A Novel Approach for Improving Cloud Liquid Water Content Profiling with Machine Learning
Abstract
1. Introduction
2. Materials and Methods
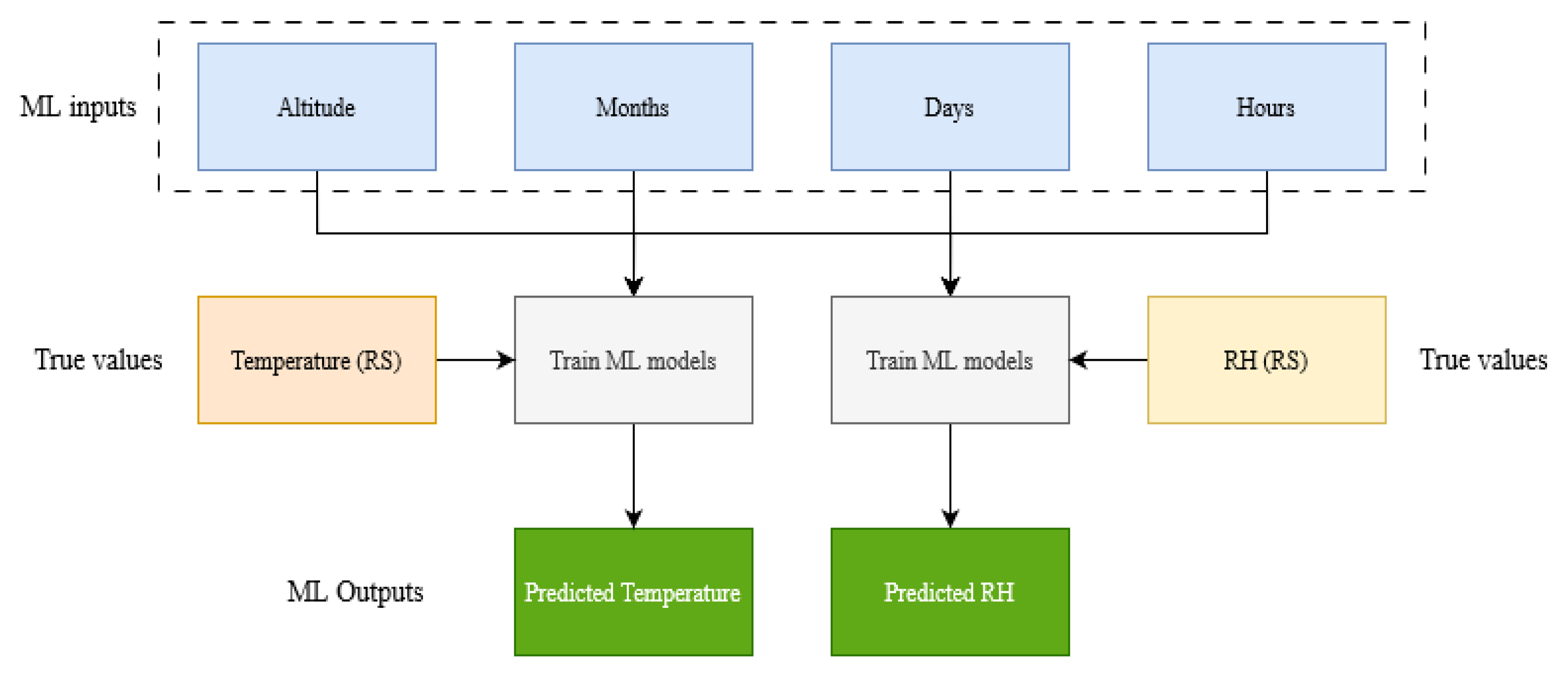
2.1. Overview of Approach and Processing Flow
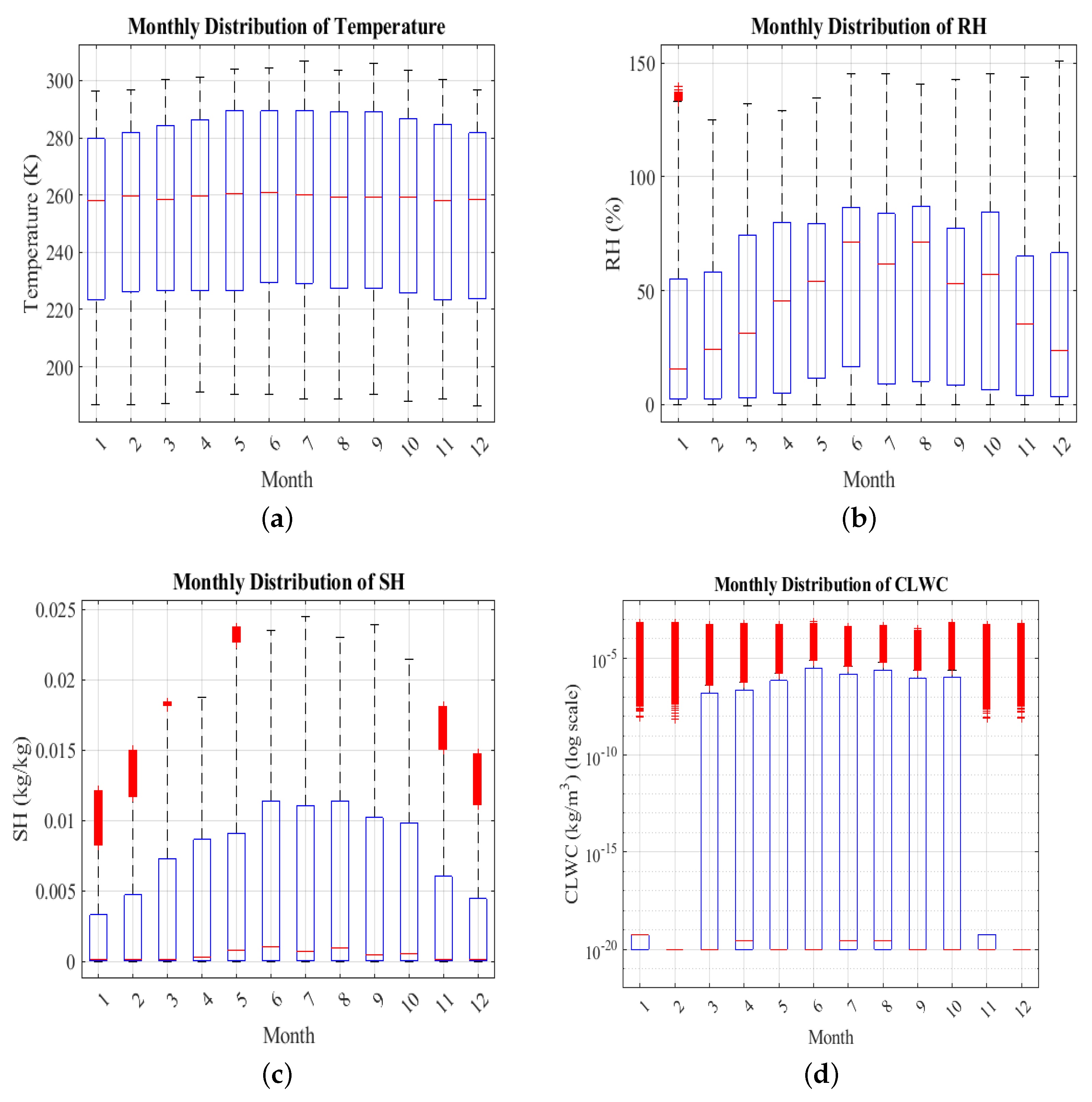
2.2. Data Description and Analysis
2.2.1. ERA5 Data
2.2.2. Radiosonde Data
2.3. Climatology of Hong Kong Area and Data Groups
2.4. Detailed Methodology
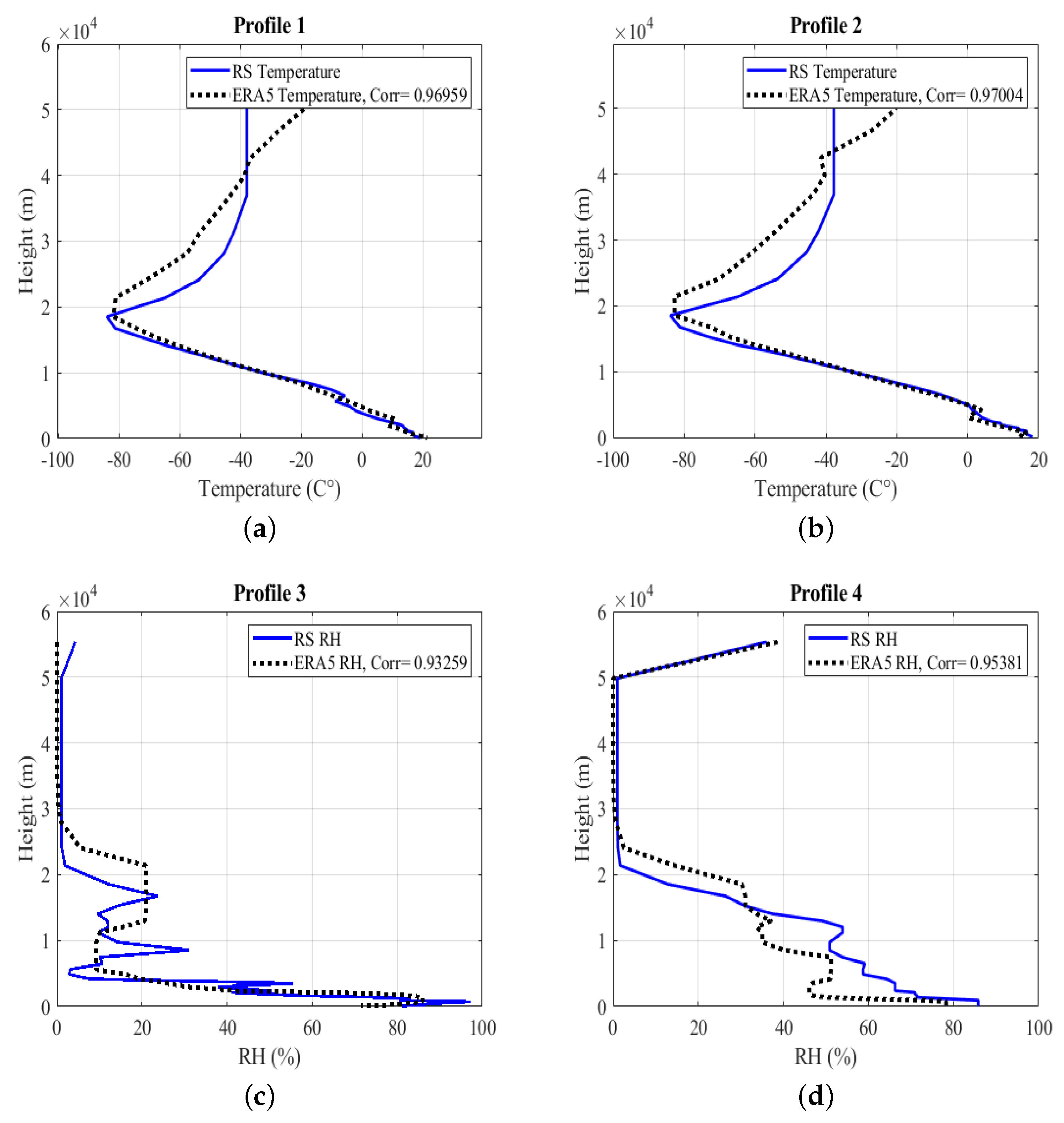
2.4.1. Correlation Between ERA5 and Radiosonde Data
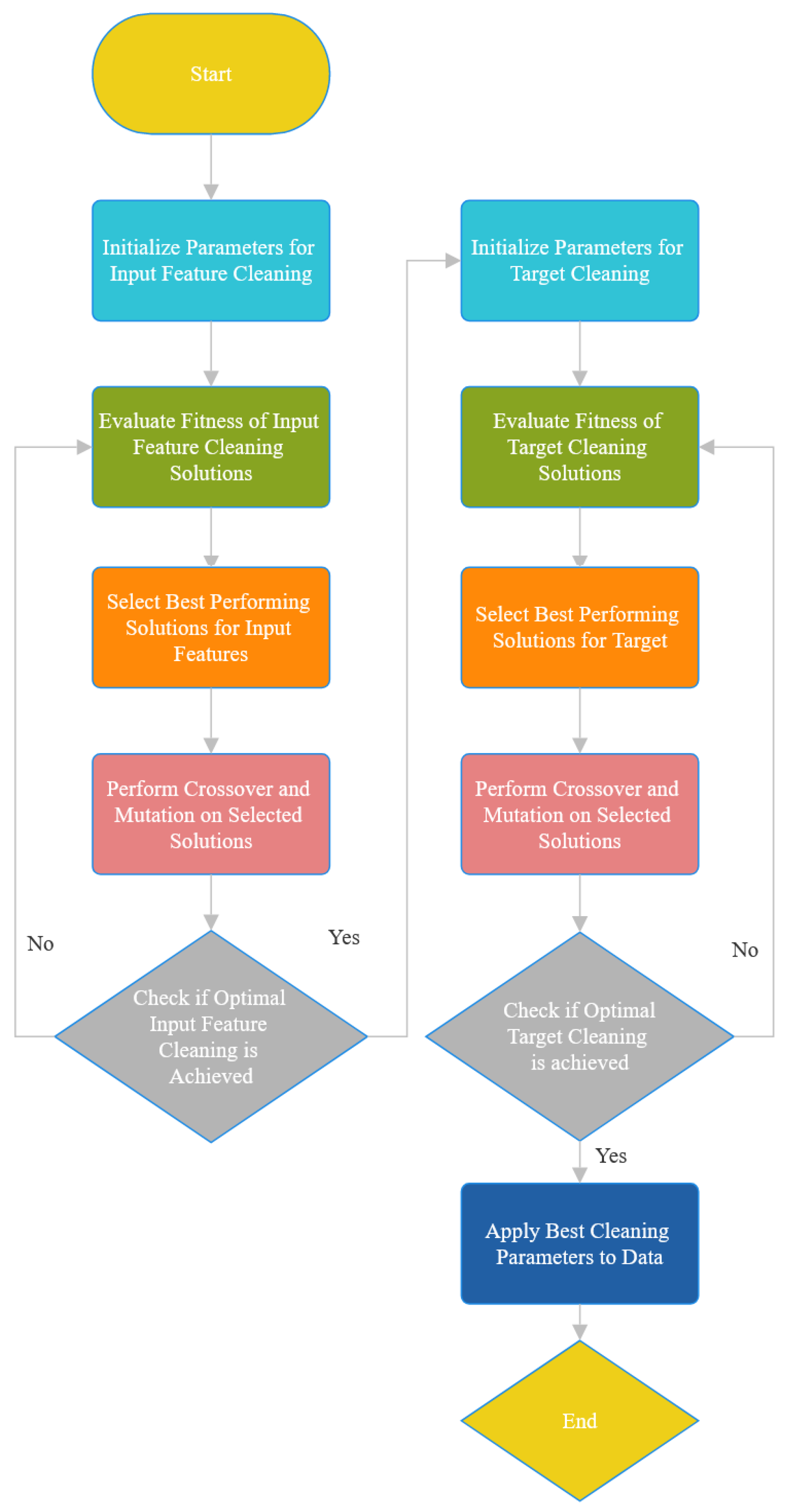
2.4.2. Data Quality Control and Prepossessing
2.4.3. Performance Evaluation Metrics for CLWC Estimation
2.4.4. ML Algorithms and Methods Used in This Study
3. Results
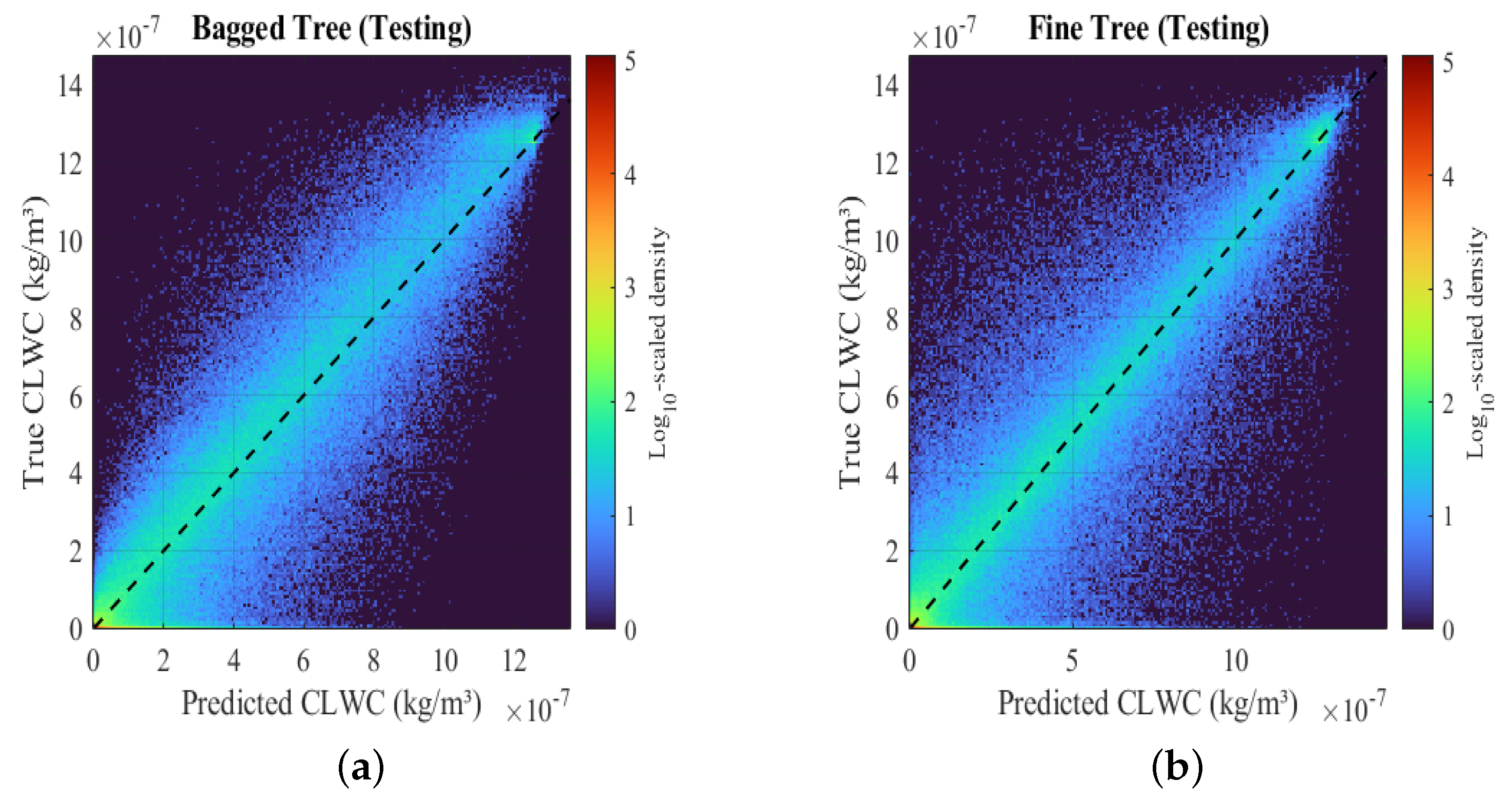
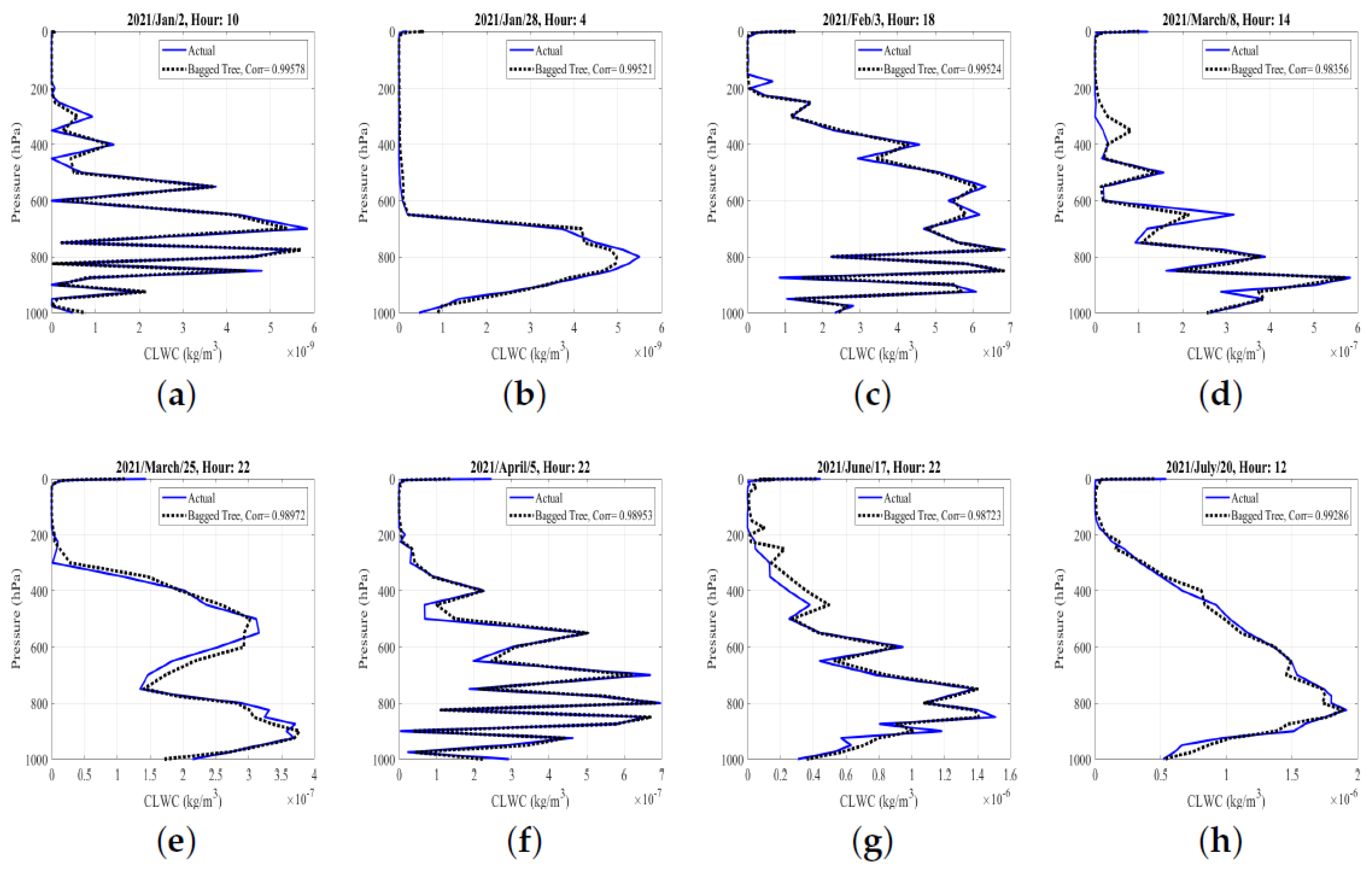
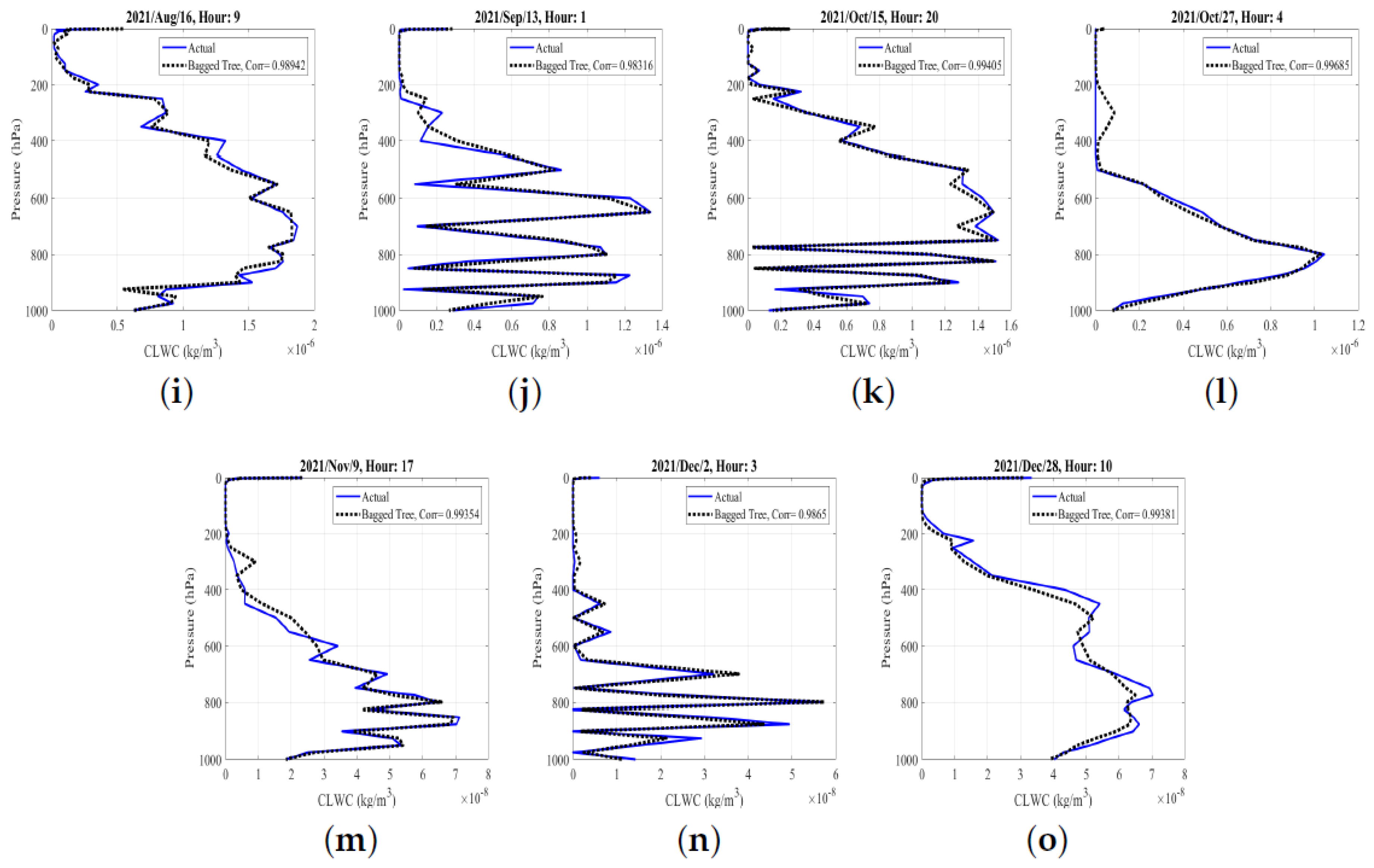
3.1. Analysis of Results Based on the Full-Year Data
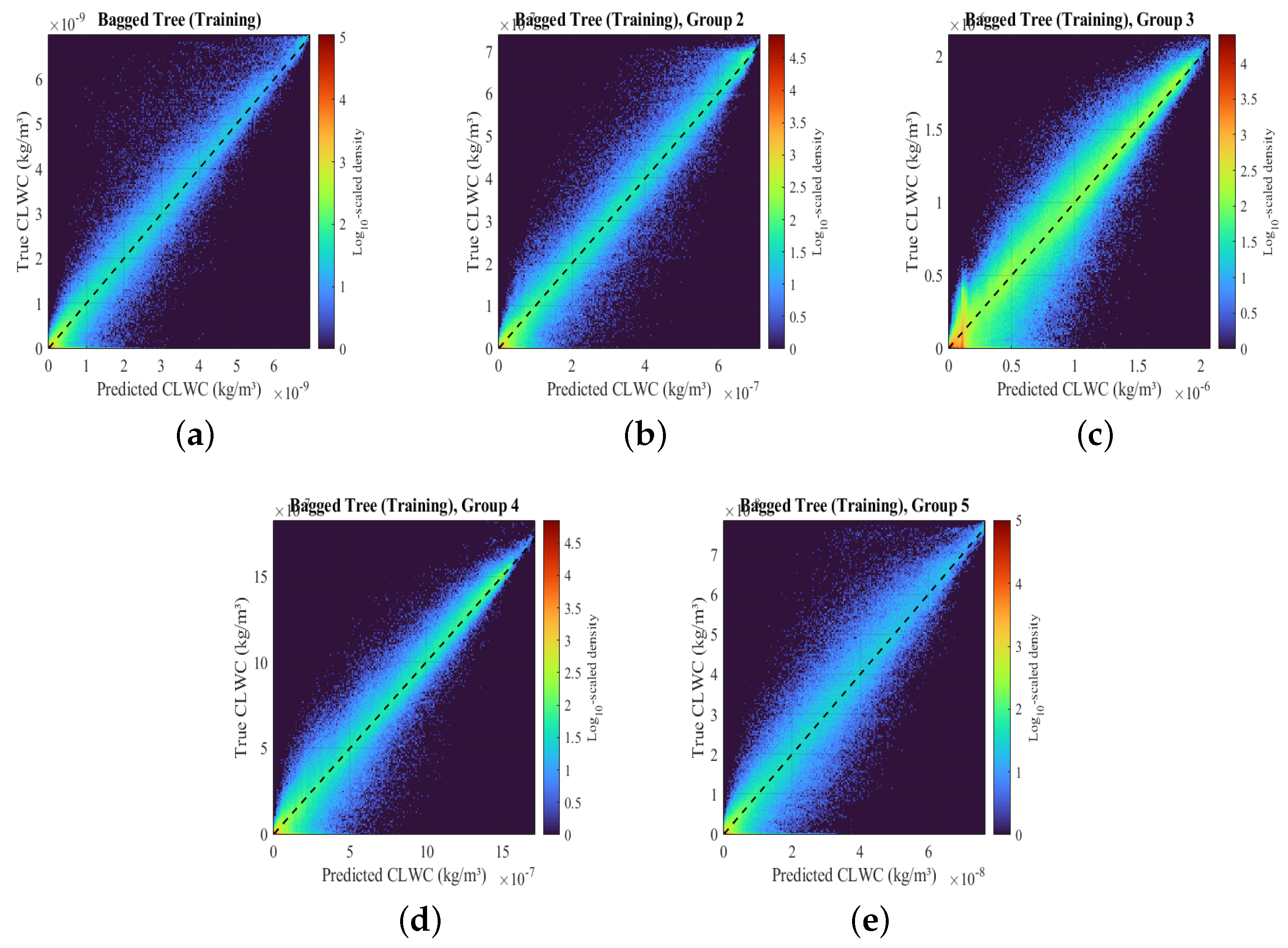
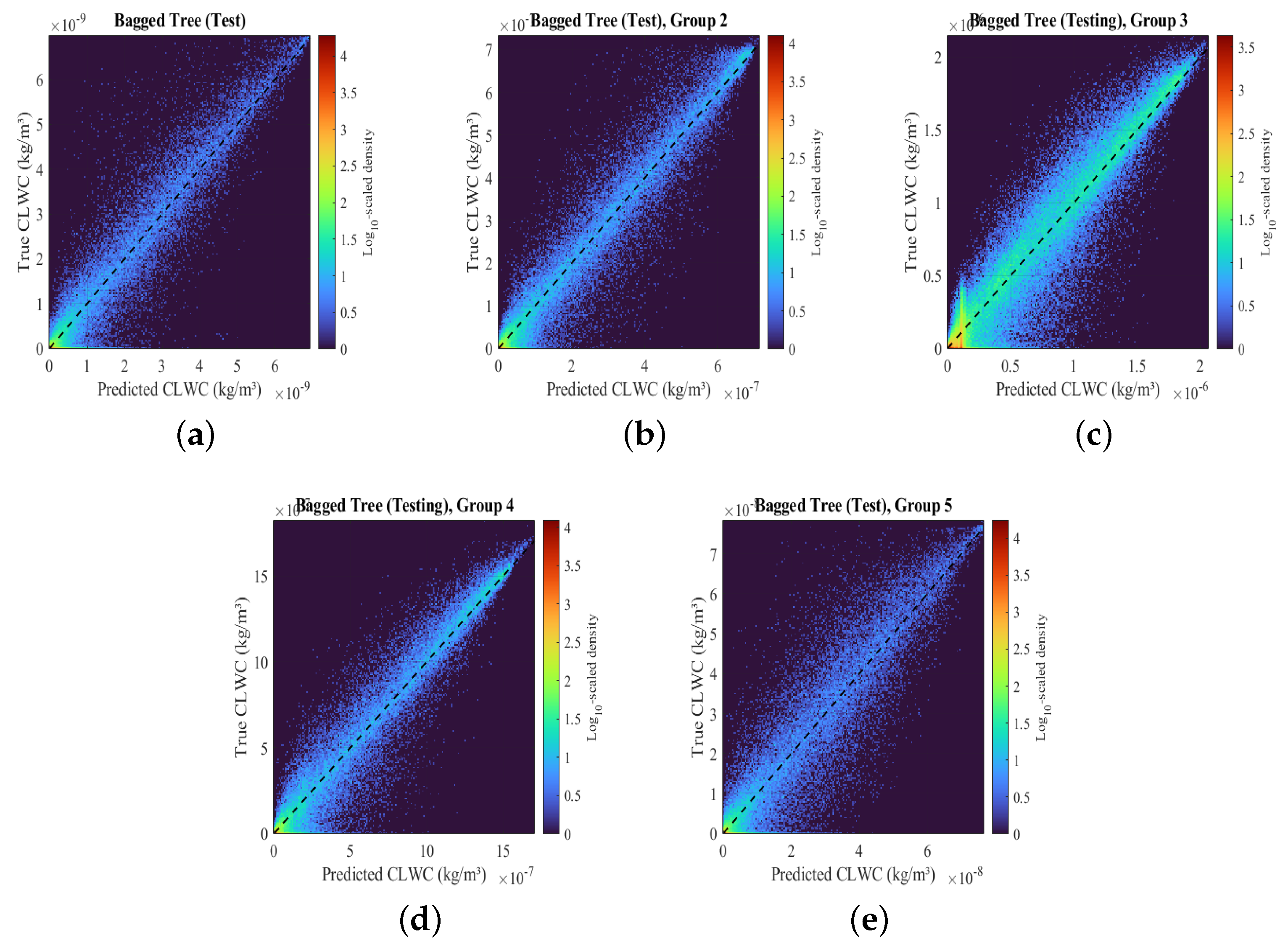
3.2. Performance Evaluations Based on Grouped Datasets
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALO | Antlion Optimization |
| CLWC | Cloud Liquid Water Content |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| ERA5 | ECMWF Reanalysis Version 5 |
| GOA | Grasshopper Optimization Algorithm |
| HKO | Hong Kong Observatory |
| LWC | Liquid Water Content |
| LWP | Liquid Water Path |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MSE | Mean Squared Error |
| R² | Coefficient of Determination |
| RH | Relative Humidity |
| RMSE | Root Mean Square Error |
| SCAMS | Scanning Microwave Spectrometer |
| TPW | Total Precipitable Water |
| WNN | Wavelet Neural Network |
Appendix A
| Model Type | Hyperparameters |
|---|---|
| Linear Regression (LR) | Linear term only |
| Fine Tree (FT) | Minimum leaf size: 4 |
| Bagged Ensemble Tree (BTT) | Minimum leaf size: 8; Number of learners: 30 |
| Wide Neural Network (WNN) | Single layer with 100 neurons; Activation function: ReLU; Iteration limit: 1000 |
| Trilayered Neural Network (TriNN) | Three layers, each with 10 neurons; Activation function: ReLU; Iteration limit: 1000 |
References
- Wallace, J.M.; Hobbs, P.V. Atmospheric Science: An Introductory Survey; Elsevier: Amsterdam, The Netherlands, 2006; Volume 92. [Google Scholar]
- Shukla, J.; Sud, Y. Effect of cloud-radiation feedback on the climate of a general circulation model. J. Atmos. Sci. 1981, 38, 2337–2353. [Google Scholar] [CrossRef]
- Techel, F.; Pielmeier, C. Point observations of liquid water content in wet snow–investigating methodical, spatial and temporal aspects. Cryosphere 2011, 5, 405–418. [Google Scholar] [CrossRef]
- Korolev, A.; Isaac, G.; Strapp, J.; Cober, S.; Barker, H. In situ measurements of liquid water content profiles in midlatitude stratiform clouds. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2007, 133, 1693–1699. [Google Scholar] [CrossRef]
- Gultepe, I.; Sharman, R.; Williams, P.D.; Zhou, B.; Ellrod, G.; Minnis, P.; Trier, S.; Griffin, S.; Yum, S.S.; Gharabaghi, B.; et al. A review of high impact weather for aviation meteorology. Pure Appl. Geophys. 2019, 176, 1869–1921. [Google Scholar] [CrossRef]
- Guo, X.; Wang, Z.; Zhao, R.; Wu, Y.; Wu, X.; Yi, X. Liquid water content measurement with SEA multi-element sensor in CARDC icing wind tunnel: Calibration and performance. Appl. Therm. Eng. 2023, 235, 121255. [Google Scholar] [CrossRef]
- Notaro, V.; Liuzzo, L.; Freni, G.; La Loggia, G. Uncertainty analysis in the evaluation of extreme rainfall trends and its implications on urban drainage system design. Water 2015, 7, 6931–6945. [Google Scholar] [CrossRef]
- Morrison, H.; van Lier-Walqui, M.; Fridlind, A.M.; Grabowski, W.W.; Harrington, J.Y.; Hoose, C.; Korolev, A.; Kumjian, M.R.; Milbrandt, J.A.; Pawlowska, H.; et al. Confronting the challenge of modeling cloud and precipitation microphysics. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001689. [Google Scholar] [CrossRef]
- Brun, E. Investigation on wet-snow metamorphism in respect of liquid-water content. Ann. Glaciol. 1989, 13, 22–26. [Google Scholar] [CrossRef]
- Thies, B.; Egli, S.; Bendix, J. The influence of drop size distributions on the relationship between liquid water content and radar reflectivity in radiation fogs. Atmosphere 2017, 8, 142. [Google Scholar] [CrossRef]
- Boucher, O.; Randall, D.; Artaxo, P.; Bretherton, C.; Feingold, G.; Forster, P.; Kerminen, V.-M.; Kondo, Y.; Liao, H.; Lohmann, U.; et al. Clouds and aerosols. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Zelinka, M.D.; Myers, T.; McCoy, D.T.; Po-Chedley, S.; Caldwell, P.M.; Ceppi, P.; Klein, S.A.; Taylor, K.E. Causes of Higher Climate Sensitivity in CMIP6 Models. Geophys. Res. Lett. 2020, 47, e2019GL085782. [Google Scholar] [CrossRef]
- Ceppi, P.; Brient, F.; Zelinka, M.D.; Hartmann, D.L. Cloud feedback mechanisms and their representation in climate models. WIREs Clim. Change 2017, 8, e465. [Google Scholar] [CrossRef]
- Emanuel, K. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 436, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Grody, N. Remote sensing of atmospheric water content from satellites using microwave radiometry. IEEE Trans. Antennas Propag. 1976, 24, 155–162. [Google Scholar] [CrossRef]
- Alishouse, J.C.; Snider, J.B.; Westwater, E.R.; Swift, C.T.; Ruf, C.S.; Snyder, S.A.; Vongsathorn, J.; Ferraro, R.R. Determination of cloud liquid water content using the SSM/I. IEEE Trans. Geosci. Remote Sens. 1990, 28, 817–822. [Google Scholar] [CrossRef]
- Greenwald, T.J.; Stephens, G.L.; Vonder Haar, T.H.; Jackson, D.L. A physical retrieval of cloud liquid water over the global oceans using Special Sensor Microwave/Imager (SSM/I) observations. J. Geophys. Res. Atmos. 1993, 98, 18471–18488. [Google Scholar] [CrossRef]
- Nimnuan, P.; Janjai, S.; Nunez, M.; Pratummasoot, N.; Buntoung, S.; Charuchittipan, D.; Chanyatham, T.; Chantraket, P.; Tantiplubthong, N. Determination of effective droplet radius and optical depth of liquid water clouds over a tropical site in northern Thailand using passive microwave soundings, aircraft measurements and spectral irradiance data. J. Atmos. Sol.-Terr. Phys. 2017, 161, 8–18. [Google Scholar] [CrossRef]
- Weng, F.; Grody, N.C. Retrieval of cloud liquid water using the special sensor microwave imager (SSM/I). J. Geophys. Res. Atmos. 1994, 99, 25535–25551. [Google Scholar]
- Weng, F.; Grody, N.C.; Ferraro, R.; Basist, A.; Forsyth, D. Cloud liquid water climatology from the Special Sensor Microwave/Imager. J. Clim. 1997, 10, 1086–1098. [Google Scholar] [CrossRef]
- Ge, J.; Du, J.; Liang, Z.; Zhu, Z.; Su, J.; Li, Q.; Mu, Q.; Huang, J.; Fu, Q. A Novel Liquid Water Content Retrieval Method Based on Mass Absorption for Single-Wavelength Cloud Radar. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4102815. [Google Scholar] [CrossRef]
- Grody, N.; Zhao, J.; Ferraro, R.; Weng, F.; Boers, R. Determination of precipitable water and cloud liquid water over oceans from the NOAA 15 advanced microwave sounding unit. J. Geophys. Res. Atmos. 2001, 106, 2943–2953. [Google Scholar] [CrossRef]
- Weng, F.; Zhao, L.; Ferraro, R.R.; Poe, G.; Li, X.; Grody, N.C. Advanced microwave sounding unit cloud and precipitation algorithms. Radio Sci. 2003, 38, 33-1–33-13. [Google Scholar] [CrossRef]
- Zhu, L.; Suomalainen, J.; Liu, J.; Hyyppä, J.; Kaartinen, H.; Haggren, H. A review: Remote sensing sensors. In Multi-Purposeful Application of Geospatial Data; IntechOpen: Rijeka, Croatia, 2018; pp. 19–42. [Google Scholar]
- Illingworth, A.; Hogan, R.; O’Connor, E.; Bouniol, D.; Brooks, M.; Delanoë, J.; Donovan, D.; Eastment, J.; Gaussiat, N.; Goddard, J.; et al. Cloudnet: Continuous evaluation of cloud profiles in seven operational models using ground-based observations. Bull. Am. Meteorol. Soc. 2007, 88, 883–898. [Google Scholar] [CrossRef]
- Dong, C.; Weng, F.; Yang, J. Assessments of cloud liquid water and total precipitable water derived from FY-3E MWTS-III and NOAA-20 ATMS. Remote Sens. 2022, 14, 1853. [Google Scholar] [CrossRef]
- Nandan, R.; Ratnam, M.V.; Kiran, V.R.; Naik, D.N. Retrieval of cloud liquid water path using radiosonde measurements: Comparison with MODIS and ERA5. J. Atmos. Sol.-Terr. Phys. 2022, 227, 105799. [Google Scholar] [CrossRef]
- Kim, M.; Cermak, J.; Andersen, H.; Fuchs, J.; Stirnberg, R. A new satellite-based retrieval of low-cloud liquid-water path using machine learning and meteosat seviri data. Remote Sens. 2020, 12, 3475. [Google Scholar] [CrossRef]
- Amaireh, A.; Zhang, Y.R. Novel Machine Learning-Based Identification and Mitigation of 5G Interference for Radar Altimeters. IEEE Access 2024, 12, 1–12. [Google Scholar] [CrossRef]
- Amaireh, A.; Zhang, Y.; Xu, D.; Bate, D. Improved Investigation of Electromagnetic Compatibility Between Radar Sensors and 5G-NR Radios. In Radar Sensor Technology XXVIII; SPIE: Bellingham, DC, USA, 2023; Volume 13048, pp. 85–98. [Google Scholar]
- Amaireh, A. Improving Radar Sensing Capabilities and Data Quality Through Machine Learning. Ph.D. Thesis, University of Oklahoma, Norman, OK, USA, 2024. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Albergel, C.; Dutra, E.; Munier, S.; Calvet, J.C.; Munoz-Sabater, J.; de Rosnay, P.; Balsamo, G. ERA-5 and ERA-Interim driven ISBA land surface model simulations: Which one performs better? Hydrol. Earth Syst. Sci. 2018, 22, 3515–3532. [Google Scholar] [CrossRef]
- Malardel, S.; Wedi, N.; Deconinck, W.; Diamantakis, M.; Kühnlein, C.; Mozdzynski, G.; Hamrud, M.; Smolarkiewicz, P. A new grid for the IFS. ECMWF Newsl. 2016, 146, 321. [Google Scholar]
- Amaireh, A.; Zhang, Y.; Chan, P. Atmospheric Humidity Estimation from Wind Profiler Radar Using a Cascaded Machine Learning Approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 6352–6371. [Google Scholar] [CrossRef]
- Hong Kong Observatory. Yearly Weather Summary 2021. Available online: https://www.hko.gov.hk/en/wxinfo/pastwx/2021/ywx2021.htm (accessed on 19 May 2024).
- Amaireh, A.; Al-Zoubi, A.S.; Dib, N.I. A new hybrid optimization technique based on antlion and grasshopper optimization algorithms. Evol. Intell. 2023, 16, 1383–1422. [Google Scholar] [CrossRef]
- Amaireh, A.; Al-Zoubi, A.S.; Dib, N.I. Sidelobe-level suppression for circular antenna array via new hybrid optimization algorithm based on antlion and grasshopper optimization algorithms. Prog. Electromagn. Res. C 2019, 93, 49–63. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Cameron, A.C.; Windmeijer, F.A. An R-squared measure of goodness of fit for some common nonlinear regression models. J. Econom. 1997, 77, 329–342. [Google Scholar] [CrossRef]




| Model Type | RMSE | MSE | R-Squared | MAE | Correlation Coefficient |
|---|---|---|---|---|---|
| Fine Tree (Temperature (°C)) | 1.3007 | 1.6917 | 0.9984 | 1.0164 | 0.9992 |
| Fine Tree (Relative humidity (%)) | 3.0501 | 9.3032 | 0.9894 | 1.8300 | 0.9965 |
| Temperature Correlation | Relative Humidity Correlation | |
|---|---|---|
| January | 0.9486 | 0.7435 |
| February | 0.9570 | 0.7495 |
| March | 0.9683 | 0.7697 |
| April | 0.9686 | 0.7404 |
| May | 0.9686 | 0.7976 |
| June | 0.9667 | 0.8159 |
| All six months | 0.9632 | 0.7808 |
| Model Type | RMSE (kg/m3) | MSE (kg/m3)2 | R2 | MAE (kg/m3) | Correlation |
|---|---|---|---|---|---|
| Fine Tree | 0.85895 | 0.9736 | |||
| Bagged Tree | 0.88800 | 0.9678 | |||
| WNN | 0.0112 | ||||
| TriNN | 0.0198 | ||||
| LR | 0.667978 | 0.8173 |
| Model Type | MAE (kg/m3) | MSE (kg/m3)2 | RMSE (kg/m3) | R2 | Correlation |
|---|---|---|---|---|---|
| Fine Tree | 0.8692 | 0.9331 | |||
| Bagged Tree | 0.8932 | 0.9452 | |||
| WNN | 0.0127 | ||||
| TriNN | 0.0227 | ||||
| LR | 0.6675 | 0.817 |
| Model Type | RMSE (kg/m3) | MSE (kg/m3)2 | R2 | MAE (kg/m3) | Correlation |
|---|---|---|---|---|---|
| Group 1 Bagged Tree | 0.9214 | 0.9602 | |||
| Group 1 Fine Tree | 0.9018 | 0.9502 | |||
| Group 1 WNN | |||||
| Group 2 Bagged Tree | 0.9431 | 0.9713 | |||
| Group 2 Fine Tree | 0.9276 | 0.9634 | |||
| Group 2 WNN | 0.0011 | ||||
| Group 3 Bagged Tree | 0.9143 | 0.9564 | |||
| Group 3 Fine Tree | 0.9105 | 0.9546 | |||
| Group 3 WNN | |||||
| Group 4 Bagged Tree | 0.9468 | 0.9733 | |||
| Group 4 Fine Tree | 0.9360 | 0.9677 | |||
| Group 4 WNN | 0.0093 | ||||
| Group 5 Bagged Tree | 0.8962 | 0.9467 | |||
| Group 5 Fine Tree | 0.8543 | 0.9257 | |||
| Group 5 WNN | 0.0222 |
| Model Type | RMSE (kg/m3) | MSE (kg/m3)2 | R2 | MAE (kg/m3) | Correlation |
|---|---|---|---|---|---|
| Group 1 Bagged Tree | 0.9257 | 0.9624 | |||
| Group 1 Fine Tree | 0.9089 | 0.9538 | |||
| Group 1 WNN | |||||
| Group 2 Bagged Tree | 0.9493 | 0.9745 | |||
| Group 2 Fine Tree | 0.9355 | 0.9674 | |||
| Group 2 WNN | 0.0212 | ||||
| Group 3 Bagged Tree | 0.9188 | 0.9588 | |||
| Group 3 Fine Tree | 0.9186 | 0.9587 | |||
| Group 3 WNN | |||||
| Group 4 Bagged Tree | 0.9509 | 0.9754 | |||
| Group 4 Fine Tree | 0.9416 | 0.9706 | |||
| Group 4 WNN | 0.0028 | ||||
| Group 5 Bagged Tree | 0.8988 | 0.9481 | |||
| Group 5 Fine Tree | 0.8601 | 0.9286 | |||
| Group 5 WNN |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amaireh, A.; Zhang, Y.; Chan, P.W.; Zrnic, D. A Novel Approach for Improving Cloud Liquid Water Content Profiling with Machine Learning. Remote Sens. 2025, 17, 1836. https://doi.org/10.3390/rs17111836
Amaireh A, Zhang Y, Chan PW, Zrnic D. A Novel Approach for Improving Cloud Liquid Water Content Profiling with Machine Learning. Remote Sensing. 2025; 17(11):1836. https://doi.org/10.3390/rs17111836
Chicago/Turabian StyleAmaireh, Anas, Yan (Rockee) Zhang, Pak Wai Chan, and Dusan Zrnic. 2025. "A Novel Approach for Improving Cloud Liquid Water Content Profiling with Machine Learning" Remote Sensing 17, no. 11: 1836. https://doi.org/10.3390/rs17111836
APA StyleAmaireh, A., Zhang, Y., Chan, P. W., & Zrnic, D. (2025). A Novel Approach for Improving Cloud Liquid Water Content Profiling with Machine Learning. Remote Sensing, 17(11), 1836. https://doi.org/10.3390/rs17111836











