VGOS Dual Linear Polarization Data Processing Techniques Applied to Differential Observation of Satellites
Abstract
1. Introduction
- The legacy S/X VLBI data processing system is incapable of processing VGOS data because of the different data format and polarization;
- Domestic DiFX implementations currently lack adequate satellite signal processing capabilities owing to access restrictions.
2. Overview of the Observation Experiment
3. Data Processing
3.1. Data Playback
3.2. Data Correlation
3.3. Data Post-Correlation
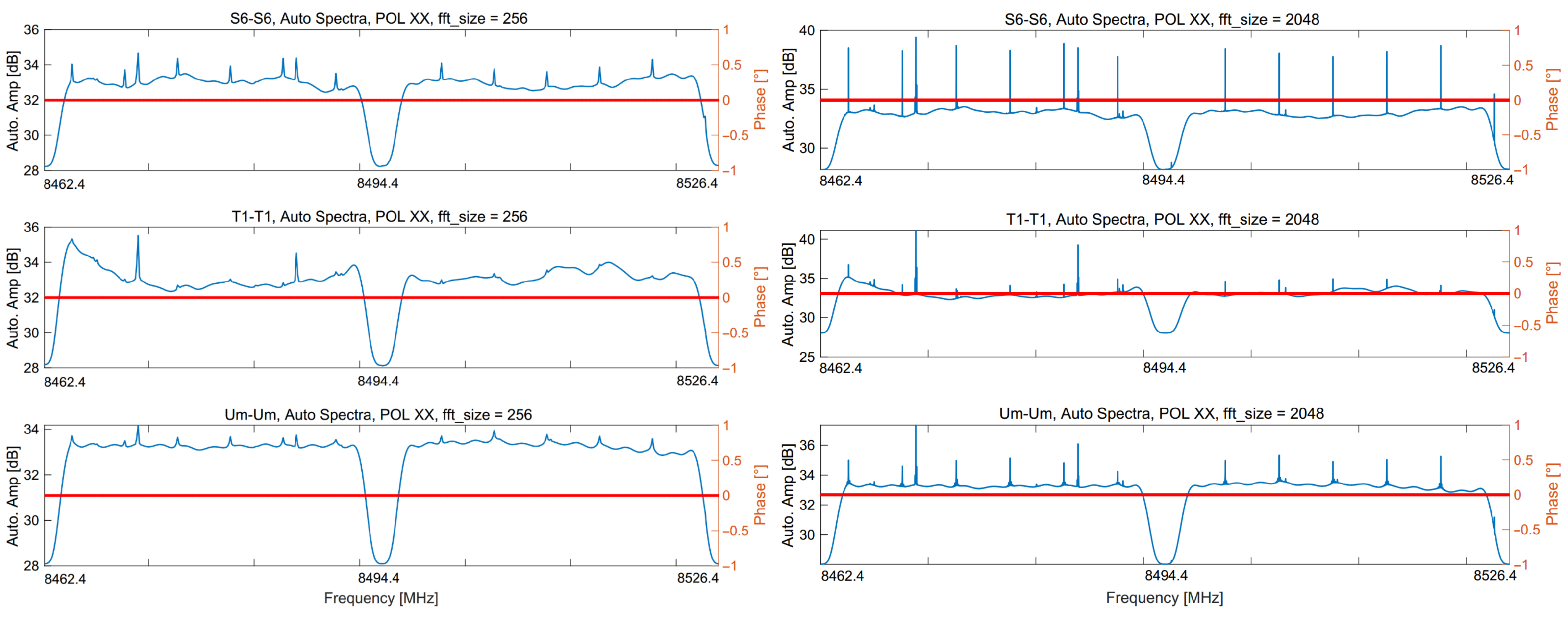
3.3.1. Auto-Correlation
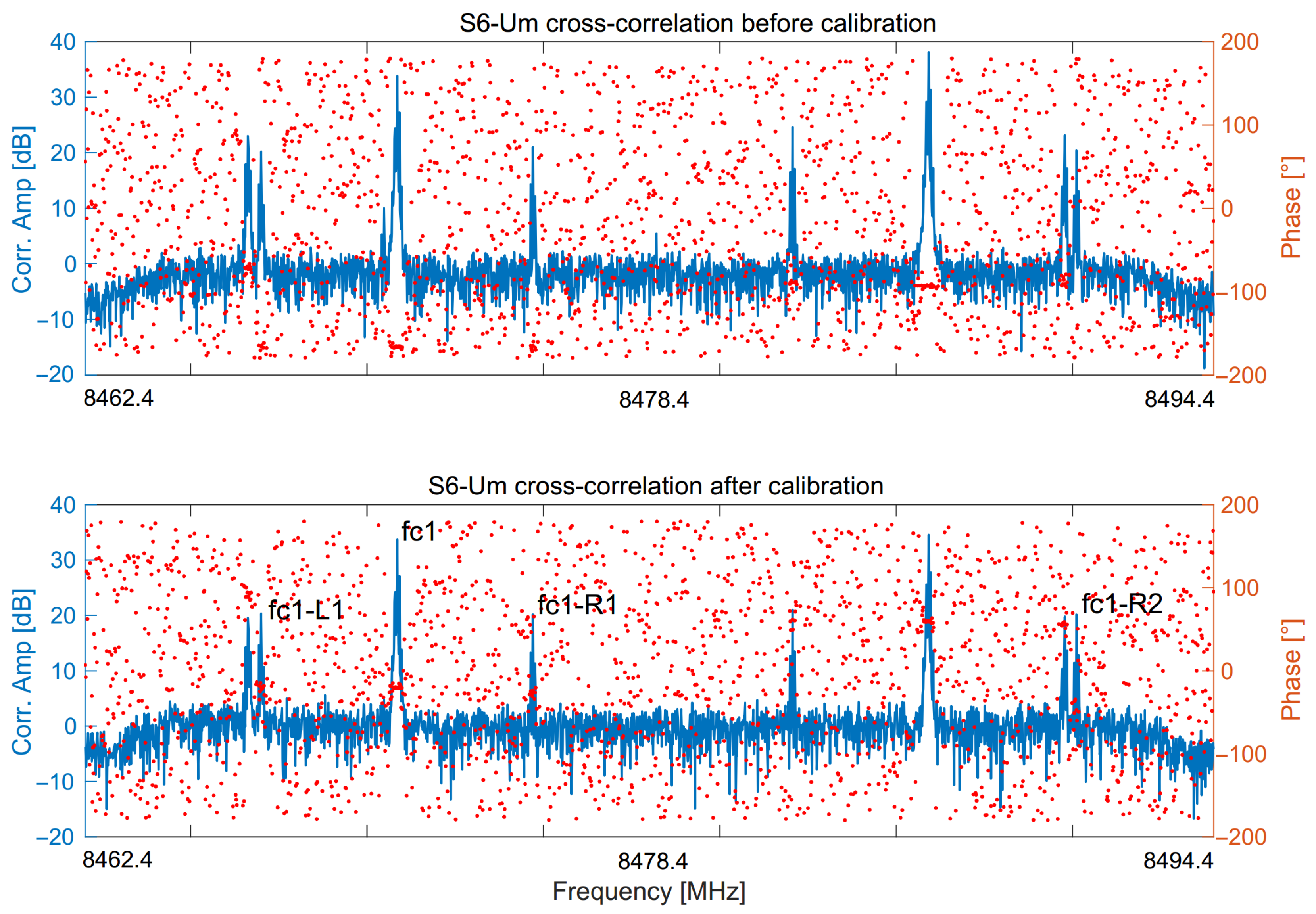
3.3.2. Cross-Correlation
- 1.
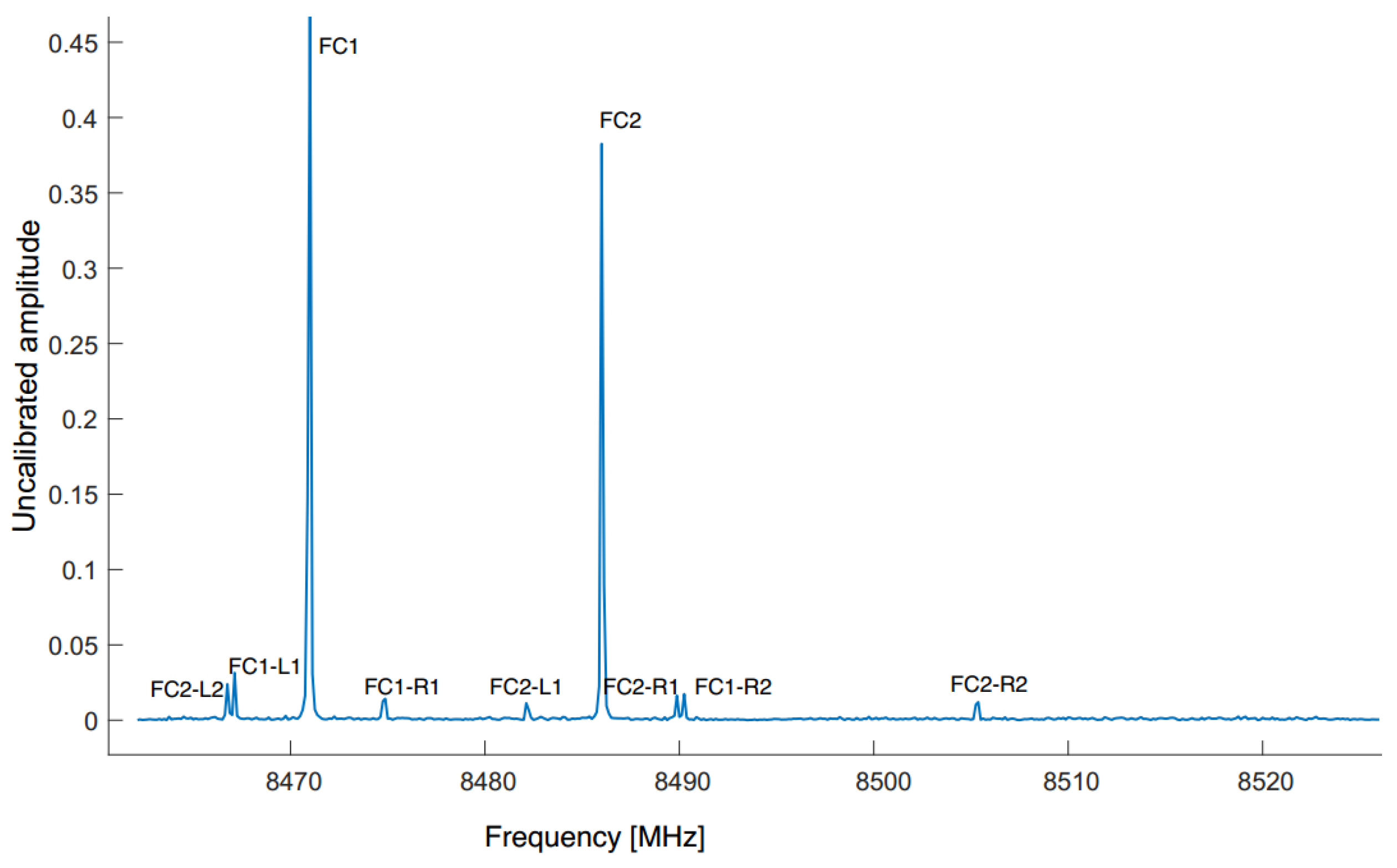
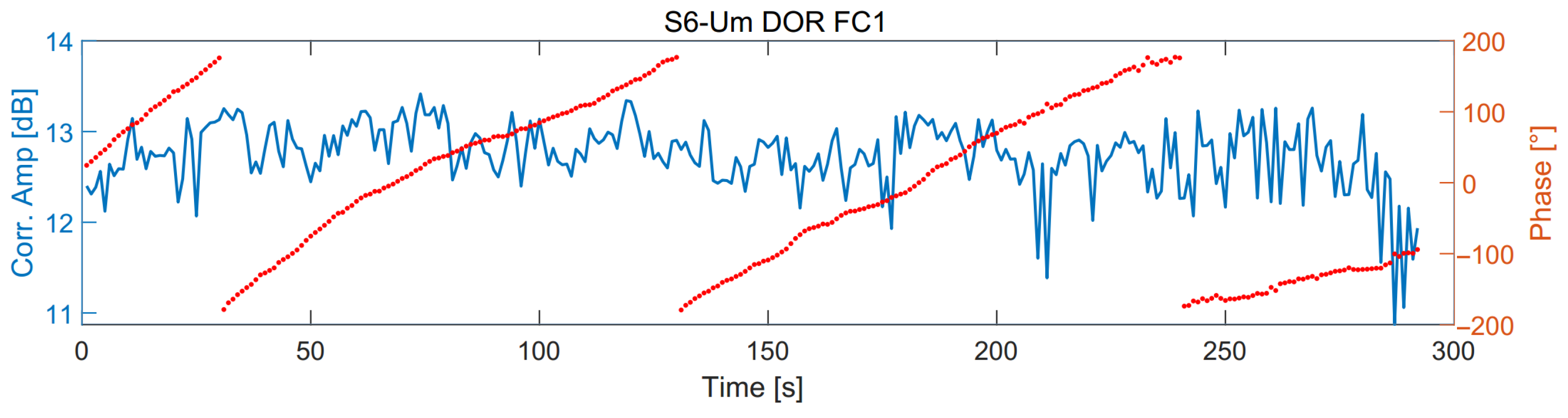
- Selection of fringe fitting data: All frequency point phases of each radio source scan were selected for processing. For each satellite scan, one carrier and its corresponding DOR tones frequency point phases were selected, thereby ensuring the maintenance of the phase variation rule. The experiment was processed for satellite scans using four frequency points of Channel 1, specifically FC1, FC1-L1, FC1-R1, and FC1-R2. The FC1-L2 of Channel 2 was not used, to avoid channel-to-channel delay.
- 2.
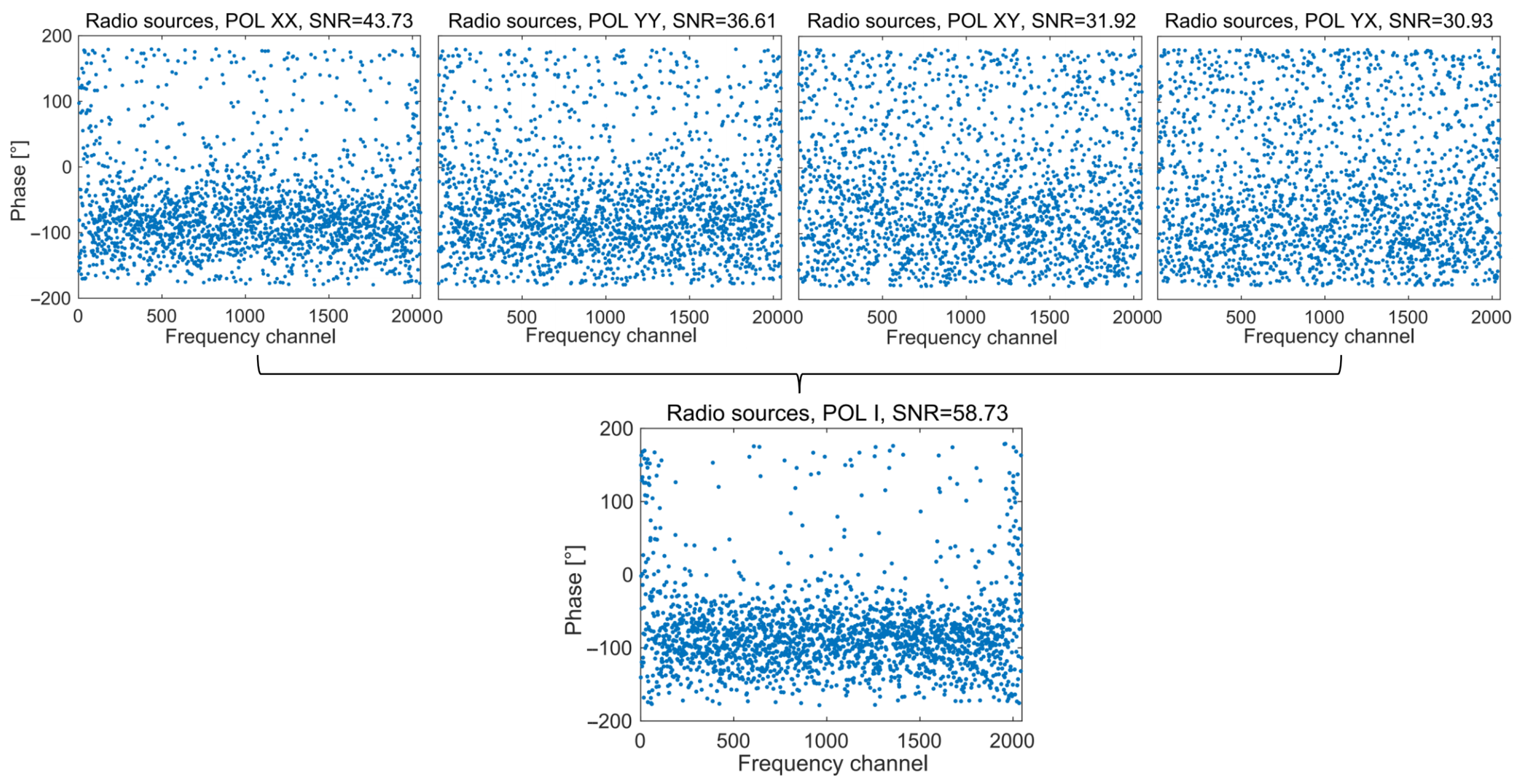
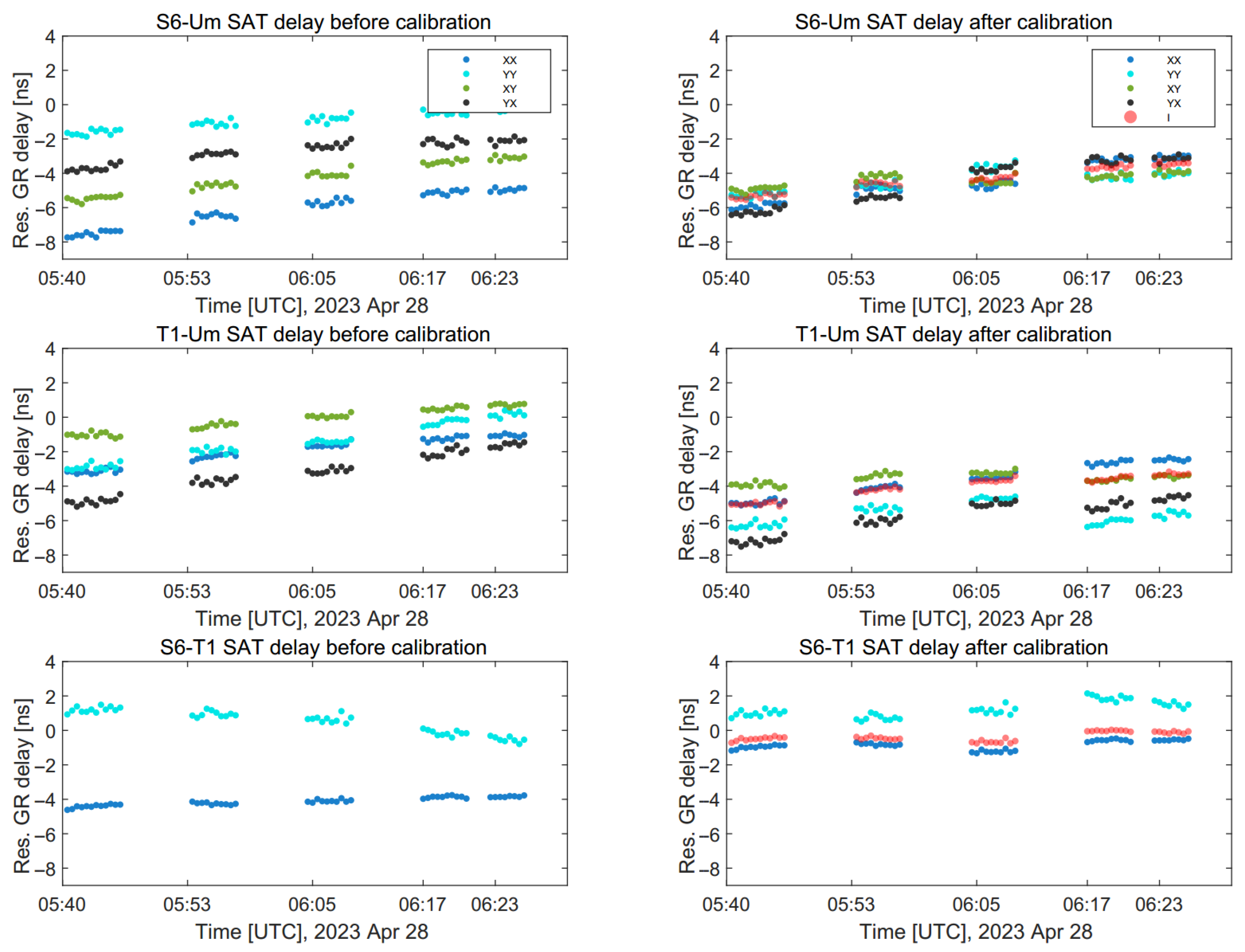
- Delay and phase calibration of the polarization products of scans: Following the first fringe fitting, the scan with a high SNR (≥30) on all polarization products was selected as the reference for the radio source signals. Calibrations were performed for all radio source scans using the delay and phase values from the reference scan. In the case of satellite scans, a radio source scan before the SAT-C5GD scan was used as the reference for delay and phase correction. In this experiment, no radio source was observed before the first SAT-C5GD scan. Therefore, the calibration for the first SAT-C5GD scan was performed with the radio source scan obtained subsequently.The experiment yielded three baselines: S6-Um, T1-Um, and S6-T1. A specialized calibration method was implemented to ensure the three-baseline residual time-delay closures. The symbols c, u, and t represent the S6, Um, and T1 stations, respectively. Using a radio source scan of the S6-Um baseline as an example, four polarization products (XcXu, YcYu, XcYu, and YcXu) were obtained after correlation. The X polarization of u was taken as the reference, i.e., the delay of () was set to zero (delay and phase were the same way; here, the delay calculation was used as an example). The X polarization delay of c () was obtained with the following:The Y polarization delay of c () was obtained with the following:Then, the Y polarization delay of u () was obtained withThese delay values were then used to correct the four polarization products of the S6-Um baseline, and the same strategy was used for phase calibration. The and (delay and phase) values of T1 were obtained from the T1-Um baseline using the same method, utilizing the X polarization of u as a reference, and the (delay/phase) values of u were not recalculated. The S6-T1 calibration values were calculated from the X and Y polarization delay/phase corresponding to c and t, which were obtained previously. is given as follows:Table 2 lists the delay/phase values used for calibration, corresponding to Channel 1 of each baseline for radio source No0009. The processing of XY/XX was unnecessary, given that the differential parallactic angle between stations S6 and T1 was essentially zero and the fringe of XY/YX was approximately non-existent.
- 3.
- Polarization combination is the combination of four polarization products into a single Stokes-I observable [24] as follows:where a and b are two stations, and p is the differential parallactic angle between stations a and b. The polarization products are the data after delay and phase calibration in Step 2. For example, in this processing, was the time-averaged cross-spectra polarization product of the Y polarization of station a with the X polarization of station b. The information of all observed scans and differential parallactic angles are presented in Table 3.
- 4.
- The fringe fitting employed the phase least-squares estimation, with the data phase obtained using the approach in Step 1. Fringe fitting was performed on the cross-correlation spectra of each polarization product and a combination of all scans. Subsequently, the residual delay and delay precision results were obtained.
4. Results and Discussion
4.1. Results
4.2. Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Niell, A.; Barrett, J.; Burns, A.; Cappallo, R.; Corey, B.; Derome, M.; Eckert, C.; Elosegui, P.; McWhirter, R.; Poirier, M.; et al. Demonstration of a Broadband Very Long Baseline Interferometer System: A New Instrument for High-Precision Space Geodesy. Radio Sci. 2018, 53, 1269–1291. [Google Scholar] [CrossRef]
- Schüler, T.; Kronschnabl, G.; Plötz, C.; Neidhardt, A.; Bertarini, A.; Bernhart, S.; La Porta, L.; Halsig, S.; Nothnagel, A. Initial Results Obtained with the First TWIN VLBI Radio Telescope at the Geodetic Observatory Wettzell. Sensors 2015, 15, 18767–18800. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Collilieux, X.; Métivier, L.; Chanard, K. ITRF2020: An augmented reference frame refining the modeling of nonlinear station motions. J. Geod. 2023, 97, 47. [Google Scholar] [CrossRef]
- Zoulida, M.; Pollet, A.; Coulot, D.; Perosanz, F.; Loyer, S.; Biancale, R.; Rebischung, P. Multi-technique combination of space geodesy observations: Impact of the Jason-2 satellite on the GPS satellite orbits estimation. Adv. Space Res. 2016, 58, 1376–1389. [Google Scholar] [CrossRef]
- Männel, B. Co-Location of Geodetic Observation Techniques in Space. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 2016. [Google Scholar]
- Delva, P.; Altamimi, Z.; Blazquez, A.; Blossfeld, M.; Böhm, J.; Bonnefond, P.; Boy, J.P.; Bruinsma, S.; Bury, G.; Chatzinikos, M.; et al. GENESIS: Co-location of geodetic techniques in space. Earth Planets Space 2023, 75, 5. [Google Scholar] [CrossRef]
- Plank, L. VLBI Satellite Tracking for the Realization of Frame Ties. Ph.D. Thesis, Vienna University of Technology, Vienna, Austria, 2014. [Google Scholar]
- Anderson, J.M.; Beyerle, G.; Glaser, S.; Liu, L.; Männel, B.; Nilsson, T.; Heinkelmann, R.; Schuh, H. Simulations of VLBI observations of a geodetic satellite providing co-location in space. J. Geod. 2018, 92, 1023–1046. [Google Scholar] [CrossRef]
- Klopotek, G.; Hobiger, T.; Haas, R.; Otsubo, T. Geodetic VLBI for precise orbit determination of Earth satellites: A simulation study. J. Geod. 2020, 94, 56. [Google Scholar] [CrossRef]
- Schunck, D.; McCallum, L.; Calves, G.M. Simulating VLBI observations to BeiDou and Galileo satellites in L-band for frame ties. J. Geod. Sci. 2024, 14, 20220168. [Google Scholar] [CrossRef]
- Sun, J.; Tang, G.S.; Shu, F.C.; Li, X.; Liu, S.; Cao, J.; Hellerschmied, A.; Böhm, J.; McCallum, L.; McCallum, J.; et al. VLBI observations to the APOD satellite. Adv. Space Res. 2018, 61, 823–829. [Google Scholar] [CrossRef]
- Hellerschmied, A.; McCallum, L.; McCallum, J.; Sun, J.; Böhm, J.; Cao, J. Observing APOD with the AuScope VLBI Array. Sensors 2018, 18, 1587. [Google Scholar] [CrossRef]
- Plank, L.; Hellerschmied, A.; McCallum, J.; Böhm, J.; Lovell, J. VLBI observations of GNSS-satellites: From scheduling to analysis. J. Geod. 2017, 91, 867–880. [Google Scholar] [CrossRef]
- Schunck, D.; McCallum, L.; Calves, G.M. On the Integration of VLBI Observations to GENESIS into Global VGOS Operations. Remote Sens. 2024, 16, 3234. [Google Scholar] [CrossRef]
- Shu, F.C.; Petrov, L.; Jiang, W.; Xia, B.; Jiang, T.; Cui, Y.; Takefuji, K.; McCallum, J.; Lovell, J.; Yi, S.O.; et al. VLBI Ecliptic Plane Survey: VEPS-1. Astrophys. J. Suppl. Ser. 2017, 230, 13. [Google Scholar] [CrossRef]
- Li, P.J.; Fan, M.; Huang, Y.; Hu, X.; Chang, S.; Shan, Q. Real-time orbit determination for transfer orbit and lunar orbit of the CE-5T1 probe. Sci. Sin. Phys. Mech. Astron. 2017, 47, 125903. [Google Scholar] [CrossRef]
- Liu, Q.; Huang, Y.; Shu, F.C.; Wang, G.; Zhang, J.; Chen, Z.; Li, P.; Ma, M.; Hong, X. VLBI technique for the orbit determination of Tianwen-1. Sci. Sin. Phys. Mech. Astron. 2022, 52, 239507. [Google Scholar] [CrossRef]
- Nothnagel, A.; Artz, T.; Behrend, D.; Malkin, Z. International VLBI Service for Geodesy and Astrometry: Delivering high-quality products and embarking on observations of the next generation. J. Geod. 2017, 91, 711–721. [Google Scholar] [CrossRef]
- McCallum, L.; Schunck, D.; McCallum, J.; McCarthy, T. An experiment to observe GNSS signals with the Australian VGOS array. Publ. Astron. Soc. Pac. 2025, 137, 045002. [Google Scholar] [CrossRef]
- Park, R.; Folkner, W.M.; Jones, D.L.; Border, J.S.; Konopliv, A.S.; Martin-Mur, T.J.; Dhawan, V.; Fomalont, E.; Romney, J.D. Very Long Baseline Array Astrometric Observations of Mars Orbiters. Astron. J. 2015, 150, 121. [Google Scholar] [CrossRef]
- Deller, A.T.; Brisken, W.F.; Phillips, C.J.; Morgan, J.; Alef, W.; Cappallo, R.; Middelberg, E.; Romney, J.; Rottmann, H.; Tingay, S.J. DiFX-2: A More Flexible, Efficient, Robust, and Powerful Software Correlator. Publ. Astron. Soc. Pac. 2011, 123, 275. [Google Scholar] [CrossRef]
- CCSDS. Recommendations for Space Data System Standards: Radio Frequency and Modulation Systems, Part 1, Earth Stations and Spacecraft, Recommended Standard 401.0-B; Consultative Committee for Space Data Systems, CCSDS Secretariat, NASA: Washington, DC, USA, 2009. [Google Scholar]
- Gan, J.Y.; Guo, S.G.; He, X.; Liu, C.; Sun, Z.; Li, J.; Ma, L.; Shu, F.; Zhang, X. Research of VGOS baseband data pre-processing system. Chin. Space Sci. Technol. 2022, 42, 46–53. [Google Scholar] [CrossRef]
- Cappallo, R. Delay and Phase Calibration in VGOS Post-Processing. In Proceedings of the International VLBI Service for Geodesy and Astrometry 2016 General Meeting, Johannesburg, South Africa, 13–17 March 2016; NASA/CP-2016-219016. pp. 61–64. [Google Scholar]
- CCSDS. Delta-DOR—Technical Characteristics and Performance, Report Concerning Space Data System Standards, Green Book, 500.1-G-2; Consultative Committee for Space Data Systems, CCSDS Secretariat, NASA: Washington, DC, USA, 2019. [Google Scholar]
- Li, T.; Liu, L.; Zheng, W.M.; Zhang, J. The Precision Analysis of the Chinese VLBI Network in Probe Delay Measurement. Res. Astron. Astrophys. 2022, 22, 035001. [Google Scholar] [CrossRef]
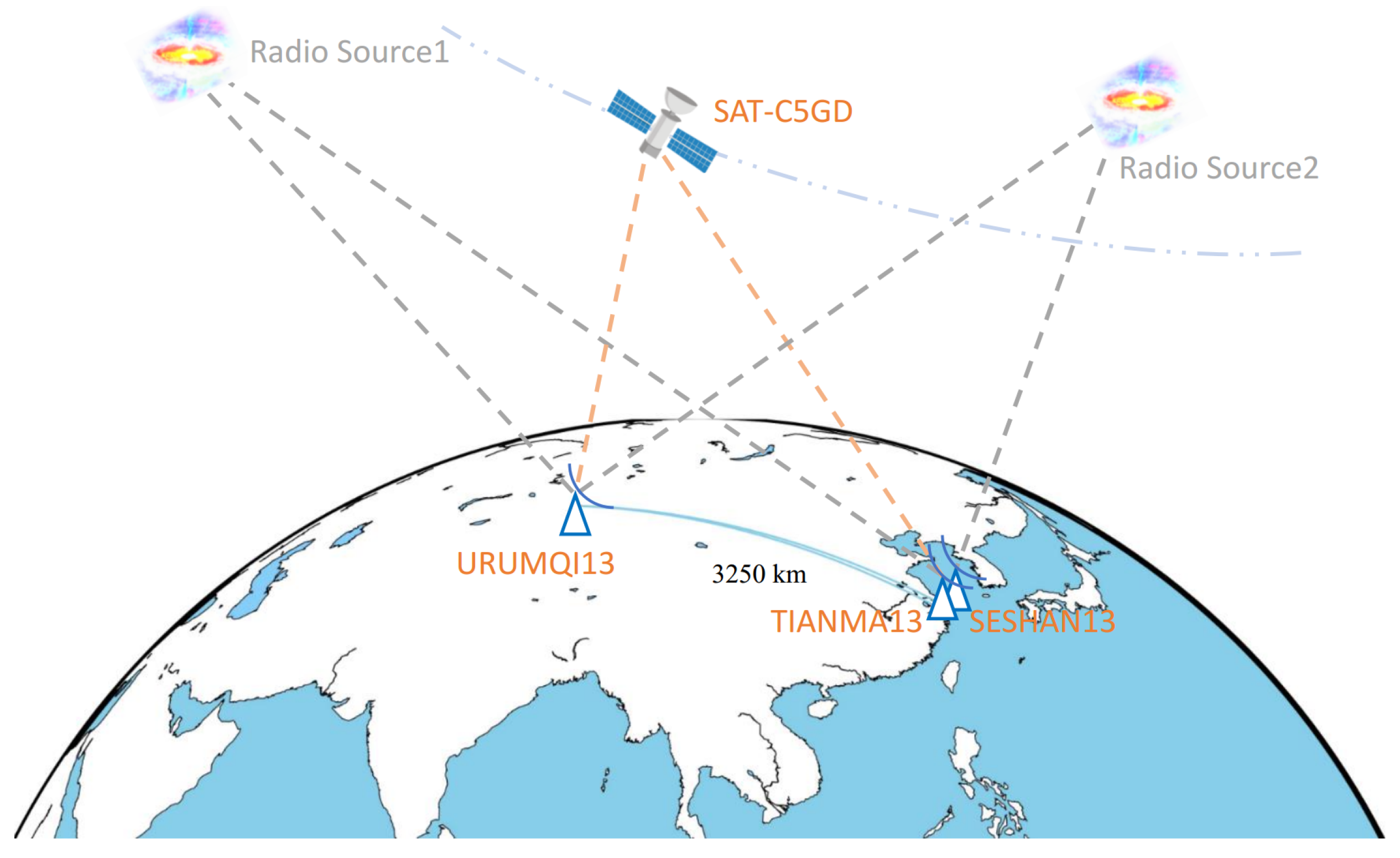
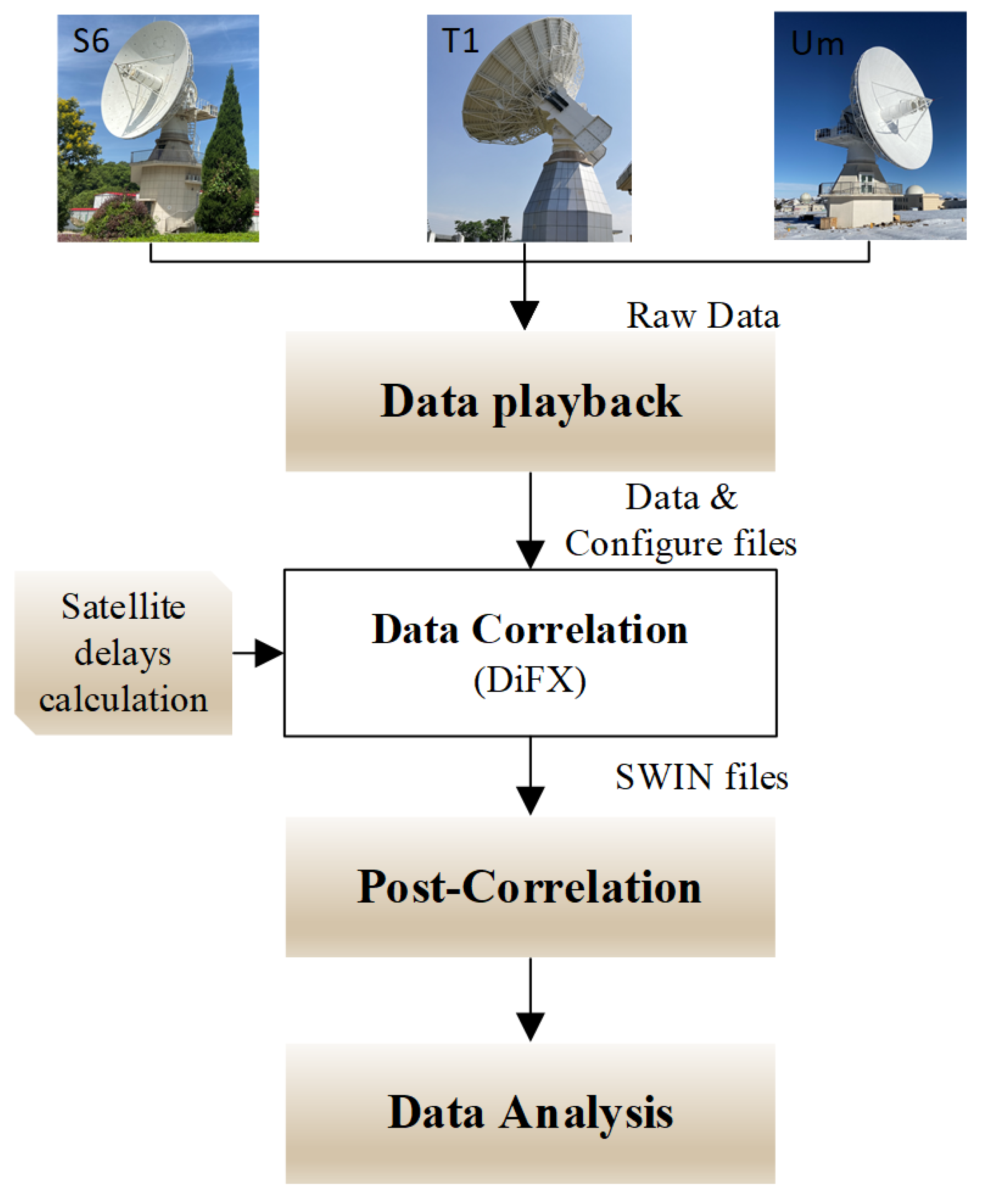


| Station Names | Station Code | Size | Year | Latitude | Longitude | Elevation |
|---|---|---|---|---|---|---|
| SESHAN13 | S6 | 13 m | 2019 | N | E | 28.0 m |
| TIANMA13 | T1 | 13.2 m | 2019 | N | E | 24.5 m |
| URUMQI13 | Um | 13 m | 2020 | N | E | 2043.4 m |
| Baseline | Parameter | XX | YY | XY | YX |
|---|---|---|---|---|---|
| S6-Um | Delay (ns) | −1.89 | 3.78 | 0.21 | 1.04 |
| Phase (rad) | 2.64 | 0.68 | −1.57 | 2.03 | |
| Delay for Calibration (ns) | −1.89 | 3.78 | 0.85 | 1.04 | |
| Phase for Calibration (rad) | 2.64 | 0.68 | 1.29 | 2.03 | |
| T1-Um | Delay (ns) | 1.40 | 2.99 | 5.43 | 3.08 |
| Phase (rad) | −1.19 | 0.29 | −2.54 | 1.64 | |
| Delay for Calibration (ns) | 1.40 | 5.82 | 4.14 | 3.08 | |
| Phase for Calibration (rad) | −1.19 | 0.29 | −2.54 | 1.64 | |
| S6-T1 | Delay (ns) | −3.77 | 0.00 | / | / |
| Phase (rad) | −2.39 | 0.24 | / | / | |
| Delay for Calibration (ns) | −3.29 | −2.04 | / | / | |
| Phase for Calibration (rad) | 3.83 | 0.39 | / | / |
| Scan No. | Duration (s) | S6-Um p (°) | T1-Um p (°) | S6-T1 p (°) | |
|---|---|---|---|---|---|
| 0738+313 | No0005 | 300 | −23.80 | −23.80 | 0.00 |
| 0738+313 | No0007 | 300 | −23.90 | −23.90 | 0.00 |
| 0738+313 | No0009 | 300 | −24.00 | −24.00 | 0.00 |
| 0552+398 | No0012 | 600 | −54.00 | −54.00 | 0.00 |
| SAT-C5GD | No0004 | 360 | −20.90 | −20.90 | 0.00 |
| No0006 | 300 | −20.70 | −20.70 | 0.00 | |
| No0008 | 300 | −20.50 | −20.50 | 0.00 | |
| No0010 | 300 | −20.20 | −20.20 | 0.00 | |
| No0011 | 240 | −20.10 | −20.10 | 0.00 |
| XX/YY/XY/YX Delay Precision (ns) | I Delay Precision (ns) | I Delay (ns) | |||||
|---|---|---|---|---|---|---|---|
| Median | Min | Max | Median | Min | Max | Median | |
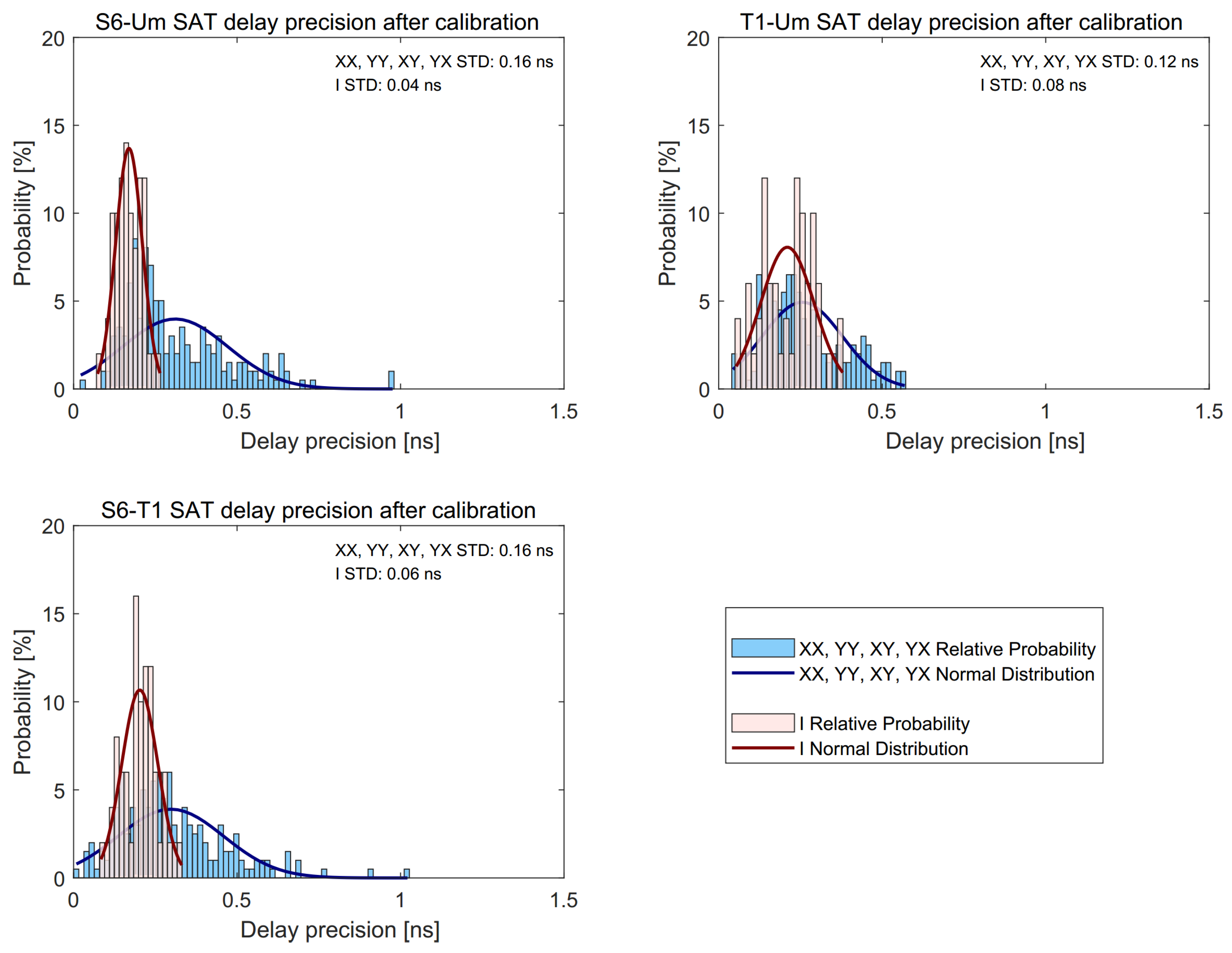
| S6-Um | 0.25 | 0.02 | 0.97 | 0.16 | 0.07 | 0.26 | −3.87 |
| T1-Um | 0.23 | 0.04 | 0.57 | 0.22 | 0.05 | 0.38 | −3.73 |
| S6-T1 | 0.27 | 0.01 | 1.02 | 0.20 | 0.08 | 0.33 | −0.43 |
| Li et al. [26] | This Study | |
|---|---|---|
| Antennas | Bj-Ur-Tm | S6-Um-T1 |
| Antennas diameter (m) | 50-26-65 | 13-13-13.2 |
| Antennas type | Legacy S/X VLBI | VGOS |
| Data processing system | CVN Legacy S/X VLBI software | Our software |
| Freq. (MHz × chan.) | 8 × 4 | 32 × 1 |
| FFT size | 8192 | 2048 |
| Integration time (s) | 30 | 30 |
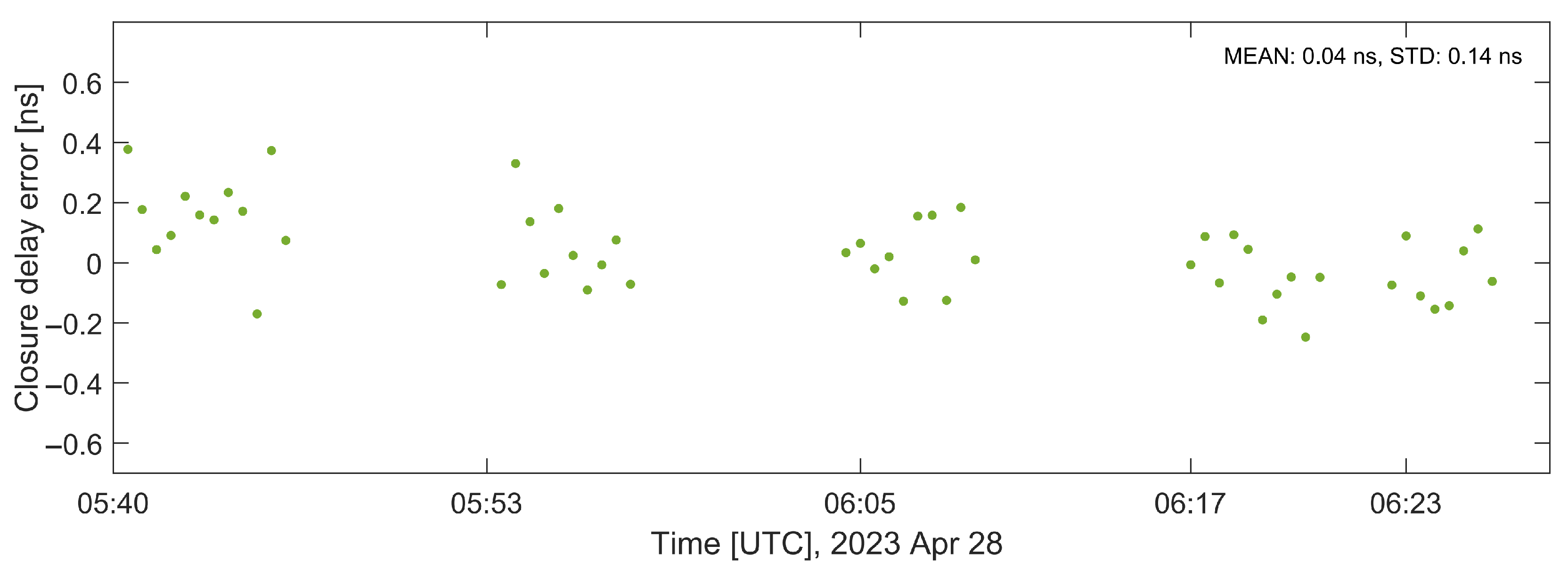
| Closure delay average (ns) | −0.02 | 0.04 |
| Closure delay STD (ns) | 0.05 | 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, J.; Shu, F.; He, X.; Huang, Y.; Tong, F.; Sun, Y. VGOS Dual Linear Polarization Data Processing Techniques Applied to Differential Observation of Satellites. Remote Sens. 2025, 17, 2319. https://doi.org/10.3390/rs17132319
Gan J, Shu F, He X, Huang Y, Tong F, Sun Y. VGOS Dual Linear Polarization Data Processing Techniques Applied to Differential Observation of Satellites. Remote Sensing. 2025; 17(13):2319. https://doi.org/10.3390/rs17132319
Chicago/Turabian StyleGan, Jiangying, Fengchun Shu, Xuan He, Yidan Huang, Fengxian Tong, and Yan Sun. 2025. "VGOS Dual Linear Polarization Data Processing Techniques Applied to Differential Observation of Satellites" Remote Sensing 17, no. 13: 2319. https://doi.org/10.3390/rs17132319
APA StyleGan, J., Shu, F., He, X., Huang, Y., Tong, F., & Sun, Y. (2025). VGOS Dual Linear Polarization Data Processing Techniques Applied to Differential Observation of Satellites. Remote Sensing, 17(13), 2319. https://doi.org/10.3390/rs17132319






