Theoretical Potential of TanSat-2 to Quantify China’s CH4 Emissions
Abstract
1. Introduction
2. Materials and Methods
2.1. Assessment of XCH4 Products
2.2. Pseudo Satellite XCH4 Observations
2.2.1. TanSat-2 Mission and Pseudo XCH4 Observations
2.2.2. Configuration of Pseudo XCH4 Error Scenarios
2.3. Inversion Framework for OSSEs
3. Results
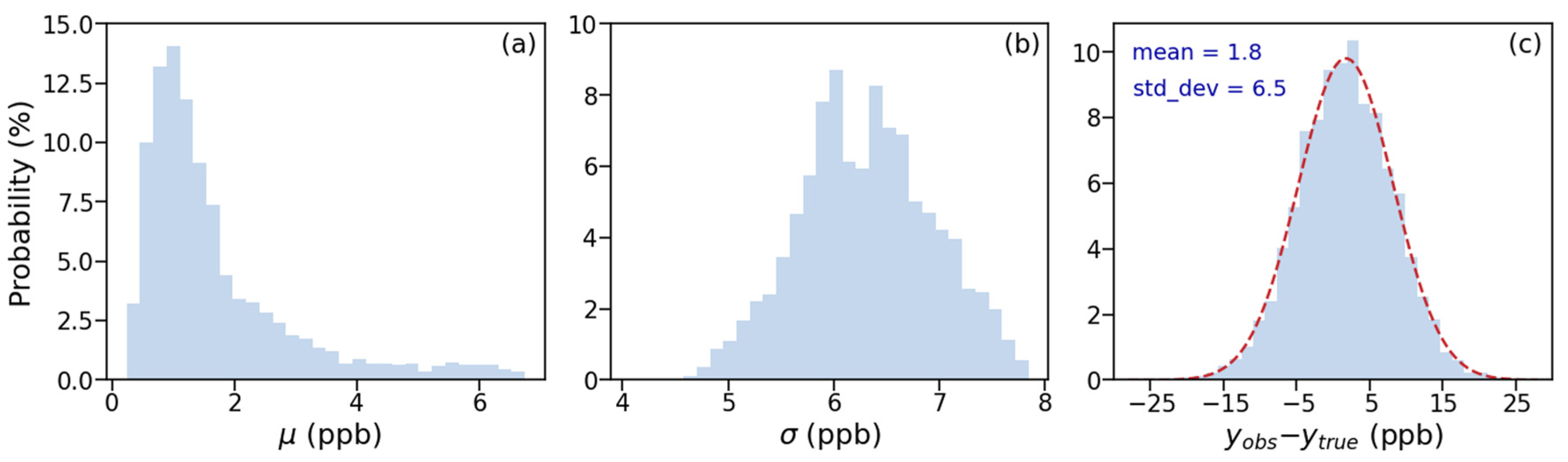
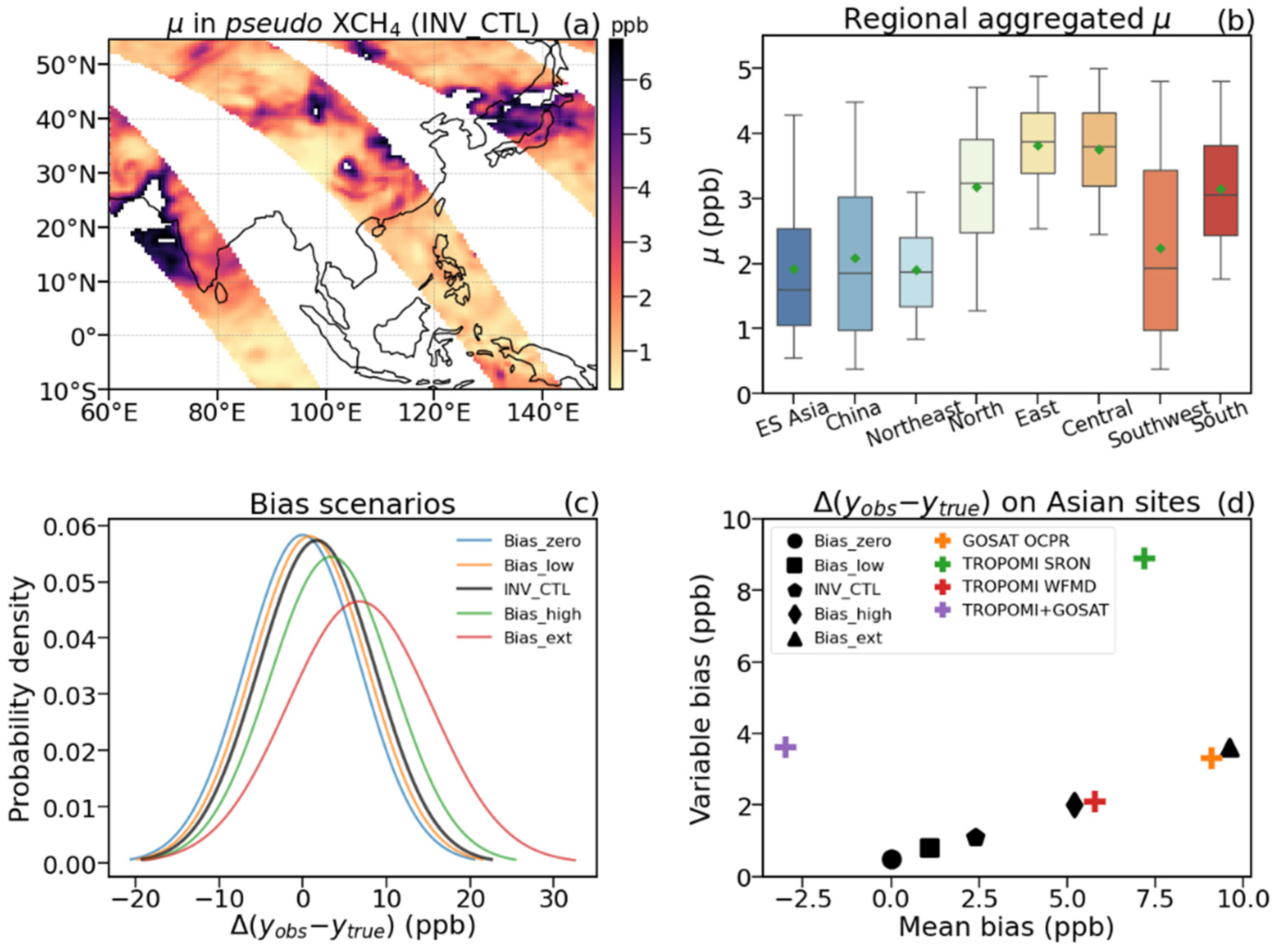
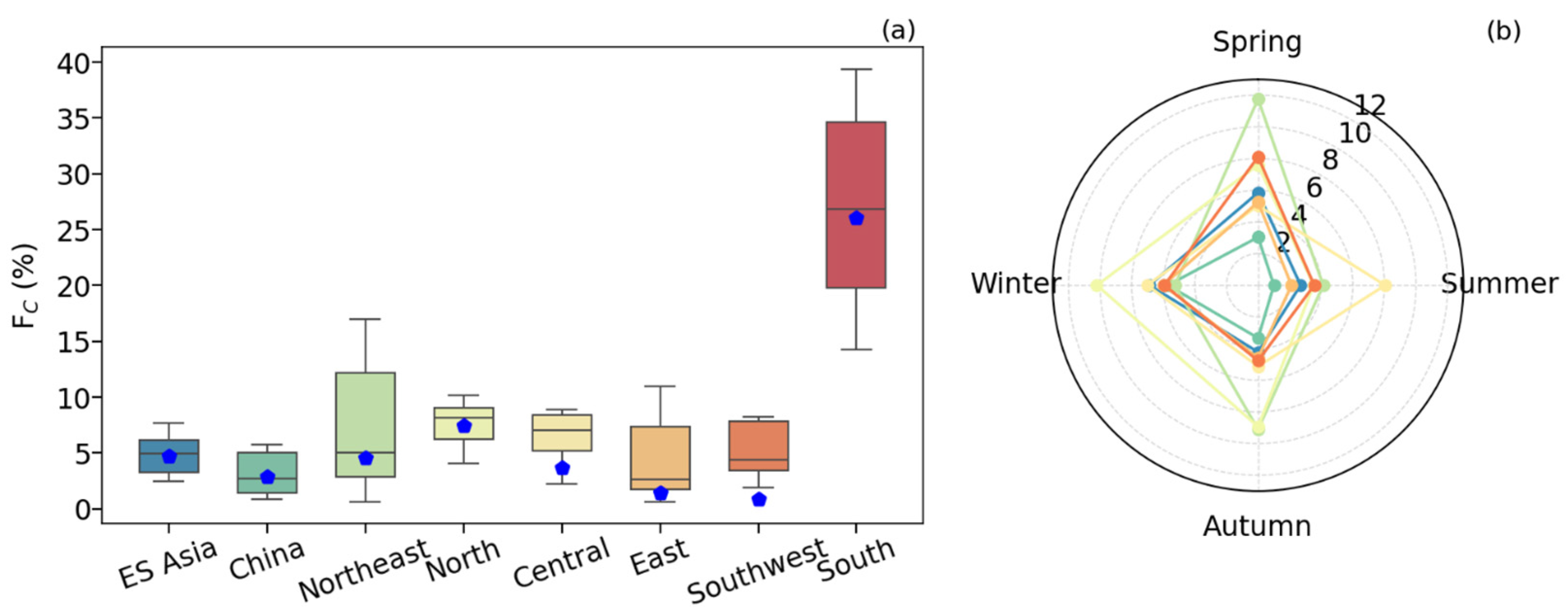
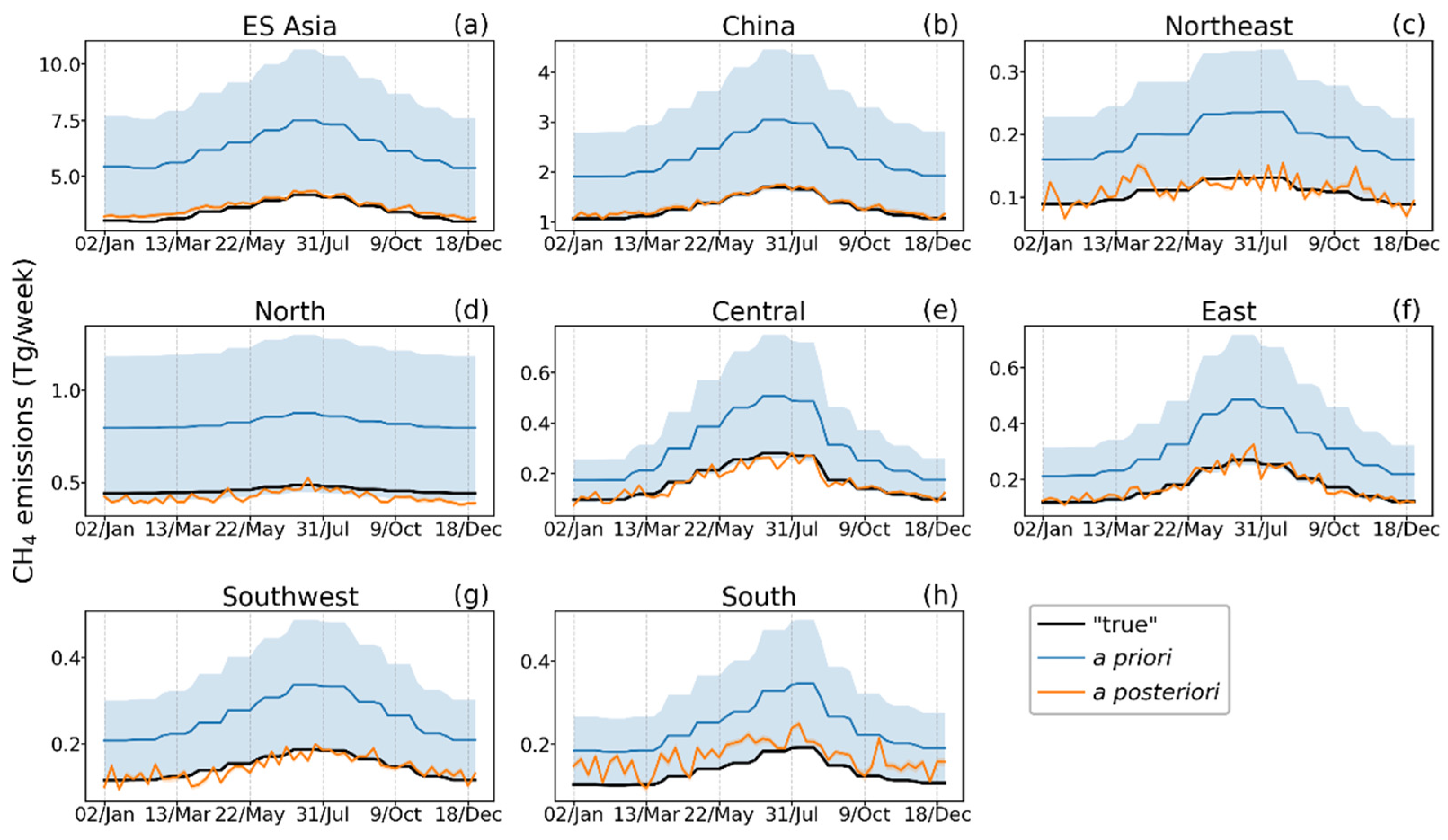
3.1. Control Experiment
3.2. Sensitivity of a Posteriori Flux Estimates to XCH4 Systematic Errors
3.3. Comparison with the Pseudo Situation of TROPOMI WFMD
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- WMO. W.M. No. 20–28 October 2024. Available online: https://library.wmo.int/records/item/69057-no-20-28-october-2024 (accessed on 13 November 2024).
- Canadell, J.; Monteiro, P.; Costa, M.; Cotrim da Cunha, L.; Cox, P.; Eliseev, A.; Henson, S.; Ishii, M.; Jaccard, S.; Koven, C.; et al. Global Carbon and Other Biogeochemical Cycles and Feedbacks; IPCC: Geneva, Switzerland, 2021. [Google Scholar]
- Nisbet, E.G.; Manning, M.R.; Dlugokencky, E.J.; Fisher, R.E.; Lowry, D.; Michel, S.E.; Myhre, C.L.; Platt, S.M.; Allen, G.; Bousquet, P.; et al. Very Strong Atmospheric Methane Growth in the 4 Years 2014–2017: Implications for the Paris Agreement. Glob. Biogeochem. Cycles 2019, 33, 318–342. [Google Scholar] [CrossRef]
- Ganesan, A.L.; Schwietzke, S.; Poulter, B.; Arnold, T.; Lan, X.; Rigby, M.; Vogel, F.R.; van der Werf, G.R.; Janssens-Maenhout, G.; Boesch, H.; et al. Advancing Scientific Understanding of the Global Methane Budget in Support of the Paris Agreement. Glob. Biogeochem. Cycles 2019, 33, 1475–1512. [Google Scholar] [CrossRef]
- Palmer, P.I.; Feng, L.; Lunt, M.F.; Parker, R.J.; Bösch, H.; Lan, X.; Lorente, A.; Borsdorff, T. The Added Value of Satellite Observations of Methane Forunderstanding the Contemporary Methane Budget. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2021, 379, 20210106. [Google Scholar] [CrossRef]
- Jacob, D.J.; Varon, D.J.; Cusworth, D.H.; Dennison, P.E.; Frankenberg, C.; Gautam, R.; Guanter, L.; Kelley, J.; McKeever, J.; Ott, L.E.; et al. Quantifying Methane Emissions from the Global Scale down to Point Sources Using Satellite Observations of Atmospheric Methane. Atmos. Chem. Phys. 2022, 22, 9617–9646. [Google Scholar] [CrossRef]
- Yokota, T.; Yoshida, Y.; Eguchi, N.; Ota, Y.; Tanaka, T.; Watanabe, H.; Maksyutov, S. Global Concentrations of CO2 and CH4 Retrieved from GOSAT: First Preliminary Results. Sola 2009, 5, 160–163. [Google Scholar] [CrossRef]
- Imasu, R.; Matsunaga, T.; Nakajima, M.; Yoshida, Y.; Shiomi, K.; Morino, I.; Saitoh, N.; Niwa, Y.; Someya, Y.; Oishi, Y.; et al. Greenhouse Gases Observing SATellite 2 (GOSAT-2): Mission Overview. Prog. Earth Planet. Sci. 2023, 10, 33. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Zhu, S.; Parker, R.J.; Liu, Y. Tropical Methane Emissions Explain Large Fraction of Recent Changes in Global Atmospheric Methane Growth Rate. Nat. Commun. 2022, 13, 1378. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Bösch, H.; Parker, R.J.; Webb, A.J.; Correia, C.S.C.; Deutscher, N.M.; Domingues, L.G.; Feist, D.G.; Gatti, L.V.; et al. Consistent Regional Fluxes of CH4 and CO2 Inferred from GOSAT Proxy XCH4: XCO2 Retrievals, 2010–2014. Atmos. Chem. Phys. 2017, 17, 4781–4797. [Google Scholar] [CrossRef]
- Zhang, Y.; Jacob, D.J.; Lu, X.; Maasakkers, J.D.; Scarpelli, T.R.; Sheng, J.-X.; Shen, L.; Qu, Z.; Sulprizio, M.P.; Chang, J.; et al. Attribution of the Accelerating Increase in Atmospheric Methane during 2010–2018 by Inverse Analysis of GOSAT Observations. Atmos. Chem. Phys. 2021, 21, 3643–3666. [Google Scholar] [CrossRef]
- Lorente, A.; Borsdorff, T.; Butz, A.; Hasekamp, O.; aan de Brugh, J.; Schneider, A.; Wu, L.; Hase, F.; Kivi, R.; Wunch, D.; et al. Methane Retrieved from TROPOMI: Improvement of the Data Product and Validation of the First 2 Years of Measurements. Atmos. Meas. Tech. 2021, 14, 665–684. [Google Scholar] [CrossRef]
- Lunt, M.F.; Palmer, P.I.; Lorente, A.; Borsdorff, T.; Landgraf, J.; Parker, R.J.; Boesch, H. Rain-Fed Pulses of Methane from East Africa during 2018–2019 Contributed to Atmospheric Growth Rate. Environ. Res. Lett. 2021, 16, 024021. [Google Scholar] [CrossRef]
- Chen, Z.; Jacob, D.J.; Nesser, H.; Sulprizio, M.P.; Lorente, A.; Varon, D.J.; Lu, X.; Shen, L.; Qu, Z.; Penn, E.; et al. Methane Emissions from China: A High-Resolution Inversion of TROPOMI Satellite Observations. Atmos. Chem. Phys. 2022, 22, 10809–10826. [Google Scholar] [CrossRef]
- Hachmeister, J.; Schneising, O.; Buchwitz, M.; Burrows, J.P.; Notholt, J.; Buschmann, M. Zonal Variability of Methane Trends Derived from Satellite Data. Atmos. Chem. Phys. 2024, 24, 577–595. [Google Scholar] [CrossRef]
- Houweling, S.; Bergamaschi, P.; Chevallier, F.; Heimann, M.; Kaminski, T.; Krol, M.; Michalak, A.M.; Patra, P. Global Inverse Modeling of CH4 Sources and Sinks: An Overview of Methods. Atmos. Chem. Phys. 2017, 17, 235–256. [Google Scholar] [CrossRef]
- Jacob, D.J.; Turner, A.J.; Maasakkers, J.D.; Sheng, J.; Sun, K.; Liu, X.; Chance, K.; Aben, I.; McKeever, J.; Frankenberg, C. Satellite Observations of Atmospheric Methane and Their Value for Quantifying Methane Emissions. Atmos. Chem. Phys. 2016, 16, 14371–14396. [Google Scholar] [CrossRef]
- Qu, Z.; Jacob, D.J.; Shen, L.; Lu, X.; Zhang, Y.; Scarpelli, T.R.; Nesser, H.; Sulprizio, M.P.; Maasakkers, J.D.; Bloom, A.A.; et al. Global Distribution of Methane Emissions: A Comparative Inverse Analysis of Observations from the TROPOMI and GOSAT Satellite Instruments. Atmos. Chem. Phys. 2021, 21, 14159–14175. [Google Scholar] [CrossRef]
- Stavert, A.R.; Saunois, M.; Canadell, J.G.; Poulter, B.; Jackson, R.B.; Regnier, P.; Lauerwald, R.; Raymond, P.A.; Allen, G.H.; Patra, P.K.; et al. Regional Trends and Drivers of the Global Methane Budget. Glob. Change Biol. 2022, 28, 182–200. [Google Scholar] [CrossRef]
- Miller, S.M.; Michalak, A.M.; Detmers, R.G.; Hasekamp, O.P.; Bruhwiler, L.M.P.; Schwietzke, S. China’s Coal Mine Methane Regulations Have Not Curbed Growing Emissions. Nat. Commun. 2019, 10, 303. [Google Scholar] [CrossRef]
- Yin, Y.; Chevallier, F.; Ciais, P.; Bousquet, P.; Saunois, M.; Zheng, B.; Worden, J.; Bloom, A.A.; Parker, R.J.; Jacob, D.J.; et al. Accelerating Methane Growth Rate from 2010 to 2017: Leading Contributions from the Tropics and East Asia. Atmos. Chem. Phys. 2021, 21, 12631–12647. [Google Scholar] [CrossRef]
- Sheng, J.; Tunnicliffe, R.; Ganesan, A.L.; Maasakkers, J.D.; Shen, L.; Prinn, R.G.; Song, S.; Zhang, Y.; Scarpelli, T.; Bloom, A.A.; et al. Sustained Methane Emissions from China after 2012 despite Declining Coal Production and Rice-Cultivated Area. Environ. Res. Lett. 2021, 16, 104018. [Google Scholar] [CrossRef]
- Liang, R.; Zhang, Y.; Chen, W.; Zhang, P.; Liu, J.; Chen, C.; Mao, H.; Shen, G.; Qu, Z.; Chen, Z.; et al. East Asian Methane Emissions Inferred from High-Resolution Inversions of GOSAT and TROPOMI Observations: A Comparative and Evaluative Analysis. Atmos. Chem. Phys. 2023, 23, 8039–8057. [Google Scholar] [CrossRef]
- Wunch, D.; Toon, G.; Blavier, J.-F.; Washenfelder, R.; Notholt, J.; Connor, B.; Griffith, D.; Sherlock, V.; Wennberg, P. The Total Carbon Column Observing Network. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2011, 369, 2087–2112. [Google Scholar] [CrossRef] [PubMed]
- Dils, B.; Buchwitz, M.; Reuter, M.; Schneising, O.; Boesch, H.; Parker, R.; Guerlet, S.; Aben, I.; Blumenstock, T.; Burrows, J.P.; et al. The Greenhouse Gas Climate Change Initiative (GHG-CCI): Comparative Validation of GHG-CCI SCIAMACHY/ENVISAT and TANSO-FTS/GOSAT CO2 and CH4 Retrieval Algorithm Products with Measurements from the TCCON. Atmos. Meas. Tech. 2014, 7, 1723–1744. [Google Scholar] [CrossRef]
- Reuter, M.; Buchwitz, M.; Schneising, O.; Noël, S.; Bovensmann, H.; Burrows, J.P.; Boesch, H.; Di Noia, A.; Anand, J.; Parker, R.J.; et al. Ensemble-Based Satellite-Derived Carbon Dioxide and Methane Column-Averaged Dry-Air Mole Fraction Data Sets (2003–2018) for Carbon and Climate Applications. Atmos. Meas. Tech. 2020, 13, 789–819. [Google Scholar] [CrossRef]
- Parker, R.J.; Webb, A.; Boesch, H.; Somkuti, P.; Barrio Guillo, R.; Di Noia, A.; Kalaitzi, N.; Anand, J.S.; Bergamaschi, P.; Chevallier, F.; et al. A Decade of GOSAT Proxy Satellite CH4 Observations. Earth Syst. Sci. Data 2020, 12, 3383–3412. [Google Scholar] [CrossRef]
- Lorente, A.; Borsdorff, T.; Martinez-Velarte, M.C.; Landgraf, J. Accounting for Surface Reflectance Spectral Features in TROPOMI Methane Retrievals. Atmos. Meas. Tech. 2023, 16, 1597–1608. [Google Scholar] [CrossRef]
- Schneising, O.; Buchwitz, M.; Hachmeister, J.; Vanselow, S.; Reuter, M.; Buschmann, M.; Bovensmann, H.; Burrows, J.P. Advances in Retrieving XCH4 and XCO from Sentinel-5 Precursor: Improvements in the Scientific TROPOMI/WFMD Algorithm. Atmos. Meas. Tech. 2023, 16, 669–694. [Google Scholar] [CrossRef]
- Balasus, N.; Jacob, D.J.; Lorente, A.; Maasakkers, J.D.; Parker, R.J.; Boesch, H.; Chen, Z.; Kelp, M.M.; Nesser, H.; Varon, D.J. A Blended TROPOMI+GOSAT Satellite Data Product for Atmospheric Methane Using Machine Learning to Correct Retrieval Biases. Atmos. Meas. Tech. 2023, 16, 3787–3807. [Google Scholar] [CrossRef]
- Zhu, S.; Yang, D.; Feng, L.; Tian, L.; Liu, Y.; Cao, J.; Wu, K.; Cai, Z.; Palmer, P.I. Towards the Optimization of TanSat-2: Assessment of a Large-Swath Methane Measurement. Remote Sens. 2025, 17, 543. [Google Scholar] [CrossRef]
- Hu, H.; Landgraf, J.; Detmers, R.; Borsdorff, T.; de Brugh, J.A.; Aben, I.; Butz, A.; Hasekamp, O. Toward Global Mapping of Methane With TROPOMI: First Results and Intersatellite Comparison to GOSAT. Geophys. Res. Lett. 2018, 45, 3682–3689. [Google Scholar] [CrossRef]
- Schneising, O.; Buchwitz, M.; Reuter, M.; Bovensmann, H.; Burrows, J.P.; Borsdorff, T.; Deutscher, N.M.; Feist, D.G.; Griffith, D.W.T.; Hase, F.; et al. A Scientific Algorithm to Simultaneously Retrieve Carbon Monoxide and Methane from TROPOMI Onboard Sentinel-5 Precursor. Atmos. Meas. Tech. 2019, 12, 6771–6802. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, P.; Nan, W.; Yang, Y.; Kumps, N.; Hermans, C.; De Mazière, M. TCCON Data from Xianghe, China; Release GGG2020R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2022. [Google Scholar]
- Liu, C.; Wang, W.; Sun, Y.; Shan, C. TCCON Data from Hefei, China; Release GGG2020R0; TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2023. [Google Scholar]
- Shiomi, K.; Kawakami, S.; Ohyama, H.; Arai, K.; Okumura, H.; Ikegami, H.; Usami, M. TCCON Data from Saga, Japan; Release GGG2020R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2022. [Google Scholar]
- Morino, I.; Ohyama, H.; Hori, A.; Ikegami, H. TCCON Data from Rikubetsu, Hokkaido, Japan; Release GGG2020R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2022. [Google Scholar]
- Morino, I.; Ohyama, H.; Hori, A.; Ikegami, H. TCCON Data from Tsukuba, Ibaraki, Japan, 125HR; Release GGG2020R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2022. [Google Scholar]
- Morino, I.; Velazco, V.A.; Hori, A.; Uchino, O.; Griffith, D.W.T. TCCON Data from Burgos, Philippines; Release GGG2020R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2022. [Google Scholar]
- Liu, Y.; Wang, J.; Yao, L.; Chen, X.; Cai, Z.; Yang, D.; Yin, Z.; Gu, S.; Tian, L.; Lu, N.; et al. The TanSat Mission: Preliminary Global Observations. Sci. Bull. 2018, 63, 1200–1207. [Google Scholar] [CrossRef]
- Yang, D.; Liu, Y.; Cai, Z.; Chen, X.; Yao, L.; Lu, D. First Global Carbon Dioxide Maps Produced from TanSat Measurements. Adv. Atmos. Sci. 2018, 35, 621–623. [Google Scholar] [CrossRef]
- Ran, Y. TanSat: A New Star in Global Carbon Monitoring from China. Sci. Bull. 2019, 64, 284–285. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Boesch, H.; Liu, Y.; Somkuti, P.; Cai, Z.; Chen, X.; Di Noia, A.; Lin, C.; Lu, N.; Lyu, D.; et al. Toward High Precision XCO2 Retrievals from TanSat Observations: Retrieval Improvement and Validation Against TCCON Measurements. J. Geophys. Res. Atmos. 2020, 125, e2020JD032794. [Google Scholar] [CrossRef]
- Yang, D.; Liu, Y.; Boesch, H.; Yao, L.; Di Noia, A.; Cai, Z.; Lu, N.; Lyu, D.; Wang, M.; Wang, J.; et al. A New TanSat XCO2 Global Product towards Climate Studies. Adv. Atmos. Sci. 2021, 38, 8–11. [Google Scholar] [CrossRef]
- Yao, L.; Yang, D.; Liu, Y.; Wang, J.; Liu, L.; Du, S.; Cai, Z.; Lu, N.; Lyu, D.; Wang, M.; et al. A New Global Solar-Induced Chlorophyll Fluorescence (SIF) Data Product from TanSat Measurements. Adv. Atmos. Sci. 2021, 38, 341–345. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, F.; Liu, Y.; Yang, D.; Wu, M.; He, W.; Wang, J.; Wang, J.; Ju, W.; Chen, J.M. Global Terrestrial Ecosystem Carbon Flux Inferred from TanSat XCO2 Retrievals. J. Remote Sens. 2022, 2022, 9816536. [Google Scholar] [CrossRef]
- Yang, D.; Hakkarainen, J.; Liu, Y.; Ialongo, I.; Cai, Z.; Tamminen, J. Detection of Anthropogenic CO2 Emission Signatures with TanSat CO2 and with Copernicus Sentinel-5 Precursor (S5P) NO2 Measurements: First Results. Adv. Atmos. Sci. 2023, 40, 1–5. [Google Scholar] [CrossRef]
- Wu, K.; Yang, D.; Liu, Y.; Cai, Z.; Zhou, M.; Feng, L.; Palmer, P.I. Evaluating the Ability of the Pre-Launch TanSat-2 Satellite to Quantify Urban CO2 Emissions. Remote Sens. 2023, 15, 4904. [Google Scholar] [CrossRef]
- Buchwitz, M.; Reuter, M.; Schneising, O.; Boesch, H.; Guerlet, S.; Dils, B.; Aben, I.; Armante, R.; Bergamaschi, P.; Blumenstock, T.; et al. The Greenhouse Gas Climate Change Initiative (GHG-CCI): Comparison and Quality Assessment of near-Surface-Sensitive Satellite-Derived CO2 and CH4 Global Data Sets. Remote Sens. Environ. 2015, 162, 344–362. [Google Scholar] [CrossRef]
- Aben, I.; Hasekamp, O.; Hartmann, W. Uncertainties in the Space-Based Measurements of CO2 Columns Due to Scattering in the Earth’s Atmosphere. J. Quant. Spectrosc. Radiat. Transf. 2007, 104, 450–459. [Google Scholar] [CrossRef]
- Butz, A.; Hasekamp, O.P.; Frankenberg, C.; Vidot, J.; Aben, I. CH4 Retrievals from Space-based Solar Backscatter Measurements: Performance Evaluation against Simulated Aerosol and Cirrus Loaded Scenes. J. Geophys. Res. 2010, 115, 2010JD014514. [Google Scholar] [CrossRef]
- Chander, G.; Hewison, T.J.; Fox, N.; Wu, X.; Xiong, X.; Blackwell, W.J. Overview of Intercalibration of Satellite Instruments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1056–1080. [Google Scholar] [CrossRef]
- von Clarmann, T.; Degenstein, D.A.; Livesey, N.J.; Bender, S.; Braverman, A.; Butz, A.; Compernolle, S.; Damadeo, R.; Dueck, S.; Eriksson, P.; et al. Overview: Estimating and Reporting Uncertainties in Remotely Sensed Atmospheric Composition and Temperature. Atmos. Meas. Tech. 2020, 13, 4393–4436. [Google Scholar] [CrossRef]
- Kiefer, M.; von Clarmann, T.; Funke, B.; García-Comas, M.; Glatthor, N.; Grabowski, U.; Kellmann, S.; Kleinert, A.; Laeng, A.; Linden, A.; et al. IMK/IAA MIPAS Temperature Retrieval Version 8: Nominal Measurements. Atmos. Meas. Tech. 2021, 14, 4111–4138. [Google Scholar] [CrossRef]
- The International GEOS-Chem User Community Geoschem/Geos-Chem: GEOS-Chem 12.5.0. 2019. Available online: http://www.geos-chem.org (accessed on 14 December 2019).
- Feng, L.; Palmer, P.; Boesch, H.; Dance, S. Estimating Surface CO2 Fluxes from Space-Borne CO2 Dry Air Mole Fraction Observations Using an Ensemble Kalman Filter. Atmos. Chem. Phys. 2009, 9, 2619–2633. [Google Scholar] [CrossRef]
- Zhu, S.; Feng, L.; Liu, Y.; Wang, J.; Yang, D. Decadal Methane Emission Trend Inferred from Proxy GOSAT XCH4 Retrievals: Impacts of Transport Model Spatial Resolution. Adv. Atmos. Sci. 2022, 39, 1343–1359. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, S.; Chen, J.; Lin, Y.; Chen, Y.; Liang, R.; Jiang, K.; Parker, R.J.; Boesch, H.; Steinbacher, M.; et al. Observed Changes in China’s Methane Emissions Linked to Policy Drivers. Proc. Natl. Acad. Sci. USA 2022, 119, e2202742119. [Google Scholar] [CrossRef]
- Yang, D.; Zhao, T.; Yao, L.; Guo, D.; Fan, M.; Ren, X.; Li, M.; Wu, K.; Wang, J.; Cai, Z.; et al. Toward Establishing a Low-Cost UAV Coordinated Carbon Observation Network (LUCCN): First Integrated Campaign in China. Adv. Atmos. Sci. 2024, 41, 1–7. [Google Scholar] [CrossRef]
- Zhao, T.; Yang, D.; Guo, D.; Wang, Y.; Yao, L.; Ren, X.; Fan, M.; Cai, Z.; Wu, K.; Liu, Y. Low-Cost UAV Coordinated Carbon Observation Network: Carbon Dioxide Measurement with Multiple UAVs. Atmos. Environ. 2024, 332, 120609. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, C.; Zhang, Y.; Lu, X.; Xiao, X.; Wang, F.; Song, J.; Guo, Y.; Leung, K.K.M.; Cao, J.; et al. Where to Place Methane Monitoring Sites in China to Better Assist Carbon Management. Npj Clim. Atmos. Sci. 2023, 6, 32. [Google Scholar] [CrossRef]




| GOSAT OCPR | TROPOMI SRON | TROPOMI WFMD | Blended TROPOMI+GOSAT | |
|---|---|---|---|---|
| Product version | v9.0 | v19_446 | v1.8 | TROPOMI v02.04.00 b GOSAT proxy v9.0 b |
| Local over pass time | 13:00 | 13:30 | 13:30 | / |
| Pixel size | 10.5 km diameter | 5.5 × 7 km2 c | 5.5 × 7 km2 c | / |
| Return time | 3 d | 1 d | 1 d | / |
| Retrieval band | 1.65 μm | 2.3 μm | 2.3 μm | / |
| Retrieval algorithm | CO2 proxy | RemoTeC | WFMD | Machine learning–LightGBM d |
| Mean bias (ppb) a | 0.0 e | −5.3 | / | −2.9 |
| Variable bias (ppb) a | 3.9 | 5.1 | 5.2 | 4.4 |
| Single-retrieval precision (ppb) a | 17.4 | 11.9 | 12.4 | 11.9 |
| Period | April 2009–December 2019 | March 2018–December 2020 | October 2017–April 2022 | January 2018–December 2021 |
| Reference f | Parker et al. (2020) [27] | Lorente et al. (2023) [28] | Schneising et al. (2023) [29] | Balasus et al. (2023) [30] |
| TCCON Site, Lat-lon Coord. (°) | GOSAT OCPR a,b | TROPOMI SRON a,c | TROPOMI WFMD a,d | Blended TROPOMI+GOSAT a | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. of Points | Bias (ppb) | Standard Deviation (ppb) | No. of Points | Bias (ppb) | Standard Deviation (ppb) | No. of Points | Bias (ppb) | Standard Deviation (ppb) | No. of Points | Bias (ppb) | Standard Deviation (ppb) | |
| Xianghe [34] (39.8, 116.96) | 106 | 7.7 | 13.4 | 49 | −5.8 | 12.9 | 567 | 6.5 | 15.1 | 468 | −6.6 | 11.7 |
| Hefei [35] (31.9, 119.17) | 0 | / | / | 48 | 8.9 | 12.9 | 54 | 2.3 | 16.3 | 49 | −2.7 | 12.3 |
| Saga [36] (33.24, 130.29) | 104 | 11.2 | 9.2 | 37 | 19.6 | 13.6 | 183 | 8.9 | 11.8 | 120 | 3.3 | 11.3 |
| Rikubetsu [37] (43.46, 143.77) | 22 | 14.1 | 13.7 | 45 | 0.4 | 21.2 | 61 | 7.1 | 16.7 | 131 | −1.1 | 10.8 |
| Tsukuba [38] (36.05, 140.12) | 59 | 5.6 | 9.1 | 130 | 3.5 | 10.1 | 147 | 5.7 | 9.5 | 142 | −3.2 | 8.3 |
| Burgos [39] (18.53, 120.65) | 42 | 7.1 | 5.7 | 10 | 16.8 | 18.4 | 25 | 4.0 | 12.1 | 68 | −7.4 | 9.1 |
| station-to-station statistics | 9.1 ± 3.3 | 10.2 ± 3.0 | 7.2 ± 8.9 | 14.8 ± 3.8 | 5.8 ± 2.1 | 13.6 ± 2.6 | −3.0 ± 3.6 | 10.6 ± 1.4 | ||||
| Sensitivity Experiments | Observation Error (ppb) | (ppb) | Sampled to TCCON Site (ppb) | ||
|---|---|---|---|---|---|
| Mean Bias | Variable Bias | ||||
| INV_CTL | 1.7 ± 1.3 | 6.8 ± 0.7 | 1.7 ± 7.0 | 2.4 | 1.1 |
| Bias_zero | 0.0 ± 0.0 | / a | 0.0 ± 6.8 | 0.0 | 0.5 |
| Bias_low | 0.9 ± 0.7 | / | 0.9 ± 6.9 | 1.1 | 0.8 |
| Bias_high | 3.4 ± 2.6 | / | 3.4 ± 7.3 | 5.2 | 2.0 |
| Bias_ext | 6.8 ± 5.1 | / | 6.8 ± 8.6 | 9.6 | 3.6 |
| Sensitivity Experiments | Spatial Coverage | Bias Scenario | Observation Error (ppb) | (ppb) | |
|---|---|---|---|---|---|
| WFMD_high | TROPOMI | Bias_high | 3.7 ± 2.8 | 9.0 ± 1.8 | 3.7 ± 9.6 |
| WFMD_med | TROPOMI | INV_CTL | 1.8 ± 1.4 | 9.0 ± 1.8 | 1.9 ± 9.3 |
| INV_CTL | TanSat-2 | INV_CTL | 1.7 ± 1.3 | 6.8 ± 0.7 | 1.7 ± 7.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Yang, D.; Feng, L.; Tian, L.; Liu, Y.; Cao, J.; Zhou, M.; Cai, Z.; Wu, K.; Palmer, P.I. Theoretical Potential of TanSat-2 to Quantify China’s CH4 Emissions. Remote Sens. 2025, 17, 2321. https://doi.org/10.3390/rs17132321
Zhu S, Yang D, Feng L, Tian L, Liu Y, Cao J, Zhou M, Cai Z, Wu K, Palmer PI. Theoretical Potential of TanSat-2 to Quantify China’s CH4 Emissions. Remote Sensing. 2025; 17(13):2321. https://doi.org/10.3390/rs17132321
Chicago/Turabian StyleZhu, Sihong, Dongxu Yang, Liang Feng, Longfei Tian, Yi Liu, Junji Cao, Minqiang Zhou, Zhaonan Cai, Kai Wu, and Paul I. Palmer. 2025. "Theoretical Potential of TanSat-2 to Quantify China’s CH4 Emissions" Remote Sensing 17, no. 13: 2321. https://doi.org/10.3390/rs17132321
APA StyleZhu, S., Yang, D., Feng, L., Tian, L., Liu, Y., Cao, J., Zhou, M., Cai, Z., Wu, K., & Palmer, P. I. (2025). Theoretical Potential of TanSat-2 to Quantify China’s CH4 Emissions. Remote Sensing, 17(13), 2321. https://doi.org/10.3390/rs17132321






