Improved Real-Time SPGA Algorithm and Hardware Processing Architecture for Small UAVs

Abstract

Real-time Synthetic Aperture Radar (SAR) imaging for small Unmanned Aerial Vehicles (UAVs) has become a significant research focus. However, limitations in Size, Weight, and Power (SwaP) restrict the imaging quality and timeliness of small UAV-borne SAR, limiting its practical application. This paper presents a non-iterative real-time Feature Sub-image Based Stripmap Phase Gradient Autofocus (FSI-SPGA) algorithm. The FSI-SPGA algorithm combines 2D Constant False Alarm Rate (CFAR) for coarse point selection and spatial decorrelation for refined point selection. This approach enables the accurate extraction of high-quality scattering points. Using these points, the algorithm constructs a feature sub-image containing comprehensive phase error information and performs a non-iterative phase error estimation based on this sub-image. To address the multifunctional, low-power, and real-time requirements of small UAV SAR, we designed a highly efficient hybrid architecture. This architecture integrates dataflow reconfigurability and dynamic partial reconfiguration and is based on an ARM + FPGA platform. It is specifically tailored to the computational characteristics of the FSI-SPGA algorithm. The proposed scheme was assessed using data from a 6 kg small SAR system equipped with centimeter-level INS/GPS. For SAR images of size 4096 × 12,288, the FSI-SPGA algorithm demonstrated a 6 times improvement in processing efficiency compared to traditional methods while maintaining the same level of precision. The high-efficiency reconfigurable ARM + FPGA architecture processed the algorithm in 6.02 s, achieving 12 times the processing speed and three times the energy efficiency of a single low-power ARM platform. These results confirm the effectiveness of the proposed solution for enabling high-quality real-time SAR imaging under stringent SwaP constraints.

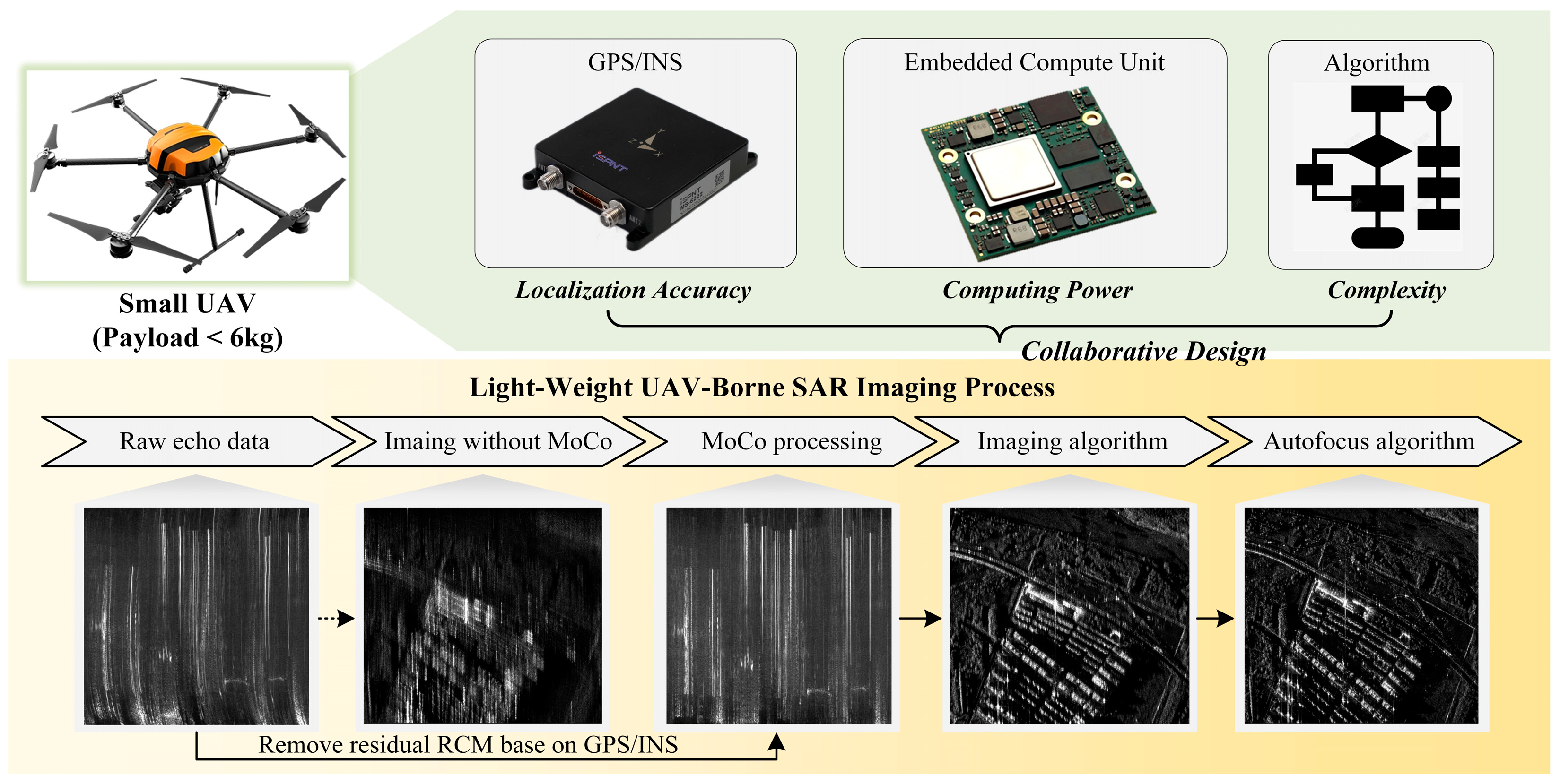
1. Introduction

SAR imaging represents a significant advancement in remote sensing, offering day-and-night, all-weather imaging capabilities that surpass those of traditional optical imaging technologies. This technology has extensive applications in military and civilian domains, such as vessel tracking, disaster assessment, and terrain surveillance [1]. Unmanned aerial vehicles (UAVs) serve as a pivotal platform for SAR applications, leveraging their flexibility, portability, and adaptability for real-time imaging, target detection, and tracking efforts.

However, due to their small and light nature, UAVs are particularly susceptible to atmospheric turbulence, which can lead to deviations from the ideal flight trajectory and result in motion errors [2,3]. In SAR systems, motion errors result in range migration and azimuth phase errors (APE) upon echo reception, significantly impairing the image resolution [4,5].

Accurate measurement and compensation of motion errors are crucial for acquiring high-precision and high-quality SAR imagery. One effective strategy is the integration of a high-precision and heavy-duty INS/GPS to concurrently capture the platform’s motion data [6,7], enabling effective motion compensation (MoCo) techniques to correct these errors. Another option is to estimate the motion error based on the echo data using the autofocus method, including the residual range cell migration (RCM) and APE, and then compensate for the error, which usually requires substantial computing power [8]. However, due to the limitations of SwaP, small UAV platforms with payloads under 7 kg cannot be equipped with high-precision INS/GPS. They cannot carry large processors with high computing power. Therefore, as shown in Figure 1, from the perspective of the system, it is necessary to comprehensively consider the INS/GPS localization accuracy, processor computing power, and algorithm complexity, and propose a real-time SAR imaging scheme that enables the completion of MoCo, imaging, and autofocus processes on a small UAV platform.

Under strict SwaP constraints, small UAV platforms, including multi-rotor configurations, typically rely on integrated light INS/GPS navigation systems that employ MEMS-IMUs to determine positional data for motion compensation in SAR imaging [9,10]. As illustrated in Figure 1, compared to the case without MoCo processing, two-step MoCo based on GPS/INS data can eliminate residual RCM errors, significantly enhancing the image quality [6,7]. However, the achievable measurement precision and sampling rate of these systems may not be sufficient to meet the demands of high-resolution SAR imaging at the Ku, Ka, and W bands, resulting in residual azimuth phase errors that can adversely impact image quality [11]. A widely adopted approach for achieving final focused SAR images is to iteratively refine defocused images through autofocus processing [12,13].

In recent years, researchers have employed data-driven autofocusing algorithms for high-precision SAR imaging. These algorithms are primarily categorized into two types: parametric and non-parametric [8].

Parametric methods assume a priori parameter models for the APE function and estimate the APE function through parameter estimation. Among parametric methods, the Map Drift (MD) algorithm is notable for its efficiency in estimating quadratic APE by analyzing sub-aperture image offsets [14,15,16]. However, it cannot estimate the higher-order APE. Another category of algorithms employs polynomial APE models based on the image quality metrics. These algorithms optimize image entropy [17,18], contrast [19], and other evaluation criteria to search for polynomial coefficients, thereby estimating the higher-order APE. Although these algorithms can accurately estimate high-order APE, they require numerous iterations, resulting in a significant computational burden and longer processing times.

The non-parametric method addresses phase errors of arbitrary forms using numerical methods, with Phase Gradient Autofocus (PGA) being the most representative technique [20]. The standard PGA algorithm encompasses four key steps: center circular shifting, windowing, phase-gradient estimation, and iterative correction. Initially proposed for spotlight-mode SAR imaging, it extracts phase errors from specifically selected points’ phase histories to enhance the focusing quality of the imagery. Enhanced PGA algorithms have been developed to accelerate the algorithm convergence. The QPGA selects high-contrast feature points to reduce the number of iterations [21], and the Weighted PGA (WPGA) enhances the phase gradient accuracy through maximum likelihood estimation [22]. To extend the applicability of the PGA to stripmap SAR, the method has been advanced by incorporating sub-aperture segmentation and phase curvature estimation, termed Stripmap PGA (SPGA) or PCA [23,24,25,26]. To enhance the performance and efficiency of the SPGA algorithm, industry scholars have adopted a range of improvement strategies. These include the use of Kalman filtering to increase the accuracy of phase error estimation [27], the employment of semidefinite relaxation for phase estimation [28], the integration PGA with the MD algorithm [29], the utilization of signal reconstruction within sub-apertures [30], and the removal of linear phase errors based on prior models [31]. Despite the satisfactory outcomes of these improvements, data dependencies and computational complexity resulting from iterations persist, making it challenging for these algorithms to meet stringent complexity requirements for real-time processing on small UAVs [8].

From an alternative perspective, advances in integrated circuit technology have significantly enhanced the performance of digital components, thereby enabling real-time Synthetic Aperture Radar (SAR) imaging and autofocus processing on-board systems. Common processors utilized in these applications include Central Processing Units (CPU), Digital Signal Processors (DSP), Graphics Processing Units (GPU), Field-Programmable Gate Arrays (FPGA), and Application-Specific Integrated Circuits (ASIC). While CPUs are designed for general computing, they exhibit limited efficiency in handling high-throughput radar signals due to the substantial instruction overhead. Conversely, DSPs improve floating-point operations and data throughput; however, they are hindered by inefficiencies in instruction parsing [32]. GPUs increase computational power with more cores, but this leads to higher power consumption [33]. Typically, the power consumption hovers around 15 watts. Implementing specialized hardware on FPGAs or ASICs provides a viable solution by optimizing the hardware for specific tasks and enhancing energy efficiency [34]. Despite exhibiting lower performance and higher power consumption than an ASIC, an FPGA’s flexibility and reconfigurability provide a superior cost-performance ratio when both cost and performance are taken into account [35]. Due to their compact size, high performance, low power consumption, and reconfigurability, FPGAs are highly appealing for on-board embedded high-performance computing. However, deploying tasks on FPGAs necessitates complex hardware circuit design, making the integration of autofocus algorithms into energy-efficient architectures challenging.

Considering the above problems, this paper proposes a lightweight real-time stripmap autofocus algorithm for kilogram-class small UAVs and an efficient hardware architecture design implementation on an ARM + FPGA platform. The primary contributions of this paper are summarized as follows:

(1) After reviewing the existing literature on PGA algorithms, we summarize the processing flow of the QW-SPGA algorithm. The FSI-SPGA was proposed in response to the iterative issues associated with the QW-SPGA algorithm. By enhancing the quality of point selection, extracting phase error feature sub-images, and performing global phase error recovery based on these feature sub-images, the algorithm significantly reduces the complexity while maintaining accuracy.

(2) Based on the characteristics of the FSI-SPGA algorithm, an efficient hardware computing architecture was designed for implementation on an FPGA. By utilizing multi-level pipelining, optimizing memory access, and employing dynamic partial reconfigurability methods, the design significantly enhances the utilization of hardware resources and energy efficiency. This architecture was implemented and validated on a Multi-Processor System on Chip (MPSoC) platform.

The remainder of this paper is organized as follows: Section 2 introduces the SAR motion error model, current autofocus methods, and associated challenges. Section 3 discusses the principles and implementation of the FSI-SPGA algorithm. Section 4 highlights the enhancements made to the FSI-SPGA algorithm and presents its hardware architecture design on an FPGA. Finally, Section 5 validates the effectiveness of the proposed scheme using real-world data from an MPSoC platform.

2. Theory and Problem Analysis

2.1. Residual Motion Error Model for SAR

The geometry of the UAV SAR data acquisition is illustrated in Figure 2, where the x-axis aligns with the course direction and the y-axis aligns with the cross-course direction. The dotted line represents the ideal trajectory of the UAV, and the yellow solid line indicates the actual trajectory.

Ideally, the aircraft moves in a straight line at a constant velocity $v$, but the realized flight trajectory often deviates from the ideal flight trajectory. It is assumed that the repetition period of the pulse is $T_a$ and the ideal flight altitude is $H$. Ideally, the antenna phase center (APC) is at $[{vt}_a,0,H]$ at the $t_a$ slow time, but due to the flight trajectory deviation of $\left[\Delta x\left(t_a\right), \Delta y\left(t_a\right), \Delta z\left(t_a\right)\right]$, the actual APC position is $[{vt}_a+\Delta x(t_a), \Delta y(t_a), H+\Delta z(t_a\left)\right]$. For the point target Q located at coordinates $(x,y,z)$, its instantaneous slope $R\left(t_a\right)$ can be expressed as [36]:

$$\begin{gathered} R\left(t_a\right)=\sqrt{{\left(v{t}_a-\Delta x\left(t_a\right)-x\right)}^2+{\left(\Delta y\left(t_a\right)-y\right)}^2+{\left(H+\Delta z\left(t_a\right)-z\right)}^2} \\ =R_0\left(t_a\right)+\Delta R\left(t_a\right), \end{gathered}$$

(1)

where $R_0\left(t_a\right)$ represents the instantaneous slant distance between the point target and the ideal trajectory, and $\Delta R\left(t_a\right)$ represents the motion error. In general, by mounting a high-precision INS/GPS on the motion platform to measure the motion error, the residual RCM and APE can be well corrected after motion compensation of the original data [11]. However, for small UAVs, due to the constraints of SwaP, only lightweight INS/GPS with low accuracy can be mounted. In this scenario, the measured position cannot be approximated to an exact value. In this paper, after range pulse compression, two-step MoCo [6,7], and residual distance migration correction based on the $\omega K$ algorithm [13], the SAR signal in the range-azimuth frequency domain can be represented as:

$$\begin{gathered} s_{rc}\left(m,n\right)=A_0\cdot w_a\left(n\cdot \Delta T_a-{\displaystyle \frac{x}{v}}\right)\cdot \mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\left[B\cdot \left(m\cdot {\Delta T}_r-{\displaystyle \frac{2r}{c}}-{\displaystyle \frac{2\Delta \tilde{R}\left(n\cdot \Delta T_a\right)}{c}}\right)\right] \\ \hspace{1em}\hspace{1em}\cdot \mathit{exp}\left[-j4\pi f_0{\displaystyle \frac{R_0\left(n\cdot \Delta T_a\right)}{c}}\right]\cdot \mathit{exp}\left[-j4\pi f_0{\displaystyle \frac{\Delta \tilde{R}\left(n\cdot \Delta T_a\right)}{c}}\right] \end{gathered}$$

(2)

$$\Delta \tilde{R}\left(n\cdot \Delta T_a\right)=\mathsf{\Delta }R\left(n\cdot \Delta T_a\right)-\mathsf{\Delta }\widehat{R}\left(n\cdot \Delta T_a\right),$$

(3)

where $\Delta T_a$ is the pulse repetition interval, $\Delta T_r$ is the distance sampling interval, and $\mathsf{\Delta }\widehat{R}\left(n\cdot \Delta T_a\right)$ is the actual measured value of the motion error. The model indicates the relationship between the phase and distance errors and determines the form in which the phase error exists.

For high-resolution SAR imaging, the analysis in Equation (2) shows that the residual RCM error is mainly caused by $\Delta \tilde{R}\left(n\cdot \Delta T_a\right).$ If the flight geometry is designed and an appropriately accurate GPS/INS is selected, such that the error $\Delta \tilde{R}\left(n\cdot \Delta T_a\right)<{\delta }_r/4$, where ${\delta }_r$ is the range resolution cell is, then the residual RCM will be transformed into APE. In the strip SAR image, the distance-compressed phase historical domain data at the k-strong point can be expressed as [27]:

$$s_k\left(t_a\right)=A_{k}rect\left({\displaystyle \frac{t_a-{\eta }_k}{T_a}}\right)\cdot \mathit{exp}\left[j\pi K_a{t}_a^2+j2\pi f_k{t}_a+j\left({{\varphi }_A}_k+{\varphi }_e\left(t_a\right)\right)\right]$$

(4)

where $A_k$ is the amplitude of the target’s scattering coefficient, ${\eta }_k$ is the slow time corresponding to the target’s azimuth position, $2\pi f_k{t}_a$ is the linear phase corresponding to the azimuth position, the ${{\phi }_A}_k$ is the phase of the target’s scattering coefficient, ${\phi }_e\left(t_a\right)$ is the azimuth phase error, $K_a$ is the azimuth frequency modulation slope, and $rect(\cdot )$ represents the rectangular window function.

2.2. Real-Time Autofocus for UAV SAR Problem Analysis

In response to the APE in question, the industry widely adopts the PGA method for its estimation and compensation. Due to the slow convergence speed of the PGA algorithm, it must undergo many iterations to achieve the ideal focusing effect, and there are many improved methods to improve the estimation accuracy and convergence speed of the PGA. The QPGA algorithm enhances the convergence speed by selecting higher-quality strong scattering points [21]. The WPGA algorithm [22,37], on the one hand, reduces the impact of weak scattering points on phase estimation through weighting. However, it precisely estimates phase errors even under low signal-to-noise ratios by leveraging the least squares method, thus improving the convergence speed of the algorithm. However, these algorithms are improved based on the traditional PGA algorithm and are mainly used for spotlight SAR. Spotlight SAR and stripmap SAR differ in that the synthetic aperture time for different scattering points within the stripmap SAR imaging scene varies, implying that the APE does not completely overlap. In order to perform a consistent estimation of phase errors for several specifically selected points within a sub-aperture, it is necessary to estimate the phase errors by taking the second derivative of the phase and then synthesizing the full-aperture phase error history through a process of double integration. Hence, the PGA technique, when applied to stripmap SAR, generally refers to the PCA algorithm [23,24,25,26,27]. For various application scenarios, many adaptive improvements have been made to the SPGA, leading to the derivation of numerous algorithms [28,29,30,31]. A non-iterative SPGA algorithm based on the removal of the linear phase was proposed in [31]. This is suitable for image defocus caused by multiple linear phase segments. While it ensures fast convergence during phase error estimation, it still follows an iterative process: point selection, azimuthal inverse compression, phase error estimation, azimuthal compression, and back to point selection. Currently, no publicly available research integrates high-quality point selection, weighting, and other general techniques to enhance the performance of the SPGA.

The QW-SPGA algorithm is summarized in this paper by combining the QPGA, WPGA, and SPGA techniques. Figure 3a shows the overall processing flow of QW-SPGA. In the process of processing the measured data, the author found that the focusing performance of the QW-SPGA was better than that of the traditional SPGA method. This paper establishes a quantitative estimation of the computational complexity of the QW-SPGA algorithm:

$$\begin{array}{l}{t}_{QW-SPGA}=\left(t_{cp}+t_{inac}+t_{es}+t_{co}\right)\times N_{iter}\\ =O\left(N_{iter}\left(MN\cdot ({4\mathit{log}}_{2}M+3+N_{ref})+KM\cdot \left(4{\mathit{log}}_{2}M+5\right)\right)\right), \end{array}$$

(5)

where $t_{cp}=O(MN\cdot N_{ref})$ represents the time taken to select the scattering point set, $t_{es}=O\left(KM\cdot \left(4{\mathit{log}}_{2}M+5\right)\right)$ represents the time taken to estimate the phase error, $t_{co}=O\left(MN\cdot \left(2+2{\mathit{log}}_{2}M\right)\right)$ represents the time taken to compensate for the image error, and $t_{inac}=O\left(MN\cdot \left(1+2{\mathit{log}}_{2}M\right)\right)$ represents the time taken to inversely compress the image azimuth. $N_{iter}$ is the number of iterations. $N_{ref}$ is the number of the reference unit in 2D CFAR. $K$ is the number of selected scatterers. $M$ and $N$ are the number of azimuth points and range points, respectively. As can be seen from Equation (5), the algorithm runtime is proportional to the iteration number $N_{iter}$.

For lightweight drones weighing around 6 kg, real-time SAR imaging with high resolution and wide-swath coverage poses significant challenges in terms of weight, power consumption, and processing efficiency. Specifically, achieving high-resolution SAR imaging with a swath width of 3.6 km and a resolution of 0.3 m while maintaining a flight speed of 12 m/s requires efficient data processing and power-management capabilities.

Given these constraints, accumulating data for two synthetic apertures of 150 m each takes 25 s. For real-time imaging, the system must simultaneously process the current data while completing the imaging, autofocus, and interpreting the previous data. The range-Doppler (RD) algorithm, accelerated by FPGA, is currently the most efficient method for SAR imaging, requiring 6 s for processing [38]. However, incorporating motion error compensation based on INS/GPS data adds an additional 3 s. Therefore, autofocus processing must be completed within a similar timeframe.

To achieve real-time autofocus, the iterative process must be minimized, with the number of iterations $N_{iter}$ approaching 1, and the error estimation time $t_{es}$ minimized. This requirement is further complicated by the power constraints of the lightweight platforms. Typically, a 6 kg drone has a battery capacity of no more than 180 Wh, with the majority of the energy allocated to flight propulsion [39]. Thus, the data processing system must operate within a power limit of 15 W.

Under these constraints, FPGA-based hardware acceleration is superior to general-purpose processors, such as CPUs and GPUs [38]. However, algorithms like QW-SPGA, which involve high computational complexity due to uncertain point selection and multiple iterations, are impractical for deployment on resource-limited FPGAs. Therefore, optimizing the hardware architecture to meet these stringent requirements is essential for the successful implementation of real-time SAR imaging on lightweight drones.

3. Lightweight Autofocusing Algorithm Design

Compared with the conventional SPGA algorithm, the QW-SPGA algorithm integrates two techniques: contrast-based high-quality point selection and weighted maximum likelihood (WML) estimation. These enhancements can improve the estimation accuracy of the phase errors during each iteration, thereby accelerating the convergence of the algorithm. In actual experiments, when the number of iterations $N_{iter}$ of the algorithm is between 6 and 8, a satisfactory focusing effect can be achieved. In the context of real-time SAR imaging using small UAVs, strict time and computational power constraints necessitate a detailed examination of the key steps involved in the QW-SPGA algorithm. This scrutiny reveals several persistent issues that warrant attention:

(1) Scattering points exhibiting high contrast along the azimuth can be selected using the maximum contrast criterion. However, this approach does not ensure the isolation of scattering points along the range, which leads to the sidelobes of the same scattering point contributing to the phase estimation multiple times.

(2) The quadratic integration of the phase curvature introduces additional noise, resulting in a loss of accuracy.

(3) In theory, the set of high-quality selected points should encompass all the information required to estimate phase errors. However, the QW-SPGA method initiates point selection at each iteration, which may not be optimal.

To address these issues, this subsection improves the QW-SPGA algorithm and proposes a non-iterative and high-precision autofocus algorithm called FSI-SPGA. The overall process of FSI-SPGA is shown in Figure 3b, which mainly includes three main steps. The specific principles and processing flow of the FSI-SPGA algorithm are presented in the following subsections.

3.1. Selection of High-Quality Scattering Points

To capture the entire azimuth phase error information, the selected scatterers must be high-quality, isolated, and complete. High quality means that the scatterers must have a high signal-to-noise ratio to yield reliable phase error data. Isolated implies that they must be sufficiently distant from other scatterers to prevent error coupling. Complete requires that the synthetic aperture periods of the scatterers fully cover the azimuth time. Considering these factors, the FSI-SPGA algorithm comprises two stages in the point selection process: coarse and fine selections, which are detailed as follows.

(1) Coarsely select scattering points

In traditional spotlight-mode SAR imaging, the PGA algorithm identifies scatterers by selecting peaks in the data of the corresponding range gates [21]. However, in the stripmap mode, the scatterers are not all in the same synthetic aperture period. To extract isolated strong scatterers across the entire image, the classic 2D CFAR algorithm from radar target detection can be used for the preliminary scatterer selection. CFAR algorithms [40] are categorized into four types based on noise estimation: Cell Averaging (CA), Ordered Statistics (OS), Greater of (GO), and Smaller of (SO). The CA-CFAR is suitable for uniform-clutter scenarios, the OS-CFAR is ideal for multi-target situations, and the GO-CFAR and SO-CFAR are designed for clutter-edge cases. However, in this study, as we only apply 2D CFAR for preliminary scatterer selection in defocused SAR images, clutter-edge scenarios are not our focus. In terms of computational complexity, for the scene depicted in Figure 4, 2D OS-CFAR has a time complexity of $O(N_a{N}_r{N}_{ref}\cdot {\mathit{log}}_2\left(N_{ref}\right))$, whereas 2D CA-CFAR only has a time complexity of $O\left(N_a{N}_r{N}_{ref}\right)$, where $N_a$ is the number of pixels in the azimuth direction, $N_r$ is the number of pixels in the range direction, and $N_{ref}$ is the number of reference cells. Moreover, practical tests indicate that when extracting phase error profiles for image focusing, the scatterer set selected by the 2D CA-CFAR is more robust than that selected by the 2D OS-CFAR. CA-CFAR is less effective in multi-target environments, but is advantageous when selecting scattering points with strong isolation and a high signal-to-noise ratio. The computational structure of the 2D CA-CFAR is optimized in Section 4.3.2 to enhance memory access and computational efficiency using FPGAs. Compared with CA-CFAR and OS-CFAR, tests on real-world data (as shown in Figure 5) reveal that, despite some differences in the selected target points between the two methods, most scatterers overlap and could cover the entire synthetic aperture time in the azimuth direction. Therefore, in this paper, a 2D CA-CFAR approach is employed for the preliminary selection of points within the image domain.

The processing procedure for the 2D CA-CFAR is illustrated in Figure 4a. The detection core traverses the power spectrum image and consists of a central, protection, and reference unit. The protection unit is specifically designed to estimate the noise energy, thereby mitigating the risk of target energy leakage. The power spectral image is formed from the raw SAR image data through a square-law geophone, i.e., $P(m,n)={\left|I\left(m,n\right)\right|}^2$, $\mathbf{I}$ is the SAR complex image matrix. When performing point-target detection, the noise energy around the central unit is first estimated as follows:

$$A\left(m,n\right)={\displaystyle \frac{1}{N_{ref}}}\sum _{n_{ref}}^{1}P\left(n_{ref}\right),$$

(6)

where $(m,n)$ represents the coordinates of the central unit, $N_{ref}=C_a{C}_r-G_a{G}_r$ is the number of reference units, and $P\left(n_{ref}\right)$ is any one of the reference units. The detection threshold can be expressed as $T(m,n)=\alpha \cdot A(m,n)$, where the threshold factor $\alpha =N_{ref}\left(P_{fa}^{-1/N_{ref}}-1\right)$, and the value is ${10}^{-4}~{10}^{-3}$ according to $P_{fa}$ the empirical false alarm rate. Finally, by comparing the energy of the central unit with the noise energy, it is judged whether the central unit is a scattering point.

(2) Finely select scattering points

After the coarse selection of points is completed, a collection of scattering points randomly distributed over the image can be formed as follows:

$$\Psi =\left\{\left(m_k,n_k,P\left(m_k,n_k\right)\right),k=\mathrm{1,2},\dots ,K\right\}.$$

(7)

To ensure the accuracy of the autofocus, the point set requires further filtering to ensure that the distance between any two points is sufficiently large, and each point is the optimal choice within its local region. For any point $\left(m_c,n_c,P\left(m_c,n_c\right)\right)\in \Psi$, as shown in Figure 4b, we define its adjacent space:

$$\left|m-m_c\right|+\left|n-n_c\right|\le d,$$

(8)

Scattering points in the adjacent space are divided into two categories: false points on the side lobes and real points competing with the candidate point. To eliminate the false point target and extract the high-energy target, the scattering point with the highest energy within the region is selected through an energy comparison. After filtering all points in $\Psi$, the final high-quality scattering point set is obtained. Figure 5a,b illustrate the outcomes of coarse and refined point selection, respectively. It is evident that the refined point selection process successfully eliminates a significant number of redundant scattering points, resulting in a uniform and high-quality set of scattering points.

3.2. Feature Sub-Image Construction

When estimating the phase error in the traditional PGA, each iteration involves multiple transformations between the image and phase history domains. Notably, estimating the phase error based on high-quality scatterers does not require the entire SAR complex image. In a defocused image, azimuth phase errors cause the main peak energy of the scatterer’s spread function to disperse. However, the extent of energy dissipation is typically within a certain range.

As shown in Figure 6c, for a standard linear frequency-modulated (LFM) signal, after pulse compression, most of the sidelobe energy is distributed within a range of 10 times the mainlobe width on either side of the mainlobe [41]. The energy of the lowest integration sidelobe is used as the threshold. Using the energy level of the lowest integrated sidelobe as a threshold, signals exceeding this threshold are extracted as the scatterer feature signal. Based on Equation (2), we introduced the quadratic and higher-order phase errors depicted in Figure 6a,b, and assessed the range of the sidelobe energy spread caused by phase errors up to 35 radians. The simulation results shown in Figure 6c indicate that the quadratic phase errors cause the most severe mainlobe widening. Consequently, the escaped sidelobe energy region is the largest, approximately six times the width of the integration sidelobe. However, pure quadratic phase errors are rare in practice. For higher-order phase errors, which are typical in practical scenarios, the sidelobe energy region is roughly four times the width of the integrated sidelobe. To address this, this paper adopts an intermediate value, using five times the width of the integrated sidelobe as the ambiguity region for independent scatterers. The ambiguity length $L$ can be approximated using the formula:

$$L=20\cdot {\displaystyle \frac{{\rho }_a}{x_a}} \cdot \alpha \cdot \beta ,$$

(9)

where ${\rho }_a$ represents the theoretical azimuth resolution, $x_a$ denotes the actual distance between two points in the azimuth direction of the SAR image, $\alpha$ is between 2 and 2.5 [41], and $\beta$ is set to 5 in this study’s scenario.

Subsequently, the fuzzy areas of all scattering points are extracted. As shown in Figure 7, the blurred areas of each scattering point are stitched together according to their azimuth coordinates to form a $K\times L$ feature sub-image, which contains the phase error information of the entire SAR image.

3.3. Phase Error Estimation

After completing the above steps, a high-quality scattering point set and the corresponding feature sub-images of size K × L are obtained. These contain sufficient information to estimate the APE when the synthetic aperture time of each scattering point coincides and encompasses the entire azimuth sampling time. This process significantly reduces the data dimension when filtering out high signal-to-noise ratio data. For APE estimation using the feature sub-images, this paper updates the scatterer positions and removes linear phase errors. These enhancements improve the accuracy of phase error estimation and reduce the image azimuth offset. Figure 8 illustrates the APE estimation process.

Firstly, the azimuth zeroing process is carried out on the feature sub-image:

$${\mathbf{I}}_0=\left[{\mathit{O}}_{K\times M} {\mathit{I}}_{sub} {\mathit{O}}_{K\times M}\right],$$

(10)

where the number of square azimuth zeros is $M=(0.8L_p-L)/2$ and $L_p$ is the number of synthetic aperture points. The azimuth inverse compression is carried out on the ${\mathbf{I}}_0$ of the zero-filled feature sub-image to obtain the distance-compressed azimuth time domain data of the feature sub-image:

$${\mathit{S}}_{\mathit{f}\mathit{e}\mathit{a}}^{\mathbf{\prime }}={\mathrm{I}\mathrm{F}\mathrm{F}\mathrm{T}}_{\mathrm{a}}\left[FF{T}_a\left({\mathit{I}}_0\right)\cdot \mathit{exp}\left\{j\mathit{\varphi }\right\}\right].$$

(11)

The phase of the azimuth matching filter corresponding to each scattering point $\left(f_m, R_k\right)$ can be expressed as:

$$\varphi \left(f_m,R_k\right)={\displaystyle \frac{{\pi \lambda R_{k}f}_m^2}{2v^2}}.$$

(12)

The energy that may be mixed with the escape from other scattering points in the time domain data ${\mathit{S}}_{\mathit{f}\mathit{e}\mathit{a}}^{\mathbf{\prime }}$, derived from the compressed azimuth time domain, can be windowed in the equivalent image signal domain to obtain the chirp signal with an error at a single scattering point:

$${\mathit{S}}_{\mathit{f}\mathit{e}\mathit{a}}^{\mathbf{″}}=IFF{T}_a\left[rec{t}_w\left(m\right)\cdot FF{T}_a\left({\mathit{S}}_{\mathit{f}\mathit{e}\mathit{a}}^{\prime }\cdot \mathit{exp}\left\{j\mathit{\varphi }\left(f_m,R_k\right)\right\}\right)\right],$$

(13)

where

$${\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}}_{\mathrm{w}}\left(m\right)=\left\{\begin{array}{c}1,-{\displaystyle \frac{L_w}{2}}-1\le m<{\displaystyle \frac{L_w}{2}}\\ 0, otherwise\end{array}\right.$$

(14)

is a rectangular window function with a window length of $L_w$, and the $L_w$ decreases proportionally in feature sub-image iterations.

After the above processing is completed, the distance compression phase history domain signal is:

$${\mathit{S}}_{\mathit{f}\mathit{e}\mathit{a}}^{\mathbf{″}}\left(k,m\right)=A_k\cdot \mathit{exp}\left(\left\{j\left(2\pi f_k\Delta T_{a}m+{\varphi }_e\left(k,m\right)\right)\right\}\right).$$

(15)

In Equation (15), the phase function consists of a linear term due to the offset of the scattering point position and an APE term due to motion error. First, it is estimated as a whole, and in order to avoid loss of accuracy, a phase gradient is used here to estimate the phase error:

$$\widehat{\dot{{\varphi }_e}}\left(k,m\right)=Angle\left({\mathit{S}}_{\mathit{f}\mathit{e}\mathit{a}}^{\prime \prime }\left(k,m\right)\cdot Conj\left({\mathit{S}}_{\mathit{f}\mathit{e}\mathit{a}}^{″}\left(k-1,m\right)\right)\right),$$

(16)

where $Angle(\cdot )$ means to find the phase, and$Conj(\cdot )$ means to take the conjugation. $\dot{{\mathit{\phi }}_{\mathit{e}}}(k,\cdot )$represents the phase gradient of the sub-aperture where the k-th scattering point is located. It is necessary to splice the phase gradient of each sub-aperture to form a complete azimuth synthesis aperture phase gradient. The specific splicing process is shown in Figure 9, where the phase gradient constant interval of each sub-aperture is first estimated:

$$\mathsf{\Delta }{\widehat{\dot{{\varphi }_e}}}_{k-1,k}={\displaystyle \frac{1}{N_p}}\sum _{i=1}^{N_p}\left(\widehat{\dot{{\varphi }_e}}\left(k,i\right)-\widehat{\dot{{\varphi }_e}}\left(k-1,L_p-N_p+i\right)\right),$$

(17)

where $N_p=m_{k-1}-m_k+L_p$ is the number of overlapping points of two adjacent sub-apertures. Then, based on the gradient interval, each sub-aperture is spliced to form a phase gradient of the synthetic aperture:

$$\widehat{\dot{{\varphi }_e}}\left(k,m\right)=\widehat{\dot{{\varphi }_e}}\left(k,m\right)-\mathsf{\Delta }{\widehat{\dot{{\varphi }_e}}}_{k-1,k},$$

(18)

where $k=\mathrm{2,3},\dots ,K$, and $m=1,\dots \dots ,L_p$. It is equivalent to completing the removal of the relative phase linearity term between the scattering points and unifying the linear phase error. Finally, the phase gradient of the overlapping parts of each sub-aperture is averaged to obtain the full aperture phase gradient estimation $\widehat{\dot{{\phi }_e}}$along the entire azimuth direction, and the gradient constant term is removed, that is, the uniform linear phase error is removed:

$$\widehat{\dot{{\varphi }_e}}\left(m\right)=\widehat{\dot{{\varphi }_e}}\left(m\right)-{\displaystyle \frac{1}{M_a}}\sum _{i=1}^{M_a}\widehat{\dot{{\varphi }_e}}\left(i\right).$$

(19)

The actual estimate is not smooth, and glitches will occur due to the low signal-to-noise ratio, so smooth filtering is required to filter out burrs. Finally, the phase error of the entire azimuth direction is obtained by phase integration:

$$\widehat{{\varphi }_e}\left(m\right)=\sum _{i=1}^m\dot{{\varphi }_e}\left(i\right).$$

(20)

Finally, the sub-image needs to be compensated to obtain the feature sub-image after this iteration:

$${\mathbf{I}}_0={\mathrm{I}\mathrm{F}\mathrm{F}\mathrm{T}}_{\mathrm{a}}\left[FF{T}_a\left({\mathit{S}}_{\mathit{f}\mathit{e}\mathit{a}}^{\prime }\cdot \widehat{{\varphi }_e}\left(m\right)\right)\cdot \mathit{exp}\left\{-j\mathit{\varphi }\left(f_m,R_k\right)\right\}\right].$$

(21)

Since both the linear phase term and the APE are corrected to a certain extent, the focus of each scattering point will increase and the position will change, so the scattering point set needs to be updated. As a rule of thumb, the scattering point position changes within a few tens of pixels, so the method of updating the scattering point set in this paper is as follows:

$$\mathsf{\Delta }{m}_k=argmax\left({\mathit{I}}_0\left(k,m\right)\cdot rec{t}_w\left(m\right)\right)-{\displaystyle \frac{L_p}{2}},$$

(22)

$$m_k=m_k+\Delta m_k.$$

(23)

After updating the azimuth positions of all scattering points sequentially, the feature sub-image undergoes cyclic shifting to align the brightest spot with the azimuth center, updating the feature sub-image. In general, after 6–8 iterations, the phase error estimation results converge.

Figure 10 illustrates the extracted feature sub-images, phase error gradients, and aggregation effects from measured data, preliminarily validating the effectiveness of the method proposed in this paper. Detailed experiments and analyses are presented in Chapter 5.

4. Architecture Design and Implementation

In Section 3, we propose the FSI-SPGA algorithm, which ensures the precision and robustness of the QW-SPGA algorithm while reducing the computational complexity to the order of magnitude of a single QW-SPGA iteration. This makes the FSI-SPGA algorithm suitable for deployment on an FPGA. However, in real-time imaging applications for small UAV SAR, autofocusing is only one aspect of the processing workflow. The onboard system must complete multiple tasks, including MoCo, SAR imaging, autofocusing, and target recognition. Under strict SWaP constraints, this paper presents a real-time imaging and autofocusing architecture for small UAV SAR based on an MPSoC. This subsection provides an overview of the hardware architecture of the digital processing system and details the deployment strategy for the FSI-SPGA algorithm.

4.1. System Hardware Architecture

As shown in Figure 11, the proposed architecture employs dynamic partial reconfiguration (DPR) to partition the FPGA into static and dynamic regions. The static region, which remains unchanged after power-up, includes data interfaces and control logic for the DAC/ADC and peripherals, SAR data transmission and preprocessing, ARM-FPGA data interaction, and reconfigurable drivers. The static region transmits bitstream files to the dynamic region for logic reconstruction and interacts with the dynamic region modules via the AXI high-speed bus. The dynamic region can be reconfigured within milliseconds, allowing hardware resources to be repurposed for different processing tasks. Time-multiplexing of resources enhances utilization and accelerates multiple non-simultaneous functions, thereby improving overall processing efficiency.

The architecture features two DDR memory sets: DDR-PS on the ARM side and DDR-PL on the FPGA side. DDR-PL is memory-mapped as a FIFO for data buffering, which is controlled by the Memory Interface Generator (MIG) within the FPGA. It caches the transmitted waveforms and preprocessed data. DDR-PS is divided into host memory for ARM data caching and device-shared memory for dynamic FPGA data caching and ARM-FPGA data exchange. The ARM can transfer data between the host memory and device shared memory, while the FPGA accesses the device shared memory via the AXI-HP bus for high-speed data transfer.

Several key issues must be addressed for the efficient implementation of the FSI-SPGA algorithm on this hardware architecture: (1) decomposition of the algorithm; (2) mapping of the decomposed processing steps onto the ARM/FPGA framework; and (3) design of hardware acceleration cores within the FPGA’s dynamic region. The subsequent subsections provide a detailed exposition of these issues.

4.2. Algorithm Decomposition and Operator Mapping

Section 3 details the FSI-SPGA algorithm to explain the principles of the algorithm. To concretely describe the algorithm’s computational processes and characteristics and to guide the design of its deployment on ARM/FPGA, this paper presents a computation graph primarily composed of matrix/vector compute blocks, as shown in Figure 11. The graph is created based on the following rules:

Each compute block represents a single operation on the data matrix or vector.

A common matrix/vector-level computational IP is treated as a compute block.

The data dependencies between the blocks can be explicitly indicated.

To elucidate the characteristics of the computational data flow and the attributes of the intermediate data, the graph includes data blocks, parameter blocks, and scatterer sets alongside the computational process blocks. The entire computational flowchart of the FSI-SPGA is divided into two parts: APE estimation and image APE correction.

The computational graph illustrates the entire process and data flow of the FSI-SPGA algorithm and serves as an input for mapping the algorithm onto the ARM + FPGA heterogeneous architecture. When mapping the various computational blocks from the graph to the processors, it is essential to first identify their computational characteristics. Computational processes can be categorized into three types based on their characteristics: compute-intensive, data-intensive, and control-intensive. Compute-intensive processes have performance bottlenecks due to computation; data-intensive processes have performance bottlenecks due to IO access; and control-intensive processes have performance bottlenecks due to complex control. For compute-intensive blocks, the performance can be enhanced by designing specific hardware acceleration cores on the FPGA. For data-intensive blocks, IO operations can be reduced by implementing multi-level hardware pipelines on the FPGA or utilizing ARM’s cache for memory access optimization. Control-intensive processes are challenging to accelerate in parallel and provide limited acceleration advantages. However, they are essential to the overall computational framework and are therefore more appropriately executed on an ARM. Based on these principles, the final mapping results of the computational blocks in the FSI-SPGA algorithm for the processors are shown in Figure 12.

4.3. Hardware Computing Unit Design Based on FPGA

4.3.1. FPGA Hardware Accelerator Model

In accordance with the computational graph and operator mapping scheme, the ARM end handles the parameter computation, data scheduling, and data flow configuration. Meanwhile, the FPGA harnesses its abundant and flexible hardware resources to function as an accelerator that is specifically designed for high-throughput data processing. Based on the overall hardware architecture of the system, as shown in Figure 13a, this paper employs a dataflow-driven hardware acceleration model. The FPGA retrieves data from the device memory through Direct Memory Access (DMA) and converts this data into a data stream. This stream is processed via dedicated multi-stage pipelined accelerator cores, achieving high-throughput parallel processing. The processed data stream is then written back to the device memory. For the aforementioned acceleration model, the processing latency of a single accelerator is determined by the ratio of the data stream to the data-stream bandwidth. This latency is influenced by both the memory access bandwidth and the processing bandwidth of the accelerator core. Consequently, the processing latency ${\tau }_s$ can be assessed using the following formula:

$${\tau }_s={\displaystyle \frac{N_m}{\mathit{min}\left(B_m\eta , \frac{f_{ker}{b}_{ker}}{D}\right)}},$$

(24)

where $N_m$ represents the amount of data to be processed, $B_m$ denotes the theoretical peak bandwidth of memory, $\eta$ is the memory access efficiency, $f_{ker}$ is the operating frequency of the accelerator core, and $b_{ker}$ is the bus width of the accelerator core. The pipeline interval $D$ refers to the interval between stages in the accelerator’s pipeline. As shown in Figure 13b, accelerators with the same operating frequency can have different hardware structures, resulting in varying pipeline intervals. The pipeline interval is inversely proportional to the processing bandwidth of the accelerator core.

For the entire task, as shown in Figure 14, there are additional considerations beyond the processing time of multiple accelerator cores. These include the data transfer time between the host memory and device memory and the switching time between different accelerators. The data transfer time $t_m$ in memory is primarily dependent on the volume of data and the effective read/write bandwidth of the memory. The switching delay $t_{rec}$ between accelerator cores requires a discussion of two switching modes. Mode 1 involves updating the Bitstream in the dynamic region of the FPGA, a process that requires additional time. Mode 2 refers to reconfiguring the data flow relationships between kernels within the dynamic region, which requires the presence of identical kernels across different accelerators. Therefore, when accelerating the entire processing task with this accelerator model, the delay $T$ can be calculated as follows:

$$T=2{\tau }_m+\sum _{i=1}^K{\tau }_s^i+\sum _{i=1}^K{\tau }_{rec}^i{p}^i,$$

(25)

where ${\tau }_s^i$ represents the data stream delay for the ii-th subtask, ${\tau }_{rec}^i$ denotes the delay for updating the bitstream for the i-th subtask, and $p_i$ indicates the switching mode for the i-th subtask, where $p^i=1$ signifies switching mode 1, and $p^i=0$ signifies switching mode 2.

To reduce the overall task delay, this paper designs an architecture with high memory access efficiency, small pipeline intervals, and high operating frequency from the perspective of a single accelerator to enhance the effective processing bandwidth. From the perspective of multiple accelerators, a reconfigurable accelerator is designed to minimize the additional time consumed by bitstream updates. By combining the computational graph of the FSI-SPGA algorithm and the design principles of hardware accelerators, this paper divides the functionality of the FPGA hardware accelerator into two parts: one part involves 2D-CFAR detection, which pertains to two-dimensional memory access operations, and the other part includes a series of computational processes such as azimuth de-skewing, azimuth inverse compression, azimuth compression, and phase compensation.

4.3.2. D-CFAR Hardware Accelerator

2D-CFAR detection is commonly used for target detection within range-doppler matrices. However, in these applications, the matrices to be detected are typically small and can be efficiently stored in a high-speed cache for processing on a frame-by-frame basis. In the FSI-SPGA algorithm, 2D-CFAR detection is primarily employed for the coarse selection of scattering points, which often requires the processing of large matrices stored in the DDR. Traditional 2D-CFAR detection necessitates two-dimensional matrix summation operations, which involve a significant amount of non-contiguous memory access. The efficiency of non-contiguous memory access in DDR is typically an order of magnitude lower than that of contiguous memory access, thereby limiting its data processing performance. To address this issue, this paper decouples the two-dimensional matrix summation into two one-dimensional summations:

$$S_{i,j}=\sum _{k=i-N}^{k=i+N}\sum _{l=j-N}^{l=j+N}{I}_{k,l}⟺L_{k,j}=\sum _{l=j-N}^{l=j+N}{I}_{k,l}, S_{i,j}=\sum _{k=i-N}^{k=i+N}{L}_{k,j},$$

(26)

where $\mathbf{I}$ represents the matrix to be processed. Based on this decoupling result, the two one-dimensional sliding summations are converted into two one-dimensional add-subtract sliding windows:

$$L_{k,j}=L_{k,j-1}-I_{k,j-N-1}+I_{k,j+N},$$

(27)

$$S_{i,j}=S_{i-1,j}-L_{i-N-1,j}+L_{i+N,j}.$$

(28)

As depicted in Figure 15, after the ARM side completes the computation of the initial values, the FPGA can process the horizontal and vertical one-dimensional add-subtract sliding windows in parallel through a Ping-Pong interleaved structure. During the execution of the Ping operation, data from the DDR is continuously input into Buffer 1 by rows and subjected to horizontal add-subtract sliding window summation, while Buffer 2 undergoes vertical add-subtract sliding window summation. By utilizing multiple add-subtract sliding window units for parallel processing, the memory access efficiency can be approximated as $B_m\eta \approx {\displaystyle \frac{f_{ker}{b}_{ker}}{D}}$. Conversely, during the Pong operation, the roles of Buffer 1 and Buffer 2 are exchanged. In this ping-pong structure, to ensure full pipeline operation of the ping-pong mechanism, it is necessary to guarantee that the delays of the Ping and Pong operations are identical, that is, $T_{ping}=T_{pong}$.

The add-subtract sliding summation pipeline unit in Figure 15a uses fixed-point numbers instead of floating-point numbers because the latter does not meet the timing requirements. To effectively use the wide dynamic range of SAR images, data mean normalization is performed first, followed by quantization with 24-bit fixed-point numbers. This provides a dynamic range of about 144 dB, which is sufficient for practical test accuracy. By using fixed-point arithmetic, the clock of the accelerator can reach 300 MHz. Utilizing this accelerator enables the rapid computation of the computation unit matrix and the protection unit matrix, thereby enhancing the data processing efficiency of the entire 2D-CFAR detection process.

4.3.3. Reconfigurable Matched Filtering (RMF) Hardware Accelerator

In the FSI-SPGA algorithm, there exists another category of computations that can be reconstructed from various combinations of vector-level computation blocks, such as FFT/IFFT, Vector Multiple (VcMul), and Phase Gradient Calculation (PGC). These computations are limited to operations in the azimuth direction, meaning that most data accesses are contiguous and involve repetitive computational blocks. For ARM, redundant instructions and limited computational resources restrict the performance of these computations. This paper leverages the high throughput and high parallelism of FPGAs by assembling data processing procedures into data streams using pre-built computational kernels. This reduces the number of times the data are read from the DDR, processed, and written back to the DDR, thereby enhancing the processing performance. For multiple processing procedures corresponding to multiple data streams, to eliminate additional reconfiguration delays, as shown in Figure 16, data output selectors (DS) and data input multiplexers (MUX) are added. By controlling the data flow structure through multiple data stream nodes, a high resource reuse rate is achieved, enabling the high-performance implementation of multiple computational functions. This paper refers to this accelerator as a reconfigurable matched-filtering hardware accelerator, which can be configured into four modes, each corresponding to one of the four computational processes.

In the RMF accelerator, the phase calculation in Equation (12) does not involve extremely large numbers; therefore, the fractional part of the floating-point numbers provides sufficient precision. The dynamic range of floating-point numbers, from ${10}^{-45}$ to ${10}^{38}$, is more than adequate for the amplitude dynamic range of SAR images. Therefore, all the data in this accelerator is in floating-point format. Although using lower-bit fixed-point numbers could enhance precision and reduce resource usage, the significant engineering effort required means that this was not pursued in this paper.

5. Experiments and Results

To validate the effectiveness of the proposed strip SAR real-time autofocus software and hardware solution in this paper, experimental data were collected based on a Ku-band UAV-mounted SAR system, and autofocus processing was performed. Additionally, the proposed embedded hardware processing framework was deployed and tested on the ZCU102 platform. This section presents the SAR system, the results of the algorithm processing experiments, and the performance evaluation of the FPGA hardware accelerator from three aspects.

5.1. SAR System

To verify the proposed algorithm, an SAR imaging experiment was conducted on a multirotor UAV based on the Ku-band SAR system developed by the Aerospace Information Innovation Institute of the Chinese Academy of Sciences, as shown in Figure 17. The SAR system includes a common antenna for the transceiver and receiver, RF front-end, digital processing machine, lightweight INS/GPS, and other key components, with a total weight of 6 kg. It uses a chirp pulse system for frontal and side-view strip SAR imaging, achieving a range resolution of 0.3 m and an azimuth resolution of 0.3 m. The specific parameters are listed in

Table 1. Main System parameters for the experiment.

Symbol	Parameters	Values (Units)
	Imaging Mode	Stripmap
	Waveform	Chirp pulses
	Band	Ku
$B$	Frequency Bandwidth	480 MHz
${\theta }_a$	Azimuth Beam Width	6°
${\theta }_i$	Incident Angle	82°
$F_s$	Sampling Rate	480 MHz
$H$	Flying Height	500 m
$v$	Platform Velocity	12 m/s

. For such small multi-rotor UAVs, high-frequency vibrations and airflow interference during flight can introduce high-frequency motion errors, causing image defocus, as shown in Figure 18a. The following subsections highlight the advantages of the proposed algorithm from the perspectives of algorithm accuracy and algorithm efficiency.

5.2. Comparison of Algorithm Accuracy

After obtaining the raw SAR echo data and the corresponding GPS/INS data, initial MoCo is applied to the raw data, and then the defocused SAR image is obtained by ωK, as shown in Figure 18a. The number of azimuth points in the image is 4096, the number of distance points is 12,288, the number of azimuth synthetic aperture points is 512, and the theoretical resolution is 0.25 m. However, motion errors cause significant resolution loss and blurring of the image. The image entropy of the entire image is 5.48. Subsequent processing using the SPGA, QW-SPGA, and FSI-SPGA methods reduces the image entropy to 5.13, 4.99, and 4.91, respectively, as shown in Figure 18b–d. In terms of the overall image focusing quality, FSI-SPGA and QW-SPGA perform similarly, and both surpassed the traditional SPGA algorithm.

As shown in Figure 19 and Figure 20, regions 1 and 2 in Figure 18 are enlarged. Figure 19a shows the image after preliminary MoCo processing. Figure 19b shows the results after applying the SPGA algorithm to SAR images that undergo MoCo processing for eight iterations. Although there is some improvement in defocusing, roads and buildings still exhibit defocusing. Figure 19c,d show the results after processing with the QW-SPGA algorithm (eight iterations) and the FSI-SPGA algorithm, respectively. Both achieve high-quality focusing on scenes such as houses, roads, and fields, significantly improving the image texture clarity.

To evaluate the image quality more intuitively and quantitatively, some targets from area 2 were selected for azimuth slice analysis, and the four targets to be analyzed were circled in red in Figure 20d. The azimuth slices corresponding to the three-point targets are shown in Figure 20e–h, and the calculation results of the resolution, peak sidelobe ratio, and integral sidelobe ratio are listed in

Table 2. Experimental results for quantitative analysis of focusing accuracy.

Autofocus Algorithm	Strong Scatterer	Azimuth PSF			Full Image
		Res. (m)	PSLR (dB)	ISLR (dB)	Entropy	Contrast	Runtime (s)
Initial MoCo	P1	0.33	−1.00	6.26	5.48	4.33	6.21
	P2	1.23	−4.21	−2.66
	P3	0.40	−1.68	4.93
	P4	0.95	−6.00	−1.08
SPGA (8 iterations)	P1	0.46	−4.42	−1.03	5.13	6.25	95.6
	P2	0.38	−9.74	−5.94
	P3	0.44	−7.88	−7.18
	P4	0.36	−13.80	−11.21
QW-SPGA (8 iterations)	P1	0.28	−12.44	−10.38	4.91	7.19	83.4
	P2	0.28	−17.48	−9.20
	P3	0.31	−10.91	−9.10
	P4	0.28	−16.91	−11.41
FSI-SPGA (1 iteration)	P1	0.30	−10.82	−7.82	4.98	7.16	6.12
	P2	0.29	−13.18	−8.47
	P3	0.29	−17.51	−10.68
	P4	0.28	−14.21	−11.61

. As shown in Figure 20 and Table 2, when comparing the target slice index, image entropy, and contrast—indicators for assessing the overall image quality—the performance of the FSI-SPGA algorithm is close to that of the QW-SPGA algorithm, and both outperform the traditional SPGA algorithm. Notably, the processing time required for FSI-SPGA is equivalent to only one iteration of the SPGA and QW-SPGA algorithms.

5.3. Algorithm Robustness Verification

To further test the robustness of the algorithm, multiple datasets are used for validation. Section 5.2 shows that the accuracy of the FSI-SPGA algorithm is close to that of the QW-SPGA algorithm, and both are better than that of the traditional SPGA algorithm. Therefore, this subsection only compares the image entropy, contrast, and processing time of the FSI-SPGA and QW-SPGA algorithms. The experimental results are presented in Figure 21 and

Table 3. Quantitative analysis results of autofocus methods.

Autofocus Algorithm	SAR Image	Entropy	Contrast	Runtime (s)
Initial MoCo	D1	6.84	10.71	3.1
	D2	5.46	27.59	3.2
	D3	6.22	21.03	3.3
	D4	6.10	11.44	3.2
QW-SPGA (8 iterations)	D1	6.62	35.15	14.5
	D2	5.07	61.12	14.2
	D3	6.10	29.01	15.1
	D4	6.06	13.59	13.9
FSI-SPGA (1 iteration)	D1	6.62	33.99	3.3
	D2	5.10	54.93	3.4
	D3	6.10	27.70	3.6
	D4	6.05	17.61	3.1

. In the three images D1, D2, and D3, which have high-quality scatterers, the image-focusing quality of the QW-SPGA and FSI-SPGA algorithms is significantly improved. For the grassy area of image D1 and the lake-island area of image D4, where there are not enough high-quality scatterers, the two algorithms do not significantly improve the image focusing quality. As shown in Table 3, the FSI-SPGA algorithm is close to the QW-SPGA algorithm in terms of image entropy and contrast, but it is nearly four times faster. These experiments show that the proposed FSI-SPGA algorithm has good processing efficiency and robustness in handling defocused SAR images with high-quality scatterers.

5.4. FPGA Hardware Accelerator Verification Experiments

To further verify the proposed hardware architecture and FPGA accelerator model, as shown in Figure 22a, the proposed FPGA hardware accelerator is implemented based on the computing core circuit of the ZCU102 evaluation board. The layout and routing results of the two key accelerators in Vivado are shown in Figure 22b,c, respectively. Their corresponding hardware resource utilization is presented in

Table 4. The resource usage of FPGA hardware.

Area	Accel	Clock	LUT	FF	BRAM	DSPs
Static Region	/	300 MHz	2591	6109	64	26
Dynamic Region	2D-CFAR		18,233	26,286	128.5	14
	RMF		82,982	129,400	472.5	379

.

The acceleration of the FSI-SPGA algorithm was implemented on the ZCU102 embedded platform. This paper used three architectures: ARM, CPU, and ARM + FPGA, to process data collected by the SAR system. As shown in Figure 23b–d, the processing results of these architectures are essentially the same. However, due to differences in the calculation accuracy of ARM/CPU instructions and FPGA-based IP calculations, minor discrepancies exist. Despite these, the image focusing quality is still significantly improved.

The performance testing results of the algorithm on hardware platforms are presented in

Table 5. The performance test results of the algorithm on a hardware platform.

Platform	Processor Model	Algorithm	Image Size (pixel × pixel)	Runtime (s)	Power (W)	PPR (pixels/J)
ARM	AMD ZU9EG (16 nm)	QW-SPGA	4 K × 12 K	566.4	2.5	37,026
			8 K × 12 K	1305.2		32,135
		FSI-SPGA	4 K × 12 K	83.4		317,630
			8 K × 12 K	162.9		325,230
CPU	AMD 5800 H (7 nm)	QW-SPGA	4 K × 12 K	56.5	30	29,694
			8 K × 12 K	130.3		25,751
		FSI-SPGA	4 K × 12 K	7.3		229,824
			8 K × 12 K	16.8		199,728
MPSoC (ARM + FPGA)	AMD ZU9EG (16 nm)	FSI-SPGA	4 K × 12 K	6.12	6.9	1,191,902
			8 K × 12 K	6.36		2,293,849

, which primarily compares the processing time, power consumption, and Performance Power Ratio (PPR) of the algorithm across different architectures. In this paper, PPR is defined as the ratio of imaging points to the energy consumed. Compared with the test results on the ARM platform, the FSI-SPGA algorithm reduces the processing delay by nearly six times and increases the PPR by nearly nine times. When comparing the performance test results between the ARM + FPGA and ARM platforms, the use of the FPGA hardware acceleration model and accelerator proposed in this paper leads to a nearly nine-fold reduction in latency and a nearly two-fold increase in PPR at 4 K × 12 K imaging points, and a nearly twenty-five-fold reduction in latency and a nearly six-fold increase in PPR at 8 K × 12 K imaging points. Compared with CPUs at advanced process nodes and high performance, the proposed solution in this paper exhibits a relatively modest improvement in processing performance but achieves a significant reduction in power consumption, resulting in an order-of-magnitude increase in PPR.

These results indicate that the FSI-SPGA algorithm demonstrates significant performance improvements on both the ARM and ARM + FPGA platforms, particularly in terms of the processing delay and PPR. The use of an FPGA hardware acceleration model and accelerator can significantly enhance the algorithm’s processing speed and energy efficiency, which is crucial for applications requiring the rapid processing of large amounts of data, such as real-time image processing and machine vision. This performance enhancement is likely attributed to the parallel processing capabilities of FPGAs and the optimized design of hardware accelerators, which can utilize hardware resources more effectively to reduce the time and energy consumption required for data processing.

6. Discussion

6.1. Analysis of Algorithm Computational Complexity and Limitations

According to Figure 3b, the theoretical calculation time of the proposed FSI-SPGA algorithm can be estimated as

$$\begin{array}{l}{t}_{FSI-SPGA}=t_{cp}+t_{inac}+t_{subes}\cdot N_{iter}+t_{co},\\ =O\left(MN\cdot ({4\mathit{log}}_{2}M+3+N_{ref})+N_{iter}K{L}_p\cdot \left(4{\mathit{log}}_2{L}_p+5\right)\right),\end{array}$$

(29)

where $t_{subes}=O\left(K{L}_p\cdot \left(4{\mathit{log}}_2{L}_p+5\right)\right)$ represents the time taken to estimate the error of the feature subgraph, $L_p$ represents the synthetic aperture points, and the meaning of the other variables is the same as that of Equation (5). Comparing Equations (5) and (29), it can be found that the algorithm proposed in this paper has no image iteration, but is replaced by feature sub-image iteration with $t_{subes}\ll t_{co}$, which greatly reduces the complexity of the algorithm, and with the increase of image size, the computational efficiency is improved more obviously, and the computational complexity is on the same order of magnitude as the azimuth compression process of SAR imaging, which can meet the real-time processing requirements. In this paper, the processing time of the two algorithms on multiple SAR images of different sizes is tested, and the results are shown in Table 5, which verifies that the algorithms have high real-time performance and strong robustness.

The FSI-SPGA algorithm is a PGA-type algorithm. It works well in scenes with isolated strong scatterers of high quality. However, it is not suitable for areas like grasslands or sea rocks, where strong scatterers are absent. Moreover, this algorithm can only correct the phase errors. As pointed out in Section 2.2, when the GPS/INS system precision is low, causing range migration errors, other algorithms for range migration compensation [36] should be applied first. In our experiment, the equivalent backscattering coefficient of the system was maintained above 20 dB. The proposed algorithm exhibited robust performance on the test data of this system. However, it may fail to accurately estimate phase errors when the signal-to-noise ratio is too low.

6.2. Analysis of Computational Performance on Hardware Architectures

Compared with low-power general-purpose processors like ARM, FPGAs come with flexible, schedulable hardware resources that can support high levels of parallel processing, and they almost entirely eliminate redundant instruction overhead. Therefore, enhancing performance through the use of Single Instruction Multiple Data (SIMD) architectures is relatively easier for FPGAs than for ARM. On the one hand, for FPGAs, non-sequential memory access can increase the data access bandwidth, which limits the performance of the computational capabilities. On the other hand, complex computational components can also lead to resource redundancy and increased power consumption. To address these two issues, this paper first constructs a computational graph of the algorithm, enabling an assessment of the computational characteristics of each process within the algorithm. This allows for an accurate description of task computational features and the extraction of hotspot computations within the FSI-SPGA algorithm that require FPGA acceleration, thus avoiding the occupation of FPGA resources by computations with low usage frequencies. Furthermore, based on a pipelined FPGA acceleration model in which data flow from DDR through multiple acceleration cores and back to DDR, two accelerators were designed: a 2D-CFAR and a reconfigurable matching filter. These designs maximize memory access efficiency and minimize pipeline intervals, achieving the expression $\mathit{max}\left(\mathit{min}\left(B_m\eta , {\displaystyle \frac{f_{ker}{b}_{ker}}{D}}\right)\right)$. Subsequently, a reconfigurable data flow structure for repeated computational units is designed to realize high resource reuse. This ensures processing delay while reducing resource redundancy and processing power consumption, ultimately leading to a multi-fold enhancement in PPR, as shown in Table 5.

7. Conclusions

Owing to SWaP limitations, small UAVs cannot carry high-precision GPS/INS systems or large processors. The traditional SPGA algorithm struggles to ensure accuracy and requires multiple iterations, which fail to meet the demands of real-time autofocus processing. To address this issue, this paper proposes a non-iterative FSI-SPGA autofocusing algorithm, verified by measured data, which significantly reduces the computational cost while maintaining accuracy. Additionally, a high-efficiency hybrid architecture combining dataflow reconfigurability and dynamic partial reconfiguration was designed based on an ARM + FPGA platform tailored to the computational characteristics of the FSI-SPGA. For 4 K × 12 K SAR images, the FSI-SPGA algorithm demonstrated a 6× increase in processing efficiency compared with traditional methods. The high-efficiency reconfigurable ARM + FPGA architecture processed the algorithm in 6.02 s, achieving 12× the processing speed and 3× the energy efficiency of a single low-power ARM platform.

Nevertheless, the proposed solution in this paper has some limitations. First, the algorithm is not applicable to scenarios lacking isolated strong scatterers. Second, regarding hardware architecture, due to engineering complexities, there is no discussion or optimization of the data precision requirements for each processing step within the algorithm, nor is there an exploration of the effects of new devices on signal processing.

With the rapid development of microelectronics technology, innovative solutions for real-time radar signal processing have been developed. The author hopes that this article will attract the attention of the industry to the design of radar signal hardware processing architectures. In the future, new solutions that integrate software and hardware could promote the advancement of radar technologies.