Burned Area Detection in the Eastern Canadian Boreal Forest Using a Multi-Layer Perceptron and MODIS-Derived Features
Abstract
1. Introduction
2. Materials and Methods
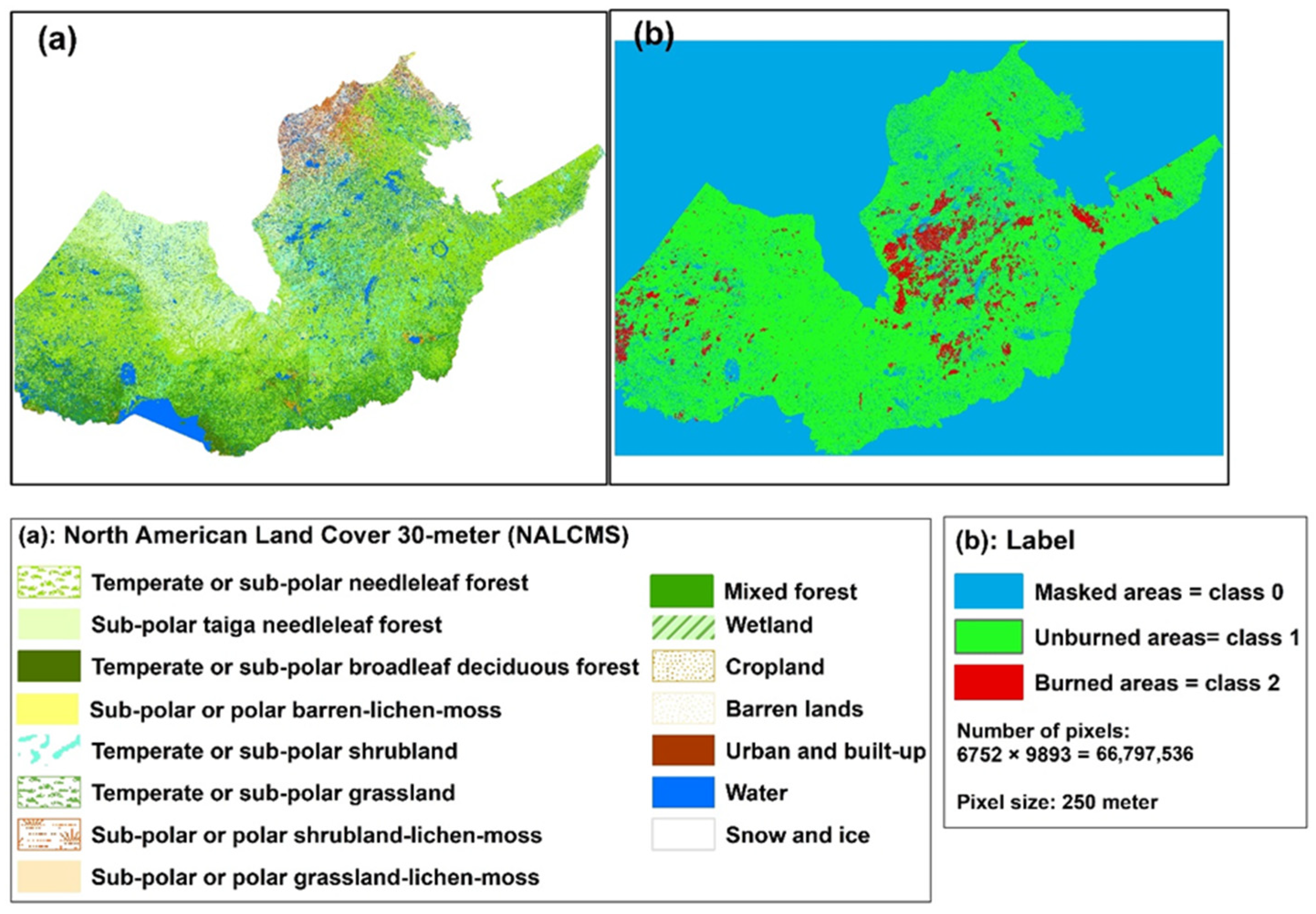
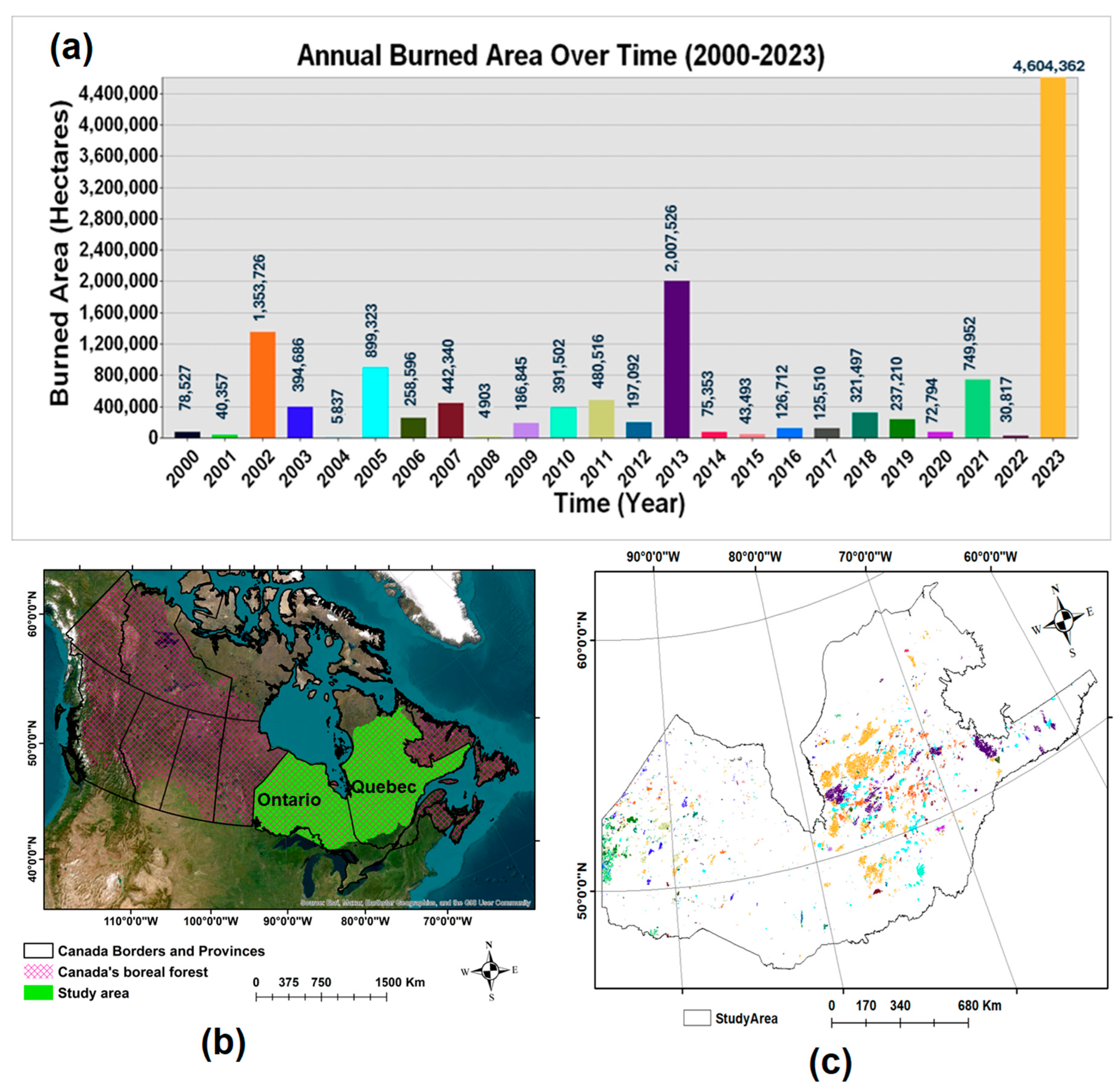
2.1. Study Area
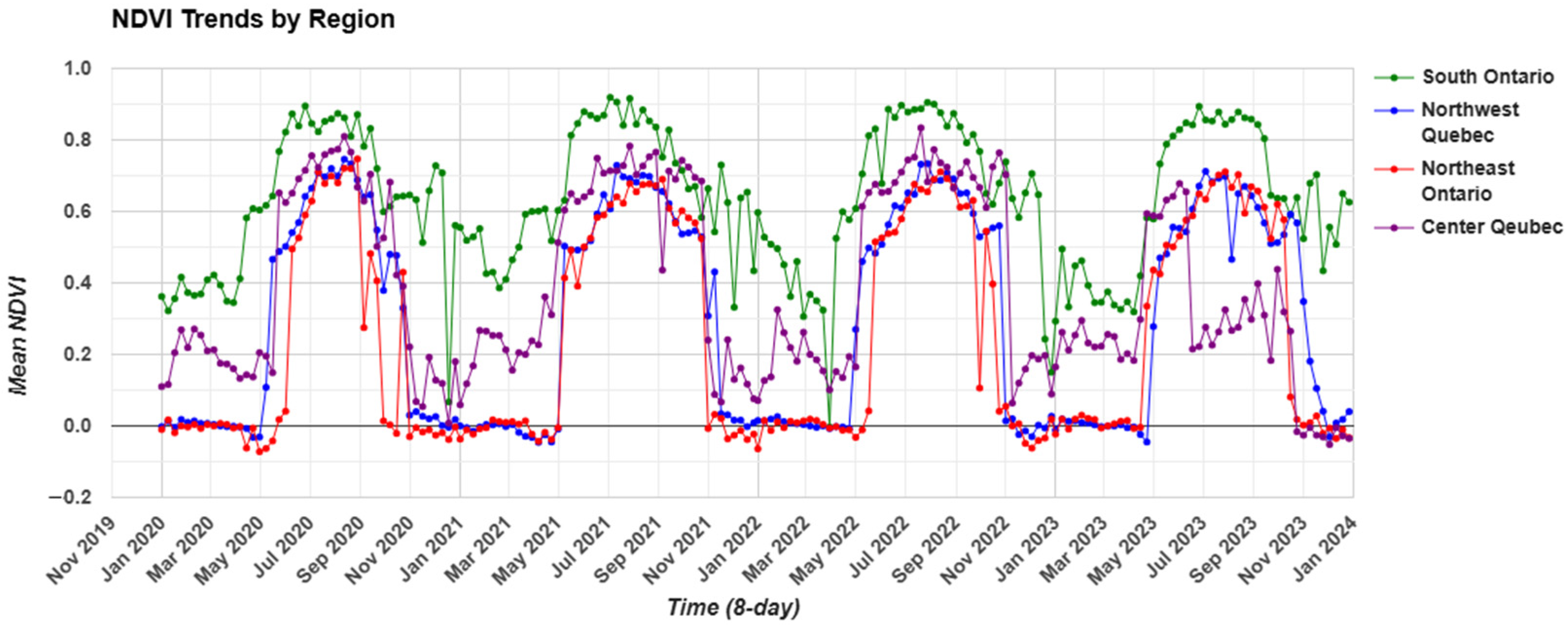
Seasonal Vegetation Dynamics and Wildfire Activity in the Eastern Canadian Boreal Forest
2.2. Source Materials
2.3. Spatial Data Extracted from the Dataset Spanning from 2000 to 2023
2.4. Preprocessing
2.5. Model Selection and Performance Evaluation (2016–2018)
2.6. Training and Hyperparameter Tuning of the Multilayer Perceptron (MLP) Model
2.6.1. Hyperparameter Tuning and Selection
2.6.2. Cross-Validation for Evaluating Model Robustness and Performance on Unseen Test Data
2.7. Assessment of MLP Model Performance
3. Results
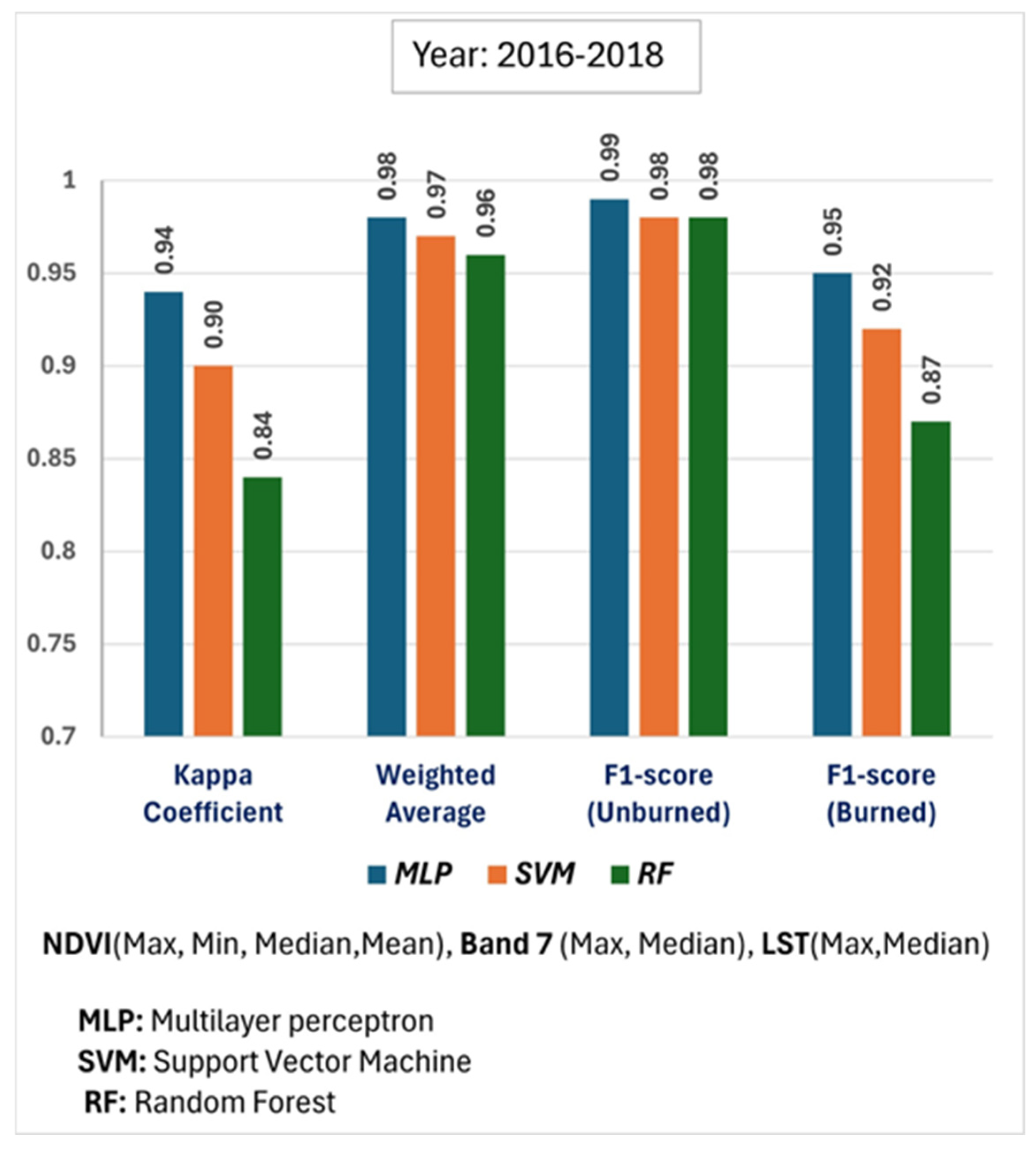
3.1. Comparative Model Performance (2016–2018)
3.1.1. Comparison of Performance Metrics Across Machine Learning Models
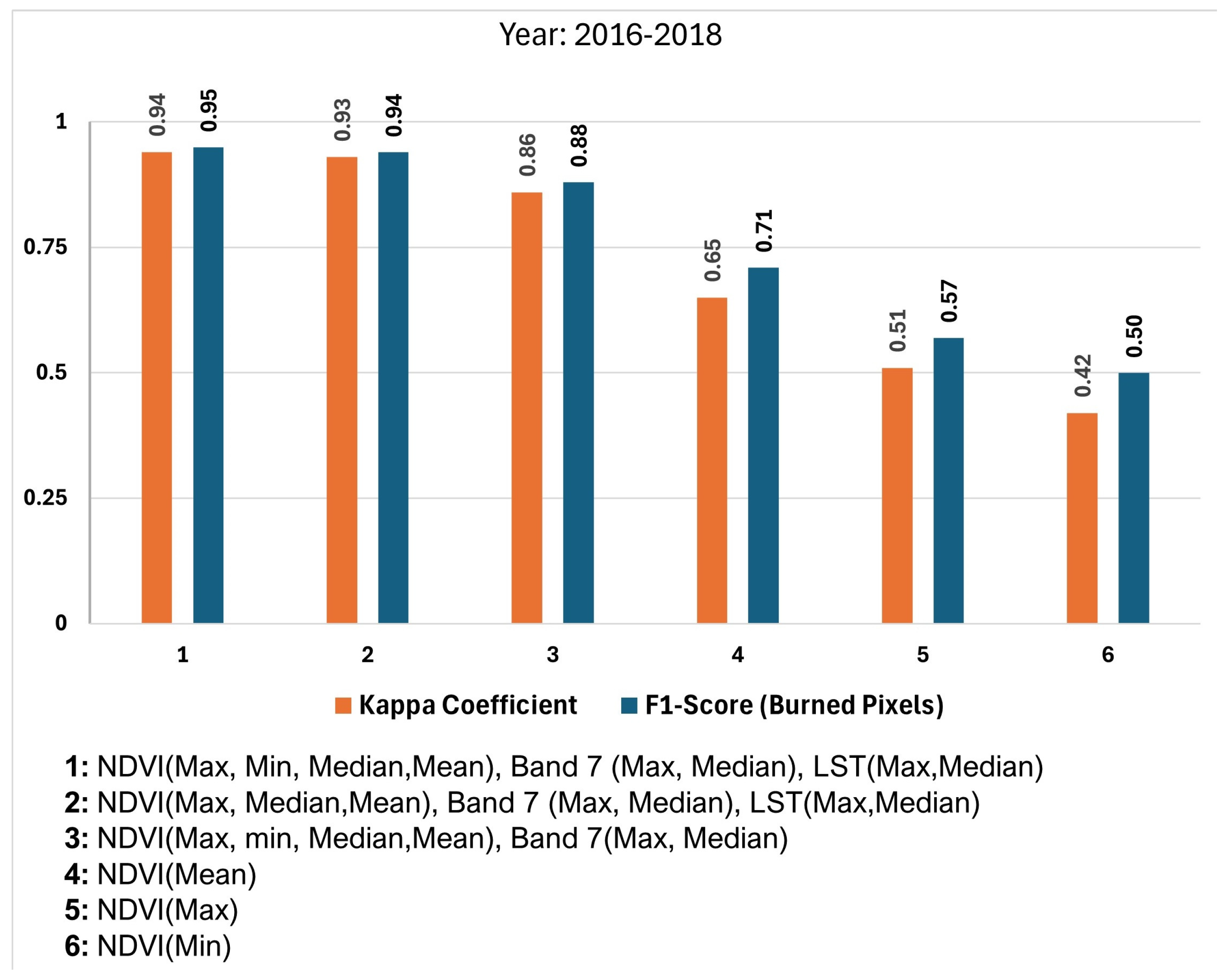
3.1.2. The Importance of Combining Multiple Biophysical Indicators for Accurate Burned Area Detection
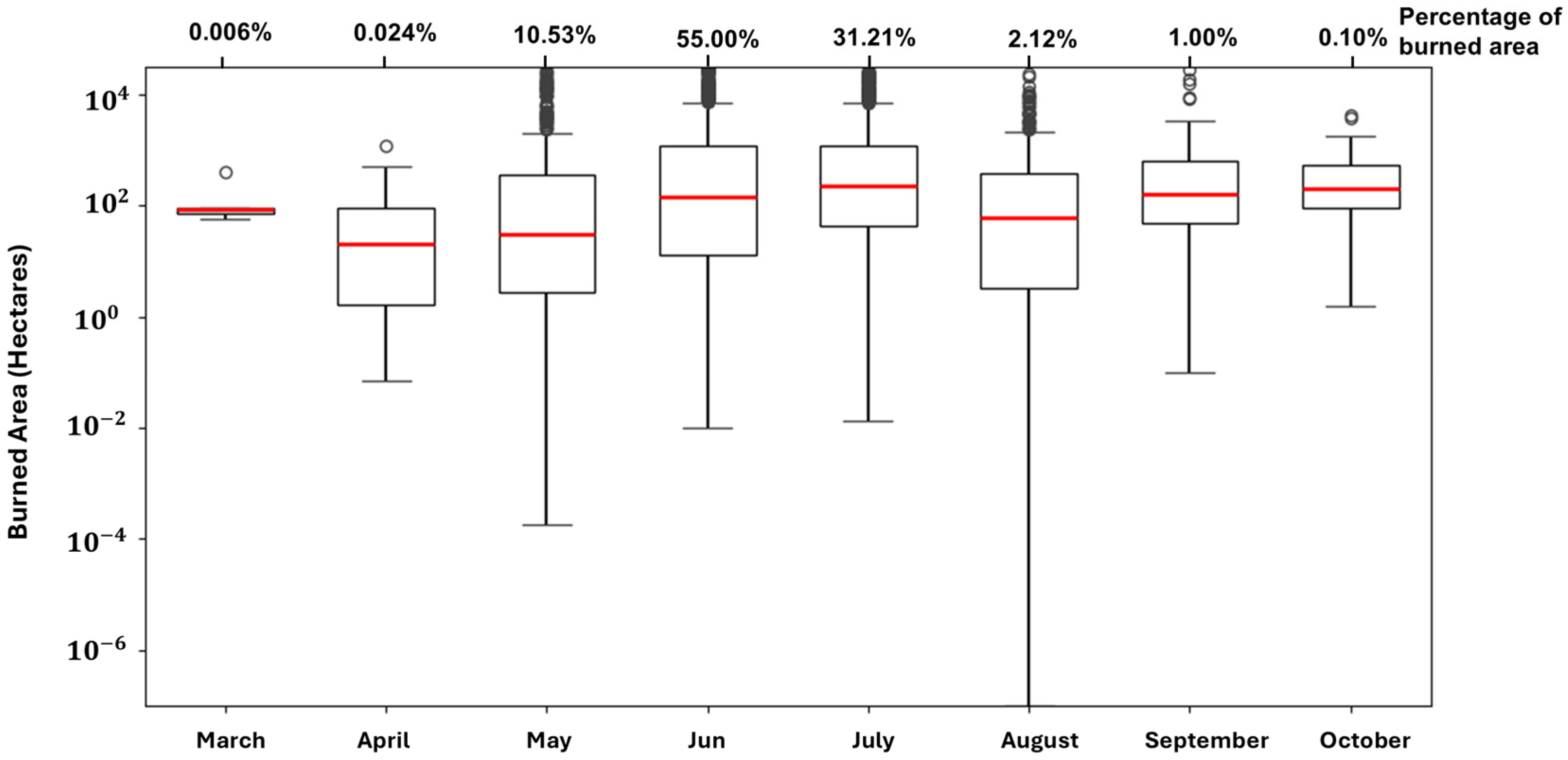
3.2. MLP Model Performance and Evaluation Across the Entire Study Area and Study Period (2000–2023)
4. Discussion
4.1. Comparative Analysis of the MLP Model for Burned Area Detection
4.2. Selecting Statistical Metrics (Max, Min, Mean, Median) for the MLP Model in Burned Area Detection
4.3. Limitations and Future Research Directions
5. Conclusions
- Superior classification performance: The MLP model consistently outperformed Support Vector Machine (SVM) and Random Forest (RF) classifiers in detecting burned areas, even under conditions of significant class imbalance.
- Multi-source feature integration: Combining biophysical indicators—the NDVI, Band 7, and LST—led to substantially higher classification accuracy than using individual features alone, highlighting the importance of integrating vegetation, spectral, and thermal data.
- Model optimization: Careful feature selection, hyperparameter tuning, and the use of deeper architectures with appropriate regularization contributed to improved model stability and predictive performance.
- Generalizability: The model demonstrated consistent and reliable performance across five-fold cross-validation, confirming its applicability for operational burned area mapping.
- Limitations: The 250 m spatial resolution of MODIS may restrict the detection of small fire events or fine-scale burn patterns. Additionally, the MLP model lacks inherent temporal modeling capabilities.
- Future research: Subsequent studies should explore temporal deep learning architectures such as Long Short-Term Memory (LSTM) or Convolutional LSTM (ConvLSTM) to capture dynamic wildfire behavior. Incorporating data from additional sensors such as Sentinel-1 SAR may further improve the detection accuracy, particularly in cloud-prone areas.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DL | Deep Learning |
| GEE | Google Earth Engine |
| HPC | High-Performance Computing |
| MLP | Multilayer Perceptron |
| NALCMS | North American Land Cover Monitoring System |
| NBAC | National Burned Area Composite |
| NDVI | Normalized Difference Vegetation Index |
| RF | Random Forest |
| LST | Land Surface Temperature |
| SVM | Support Vector Machines |
Appendix A
Appendix A.1
Appendix A.2
| Reference | ||||||
|---|---|---|---|---|---|---|
| Class | 1 | 2 | … | Ʃ | ||
| Prediction | 1 | … | ||||
| 2 | … | |||||
| … | … | … | … | … | ||
| … | ||||||
| Ʃ | M | |||||
Appendix A.3

Appendix A.4
| Year | Class 0 (Water/Non-Study) | Class 1 (Unburned) | Class 2 (Burned) |
|---|---|---|---|
| 2000 | 40,410,779 | 26,375,280 | 11,477 |
| 2001 | 40,410,779 | 26,380,309 | 6448 |
| 2002 | 40,410,779 | 26,182,241 | 204,516 |
| 2003 | 40,410,779 | 26,324,314 | 62,443 |
| 2004 | 40,410,779 | 26,385,843 | 914 |
| 2005 | 40,410,779 | 26,253,981 | 132,776 |
| 2006 | 40,410,779 | 26,347,766 | 38,991 |
| 2007 | 40,410,779 | 26,319,596 | 67,161 |
| 2008 | 40,410,779 | 26,386,030 | 727 |
| 2009 | 40,410,779 | 26,359,113 | 27,644 |
| 2010 | 40,410,779 | 26,329,989 | 56,768 |
| 2011 | 40,410,779 | 26,316,363 | 70,394 |
| 2012 | 40,410,779 | 26,357,704 | 29,053 |
| 2013 | 40,410,779 | 26,097,745 | 289,012 |
| 2014 | 40,410,779 | 26,376,832 | 9925 |
| 2015 | 40,410,779 | 26,379,865 | 6892 |
| 2016 | 40,410,779 | 26,370,345 | 16,412 |
| 2017 | 40,410,779 | 26,367,137 | 19,620 |
| 2018 | 40,410,779 | 26,341,623 | 45,134 |
| 2019 | 40,410,779 | 26,346,650 | 40,107 |
| 2020 | 40,410,779 | 26,375,593 | 11,164 |
| 2021 | 40,410,779 | 26,277,629 | 109,128 |
| 2022 | 40,410,779 | 26,382,594 | 4163 |
| 2023 | 40,410,779 | 25,700,600 | 686,157 |
| Combined Labels | 40,410,779 | 24,504,452 | 1,882,305 |
Appendix A.5
- Multilayer Perceptron (MLP):
- Hidden layers: 2;
- Neurons per layer: 100;
- Activation: ReLU;
- Solver: Adam;
- Alpha (L2 penalty): 0.0001.
- Support Vector Machine (SVM):
- Penalty parameter (C): 2;
- Kernel: Polynomial;
- Degree: 3;
- Coef0: 1.
- Random Forest (RF):
- Number of estimators: 200;
- Criterion: Gini;
- Max depth: 10;
- Min samples split: 2.
References
- Flannigan, M.; Stocks, B.; Turetsky, M.; Wotton, M. Impacts of Climate Change on Fire Activity and Fire Management in the Circumboreal Forest. Glob. Chang. Biol. 2009, 15, 549–560. [Google Scholar] [CrossRef]
- Rogers, B.M.; Balch, J.K.; Goetz, S.J.; Lehmann, C.E.R.; Turetsky, M. Focus on Changing Fire Regimes: Interactions with Climate, Ecosystems, and Society. Environ. Res. Lett. 2020, 15, 030201. [Google Scholar] [CrossRef]
- Lee, H.; Calvin, K.; Dasgupta, D.; Krinner, G.; Mukherji, A.; Thorne, P.; Trisos, C.; Romero, J.; Aldunce, P.; Barret, K.; et al. Climate Change 2023: Synthesis Report. In Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- Sayedi, S.S.; Abbott, B.W.; Vannière, B.; Leys, B.; Colombaroli, D.; Romera, G.G.; Słowiński, M.; Aleman, J.C.; Blarquez, O.; Feurdean, A.; et al. Assessing Changes in Global Fire Regimes. Fire Ecol. 2024, 20, 18. [Google Scholar] [CrossRef]
- Brandt, J.P. The Extent of the North American Boreal Zone. Environ. Rev. 2009, 17, 101–161. [Google Scholar] [CrossRef]
- Wang, Y. The Effect of Climate Change on Forest Fire Danger and Severity in the Canadian Boreal Forests for the Period 1976–2100. J. Geophys. Res. Atmos. 2024, 129, 1–20. [Google Scholar] [CrossRef]
- Veraverbeke, S.; Rogers, B.M.; Goulden, M.L.; Jandt, R.R.; Miller, C.E.; Wiggins, E.B.; Randerson, J.T. Lightning as a Major Driver of Recent Large Fire Years in North American Boreal Forests. Nat. Clim. Chang. 2017, 7, 529–534. [Google Scholar] [CrossRef]
- Coogan, S.C.P.; Robinne, F.N.; Jain, P.; Flannigan, M.D. Scientists’ Warning on Wildfire—A Canadian Perspective. Can. J. For. Res. 2019, 49, 1015–1023. [Google Scholar] [CrossRef]
- Hanes, C.C.; Wang, X.; Jain, P.; Parisien, M.A.; Little, J.M.; Flannigan, M.D. Fire-Regime Changes in Canada over the Last Half Century. Can. J. For. Res. 2019, 49, 256–269. [Google Scholar] [CrossRef]
- Villaverde Canosa, I.; Ford, J.; Paavola, J.; Burnasheva, D. Community Risk and Resilience to Wildfires: Rethinking the Complex Human-Climate-Fire Relationship in High-Latitude Regions. Sustainability 2024, 16, 957. [Google Scholar] [CrossRef]
- Xu, Y.; Zhuang, Q.; Zhao, B.; Billmire, M.; Cook, C.; Graham, J.; French, N.H.; Prinn, R. Impacts of Wildfires on Boreal Forest Ecosystem Carbon Dynamics from 1986 to 2020. Environ. Res. Lett. 2024, 19, 064023. [Google Scholar] [CrossRef]
- Peng, C.; Apps, M.J. Modelling the Response of Net Primary Productivity (NPP) of Boreal Forest Ecosystems to Changes in Climate and Fire Disturbance Regimes. Ecol. Modell. 1999, 122, 175–193. [Google Scholar] [CrossRef]
- Bowman, D.M.J.S.; Kolden, C.A.; Abatzoglou, J.T.; Johnston, F.H.; van der Werf, G.R.; Flannigan, M. Vegetation Fires in the Anthropocene. Nat. Rev. Earth Environ. 2020, 1, 500–515. [Google Scholar] [CrossRef]
- Byrne, B.; Liu, J.; Bowman, K.W.; Pascolini-Campbell, M.; Chatterjee, A.; Pandey, S.; Miyazaki, K.; van der Werf, G.R.; Wunch, D.; Wennberg, P.O.; et al. Carbon Emissions from the 2023 Canadian Wildfires. Nature 2024, 633, 835–839. [Google Scholar] [CrossRef] [PubMed]
- Jain, P.; Barber, Q.E.; Taylor, S.W.; Whitman, E.; Castellanos Acuna, D.; Boulanger, Y.; Chavardès, R.D.; Chen, J.; Englefield, P.; Flannigan, M.; et al. Drivers and Impacts of the Record-Breaking 2023 Wildfire Season in Canada. Nat. Commun. 2024, 15, 6764. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Flannigan, M.D.; Guindon, L.; Swystun, T.; Castellanos-Acuna, D.; Wu, W.; Wang, G. Canadian Forests Are More Conducive to High-Severity Fires in Recent Decades. Science 2025, 387, 91–97. [Google Scholar] [CrossRef]
- Marceau, D.J.; Hay, G.J. Remote Sensing Contributions to the Scale Issue. Can. J. Remote Sens. 1999, 25, 357–366. [Google Scholar] [CrossRef]
- Coops, N.C.; Shang, C.; Wulder, M.A.; White, J.C.; Hermosilla, T. Change in Forest Condition: Characterizing Non-Stand Replacing Disturbances Using Time Series Satellite Imagery. For. Ecol. Manag. 2020, 474, 118370. [Google Scholar] [CrossRef]
- Gómez, I.; Pilar Martín, M. Prototyping an Artificial Neural Network for Burned Area Mapping on a Regional Scale in Mediterranean Areas Using MODIS Images. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 741–752. [Google Scholar] [CrossRef]
- Van, L.N.; Tran, V.N.; Nguyen, G.V.; Yeon, M.; Do, M.T.T.; Lee, G. Enhancing Wildfire Mapping Accuracy Using Mono-Temporal Sentinel-2 Data: A Novel Approach through Qualitative and Quantitative Feature Selection with Explainable AI. Ecol. Inform. 2024, 81, 102601. [Google Scholar] [CrossRef]
- Liu, J.; Heiskanen, J.; Maeda, E.E.; Pellikka, P.K.E. Burned Area Detection Based on Landsat Time Series in Savannas of Southern Burkina Faso. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 210–220. [Google Scholar] [CrossRef]
- Giglio, L.; Schroeder, W.; Justice, C.O. The Collection 6 MODIS Active Fire Detection Algorithm and Fire Products. Remote Sens. Environ. 2016, 178, 31–41. [Google Scholar] [CrossRef] [PubMed]
- Hall, R.J.; Skakun, R.S.; Metsaranta, J.M.; Landry, R.; Fraser, R.H.; Raymond, D.; Gartrell, M.; Decker, V.; Little, J. Generating Annual Estimates of Forest Fire Disturbance in Canada: The National Burned Area Composite. Int. J. Wildland Fire 2020, 29, 878–891. [Google Scholar] [CrossRef]
- Guindon, L.; Bernier, P.; Gauthier, S.; Stinson, G.; Villemaire, P.; Beaudoin, A. Missing Forest Cover Gains in Boreal Forests Explained. Ecosphere 2018, 9, e02094. [Google Scholar] [CrossRef]
- Lizundia-Loiola, J.; Otón, G.; Ramo, R.; Chuvieco, E. A Spatio-Temporal Active-Fire Clustering Approach for Global Burned Area Mapping at 250 m from MODIS Data. Remote Sens. Environ. 2020, 236, 111493. [Google Scholar] [CrossRef]
- Fraser, R.H.; Li, Z.; Cihlar, J. Hotspot and NDVI Differencing Synergy (HANDS): A New Technique for Burned Area Mapping over Boreal Forest. Remote Sens. Environ. 2000, 74, 362–376. [Google Scholar] [CrossRef]
- Verbesselt, J.; Zeileis, A.; Herold, M. Near Real-Time Disturbance Detection Using Satellite Image Time Series. Remote Sens. Environ. 2012, 123, 98–108. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.L. Quality Assessment and Validation of the MODIS Global Land Surface Temperature. Int. J. Remote Sens. 2004, 25, 261–274. [Google Scholar] [CrossRef]
- Karnieli, A.; Agam, N.; Pinker, R.T.; Anderson, M.; Imhoff, M.L.; Gutman, G.G.; Panov, N.; Goldberg, A. Use of NDVI and Land Surface Temperature for Drought Assessment: Merits and Limitations. J. Clim. 2010, 23, 618–633. [Google Scholar] [CrossRef]
- Joshi, R.C.; Ryu, D.; Sheridan, G.J.; Lane, P.N.J. Modeling Vegetation Water Stress over the Forest from Space: Temperature Vegetation Water Stress Index (TVWSI). Remote Sens. 2021, 13, 4635. [Google Scholar] [CrossRef]
- Van Leeuwen, W.J.D.; Orr, B.J.; Marsh, S.E.; Herrmann, S.M. Multi-Sensor NDVI Data Continuity: Uncertainties and Implications for Vegetation Monitoring Applications. Remote Sens. Environ. 2006, 100, 67–81. [Google Scholar] [CrossRef]
- Abuzar, M.; Sheffield, K.; McAllister, A. Feasibility of Using SWIR-Transformed Reflectance (STR) in Place of Surface Temperature (Ts) for the Mapping of Irrigated Landcover. Land 2024, 13, 633. [Google Scholar] [CrossRef]
- Ghali, R.; Akhloufi, M.A. Deep Learning Approaches for Wildland Fires Remote Sensing: Classification, Detection, and Segmentation. Remote Sens. 2023, 15, 1821. [Google Scholar] [CrossRef]
- Pinto, M.M.; Libonati, R.; Trigo, R.M.; Trigo, I.F.; DaCamara, C.C. A Deep Learning Approach for Mapping and Dating Burned Areas Using Temporal Sequences of Satellite Images. ISPRS J. Photogramm. Remote Sens. 2020, 160, 260–274. [Google Scholar] [CrossRef]
- Marjani, M.; Ahmadi, S.A.; Mahdianpari, M. FirePred: A Hybrid Multi-Temporal Convolutional Neural Network Model for Wildfire Spread Prediction. Ecol. Inform. 2023, 78, 102282. [Google Scholar] [CrossRef]
- Al-Dabbagh, A.M.; Ilyas, M. Uni-Temporal Sentinel-2 Imagery for Wildfire Detection Using Deep Learning Semantic Segmentation Models. Geomat. Nat. Hazards Risk 2023, 14, 2196370. [Google Scholar] [CrossRef]
- Akbari Asanjan, A.; Memarzadeh, M.; Lott, P.A.; Rieffel, E.; Grabbe, S. Probabilistic Wildfire Segmentation Using Supervised Deep Generative Model from Satellite Imagery. Remote Sens. 2023, 15, 2718. [Google Scholar] [CrossRef]
- Kang, Y.; Jang, E.; Im, J.; Kwon, C. A Deep Learning Model Using Geostationary Satellite Data for Forest Fire Detection with Reduced Detection Latency. GISci Remote Sens. 2022, 59, 2019–2035. [Google Scholar] [CrossRef]
- Hu, X.; Ban, Y.; Nascetti, A. Uni-Temporal Multispectral Imagery for Burned Area Mapping with Deep Learning. Remote Sens. 2021, 13, 1509. [Google Scholar] [CrossRef]
- Prabowo, Y.; Sakti, A.D.; Pradono, K.A.; Amriyah, Q.; Rasyidy, F.H.; Bengkulah, I.; Ulfa, K.; Candra, D.S.; Imdad, M.T.; Ali, S. Deep Learning Dataset for Estimating Burned Areas: Case Study, Indonesia. Data 2022, 7, 78. [Google Scholar] [CrossRef]
- Seydi, S.T.; Hasanlou, M.; Chanussot, J. Dsmnn-Net: A Deep Siamese Morphological Neural Network Model for Burned Area Mapping Using Multispectral Sentinel-2 and Hyperspectral Prisma Images. Remote Sens. 2021, 13, 5138. [Google Scholar] [CrossRef]
- Brand, A.K.; Manandhar, A. Semantic Segmentation of Burned Areas in Satellite Images Using a U-Net-Based Convolutional Neural Network. In Proceedings of the XXIV ISPRS Congress (2021 Edition), The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Nice, France, 5–9 July 2021; Volume XLIII-B3-2021, pp. 47–53. [Google Scholar] [CrossRef]
- Seydi, S.T.; Hasanlou, M.; Chanussot, J. Burnt-Net: Wildfire Burned Area Mapping with Single Post-Fire Sentinel-2 Data and Deep Learning Morphological Neural Network. Ecol. Indic. 2022, 140, 108999. [Google Scholar] [CrossRef]
- Cho, A.Y.; Park, S.E.; Kim, D.J.; Kim, J.; Li, C.; Song, J. Burned Area Mapping Using Unitemporal PlanetScope Imagery with a Deep Learning Based Approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 242–253. [Google Scholar] [CrossRef]
- Padilla, M.; Stehman, S.V.; Ramo, R.; Corti, D.; Hantson, S.; Oliva, P.; Alonso-Canas, I.; Bradley, A.V.; Tansey, K.; Mota, B.; et al. Comparing the Accuracies of Remote Sensing Global Burned Area Products Using Stratified Random Sampling and Estimation. Remote Sens. Environ. 2015, 160, 114–121. [Google Scholar] [CrossRef]
- Badda, H.; Cherif, E.K.; Boulaassal, H.; Wahbi, M.; Yazidi Alaoui, O.; Maatouk, M.; Bernardino, A.; Coren, F.; El Kharki, O. Improving the Accuracy of Random Forest Classifier for Identifying Burned Areas in the Tangier-Tetouan-Al Hoceima Region Using Google Earth Engine. Remote Sens. 2023, 15, 4226. [Google Scholar] [CrossRef]
- Belenguer-Plomer, M.A.; Tanase, M.A.; Chuvieco, E.; Bovolo, F. CNN-Based Burned Area Mapping Using Radar and Optical Data. Remote Sens. Environ. 2021, 260, 112468. [Google Scholar] [CrossRef]
- Ghali, R.; Akhloufi, M.A. Deep Learning Approaches for Wildland Fires Using Satellite Remote Sensing Data: Detection, Mapping, and Prediction. Fire 2023, 6, 192. [Google Scholar] [CrossRef]
- Boucher, J.; Beaudoin, A.; Hébert, C.; Guindon, L.; Bauce, É. Assessing the Potential of the Differenced Normalized Burn Ratio (DNBR) for Estimating Burn Severity in Eastern Canadian Boreal Forests. Int. J. Wildland Fire 2017, 26, 32–45. [Google Scholar] [CrossRef]
- Skakun, R.; Castilla, G.; Metsaranta, J.; Whitman, E.; Rodrigue, S.; Little, J.; Groenewegen, K.; Coyle, M. Extending the National Burned Area Composite Time Series of Wildfires in Canada. Remote Sens. 2022, 14, 3050. [Google Scholar] [CrossRef]
- Pettorelli, N.; Ryan, S.; Mueller, T.; Bunnefeld, N.; Jedrzejewska, B.; Lima, M.; Kausrud, K. The Normalized Difference Vegetation Index (NDVI): Unforeseen Successes in Animal Ecology. Clim. Res. 2011, 46, 15–27. [Google Scholar] [CrossRef]
- Jones, M.W.; Abatzoglou, J.T.; Veraverbeke, S.; Andela, N.; Lasslop, G.; Forkel, M.; Smith, A.J.P.; Burton, C.; Betts, R.A.; van der Werf, G.R.; et al. Global and Regional Trends and Drivers of Fire Under Climate Change. Rev. Geophys. 2022, 60, 1–76. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Chuvieco, E.; Yue, C.; Heil, A.; Mouillot, F.; Alonso-Canas, I.; Padilla, M.; Pereira, J.M.; Oom, D.; Tansey, K. A New Global Burned Area Product for Climate Assessment of Fire Impacts. Glob. Ecol. Biogeogr. 2016, 25, 619–629. [Google Scholar] [CrossRef]
- Goetz, S.J.; Bunn, A.G.; Fiske, G.J.; Houghton, R.A. Satellite-Observed Photosynthetic Trends across Boreal North America Associated with Climate and Fire Disturbance. Proc. Natl. Acad. Sci. USA 2005, 102, 13521–13525. [Google Scholar] [CrossRef]
- Smith, C.W.; Panda, S.K.; Bhatt, U.S.; Meyer, F.J.; Badola, A.; Hrobak, J.L. Assessing Wildfire Burn Severity and Its Relationship with Environmental Factors: A Case Study in Interior Alaska Boreal Forest. Remote Sens. 2021, 13, 1966. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Justice, C.O.; Giglio, L.; Korontzi, S.; Owens, J.; Morisette, J.T.; Roy, D.; Descloitres, J.; Alleaume, S.; Petitcolin, F.; Kaufman, Y. The MODIS Fire Products. Remote Sens. Environ. 2002, 83, 244–262. [Google Scholar] [CrossRef]
- Hawbaker, T.J.; Radeloff, V.C.; Syphard, A.D.; Zhu, Z.; Stewart, S.I. Detection Rates of the MODIS Active Fire Product in the United States. Remote Sens. Environ. 2008, 112, 2656–2664. [Google Scholar] [CrossRef]
- Wang, L.; Bartlett, P.; Pouliot, D.; Chan, E.; Lamarche, C.; Wulder, M.A.; Defourny, P.; Brady, M. Comparison and Assessment of Regional and Global Land Cover Datasets for Use in CLASS over Canada. Remote Sens. 2019, 11, 2286. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Zeng, C.; Li, X.; Wei, Y. Missing Data Reconstruction in Remote Sensing Image with a Unified Spatial-Temporal-Spectral Deep Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4274–4288. [Google Scholar] [CrossRef]
- Shalabi, L.A.; Shaaban, Z.; Kasasbeh, B. Data Mining: A Preprocessing Engine. J. Comput. Sci. 2006, 2, 735–739. [Google Scholar] [CrossRef]
- Cabello-Solorzano, K.; Ortigosa de Araujo, I.; Peña, M.; Correia, L.; Tallón-Ballesteros, A.J. The Impact of Data Normalization on the Accuracy of Machine Learning Algorithms: A Comparative Analysis. In Proceedings of the 18th International Conference on Soft Computing Models in Industrial and Environmental Applications (SOCO 2023), Cáceres, Spain, 12–14 September 2023; Rivas, A.P., García, G.C., Abraham, A., De Paz Santana, J.F., Eds.; Lecture Notes in Networks and Systems. Springer: Cham, Switzerland, 2023; Volume 750, pp. 344–353. [Google Scholar] [CrossRef]
- Chuvieco, E.; Giglio, L.; Justice, C. Global Characterization of Fire Activity: Toward Defining Fire Regimes from Earth Observation Data. Glob. Change Biol. 2008, 14, 1488–1502. [Google Scholar] [CrossRef]
- Zhang, P.; Ban, Y.; Nascetti, A. Learning U-Net without Forgetting for near Real-Time Wildfire Monitoring by the Fusion of SAR and Optical Time Series. Remote Sens. Environ. 2021, 261, 112467. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, M.; Liu, K. Deep Neural Networks for Global Wildfire Susceptibility Modelling. Ecol. Indic. 2021, 127, 107735. [Google Scholar] [CrossRef]
- Murat, H.S. A Brief Review of Feed-Forward Neural Networks. Commun. Fac. Sci. Univ. Ank. 2006, 50, 11–17. [Google Scholar] [CrossRef]
- Florath, J.; Keller, S. Supervised Machine Learning Approaches on Multispectral Remote Sensing Data for a Combined Detection of Fire and Burned Area. Remote Sens. 2022, 14, 657. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tatnall, A.R.L. Introduction Neural Networks in Remote Sensing. Int. J. Remote Sens. 1997, 18, 699–709. [Google Scholar] [CrossRef]
- El-Hassani, F.Z.; Amri, M.; Joudar, N.E.; Haddouch, K. A New Optimization Model for MLP Hyperparameter Tuning: Modeling and Resolution by Real-Coded Genetic Algorithm. Neural Process Lett. 2024, 56, 105. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Stathakis, D. How Many Hidden Layers and Nodes? Int. J. Remote Sens. 2009, 30, 2133–2147. [Google Scholar] [CrossRef]
- Gao, K.; Feng, Z.; Wang, S. Using Multilayer Perceptron to Predict Forest Fires in Jiangxi Province, Southeast China. Discret. Dyn. Nat. Soc. 2022, 2022, 6930812. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Ni, S.; Wei, X.; Zhang, N.; Chen, H. Algorithm-Hardware Co-Optimization and Deployment Method for Field-Programmable Gate-Array-Based Convolutional Neural Network Remote Sensing Image Processing. Remote Sens. 2023, 15, 5784. [Google Scholar] [CrossRef]
- Bottou, L. Large-Scale Machine Learning with Stochastic Gradient Descent. In Proceedings of the 19th International Conference on Computational Statistics (COMPSTAT 2010), Paris, France, 22–27 August 2010; Lechevallier, Y., Saporta, G., Eds.; Physica-Verlag HD: Heidelberg, Germany, 2010; pp. 177–186. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Saito, T.; Rehmsmeier, M. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Society Ser. B (Methodol.) 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence (IJCAI 1995), Montreal, QC, Canada, 20–25 August 1995; Volume 2, pp. 1137–1145. [Google Scholar]
- Agrawal, N.; Nelson, P.V.; Low, R.D. A Novel Approach for Predicting Large Wildfires Using Machine Learning towards Environmental Justice via Environmental Remote Sensing and Atmospheric Reanalysis Data across the United States. Remote Sens. 2023, 15, 5501. [Google Scholar] [CrossRef]
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Aryal, J. Forest Fire Susceptibility and Risk Mapping Using Social/Infrastructural Vulnerability and Environmental Variables. Fire 2019, 2, 50. [Google Scholar] [CrossRef]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of Quantity Disagreement and Allocation Disagreement for Accuracy Assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Kondylatos, S.; Prapas, I.; Ronco, M.; Papoutsis, I.; Camps-Valls, G.; Piles, M.; Fernández-Torres, M.Á.; Carvalhais, N. Wildfire Danger Prediction and Understanding With Deep Learning. Geophys. Res. Lett. 2022, 49, 1–11. [Google Scholar] [CrossRef]
- Abid, N.; Malik, M.I.; Shahzad, M.; Shafait, F.; Ali, H.; Ghaffar, M.M.; Liwicki, M. Burnt Forest Estimation from Sentinel-2 Imagery of Australia Using Unsupervised Deep Learning. In Proceedings of the 2021 Digital Image Computing: Techniques and Applications (DICTA), Gold Coast, Australia, 29 November–1 December 2021; IEEE: New York, NY, USA, 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Digavinti, J.; Manikiam, B. Satellite Monitoring of Forest Fire Impact and Regeneration Using NDVI and LST. J. Appl. Remote Sens. 2021, 15, 042412. [Google Scholar] [CrossRef]
- Tang, Z.; Xia, X.; Huang, Y.; Lu, Y.; Guo, Z. Estimation of National Forest Aboveground Biomass from Multi-Source Remotely Sensed Dataset with Machine Learning Algorithms in China. Remote Sens. 2022, 14, 5487. [Google Scholar] [CrossRef]
- Omar, N.; Al-Zebari, A.; Sengur, A. Deep Learning Approach to Predict Forest Fires Using Meteorological Measurements. In Proceedings of the 2021 2nd International Informatics and Software Engineering Conference (IISEC), Ankara, Turkey, 16–17 December 2021; IEEE: New York, NY, USA, 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, M.; Liu, K. Dynamic Prediction of Global Monthly Burned Area with Hybrid Deep Neural Networks. Ecol. Appl. 2022, 32, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhou, C.; Zhang, G.; Yang, Z.; Pang, Z.; Luo, Y. A Novel Framework for Forest Above-Ground Biomass Inversion Using Multi-Source Remote Sensing and Deep Learning. Forests 2024, 15, 456. [Google Scholar] [CrossRef]

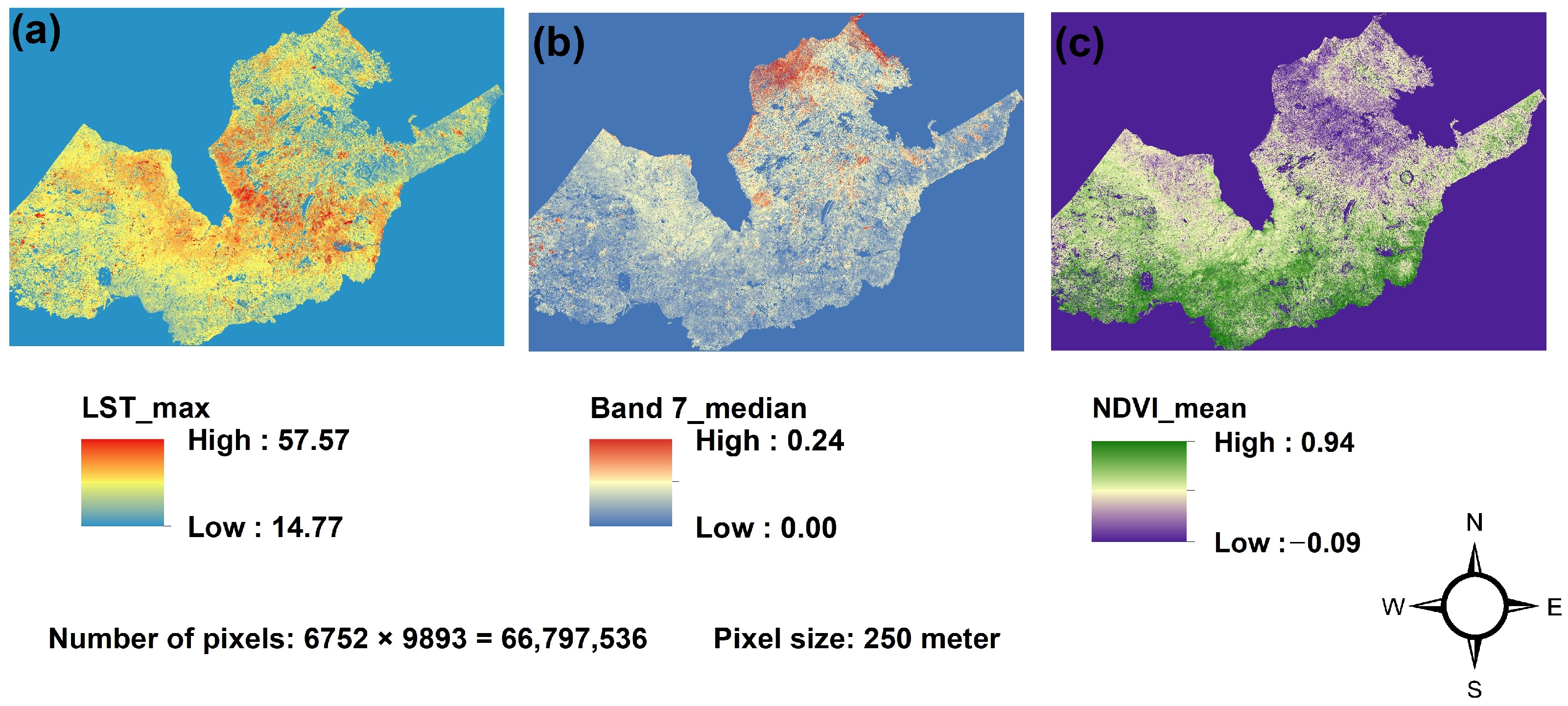
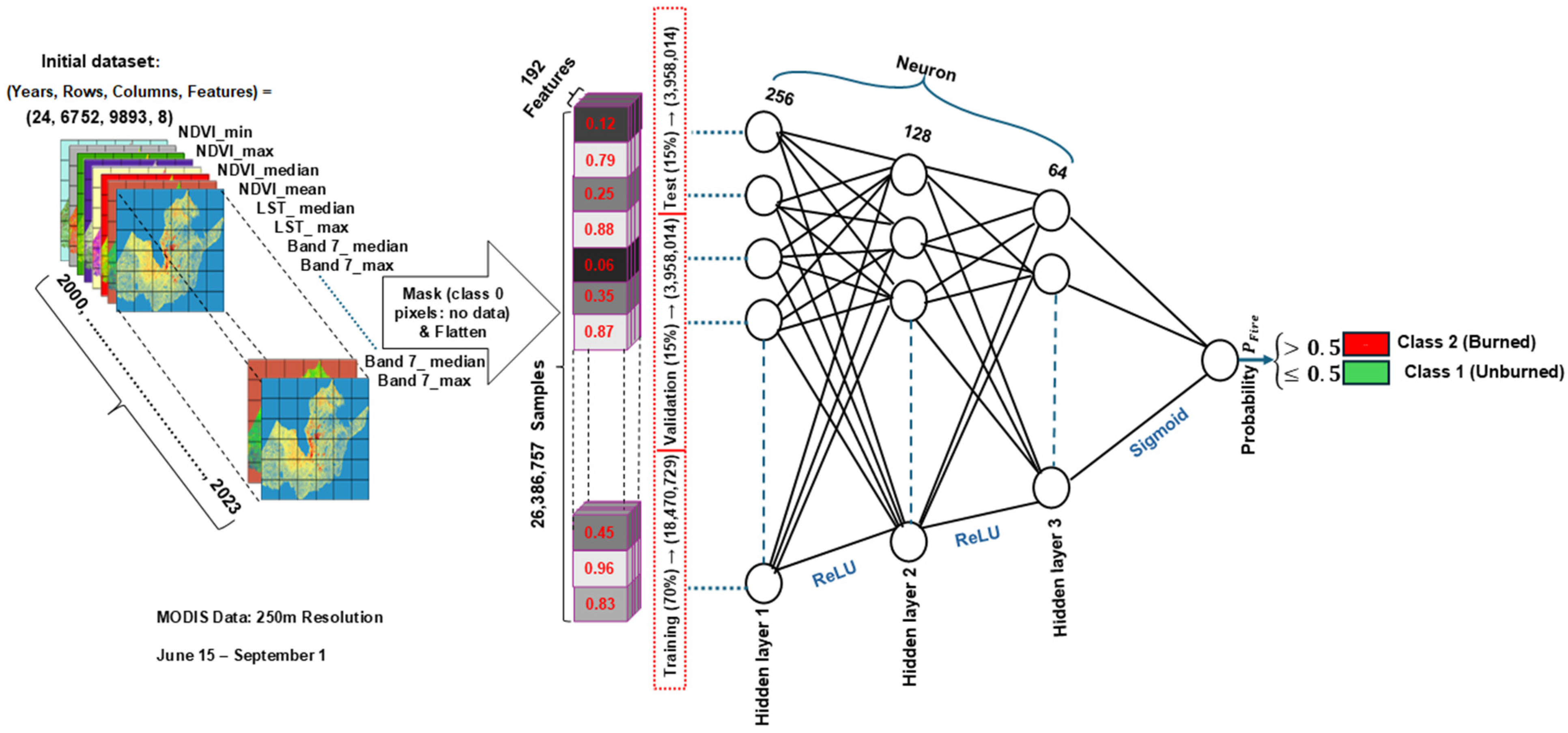

| Feature Name | Source Google Earth Engine | Bands Used | Spatial Resolution | Temporal Resolution |
|---|---|---|---|---|
| NDVI_max NDVI_min NDVI_median NDVI_mean | MOD13Q1.061 & MYD13Q1.061 | Band 1 (Red, 620–670 nm) & Band 2 (NIR, 841–876 nm) | 250 m | 16-Day |
| B7_max B7_median | MOD13Q1 V6.1 & MYD13Q1 V6.1 | Band 7 (Shortwave Infrared) (2.105–2.155 µm) | 500 m | 16-Day |
| LST_max LST_median | MOD11A1.061 & MYD11A1.061 | Thermal Infrared (TIR): Band 31 (10.78–11.28 µm) Band 32 (11.77–12.27 µm) | 1 Km | Daily |
| Hyperparameter | Values2 |
|---|---|
| Hidden Layer Sizes | [(128, 64, 32), (256, 128, 64), (64, 32)] |
| Alpha (Regularization Strength) | [0.0001, 0.001, 0.01] |
| Activation Functions | [‘ReLU’] |
| Solvers (Optimization Algorithms) | [‘Adam’, ‘SGD’] |
| Rank | Tuning Configuration | Cohen’s Kappa | F1-Score (Burned Pixels) | Hidden Layers | Optimizer | Regularization (α) |
|---|---|---|---|---|---|---|
| 1 | Tuning 14 | 0.8890 | 0.90 | (256, 128, 64) | SGD | 0.0001 |
| 2 | Tuning 15 | 0.8847 | 0.89 | (256, 128, 64) | SGD | 0.001 |
| 3 | Tuning 11 | 0.8890 | 0.89 | (128, 64, 32) | SGD | 0.0001 |
| 4 | Tuning 12 | 0.8811 | 0.89 | (128, 64, 32) | SGD | 0.001 |
| 5 | Tuning 16 | 0.8775 | 0.89 | (256, 128, 64) | SGD | 0.01 |
| 6 | Tuning 13 | 0.8750 | 0.88 | (128, 64, 32) | SGD | 0.01 |
| 7 | Tuning 05 | 0.8704 | 0.88 | (256, 128, 64) | Adam | 0.001 |
| 8 | Tuning 17 | 0.8697 | 0.88 | (64, 32) | SGD | 0.0001 |
| 9 | Tuning 01 | 0.8692 | 0.88 | (128, 64, 32) | Adam | 0.0001 |
| 10 | Tuning 18 | 0.8684 | 0.88 | (64, 32) | SGD | 0.001 |
| 11 | Tuning 07 | 0.8666 | 0.88 | (64, 32) | Adam | 0.0001 |
| 12 | Tuning 04 | 0.8664 | 0.88 | (256, 128, 64) | Adam | 0.0001 |
| 13 | Tuning 02 | 0.8663 | 0.88 | (128, 64, 32) | Adam | 0.001 |
| 14 | Tuning 19 | 0.8631 | 0.87 | (64, 32) | SGD | 0.01 |
| 15 | Tuning 08 | 0.8592 | 0.87 | (64, 32) | Adam | 0.001 |
| 16 | Tuning 06 | 0.8502 | 0.86 | (256, 128, 64) | Adam | 0.01 |
| 17 | Tuning 09 | 0.8417 | 0.85 | (64, 32) | Adam | 0.01 |
| 18 | Tuning 03 | 0.8399 | 0.85 | (128, 64, 32) | Adam | 0.01 |
| Precision | Recall | F1-Score | Support | |
|---|---|---|---|---|
| Class 1 | 0.99 | 0.99 | 0.99 | 3,675,668 |
| Class 2 | 0.89 | 0.89 | 0.89 | 282,346 |
| Macro average | 0.94 | 0.94 | 0.94 | 3,958,014 |
| Weighted average | 0.98 | 0.98 | 0.98 | |
| Overall Accuracy | 0.9846 | |||
| Kappa Coefficient | 0.8839 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meimand, H.M.; Chen, J.; Kneeshaw, D.; Bakhtyari, M.; Peng, C. Burned Area Detection in the Eastern Canadian Boreal Forest Using a Multi-Layer Perceptron and MODIS-Derived Features. Remote Sens. 2025, 17, 2162. https://doi.org/10.3390/rs17132162
Meimand HM, Chen J, Kneeshaw D, Bakhtyari M, Peng C. Burned Area Detection in the Eastern Canadian Boreal Forest Using a Multi-Layer Perceptron and MODIS-Derived Features. Remote Sensing. 2025; 17(13):2162. https://doi.org/10.3390/rs17132162
Chicago/Turabian StyleMeimand, Hadi Mahmoudi, Jiaxin Chen, Daniel Kneeshaw, Mohammadreza Bakhtyari, and Changhui Peng. 2025. "Burned Area Detection in the Eastern Canadian Boreal Forest Using a Multi-Layer Perceptron and MODIS-Derived Features" Remote Sensing 17, no. 13: 2162. https://doi.org/10.3390/rs17132162
APA StyleMeimand, H. M., Chen, J., Kneeshaw, D., Bakhtyari, M., & Peng, C. (2025). Burned Area Detection in the Eastern Canadian Boreal Forest Using a Multi-Layer Perceptron and MODIS-Derived Features. Remote Sensing, 17(13), 2162. https://doi.org/10.3390/rs17132162






