PhA-MOE: Enhancing Hyperspectral Retrievals for Phytoplankton Absorption Using Mixture-of-Experts
Abstract
1. Introduction
- Examine various preprocessing methods for spectral data and introduce an innovative method for in situ spectral feature extraction and enhancement, further providing benchmark comparisons for different neural networks.
- Present the first known MOE application in ocean color remote sensing, featuring a novel specialized structure design and training scheme for prediction.
- Establish a systematic experiment and evaluation of prediction by comparing the performance of PhA-MOE against other state-of-the-art (SOTA) learning-based approaches, thereby validating its effectiveness and robustness.
- Apply the PhA-MOE framework to real hyperspectral PACE-OCI imagery for the first time and validate its performance using match-up field data, enabling the study of spatio-temporal variations of in an optically complex estuary.
2. Data
2.1. Dataset
2.1.1. GLORIA Data
2.1.2. Field Collection in Gulf Estuaries
2.1.3. Satellite Data
2.2. Data Preprocessing
- Robust Scaler (Rob): The robust scaler is designed to mitigate the influence of outliers by scaling the data based on the interquartile range, calculated aswhere z is a data sample at a given wavelength , such as or . Here, , , and are the median, first, and third quartiles, respectively. It is important to note that, since are computed from training samples and Equation (3) represents a linear transformation, the predicted can be rescaled back to the original domain without any loss of information.
- Logarithmic Scaler (Log): The log transformation is another form of linear normalization, commonly used to scale data within a specified range (e.g., to [−1,1]), and expressed as
3. Method
3.1. Motivation for Applying MOE to Prediction
3.2. PhA-MOE Model for Retrieval
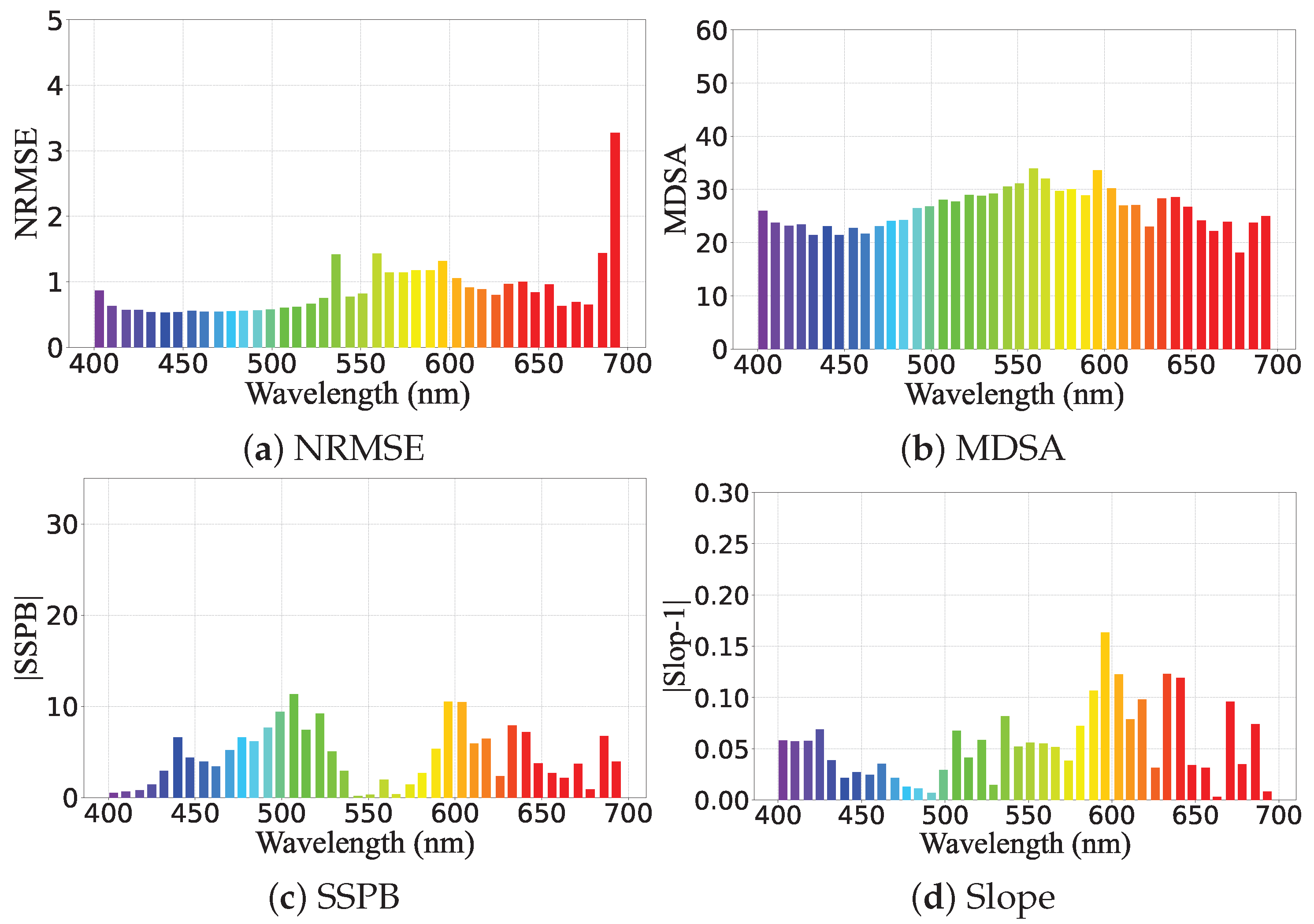
3.3. Evaluation Metrics
4. Results
4.1. Baseline
4.2. Evaluation of Various Preprocessing Methods
4.3. Comparison of Different Learning Frameworks
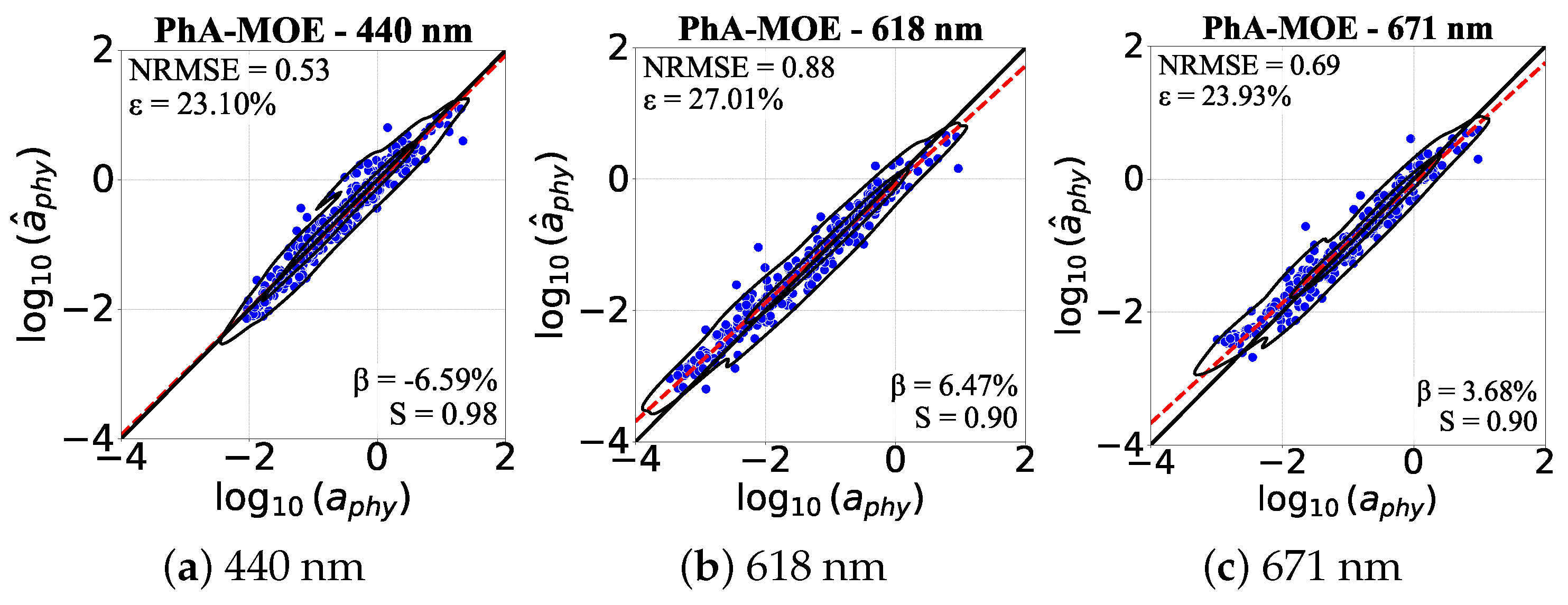
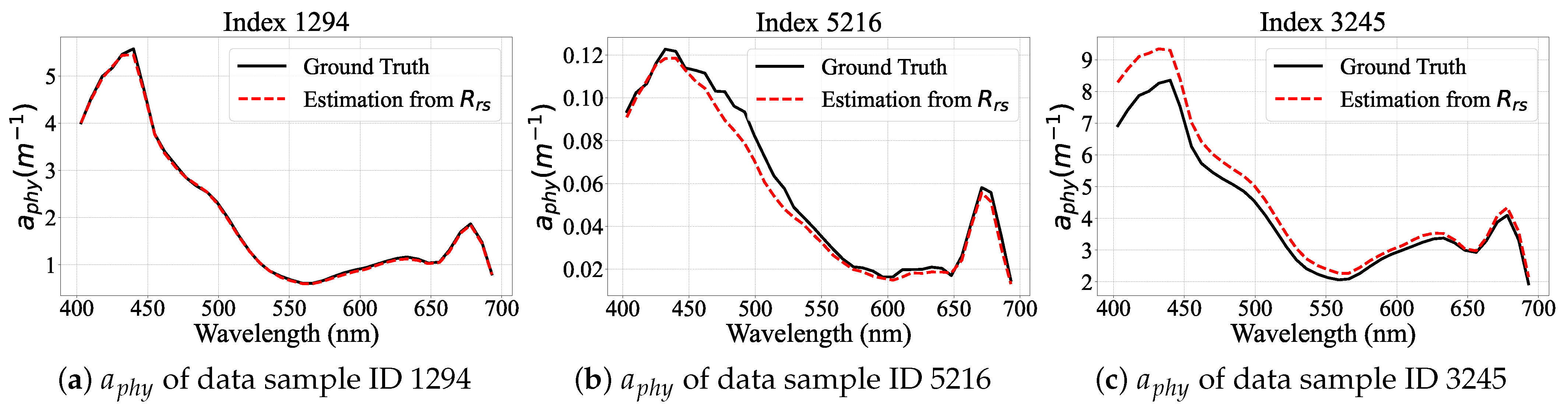
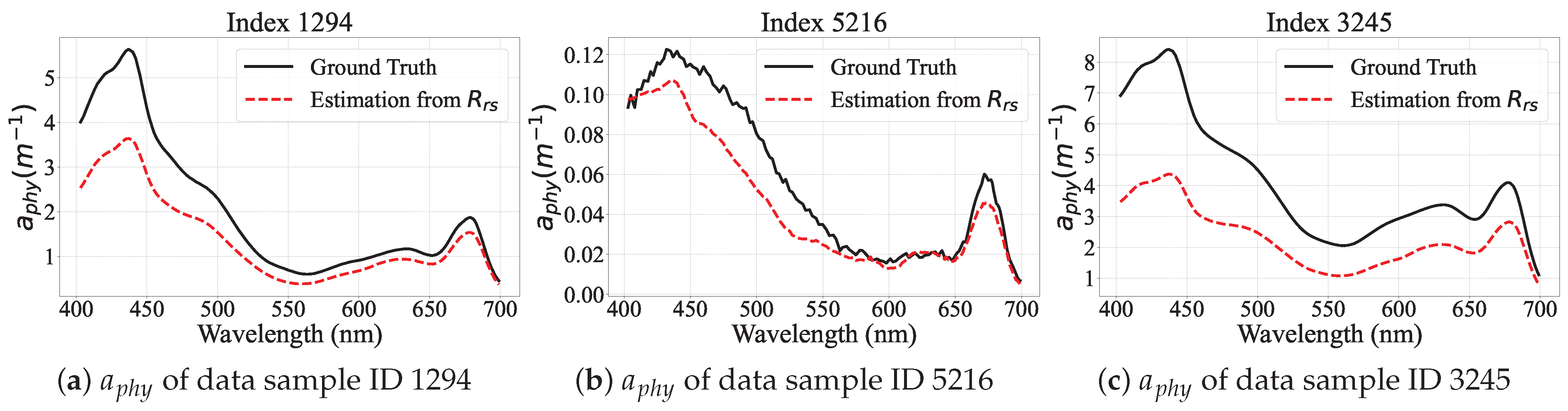
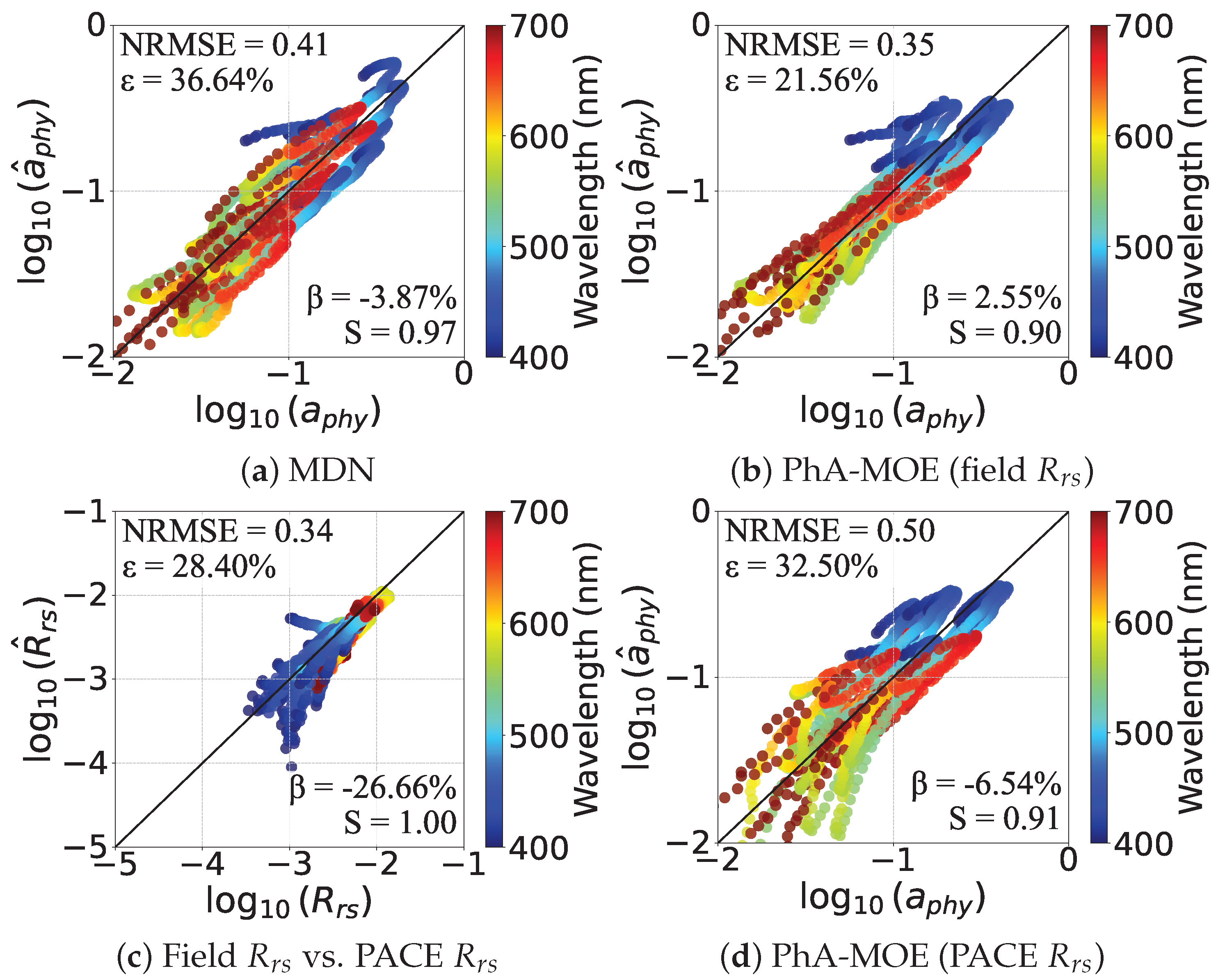
Performance Visualization of PhA-MOE model
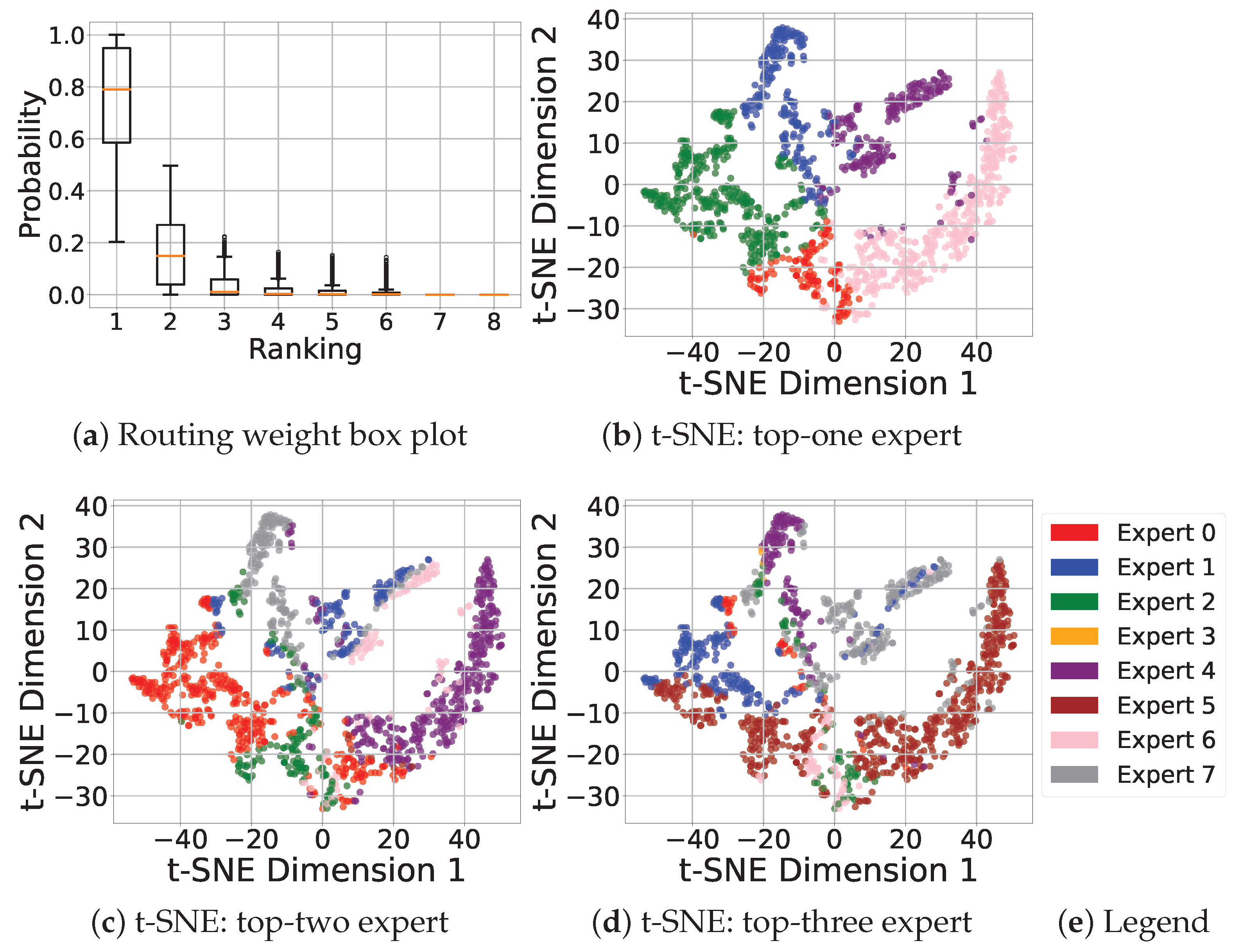
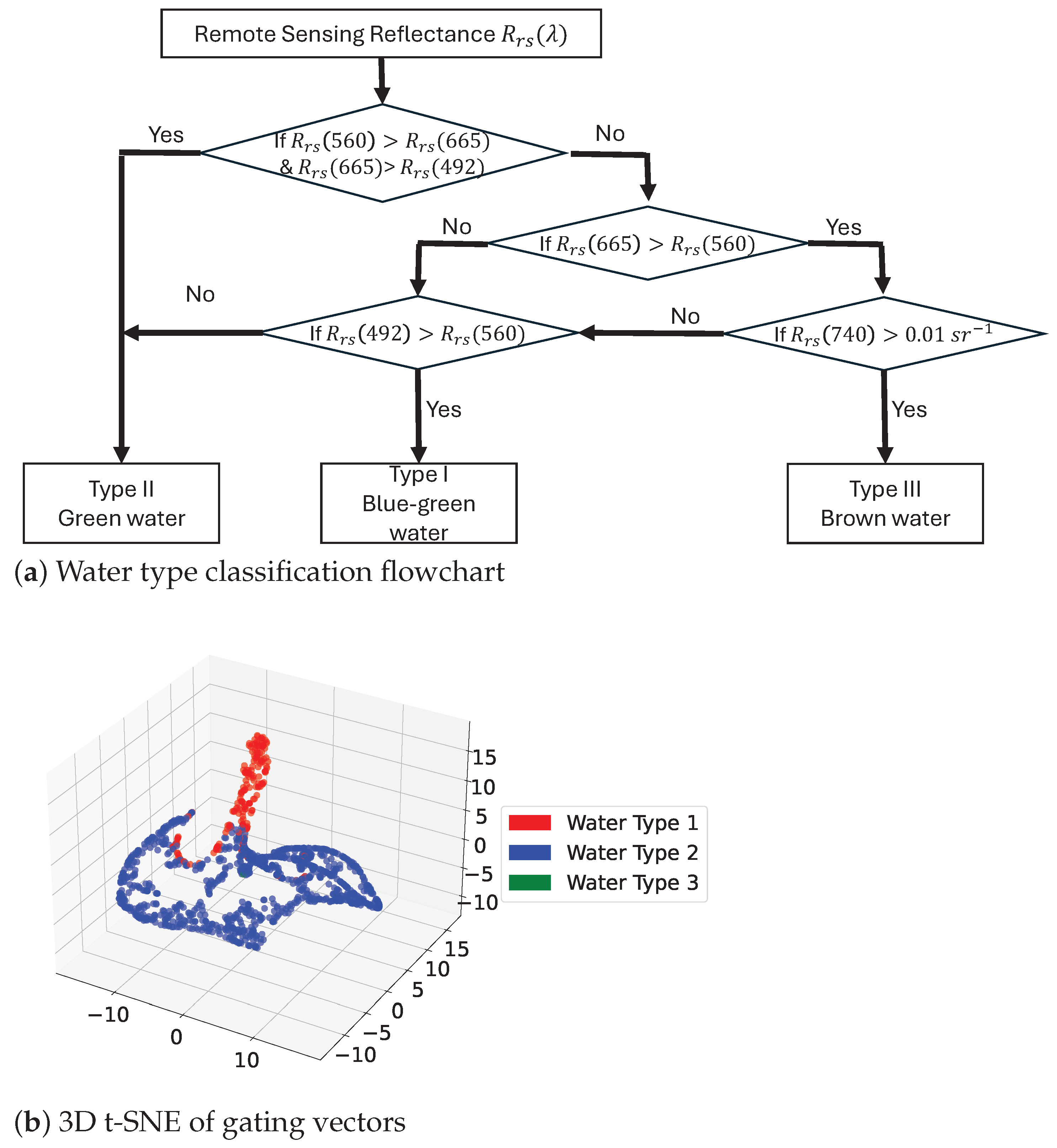
4.4. Visualization of MOE Learning
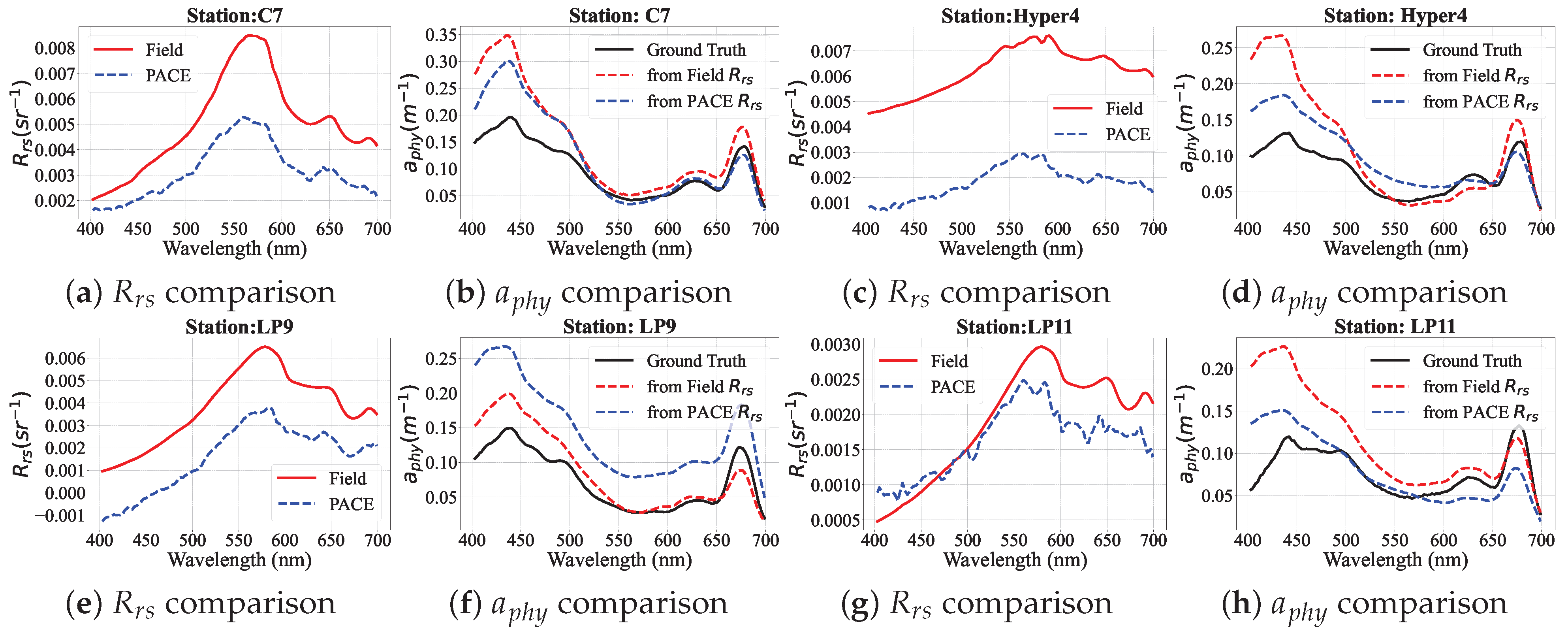
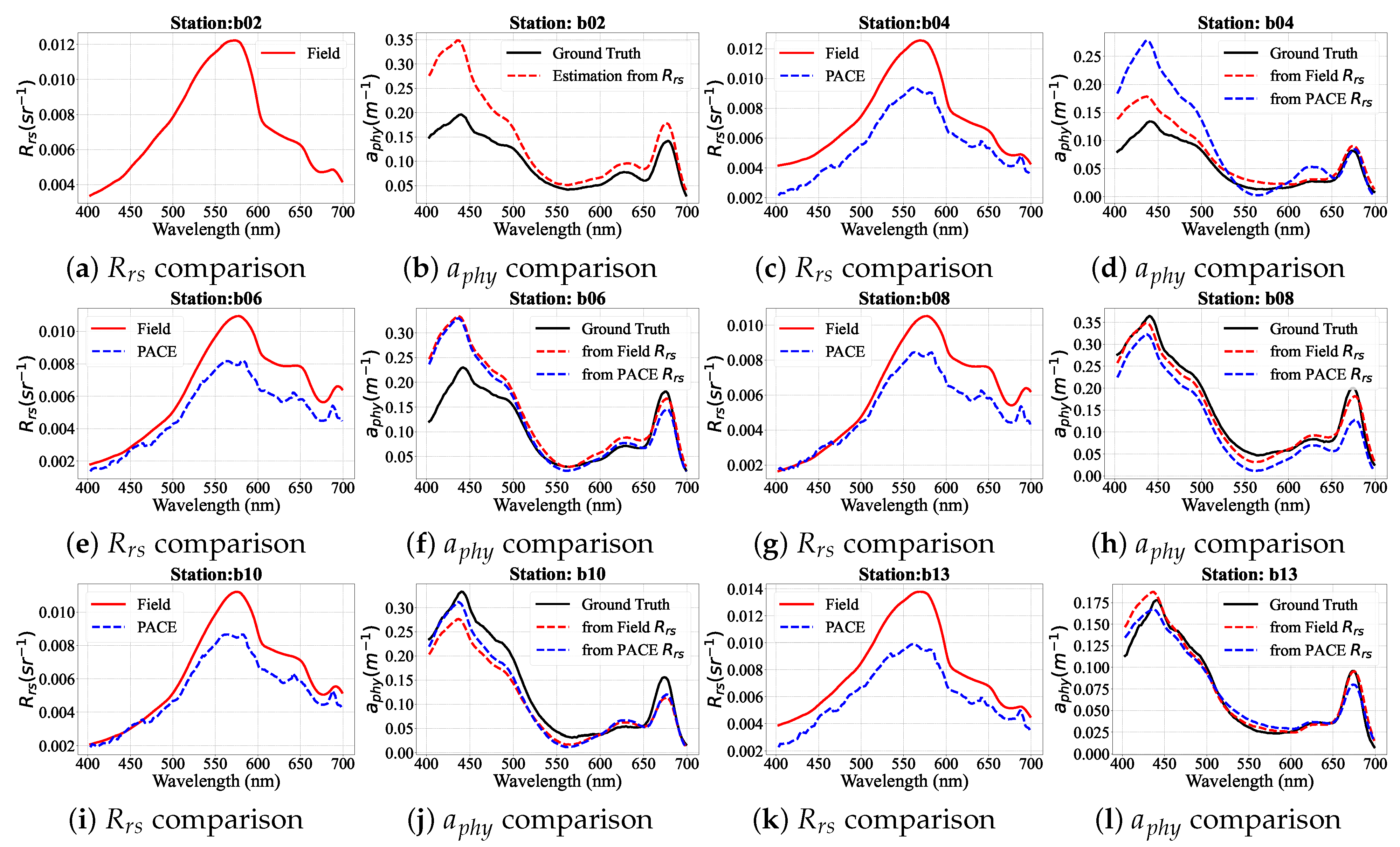
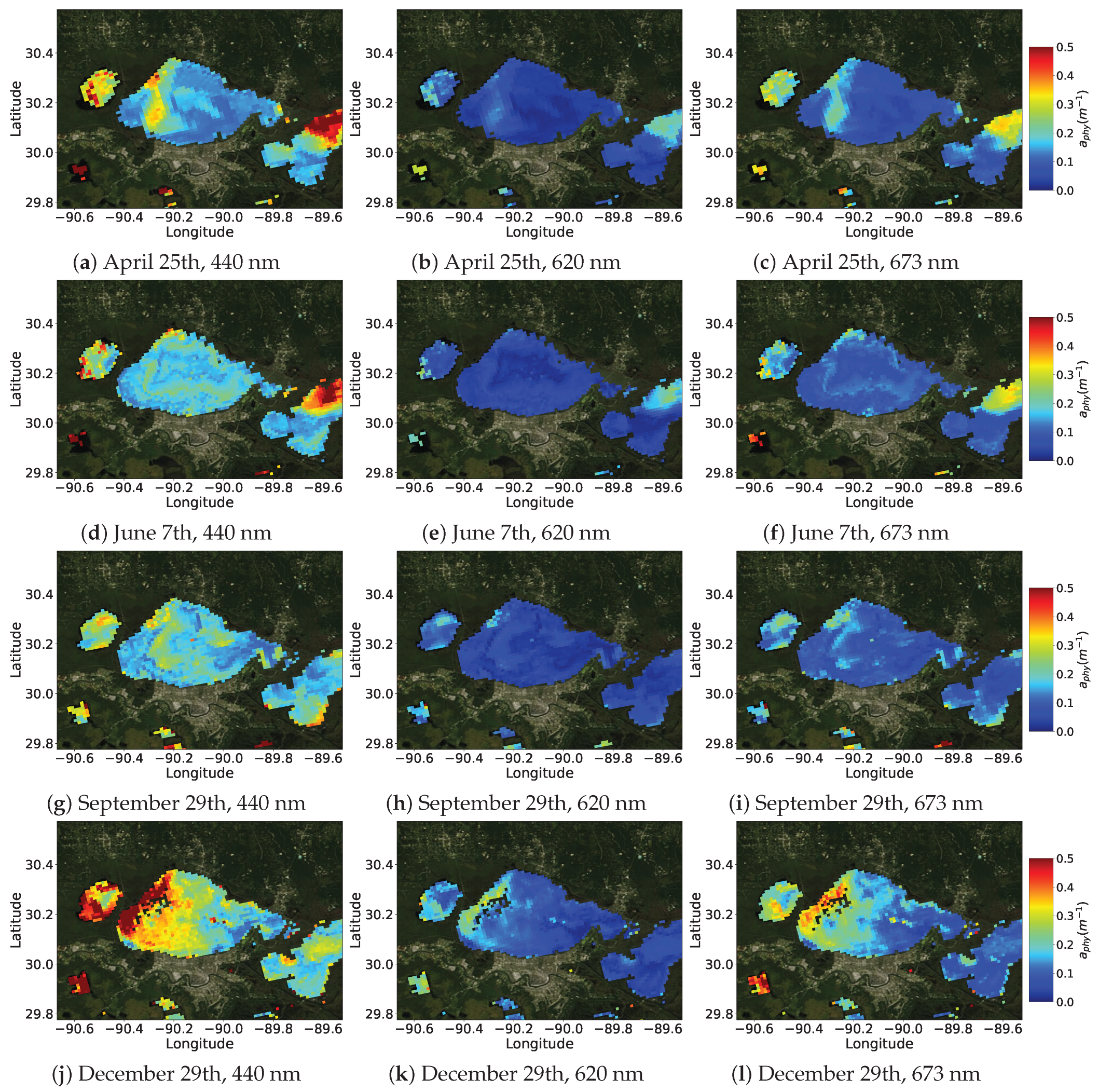
4.5. PhA-MOE Implementation on Field and PACE-OCI Observations
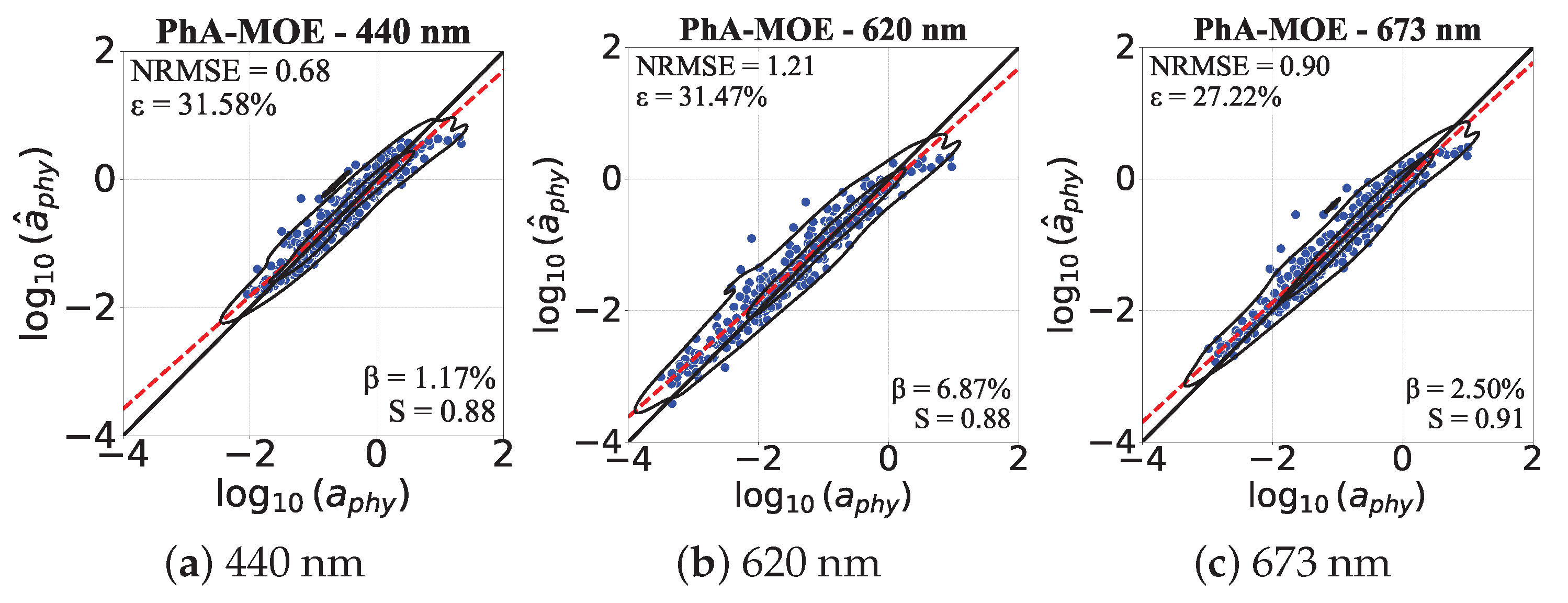
4.5.1. Comparison of Generalizability Between PhA-MOE and MDN
4.5.2. PhA-MOE for Map Prediction
5. Discussion
5.1. Data Preprocessing
5.2. Model Implementation of Satellite Imagery
5.3. Interpretability of MOE Structure
5.4. Potentials to Large Phytoplankton Foundation Models
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IOPs | Inherent Optical Properties |
| Phytoplankton Absorption Coefficient | |
| PPC | Phytoplankton Community Composition |
| MOE | Mixture of Experts |
| OCI | Ocean Color Instrument |
| PACE | Plankton, Aerosol, Cloud, Ocean Ecosystem |
| EMIT | Earth Surface Mineral Dust Source Investigation |
| SBG | Surface Biology Geology |
| HAB | Harmful Algal Bloom |
| Remote Sensing Reflectance | |
| IOP | Inherent Optical Properties |
| QAA | Quasi Analytical Algorithm |
| GIOP | Generalized IOP Inversion |
| CDOM | Colored Dissolved Organic Matter |
| NAP | Non-Algal Particles |
| AI | Artificial Intelligence |
| Chla | Chlorophyll-a |
| MDN | Mixture Density Network |
| TSS | Total Suspended Solids |
| PC | Phycocyanin |
| MLP | Multi-Layer Perceptron |
| QFT | Quantitative Filter Pad Technique |
| AOP | Apparent Optical Property |
| SOTA | State-of-the-Art |
| VAE | Variational Autoencoder |
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
Appendix A. Technical Details of PhA-MOE
- MOE-based Embedding:
- MDN-based Predictor:
- Loss Function:
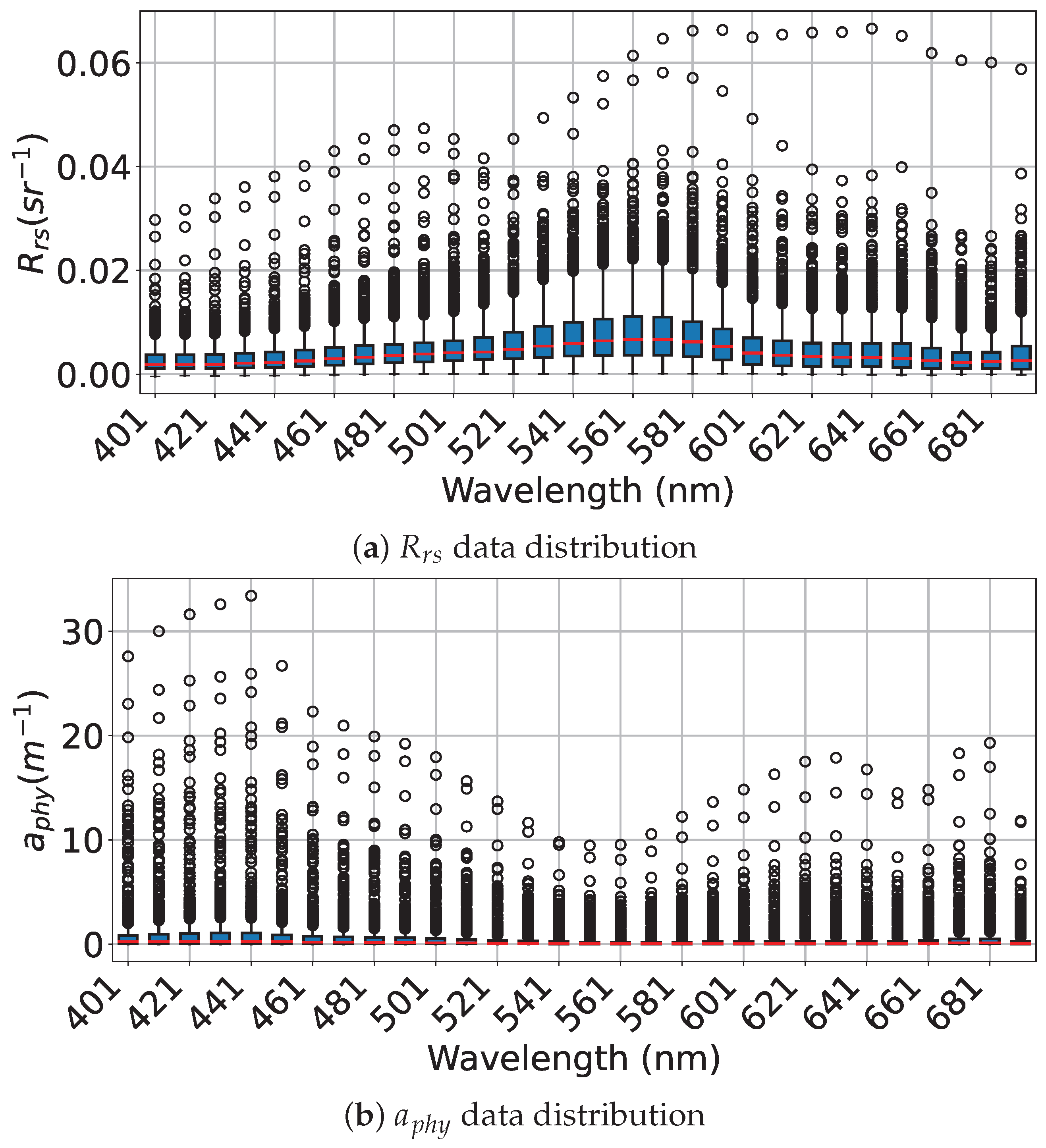
Appendix B. Box Plot Visualizations of Preprocessed Rrs and aphy

Appendix C. Stability Analysis Across Random Seeds
| Resolution | Model | ↓ | |||
|---|---|---|---|---|---|
| EMIT | MDN | 0.3487 | 0.1009 | 0.5163 | 0.6850 |
| PhA-MOE | 0.2359 | 0.0723 | 0.5226 | 0.5054 | |
| MLP | 0.4053 | 0.1270 | 0.4134 | 0.1924 | |
| VAE | 0.2395 | 0.1488 | 0.7382 | 0.3965 | |
| PACE | MDN | 0.1464 | 0.1206 | 0.4386 | 0.4120 |
| PhA-MOE | 0.0958 | 0.0843 | 0.2092 | 0.2631 | |
| MLP | 0.3288 | 0.1245 | 0.4551 | 0.1956 | |
| VAE | 0.4323 | 0.1555 | 0.6426 | 0.4813 |
References
- Henson, S.A.; Cael, B.; Allen, S.R.; Dutkiewicz, S. Future phytoplankton diversity in a changing climate. Nat. Commun. 2021, 12, 5372. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; D’Sa, E.J.; Maiti, K.; Rivera-Monroy, V.H.; Xue, Z. Biogeographical trends in phytoplankton community size structure using adaptive sentinel 3-OLCI chlorophyll a and spectral empirical orthogonal functions in the estuarine-shelf waters of the northern Gulf of Mexico. Remote Sens. Environ. 2021, 252, 112154. [Google Scholar] [CrossRef]
- Xi, H.; Hieronymi, M.; Röttgers, R.; Krasemann, H.; Qiu, Z. Hyperspectral Differentiation of Phytoplankton Taxonomic Groups: A Comparison between Using Remote Sensing Reflectance and Absorption Spectra. Remote Sens. 2015, 7, 14781–14805. [Google Scholar] [CrossRef]
- Liu, B.; D’Sa, E.J.; Joshi, I.D. Floodwater impact on Galveston Bay phytoplankton taxonomy, pigment composition and photo-physiological state following Hurricane Harvey from field and ocean color (Sentinel-3A OLCI) observations. Biogeosciences 2019, 16, 1975–2001. [Google Scholar] [CrossRef]
- Dierssen, H.M.; Ackleson, S.G.; Joyce, K.E.; Hestir, E.L.; Castagna, A.; Lavender, S.; McManus, M.A. Living up to the hype of hyperspectral aquatic remote sensing: Science, resources and outlook. Front. Environ. Sci. 2021, 9, 649528. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Roesler, C.S.; Boss, E. Spectral beam attenuation coefficient retrieved from ocean color inversion. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Werdell, P.J.; Franz, B.A.; Bailey, S.W.; Feldman, G.C.; Boss, E.; Brando, V.E.; Dowell, M.; Hirata, T.; Lavender, S.J.; Lee, Z.; et al. Generalized ocean color inversion model for retrieving marine inherent optical properties. Appl. Opt. 2013, 52, 2019–2037. [Google Scholar] [CrossRef]
- Zhu, Q.; Shen, F.; Shang, P.; Pan, Y.; Li, M. Hyperspectral remote sensing of phytoplankton species composition based on transfer learning. Remote Sens. 2019, 11, 2001. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Binding, C.; Gurlin, D.; Li, L.; Bresciani, M.; Giardino, C. Hyperspectral retrievals of phytoplankton absorption and chlorophyll-a in inland and nearshore coastal waters. Remote Sens. Environ. 2021, 253, 112200. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: San Diego, CA, USA, 1994. [Google Scholar]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. Atmos. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Roesler, C.; Pery, M. In situ phytoplankton absorption, fluorescence emission, and particulate backscattering spectra determined from reflectance. J. Geophys. Res. 1995, 100. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Hà, N.; et al. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- O’Shea, R.E.; Pahlevan, N.; Smith, B.; Boss, E.; Gurlin, D.; Alikas, K.; Kangro, K.; Kudela, R.M.; Vaičiūtė, D. A hyperspectral inversion framework for estimating absorbing inherent optical properties and biogeochemical parameters in inland and coastal waters. Remote Sens. Environ. 2023, 295, 113706. [Google Scholar] [CrossRef]
- Lehmann, M.K.; Gurlin, D.; Pahlevan, N.; Alikas, K.; Conroy, T.; Anstee, J.; Balasubramanian, S.V.; Barbosa, C.C.; Binding, C.; Bracher, A.; et al. GLORIA-A globally representative hyperspectral in situ dataset for optical sensing of water quality. Sci. Data 2023, 10, 100. [Google Scholar] [CrossRef]
- Roesler, C.; Stramski, D.; D’Sa, E.; Röttgers, R.; Reynolds, R.A. Spectrophotometric Measurements of Particulate Absorption Using Filter Pads; IOCCG: Washington, DC, USA, 2018. [Google Scholar]
- Zhou, K.; Liu, Z.; Qiao, Y.; Xiang, T.; Loy, C.C. Domain Generalization: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 4396–4415. [Google Scholar] [CrossRef]
- Zhou, K.; Yang, Y.; Qiao, Y.; Xiang, T. Domain Adaptive Ensemble Learning. IEEE Trans. Image Process. 2021, 30, 8008–8018. [Google Scholar] [CrossRef]
- Ding, Z.; Fu, Y. Deep Domain Generalization With Structured Low-Rank Constraint. IEEE Trans. Image Process. 2018, 27, 304–313. [Google Scholar] [CrossRef]
- Yuksel, S.E.; Wilson, J.N.; Gader, P.D. Twenty Years of Mixture of Experts. IEEE Trans. Neural Networks Learn. Syst. 2012, 23, 1177–1193. [Google Scholar] [CrossRef]
- Yi, L.; Yu, H.; Ren, C.; Zhang, H.; Wang, G.; Liu, X.; Li, X. pFedMoE: Data-level personalization with mixture of experts for model-heterogeneous personalized federated learning. arXiv 2024, arXiv:2402.01350. [Google Scholar]
- Huo, Z.; Zhang, L.; Khera, R.; Huang, S.; Qian, X.; Wang, Z.; Mortazavi, B.J. Sparse Gated Mixture-of-Experts to Separate and Interpret Patient Heterogeneity in EHR data. In Proceedings of the 2021 IEEE EMBS International Conference on Biomedical and Health Informatics (BHI), Athens, Greece, 27–30 July 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Eavani, H.; Hsieh, M.K.; An, Y.; Erus, G.; Beason-Held, L.; Resnick, S.; Davatzikos, C. Capturing heterogeneous group differences using mixture-of-experts: Application to a study of aging. NeuroImage 2016, 125, 498–514. [Google Scholar] [CrossRef]
- Mu, S.; Lin, S. A comprehensive survey of mixture-of-experts: Algorithms, theory, and applications. arXiv 2025, arXiv:2503.07137. [Google Scholar]
- Gould, R.W.; Arnone, R.A.; Sydor, M. Absorption, Scattering, and, Remote-Sensing Reflectance Relationships in Coastal Waters: Testing a New Inversion Algorith. J. Coast. Res. 2001, 17, 328–341. [Google Scholar]
- Naik, P.; D’Sa, E. Phytoplankton Light Absorption of Cultures and Natural Samples: Comparisons Using Two Spectrophotometers. Opt. Express 2012, 20, 4871–4886. [Google Scholar] [CrossRef] [PubMed]
- Stramski, D.; Reynolds, R.A.; Kaczmarek, S.; Uitz, J.; Zheng, G. Correction of pathlength amplification in the filter-pad technique for measurements of particulate absorption coefficient in the visible spectral region. Appl. Opt. 2015, 54, 6763–6782. [Google Scholar] [CrossRef]
- Dierssen, H.; Bracher, A.; Brando, V.; Loisel, H.; Ruddick, K. Data Needs for Hyperspectral Detection of Algal Diversity Across the Globe. Oceanography 2020, 33, 74–79. [Google Scholar] [CrossRef]
- Liu, B.; Wu, Q. HyperCoast: A Python Package for Visualizing and Analyzing Hyperspectral Data in Coastal Environments. J. Open Source Softw. 2024, 9, 7025. [Google Scholar] [CrossRef]
- Singh, D.; Singh, B. Investigating the impact of data normalization on classification performance. Appl. Soft Comput. 2020, 97, 105524. [Google Scholar] [CrossRef]
- Cabello-Solorzano, K.; Ortigosa de Araujo, I.; Peña, M.; Correia, L.; Tallón-Ballesteros, A.J. The impact of data normalization on the accuracy of machine learning algorithms: A comparative analysis. In Proceedings of the International Conference on Soft Computing Models in Industrial and Environmental Applications; Springer: Cham, Switzerland, 2023; pp. 344–353. [Google Scholar]
- Koprinkova, P.; Petrova, M. Data-scaling problems in neural-network training. Eng. Appl. Artif. Intell. 1999, 12, 281–296. [Google Scholar] [CrossRef]
- Jacobs, R.A.; Jordan, M.I.; Nowlan, S.J.; Hinton, G.E. Adaptive Mixtures of Local Experts. Neural Comput. 1991, 3, 79–87. [Google Scholar] [CrossRef]
- Jordan, M.I.; Jacobs, R.A. Hierarchical Mixtures of Experts and the EM Algorithm. Neural Comput. 1994, 6, 181–214. [Google Scholar] [CrossRef]
- Dai, Y.; Li, X.; Liu, J.; Tong, Z.; Duan, L.Y. Generalizable Person Re-Identification with Relevance-Aware Mixture of Experts. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 16145–16154. [Google Scholar]
- Li, B.; Shen, Y.; Yang, J.; Wang, Y.; Ren, J.; Che, T.; Zhang, J.; Liu, Z. Sparse Mixture-of-Experts are Domain Generalizable Learners. In Proceedings of the the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Wang, M.; Yuan, J.; Wang, Z. Mixture-of-Experts Learner for Single Long-Tailed Domain Generalization. In Proceedings of the Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; MM ’23. pp. 290–299. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, K.Y.; Yao, T.; Yi, R.; Ding, S.; Ma, L. Adaptive Mixture of Experts Learning for Generalizable Face Anti-Spoofing. In Proceedings of the Proceedings of the 30th ACM International Conference on Multimedia; Lisboa, Portugal, 10–14 October 2022, MM ’22; pp. 6009–6018. [CrossRef]
- Enzweiler, M.; Gavrila, D.M. A Multilevel Mixture-of-Experts Framework for Pedestrian Classification. IEEE Trans. Image Process. 2011, 20, 2967–2979. [Google Scholar] [CrossRef] [PubMed]
- Doersch, C. Tutorial on Variational Autoencoders. arXiv 2016. [Google Scholar] [CrossRef]
- Shazeer, N.; Mirhoseini, A.; Maziarz, K.; Davis, A.; Le, Q.V.; Hinton, G.E.; Dean, J. Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Balasubramanian, S.V.; Pahlevan, N.; Smith, B.; Binding, C.; Schalles, J.; Loisel, H.; Gurlin, D.; Greb, S.; Alikas, K.; Randla, M.; et al. Robust algorithm for estimating total suspended solids (TSS) in inland and nearshore coastal waters. Remote Sens. Environ. 2020, 246, 111768. [Google Scholar] [CrossRef]
- Lohrenz, S.E.; Weidemann, A.D.; Tuel, M. Phytoplankton spectral absorption as influenced by community size structure and pigment composition. J. Plankton Res. 2003, 25, 35–61. [Google Scholar] [CrossRef]
- Ahonen, S.; Jones, R.; Seppälä, J.; Vuorio, K.; Tiirola, M.; Vähätalo, A. Phytoplankton absorb mainly red light in lakes with high chromophoric dissolved organic matter. Limnol. Oceanogr. 2025, 70, 1359–1374. [Google Scholar] [CrossRef]
- Lou, J.; Liu, B.; Xiong, Y.; Zhang, X.; Yuan, X. Variational Autoencoder Framework for Hyperspectral Retrievals (Hyper-VAE) of Phytoplankton Absorption and Chlorophyll a in Coastal Waters for NASA’s EMIT and PACE Missions. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–16. [Google Scholar] [CrossRef]
- Liu, B.; D’Sa, E.J.; Joshi, I. Multi-decadal trends and influences on dissolved organic carbon distribution in the Barataria Basin, Louisiana from in-situ and Landsat/MODIS observations. Remote Sens. Environ. 2019, 228, 183–202. [Google Scholar] [CrossRef]
- Popescu, M.C.; Balas, V.E.; Perescu-Popescu, L.; Mastorakis, N. Multilayer perceptron and neural networks. WSEAS Trans. Cir. Sys. 2009, 8, 579–588. [Google Scholar]




| Model | EMIT | PACE |
|---|---|---|
| MLP | 6 layers, 256 neurons each | 4 layers with (256, 512, 512, 256) neurons |
| VAE Encoder | 2 layers with (512, 256) neurons | 2 layers with (512, 256) neurons |
| VAE Decoder | 2 layers, 256 neurons each | 2 layers, 256 neurons each |
| MDN | 5 layers, 256 neurons each | 6 layers, 256 neurons each |
| PhA-MOE | MOE part: 8 experts, each has two layers with 256 neurons each | |
| MDN part: 3 layers, 256 neurons each | 4 layers, 256 neurons each | |
| Preprocessing Methods | Models | |||
|---|---|---|---|---|
| PhA-MOE | MDN | MLP | VAE | |
| Rob-WL-Log-WL | 1.17 | 1.25 | 7.35 | 5.08 |
| Rob-WB-Log-WB | 1.51 | 1.63 | 8.19 | 8.61 |
| Rob-WL-Rob-WL | 3.71 | 9.06 | 4.56 | 9.71 |
| Rob-WB-Rob-WB | 5.77 | 5.22 | 4.34 | 8.12 |
| Log-WL-Log-WL | 1.88 | 1.71 | 8.12 | 10.92 |
| Log-WB-Log-WB | 5.22 | 1.89 | 22.56 | 12.93 |
| No preprocessing | 1.43 | 2.01 | 7.23 | 13.53 |
| Preprocessing Methods | Models | |||
|---|---|---|---|---|
| PhA-MOE | MDN | MLP | VAE | |
| Rob-WL-Log-WL | 1.93 | 2.49 | 8.04 | 6.79 |
| Rob-WB-Log-WB | 1.46 | 1.72 | 7.88 | 9.69 |
| Rob-WL-Rob-WL | 28.20 | 25.10 | 6.58 | 8.54 |
| Rob-WB-Rob-WB | 29.59 | 29.45 | 5.13 | 9.36 |
| Log-WL-Log-WL | 51.96 | 63.77 | 8.66 | 14.77 |
| Log-WB-Log-WB | 76.67 | 54.95 | 8.89 | 12.67 |
| No preprocessing | 15.75 | 14.43 | 4.57 | 14.50 |
| Resolution | Model | NRMSE ↓ | |||
|---|---|---|---|---|---|
| EMIT | MDN | 1.25 | 28.37 | 8.18 | 0.088 |
| PhA-MOE | 1.17 | 28.35 | 6.92 | 0.085 | |
| MLP | 4.35 | 69.15 | 30.27 | 0.37 | |
| VAE | 5.08 | 50.64 | 17.55 | 0.23 | |
| PACE | MDN | 1.72 | 41.25 | 12.79 | 0.13 |
| PhA-MOE | 1.46 | 39.08 | 8.55 | 0.13 | |
| MLP | 4.57 | 55.09 | 25.42 | 0.33 | |
| VAE | 6.79 | 46.17 | 17.05 | 0.23 |
| Phase | Model | NRMSE ↓ | |||
|---|---|---|---|---|---|
| Before Fine-tuning | MDN (avg) | 1.68 | 44.41 | 32.79 | 0.12 |
| PhA-MOE (avg) | 1.50 | 41.46 | 35.33 | 0.10 | |
| MDN (best) | 1.20 | 51.35 | 48.27 | 0.10 | |
| PhA-MOE (best) | 1.06 | 38.87 | 27.48 | 0.10 | |
| After Fine-tuning | MDN (avg) | 0.56 | 29.70 | 6.83 | 0.09 |
| PhA-MOE (avg) | 0.50 | 28.65 | 7.80 | 0.11 | |
| MDN (best) | 0.41 | 36.64 | 3.87 | 0.03 | |
| PhA-MOE (best) | 0.35 | 21.56 | 2.55 | 0.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Liu, B.; Gao, S.; Li, J.; Zhou, Y.; Zhang, S.; Ding, Z. PhA-MOE: Enhancing Hyperspectral Retrievals for Phytoplankton Absorption Using Mixture-of-Experts. Remote Sens. 2025, 17, 2103. https://doi.org/10.3390/rs17122103
Wang W, Liu B, Gao S, Li J, Zhou Y, Zhang S, Ding Z. PhA-MOE: Enhancing Hyperspectral Retrievals for Phytoplankton Absorption Using Mixture-of-Experts. Remote Sensing. 2025; 17(12):2103. https://doi.org/10.3390/rs17122103
Chicago/Turabian StyleWang, Weiwei, Bingqing Liu, Song Gao, Jiang Li, Yueling Zhou, Songyang Zhang, and Zhi Ding. 2025. "PhA-MOE: Enhancing Hyperspectral Retrievals for Phytoplankton Absorption Using Mixture-of-Experts" Remote Sensing 17, no. 12: 2103. https://doi.org/10.3390/rs17122103
APA StyleWang, W., Liu, B., Gao, S., Li, J., Zhou, Y., Zhang, S., & Ding, Z. (2025). PhA-MOE: Enhancing Hyperspectral Retrievals for Phytoplankton Absorption Using Mixture-of-Experts. Remote Sensing, 17(12), 2103. https://doi.org/10.3390/rs17122103







