UIMM-Tracker: IMM-Based with Uncertainty Detection for Video Satellite Infrared Small-Target Tracking
Abstract
1. Introduction
2. Related Works
2.1. Small-Target Tracking in Video Satellites
2.2. Infrared Small-Target Tracking
2.3. Application of Uncertainty Measurement
3. Method
3.1. Overview
| Algorithm 1 UIMM-Tracker execution process | |
| Input: Image sequence 1~n, Detection result , Detection uncertainty covariance | |
| Output: Trajectory , The mean of the updated , updated state covariance , fused state mean , fused state covariance , Markov transition matrix , model probability | |
| Initial: CT model control variable , Markov transition matrix , model probability , target initial state mean , Initial state covariance = . | |
| 1 for k in 1~t do | |
| 2 | Uncertainty of Measurement Detection Result d: ; |
| 3 | Input Interaction and Filtering; |
| 4 | Calculate the mixed state mean and mixed covariance for model j based on the updated state mean and updated state covariance of all models; #(1)~(4) |
| 5 | Obtain the sigma points of the UKF based on and ; #(5) |
| 6 | Obtain the predicted mean and predicted covariance ; #(6)~(8) |
| 7 | Calculate the observation predicted mean and observation predicted covariance ; #(9)~(11) |
| 8 | Data Association; |
| 9 | Combine NWD and IoU distance to calculate the cost of trajectory and detection ; #(12)~(15) |
| 10 | Iterate over p and q to obtain the cost matrix ; |
| 11 | Calculate the scale cost for ambiguous matches of trajectory and detection ; #(16) |
| 12 | Calculate the scale cost for ambiguous matches of trajectory and detection ; #(17)~(18) |
| 13 | Combine the scale cost and energy cost to obtain the additional cost matrix U; #(19) |
| 14 | Integrate the cost matrix and apply Hungarian matching to obtain the association result ; |
| 15 | Model Probability Update; |
| 16 | Calculate the cross-covariance between the predicted mean and the association result ; #(20) |
| 17 | Calculate the Kalman gain ; #(21) |
| 18 | Calculate the updated state mean and updated state covariance ; #(22)~(23) |
| 19 | Data Fusion; |
| 20 | Calculate the likelihood probability using , and ; #(24) |
| 21 | Calculate the model probability using , Markov transition probability , and the model probability ; #(25) |
| 22 | Calculate the fused state mean and fused covariance using , , and ; #(26)~(27) |
| 23 | Dynamic Markov Transition Matrix; |
| 24 | Calculate the state prediction error using the observation predicted mean and the association result ; |
| 25 | Calculate the normalized likelihood probability ; |
| 26 | Calculate the rate of change of model probability ; |
| 27 | Calculate the Markov transition probability matrix ; #(28)~(29) |
| 28 | Filling Discontinuous Trajectories; |
| 29 | For discontinuous trajectories from time t1 to t2, use the fused state mean at time t2 and the predicted mean to correct the prediction error. #(30) |
| 30 end | |
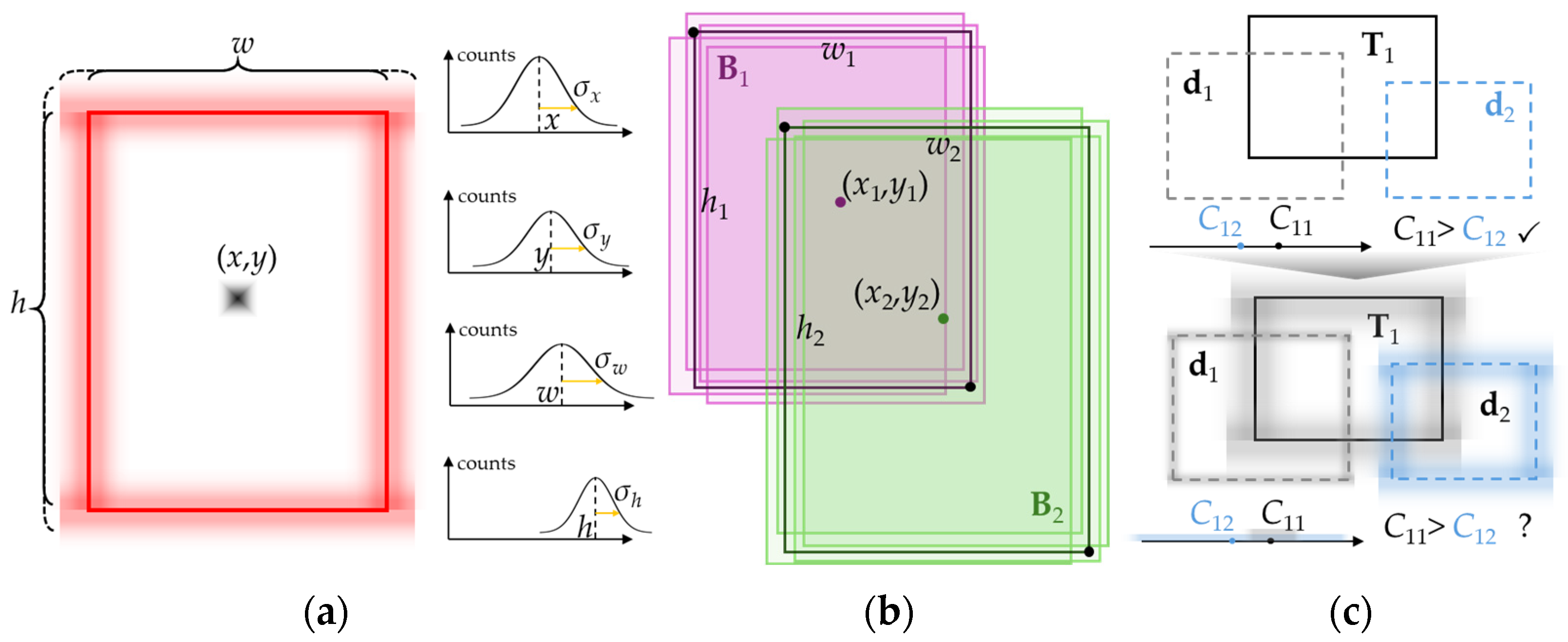
3.2. Uncertainty Measurement of Detection Results
3.3. Input Interaction and Filtering
3.4. Data Association
3.5. Model Probability Update and Data Fusion
3.6. Dynamic Markov Transition Matrix
3.7. Method for Filling Discontinuous Trajectories
4. Experiments and Results
4.1. Experimental Setting
4.1.1. Datasets
4.1.2. Comparison Methods
4.1.3. Evaluation Metrics
4.1.4. Implementation Details
4.2. Comparison with Various Methods
4.2.1. Quantitative Analysis
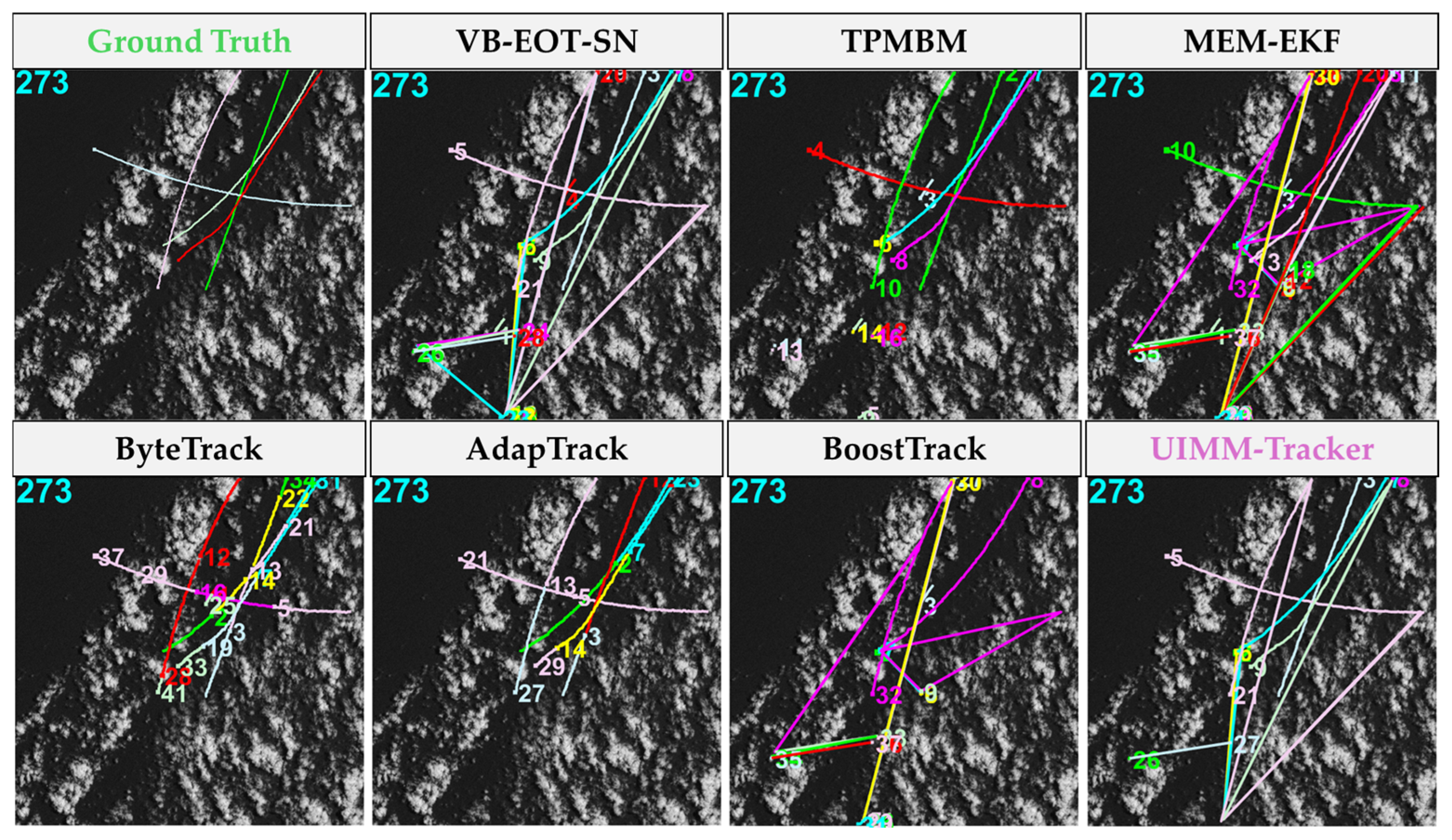
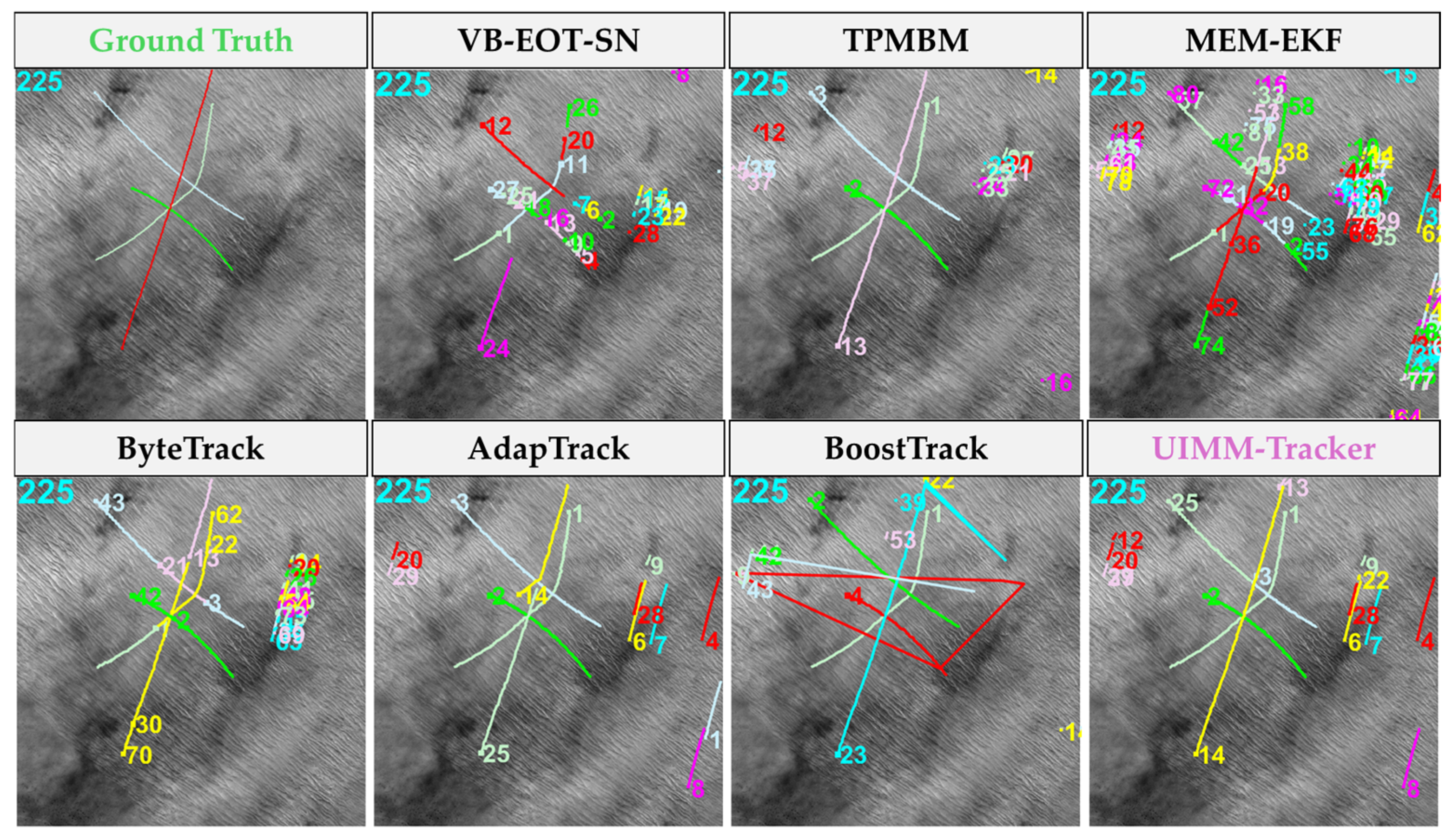
4.2.2. Qualitative Analysis
4.2.3. Efficiency Comparison
4.3. The Ablation Study
4.3.1. Impact of Detection Uncertainty
4.3.2. The Impact of the Markov Transition Matrix
4.3.3. The Impact of Association Methods
4.3.4. The Impact of Multi-Model
4.3.5. Comparison of Tracking Performance Under Different Detection Qualities
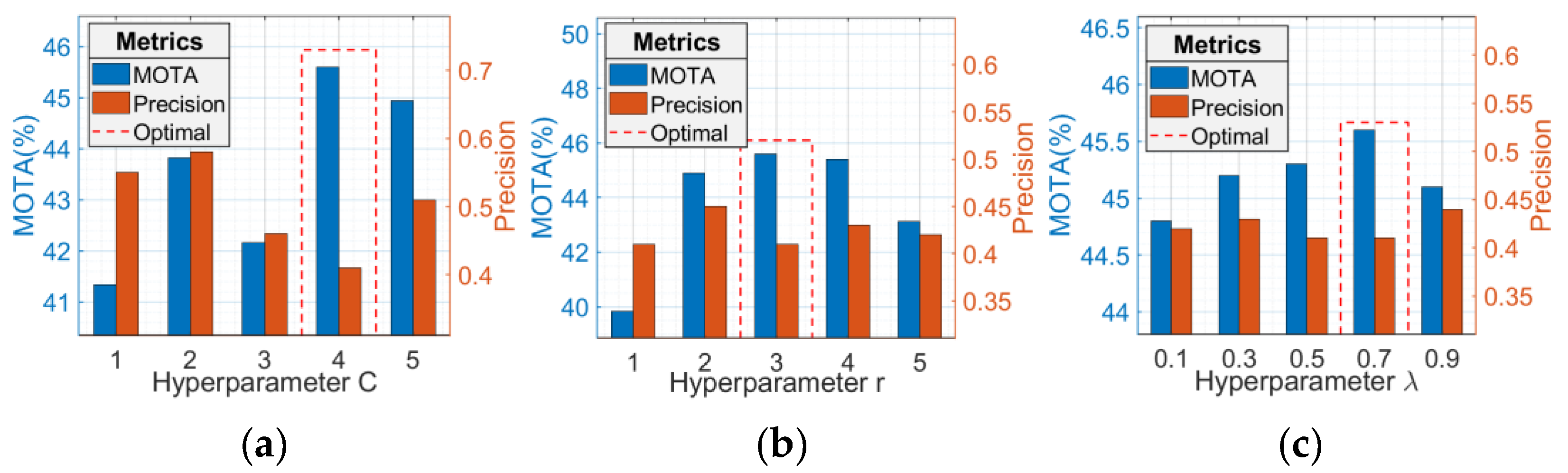
4.3.6. Analysis of Model Hyperparameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kallenborn, Z.; Plichta, M. Breaking the Shield: Countering Drone Defenses. Jt. Force Q. 2024, 113, 26–35. [Google Scholar]
- Jones, M.W.; Kelley, D.I.; Burton, C.A.; Di Giuseppe, F.; Barbosa, M.L.F.; Brambleby, E.; Hartley, A.J.; Lombardi, A.; Mataveli, G.; McNorton, J.R.; et al. State of Wildfires 2023–2024. Earth Syst. Sci. Data 2024, 16, 3601–3685. [Google Scholar] [CrossRef]
- Shi, T.; Gong, J.; Hu, J.; Sun, Y.; Bao, G.; Zhang, P.; Wang, J.; Zhi, X.; Zhang, W. Progressive Class-Aware Instance Enhancement for Aircraft Detection in Remote Sensing Imagery. Pattern Recognit. 2025, 164, 111503. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, R.; Zou, L.; Tang, H. Hierarchical Distribution-Based Exemplar Replay for Incremental SAR Automatic Target Recognition. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 6576–6588. [Google Scholar] [CrossRef]
- Hu, J.; Wei, Y.; Chen, W.; Zhi, X.; Zhang, W. CM-YOLO: Typical Object Detection Method in Remote Sensing Cloud and Mist Scene Images. Remote Sens. 2025, 17, 125. [Google Scholar] [CrossRef]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared Patch-Image Model for Small Target Detection in a Single Image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef]
- Huang, Y.; Zhi, X.; Hu, J.; Yu, L.; Han, Q.; Chen, W.; Zhang, W. FDDBA-NET: Frequency Domain Decoupling Bidirectional Interactive Attention Network for Infrared Small Target Detection. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 5004416. [Google Scholar] [CrossRef]
- Nicola, M.; Gobetto, R.; Bazzacco, A.; Anselmi, C.; Ferraris, E.; Russo, A.; Masic, A.; Sgamellotti, A. Real-Time Identification and Visualization of Egyptian Blue Using Modified Night Vision Goggles. Rend. Fis. Acc. Lincei 2024, 35, 495–512. [Google Scholar] [CrossRef]
- Zhou, X.; Li, L.; Yu, J.; Gao, L.; Zhang, R.; Hu, Z.; Chen, F. Multimodal Aircraft Flight Altitude Inversion from SDGSAT-1 Thermal Infrared Data. Remote Sens. Environ. 2024, 308, 114178. [Google Scholar] [CrossRef]
- Zhang, R.; Li, H.; Duan, K.; You, S.; Liu, K.; Wang, F.; Hu, Y. Automatic Detection of Earthquake-Damaged Buildings by Integrating UAV Oblique Photography and Infrared Thermal Imaging. Remote Sens. 2020, 12, 2621. [Google Scholar] [CrossRef]
- Huang, Y.; Zhi, X.; Hu, J.; Yu, L.; Han, Q.; Chen, W.; Zhang, W. LMAFormer: Local Motion Aware Transformer for Small Moving Infrared Target Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–17. [Google Scholar] [CrossRef]
- Kou, R.; Wang, C.; Yu, Y.; Peng, Z.; Huang, F.; Fu, Q. Infrared Small Target Tracking Algorithm via Segmentation Network and Multistrategy Fusion. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Li, X.; Lv, C.; Wang, W.; Li, G.; Yang, L.; Yang, J. Generalized Focal Loss: Towards Efficient Representation Learning for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 3139–3153. [Google Scholar] [CrossRef]
- Xie, X.; Xi, J.; Yang, X.; Lu, R.; Xia, W. STFTrack: Spatio-Temporal-Focused Siamese Network for Infrared UAV Tracking. Drones 2023, 7, 296. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian Method for the Assignment Problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Psalta, A.; Tsironis, V.; Karantzalos, K. Transformer-Based Assignment Decision Network for Multiple Object Tracking. Comput. Vis. Image Underst. 2024, 241, 103957. [Google Scholar] [CrossRef]
- Zou, Z.; Hao, J.; Shu, L. Rethinking Bipartite Graph Matching in Realtime Multi-object Tracking. In Proceedings of the 2022 Asia Conference on Algorithms, Computing and Machine Learning (CACML), Hangzhou, China, 25–27 March 2022; pp. 713–718. [Google Scholar]
- Rezatofighi, S.H.; Milan, A.; Zhang, Z.; Shi, Q.; Dick, A.; Reid, I. Joint Probabilistic Data Association Revisited. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3047–3055. [Google Scholar]
- Kim, C.; Li, F.; Ciptadi, A.; Rehg, J.M. Multiple Hypothesis Tracking Revisited. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Yi, K.; Luo, K.; Luo, X.; Huang, J.; Wu, H.; Hu, R.; Hao, W. UCMCTrack: Multi-Object Tracking with Uniform Camera Motion Compensation. Proc. AAAI Conf. Artif. Intell. 2024, 38, 6702–6710. [Google Scholar] [CrossRef]
- Hess, R.; Fern, A. Discriminatively Trained Particle Filters for Complex Multi-Object Tracking. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 240–247. [Google Scholar]
- Moraffah, B.; Papandreou-Suppappola, A. Bayesian Nonparametric Modeling for Predicting Dynamic Dependencies in Multiple Object Tracking. Sensors 2022, 22, 388. [Google Scholar] [CrossRef]
- Lee, I.H.; Park, C.G. Integrating Detection and Tracking of Infrared Aerial Targets with Random Finite Sets. In Proceedings of the 2024 24th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 29 October–1 November 2024; pp. 661–666. [Google Scholar]
- Wang, C.; Wang, Y.; Wang, Y.; Wu, C.-T.; Yu, G. muSSP: Efficient Min-cost Flow Algorithm for Multi-object Tracking. Neural Inf. Process. Syst. 2019, 32, 423–432. [Google Scholar]
- Zhou, H.; Ouyang, W.; Cheng, J.; Wang, X.; Li, H. Deep Continuous Conditional Random Fields With Asymmetric Inter-Object Constraints for Online Multi-Object Tracking. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 1011–1022. [Google Scholar] [CrossRef]
- Bozorgtabar, B.; Goecke, R. Efficient Multi-Target Tracking via Discovering Dense Subgraphs. Comput. Vis. Image Underst. 2016, 144, 205–216. [Google Scholar] [CrossRef]
- Yang, Z.; Nie, H.; Liu, Y.; Bian, C. Robust Tracking Method for Small and Weak Multiple Targets Under Dynamic Interference Based on Q-IMM-MHT. Sensors 2025, 25, 1058. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, R.; Zhang, D.; Li, M.; Cao, J.; Zheng, Z. CATrack: Condition-Aware Multi-Object Tracking with Temporally Enhanced Appearance Features. Knowl.-Based Syst. 2025, 308, 112760. [Google Scholar] [CrossRef]
- Huang, M.; Li, X.; Hu, J.; Peng, H.; Lyu, S. Tracking Multiple Deformable Objects in Egocentric Videos. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 1461–1471. [Google Scholar]
- Zhang, J.; Wang, H.; Cui, F.; Liu, Y.; Liu, Z.; Dong, J. Research into Ship Trajectory Prediction Based on An Improved LSTM Network. J. Mar. Sci. Eng. 2023, 11, 1268. [Google Scholar] [CrossRef]
- Ma, J.; Chen, X.; Bao, W.; Xu, J.; Wang, H. MADiff: Motion-Aware Mamba Diffusion Models for Hand Trajectory Prediction on Egocentric Videos. arXiv 2024, arXiv:2409.02638. [Google Scholar] [CrossRef]
- Qin, Z.; Zhou, S.; Wang, L.; Duan, J.; Hua, G.; Tang, W. MotionTrack: Learning Robust Short-Term and Long-Term Motions for Multi-Object Tracking. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 17939–17948. [Google Scholar]
- Li, X.; Liu, D.; Wu, Y.; Wu, X.; Zhao, L.; Gao, J. Fast-Poly: A Fast Polyhedral Framework For 3D Multi-Object Tracking. IEEE Robot. Autom. Lett. 2024, 9, 10519–10526. [Google Scholar] [CrossRef]
- Hua, B.; Yang, G.; Wu, Y.; Chen, Z. Angle-Only Target Tracking Method for Optical Imaging Micro-/Nanosatellite Based on APSO-SSUKF. Space Sci. Technol. 2022, 2022, 9898147. [Google Scholar] [CrossRef]
- Yu, C.; Feng, Z.; Wu, Z.; Wei, R.; Song, B.; Cao, C. HB-YOLO: An Improved YOLOv7 Algorithm for Dim-Object Tracking in Satellite Remote Sensing Videos. Remote Sens. 2023, 15, 3551. [Google Scholar] [CrossRef]
- Wang, B.; Sui, H.; Ma, G.; Zhou, Y. MCTracker: Satellite Video Multi-Object Tracking Considering Inter-Frame Motion Correlation and Multi-Scale Cascaded Feature Enhancement. ISPRS J. Photogramm. Remote Sens. 2024, 214, 82–103. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, C.; Liu, L.; Shi, Z.; Zou, Z. MetaEarth: A Generative Foundation Model for Global-Scale Remote Sensing Image Generation. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 1764–1781. [Google Scholar] [CrossRef]
- Revach, G.; Shlezinger, N.; Ni, X.; Escoriza, A.L.; van Sloun, R.J.G.; Eldar, Y.C. KalmanNet: Neural Network Aided Kalman Filtering for Partially Known Dynamics. IEEE Trans. Signal Process. 2022, 70, 1532–1547. [Google Scholar] [CrossRef]
- Xinlong, L.; Hamdulla, A. Research on Infrared Small Target Tracking Method. In Proceedings of the 2020 12th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Phuket, Thailand, 28–29 February 2020; pp. 610–614. [Google Scholar]
- Shan, J.; Yang, Y.; Liu, H.; Liu, T. Infrared Small Target Tracking Based on OSTrack Model. IEEE Access 2023, 11, 123938–123946. [Google Scholar] [CrossRef]
- Ye, B.; Chang, H.; Ma, B.; Shan, S.; Chen, X. Joint Feature Learning and Relation Modeling for Tracking: A One-Stream Framework. arXiv 2022, arXiv:2203.11991. [Google Scholar] [CrossRef]
- Fan, J.; Wei, J.; Huang, H.; Zhang, D.; Chen, C. IRSDT: A Framework for Infrared Small Target Tracking with Enhanced Detection. Sensors 2023, 23, 4240. [Google Scholar] [CrossRef]
- Shuai, B.; Berneshawi, A.; Li, X.; Modolo, D.; Tighe, J. SiamMOT: Siamese Multi-Object Tracking. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 12367–12377. [Google Scholar]
- Qian, K.; Zhang, S.; Ma, H.; Sun, W. SiamIST: Infrared Small Target Tracking Based on an Improved SiamRPN. Infrared Phys. Technol. 2023, 134, 104920. [Google Scholar] [CrossRef]
- Zhang, L.; Lin, W.; Shen, Z.; Zhang, D.; Xu, B.; Wang, K.; Chen, J. Infrared Dim and Small Target Sequence Dataset Generation Method Based on Generative Adversarial Networks. Electronics 2023, 12, 3625. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, L.; Sheng, W.; Wang, Y.; Xiao, C.; Ma, C.; An, W. Heterogeneous Graph Transformer for Multiple Tiny Object Tracking in RGB-T Videos. IEEE Trans. Multimed. 2024, 26, 9383–9397. [Google Scholar] [CrossRef]
- Tang, X.; Zhong, G.; Li, S.; Yang, K.; Shu, K.; Cao, D.; Lin, X. Uncertainty-Aware Decision-Making for Autonomous Driving at Uncontrolled Intersections. IEEE Trans. Intell. Transp. Syst. 2023, 24, 9725–9735. [Google Scholar] [CrossRef]
- Chen, M.; Chen, M.; Yang, Y. UAHOI: Uncertainty-Aware Robust Interaction Learning for HOI Detection. Comput. Vis. Image Underst. 2024, 247, 104091. [Google Scholar] [CrossRef]
- Kath, H.; Serafini, P.P.; Campos, I.B.; Gouvêa, T.S.; Sonntag, D. Leveraging Transfer Learning and Active Learning for Data Annotation in Passive Acoustic Monitoring of Wildlife. Ecol. Inform. 2024, 82, 102710. [Google Scholar] [CrossRef]
- Rong, Q.; Wu, H.; Otkur, A.; Yue, W.; Su, M. A Novel Uncertainty Analysis Method to Improve the Accuracy of Agricultural Grey Water Footprint Evaluation Considering the Influence of Production Conditions. Ecol. Indic. 2023, 154, 110641. [Google Scholar] [CrossRef]
- Maleki Varnosfaderani, S.; Forouzanfar, M. The Role of AI in Hospitals and Clinics: Transforming Healthcare in the 21st Century. Bioengineering 2024, 11, 337. [Google Scholar] [CrossRef]
- Mays, D.J.; Elsayed, S.A.; Hassanein, H.S. Uncertainty-Aware Multitask Allocation for Parallelized Mobile Edge Learning. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 3597–3602. [Google Scholar]
- Zhou, H.; Yu, J.; Yang, W. Dual Memory Units with Uncertainty Regulation for Weakly Supervised Video Anomaly Detection. Proc. AAAI Conf. Artif. Intell. 2023, 37, 3769–3777. [Google Scholar] [CrossRef]
- Ying, X.; Xiao, C.; Li, R.; He, X.; Li, B.; Li, Z.; Wang, Y.; Hu, M.; Xu, Q.; Lin, Z.; et al. Visible-Thermal Tiny Object Detection: A Benchmark Dataset and Baselines 2024. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 6088–6096. [Google Scholar] [CrossRef]
- Ying, X.; Liu, L.; Lin, Z.; Shi, Y.; Wang, Y.; Li, R.; Cao, X.; Li, B.; Zhou, S. Infrared Small Target Detection in Satellite Videos: A New Dataset and A Novel Recurrent Feature Refinement Framework. IEEE Trans. Geosci. Remote Sens 2024, 63, 1–18. [Google Scholar] [CrossRef]
- Zhang, L.; Lan, J. Extended Object Tracking Using Random Matrix With Skewness. IEEE Trans. Signal Process. 2020, 68, 5107–5121. [Google Scholar] [CrossRef]
- Xia, Y.; García-Fernández, Á.F.; Meyer, F.; Williams, J.L.; Granström, K.; Svensson, L. Trajectory PMB Filters for Extended Object Tracking Using Belief Propagation. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 9312–9331. [Google Scholar] [CrossRef]
- Garcia-Fernandez, A.F.; Svensson, L. Tracking Multiple Spawning Targets Using Poisson Multi-Bernoulli Mixtures on Sets of Tree Trajectories. IEEE Trans. Signal Process. 2022, 70, 1987–1999. [Google Scholar] [CrossRef]
- Granstrom, K.; Svensson, L.; Xia, Y.; Williams, J.; García-Fernández, Á.F. Poisson Multi-Bernoulli Mixtures for Sets of Trajectories. IEEE Trans. Aerosp. Electron. Syst. 2024, 61, 5178–5194. [Google Scholar] [CrossRef]
- García-Fernández, Á.F.; Särkkä, S. Gaussian Multi-Target Filtering with Target Dynamics Driven by a Stochastic Differential Equation. arXiv 2024, arXiv:2411.19814. [Google Scholar] [CrossRef]
- Yang, S.; Baum, M. Tracking the Orientation and Axes Lengths of an Elliptical Extended Object. IEEE Trans. Signal Process. 2019, 67, 4720–4729. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, P.; Jiang, Y.; Yu, D.; Weng, F.; Yuan, Z.; Luo, P.; Liu, W.; Wang, X. ByteTrack: Multi-object Tracking by Associating Every Detection Box. In Computer Vision—ECCV 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Lecture Notes in Computer Science; Springer Nature: Cham, Switzerland, 2022; Volume 13682, pp. 1–21. ISBN 978-3-031-20046-5. [Google Scholar]
- Shim, K.; Hwang, J.; Ko, K.; Kim, C. A Confidence-Aware Matching Strategy For Generalized Multi-Object Tracking. In Proceedings of the 2024 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 27–30 October 2024; pp. 4042–4048. [Google Scholar]
- Shim, K.; Ko, K.; Hwang, J.; Kim, C. Adaptrack: Adaptive Thresholding-Based Matching for Multi-Object Tracking. In Proceedings of the 2024 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 27 September 2024. [Google Scholar]
- Huang, H.-W.; Yang, C.-Y.; Sun, J.; Kim, P.-K.; Kim, K.-J.; Lee, K.; Huang, C.-I.; Hwang, J.-N. Iterative Scale-Up ExpansionIoU and Deep Features Association for Multi-Object Tracking in Sports. In Proceedings of the 2024 IEEE/CVF Winter Conference on Applications of Computer Vision Workshops (WACVW), Waikoloa, HI, USA, 1–6 January 2024; pp. 163–172. [Google Scholar]
- Stanojevic, V.D. BoostTrack: Boosting the Similarity Measure and Detection Confidence for Improved Multiple Object Tracking. Mach. Vis. Appl. 2024, 35, 1–15. [Google Scholar] [CrossRef]
- Kasturi, R.; Goldgof, D.; Soundararajan, P.; Manohar, V.; Garofolo, J.; Bowers, R.; Boonstra, M.; Korzhova, V.; Zhang, J. Framework for Performance Evaluation of Face, Text, and Vehicle Detection and Tracking in Video: Data, Metrics, and Protocol. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 319–336. [Google Scholar] [CrossRef] [PubMed]
- Luiten, J.; Ošep, A.; Dendorfer, P.; Torr, P.; Geiger, A.; Leal-Taixé, L.; Leibe, B. HOTA: A Higher Order Metric for Evaluating Multi-object Tracking. Int. J. Comput. Vis. 2021, 129, 548–578. [Google Scholar] [CrossRef]
- Ristani, E.; Solera, F.; Zou, R.; Cucchiara, R.; Tomasi, C. Performance Measures and a Data Set for Multi-target, Multi-camera Tracking. In Computer Vision—ECCV 2016 Workshops; Hua, G., Jégou, H., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2016; Volume 9914, pp. 17–35. ISBN 978-3-319-48880-6. [Google Scholar]
- Bernardin, K.; Stiefelhagen, R. Evaluating Multiple Object Tracking Performance: The CLEAR MOT Metrics. EURASIP J. Image Video Process. 2008, 2008, 246309. [Google Scholar] [CrossRef]
- Chen, S.; Ji, L.; Zhu, S.; Ye, M.; Ren, H.; Sang, Y. Toward Dense Moving Infrared Small Target Detection: New Datasets and Baseline. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5005513. [Google Scholar] [CrossRef]
- Sun, H.; Bai, J.; Yang, F.; Bai, X. Receptive-Field and Direction Induced Attention Network for Infrared Dim Small Target Detection With a Large-Scale Dataset IRDST. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5000513. [Google Scholar] [CrossRef]
- Li, B.; Xiao, C.; Wang, L.; Wang, Y.; Lin, Z.; Li, M.; An, W.; Guo, Y. Dense Nested Attention Network for Infrared Small Target Detection. IEEE Trans. Image Process. 2023, 32, 1745–1758. [Google Scholar] [CrossRef]
- Chen, S.; Ji, L.; Zhu, J.; Ye, M.; Yao, X. SSTNet: Sliced Spatio-Temporal Network with Cross-Slice ConvLSTM for Moving Infrared Dim-Small Target Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5000912. [Google Scholar] [CrossRef]



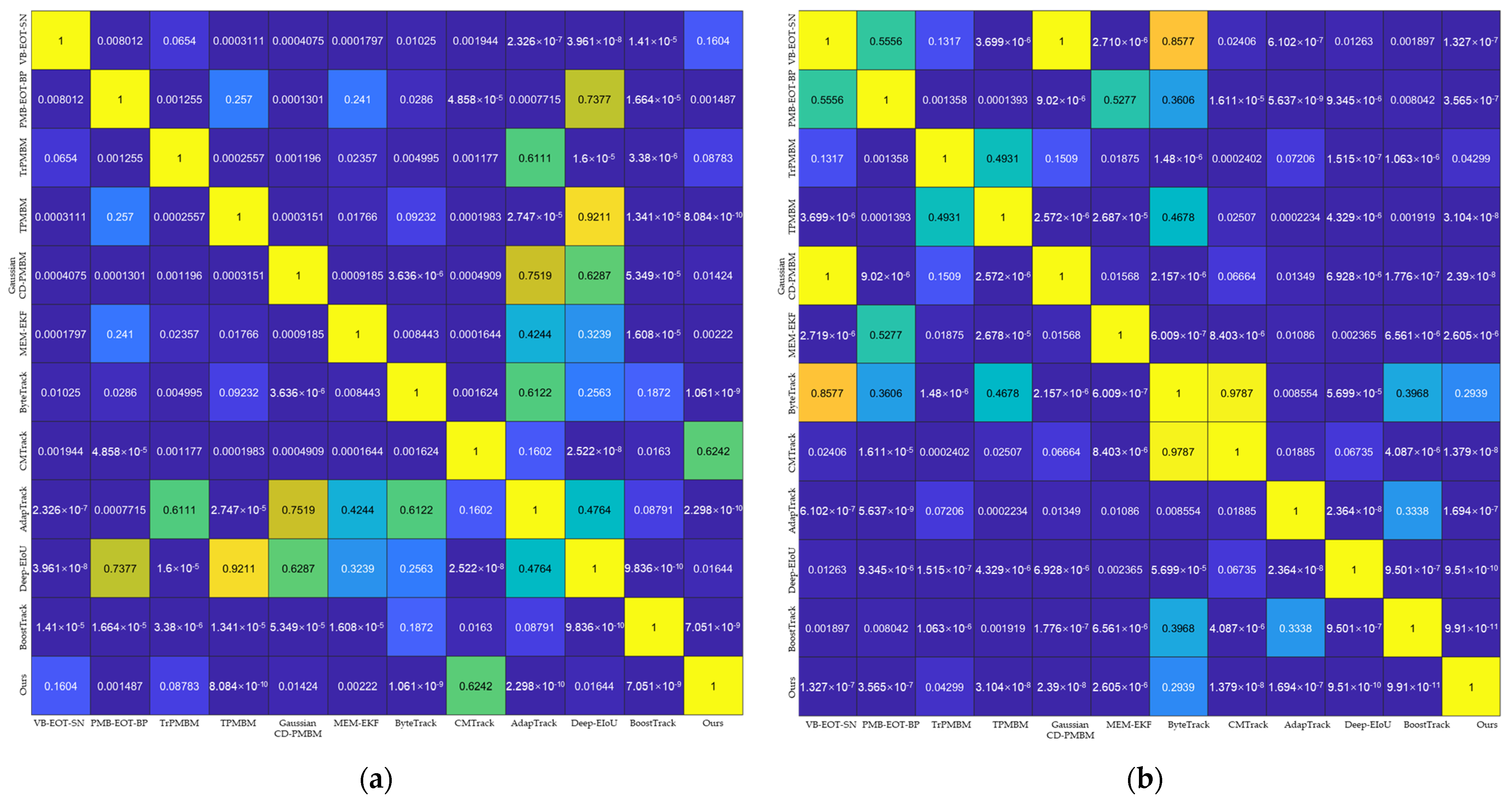


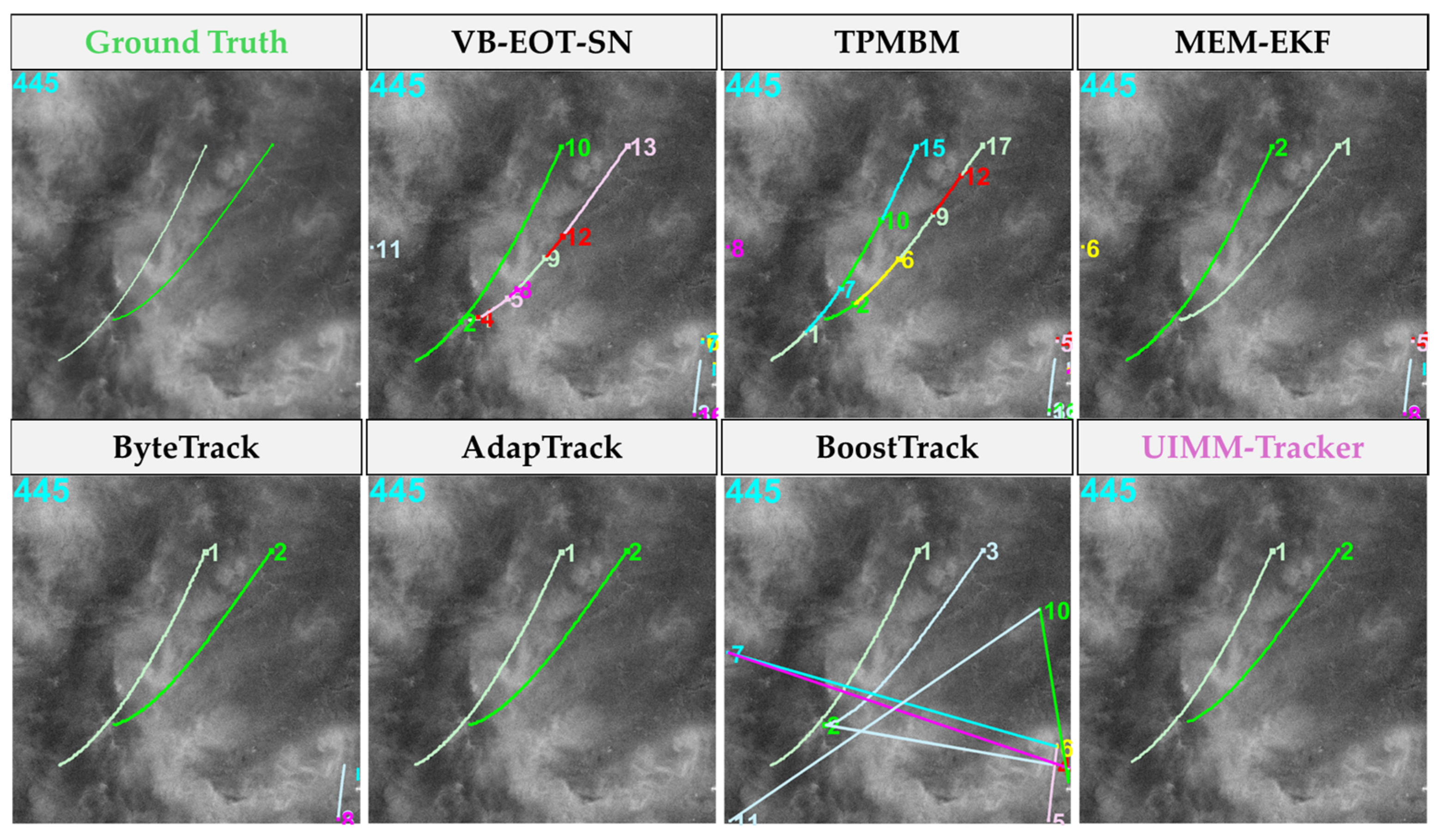


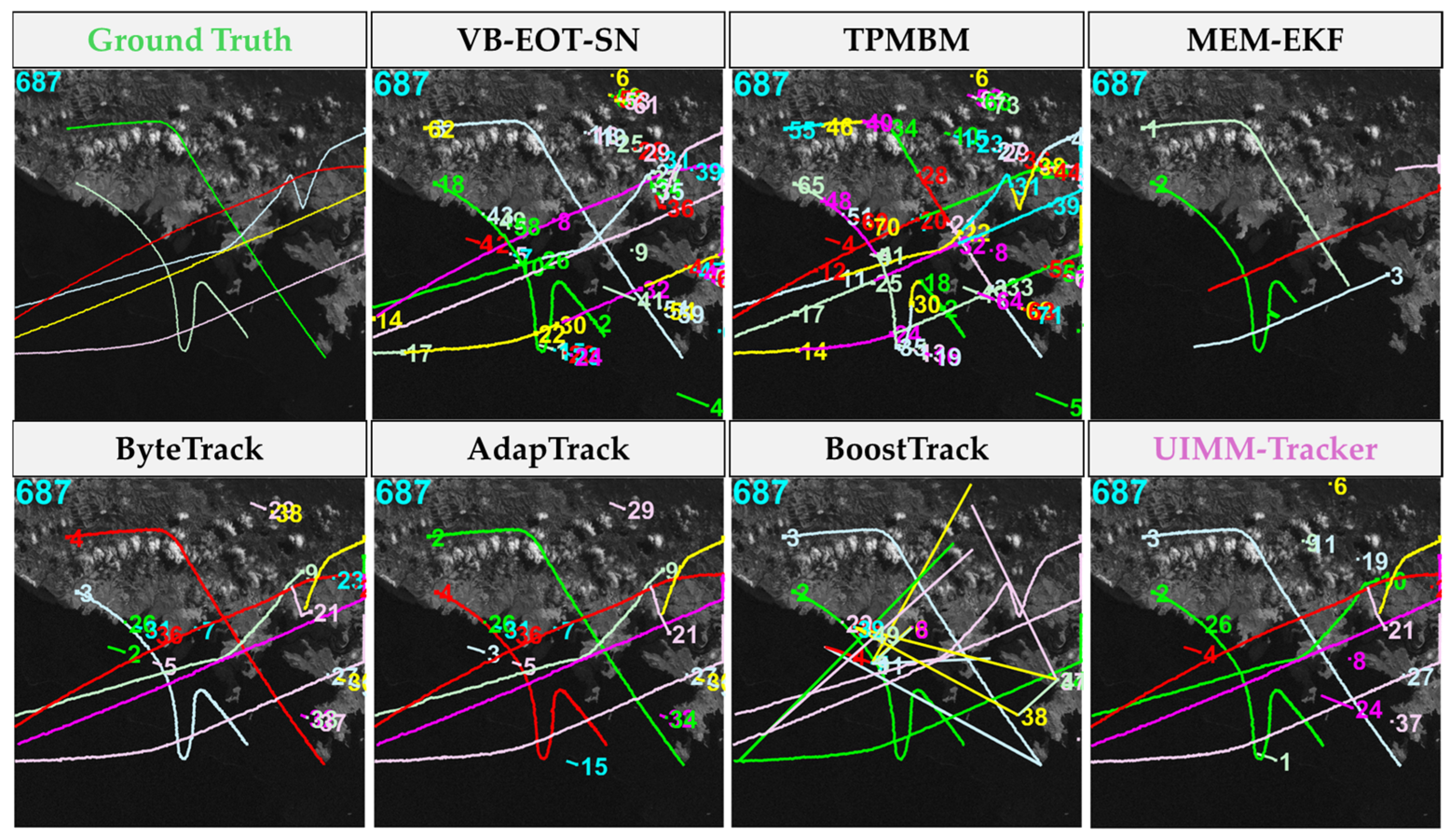

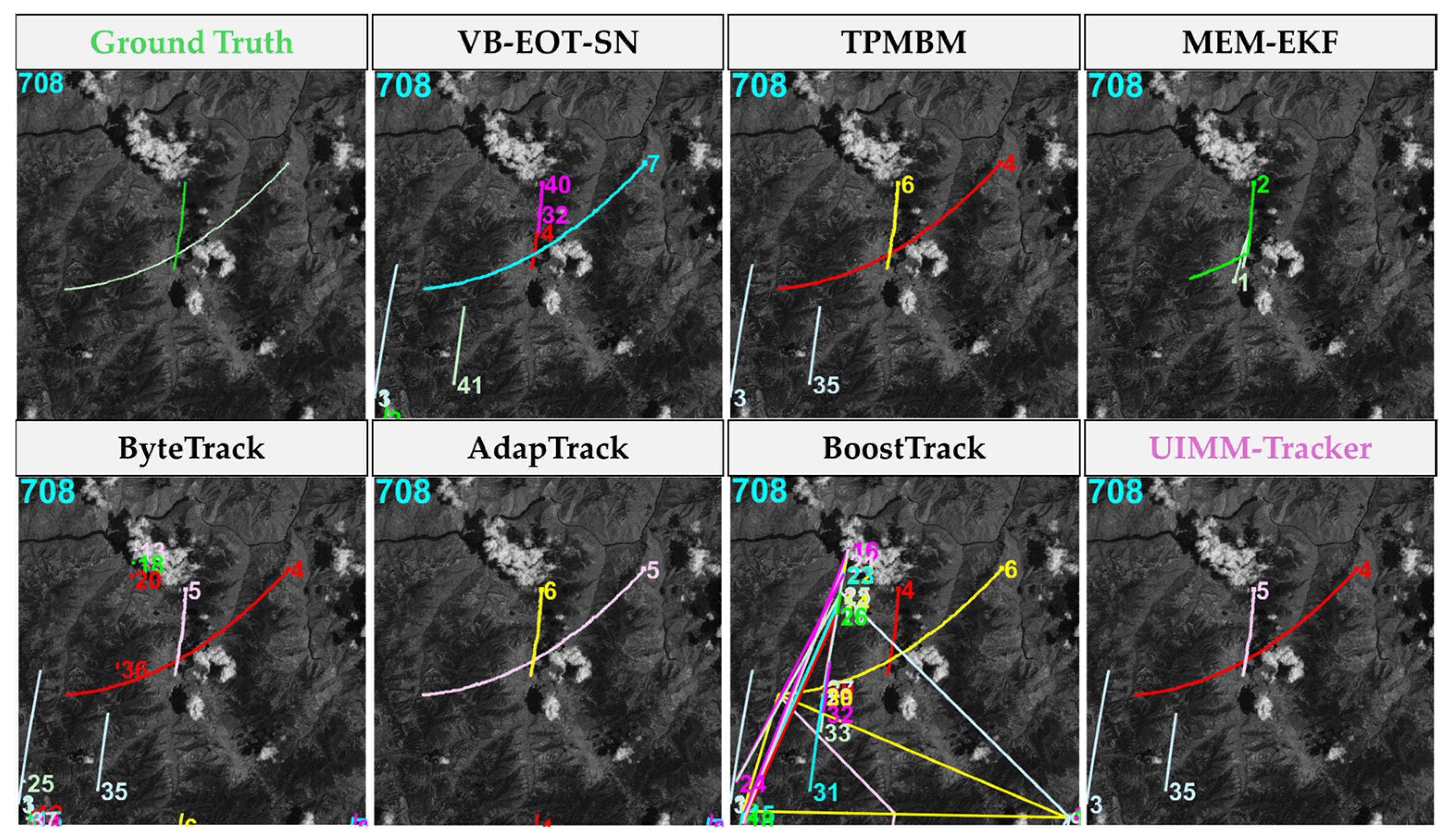
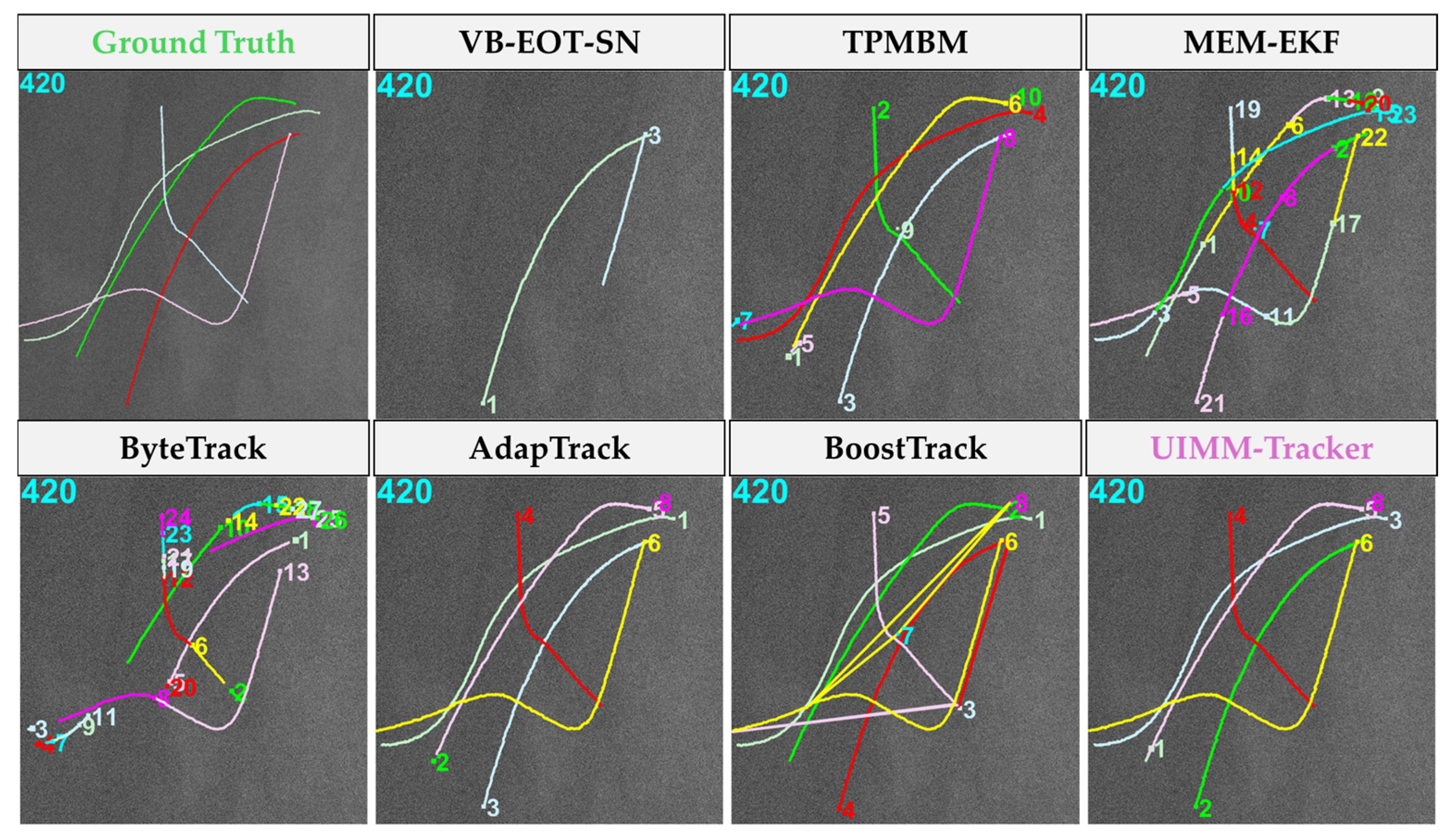

| Method | MOTA ↑ | HOTA ↑ | AssA ↑ | IDF1 ↑ | IDs ↓ | Precision ↓ |
|---|---|---|---|---|---|---|
| VB-EOT-SN [56] | 37.2 | 46.1 | 50.0 | 62.1 | 51 | 0.82 |
| PMB-EOT-BP [57] | 41.8 | 54.3 | 52.5 | 63.2 | 44 | 0.90 |
| TrPMBM [58] | 40.5 | 52.7 | 52.6 | 61.6 | 39 | 0.93 |
| TPMBM [59] | 45.3 | 55.8 | 56.1 | 67.2 | 38 | 1.19 |
| Gaussian CD-PMBM [60] | 44.7 | 53.9 | 55.1 | 67.3 | 39 | 1.31 |
| MEM-EKF [61] | 35.0 | 44.5 | 50.4 | 59.7 | 68 | 0.74 |
| ByteTrack [62] | 45.0 | 55.2 | 54.9 | 66.3 | 41 | 0.88 |
| CMTrack [63] | 44.4 | 52.9 | 53.8 | 63.6 | 40 | 0.85 |
| AdapTrack [64] | 46.1 | 54.7 | 56.2 | 67.9 | 42 | 1.55 |
| Deep-EIoU [65] | 43.8 | 54.6 | 54.7 | 65.1 | 43 | 0.92 |
| BoostTrack [66] | 27.2 | 33.1 | 32.6 | 41.9 | 84 | 1.48 |
| UIMM-Tracker | 45.6 | 56.2 | 55.7 | 68.5 | 35 | 0.41 |
| Seq | Frames | Size | Target Number | Target Condition | Background Condition |
|---|---|---|---|---|---|
| (1) | 273 | 1024 × 1024 | 5 | Regular motion High speed Small scale | Cloud–Sea background Complex structure Gradually changing background |
| (2) | 225 | 4 | Regular motion Moderate speed Weak energy | Striped background Slow movement Complex structure | |
| (3) | 157 | 6 | Trajectory crossing Varying motion speeds Small scale | Fragmented cloud background High noise Rotating background | |
| (4) | 445 | 2 | Continuous acceleration Weak energy Small scale | Irregular cloud background High contrast High noise | |
| (5) | 586 | 4 | High maneuverability Varying motion speeds Weak energy | Farmland background Inconsistent light and shadow Weak noise | |
| (6) | 378 | 4 | Trajectory crossing Varying motion speeds Varying scales | Cloud–Sea background High contrast High noise | |
| (7) | 687 | 7 | Move across backgrounds Varying motion states Moderate speed | Land–Sea–Cloud background Complex terrain Inconsistent light and shadow | |
| (8) | 499 | 7 | Significant differences in speeds High maneuverability Presence of dense regions | Urban river background High-temperature false alarm source High contrast | |
| (9) | 708 | 2 | Slow motion Fluctuating energy levels Continuously changing scales | Mountainous background Uneven illumination Clutter from structures such as ridges | |
| (10) | 420 | 5 | Significant differences in motion states High maneuverability Presence of sudden speed changes | Land–Sea background High noise Uneven illumination |
| Method | MOTA ↑|Precision ↓ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Seq1 | Seq2 | Seq3 | Seq4 | Seq5 | Seq6 | Seq7 | Seq8 | Seq9 | Seq10 | |
| VB-EOT-SN [56] | 37.1|1.05 | 36.2|0.82 | 39.2|0.69 | 41.5|0.73 | 42.4|0.81 | 32.8|0.89 | 40.9|0.77 | 30.6|0.89 | 41.4|0.94 | 30.9|0.91 |
| PMB-EOT-BP [57] | 44.1|0.69 | 42.1|1.05 | 46.9|0.98 | 38.9|0.91 | 46.5|0.92 | 37.6|0.79 | 45.3|0.87 | 36.9|1.06 | 38.3|0.92 | 38.5|0.71 |
| TrPMBM [58] | 43.4|0.93 | 37.8|0.84 | 40.3|0.92 | 38.8|0.96 | 44.5|0.97 | 37.9|0.90 | 41.4|0.89 | 37.3|1.05 | 38.8|0.78 | 42.7|0.97 |
| TPMBM [59] | 48.7|1.38 | 50.3|1.22 | 41.8|0.93 | 40.0|0.97 | 49.7|1.44 | 47.6|0.82 | 45.1|1.15 | 39.9|0.92 | 46.2|1.50 | 44.8|1.26 |
| Gaussian CD-PMBM [60] | 49.8|1.31 | 44.2|1.30 | 44.4|1.42 | 44.7|1.22 | 48.1|1.13 | 44.3|1.17 | 42.7|1.28 | 40.1|1.49 | 45.6|1.48 | 45.1|1.51 |
| MEM-EKF [61] | 35.6|0.86 | 36.4|0.63 | 35.8|0.64 | 32.1|0.68 | 40.2|0.69 | 34.8|0.72 | 31.9|0.70 | 38.7|0.83 | 32.3|0.82 | 33.2|0.72 |
| ByteTrack [62] | 43.9|0.82 | 41.6|0.79 | 46.6|0.87 | 42.8|0.90 | 48.4|0.92 | 47.0|0.91 | 47.7|0.78 | 42.1|1.04 | 45.3|0.79 | 44.6|0.99 |
| CMTrack [63] | 41.7|0.89 | 43.5|0.91 | 45.0|0.82 | 43.3|0.94 | 47.1|0.75 | 44.8|0.89 | 47.0|0.69 | 41.8|1.05 | 44.5|0.81 | 45.3|0.75 |
| AdapTrack [64] | 43.1|1.54 | 43.7|1.70 | 46.0|1.86 | 44.8|1.58 | 49.6|1.25 | 48.3|1.38 | 49.2|1.24 | 45.1|1.83 | 46.0|1.60 | 45.2|1.52 |
| Deep-EIoU [65] | 42.0|0.99 | 44.5|1.12 | 43.0|0.92 | 42.6|0.93 | 45.4|0.97 | 44.1|0.87 | 45.2|0.74 | 42.0|0.99 | 44.3|0.81 | 44.9|0.88 |
| BoostTrack [66] | 26.6|1.67 | 26.7|1.48 | 27.3|1.61 | 23.6|1.54 | 27.4|1.54 | 30.9|1.47 | 27.1|1.24 | 25.5|1.69 | 27.3|1.32 | 29.6|1.25 |
| UIMM-Tracker | 40.5|0.50 | 44.8|0.48 | 46.6|0.43 | 44.1|0.45 | 51.2|0.46 | 48.4|0.34 | 48.9|0.32 | 42.4|0.56 | 46.1|0.33 | 45.7|0.35 |
| Methods | MOTA ↑ | HOTA ↑ | Precision ↓ | Time (s) ↓ |
|---|---|---|---|---|
| VB-EOT-SN [56] | 37.2 | 46.1 | 0.82 | 2.65 |
| PMB-EOT-BP [57] | 41.8 | 54.3 | 0.90 | 9.07 |
| TrPMBM [58] | 40.5 | 52.7 | 0.93 | 18.63 |
| TPMBM [59] | 45.3 | 55.8 | 1.19 | 17.29 |
| Gaussian CD-PMBM [60] | 44.7 | 53.9 | 1.31 | 17.95 |
| MEM-EKF [61] | 35.0 | 44.5 | 0.74 | 1.71 |
| ByteTrack [62] | 45.0 | 55.2 | 0.88 | 1.42 |
| CMTrack [63] | 44.4 | 52.9 | 0.85 | 2.47 |
| AdapTrack [64] | 46.1 | 54.7 | 1.55 | 1.51 |
| Deep-EIoU [65] | 43.8 | 54.6 | 0.92 | 0.93 |
| BoostTrack [66] | 27.2 | 33.1 | 1.48 | 4.18 |
| UIMM-Tracker | 45.6 | 56.2 | 0.41 | 2.81 |
| The Method for Obtaining | MOTA ↑ | HOTA ↑ | AssA ↑ | IDF1 ↑ | IDs ↓ | Precision ↓ |
|---|---|---|---|---|---|---|
| Without | 40.4 | 50.7 | 49.8 | 58.1 | 52 | 0.84 |
| from prior | 45.0 | 55.1 | 55.4 | 67.8 | 38 | 0.52 |
| from detections | 45.6 | 56.2 | 55.7 | 68.5 | 35 | 0.41 |
| Markov Transition Matrix Construction Methods | MOTA ↑ | HOTA ↑ | AssA ↑ | IDF1 ↑ | IDs ↓ | Precision ↑ | ||
|---|---|---|---|---|---|---|---|---|
| ✗ | ✗ | ✗ | 35.2 | 47.5 | 51.4 | 62.2 | 59 | 0.67 |
| ✗ | ✓ | ✓ | 44.1 | 53.4 | 55.9 | 68.1 | 42 | 0.45 |
| ✓ | ✗ | ✓ | 44.6 | 53.5 | 55.3 | 68.2 | 43 | 0.44 |
| ✓ | ✓ | ✗ | 40.3 | 51.2 | 53.6 | 65.4 | 50 | 0.55 |
| ✓ | ✓ | ✓ | 45.6 | 56.2 | 55.7 | 68.5 | 35 | 0.41 |
| Cost Calculation Methods | MOTA ↑ | HOTA ↑ | AssA ↑ | IDF1 ↑ | IDs ↓ | Precision ↑ | ||
|---|---|---|---|---|---|---|---|---|
| Uncertainty | ||||||||
| ✗ | -- | -- | 42.5 | 51.3 | 50.5 | 63.7 | 49 | 0.64 |
| ✓ | ✗ | ✓ | 44.7 | 54.4 | 54.8 | 67.2 | 41 | 0.46 |
| ✓ | ✓ | ✗ | 45.4 | 56.5 | 54.3 | 67.0 | 39 | 0.44 |
| ✓ | ✓ | ✓ | 45.6 | 56.2 | 55.7 | 68.5 | 35 | 0.41 |
| Motion Model | MOTA ↑ | HOTA ↑ | AssA ↑ | IDF1 ↑ | IDs ↓ | Precision ↑ | ||
|---|---|---|---|---|---|---|---|---|
| CV | CA | CT | ||||||
| ✓ | ✗ | ✗ | 39.4 | 48.7 | 46.2 | 58.8 | 65 | 0.75 |
| ✗ | ✓ | ✗ | 44.2 | 54.5 | 53.6 | 65.1 | 40 | 0.49 |
| ✗ | ✗ | ✓ | 26.3 | 34.8 | 39.2 | 41.4 | 116 | 1.66 |
| ✓ | ✓ | ✓ | 45.6 | 56.2 | 55.7 | 68.5 | 35 | 0.41 |
| Detector | Precision (%) | Recall (%) | MOTA ↑ | HOTA ↑ | AssA ↑ | IDF1 ↑ | IDs ↓ | Precision ↓ |
|---|---|---|---|---|---|---|---|---|
| RDIAN [72] | 79.98 | 65.83 | 38.4 | 46.5 | 49.2 | 64.8 | 46 | 0.41 |
| DNANet [73] | 80.84 | 71.97 | 42.7 | 55.8 | 52.4 | 67.0 | 45 | 0.42 |
| LMAFormer [11] | 81.06 | 71.29 | 42.6 | 55.1 | 52.3 | 66.9 | 38 | 0.40 |
| SSTNet [74] | 83.95 | 69.51 | 43.3 | 53.6 | 52.8 | 67.2 | 36 | 0.43 |
| LASNet [71] | 85.32 | 73.64 | 45.6 | 56.2 | 55.7 | 68.5 | 35 | 0.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Zhi, X.; Xu, Z.; Chen, W.; Han, Q.; Hu, J.; Sui, Y.; Zhang, W. UIMM-Tracker: IMM-Based with Uncertainty Detection for Video Satellite Infrared Small-Target Tracking. Remote Sens. 2025, 17, 2052. https://doi.org/10.3390/rs17122052
Huang Y, Zhi X, Xu Z, Chen W, Han Q, Hu J, Sui Y, Zhang W. UIMM-Tracker: IMM-Based with Uncertainty Detection for Video Satellite Infrared Small-Target Tracking. Remote Sensing. 2025; 17(12):2052. https://doi.org/10.3390/rs17122052
Chicago/Turabian StyleHuang, Yuanxin, Xiyang Zhi, Zhichao Xu, Wenbin Chen, Qichao Han, Jianming Hu, Yi Sui, and Wei Zhang. 2025. "UIMM-Tracker: IMM-Based with Uncertainty Detection for Video Satellite Infrared Small-Target Tracking" Remote Sensing 17, no. 12: 2052. https://doi.org/10.3390/rs17122052
APA StyleHuang, Y., Zhi, X., Xu, Z., Chen, W., Han, Q., Hu, J., Sui, Y., & Zhang, W. (2025). UIMM-Tracker: IMM-Based with Uncertainty Detection for Video Satellite Infrared Small-Target Tracking. Remote Sensing, 17(12), 2052. https://doi.org/10.3390/rs17122052







