Large Quantities of Acoustic Multibeam Bathymetric Point Clouds: Organizing Method for Efficient Storage and Retrieval
Abstract
1. Introduction
2. Methods
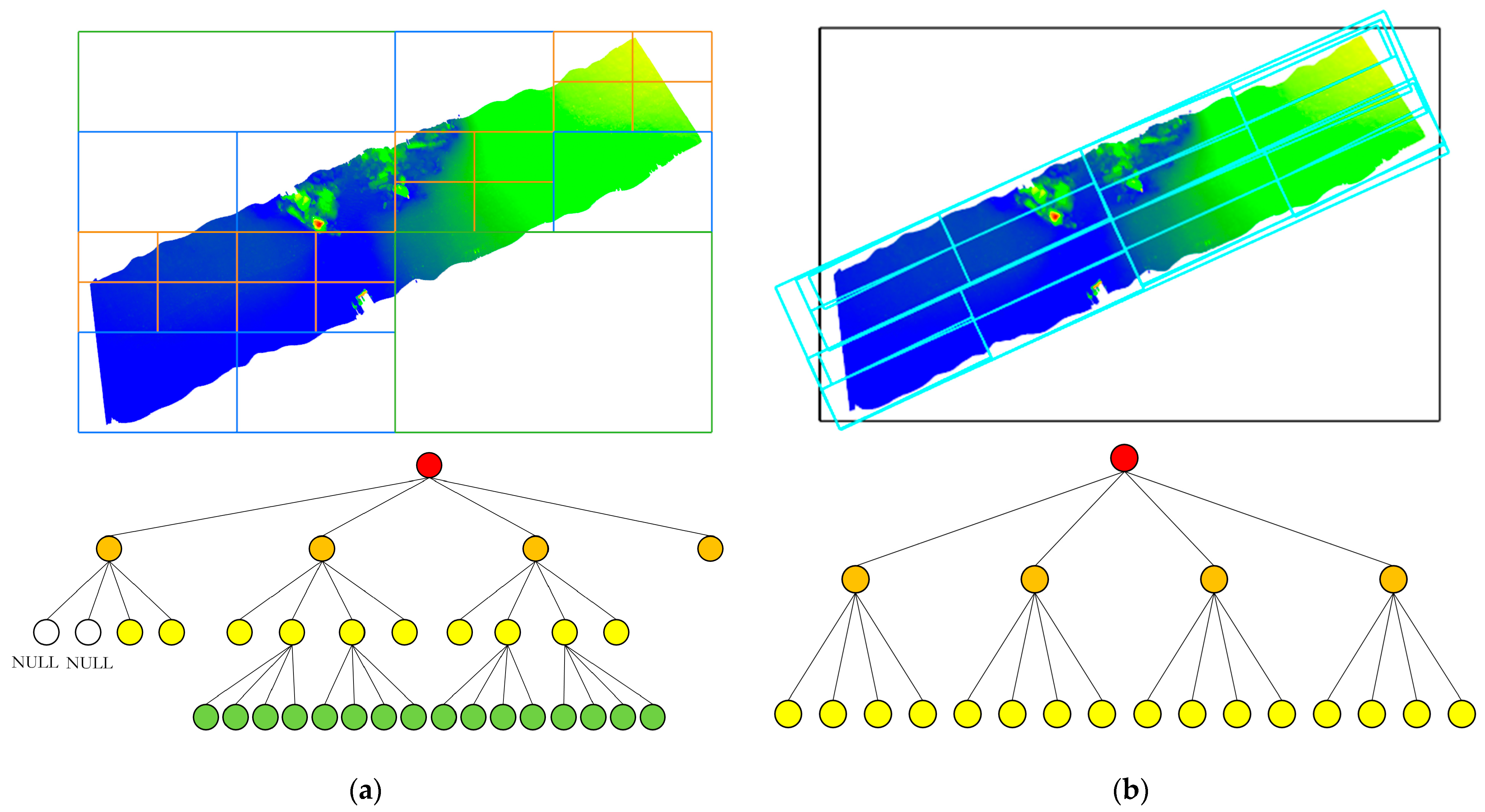
2.1. Quadtree Structure
2.2. Oriented Bounding Box and Oriented Quadtree
- The principal axis orientation of the point cloud is determined by performing PCA on the raw point cloud data. The main steps of PCA are as follows:
- 1.1
- Calculate the center of mass of the point cloud as shown in Equation (1).where and refer to the average x-coordinate and y-coordinate of all points, respectively; n is the number of points.
- 1.2
- Translate the point cloud data to the center of mass as shown in Equation (2) so that the center of mass is located at the origin of the coordinates.where is the centralized point and is the original point.
- 1.3
- Construct the covariance matrix of the centered point cloud data and calculate the covariance matrix as shown in Equation (3).where the superscript T represents the matrix transpose.
- 1.4
- The eigenvalue decomposition of the covariance matrix is performed to solve for the eigenvectors as shown in Equation (4).where is the eigenvalue, and is the corresponding eigenvector.
- 1.5
- Arrange the eigenvalues in descending order and obtain the corresponding eigenvectors and the principal axis direction of the point cloud data.
- Rotate the centralized point cloud along the coordinate origin by the major axis square degree so that the major direction of the rotated point cloud aligns with the coordinate axis to obtain the rotated point cloud .
- At this point, the main direction of the rotated point cloud has been aligned with the coordinate axes, so the AABB (axis-aligned bounding box) is calculated for the rotated point cloud.
- Rotate the AABB back to the corresponding position of the original point cloud and perform decentralization processing. The resulting oriented bounding box is the OBB (oriented bounding box) of the original point cloud.
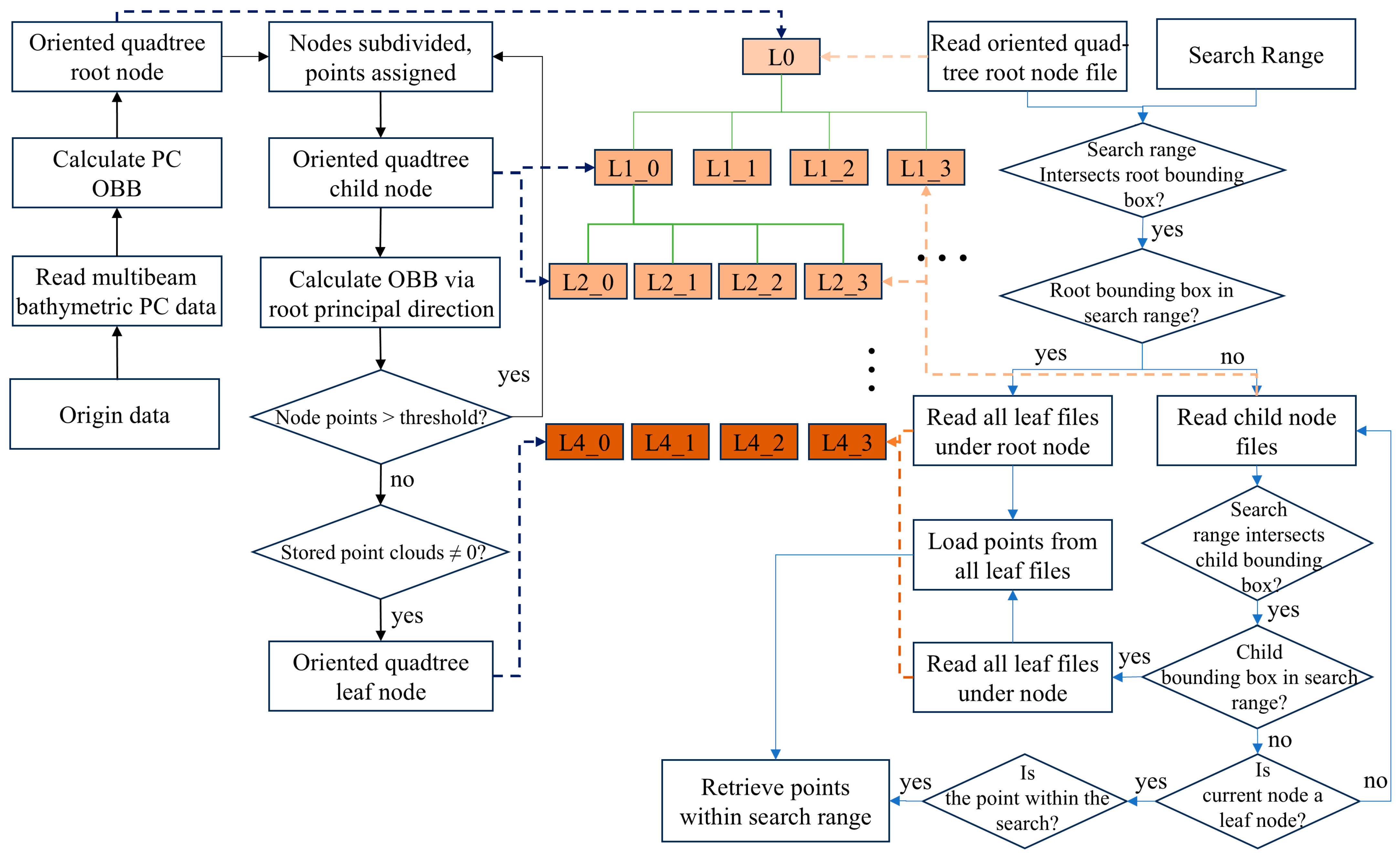
2.3. Construction and Retrieval of Defined Index Files
- The multibeam bathymetric point cloud data are accessed using memory mapping technology, with the coordinates of the first point serving as the reference offset. Subsequently, the coordinates of all following points are adjusted by subtracting this offset to obtain the relative offset point cloud data. This step aims to reduce the numerical range in subsequent calculations, improving computational efficiency and accuracy. Next, the segmentation threshold is initialized and set at 2.5% of the total number of points in the original point cloud data for this experiment.
- Calculate the oriented bounding box of the point cloud and record its principal axis direction. Use this oriented bounding box as the root node of the quadtree, then divide the space into four equal parts based on the oriented bounding box, assigning the corresponding point set in each area to the four child nodes of the current node. Recalculate the bounding box of the child nodes according to the principal axis direction of the original point cloud. If the number of points in a child node exceeds the threshold, continue subdividing the quadtree until all leaf nodes contain fewer points than the threshold.
- In constructing the oriented quadtree index, the offset and oriented bounding box information of the root node and its child nodes are recorded in the root node file. The child node files contain the oriented bounding box information and its corresponding child nodes. For leaf nodes, the files include the oriented bounding box data, neighboring node information, and point-set details. As shown in Table 1, this oriented quadtree index information is iteratively serialized to the computer’s hard disk, creating the external oriented quadtree index file. This process completes the establishment of the oriented quadtree spatial index. This process not only completes the construction of the oriented quadtree spatial index but also ensures efficient storage and fast access to the index data.
| Algorithm 1. External memory oriented quadtree index construction |
| Input: Points, oriented bounding box (OBB), maxPointsPerNode and mainDirection Function QuadTreeSegmentation(Points, OBB, maxPointsPerNode, mainDirection): if size(Points) < maxPointsPerNode Create a leaf node and store Points in it return leaf node end if Initialize: Sub-obbs list SubOBBs = ComputeSubOBBs(OBB) Initialize: Sub-points list SubPoints = [[], [], [], []] for each point p in Points: Determine sub-obb p belongs to and add p to the corresponding Sub Points[i] end for Recalculate SubOBBs using mainDirection, SubPoints for each sub-region i (from 1 to 4): if SubPoints[i] is not empty: SubNode = QuadTreeSegmentation(SubPoints[i], SubOBBs[i], maxPointsPer Node, mainDirection) Add SubNode to the children of Node end if end for return Node Function ComputeSubOBBs(OBB): Center = Calculate the center point of the OBB Side-center-point list SideCenters = Calculate the side center points of the OBB OBBs = Calculate the first sub-boundary using OBB, Center and SideCenters return OBBs End Function # Initialize the quadtree segmentation process RootNode = QuadTreeSegmentation(Points, OBB, maxPointsPerNode, mainDirection) |
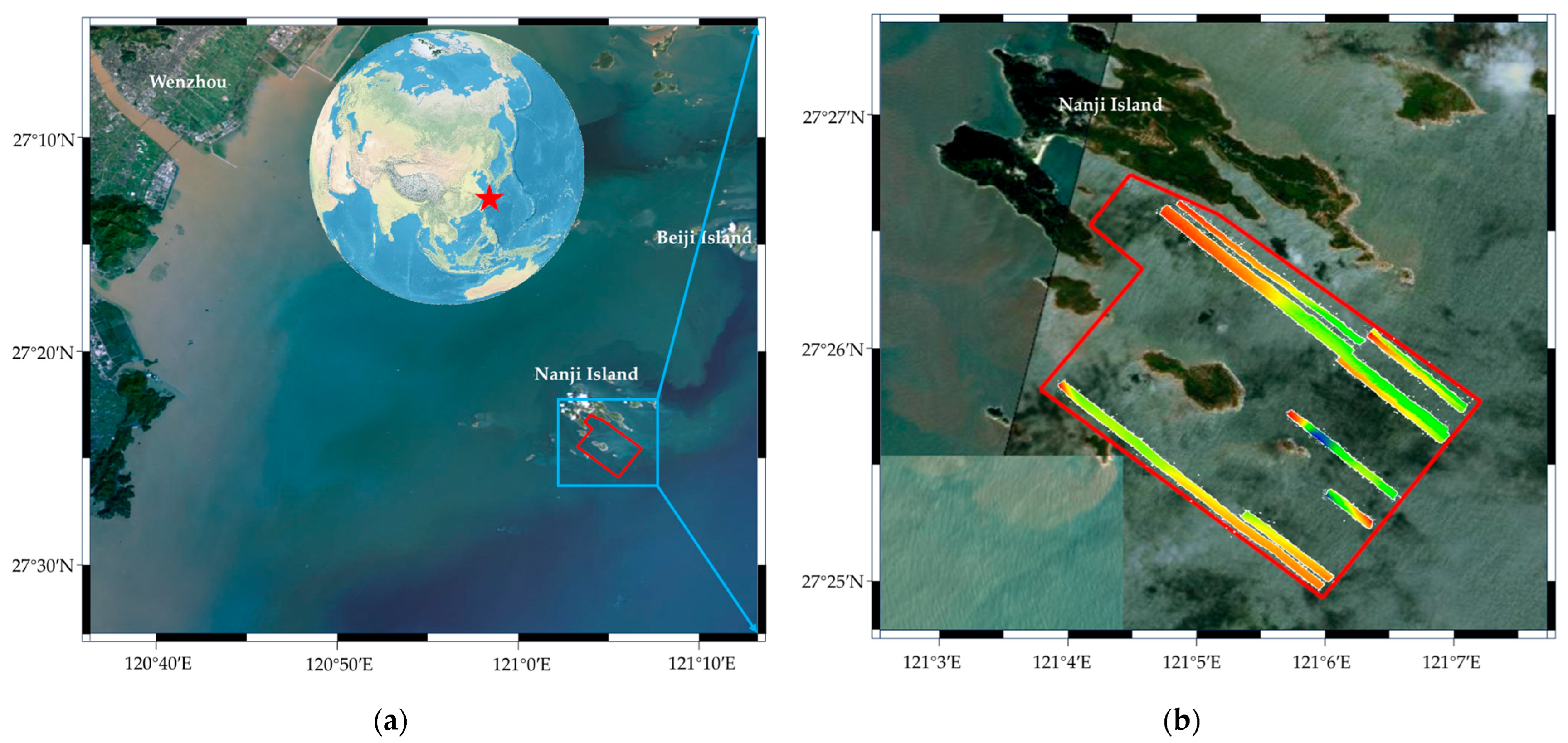
3. Results
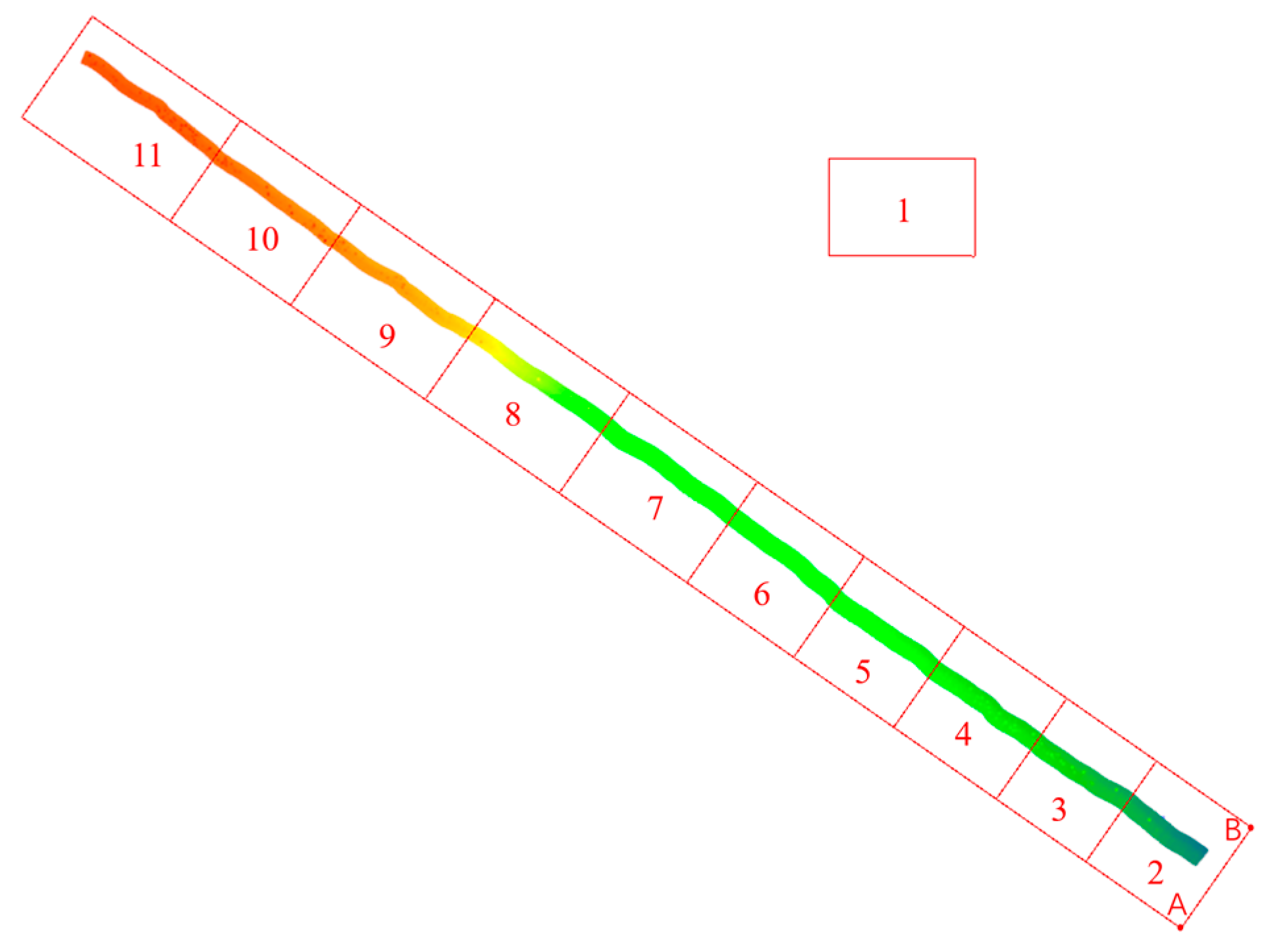
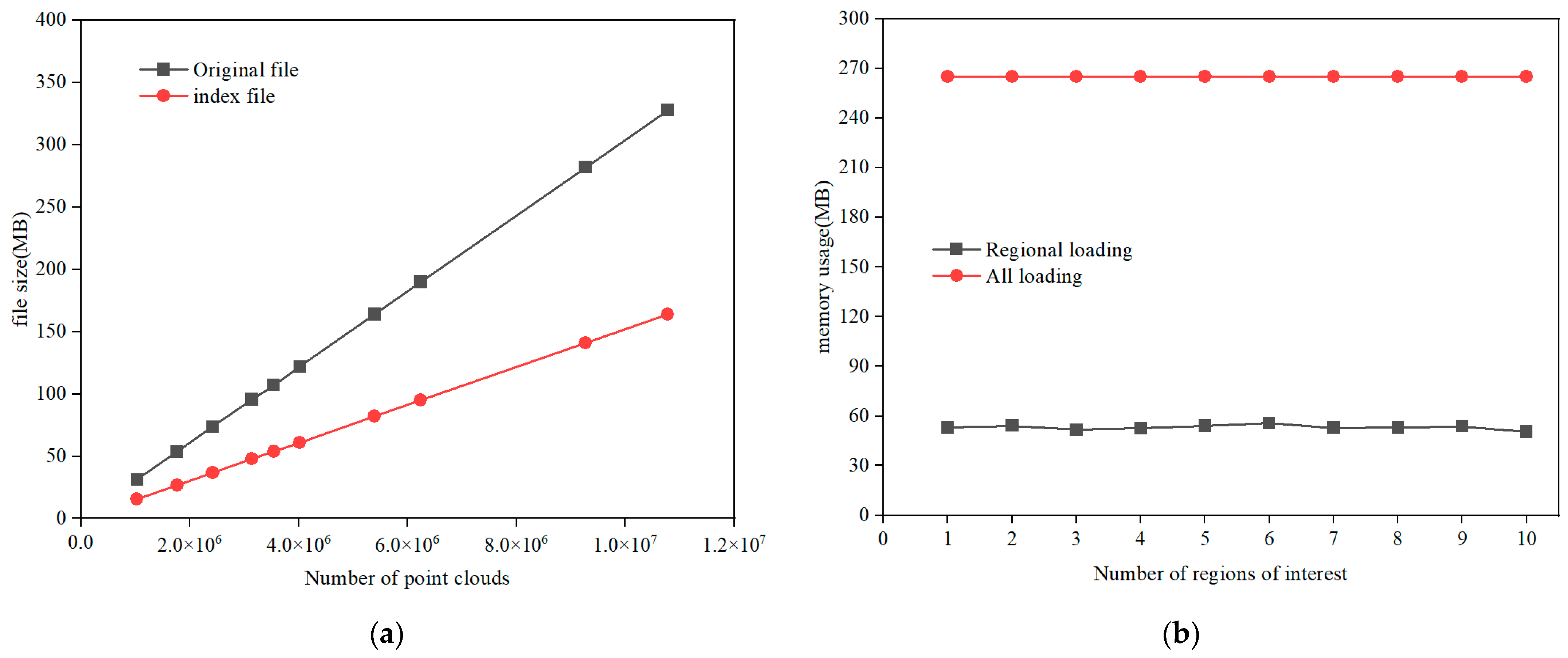
3.1. Analysis of Index Construction and Retrieval Time
3.2. Analysis of Internal and External Storage Occupancy
4. Discussion
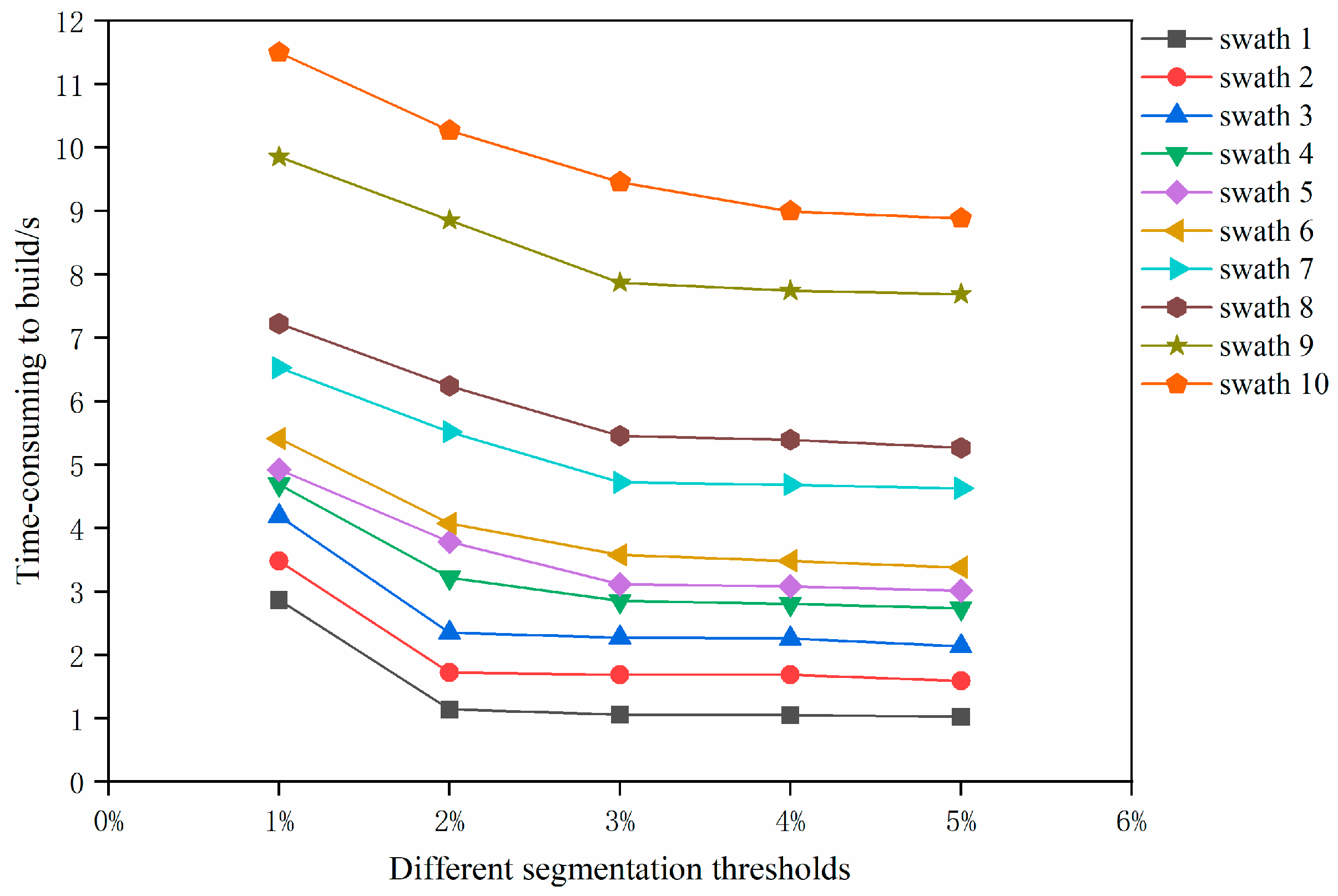
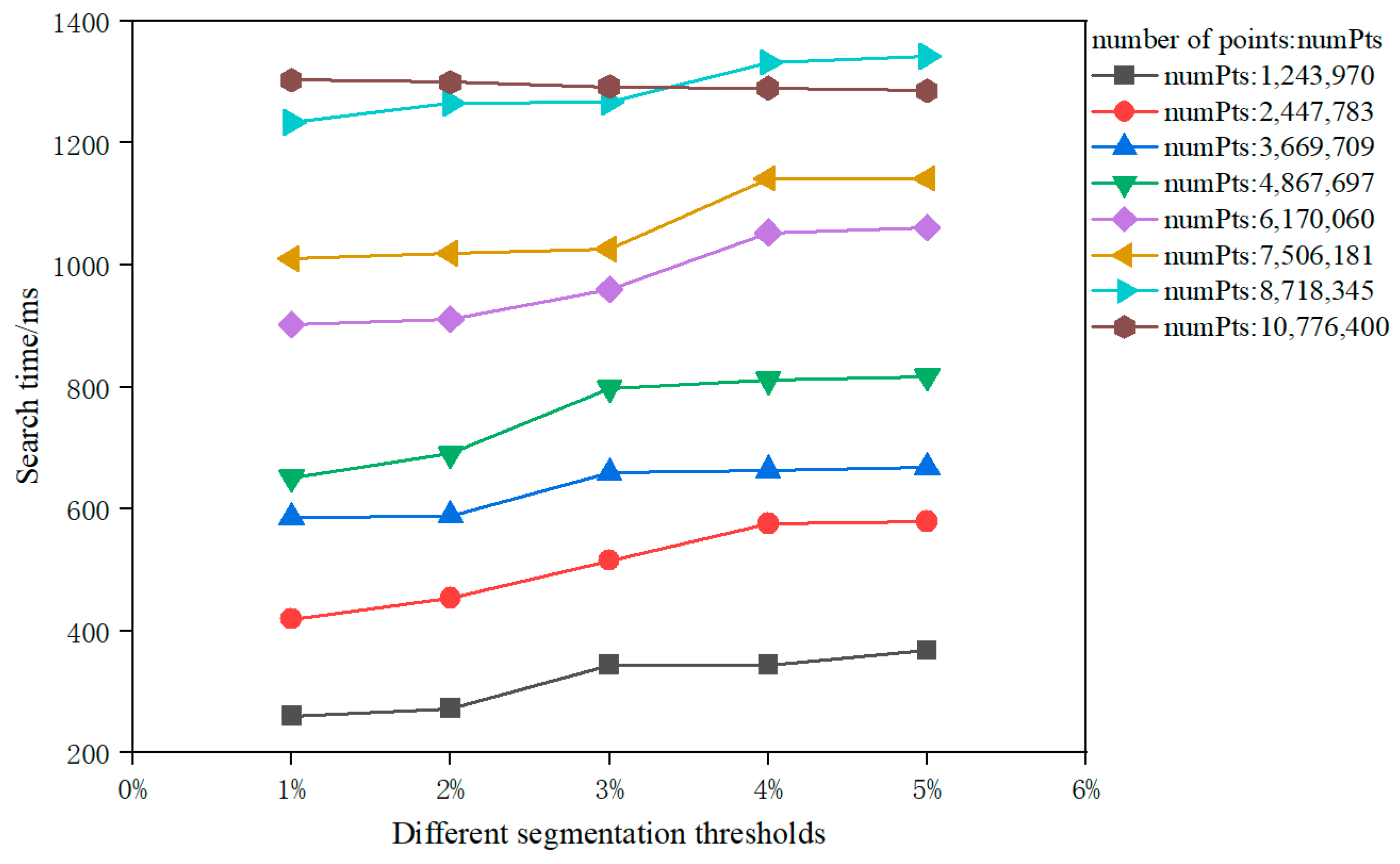
4.1. Effects of the Different Segmentation Thresholds
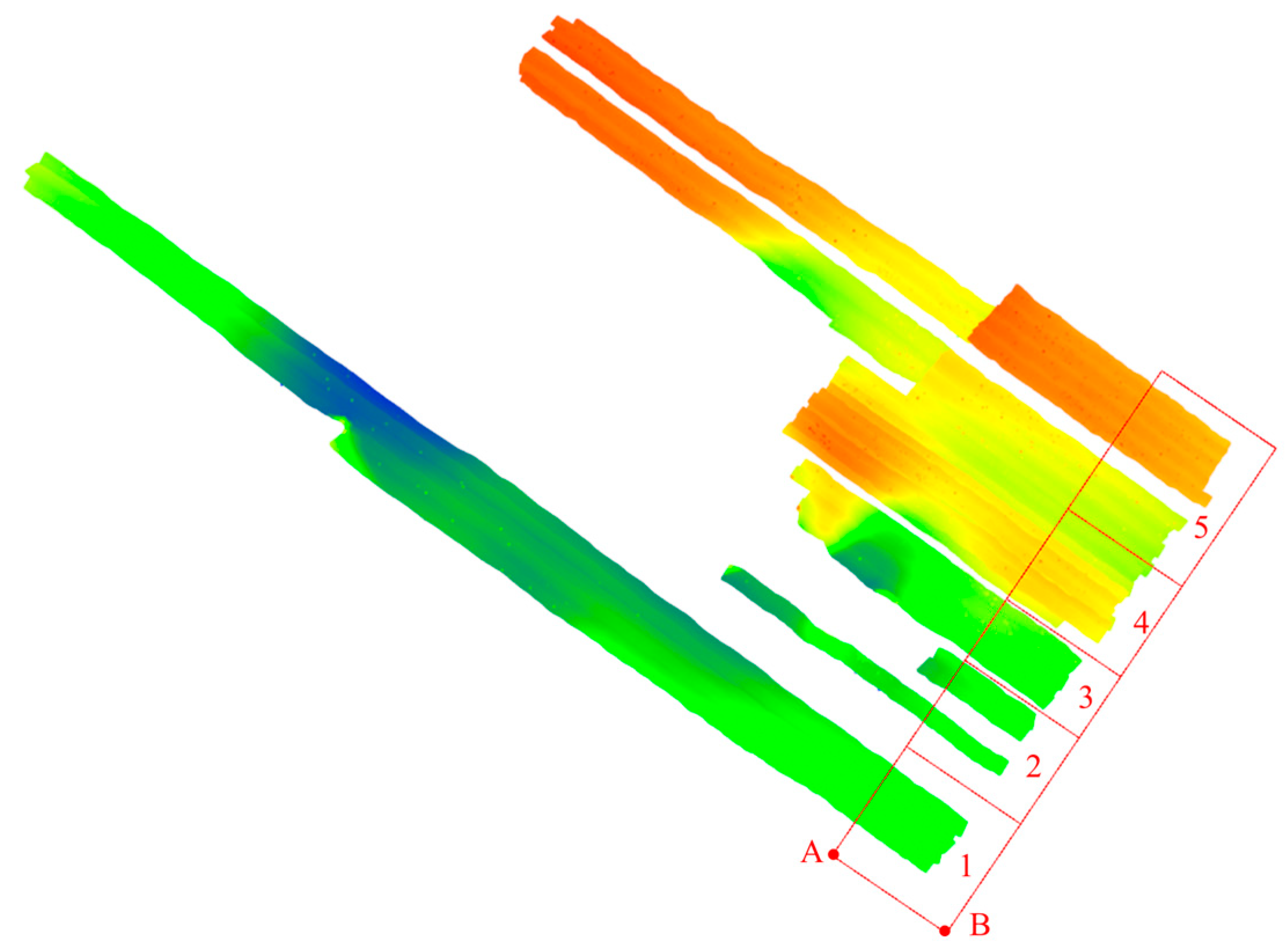
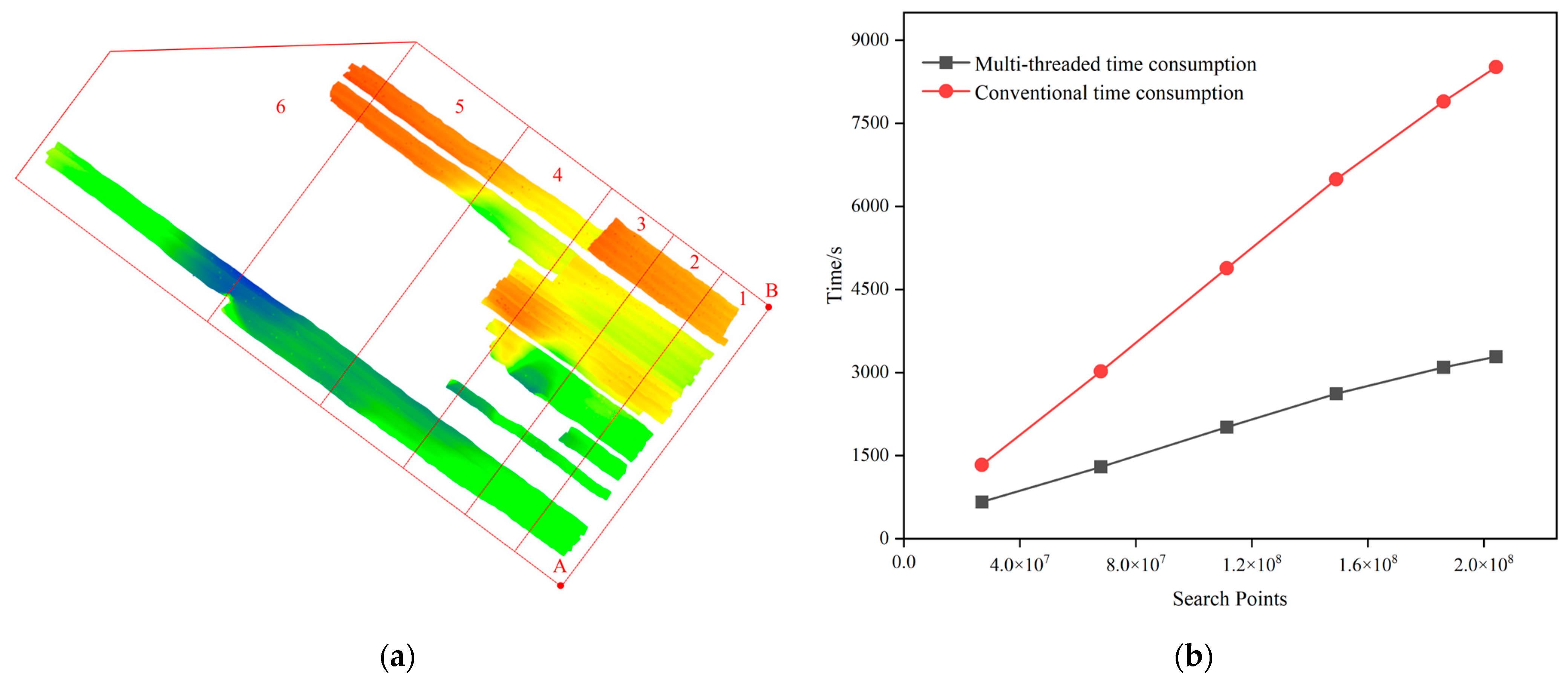
4.2. Combining Multi-Threading Technology for Multiple Swathes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Šiljeg, A.; Marić, I.; Domazetović, F.; Cukrov, N.; Lovrić, M.; Panđa, L. Bathymetric Survey of the St. Anthony Channel (Croatia) Using Multibeam Echosounders (MBES)—A New Methodological Semi-Automatic Approach of Point Cloud Post-Processing. J. Mar. Sci. Eng. 2022, 10, 101. [Google Scholar] [CrossRef]
- Rowley, T.; Ursic, M.; Konsoer, K.; Langendoen, E.; Mutschler, M.; Sampey, J.; Pocwiardowski, P. Comparison of terrestrial lidar, SfM, and MBES resolution and accuracy for geomorphic analyses in physical systems that experience subaerial and subaqueous conditions. Geomorphology 2020, 355, 107056. [Google Scholar] [CrossRef]
- Wang, M.; Wu, Z.; Yang, F.; Ma, Y.; Wang, X.H.; Zhao, D. Multifeature Extraction and Seafloor Classification Combining LiDAR and MBES Data around Yuanzhi Island in the South China Sea. Sensors 2018, 18, 3828. [Google Scholar] [CrossRef] [PubMed]
- Hughes Clarke, J.E. First wide-angle view of channelized turbidity currents links migrating cyclic steps to flow characteristics. Nat. Commun. 2016, 7, 11896. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Li, Q.; Zhu, H.; Yang, F.; Wu, Z. Acoustic Deep-Sea Seafloor Characterization Accounting for Heterogeneity Effect. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3034–3042. [Google Scholar] [CrossRef]
- Stateczny, A.; Błaszczak-Bąk, W.; Sobieraj-Żłobińska, A.; Motyl, W.; Wisniewska, M. Methodology for Processing of 3D Multibeam Sonar Big Data for Comparative Navigation. Remote Sens. 2019, 11, 2245. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L.; Fang, T.; Mathiopoulos, P.T.; Tong, X.; Qu, H.; Xiao, Z.; Li, F.; Chen, D. A Multiscale and Hierarchical Feature Extraction Method for Terrestrial Laser Scanning Point Cloud Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2409–2425. [Google Scholar] [CrossRef]
- Scheiblauer, C.; Wimmer, M. Out-of-core selection and editing of huge point clouds. Comput. Graph. 2011, 35, 342–351. [Google Scholar] [CrossRef]
- Baert, J.; Lagae, A.; Dutré, P. Out-of-core construction of sparse voxel octrees. In Proceedings of the 5th High-Performance Graphics Conference, Anaheim, CA, USA, 19–21 July 2013; pp. 27–32. [Google Scholar]
- Richter, R.; Kyprianidis, J.E.; Döllner, J. Out-of-Core GPU-based Change Detection in Massive 3D Point Clouds. Trans. GIS 2012, 17, 724–741. [Google Scholar] [CrossRef]
- Derigs, U.; Metz, A. An in-core/out-of-core method for solving large scale assignment problems. Z. Oper. Res. 1986, 30, A181–A195. [Google Scholar] [CrossRef]
- Zhang, Y.; Lv, X.Q. In-core and Out-of-core Exchange Rendering Technique of Large-scale Point Cloud. Comput. Eng. 2014, 40, 49–54. [Google Scholar]
- Zhang, Y.; Taylor, M.; Sarkar, T.K.; Moon, H.; Yuan, M. Solving large complex problems using a higher-order basis: Parallel in-core and out-of-core integral-equation solvers. IEEE Antennas Propag. Mag. 2008, 50, 13–30. [Google Scholar] [CrossRef]
- van Oosterom, P.; Martinez-Rubi, O.; Ivanova, M.; Horhammer, M.; Geringer, D.; Ravada, S.; Tijssen, T.; Kodde, M.; Gonçalves, R. Massive point cloud data management: Design, implementation and execution of a point cloud benchmark. Comput. Graph. 2015, 49, 92–125. [Google Scholar] [CrossRef]
- Huang, H.C. Construction of Multi-resolution Spatial Data Organization for Ultralarge-scale 3D Laser Point Cloud. Sens. Mater. 2023, 35, 87–102. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, X.P.; Ma, X.Y.; Ye, K.; Liu, Y.W. Data Analysis System of Oblique Photography Based on OpenSceneGraph. In Proceedings of the 2017 2nd International Conference on Electrical, Control and Automation Engineering (ECAE 2017), Xiamen, China, 24–25 December 2017; pp. 282–285. [Google Scholar]
- Guimaraes, N.; Pádua, L.; Adao, T.; Hruska, J.; Peres, E.; Sousa, J.J. VisWebDrone: A Web Application for UAV Photogrammetry Based on Open-Source Software. ISPRS Int. J. GEO-Inf. 2020, 9, 679. [Google Scholar] [CrossRef]
- Yixuan, W.; Xudong, L.; Fenglin, Z.; Zhehui, J.; Yong, T.; Huijie, Z. Design of point cloud data structures for efficient processing of large-scale point clouds. In Proceedings of the International Conference on Optical and Photonic Engineering (icOPEN 2023), Singapore, 27 November–1 December 2023; SPIE: Bellingham, WA, USA; p. 130690. [Google Scholar]
- Goswami, P.; Erol, F.; Mukhi, R.; Pajarola, R.; Gobbetti, E. An efficient multi-resolution framework for high quality interactive rendering of massive point clouds using multi-way kd-trees. Vis. Comput. 2012, 29, 69–83. [Google Scholar] [CrossRef]
- Anbin, Y.; Wensheng, M. Index model based on top-down greedy splitting R-tree and three-dimensional quadtree for massive point cloud management. J. Appl. Remote Sens. 2019, 13, 028501. [Google Scholar] [CrossRef]
- Ding, L.; Qiao, B.; Wang, G.; Chen, C. An Efficient Quad-Tree Based Index Structure for Cloud Data Management; Springer: Berlin/Heidelberg, Germany, 2011; pp. 238–250. [Google Scholar]
- Elseberg, J.; Borrmann, D.; Nüchter, A. One billion points in the cloud—An octree for efficient processing of 3D laser scans. ISPRS J. Photogramm. Remote Sens. 2013, 76, 76–88. [Google Scholar] [CrossRef]
- Bentley, J.L. K-d trees for semidynamic point sets. In Proceedings of the Sixth Annual Symposium on Computational Geometry, Berkley, CA, USA, 6–8 June 1990; pp. 187–197. [Google Scholar]
- Wang, W.; Zhang, Y.; Ge, G.; Jiang, Q.; Wang, Y.; Hu, L. A Hybrid Spatial Indexing Structure of Massive Point Cloud Based on Octree and 3D R*-Tree. Appl. Sci. 2021, 11, 9581. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, Y.; Dong, Z.; Li, J.; Chen, Y.; Tang, Q.; Huang, G.; Tao, J. An Optimal Denoising Method for Spaceborne Photon-Counting LiDAR Based on a Multiscale Quadtree. Remote Sens. 2024, 16, 2475. [Google Scholar] [CrossRef]
- Han, S. Towards Efficient Implementation of an Octree for a Large 3D Point Cloud. Sensors 2018, 18, 4398. [Google Scholar] [CrossRef] [PubMed]
- Amorim, P.H.J.; de Moraes, T.F.; da Silva, J.V.L.; Pedrini, H. Out-of-Core Rendering of Large Volumetric Data Sets at Multiple Levels of Detail. In Multi-Modality Imaging: Applications and Computational Techniques; Abreu de Souza, M., Remigio Gamba, H., Pedrini, H., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 191–215. [Google Scholar]
- Schütz, M.; Ohrhallinger, S.; Wimmer, M. Fast Out-of-Core Octree Generation for Massive Point Clouds. Comput. Graph. Forum 2020, 39, 155–167. [Google Scholar] [CrossRef]
- Ghazizadeh, M.A.; Mohammadian, A.; Kurganov, A. An adaptive well-balanced positivity preserving central-upwind scheme on quadtree grids for shallow water equations. Comput. Fluids 2020, 208, 104633. [Google Scholar] [CrossRef]
- Wang, J.; Tang, Y.; Jin, S.; Bian, G.; Zhao, X.; Peng, C. A Method for Multi-Beam Bathymetric Surveys in Unfamiliar Waters Based on the AUV Constant-Depth Mode. J. Mar. Sci. Eng. 2023, 11, 1466. [Google Scholar] [CrossRef]
- Hamilton, T.; Beaudoin, J.; Clarke, J.H. A more precise algorithm to account for non-concentric multibeam array geometry. In Proceedings of the Canadian Hydrographic Conference, St. John’s, NL, Canada, 14–17 April 2014. [Google Scholar]
- Bu, X.; Yang, F.; Ma, Y.; Wu, D.; Zhang, K.; Xu, F. Simplified calibration method for multibeam footprint displacements due to non-concentric arrays. Ocean. Eng. 2020, 197, 106862. [Google Scholar] [CrossRef]
- Yang, L.J.; Cui, J.L.; Yang, Z.Q.; Zhai, G.C.; Wang, C. Multi-level index structure based on spatial distribution characteristics of point cloud. Laser Infrared 2023, 53, 137–145. [Google Scholar]
- Beltrami, M.; da Silva, A.C.L. A grid-quadtree model selection method for support vector machines. Expert Syst. Appl. 2020, 146, 113172. [Google Scholar] [CrossRef]
- Samet, H. The Quadtree and Related Hierarchical Data Structures. ACM Comput. Surv. 1984, 16, 187–260. [Google Scholar] [CrossRef]
- Gottschalk, S.; Lin, M.C.; Manocha, D. OBBTree: A hierarchical structure for rapid interference detection. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 4–9 August 1996; pp. 171–180. [Google Scholar]
- Chang, J.-W.; Wang, W.; Kim, M.-S. Efficient collision detection using a dual OBB-sphere bounding volume hierarchy. Comput. Aided Des. 2010, 42, 50–57. [Google Scholar] [CrossRef]
- Wang, W.; Ma, J.; Liu, W. Research and Application of Collision Detection Based on Oriented Bounding Box. Comput. Simul. 2009, 26, 180–183+312. [Google Scholar]
- Siwei, H.; Baolong, L. Review of Bounding Box Algorithm Based on 3D Point Cloud. Int. J. Adv. Netw. Monit. Control. 2021, 6, 18–23. [Google Scholar] [CrossRef]
- Song, N.Y.; Son, Y.; Han, H.; Yeom, H.Y. Efficient Memory-Mapped I/O on Fast Storage Device. ACM Trans. Storage 2016, 12, 1–27. [Google Scholar] [CrossRef]
- Evans, N. Verifying QThreads: Is Model Checking viable for User-Level Tasking runtimes? In Proceedings of the 2nd IEEE/ACM International Workshop on Software Correctness for High-Performance Computing (HPC) Applications, Dallas, TX, USA, 12 November 2018; pp. 25–32. [Google Scholar]


| Root Node | Child Node | Leaf Node |
|---|---|---|
| Point cloud offset | Oriented bounding box information | Oriented bounding box information |
| Oriented bounding box information | Subnode file information | Neighbor node file information |
| Subnode file information | Current node point set information |
| Swath Number | Number of Point Clouds | Traditional Quadtree (s) | Conventional Oriented Quadtree (s) | Improved Oriented Quadtree (s) | Constructing Quadtree (s) |
|---|---|---|---|---|---|
| 1 | 1,026,000 | 0.581 | 3.063 | 1.107 | 0.515 |
| 2 | 1,760,000 | 0.864 | 4.751 | 1.698 | 0.694 |
| 3 | 2,417,200 | 1.152 | 6.554 | 2.306 | 0.905 |
| 4 | 3,137,600 | 1.325 | 8.212 | 2.995 | 1.182 |
| 5 | 3,538,800 | 1.489 | 9.218 | 3.352 | 1.331 |
| 6 | 4,016,000 | 1.629 | 10.470 | 3.687 | 1.427 |
| 7 | 5,388,800 | 2.010 | 14.593 | 5.100 | 1.897 |
| 8 | 6,235,600 | 2.136 | 18.007 | 5.545 | 1.947 |
| 9 | 9,267,600 | 3.687 | 25.824 | 8.221 | 2.829 |
| 10 | 10,776,400 | 4.102 | 31.039 | 9.741 | 3.515 |
| Swath Number | Number of Point Clouds | Traditional Quadtree (s) | Conventional Oriented Quadtree (s) | Improved Oriented Quadtree (s) |
|---|---|---|---|---|
| 1 | 1,026,000 | 4/106 | 3/85 | 3/85 |
| 2 | 1,760,000 | 5/120 | 3/85 | 3/85 |
| 3 | 2,417,200 | 5/132 | 4/101 | 4/101 |
| 4 | 3,137,600 | 5/125 | 4/89 | 4/89 |
| 5 | 3,538,800 | 5/125 | 4/81 | 4/81 |
| 6 | 4,016,000 | 5/132 | 3/85 | 3/85 |
| 7 | 5,388,800 | 5/125 | 4/88 | 4/88 |
| 8 | 6,235,600 | 5/123 | 4/137 | 4/137 |
| 9 | 9,267,600 | 6/185 | 4/125 | 4/125 |
| 10 | 10,776,400 | 6/176 | 5/124 | 5/124 |
| Retrieval Region | Point Number | Traditional Quadtree (ms) | Conventional Oriented Quadtree (ms) | Improved Oriented Quadtree (ms) | TRAVERSAL (ms) |
|---|---|---|---|---|---|
| 1 | 0 | 0.11 | 0.10 | 0.10 | 212 |
| 2 | 1,075,204 | 53 | 51 | 52 | 241 |
| 3 | 2,176,067 | 94 | 79 | 82 | 259 |
| 4 | 3,393,547 | 145 | 118 | 118 | 282 |
| 5 | 4,219,178 | 192 | 159 | 162 | 315 |
| 6 | 5,003,093 | 214 | 173 | 180 | 331 |
| 7 | 6,220,027 | 277 | 238 | 233 | 363 |
| 8 | 7,047,486 | 311 | 248 | 251 | 378 |
| 9 | 8,021,641 | 391 | 321 | 320 | 401 |
| 10 | 9,028,699 | 429 | 333 | 335 | 426 |
| 11 | 10,776,400 | 456 | 360 | 361 | 453 |
| Swath Number | Number of Point Clouds | 1% of Total Point Clouds | 2% of Total Point Clouds | 3% of Total Point Clouds | 4% of Total Point Clouds | 5% of Total Point Clouds |
|---|---|---|---|---|---|---|
| 1 | 1,026,000 | 4/304 | 3/100 | 3/84 | 3/80 | 3/72 |
| 2 | 1,760,000 | 4/292 | 3/92 | 3/84 | 3/80 | 3/68 |
| 3 | 2,417,200 | 4/300 | 3/104 | 3/84 | 3/80 | 3/64 |
| 4 | 3,137,600 | 4/288 | 4/140 | 3/84 | 3/80 | 3/60 |
| 5 | 3,538,800 | 4/280 | 4/172 | 3/80 | 3/68 | 3/64 |
| 6 | 4,016,000 | 4/280 | 4/156 | 3/84 | 3/76 | 3/56 |
| 7 | 5,388,800 | 5/266 | 4/179 | 3/71 | 3/68 | 3/64 |
| 8 | 6,235,600 | 5/255 | 4/171 | 3/88 | 3/64 | 3/60 |
| 9 | 9,267,600 | 5/251 | 4/183 | 4/80 | 3/64 | 3/64 |
| 10 | 10,776,400 | 5/270 | 4/186 | 4/111 | 3/67 | 3/55 |
| Retrieval Region | Number of Coverage Swathes | Point Number | Multi-Threaded Time Consumption (ms) | Conventional Time Consumption (ms) | Improve Efficiency |
|---|---|---|---|---|---|
| 1 | 5 | 3,509,194 | 163 | 200 | 18% |
| 2 | 8 | 5,582,571 | 167 | 271 | 38% |
| 3 | 13 | 9,001,712 | 207 | 431 | 52% |
| 4 | 25 | 18,365,086 | 359 | 890 | 60% |
| 5 | 39 | 32,956,272 | 641 | 1575 | 60% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, X.; Dou, S.; Zhang, J.; Yun, T.; Zhu, Y.; Huang, Y.; Cui, X. Large Quantities of Acoustic Multibeam Bathymetric Point Clouds: Organizing Method for Efficient Storage and Retrieval. Remote Sens. 2025, 17, 2039. https://doi.org/10.3390/rs17122039
Bu X, Dou S, Zhang J, Yun T, Zhu Y, Huang Y, Cui X. Large Quantities of Acoustic Multibeam Bathymetric Point Clouds: Organizing Method for Efficient Storage and Retrieval. Remote Sensing. 2025; 17(12):2039. https://doi.org/10.3390/rs17122039
Chicago/Turabian StyleBu, Xianhai, Shuaibing Dou, Jianxing Zhang, Tianyu Yun, Yabing Zhu, Yi Huang, and Xiaodong Cui. 2025. "Large Quantities of Acoustic Multibeam Bathymetric Point Clouds: Organizing Method for Efficient Storage and Retrieval" Remote Sensing 17, no. 12: 2039. https://doi.org/10.3390/rs17122039
APA StyleBu, X., Dou, S., Zhang, J., Yun, T., Zhu, Y., Huang, Y., & Cui, X. (2025). Large Quantities of Acoustic Multibeam Bathymetric Point Clouds: Organizing Method for Efficient Storage and Retrieval. Remote Sensing, 17(12), 2039. https://doi.org/10.3390/rs17122039







