Mapping Mountain Permafrost via GPR-Augmented Machine Learning in the Northeastern Qinghai–Tibet Plateau
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Field Observations
2.2. Environmental Variables and Data Preprocessing
2.3. Machine Learning Modeling and Evaluation
3. Results
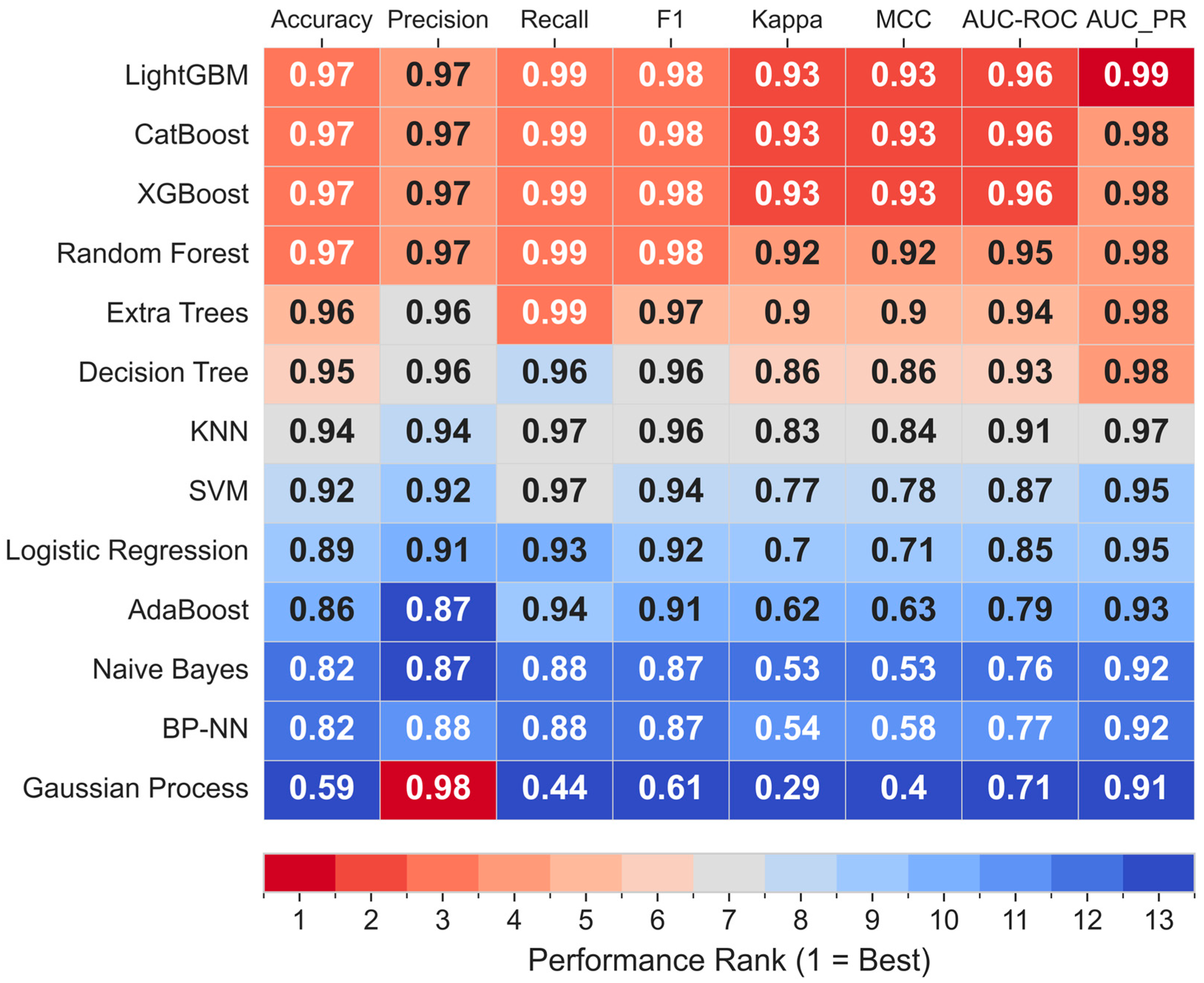
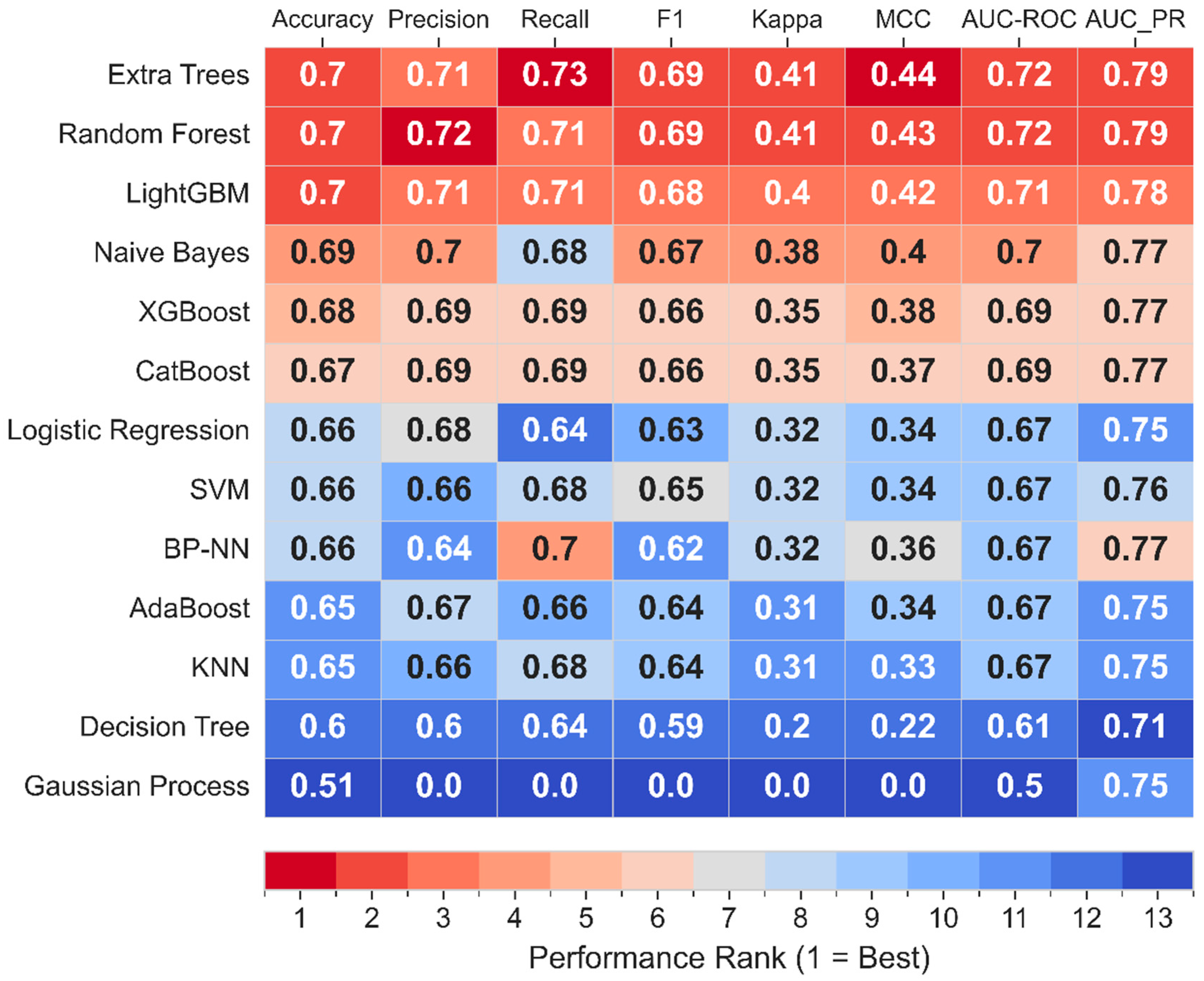
3.1. Model Performance Comparison of 13 Algorithms
3.2. Spatial Prediction Comparison of the Top Models
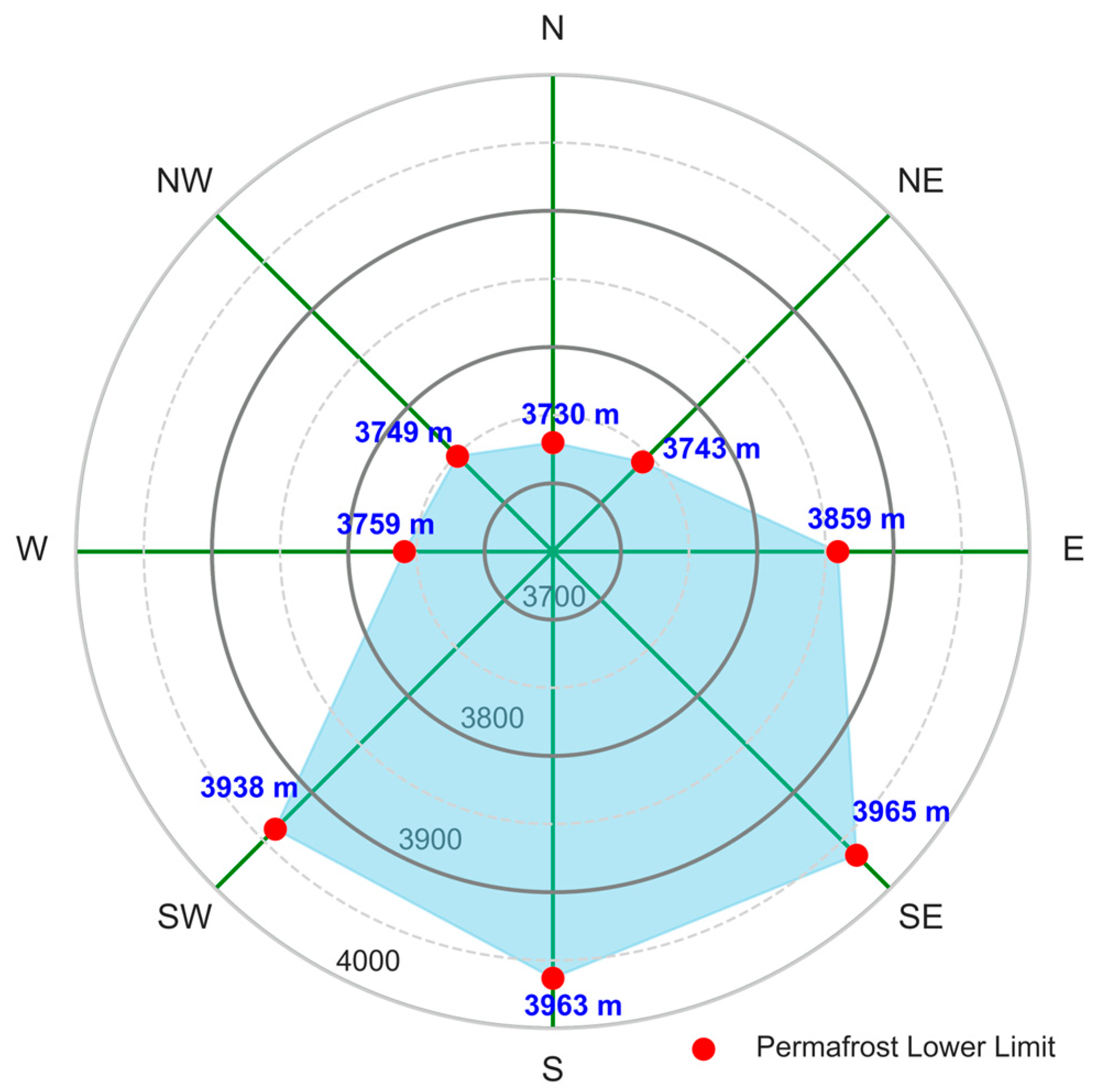
3.3. Aspect-Dependent Lower Elevation Limits of Modeled Permafrost
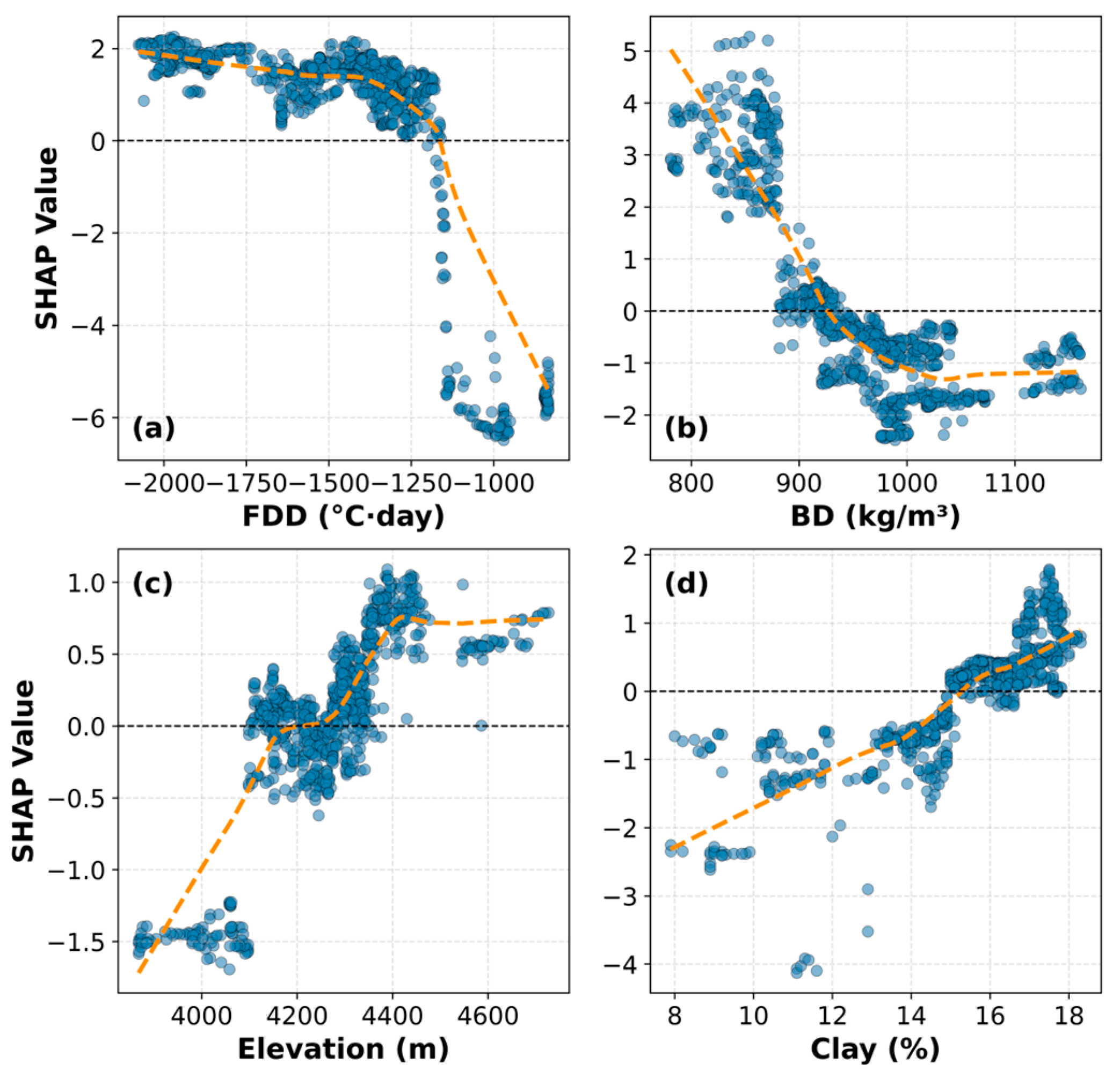
3.4. Feature Contributions Interpreted by SHAP in the LightGBM Model
4. Discussion
4.1. Comparison with Previous Studies
4.2. Added Value of GPR-Augmented Training Data
4.3. Feature Contributions and Environmental Controls
4.4. Limitations and Outlook
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hugelius, G.; Loisel, J.; Chadburn, S.; Jackson, R.B.; Jones, M.; MacDonald, G.; Marushchak, M.; Olefeldt, D.; Packalen, M.; Siewert, M.B.; et al. Large Stocks of Peatland Carbon and Nitrogen Are Vulnerable to Permafrost Thaw. Proc. Natl. Acad. Sci. USA 2020, 117, 20438–20446. [Google Scholar] [CrossRef] [PubMed]
- Vonk, J.E.; Tank, S.E.; Bowden, W.B.; Laurion, I.; Vincent, W.F.; Alekseychik, P.; Amyot, M.; Billet, M.F.; Canário, J.; Cory, R.M.; et al. Reviews and Syntheses: Effects of Permafrost Thaw on Arctic Aquatic Ecosystems. Biogeosciences 2015, 12, 7129–7167. [Google Scholar] [CrossRef]
- Zhang, T. Influence of the Seasonal Snow Cover on the Ground Thermal Regime: An Overview. Rev. Geophys. 2005, 43, 2004RG000157. [Google Scholar] [CrossRef]
- Miner, K.R.; Turetsky, M.R.; Malina, E.; Bartsch, A.; Tamminen, J.; McGuire, A.D.; Fix, A.; Sweeney, C.; Elder, C.D.; Miller, C.E. Permafrost Carbon Emissions in a Changing Arctic. Nat. Rev. Earth Environ. 2022, 3, 55–67. [Google Scholar] [CrossRef]
- Turetsky, M.R.; Abbott, B.W.; Jones, M.C.; Anthony, K.W.; Olefeldt, D.; Schuur, E.A.G.; Grosse, G.; Kuhry, P.; Hugelius, G.; Koven, C.; et al. Carbon Release through Abrupt Permafrost Thaw. Nat. Geosci. 2020, 13, 138–143. [Google Scholar] [CrossRef]
- Biskaborn, B.K.; Smith, S.L.; Noetzli, J.; Matthes, H.; Vieira, G.; Streletskiy, D.A.; Schoeneich, P.; Romanovsky, V.E.; Lewkowicz, A.G.; Abramov, A.; et al. Permafrost Is Warming at a Global Scale. Nat. Commun. 2019, 10, 264. [Google Scholar] [CrossRef]
- Smith, S.L.; O’Neill, H.B.; Isaksen, K.; Noetzli, J.; Romanovsky, V.E. The Changing Thermal State of Permafrost. Nat. Rev. Earth Environ. 2022, 3, 10–23. [Google Scholar] [CrossRef]
- Liljedahl, A.K.; Boike, J.; Daanen, R.P.; Fedorov, A.N.; Frost, G.V.; Grosse, G.; Hinzman, L.D.; Iijma, Y.; Jorgenson, J.C.; Matveyeva, N.; et al. Pan-Arctic Ice-Wedge Degradation in Warming Permafrost and Its Influence on Tundra Hydrology. Nat. Geosci. 2016, 9, 312–318. [Google Scholar] [CrossRef]
- Mu, C.; Abbott, B.W.; Norris, A.J.; Mu, M.; Fan, C.; Chen, X.; Jia, L.; Yang, R.; Zhang, T.; Wang, K.; et al. The Status and Stability of Permafrost Carbon on the Tibetan Plateau. Earth Sci. Rev. 2020, 211, 103433. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, T.; Frauenfeld, O.W.; Mu, C.; Wang, K.; Wu, X.; Guo, D.; Luo, J.; Hjort, J.; Aalto, J.; et al. Active Layer Thickness and Permafrost Area Projections for the 21st Century. Earth’s Future 2023, 11, e2023EF003573. [Google Scholar] [CrossRef]
- Wang, T.; Yang, D.; Yang, Y.; Zheng, G.; Jin, H.; Li, X.; Yao, T.; Cheng, G. Pervasive Permafrost Thaw Exacerbates Future Risk of Water Shortage Across the Tibetan Plateau. Earth’s Future 2023, 11, e2022EF003463. [Google Scholar] [CrossRef]
- Nicolsky, D.J.; Romanovsky, V.E. Modeling Long-term Permafrost Degradation. J. Geophys. Res. Earth Surf. 2018, 123, 1756–1771. [Google Scholar] [CrossRef]
- Obu, J.; Westermann, S.; Bartsch, A.; Berdnikov, N.; Christiansen, H.H.; Dashtseren, A.; Delaloye, R.; Elberling, B.; Etzelmüller, B.; Kholodov, A.; et al. Northern Hemisphere Permafrost Map Based on TTOP Modelling for 2000–2016 at 1 km2 Scale. Earth Sci. Rev. 2019, 193, 299–316. [Google Scholar] [CrossRef]
- Zou, D.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.; Wu, T.; Wu, J.; Xie, C.; Wu, X.; Pang, Q.; et al. A New Map of Permafrost Distribution on the Tibetan Plateau. Cryosphere 2017, 11, 2527–2542. [Google Scholar] [CrossRef]
- Boeckli, L.; Brenning, A.; Gruber, S.; Noetzli, J. Permafrost Distribution in the European Alps: Calculation and Evaluation of an Index Map and Summary Statistics. Cryosphere 2012, 6, 807–820. [Google Scholar] [CrossRef]
- Deluigi, N.; Lambiel, C.; Kanevski, M. Data-Driven Mapping of the Potential Mountain Permafrost Distribution. Sci. Total Environ. 2017, 590–591, 370–380. [Google Scholar] [CrossRef]
- Sun, W.; Cao, B.; Hao, J.; Wang, S.; Clow, G.D.; Sun, Y.; Fan, C.; Zhao, W.; Peng, X.; Yao, Y.; et al. Two-Dimensional Simulation of Island Permafrost Degradation in Northeastern Tibetan Plateau. Geoderma 2023, 430, 116330. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Kamrava, S.; Bai, T.; Sahimi, M. Machine Learning in Geo- and Environmental Sciences: From Small to Large Scale. Adv. Water Resour. 2020, 142, 103619. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Cheng, G. Climate Warming over the Past Half Century Has Led to Thermal Degradation of Permafrost on the Qinghai–Tibet Plateau. Cryosphere 2018, 12, 595–608. [Google Scholar] [CrossRef]
- Wang, X.; Ran, Y.; Pang, G.; Chen, D.; Su, B.; Chen, R.; Li, X.; Chen, H.W.; Yang, M.; Gou, X.; et al. Contrasting Characteristics, Changes, and Linkages of Permafrost between the Arctic and the Third Pole. Earth-Sci. Rev. 2022, 230, 104042. [Google Scholar] [CrossRef]
- Baral, P.; Haq, M.A. Spatial Prediction of Permafrost Occurrence in Sikkim Himalayas Using Logistic Regression, Random Forests, Support Vector Machines and Neural Networks. Geomorphology 2020, 371, 107331. [Google Scholar] [CrossRef]
- Li, X.; Ji, Y.; Zhou, G.; Zhou, L.; Li, X.; He, X.; Tian, Z. A New Method for Bare Permafrost Extraction on the Tibetan Plateau by Integrating Machine Learning and Multi-Source Information. Remote Sens. 2023, 15, 5328. [Google Scholar] [CrossRef]
- Popescu, R.; Filhol, S.; Etzelmüller, B.; Vasile, M.; Pleșoianu, A.; Vîrghileanu, M.; Onaca, A.; Șandric, I.; Săvulescu, I.; Cruceru, N.; et al. Permafrost Distribution in the Southern Carpathians, Romania, Derived from Machine Learning Modeling. Permafr. Periglac. Process. 2024, 35, 243–261. [Google Scholar] [CrossRef]
- Șerban, R.-D.; Șerban, M.; He, R.; Jin, H.; Li, Y.; Li, X.; Wang, X.; Li, G. 46-Year (1973–2019) Permafrost Landscape Changes in the Hola Basin, Northeast China Using Machine Learning and Object-Oriented Classification. Remote Sens. 2021, 13, 1910. [Google Scholar] [CrossRef]
- Sheng, Q.; Zhang, Y.; Li, K.; Ling, X.; Li, J. Exploring the Seasonal Comparison of Land Surface Temperature Dominant Factors in the Tibetan Plateau. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, X-1-2024, 197–203. [Google Scholar] [CrossRef]
- Cao, B.; Gruber, S.; Zhang, T.; Li, L.; Peng, X.; Wang, K.; Zheng, L.; Shao, W.; Guo, H. Spatial Variability of Active Layer Thickness Detected by Ground-penetrating Radar in the Qilian Mountains, Western China. J. Geophys. Res. Earth Surf. 2017, 122, 574–591. [Google Scholar] [CrossRef]
- Du, E.; Zhao, L.; Zou, D.; Li, R.; Wang, Z.; Wu, X.; Hu, G.; Zhao, Y.; Liu, G.; Sun, Z. Soil Moisture Calibration Equations for Active Layer GPR Detection—A Case Study Specially for the Qinghai–Tibet Plateau Permafrost Regions. Remote Sens. 2020, 12, 605. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, K.; Bagheri, M.; Burken, J.G.; Gu, A.; Li, B.; Ma, X.; Marrone, B.L.; Ren, Z.J.; Schrier, J.; et al. Machine Learning: New Ideas and Tools in Environmental Science and Engineering. Environ. Sci. Technol. 2021, 55, 12741–12754. [Google Scholar] [CrossRef]
- Haberkorn, A.; Kenner, R.; Noetzli, J.; Phillips, M. Changes in Ground Temperature and Dynamics in Mountain Permafrost in the Swiss Alps. Front. Earth Sci. 2021, 9, 626686. [Google Scholar] [CrossRef]
- Liu, G.; Zhao, L.; Xie, C.; Zou, D.; Wu, T.; Du, E.; Wang, L.; Sheng, Y.; Zhao, Y.; Xiao, Y.; et al. The Zonation of Mountain Frozen Ground under Aspect Adjustment Revealed by Ground-Penetrating Radar Survey—A Case Study of a Small Catchment in the Upper Reaches of the Yellow River, Northeastern Qinghai–Tibet Plateau. Remote Sens. 2022, 14, 2450. [Google Scholar] [CrossRef]
- Angelopoulos, M.C.; Pollard, W.H.; Couture, N.J. The Application of CCR and GPR to Characterize Ground Ice Conditions at Parsons Lake, Northwest Territories. Cold Reg. Sci. Technol. 2013, 85, 22–33. [Google Scholar] [CrossRef]
- Yang, J.; Dong, J.; Xiao, X.; Dai, J.; Wu, C.; Xia, J.; Zhao, G.; Zhao, M.; Li, Z.; Zhang, Y.; et al. Divergent Shifts in Peak Photosynthesis Timing of Temperate and Alpine Grasslands in China. Remote Sens. Environ. 2019, 233, 111395. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Liu, W.; Li, Z. 1 Km Monthly Temperature and Precipitation Dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, G.-L.; Song, X.; Li, D.; Zhao, Y.; Yang, J.; Wu, H.; Yang, F. High-Resolution and Three-Dimensional Mapping of Soil Texture of China. Geoderma 2020, 361, 114061. [Google Scholar] [CrossRef]
- Li, S.; Cheng, G. Map of Frozen Ground on Qinghai-Xizang Plateau; Gansu Culture Press: Lanzhou, China, 1996. [Google Scholar]
- Li, W.; Weng, B.; Yan, D.; Lai, Y.; Li, M.; Wang, H. Underestimated Permafrost Degradation: Improving the TTOP Model Based on Soil Thermal Conductivity. Sci. Total Environ. 2023, 854, 158564. [Google Scholar] [CrossRef]
- Liu, Y.; Ran, Y.; Li, X.; Che, T.; Wu, T. Multisite Evaluation of Physics-Informed Deep Learning for Permafrost Prediction in the Qinghai-Tibet Plateau. Cold Reg. Sci. Technol. 2023, 216, 104009. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Cheng, G.; Nan, Z.; Che, J.; Sheng, Y.; Wu, Q.; Jin, H.; Luo, D.; Tang, Z.; et al. Mapping the Permafrost Stability on the Tibetan Plateau for 2005–2015. Sci. China Earth Sci. 2021, 64, 62–79. [Google Scholar] [CrossRef]
- Zhang, Y.-Z.; Liang, S.-J.; Chen, J.-B.; Wang, M.; Jia, M.-T.; Jiang, Y.-T. Enhancing Artificial Permafrost Table Predictions Using Integrated Climate and Ground Temperature Data: A Case Study from the Qinghai-Xizang Highway. Cold Reg. Sci. Technol. 2025, 229, 104341. [Google Scholar] [CrossRef]
- Shen, Y.; Zuo, R.; Liu, J.; Tian, Y.; Wang, Q. Characterization and Evaluation of Permafrost Thawing Using GPR Attributes in the Qinghai-Tibet Plateau. Cold Reg. Sci. Technol. 2018, 151, 302–313. [Google Scholar] [CrossRef]
- Wu, T.; Wang, Q.; Watanabe, M.; Chen, J.; Battogtokh, D. Mapping Vertical Profile of Discontinuous Permafrost with Ground Penetrating Radar at Nalaikh Depression, Mongolia. Environ. Geol. 2009, 56, 1577–1583. [Google Scholar] [CrossRef]
- Obu, J. How Much of the Earth’s Surface Is Underlain by Permafrost? J. Geophys. Res. Earth Surf. 2021, 126, e2021JF006123. [Google Scholar] [CrossRef]
- Hu, G.; Zhao, L.; Li, R.; Park, H.; Wu, X.; Su, Y.; Guggenberger, G.; Wu, T.; Zou, D.; Zhu, X.; et al. Water and Heat Coupling Processes and Its Simulation in Frozen Soils: Current Status and Future Research Directions. Catena 2023, 222, 106844. [Google Scholar] [CrossRef]
- Gao, K.; Tang, Y.; Chen, D.; Wang, J.; Duan, A. Influence of Arctic Sea Ice and Interdecadal Pacific Oscillation on the Recent Increase of Winter Extreme Snowfall in Northeast China. Atmos. Res. 2023, 295, 107030. [Google Scholar] [CrossRef]
- Li, R.; Ma, J.; Wu, T.; Wang, Q.; Wu, X.; Zhao, L.; Wang, S.; Hu, G.; Liu, W.; Jiao, Y.; et al. The Spatiotemporal Variations of Freezing Index and Its Relationship with Permafrost Degradation over the Qinghai–Tibet Plateau from 1977 to 2016. Theor. Appl. Clim. 2024, 155, 985–998. [Google Scholar] [CrossRef]
- Martin, L.C.P.; Nitzbon, J.; Aas, K.S.; Etzelmüller, B.; Kristiansen, H.; Westermann, S. Stability Conditions of Peat Plateaus and Palsas in Northern Norway. J. Geophys. Res. Earth Surf. 2019, 124, 705–719. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Prabhat Deep Learning and Process Understanding for Data-Driven Earth System Science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Beddrich, J.; Gupta, S.; Wohlmuth, B.; Chiogna, G. The Importance of Topographic Gradients in Alpine Permafrost Modeling. Adv. Water Resour. 2022, 170, 104321. [Google Scholar] [CrossRef]
- Bergen, K.J.; Johnson, P.A.; De Hoop, M.V.; Beroza, G.C. Machine Learning for Data-Driven Discovery in Solid Earth Geoscience. Science 2019, 363, eaau0323. [Google Scholar] [CrossRef]

| Variable | Code | Description/Relevance | Data Source |
|---|---|---|---|
| Climatic factors | |||
| Land surface temperature | LST | Proxy for near-surface energy input and surface heat budget | MODIS MOD11A1 (2003–2019) |
| Thawing degree days | TDD | Cumulative thermal energy during thaw season; key driver of permafrost degradation | Derived from MODIS |
| Freezing degree days | FDD | Accumulated freezing intensity; indicator of freeze duration | Derived from MODIS |
| Mean annual temperature | AT | Highly collinear with TDD; retained to enhance climatic context | Peng et al. [34] |
| Annual precipitation | Pre | Reflects hydrothermal conditions; potentially influences vegetation and insulation | Peng et al. [34] |
| Topographic factors | |||
| Elevation | DEM | Controls surface temperature and soil water content via lapse rate | ASTER GDEM v2 |
| Slope | Slope | Influences runoff and snow redistribution | Derived from DEM |
| Aspect | Aspect | Affects solar exposure and snowmelt timing | Derived from DEM |
| Topographic Wetness Index | TWI | Proxy for water accumulation and soil moisture | DEM-derived |
| Solar radiation | Sola | Controls energy input; relevant for melt and insulation processes | GIS-based solar model |
| Latitude | Lat | Proxy for regional climate gradient | ASTER |
| Longitude | Lon | Captures east–west climatic and vegetative differences | ASTER |
| Surface condition factors | |||
| Normalized Difference Vegetation Index | NDVI | Proxy for vegetation cover; alters insulation and latent heat flux | Landsat 8 (2013–2015) |
| Normalized Difference Water Index | NDWI | Indicator of surface water content and wetness | Landsat 8 (2013–2015) |
| Normalized Difference Moisture Index | NDMI | Proxy for canopy and surface moisture | Landsat 8 (2013–2015) |
| Bulk density | BD | Key determinant of soil thermal conductivity | Liu et al. [35] |
| Sand content | Snd | Affects porosity, drainage, and freeze–thaw dynamics | |
| Clay content | Clay | Influences heat capacity and moisture retention | |
| Organic carbon density | Soc | Related to soil insulation and carbon storage; collinear with BD in some cases | |
| Gravel fraction | Cf | Impacts soil heat flux and infiltration pathways |
| Category | Abbreviation | Model Name | Key Characteristics |
|---|---|---|---|
| Tree-Based Models | RF | Random Forest | Ensemble of decision trees based on bagging; robust to overfitting and handles high-dimensional data effectively. |
| ET | Extremely Randomized Trees | Similar to RF but with more randomized splits; faster training and reduced variance. | |
| DT | Decision Tree | Single-tree structure; highly interpretable but prone to overfitting on complex datasets. | |
| Boosting-Based Models (GBDT) | XGBoost | Extreme Gradient Boosting | Highly efficient; incorporates advanced regularization techniques to prevent overfitting; excels in handling large datasets with complex patterns. |
| LightGBM | Light Gradient Boosting Machine | Optimized for speed and memory efficiency; uses histogram-based learning; particularly suitable for large dataset. | |
| CatBoost | CatBoost | Specifically designed for categorical feature encoding and high performance; reduces the need for extensive preprocessing. | |
| AdaBoost | Adaptive Boosting | Using weighted weak classifiers to improve overall prediction accuracy. | |
| Linear and Kernel-Based Models | LR | Logistic Regression | Linear model for binary classification; simple, interpretable, and works well with linearly separable data. |
| SVM | Support Vector Machine | Kernel-based method for both linear and nonlinear classification; effective for small dataset with clear margins of separations. | |
| GP | Gaussian Process | Probabilistic non-parametric Bayesian model; provides uncertainty estimates but computationally expensive. | |
| Other Models | BP-NN | BP Neural Network | Multi-layer perceptron; a classical neural network; suitable for capturing complex, nonlinear relationships in data. |
| KNN | K-Nearest Neighbors | Non-parametric model relying on distance measures; sensitive to the choice of k and feature scaling. | |
| NB | Naive Bayes | Simple probabilistic classifier based on Bayes’ theorem; assumes feature independence; included as a baseline for evaluating model performance in structured environmental data. |
| Performance Parameters | Formula | Description |
|---|---|---|
| Accuracy | The proportion of correctly classified samples among all samples, reflecting the overall predictive capability. | |
| Precision | The proportion of predicted positive samples that are true positives. | |
| Recall | The proportion of actual positive samples correctly identified. | |
| F1 Score | The harmonic mean of precision and recall, balancing both metrics. | |
| Cohen’s Kappa | Measures agreement between predicted and observed classifications, considering chance agreement. | |
| MCC | A balanced metric considering all four confusion matrix elements, suitable for imbalanced data. | |
| AUC-ROC | Area under the ROC curve, measuring the ability to distinguish between positive and negative classes. | |
| AUC-PR | Area under the precision–recall curve, particularly useful for evaluating imbalanced data. |
| Elevation Band | Area Proportion (%) | Observation Sites | Permafrost Proportion (%) | |||
|---|---|---|---|---|---|---|
| LightGBM | CatBoost | XGBoost | Random Forest | |||
| 3000–3500 m | 0.07 | 0 | 0 | 0 | 0 | 0 |
| 3500–4000 m | 7.79 | 40 | 0.79 | 2.66 | 1.74 | 0 |
| 4000–4500 m | 63.64 | 927 | 65.27 | 68.28 | 70.12 | 65.18 |
| 4500–5000 m | 28.35 | 48 | 94.83 | 97.58 | 95.59 | 96.63 |
| 5000–5500 m | 0.16 | 0 | 99.98 | 99.98 | 99.98 | 99.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Liu, G.; Hu, G.; Zou, D.; Li, R.; Du, E.; Wu, T.; Wu, X.; Zhao, G.; Zhao, Y.; et al. Mapping Mountain Permafrost via GPR-Augmented Machine Learning in the Northeastern Qinghai–Tibet Plateau. Remote Sens. 2025, 17, 2015. https://doi.org/10.3390/rs17122015
Xiao Y, Liu G, Hu G, Zou D, Li R, Du E, Wu T, Wu X, Zhao G, Zhao Y, et al. Mapping Mountain Permafrost via GPR-Augmented Machine Learning in the Northeastern Qinghai–Tibet Plateau. Remote Sensing. 2025; 17(12):2015. https://doi.org/10.3390/rs17122015
Chicago/Turabian StyleXiao, Yao, Guangyue Liu, Guojie Hu, Defu Zou, Ren Li, Erji Du, Tonghua Wu, Xiaodong Wu, Guohui Zhao, Yonghua Zhao, and et al. 2025. "Mapping Mountain Permafrost via GPR-Augmented Machine Learning in the Northeastern Qinghai–Tibet Plateau" Remote Sensing 17, no. 12: 2015. https://doi.org/10.3390/rs17122015
APA StyleXiao, Y., Liu, G., Hu, G., Zou, D., Li, R., Du, E., Wu, T., Wu, X., Zhao, G., Zhao, Y., & Zhao, L. (2025). Mapping Mountain Permafrost via GPR-Augmented Machine Learning in the Northeastern Qinghai–Tibet Plateau. Remote Sensing, 17(12), 2015. https://doi.org/10.3390/rs17122015










