Abstract
Due to its capacity of long-time automatic observation, the Vaisala CL51 Ceilometer, which is a simple single wavelength lidar, has great potential to retrieve aerosol vertical profiles. However, the backscattering signals from ceilometers around 910 nm, which are seriously affected by background signals and water vapor absorption, strongly limits the performance of aerosol retrievals. To overcome this issue, a signal correction process would be crucial to reduce errors of backscattering signals of the CL51 ceilometer. Herein, we develop a signal correction method including background signal correction and efficient water vapor correction. Using the profile observed by the collocated Raman lidar as reference data, we demonstrate that the signal correction significantly improves the accuracy of aerosol measurements from the ceilometer, reducing the median relative error between the two instruments from 29.34% to 21.54%. Although the median error remains slightly above the generally acceptable level, the improvement is nonetheless evident and meaningful. We further indicate that the water vapor correction, based on the humidity profiles, has effectively scaled the underestimated ceilometer backscatter profiles, particularly under humid conditions. The water correction method is validated in Leipzig, and the results imply the effectiveness of water vapor correction in different locations. For individual profiles, at around 1.3 km, where the largest profile differences occur, the relative error between the original CL61 and PollyXT decreases from 28.0% to 13.2% after water vapor correction. Our findings underscore the importance of the ceilometer in capturing the vertical distribution of aerosols through refined signal processing, offering a practical approach for observing the atmosphere.
1. Introduction
The vertical profile of aerosols is a crucial characteristic, playing a significant role in radiative forcing estimation, climate impact assessment, and air pollution studies. Lidar observation is commonly used in aerosol vertical profile retrieval. However, the lidar equipment is relatively expensive and requires manual maintenance. As a widely deployed simple lidar, the ceilometer provides extensive aerosol observation data near the surface and enhances our ability to monitor aerosol vertical profiles.
Ceilometers are simple elastic single-wavelength backscatter lidars originally designed to detect cloud-base height with the emitted wavelength between 900 nm and 1100 nm. They are much cheaper than advanced aerosol lidars and could operate 24/7 under all weather conditions automatically, thus becoming more widespread and denser with continuous measurements. Such advantages widen the application of ceilometers which are widely distributed in lidar networks, airports and weather bureau in America and Asia, and could serve as supplements of sparse aerosol lidar measurement. An important ceilometer network is the Automatic Lidars and Ceilometers (ALC) with nearly 300 ceilometers in the E-PROFILE program of European Meteorological Services Network (EUMETNET).
Although ceilometers are originally designed to determine cloud base height, they have also been widely used in aerosol-related studies such as volcanic ash monitoring [1], desert dust transport [2,3] and mixing layer heights determination from ceilometer signals [4,5,6,7]. More importantly, the ceilometers can be of much help for measuring aerosol vertical profiles as supplement of aerosol lidars which are pricy and quite limited [8,9,10]. However, it is still challenging because of the low signal processing quality of ceilometers [11]. The processing of ceilometer signals mainly involves two components: background correction and water vapor correction. Background correction aims to mitigate noise from instruments and the environment, primarily caused by instrument dark current signals. Water vapor correction addresses the impact of water vapor absorption, particularly when the emitted radiation from ceilometers (such as the Vaisala CL51 and CL61) is near the water vapor absorption band. Signal correction is of great importance for subsequent aerosol optical depth (AOD) inversion, and substantial research efforts have been dedicated to this area.
The ceilometer operates at a single wavelength, and the retrieval of aerosol backscattering coefficients requires the assumption of a constant lidar ratio. This assumption introduces a certain level of uncertainty into the retrieval. To constrain the inversion and improve accuracy, ancillary data such as optical depth measurements are needed. The error introduced by lidar ratio estimation is an unavoidable limitation in aerosol profile retrieval based on the ceilometer. Nevertheless, in regions without access to high-precision lidar systems, aerosol profiles derived from ceilometer observations remain valuable for atmospheric monitoring. According to Wiegner et al. [11], a relative error in the retrieved backscattering coefficient on the order of 10% is considered acceptable.
Background signals could induce large errors in aerosol remote sensing especially for the backward approach. Some studies tried to temporally average backscattering signal to improve the signal-to-noise ratio (SNR), and others chose to smooth signals in logarithmic scale over altitude due to exponentially decreasing air density [12,13]. Although the aforementioned methods enhance the signal-to-noise ratio (SNR) of backscattering signal, they struggle to correct the background signal, which predominantly comprises dark current signal. To automate the processing of ceilometer signal, the background signal is generally acquired using a “termination hood” or various signal processing methods. Kotthaus et al. [14] took the total backscatter signals measured in clear midnight as an estimate for the background signal above 2.4 km. Later, Marcos et al. [10] improved this method with two steps (estimating dark signal and reducing the uncertainty introduced by the dark noise estimation assumption) and Raman lidar measurements. Although the two steps method is more complex, it can determine the background signal accurately between 1 km and 2.4 km. In addition, Bedoya-Velásquez et al. [8] analyzed the spatial characteristics of noises and found backscatter signal oscillation above 9 km because of atmosphere background light. In this study, we develop a background correcting method by combining the dark signal correcting method of Kotthaus and shifted signal correcting method of Bedoya-Velásquez. By simultaneously eliminating dark signal and atmosphere background noise, the ceilometer signal can be automatically corrected requiring no additional instruments.
For the Vaisala CL51 ceilometer, the emitting wavelength is close to the absorption band of water vapor and the absorption cross-section of water vapor varies within this wavelength range. The emission wavelength of the Vaisala CL51 ceilometer is around 910 nm, and the effect of water vapor absorption need to be corrected. According to Wiegner et al. [11], the error in estimating extinction/backscattering coefficient can reach more than 20% if water vapor correction is ignored. Thus, Wiegner and Gasteiger [15] developed a water vapor correction scheme for ceilometer data calibration (WAPL), utilizing data from a high-resolution transmission molecular absorption database (HITRAN), radiosonde measurement, and the atmospheric radiative transfer simulator (ARTS). Wiegner et al. [16] validated the WAPL method in Germany, and the experiment obtained good results on CL51 ceilometers, while it was not always successful in the case of CL31 and CS135 validation. Although these studies proposed some available water vapor correction methods, they did not perform consistently across different climate zones due to varying meteorological conditions, laser wavelength drift, and other factors. Moreover, operations of the radiative transfer model used in those correction methods are time-consuming and inapplicable for near real-time correction. The WAPL method has been developed to increase the efficiency of calculating absorption coefficients but the mean absorption cross-section table calculated by the WAPL method is not suitable for different climate zones [15]. The absorption cross-section table needs to be recalculated for different places. Based on the band absorption theory, we establish an empirical model that connects the total absorption and the integrated water vapor (IWV) in this study. This empirical model facilitates near real-time ceilometer data processing, and is easy to implement across different climate zones.
In this study, a background signal and water vapor correction method is developed for Vaisala CL51 ceilometer measurements. By estimating dark signals and background signals from the ceilometer’s backscattering profile, we automatically correct the ceilometer’s signal, requiring no additional instruments. Different from the aforementioned WAPL method by keeping the water absorption cross-section table, this study tries to establish a statistical model based on empirical relations between absorptivity and absorber concentration. The comparison between the processed ceilometer signal and lidar proves the empirical statistical model to be effective for water vapor correction, thus providing a simpler way for real-time signal processing. The statistical model of water vapor transmission is also applied to ceilometer data in Leipzig to validate their effectiveness in different locations. The signal correction method developed in this study enables signal processing for aerosol backscattering coefficient retrieval.
This article is organized as follows. Section 2 introduces the instruments and data. Section 3 describes the methodology and method used in the ceilometer signal correction procedure and data processing method in validation. In Section 4, the results of ceilometers and lidar are compared for method validation. In addition, we analyze the impact of signal correction on the backscattering coefficient and validate the adaption of the water correction model in Leipzig. Finally, Section 5 discuss the signal correction method proposed in this study.
2. Instrumentation and Data
2.1. Ceilometer
In this study, a Vaisala CL51 ceilometer installed on the rooftop of Wuhan University, China (30.5°N, 114.4°E), is used for signal correction and method development. The CL51 emits laser pulses (910 ± 10 nm at 25 °C, full width at half maximum: 3.4 nm) using an InGaAs diode laser, with backscattered signals detected by a silicon avalanche photodiode (APD). The APD receiver of the CL51 ceilometer operates in analog mode, and the vendor software provides an overlap function to correct for incomplete overlap between the telescope’s field of view and the laser beam [11,14,17]. Owing to its coaxial optical path design and relatively wide FOV compared to the Raman lidar, the CL51 ceilometer provides a high degree of overlap between the transmitted and received signals, even at low altitudes near the instrument. Consequently, the blind zone is small, and no overlap function is applied to the CL51 signal in this study.
Level 2 data from the CL51 provide range-corrected signals up to 15,400 m, with a vertical resolution of 10 m and a temporal resolution of 16 s. Two CL51 ceilometers, CL51-1 (July 2019–June 2020) and CL51-2 (December 2020–July 2021), are used to assess the proposed signal correction method. Minimal differences in corrected results between the two devices confirm the method’s applicability.
To validate the water vapor correction method in different locations, data from a Vaisala CL61 ceilometer in Leipzig (51.4°N, 12.4°E) are used. The CL61 operates similarly to the CL51, emitting at 910 nm and providing continuous atmospheric observations. According to Cloudnet data, the CL61’s attenuated backscatter coefficient profiles have a vertical resolution of 4.80 m and a temporal resolution of 1 min. The processed CL61 data are provided by ACTRIS Cloudnet.
2.2. Microwave Radiometer
In this study, an RPG-HATPRO microwave radiometer is used to derive atmospheric temperature and humidity profiles. This passive sensor measures temperature in the V-band (51.26–58.00 GHz) and absolute humidity in the K-band (22.24–31.40 GHz) with 21 detection channels across seven receivers. It is also equipped with infrared instruments and ground weather sensors to provide cloud-base height and surface pressure.
The radiometer and ceilometer conducted simultaneous measurements in the same location. The radiometer primarily provides temperature and humidity profiles, as well as surface meteorological data, for ceilometer signal correction. Profiles extend from 0 to 10 km, with a vertical resolution of 10–300 m depending on altitude, covering the ceilometer detection range. The temporal resolution is approximately 1 min. Merra-2 data supplement this study by providing pressure profiles. Including the M2I3NPASM dataset, Merra-2 provides pressure, humidity, and temperature profiles with a spatial resolution of 0.5° × 0.625° and a temporal resolution of 3 h. The vertical resolution is interpolated to match that of the radiometer, and temporal variations are calculated. All prepared data undergo simple signal filtering to reduce systematic noise, yielding hourly pressure, humidity, and temperature profiles.
Additionally, another RPG-HATPRO microwave radiometer in Leipzig is used to validate the water vapor correction method in different locations. This radiometer, with the same vertical and temporal resolution as the one in Wuhan, provides absolute humidity profiles. The Leipzig data are sourced from ACTRIS Cloudnet.
2.3. Lidar Data
A single-band polarization lidar is used for correction method verification which operates at wavelength of 532 nm. The lidar provides aerosol profiles that serve as reference data. It observes at a distance of 1 km from the ceilometer CL51 in Wuhan. This instrument offers range-corrected signals and depolarization products from the surface up to 60 km, with a temporal resolution of 1 min and vertical resolution of 30 m [18]. Strict cloud filtering strategies are applied to eliminate cloud-contaminated profiles [10]. Additionally, lidar observations at an altitude above 540 m are selected to avoid effects of incomplete overlap near the ground.
A Raman polarization lidar in Leipzig is used to validate the water vapor correction method in different locations. The PollyXT lidar, operating at a wavelength of 1064 nm, provides reference backscattering coefficient values for atmospheric observations. It features a temporal resolution of 0.5 min and a vertical resolution of 7.47 m. With a maximum detection height of 26,900 m, the PollyXT lidar fully covers the detection range of the CL61. The PollyXT data are provided by ACTRIS Cloudnet.
2.4. CE318T Photometer
The CE318T photometer is an instrument for multispectral atmospheric photometry from the French manufacturer Cimel. It measures irradiance quantitatively and automatically by tracking the sun, the moon, and the sky. Later, these measurements are applied to retrieve aerosol properties, such as Aerosol Optical Depth (AOD), Volume Size Distribution (VSD), and so on. Thus, the CE318T photometer is widely used in AERONET, SONET, and other global aerosol networks.
In this study, the CE318T photometer is co-located with the CL51 ceilometer and provides AOD in four spectral channels (340 nm, 440 nm, 870 nm, and 1020 nm). The AOD is regarded as a constraint to determine the concentration of atmospheric aerosols in the least square method. In addition, the components of aerosols are mainly water-soluble aerosol, soot aerosol, and mineral aerosol in Wuhan according to the references [19,20]. Their extinction coefficients and backscatter coefficients are calculated based on the theory of Mie Scattering, the lognormal distribution function, and assumptive microphysical properties. The above optical properties are used to calculate the lidar ratios and Angstrom exponent.
3. Methodology and Theory
The signal correction procession only considers the elastic backscattering scattering of lidar signal. The elastic lidar equation is shown as Equation (1):
The elastic lidar equation describes the scattering and absorption processes of lidar signal in the atmosphere [21]. The range-corrected signal is equal to the multiplication of backscattered original signal and the square of the height from the ceilometer z. is the ceilometer calibration constant, affected by the laser emission power, the pulse duration, the active area of the receiver, and the receiver’s efficiencies. The backscattering coefficient of aerosols and air molecules represent the scattering efficiency of lidar signal. The attenuation of lidar signal is expressed by the two-way transmission of air molecules and aerosols and water vapor . is the background signal from environment and ceilometer APD receiver.
According to the Klett–Fernald–Sasano method [22,23,24], Equation (1) can be used to retrieve aerosols after the water vapor correction and background correction. For the subsequent aerosol retrieval and signal correction, the necessary parameters, and , need to be calculated from meteorological observations and ceilometer data.
In this section, the principles of background signal and the water vapor two-way transmission calculations are introduced in detail to realize the automatic correction of the CL51 ceilometer range-corrected signals. In addition, the signal processing method used for validation with lidar data is described.
3.1. Background Signal Estimation Method
As shown in Equation (1), the background signal should be removed from the original profiles of the Vaisala CL51 ceilometer in the first place. The background signal contains two parts: the instrument-related dark current signal and the shifted signal according to Kotthaus et al. [14].
The main component of is the dark current signal, which always exists with or without the light and return signals. Although the dark current signal is theoretically expected to be range-independent, the internal characteristics of the ceilometer, such as altitude-dependent averaging time intervals, cause the dark current signal to vary with height. The manufacturer Vaisala provides an element named “termination hood” for its measurements. However, this element needs manual operation and is probably unavailable for the long-term updates of . Therefore, in this study, is estimated at profiles around midnight in the clear sky [10,14]. In this study, statistical characteristics of backscatter signals from the ceilometers is obtained to determine values of between 22:00 and 2:00 local time. In addition, a cloud filtering strategy is employed to avoid cloud influence as follows. First, the range-corrected signal is limit to an altitude between 0.5 km and 3.2 km. Subsequently, if the maximum value of exceeds twenty times the value at 0.3 km above and below, the profile is rejected as this condition indicate the cloud contamination. Finally, the profile around midnight are all rejected if more than 2/3 profiles are contaminated by clouds.
is a non-negligible bias which leads to serious negative values in ceilometer signal. Although aims at emphasizing the cloud base height and facilitates clearer cloud base height detection, it occasionally renders the backscattering signals of thin clouds negative, making backscattering signals unavailable at high altitudes. In the aerosol profile retrieval, introduces a non-negligible error that must be removed. value varies with the atmospheric background signal, thus shows significant diurnal differences characteristics. After the determination of , is calculated as a constant for every measured profile in this study. According to Kotthaus et al. [14], is estimated as the mean value of minus between 7 and 9 km without clouds.
After estimating the dark signal , can be determined using ceilometer signal and between 7 and 9 km under cloud-free condition, following Equation (3).
3.2. Water Vapor Absorption Calculation
After the background correction, according to Wiegner and Gasteiger [15], Equation (1) is revised as follows:
To eliminate the water vapor absorption effect along the laser propagation path, the two-way water vapor transmission needs to be calculated. Since the absorption spectrum of water vapor around 910 nm is much narrower than the width of the emission spectrum of the ceilometers, and is wavelength dependent within the CL51 emission spectrum, is estimated by calculating water vapor absorption at each wavelength and combining the absorption with the weight based on the spectral shape distribution. Thus, the fundamental principle of water vapor absorption calculation can be expressed by Equations (5) and (6):
where is the weight at the wavelength ; is the water vapor number concentration; is the mean absorption cross-section of water molecule. In this study, based on the ceilometer emission spectrum, the distribution of is assumed to be a Gaussian-shaped emission spectrum with full width at half maximum of 3.4 nm (). In addition, and are calculated based on meteorological data provided by microwave radiometer and the HITRAN database respectively.
A Python library named HAPI (HITRAN Application Programming Interface) [25] is applied to process the spectroscopic data from HITRAN instead of ARTS-simulations by Wiegner and Gasteiger [15]. In the water vapor absorption calculation process, the spectral resolution is set to to calculate the two-way transmission.
However, invoking HITRAN and making a hyperspectral calculation requires lots of time and needs numerous meteorological data. Therefore, different statistical models between integrated water vapor (IWV) and are analyzed in this study to achieve simple and efficient calculations. IWV is the integration of absolute humidity along the laser propagation path with unit of . The absolute humidity profile could be provided by the microwave radiometer. Constructing the statistical model between IWV and water vapor two-way transmission is considerably less time-consuming than conducting absorption calculation at every wavelength for every ceilometer observation. In addition, the study on the absorption band model theory provides a rationale for constructing a statistical model in the ceilometer CL51 emission band [26,27]. From the point of view of eliminating the water vapor absorbing effect, the total absorption of the ceilometer emission band is the desired result. Correlating the band absorption coefficient and IWV with the statistical model provides great convenience for direct use.
In previous studies, statistical models between band absorption and IWV have been studied. Five kinds of statistical model are compared in this study for water vapor correction. Except for the quantic polynomial model used for comparison, all the others are statistical fitting models commonly used in previous studies, or statistical models based on experimental theories.
Goody’s model of band absorption provides a simple and accurate expression for the mean spectral transmission of water vapor [28]. It can be approximately expressed by Equation (7) [29]:
where is the effective water vapor transmission; w is the integrated water vapor (IWV); a and b are empirical constants. Equation (7) is widely used to retrieve water vapor concentration with photometers and sky radiometers [30,31,32,33,34,35]. However, its coefficients and depend on the vertical distribution of meteorological elements at different times. Thus, the coefficients a and b vary over time, making Equation (7) unsuitable for simulating the water vapor transmittance.
Based on the water vapor correction principle and Equation (7), the selected statistical model should satisfy the demands below:
- (1)
- To achieve an efficient calculation, the statistical model should be a simple variant of a fundamental function, such as the power function or the logarithmic function.
- (2)
- According to the requirement for describing the function’s variation, at least two parameters are used in the model to describe the relationship between and IWV.
- (3)
- The effective transmission reaches 100% in the absence of water vapor in the atmosphere (IWV = 0).
- (4)
- Showing similar Taylor expansion as exponential formula Equation (7).
According to the selection rules, the binomial model Equation (8) and logarithmic model Equation (9) are chosen in this study. They align with the study of the absorption band model by Edward et al. [26] under the assumption of a non-rigid rotator at different absorber concentrations. Under this assumption, three asymptotic relations between transmission and IWV can be derived: the linear relation at low values of , the square root relation at moderate values, and the logarithmic relation at high values. The absorption band model justifies the use of Equations (8) and (9) for water vapor correction. In addition, other experimental data of the band absorption also display a binomial and logarithmic empirical relation under different absorber concentrations [27].
In that way, binomial expression and logarithmic form are chosen in this study as follows:
In addition to Equations (7)–(10) [36], fifth-order polynomial equations are also compared with each other. Equation (10) is the form of correction function according to Hopkin et al. used in ceilometer data processing.
Since the transmittance must decrease as the IWV increases, all the compared models show a monotonically decreasing function. From this perspective, the sign of the model parameter can be determined. The statistical models were compared, and the model parameters and Taylor expansions are shown in Table 1.

Table 1.
Model functions, model parameters, and their Taylor expansions (level n at w = 0).
3.3. Validation Process
To validate the signal corrections for the CL51 ceilometer, range-corrected signals are compared with the extrapolated signals from the Raman polarization lidar. After background correction and water vapor correction, some necessary treatments on profiles are taken to compare the profiles between the ceilometer and the lidar. First of all, due to the differing backscattering characteristics of the 532 nm lidar and the 910 nm ceilometer, the signal conversion algorithm introduced by Wiegner et al. [16] is applied to enable the signal translation between the two wavelengths. In this conversion process, AOD data provided by the photometer are used to estimate the Angstrom exponent. Through the signal conversion algorithm, the range-corrected signal of the lidar at a wavelength of 532 nm can be extrapolated to 910 nm. After the signal convention process, profiles from the ceilometer and the lidar are normalized because of their different emission power. Normalization is a linear transformation that scales data to the range [−1, 1] by mapping the minimum value to −1, the maximum to 1, and adjusting all other values proportionally based on their relative position between the maximum and minimum. In this way, the difference in emission power between the ceilometer and the lidar is eliminated, allowing for direct comparison.
Secondly, all profiles from the ceilometer are interpolated to get the same vertical resolution as the lidar does. In addition, the suitable range for the validation is changeable in different conditions. The minimum height is 540 m above sea level to avoid the effects of the incomplete lidar view field overlap, and the maximum height depends on the negative values of ceilometer signals.
Furthermore, to evaluate the impact of the signal correction procedure on backscattering coefficient profiles, the profiles derived from the corrected ceilometer signal are compared with those from the original signal. The backscattering coefficient profiles are retrieved using the backward integration form of the Fernald algorithm, as presented in Equation (11) [22].
In Equation (11), the subscripts a and m represent aerosols and air molecules, respectively. RCS′(z) is the range-corrected signal after the signal correction procedure. The lidar ratio (S) is defined as the ratio of extinction coefficient and backscattering coefficient (). For effectiveness evaluation, the lidar ratio for air molecules is fixed at , and the aerosol lidar ratio at 910 nm in Wuhan is estimated based on photometer observations, as detailed in Section 3.4 [37]. Accordingly, the forward integration form of the Fernald algorithm is used to retrieve the aerosol backscattering coefficient profile, starting from the surface and progressively calculating the backscattering coefficient upward.
3.4. Lidar Ratio Calculation
The lidar ratio is a necessary constant in Klett–Fernald algorithm. In general, the lidar ratio has a relatively minor impact on the retrieval of aerosol backscattering profiles, but it plays a more significant role in the retrieval of extinction profiles. Moreover, the lidar ratio varies with different aerosol mixtures. In this study, the AOD observed by the photometer is used as a constraint, under the assumption that the aerosol mixture is vertically homogeneous. The number concentrations of individual aerosol components are estimated using a least-squares approach, which is then used to derive the lidar ratio at 910 nm.
Aerosols in Wuhan are primarily composed of water-soluble aerosol, soot aerosol, and mineral aerosol. The relevant parameters are listed in Table 2. According to the research by Hess et al. [19], water-soluble and soot aerosols are the dominant components in continental or urban regions, and are suitable for characterizing aerosols in areas heavily influenced by anthropogenic pollution, while mineral aerosol mainly represents mineral particles such as those found in dust storms.

Table 2.
Microphysical properties of the three aerosol components.
The monthly lidar ratios in Wuhan for the year 2021 are presented as a boxplot in Figure 1. As shown in Figure 1, the estimated lidar ratios are further aggregated into a monthly estimation, and the monthly median value is adopted to minimize the influence of outliers. On the one hand, the use of representative monthly estimates ensures the reliability and accuracy of the retrieved aerosol backscattering coefficient profiles. On the other hand, the monthly lidar ratio enables aerosol vertical profile retrieval using ceilometer data, even when sun photometer measurements are missing or affected by unfavorable observational conditions, thereby ensuring more continuous and complete retrieval results.

Figure 1.
Monthly lidar ratio boxplot in Wuhan, 2021. The red line represents estimated lidar ratio in each month.
The estimated lidar ratio introduces a certain degree of error into the Klett–Fernald algorithm. To quantitatively assess the impact of the lidar ratio uncertainty on backscattering coefficient retrieval, a sensitivity analysis was conducted to elucidate its influence. Taking December as an example, where the median lidar ratio (Sa) was 65.79, a sensitivity analysis was performed using data from 27 December. Assuming a 10% relative error in the lidar ratio, the resulting changes in backscattering coefficient retrieval are evaluated. When the lidar ratio increases and decreases by 10%, the corresponding average relative errors in the retrieved backscattering coefficients are 10.92% and 13.92%, respectively. These results highlight the importance of accurate lidar ratio estimation.
4. Results and Method Validation
This section aims to introduce the signal correction method established in this study, and to investigate the influence of the background correction and water vapor correction on the quality of range-corrected signals. The applicability of water vapor correction is analyzed in different humidity conditions. Furthermore, the impact of the signal correction method on the backscattering coefficient profiles is evaluated with the Fernald algorithm. Additionally, to assess the effectiveness of the water vapor correction method in different locations, the statistical model of water vapor transmission is applied to the backscattering coefficient data observed by the ceilometer in Leipzig and validated using the co-located Raman lidar (PollyXT).
4.1. Signal Correction Method
4.1.1. Background Signal Estimation
As previously mentioned, the background signal is estimated using the backscattering signal from the clear midnight sky. Figure 2 and Figure 3 present the frequency distribution of backscattering signals around midnight (22:00–2:00) for CL51-1 and CL51-2, respectively. The top row presents the frequency distribution histograms of signal values from each height, while the bottom row shows the corresponding Q–Q plots. In the histograms, the x–axis represents the ceilometer backscattering signal intensity, while the y–axis denotes the frequency density, calculated as frequency divided by bin width. The Q–Q plot (quantile–quantile plot) is employed to compare the distribution of the backscattering signal with a theoretical normal distribution. This is achieved by plotting the quantiles of the observed data against those of the reference distribution to check the normality of data.

Figure 2.
Histograms (upper row) and Q-Q plots (bottom row) of signal values at different from CL51-1 on March 2020 at midnight under clear sky conditions. The red line in Q-Q plots denotes the ideal normal distribution.
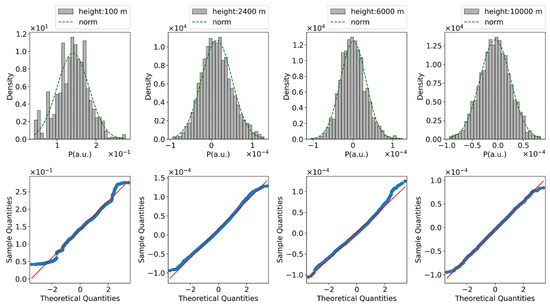
Figure 3.
Similar to Figure 2, but for CL51-2 on March 2021. The red line in Q-Q plots denotes the ideal normal distribution.
Results from the two ceilometers show a nearly perfect normal distribution at a height of 10,000 m, where there are no aerosols and clouds. Different from that, the distribution shows a slight deviation at lower heights of 6000 m and 2400 m. This deviated skewed distribution could be caused by backscattering signals of occasional aerosols and thin clouds. However, the Q-Q plots distribute around the straight line, indicating the signal values still conform to normal distribution, but the expected value is not equal to 0. In addition, more aerosols play a leading role in the near-surface detections of the ceilometer, which results in irregular values and a multimodal distribution. As demonstrated by Kotthaus et al. [14], a constant equal to at 2.4 km is used for lower altitude in this study, as estimating a dark signal from a backscattering signal at a lower altitude is challenging due to the influence of an aerosol. In a word, the time-dependent signal is likely to follow a normal distribution at higher heights, and the estimation is easily affected by aerosols. Therefore, the median value of return signals around midnight under the clear sky condition of each month is used to estimate . Figure 2 and Figure 3 show the backscattering signal on March 2020 and March 2021, respectively. The dark signal of each month is estimated and stored for rapid background signal correction.
The final result of the dark signal monthly estimation is shown in Figure 4. While the dark current signal is theoretically expected to be range-independent, the observed range dependence is likely attributable to altitude-dependent variations in the CL51’s signal processing. Because the dark signal is sensitive to temperature changes, the dark signal profiles show significant monthly differences. Figure 4 shows the median values of the backscattering signal at midnight, revealing significant monthly variations. Generally, the dark signal shows little difference during November–December and January–March when the temperature is low, and the dark signal increases with higher environmental temperature. The dark signal is the most obvious in June–September when the temperature is high, which is caused by the higher thermal excitation effect in the ceilometer Si-APD receiver. In addition, the smooth profiles are final results with logarithmic smoothing. At 5 km and 7 km, due to the instrumental data storage step, unstable spikes appear, which is consistent with the conclusions of Kotthaus et al. [14] studies. Notably, the monthly dark signal profiles intersect at approximately 13 km, while the peak values are commonly around 4 km. This differs from the dark current profiles reported in previous studies, highlighting the importance of estimating the dark current signal for individual ceilometers.
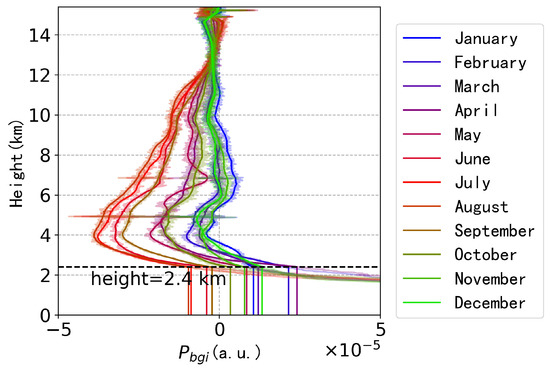
Figure 4.
Ceilometer monthly dark signal profile.
After the dark signal estimation, the shifted signal can be calculated by the original signal and the dark signal with Equation (3). The effect of background correction on the ceilometer signal is validated later. On the whole, the background correction procedure can estimate the background signal presented in the ceilometer measurements at low altitude and slightly enlarge the effective detection range.
A sensitivity analysis of the background signal was conducted separately for April and December, assuming a ±10% relative error to evaluate its impact on the retrieved backscattering coefficient. In December, a −10% error in the background signal results in a 2.38% relative error in the backscattering coefficient, while a +10% error leads to a 2.11% deviation. In April, the corresponding errors increase to 3.16% and 2.96%, respectively, mainly due to a higher dark current during this period, which introduces greater uncertainty.
4.1.2. Water Vapor Transmission Model
After five models are selected in Section 3.2, evaluation metrics such as SSE (the sum of squares due to error), MSE (mean squared error), RMSE (root mean squared error), and R2 are calculated for quantitative analysis in Table 3 to select the optimal statistical model. In order to ensure the accuracy of the algorithm, the ten-fold cross-validation method is adopted in this study [38].

Table 3.
Results of 10-fold cross validation for five models.
Ten-fold cross-validation is a commonly used model evaluation method, primarily aimed at assessing a model’s generalization ability on unseen data. The core idea is to divide the dataset into several parts and repeatedly train and validate the model on different subsets. This helps reduce the bias caused by random data splits and improves the stability and reliability of the evaluation.
As mentioned in Section 3.2, calculated by HAPI, the two-way transmission is employed to establish a statistical model with IWV. To assess the robustness and generalization ability of the statistical model relating the to the IWV, a 10-fold cross-validation approach is employed. Specifically, the full dataset is randomly partitioned into ten equal subsets. In each iteration, nine subsets are used for training the model, while the remaining one is reserved for validation. This process is repeated ten times, with each subset used once as the validation set.
For each fold, the model performance is evaluated using error metrics such as the SSE, MSE, RMSE, and R2. The final evaluation results are obtained by averaging the performance metrics across all ten folds. This method ensures that the model’s predictive capability is not overly dependent on a particular subset of the data and helps to minimize the risk of overfitting.
As shown in Table 3, the quintic polynomial (polynomial_5) outperforms both and due to its lower RMSE and higher R2. However, the two best results are from and , which are both established in this study. Notably, the RMSE of is about 21% lower than RMSE of . This indicates logarithmic model (Equation (9)) has the greatest prediction of the water vapor transmission.
Although all of the five models have R2 more than 0.98 in Table 3, they do not work well in all conditions. Thus, typical models are analyzed graphically in the scatter plots of Figure 5 and residual plots of Figure 6. The two-way transmission data and IWV are calculated from metrological data observed by the microwave radiometer and HITRAN database. According to Figure 5a,d and Figure 6a,d, and obviously underestimate the two-way transmission when IWV is more than 6 g/cm2. On the contrary, the transmission is overvalued by Equation (8), as observed in Figure 5b and Figure 6b. Moreover, Figure 5e and Figure 6e indicate an unsatisfactory fitting result of the quantic polynomial in spite of RMSE being equal to 0.0091 and R2 being equal to 0.9958, because its residuals change regularly like a wave as the IWV increases. Considering the higher IWV leads to the lower effective water vapor transmittance and results in the greater influence of water vapor on the ceilometer profile, is more suitable for the water vapor correction work of the ceilometer. As illustrated in Figure 6c, the residual plots are approximately symmetrically distributed around the x–axis, indicating that the errors introduced by the water vapor correction tend to be canceled out when averaged. The maximum residual associated with Equation (12) is 0.031, suggesting that the transmission error caused by water vapor correction remains below 0.031.


Figure 5.
Scatter plots of two-way transmissivity and IWV for different models, along with the fitting curves. (a–e) represent the fitting performance of Equations (7)–(10) and the quantic polynomial respectively.

Figure 6.
Scatter plots of residual and IWV for different models, along with the fitting curves. (a–e) represent the fitting residual of Equations (7)–(10) and the quantic polynomial respectively.
On the whole, is the optimal choice to predict the water vapor transmission according to Table 3, and Figure 5 and Figure 6. This results in an excellent fitting curve based on the logarithmic relationship, especially at high values of IWV. This phenomenon is consistent with conclusions of segmented studies on band absorption theory [26,27].
Based on the above analysis, the final equation determined for the water vapor correction is as follows:
where is the two-way transmission of water vapor; is the integrated water vapor from ground to height z, in g/cm2. Equation (12) is used to estimate the water vapor transmittance in water vapor correction. The absolute humidity profile provided by the microwave radiometer enables the calculation of water vapor transmittance with high spatial and temporal resolution. Since the ceilometer and radiometer conduct simultaneous observations in the same location, the water vapor correction can be performed in real time. The water vapor correction procedure helps to obtain an actual backscattering signal, especially under high water vapor concentration circumstances.
4.2. Validation with Lidar Observation in Wuhan
After normalization and height interpolation, SSE, RMSE, and symmetric Mean Absolute Percentage Error (SMAPE) between the lidar and ceilometer profiles are calculated for a quantitative evaluation. Generally, the application of the signal correction technique improves the agreement between the ceilometer and lidar backscattering profiles. In Figure 7, Figures (a) to (c) show comparisons between lidar data and CL51 data: (a) the original CL51 data, (b) the background-corrected CL51 data, and (c) the CL51 data after both background and water vapor corrections. To validate the procedure of background correction and water vapor correction, lidar data from five days in January, April, July, and October are selected and compared with related ceilometer data. The detailed analysis is as follows.
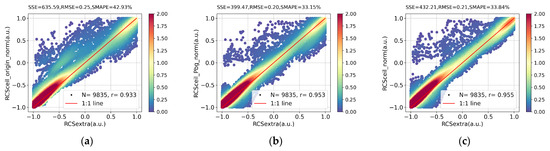
Figure 7.
Scatter plots of paired range-corrected signals measured by the Vaisala CL51 ceilometer (RCSceil, y–axis) and the lidar (RCSextra, x–axis). Each profile is normalized to a range of −1 to 1. (a) Original CL51 signal compared with lidar data; (b) background-corrected CL51 signal compared with lidar data; (c) CL51 signal after both background and water vapor corrections compared with lidar data.
As shown in Figure 7, the impact of background noise on the ceilometer is noticeable, so it is necessary to improve the data quality of ceilometer through background correction as Figure 7a,b show. In Figure 7a, dense points on the left of center and their normalized values from the CL51 ceilometer are obviously larger than those from the lidar. The further analysis suggests that most of the particular points are from various profiles measured on 29 April and 30 April 2021. Those profiles all have thin aerosol layers in a higher place than usual, at a height between about 2.5 km and 5 km. At this height, the dark current signal contributes a lot to backscattering signal profiles (as Figure 4 shows), while the aerosol caused backscattering signals that were not as strong as near the surface. This reduced the SNR of the data and led to serious errors in the profile. Thus, after the background correction, RMSE decreased from 0.25 to 0.20, and SMAPE decreased from 42.93% to 33.15% in Figure 7b. In addition, this means background correction can improve the ability to identify the maximum height of layers and retrieve aerosol properties, rather than ignoring negative values of original signals above the comparison range.
As shown in Figure 7b,c, the effect of water vapor correction is visually noticeable: it adjusts the scattered data points closer to the diagonal, particularly in the top-right region, where the points shift toward red, indicating improved agreement between the lidar and ceilometer. However, quantitatively, the water correction procedure only slightly improves the consistency of signal profiles between the ceilometer and the lidar, with r increasing from 0.953 to 0.955. In addition, the error metrics increase following the application of water vapor correction. This suggests that the error introduced by the statistical model may outweigh the benefits of the water vapor correction under low humidity. The cases under high humidity are considered separately in Figure 8.
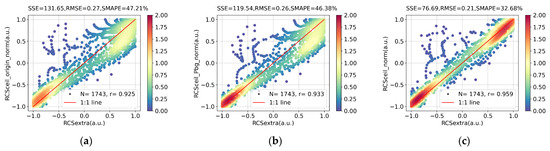
Figure 8.
Same as Figure 7, but for cases where IWV > 3 g/cm2. (a) Original CL51 signal compared with lidar data; (b) background-corrected CL51 signal compared with lidar data; (c) CL51 signal after both background and water vapor corrections compared with lidar data.
As shown in Figure 8, for cases where IWV > 3 g/cm2, the water vapor correction is particularly noticeable. In these cases, the original signal points become increasingly scattered as the normalized values increase. Additionally, the center of these points lies below the 1:1 line in the top-right corner, indicating smaller normalized values from the ceilometer. These significant discrepancies lead to an RMSE of 0.26 and SMAPE of 46.38%. However, the water vapor correction brings the discrete data points closer to the diagonal, improving the consistency of signal profiles between the ceilometer and lidar, as seen in Figure 8c. The RMSE and SMAPE decrease to 0.21 and 32.68%, respectively. Moreover, r increases from 0.933 to 0.959. These results show the importance of water vapor correction in high humidity conditions, highlighting the significant impact of water vapor absorption on the ceilometer, particularly at high IWV values.
The above results suggest the necessity and effectiveness of signal correction in order to account for background signals and water vapor absorption effects on the ceilometer signals. These normalized range-corrected signals from the ceilometer have no pronounced changes and even get a little worse after water vapor corrections when they are compared with signals from the lidar. However, as Figure 7 shows, this error is very slight and can usually be ignored. The main cause is, perhaps, the errors introduced by approximations in water vapor correction. Under high humidity, as Figure 8 shows, the water vapor correction is necessary and improves the quality of ceilometer signal effectively.
In this study, the Pearson Correlation Coefficient and Mean Euclidean Distance are computed to show the similarity of profiles in each pair. Pearson Correlation Coefficient is a measurement of the linear correlation between two variables, ranging from −1 to 1. It is calculated to show linear relationship between two variables. Mean Euclidean Distance is a measurement of the straight-line distance between two points in Euclidean space. Euclidean distance quantifies how far apart two points are, and it is often used to compare similarity or dissimilarity between observations. Figure 9 shows the frequency histograms of the Pearson Correlation Coefficient and Mean Euclidean Distance after different signal processions.

Figure 9.
Frequency distributions of (a) Pearson correlation coefficient and (b) mean Euclidean distance for each pair of profiles: the original profiles from the ceilometer (green); profiles after the background correction (orange); profiles after the background correction and water vapor correction (blue). “Counts” is the number of comparable profiles.
As shown in Figure 9, the Pearson coefficient for most profiles exceeds 0.98, while the Euclidean distance remains below 0.2. Therefore, the discussion primarily focuses on the percentage of profiles meeting these criteria. Notably, both metrics improve after water vapor correction, indicating that the correction enhances the consistency between ceilometer and Raman lidar profiles.
Furthermore, background correction leads to an increase in the Pearson Correlation Coefficient from 0.58 to 0.59, and the Mean Euclidean Distance from 0.64 to 0.70, as shown in Figure 9. These results suggest that background correction not only slightly refines the profile shape (as indicated by the Pearson coefficient increase in Figure 9a) but also reduces the discrepancy in signal magnitude between the ceilometer and lidar profiles (as reflected by the increase in Mean Euclidean Distance in Figure 9b). In addition, the water vapor correction leads to an increase in the Pearson Correction Coefficient from 0.59 to 0.65, and the Mean Euclidean Distance from 0.64 to 0.70, indicating the effectiveness of water vapor correction in improving the consistency between ceilometer and Raman lidar profiles. Overall, both water vapor correction and background correction play a role in improving the ceilometer’s backscattering profile.
In addition to the comparison of normalized signals, comparisons of backscattering coefficients retrieved from lidar and ceilometer observation are shown in Figure 10. The cross-comparison is conducted by matching the lidar data with the ceilometer data at the same height and time. In Figure 10, Figures (a) to (c) show backscattering coefficients comparisons between lidar and CL51: (a) the original CL51 data, (b) the background-corrected CL51 data, and (c) the CL51 data after both background and water vapor corrections. The detailed analysis is as follows.

Figure 10.
Scatter plots of paired backscattering coefficients by the Vaisala CL51 ceilometer (βceil, y–axis) and the lidar (βextra, x–axis). (a) Backscattering coefficients retrieved from original CL51 signal compared with lidar; (b) backscattering coefficients retrieved from background-corrected CL51 signal compared with lidar; (c) backscattering coefficients retrieved from CL51 signal after both background and water vapor corrections compared with lidar.
With the implementation of the signal correction procedures, the discrepancy between the backscattering coefficients retrieved from the lidar and the ceilometer is notably reduced. After applying the background correction, as shown in Figure 10a,b, the SSE reduces from to , and RMSE reduces from to . With Raman lidar observations as a reference, this indicates that the background correction effectively reduces systematic errors in the backscattering coefficients retrieved from ceilometer. The following water vapor correction, as shown in Figure 10b,c, the SSE reduces from to , and RMSE reduces from to . With Raman lidar data as the reference, these results demonstrate that the water vapor correction also plays a critical role in improving the accuracy of aerosol measurement from ceilometer. To mitigate the influence of extreme values, the median relative error is used to represent the agreement between ceilometer and lidar measurements. The median relative error decreases from 29.34% for the original ceilometer observations to 21.54% after signal correction, indicating improved agreement with Raman lidar data. Although the median error remains slightly above the generally acceptable level (on the order of 10%), the improvement is nonetheless evident and meaningful.
According to the above analysis, the proper usage of corrections improves the quality of range-corrects signals from the CL51 ceilometer. Since the background correction only depends on the ceilometer data, and the calculation is relatively simple, it is recommended to always apply the background correction. The effectiveness of water vapor correction based on the statistical model is noticeable under high humidity. However, the effect of water vapor correction is relatively limited under low humidity and induces minor error as shown in Figure 7. According to the statistical model in Equation (12), the two-way transmission remains relatively high under low humidity conditions, resulting in minimal modifications to the ceilometer data profile after water vapor correction. Nonetheless, applying the water vapor correction consistently is still recommended to ensure accuracy across varying atmospheric conditions. Overall, the comparison of backscattering coefficient profiles demonstrates the effectiveness of the proposed signal correction procedures. Using Raman lidar-retrieved backscattering coefficients as reference data, both the background signal correction and water vapor correction improves the accuracy of aerosol profiles from the ceilometer. Quantitative evaluations using RMSE consistently show that the combined correction approach leads to a closer match with reference lidar data, indicating enhanced accuracy in aerosol profiles derived from ceilometer observations. These results confirm the potential of the proposed correction method to enhance the reliability of ceilometer-based aerosol observations.
4.3. Impact of Signal Correction Method Analysis
To evaluate the impact of signal correction method on the atmospheric backscattering coefficient retrieval, the backscattering coefficient is calculated using CL51 ceilometer in Wuhan with Fernald algorithm (Equation (11)). The backscattering coefficient profiles retrieved from ceilometer signal before and after correction are compared. For validation, the observation on 27 December 2020 is used. The backscattering coefficient profiles before and after correction, along with their differences, are shown in Figure 11.
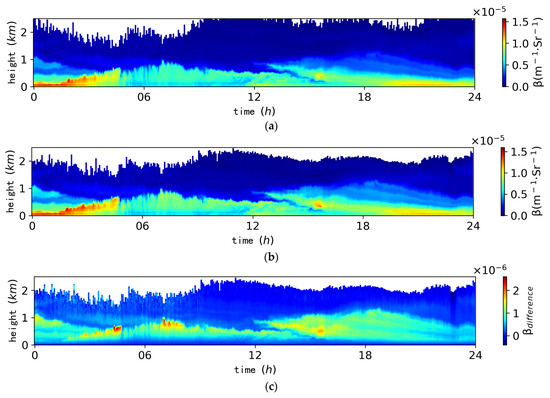
Figure 11.
Impact of signal correction method on retrieved backscattering coefficient profiles: (a) without signal correction, (b) with signal correction, (c) difference between Figures (a,b).
From Figure 11a to Figure 11b, it is evident that the signal correction procedure alters the overall backscattering coefficient profiles, especially in regions with the highest backscattering coefficient values. Compared to Figure 11a, the profiles in Figure 11b exhibit an enhancement in the aerosol accumulation region, a pattern also observed in Figure 11c. The most significant difference between the retrieved backscattering coefficients with and without signal correction occurs in aerosol-rich areas.
Notably, in Figure 11c, from UTC 12:00 to UTC 24:00, the signal correction procedure amplifies the backscattering signals in aerosol layers. This suggests that the correction method can modify signals and help aerosol detection in the upper atmosphere. Furthermore, after signal correction, the backscattering coefficient profiles show an average difference of 20.78% compared to the original signal, highlighting the necessity of the correction process.
Overall, the signal correction procedure is important for removing the effects of water vapor and background signals on the retrieved aerosol backscatter profiles for the CL51 ceilometer. The correction method developed in this study effectively mitigates the influence of dark signals and water vapor absorption on ceilometer measurements.
4.4. Water Vapor Correction Method Validation in Leipzig
After the validation of the ceilometer signal correction method, the effectiveness of the water vapor transmission statistical model is evaluated in different locations in Leipzig, Germany (51.4°N, 12.4°E). In this test, the CL61 ceilometer provides the data requiring correction, while the PollyXT lidar data serve as the reference. It should be noticed that the CL61 data of Cloudnet only provide the attenuated backscattering coefficient profiles rather than range corrected signals (RCS). Without access to the original signal, the estimation of background signal is impracticable. However, based on the Equation (4), the water vapor correction procedure can still be applied to the backscattering coefficient. The effectiveness of the water vapor correction can be assessed by comparing the backscattering coefficients before and after the correction. The relationship between the backscattering coefficient before and after water vapor correction is given by Equation (13).
The CL61 ceilometer observes the backscattering coefficient profile which is affected by water vapor absorption. With the statistical model Equation (12), the transmission of water vapor can be estimated with the absolute humidity data provided by the microwave radiometer. The CL61 ceilometer and the radiometer operate simultaneously in the same location, with the humidity profiles used to calculate water vapor transmission at different heights in real time. Lidar data are used to validate the effectiveness of statistical model-based water vapor correction. Because of the different resolution of CL61 and PollyXT, the temporal and vertical resolutions are adjusted to 5 min and 30 m, respectively, for comparison. Additionally, because the Rayleigh scattering intensity is inversely proportional to the fourth power of the wavelength, the backscattering coefficient of PollyXT must be scaled according to the wavelength ratio relative to the ceilometer. Figure 12 presents a comparison of the backscattering coefficients between PollyXT and CL61. To better illustrate the difference between two instruments, the backscattering coefficients are expressed in base-10 logarithmic scale. The data are filtered according to the quality flag of radiometer data; if no valid observations are available in the 5-min interval, the corresponding data point is removed. In the Figure, the red line represents the 1:1 line and the color scale indicates the density of data points. Gray data points denote the situation where the backscattering coefficient from two instruments at the same height and time differs by more than an order of magnitude. The PollyXT observation data near the ground exhibit errors with the backscattering coefficient showing NaN values at low height. Therefore, only an observation above 200 m is used for comparison in this study.
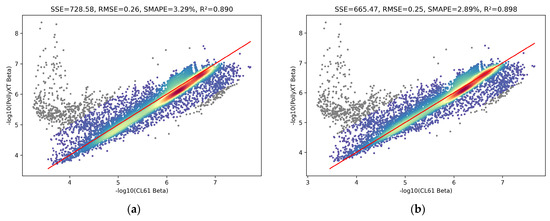
Figure 12.
Comparison of backscattering coefficients between PollyXT and CL61 on 21 December 2024: (a) without water vapor correction and (b) with water vapor correction.
Figure 12 presents a comparison of backscattering coefficients between PollyXT and CL61 in Leipzig on 21 December 2024. As shown in Figure 12, the water correction slightly improves the correlation of backscattering coefficients between the two instruments, with R2 increasing from 0.890 to 0.898. After applying the correction, the dense region of data points is more symmetrically distributed around the 1:1 line. In addition, all error metrics (SSE, RMSE, SMAPE) decrease after the water vapor correction procedure. Most of the gray data points are positioned above the 1:1 line, indicating that the backscattering coefficients retrieved from CL61 are much higher than those from PollyXT at these points. Further analysis reveals that these points primarily correspond to regions with high backscattering coefficients, suggesting a higher concentration of aerosols. In such cases, the Rayleigh scattering theory is no longer sufficient to explain the scattering intensity differences caused by different instrument wavelengths, and Mie scattering theory becomes more appropriate. Aerosol particles will cause much higher backscattering coefficient at a short wavelength of CL61, which is consistent with the trends observed in Figure 12.
The effect of water vapor correction is more obvious in circumstances where fewer large particles exist. For instance, observations in Leipzig on 22 January 2025 provide further insights, as shown in Figure 13.
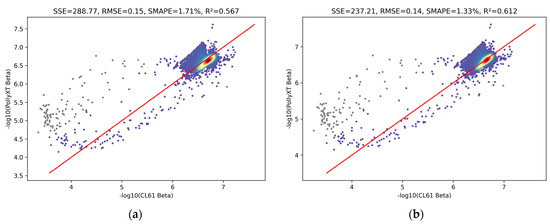
Figure 13.
Comparison of backscattering coefficients between PollyXT and CL61 on 22 January 2025: (a) without water vapor correction and (b) with water vapor correction.
As shown in Figure 13, after applying the water vapor correction, the data points are more evenly distributed around the 1:1 line, with the line directly passing through the center of the dense data zone. R2 increases from 0.567 to 0.612, and all the error metrics significantly decrease with the water vapor correction procedure. Most of the data points are concentrated within the range of 6 to 7, corresponding to a backscattering coefficient in the order of ~10−7. The water vapor correction procedure effectively compensates for the absorption of the ceilometer laser at 910 nm caused by water vapor.
In addition, an individual backscattering profile from Leipzig is presented to visually demonstrate the effect of water vapor correction. In Figure 14, the original ceilometer backscattering profile, the water vapor corrected ceilometer backscattering profile, and the corresponding lidar backscattering profile are drawn in blue, red, black, respectively, to validate the effectiveness of correction. The data were collected in Leipzig on 21 December 2024, at 17:30 (UTC+0), with a 5 min averaging interval. As illustrated in Figure 14, after applying the water vapor correction, the RMSE between the backscattering coefficients retrieved by the CL61 ceilometer and PollyXT lidar decreased from to , indicating a reduction in the error introduced by water vapor absorption. From the profile, aerosol concentration is relatively low near the surface, increasing rapidly to a first peak around 1 km. Above 1 km, the concentration exhibits an oscillatory decline, with a second peak observed at approximately 2.3 km. Specifically, taking the backscattering coefficient at approximately 1.3 km as an example, where the largest differences among profiles are observed, the relative error between the original CL61 profile and PollyXT is 28.0%. After applying the water vapor correction, the relative error is reduced to 13.2%. According to Wiegner et al. [11], a relative error of around 10% is considered acceptable for backscattering coefficients retrieved from ceilometers. Therefore, the corrected profile is in an acceptable range.

Figure 14.
Comparison of backscattering coefficients between PollyXT and CL61 on 21 December 2024, at 17:30. Original ceilometer profile, the water vapor corrected ceilometer profile, and the corresponding lidar profile are drawn in blue, red, and black, respectively.
Generally speaking, the statistical model established in this study performs well in different locations. By capturing the relationship between IWV and two-way water vapor transmission, the model enhances the efficiency of the water vapor correction process. Comparisons with PollyXT lidar data indicate that the corrected data exhibit higher similarity to the reference data and reduced error.
5. Discussion
The signal correction process is essential in the aerosol backscattering coefficient measurement based on the CL51 ceilometer. After applying the signal correction, using Raman lidar observations as reference data, the accuracy of backscattering coefficients derived from the ceilometer is enhanced. To enhance the quality of ceilometer backscattering signals, the background correction and water vapor correction are carried out for the Vaisala CL51 ceilometer using auxiliary data from a microwave radiometer and Merra-2. To realize efficient water vapor correction, the statistical model between water vapor transmission and IWV is constructed. Later, the results after signal corrections are validated by profiles from the lidar in 2021, and the impact of signal correction on backscattering coefficient retrieval is analyzed. In addition, the effect of the water correction method in different locations is validated using data from Leipzig. The main conclusions can be summarized as follows.
According to analysis, backscatter signals at midnight are in irregular distribution near the ground, in positive skew distribution at intermediate heights and in normal distribution at the top. These distributions are caused by the dark signal, some aerosols, and occasional clouds. Therefore, the median of high-altitude signals is chosen to estimate the profile of dark signal for the background correction, and the shifted signal is calculated by backscattering signal and dark signal. In the comparison between the normalized profile of the ceilometer and lidar, the background correction can reduce the RMSE from 0.25 to 0.20, and the SMAPE from 42.93% to 33.15%. The background correction can correct the signal profiles of the CL51 ceilometer.
As for the water vapor correction, meteorological data of the microwave radiometer and Merra-2 can be used to calculate the integrated water vapor (IWV, g/cm2) and two-way effective transmission based on HITRAN. Later, several statistical models between the transmission and IWV are analyzed to approximate the transmission simply and efficiently. As a result, the approximation of the logarithmic relationship in Equation (12) is the best because it leads to minimum errors under high humidity. This approximation improves the calculating efficiency of two-way effective transmission and realizes near-real time water vapor correction. Under high humidity, the effect of water correction procedure is non-negligible, with r increasing from 0.933 to 0.959. In addition, water vapor correction has an important influence on the shapes of the range-corrected signal profiles. It enhances the percentage of Pearson Correlation Coefficient exceeding 0.98, and the percentage of Mean Euclidean Distance within 0.2. The water vapor correction can correct the signal profiles of the CL51 ceilometer. The comparison of backscattering coefficients between the ceilometer and Raman lidar demonstrates improved agreement after signal correction, with the median relative error reducing from 29.34% to 21.54%. Although this remains slightly above the generally accepted threshold, the improvement is still evident and meaningful. Furthermore, the test of water correction in Leipzig validate signal correction’s effectiveness in different location. The water vapor correction method proposed in this study is applicable for correcting ceilometer signals with a central wavelength of 910 nm. At around 1.3 km, water vapor correction reduces the relative error between CL61 and PollyXT from 28.0% to 13.2%, bringing it close to the acceptable level.
On the whole, the proper usage of two corrections is advised on aerosol retrievals for the CL51 ceilometer in this study. Since the background correction only depends on the ceilometer, and the calculation is relatively simple, it is recommended to always carry out the background correction step. As for water vapor correction, some minor errors in the correction reduce accuracy of the profiles with small IWV. However, due to the relatively high two-way transmission under low humidity conditions, the water vapor correction introduces only minor modifications to the ceilometer data profile. To maintain accuracy across varying atmospheric conditions, consistent application of the water vapor correction is still recommended.
In summary, we successfully implemented background correction and water vapor correction on the Vaisala CL51 ceilometer, achieving signal processing and aerosol backscattering coefficients retrieval. The background signal is eliminated automatically with the ceilometer profile and the statistical model between transmittance and IWV is constructed to realize near real-time water vapor correction. However, there are some drawbacks in this study. The effective range of background correction is limited. It is worth noting that the background signal exhibited sensitivity to the operating temperature of the ceilometer, as shown in Figure 4. This implies that diurnal temperature variations may introduce fluctuations in the background level, potentially affecting the accuracy of backscatter retrievals. While active temperature control of the detector would offer the most robust solution to this issue, it is not feasible for our current commercial ceilometer system. In future work, we could explore alternative approaches, such as time-dependent background modeling, to reduce the impact of this effect on backscatter retrievals. Furthermore, the water vapor correction method relies on meteorological data, and its applicability in dry climate regions has not been thoroughly evaluated. Due to potential limitations in the existing model under low humidity, its implementation in such conditions may introduce some degree of error. Therefore, in dry climate regions, the water vapor transmission model may require reconstruction to ensure accuracy. The results presented in this paper represent a preliminary study on the innovative aerosol profile retrieval method based on ceilometer data. Currently, further research is constrained by accessibility to ceilometer, lidar, and humidity profile data. In future work, water vapor profiles obtained from satellite observations and standard atmospheric models will be used to assess the feasibility of performing water vapor correction in the absence of radiometer measurements. Additionally, data from a wider range of observational sites will be utilized to further evaluate the applicability of the proposed water vapor correction method across different climate regions.
Author Contributions
Conceptualization, S.L. (Siwei Li); methodology, S.L. (Siwei Li) and X.Z.; software, J.C. and X.Z.; validation, J.C., S.L. (Siwei Li), X.Z., G.S. and S.L. (Shuangliang Li); formal analysis, J.C.; investigation, J.C., S.L. (Siwei Li) and X.Z.; resources, J.C., G.S. and S.L. (Shuangliang Li); data curation, J.C.; writing—original draft preparation, J.C. and X.Z.; writing—review and editing, J.C.; visualization, J.C. and X.Z.; supervision, S.L. (Siwei Li); project administration, S.L. (Siwei Li); funding acquisition, S.L. (Siwei Li). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The National Natural Science Foundation of China, grant number 41975022.
Data Availability Statement
The Merra-2 data used in this study is provided with NASA, and is publicly available at https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2/ (accessed on 28 December 2021). The PollyXT data and CL61 data used in this study are provided by ACTRIS Cloudnet and available at https://cloudnet.fmi.fi/ (accessed on 11 February 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Flentje, H.; Claude, H.; Elste, T.; Gilge, S.; Köhler, U.; Plass-Dülmer, C.; Steinbrecht, W.; Thomas, W.; Werner, A.; Fricke, W. The Eyjafjallajökull eruption in April 2010—Detection of volcanic plume using in-situ measurements, ozone sondes and lidar-ceilometer profiles. Atmos. Chem. Phys. 2010, 10, 10085–10092. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Paliatsos, A.G.; Kappos, N.; Kasselouri, B. A Case of African Dust Transport over Athens Captured by a Ceilometer. In Advances in Meteorology, Climatology and Atmospheric Physics; Helmis, C.G., Nastos, P.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1011–1018. [Google Scholar]
- Nikolay, K.; Tsvetina, E.; Ivan, G.; Atanaska, D.; Danko, I.; Ventsislav, D.; Plamen, S.; Doyno, P. Ceilometer observation of Saharan dust over mountain valley of Sofia, Bulgaria. In Proceedings of the 18th International School on Quantum Electronics: Laser Physics and Applications, Sozopol, Bulgaria, 29 September–3 October 2014; SPIE: Bellingham, WA, USA, 2015; Volume 9447, p. 94470Q. [Google Scholar]
- Geiß, A. Automated Calibration of Ceilometer Data and Its Applicability for Quantitative Aerosol Monitoring. Ph.D. Thesis, Ludwig Maximilian University of Munich, Munich, Germany, 2016. [Google Scholar]
- Knepp, T.N.; Szykman, J.J.; Long, R.; Duvall, R.M.; Krug, J.; Beaver, M.; Cavender, K.; Kronmiller, K.; Wheeler, M.; Delgado, R.; et al. Assessment of mixed-layer height estimation from single-wavelength ceilometer profiles. Atmos. Meas. Tech. 2017, 10, 3963–3983. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Hong, J.; Lee, K.; Hong, J.; Velasco, E.; Lim, Y.J.; Lee, J.B.; Nam, K.; Park, J. Ceilometer Monitoring of Boundary-Layer Height and Its Application in Evaluating the Dilution Effect on Air Pollution. Bound.-Layer Meteor. 2019, 172, 435–455. [Google Scholar] [CrossRef]
- Li, S.; Joseph, E.; Min, Q.; Yin, B.; Sakai, R.; Payne, M.K. Remote sensing of PM2. 5 during cloudy and nighttime periods using ceilometer backscatter. Atmos. Meas. Tech. 2017, 10, 2093–2104. [Google Scholar] [CrossRef]
- Bedoya-Velásquez, A.E.; Herreras-Giralda, M.; Román, R.; Wiegner, M.; Lefebvre, S.; Toledano, C.; Huet, T.; Ceolato, R. Ceilometer inversion method using water-vapor correction from co-located microwave radiometer for aerosol retrievals. Atmos. Res. 2021, 250, 105379. [Google Scholar] [CrossRef]
- Cazorla, A.; Casquero-Vera, J.A.; Román, R.; Guerrero-Rascado, J.L.; Toledano, C.; Cachorro, V.E.; Orza, J.A.G.; Cancillo, M.L.; Serrano, A.; Titos, G.; et al. Near-real-time processing of a ceilometer network assisted with sun-photometer data: Monitoring a dust outbreak over the Iberian Peninsula. Atmos. Chem. Phys. 2017, 17, 11861–11876. [Google Scholar] [CrossRef]
- Marcos, C.R.; Gómez-Amo, J.L.; Peris, C.; Pedrós, R.; Utrillas, M.P.; Martínez-Lozano, J.A. Analysis of four years of ceilometer-derived aerosol backscatter profiles in a coastal site of the western Mediterranean. Atmos. Res. 2018, 213, 331–345. [Google Scholar] [CrossRef]
- Wiegner, M.; Madonna, F.; Binietoglou, I.; Forkel, R.; Gasteiger, J.; Geiß, A.; Pappalardo, G.; Schäfer, K.; Thomas, W. What is the benefit of ceilometers for aerosol remote sensing? An answer from EARLINET. Atmos. Meas. Tech. 2014, 7, 1979–1997. [Google Scholar] [CrossRef]
- Ioannis, B.; Aldo, A.; Giuseppe, D.; Aldo, G.; Fabio, M.; Lucia, M.; Gelsomina, P. Examination of possible synergy between lidar and ceilometer for the monitoring of atmospheric aerosols. In Proceedings of the Lidar Technologies, Techniques, and Measurements for Atmospheric Remote Sensing VII, Prague, Czech Republic, 19–22 September 2011; SPIE: Bellingham, WA, USA, 2011; Volume 8182, p. 818209. [Google Scholar]
- Lopatin, A.; Dubovik, O.; Chaikovsky, A.; Goloub, P.; Lapyonok, T.; Tanré, D.; Litvinov, P. Enhancement of aerosol characterization using synergy of lidar and sun-photometer coincident observations: The GARRLiC algorithm. Atmos. Meas. Tech. 2013, 6, 2065–2088. [Google Scholar] [CrossRef]
- Kotthaus, S.; O’Connor, E.; Münkel, C.; Charlton-Perez, C.; Haeffelin, M.; Gabey, A.M.; Grimmond, C.S.B. Recommendations for processing atmospheric attenuated backscatter profiles from Vaisala CL31 ceilometers. Atmos. Meas. Tech. 2016, 9, 3769–3791. [Google Scholar] [CrossRef]
- Wiegner, M.; Gasteiger, J. Correction of water vapor absorption for aerosol remote sensing with ceilometers. Atmos. Meas. Tech. 2015, 8, 3971–3984. [Google Scholar] [CrossRef]
- Wiegner, M.; Mattis, I.; Pattantyús-Ábrahám, M.; Bravo-Aranda, J.A.; Poltera, Y.; Haefele, A.; Hervo, M.; Görsdorf, U.; Leinweber, R.; Gasteiger, J.; et al. Aerosol backscatter profiles from ceilometers: Validation of water vapor correction in the framework of CeiLinEx2015. Atmos. Meas. Tech. 2019, 12, 471–490. [Google Scholar] [CrossRef]
- Hervo, M.; Poltera, Y.; Haefele, A. An empirical method to correct for temperature-dependent variations in the overlap function of CHM15k ceilometers. Atmos. Meas. Tech. 2016, 9, 2947–2959. [Google Scholar] [CrossRef]
- Kong, W.; Yi, F. Convective boundary layer evolution from lidar backscatter and its relationship with surface aerosol concentration at a location of a central China megacity. J. Geophys. Res. Atmos. 2015, 120, 7928–7940. [Google Scholar] [CrossRef]
- Hess, M.; Koepke, P.; Schult, I. Optical Properties of Aerosols and Clouds: The Software Package OPAC. Bull. Am. Meteorol. Soc. 1998, 79, 831–844. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, B.; Shi, G.; Li, S.; Di, H.; Yan, Q.; Hua, D. Correlation between the lidar ratio and the Ångström exponent of various aerosol types. Particuology 2018, 40, 62–69. [Google Scholar] [CrossRef]
- Collis, R.T.H.; Russell, P.B. Lidar measurement of particles and gases by elastic backscattering and differential absorption. In Laser Monitoring of the Atmosphere; Hinkley, E.D., Ed.; Springer: Berlin/Heidelberg, Germany, 1976; pp. 71–151. [Google Scholar]
- Fernald, F.G. Analysis of atmospheric lidar observations: Some comments. Appl. Opt. 1984, 23, 652–653. [Google Scholar] [CrossRef]
- Klett, J.D. Stable analytical inversion solution for processing lidar returns. Appl. Opt. 1981, 20, 211–220. [Google Scholar] [CrossRef]
- Sasano, Y.; Browell, E.V.; Ismail, S. Error caused by using a constant extinction/backscattering ratio in the lidar solution. Appl. Opt. 1985, 24, 3929–3932. [Google Scholar] [CrossRef]
- Kochanov, R.V.; Gordon, I.E.; Rothman, L.S.; Wcisło, P.; Hill, C.; Wilzewski, J.S. HITRAN Application Programming Interface (HAPI): A comprehensive approach to working with spectroscopic data. J. Quant. Spectrosc. Radiat. Transf. 2016, 177, 15–30. [Google Scholar] [CrossRef]
- Edwards, D.K.; Menard, W.A. Comparison of Models for Correlation of Total Band Absorption. Appl. Opt. 1964, 3, 621–625. [Google Scholar] [CrossRef]
- Howard, J.N.; Burch, D.E.; Williams, D. Infrared Transmission of Synthetic Atmospheres. III. Absorption by Water Vapor. J. Opt. Soc. Am. 1956, 46, 242–245. [Google Scholar] [CrossRef]
- Goody, R.M. A statistical model for water-vapour absorption. Q. J. R. Meteorol. Soc. 1952, 78, 165–169. [Google Scholar] [CrossRef]
- Gates, D.M.; Harrop, W.J. Infrared transmission of the atmosphere to solar radiation. Appl. Opt. 1963, 2, 887–898. [Google Scholar] [CrossRef]
- Bruegge, C.J.; Conel, J.E.; Green, R.O.; Margolis, J.S.; Holm, R.G.; Toon, G. Water vapor column abundance retrievals during FIFE. J. Geophys. Res. Atmos. 1992, 97, 18759–18768. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, T.; Wu, Y.; Wang, Q.; Gao, T. Accuracy Analysis of the Aerosol Backscatter Coefficient Profiles Derived from the CYY-2B Ceilometer. Adv. Meteorol. 2018, 2018, 9738197. [Google Scholar] [CrossRef]
- Thome, K.J.; Smith, M.W.; Palmer, J.M.; Reagan, J.A. Three-channel solar radiometer for the determination of atmospheric columnar water vapor. Appl. Opt. 1994, 33, 5811–5819. [Google Scholar] [CrossRef]
- Uchiyama, A.; Yamazaki, A.; Kudo, R. Column Water Vapor Retrievals from Sky Radiometer (POM-02) 940 nm Data. J. Meteorol. Soc. Jpn. Ser. II 2014, 92A, 195–203. [Google Scholar] [CrossRef]
- Uchiyama, A.; Matsunaga, T.; Yamazaki, A. The instrument constant of sky radiometers (POM-02)—Part 1: Calibration constant. Atmos. Meas. Tech. 2018, 11, 5363–5388. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, B.; Chen, D.; Li, J.; Zhao, G. Influence of Filter Band Function on Retrieval of Aerosol Optical Depth from Sunphotometer Data. J. Atmos. Ocean. Technol. 2013, 30, 929–941. [Google Scholar] [CrossRef]
- Hopkin, E.; Illingworth, A.J.; Charlton-Perez, C.; Westbrook, C.D.; Ballard, S. A robust automated technique for operational calibration of ceilometers using the integrated backscatter from totally attenuating liquid clouds. Atmos. Meas. Tech. 2019, 12, 4131–4147. [Google Scholar] [CrossRef]
- Wang, W.; Gong, W.; Mao, F.; Pan, Z.; Liu, B. Measurement and study of lidar ratio by using a raman lidar in central China. Int. J. Environ. Res. Public Health 2016, 13, 508. [Google Scholar] [CrossRef] [PubMed]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; Morgan Kaufmann Publishers Inc.: Montreal, QC, Canada, 1995; Volume 2, pp. 1137–1143. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).