PSNet: Patch-Based Self-Attention Network for 3D Point Cloud Semantic Segmentation

Abstract

LiDAR-captured 3D point clouds are widely used in self-driving cars and smart cities. Point-based semantic segmentation methods allow for more efficient use of the rich geometric information contained in 3D point clouds, so it has gradually replaced other methods as the mainstream deep learning method in 3D point cloud semantic segmentation. However, existing methods suffer from limited receptive fields and feature misalignment due to hierarchical downsampling. To address these challenges, we propose PSNet, a novel patch-based self-attention network that significantly expands the receptive field while ensuring feature alignment through a patch-aggregation paradigm. PSNet combines patch-based self-attention feature extraction with common point feature aggregation (CPFA) to implicitly model large-scale spatial relationships. The framework first divides the point cloud into overlapping patches to extract local features via multi-head self-attention, then aggregates features of common points across patches to capture long-range context. Extensive experiments on Toronto-3D and Complex Scene Point Cloud (CSPC) datasets validate PSNet’s state-of-the-art performance, achieving overall accuracies (OAs) of 98.4% and 97.2%, respectively, with significant improvements in challenging categories (e.g., +32.1% IoU for fences). Experimental results on the S3DIS dataset show that PSNet attains competitive mIoU accuracy (71.2%) while maintaining lower inference latency (7.03 s). The PSNet architecture achieves a larger receptive field coverage, which represents a significant advantage over existing methods. This work not only reveals the mechanism of patch-based self-attention for receptive field enhancement but also provides insights into attention-based 3D geometric learning and semantic segmentation architectures. Furthermore, it provides substantial references for applications in autonomous vehicle navigation and smart city infrastructure management.

1. Introduction

Benefiting from the synergistic development of sensor technology and artificial intelligence, the 3D point cloud, as the main data format of LiDAR, is playing an increasingly significant role in the field of autonomous driving [1]. Compared with binocular cameras and RGB-D cameras, LiDAR is not easily affected by some external conditions such as weather and illumination, and it can provide a 3D point cloud containing clear ground objects and rich spatial details [2]. The latent features of the 3D point cloud can be extracted by the 3D point cloud semantic segmentation method, which can assign a specific semantic label to each point and help the machine to discriminate the region of interest (ROI). As a hot research topic for scholars in the 3D field, 3D point cloud semantic segmentation methods have been widely used in many ubiquitous receptive fields such as robotics, autonomous driving, smart cities, and augmented reality [3].

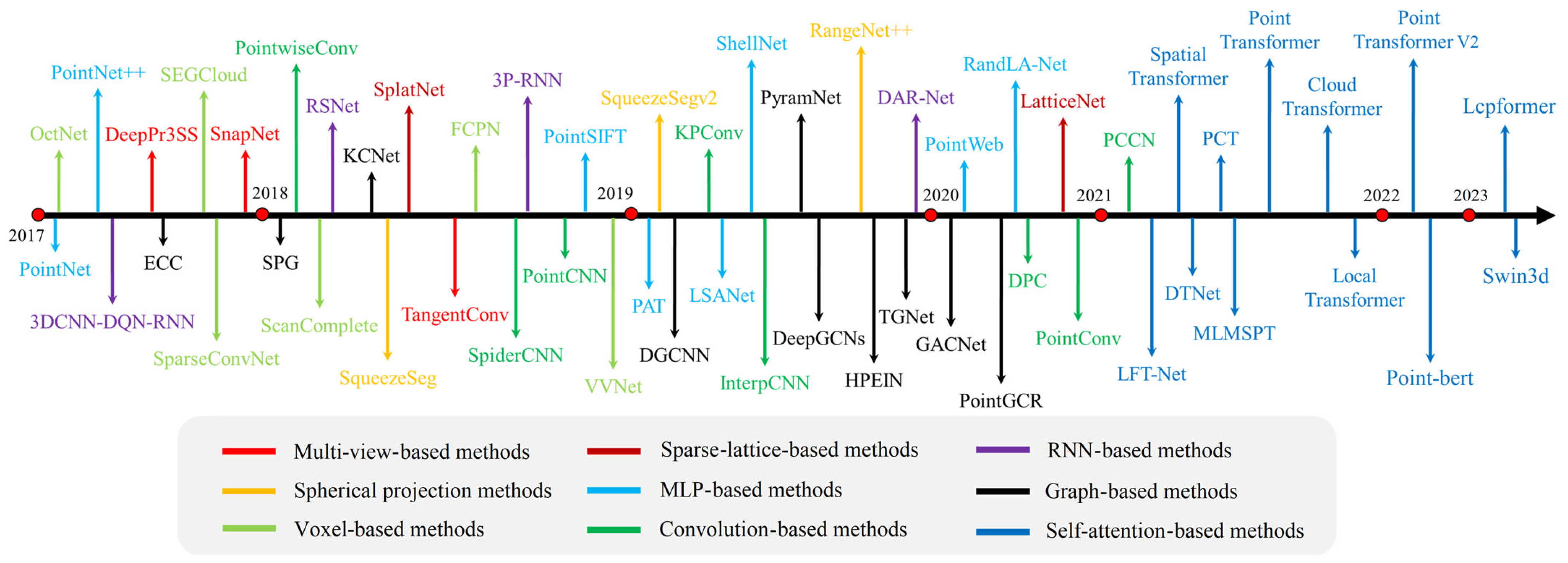
Semantic segmentation in 3D point clouds is more challenging than semantic segmentation in 2D images. First of all, the 3D point cloud is distributed in a Euclidean space, which makes the amount of data contained in the 3D point cloud much larger than that of the 2D image. Second, unlike gridded images, the distribution of the 3D point cloud is irregular. Its data density is not uniform, which easily leads to a long-tailed distribution [4]. Third, the 3D point cloud is discrete, and its structural characteristics are not clear. This makes 3D point clouds lack texture information similar to that evident in 2D images. The above characteristics will bring significant challenges to the task of semantic segmentation of point clouds. Traditional 3D point cloud semantic segmentation methods usually rely on hand-crafted features, in which it is difficult to fully express the shape and texture information contained in the point cloud [5,6]. This is insufficient in terms of speed and accuracy to meet the semantic segmentation requirements brought by massive point clouds. Fortunately, deep learning has gradually been applied to 3D vision tasks due to its powerful feature expression capabilities [2]. At present, 3D point cloud semantic segmentation methods based on deep learning mainly include projection-based methods, discretization-based methods, and point-based methods [1]. Figure 1 shows some typical 3D point cloud semantic segmentation methods based on deep learning in chronological order.

Projection-based semantic segmentation methods mainly include multi-view projection and spherical projection methods. Usually, two-dimensional image processing methods, such as convolution, are adopted to process the projected image of the point cloud, and then the two-dimensional semantic segmentation result is back-projected to the point cloud feature space. Tatarchenko et al. [7] proposed the TangentConv method, which projects the local surface around each point onto a tangent plane to obtain a tangent image, and then uses convolution to extract the features of the tangent image. Milioto et al. [8] proposed RangeNet++, which performs spherical projection on the input point cloud to obtain a range image, and then performs semantic segmentation on the range image. Projection-based methods are prone to loss of geometric features, and their performance depends on the choice of viewpoint and the angle of projection.

Discretization-based semantic segmentation methods usually convert point clouds into dense or sparse discrete representations, commonly known as voxel and sparse lattice methods. Graham et al. [9] proposed a sparse convolution operation, where the convolution operation is performed only on occupied voxels. Su et al. [10] proposed SPLATNet, which uses bilateral convolutional layers as the base module to transform point clouds into a sparse lattice space and extract features using bilateral convolutional layers. Discretization-based methods tend to have a high computational cost and memory footprint [2].

The point-based semantic segmentation method directly uses the raw point cloud as the input of the model, and completely retains the rich geometric information in the 3D point cloud [1]. It can be classified into multilayer perceptron (MLP)-based methods, convolution-based methods, recurrent neural network (RNN)-based methods, graph-based methods, and self-attention-based methods. Qi et al. [11] proposed PointNet++ to extract and integrate features over nested partitions of the input point set. Engelmann et al. [12] introduce a dilated point convolution (DPC) operation to aggregate nearby point features. Ye et al. [13] capture long-range spatial dependencies based on bidirectional recurrent neural networks. Ma et al. [14] adopted an undirected graph to capture global contextual information. Point Transformer V2 [15] introduces novel group vector attention and lightweight partition-based pooling methods to achieve better spatial alignment and more efficient sampling. LCPFormer [16] is equipped with the Local Context Propagation (LCP) module, which enhances the ability of the model to capture comprehensive and discriminative local structural information. Sufficient studies have shown that the point-based semantic segmentation method is more helpful in achieving satisfactory segmentation results. As the mainstream 3D point cloud semantic segmentation method, it is gradually replacing the projection-based semantic segmentation method and the voxel-based semantic segmentation method.

However, existing point-based 3D point cloud semantic segmentation methods still have some limitations. On the one hand, these methods need to find a certain number of neighbors. However, the comparative experiments of Engelmann et al. [12] found that when the number of nearest neighbors is fixed at 16, the receptive field of the model is still small even if many layers are stacked. The restricted receptive field makes the model unable to directly model large-scale spatial relationships. On the other hand, the downsampling process of mainstream semantic segmentation frameworks inevitably results in the loss of local information of point clouds. Moreover, the interpolation operation during the upsampling process may also cause misalignment of features. Addressing these two major challenges, the core objective of this study is to enhance the model’s receptive field and prevent feature misalignment during downsampling through a novel patch-aggregation paradigm. Therefore, this paper proposes a novel self-attention network for 3D point cloud semantic segmentation, which adopts a new paradigm, patch-based self-attention feature extraction and common point feature aggregation (CPFA), instead of stepwise downsampling and upsampling operations. It can learn local features and long-range dependencies more fully. The main contributions of the paper are briefly summarized as follows: (1) We propose a patch-based self-attention network (PSNet) to segment 3D point clouds. It uses a self-attention module to extract local feature information within patches and losslessly exploits the spatial information of the raw data. (2) We design a CPFA component. It can aggregate common point features belonging to different patches to capture long-range spatial dependencies, and eliminate feature bias. (3) Based on Toronto-3D and CSP datasets and a variety of classic point cloud semantic segmentation algorithms, extensive performance evaluations and comparisons are carried out to verify the advancement and effectiveness of the proposed method.

2. Related Works

2.1. Self-Attention Mechanism

The self-attention mechanism [17,18] is a variant of the attention mechanism [19,20,21], which is the core module of the Transformer [22,23]. It was originally proposed to solve the problem of modeling long-distance dependencies in the field of natural language processing [24]. The self-attention mechanism is based on the soft attention mechanism [25] in the key–value pair mode, and maps the input information to three different feature vector spaces of key (K), value (V), and query (Q), thereby calculating the attention coefficient and capturing contextual information. In particular, the multi-head self-attention mechanism [22] is popular due to its performance advantages. The essence of the multi-head self-attention mechanism is the parallel mapping of multiple independent attention modules, which allows the complex relationships of input information to be modeled in different feature subspaces [26]. DeepSeek [27] employs the multi-head latent attention mechanism, which integrates low-rank key–value joint compression to enhance inference efficiency. These advancements collectively demonstrate the adaptability of self-attention frameworks in modeling complex spatial and semantic relationships, laying the theoretical foundation for their extension to 3D geometric learning tasks such as point cloud segmentation.

2.2. Downsampling Method

The mainstream point cloud semantic segmentation methods introduce a downsampling process in order to expand the receptive field and improve the computational efficiency [28]. In general, in the encoder of the model, a series of downsampling methods such as random sampling [29], farthest point sampling [26,30] or learning-based sampling [31,32] are used to discard some points in the input data in order to map features layer by layer to a higher features space to gradually acquire a larger receptive field and extract higher-level abstract semantic features. In the decoder of the model, upsampling is performed by interpolation to restore the abstract features obtained in downsampling to the original size of the input data [11]. However, the downsampling process continuously loses the local information of the input data, and the upsampling process may lead to feature bias in the point cloud data. These operations will generate a negative effect on the final semantic segmentation result. The recently proposed SliceSamp [33] algorithm integrates feature slicing with depthwise separable convolutions, achieving enhanced computational efficiency while preserving information integrity. Swin Transformer [30] attempts to mitigate information loss through patch-based operations, yet it still faces challenges in global feature aggregation.

3. Methods

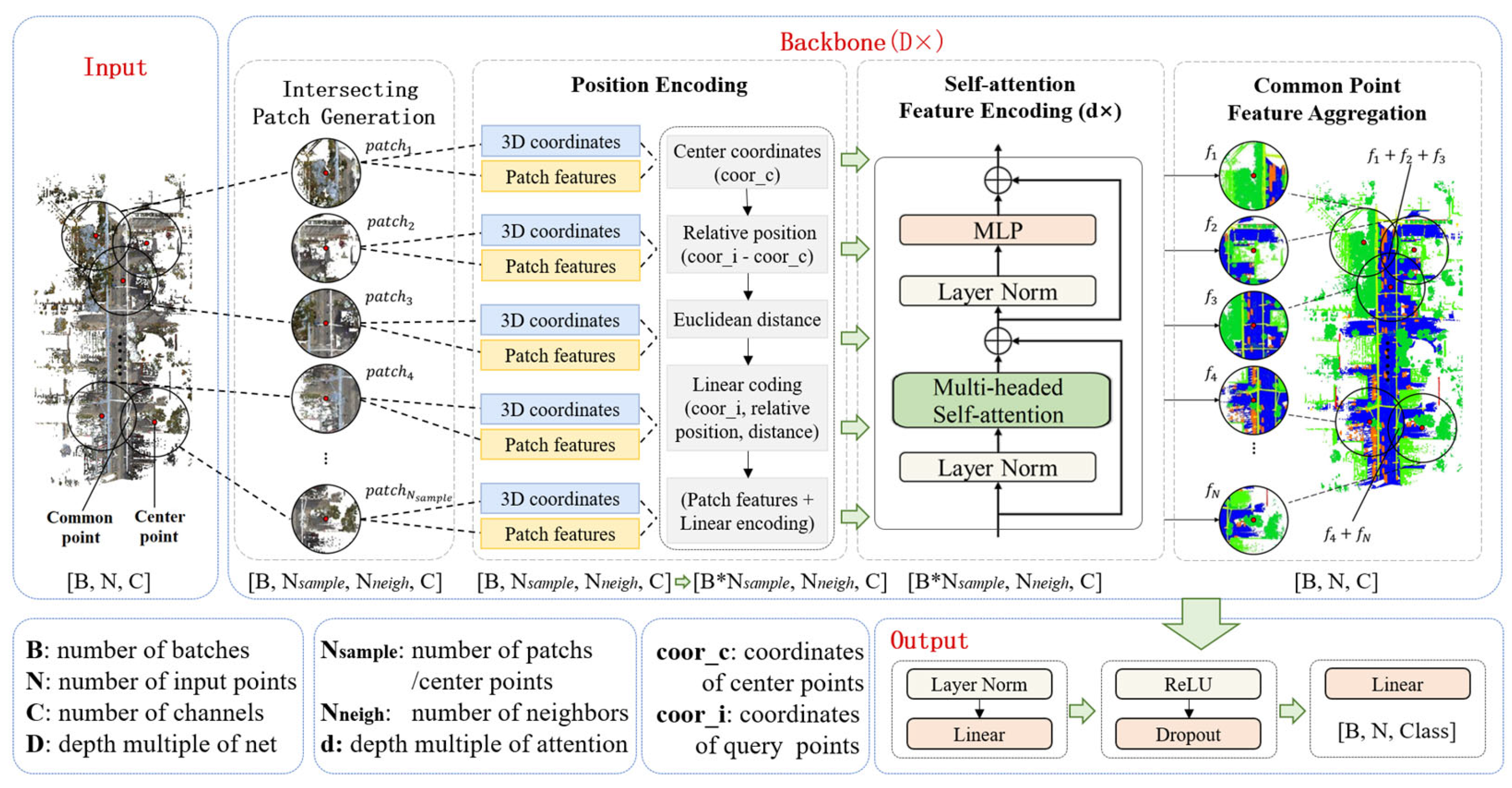
To address the limitations of existing methods caused by traditional sampling paradigms—such as insufficient receptive fields and feature misalignment—we propose a patch-based self-attention network (PSNet) for 3D point cloud semantic segmentation. The backbone (depth of 4) of the model consists of four key components: intersecting patch generation (IPG), position encoding (PE), self-attention feature encoding (SFE, depth of 2), and common point feature aggregation (CPFA). PSNet employs the multi-head self-attention layer of the Vision Transformer as its core feature extraction component. In this study, we introduce a novel paradigm that replaces the conventional stepwise downsampling and upsampling operations with intersecting patch-based self-attention feature extraction and common point feature aggregation. This paradigm effectively addresses challenges such as difficulty in modeling large-scale spatial relationships, information loss, and feature misalignment commonly encountered in downsampling–upsampling architectures. Figure 2 illustrates the overall architecture of PSNet for the task of 3D point cloud semantic segmentation.

3.1. Intersecting Patch Generation (IPG)

To address the limited receptive field in existing methods and reduce the computational effort in the self-attention feature extraction process, we innovatively propose an intersecting patch generation strategy. We introduce the patching mechanism [34] in the Visual Transformer model to generate multiple intersecting point cloud patches from the input of the model. The execution workflow of this component is as follows: First, a probabilistic sampling algorithm is applied to obtain a set of input points (81,920 points per batch). Subsequently, the farthest point sampling (FPS) algorithm is employed to select ${\mathrm{N}}_{\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}$ (${\mathrm{N}}_{\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}$ = 256) center points from the input point cloud. By utilizing farthest point sampling (FPS) for center point selection, representative coverage across both sparse and dense regions is ensured. For each of these centers, ${\mathrm{N}}_{\mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}}$ (${\mathrm{N}}_{\mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}}$ = 400) neighboring points are retrieved to form a compact point set—referred to as a point cloud patch—enabling subsequent local self-attention operations within each patch. During the patch generation process, the indices of each point in the original input point cloud are recorded for every generated patch. This facilitates the mapping of per-patch features back to the original input space in the later common point feature aggregation stage. This component replaces the conventional approach of progressively downsampling the entire input point cloud, thereby reducing computational complexity and mitigating issues of information loss and feature misalignment commonly associated with downsampling procedures. Moreover, during the intersecting patch generation phase, it is essential to ensure that every point in the input point cloud is included in at least one patch to prevent information loss. Specifically, this study ensures full coverage by setting the product of ${\mathrm{N}}_{\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}$ and ${\mathrm{N}}_{\mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}}$ to be greater than the number of input points per batch. Under this configuration, certain points may belong to multiple patches—these are referred to as common points. The farthest point sampling ensures representative coverage across density variations, while fixed-size neighborhoods with learned attention weights maintain consistent feature extraction. The intersecting patch generation component in Figure 2 illustrates the process of generating intersecting patches.

3.2. Position Encoding (PE)

Compared with the algorithms of recurrent neural network series, self-attention does not easily learn the sequence of data. The position encoding component can encode the position of points inside each point cloud patch to alleviate the above problem [22]. As depicted in Figure 2, for each point cloud patch, the input to the position encoding component comprises the 3D coordinates (x, y, z) of the points within the patch, which has a dimension of (${\mathrm{N}}_{\mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}}$, 3), and the corresponding point cloud patch features with a dimension of (${\mathrm{N}}_{\mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}}$, C). During the position encoding process, the relative position ($p_{rel,i}$) of each query point ($p_i$) with respect to the center point ($p_c$) is firstly calculated according to Equation (1). This relative position is defined as the coordinate offset between the 3D coordinate ($p_{coor,i}$) of query point ($p_i$) and the 3D coordinate ($p_{coor,c}$) of the center point ($p_c$). Concurrently, the Euclidean distance from each point to the center point is calculated based on Equation (2). Subsequently, the fused position vector for each point is obtained by adding the absolute coordinates, the relative position vector, and the Euclidean distance of $p_i$ and $p_c$. Finally, as illustrated in Equation (4), a linear layer is utilized to encode this fused position vector into the same dimension as the input patch features. The resulting positional encoding vector is then added to the feature vector ($p_{f,i}$) of each point, thereby yielding the output $f_{pos,i}$ of the position encoding component.

$$p_{rel, i}=p_{coor, i}-p_{coor, c}$$

(1)

$${dist}_i=\left|\right| p_{coor, i}-p_{coor, c} \left|\right|$$

(2)

$$r_i=p_{coor, i}\oplus p_{rel, i}\oplus {dist}_i$$

(3)

$$f_{pos,i}=Linear\left(r_i\right)+p_{f, i}$$

(4)

where $p_{rel,i}$ denotes the relative coordinates of each query point ($p_i$) and center point ($p_c$). $p_{coor,i}$ and $p_{coor,c}$ denote the coordinates of $p_i$ and $p_c$, respectively. $\left|\right|\cdot \left|\right|$ denotes the calculation of the Euclidean distance ${dist}_i$ of $p_i$, and $p_c$. $r_i$ denotes the position vector of $p_i$. $\oplus$ denotes the sum operation. $f_{pos,i}$ denotes the position encoding output of $p_i$. $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}$ denotes the convolution operation. $p_{f,i}$ denotes the feature vector of $p_i$.

3.3. Self-Attention Feature Encoding (SFE)

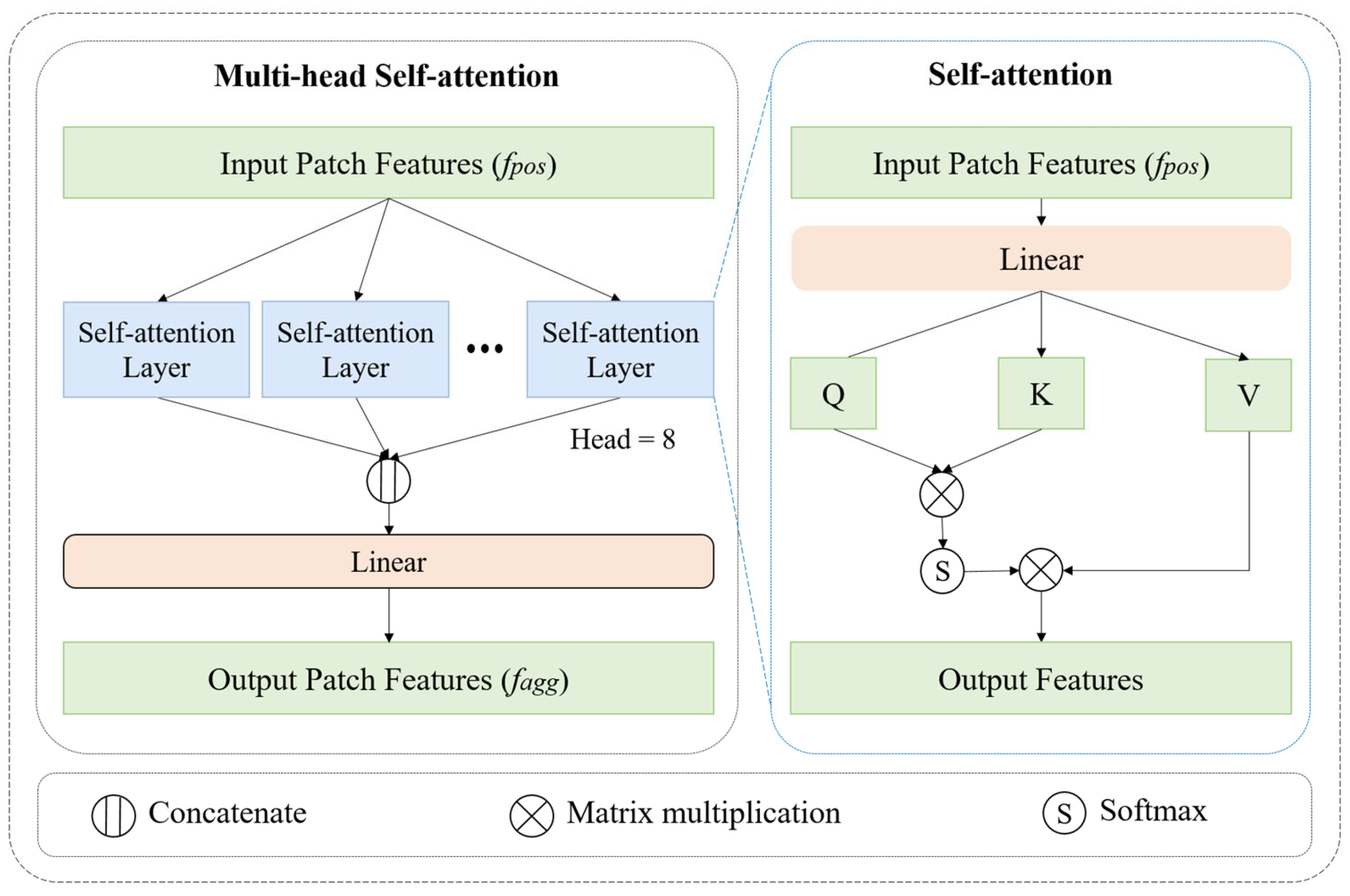
Figure 2 illustrates the internal structure of the self-attention feature encoding component, which is used to encode the internal features of each point cloud patch. The component receives as input the features $f_{pos}$ of each point fused with position information. It first updates the features of each point inside the point cloud patch through a normalization layer and a multi-head self-attention layer. The output $f_{agg}$ of the feature encoding component is then obtained through a normalization layer and a fully connected layer, while a residual connection is introduced during the feature encoding process to fuse the input features with the intermediate features generated during the feature encoding process.

Figure 3 presents the detailed architecture of the multi-head self-attention module within the self-attention feature encoding component. In this study, the self-attention feature encoding component is designed with a depth of 2 layers, and the number of heads in the multi-head self-attention module is set to 8. The module performs multiple independent self-attention computations on the input feature tensor ($f_{pos}$). Subsequently, the results from these parallel computations are concatenated. Finally, a linear layer is applied to project the concatenated features back to the same dimension as the input, resulting in the output tensor of shape (${\mathrm{N}}_{\mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}}$, C), which serves as the final output of the self-attention feature encoding component.

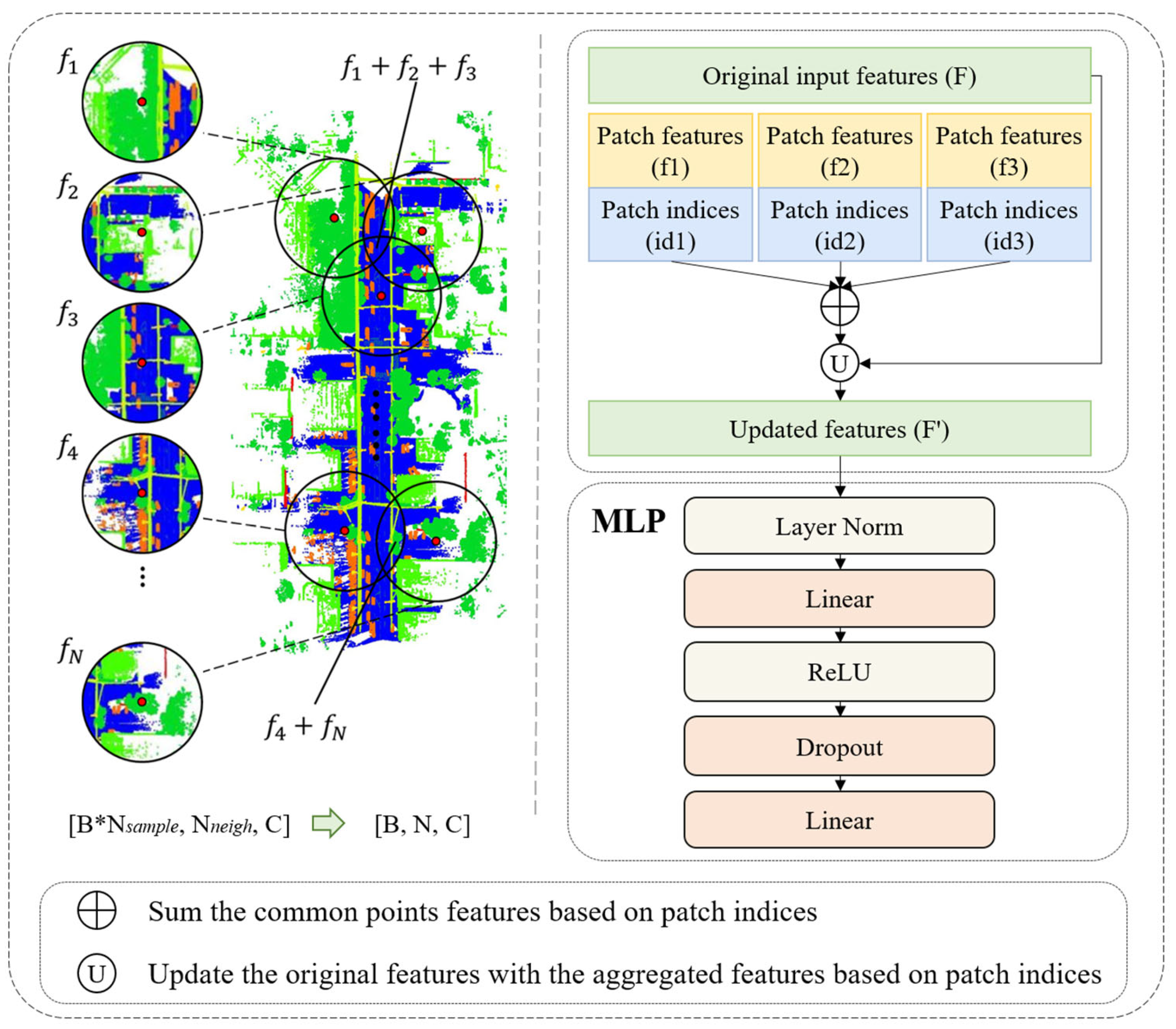
3.4. Common Point Feature Aggregation (CPFA)

The CPFA component is responsible for aggregating the attention features of each point cloud patch to update per-point features, thereby obtaining comprehensive features for all points in the current batch of input point cloud data. This aggregation process consists of three key steps: (1) Feature summation of common points across different patches based on point indices obtained during the intersecting patch generation phase. As illustrated in Figure 4, f₁, f₂, and f₃ represent three distinct patch features from the same input batch, where f₁ + f₂ + f₃ denotes the elementwise addition of features from different patches according to corresponding point indices, resulting in aggregated features for common points. (2) Projection of the aggregated features back to the original point cloud using point indices to overwrite the initial features, yielding updated features for each point. (3) Processing the updated features through an MLP module to further enhance the fused features of the current batch. This component effectively combines features of common points across different patches while preserving the intrinsic characteristics of point sets within individual patches. It achieves long-range feature aggregation for the current point cloud batch while simultaneously learning local spatial representations of point sets within different patches. Moreover, it can also further enhance robustness by aggregating features across density-varying regions.

3.5. Loss Function

In the 3D point cloud semantic segmentation task, multicategory cross-entropy loss is often used to measure the learning effectiveness of the model. We use a weighted cross-entropy loss (WCEL) function to address the potential impact of the category imbalance problem on the experimental results. To address the phenomenon of unbalanced samples of each category in the dataset, we introduce a category weight prior in the multicategory cross-entropy loss function. The specific calculation formula is as follows.

$$r_c={\displaystyle \frac{n_c}{{\sum }_{c=1}^M{n}_c}}$$

(5)

$$w_c={\displaystyle \frac{1}{r_c}}$$

(6)

$$y_{ic}=\left\{\begin{array}{c}1 if {label}_i=c\\ 0 else \end{array}\right.$$

(7)

$$WCEL=-{\displaystyle \frac{1}{N}}\sum _{i=1}^N\sum _{c=1}^M{w}_c{y}_{ic}\log \left(p_{ic}\right)$$

(8)

where $r_c$ denotes the proportion of samples in category c. $n_c$ denotes the number of samples in category c, and M denotes the number of categories. $w_c$ denotes the weight of samples in category c. $y_{ic}$ is an indicator function that takes 1 if the ground truth of sample i is c, and 0 otherwise. N denotes the number of samples, and $p_{ic}$ denotes the probability that sample i is predicted to be in category c.

4. Results

4.1. Datasets

Three open-access datasets were selected for algorithm validation experiments: the Toronto-3D dataset [35], the Complex Scene Point Cloud (CSPC) dataset [36], and the Stanford Large-Scale 3D Indoor Spaces (S3DIS) dataset.

Toronto-3D is a large urban outdoor point cloud dataset collected by the Mobile Laser System (MLS), which includes four areas, L001, L002, L003, and L004, with a total of 78.3 million points. It is divided into eight categories, including road, road markings, natural, building, utility line, poles, car, and fence. It has 10 attributes, including 3D location, RGB color, intensity, GPS time, scan angle level, and category.

CSPC is a LiDAR dataset for semantic segmentation of large-scale complex outdoor scenes, including Scene1, Scene2, Scene3, Scene4, and Scene5, with a total of about 68 million points. It is divided into six categories, including ground, car, building, vegetation, bridge, and utility pole. The points in the dataset have six attributes, which represent 3D position and RGB color. The category imbalance problem in these two datasets poses a challenge to the semantic segmentation approach.

S3DIS is a widely adopted benchmark dataset designed to facilitate research in indoor point cloud semantic segmentation. It comprises six large-scale indoor environments, labeled as Area 1 through Area 6, encompassing a total of 271 rooms across 11 scene types, including offices, conference rooms, corridors, and other common indoor spaces. The dataset contains over 695 million annotated points, each represented by its 3D spatial coordinates and corresponding RGB color values. S3DIS defines a comprehensive set of 13 semantic categories, which include both architectural elements—such as ceilings, walls, and floors—and movable objects—such as tables, chairs, sofas, and clutter. These semantic annotations enable fine-grained understanding and analysis of complex indoor scenes at the point level. Due to its high object density, significant variability in spatial layouts, and extensive annotation coverage, S3DIS offers a robust and realistic benchmark for evaluating semantic segmentation algorithms on large-scale indoor point cloud data. It has become an essential resource for advancing research in 3D scene understanding, particularly in applications such as indoor navigation, augmented reality, and intelligent environment perception.

4.2. Implementation Details

In the experiments on the Toronto-3D dataset, three regions, L001, L003, and L004, were used for model training, and L002 was used for testing. We compared the experimental results of six semantic segmentation methods, PointNet++ [11], DGCNN [37], KPFCNN [38], MS-PCNN [14], TGNet [39], and MS-TGNet [35], from the paper on the Toronto-3D dataset. In the experiments on the CSPC dataset, Scene1, Scene3, and Scene4 were used for training, while Scene2 and Scene5 were used for testing. We compared the experimental results of SnapNet [40], PointNet++ [11], 3D CNN [41], DeepNet [5], and KPConv [38], the five semantic segmentation methods in the CSPC dataset paper. In addition, comparative experiments were conducted in the above two datasets using representative RandLA-Net [29] and Point Transformer [42] methods. In the experiments on the indoor scene dataset S3DIS, Areas 1, 2, 3, 4, and 6 were used for training, and Area 5 was reserved for testing. We compare the point cloud semantic segmentation performance in terms of mAcc and mIoU, model complexity in terms of the number of parameters (Params), and average wall-time latency of several recent state-of-the-art (SOTA) methods, including KPConv [38], PAConv [43], Point Transformer [42], Fast Point Transformer [44], Stratified Transformer [45], and PointNeXt-XL [46]. In this study, the model was trained on preprocessed point clouds that underwent voxel grid downsampling. Following established practices in the existing studies, we carefully selected grid resolutions of 0.01m for Toronto-3D, 0.03m for CSPC, and 0.04m for S3DIS to optimally balance point cloud density with computational efficiency.

For the model parameter setting, the number of points N in each input batch was set to 81,920. The number of center points (${\mathrm{N}}_{\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}$), selected using the farthest point sampling algorithm, was set to 256. The number of neighboring points (${\mathrm{N}}_{\mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}}$) for each centroid was set to 400. A critical implementation requirement is that the product of the number of center points and neighboring points must be greater than the number of points (N = 81,920) per input batch, which guarantees sufficient patch overlap for effective feature aggregation via the CPFA module. The initial learning rate was set to 0.01.

4.3. Evaluation Metrics

To verify the effectiveness of our method, three representative evaluation metrics are used to evaluate the performance of our method and other methods, including the Intersection over Union (IoU), the Mean Intersection over Union (mIoU), and the overall accuracy (OA) of each category. mIoU represents the average value of the IoU for all categories. The calculation methods of the above evaluation metrics are shown below.

$$OA={\displaystyle \frac{{\sum }_{i=1}^C{mat}_{i,i}}{{\sum }_{i=1}^C{\sum }_{j=1}^C{mat}_{i,j}}}$$

(9)

$${IoU}_c={\displaystyle \frac{{mat}_{c,c}}{{\sum }_{i=1}^C{mat}_{i,c}+{\sum }_{j=1}^C{mat}_{c,j}-{mat}_{c,c}}},c=\mathrm{1,2},\dots C$$

(10)

$$mIoU={\displaystyle \frac{{\sum }_{c=1}^C{IoU}_c}{C}}$$

(11)

where C denotes the number of categories. mat denotes the confusion matrix used for evaluation, whose rows denote the true labels and whose columns denote the predicted results. ${mat}_{i,j}$ denotes the number of points in category i that are predicted to be in category j.

4.4. Performance Comparison

Table 1. Semantic segmentation performance comparison on the L002 region of Toronto-3D.

Methods	IoU								mIoU	OA
	Road	Road Marking	Natural	Building	Utility Line	Pole	Car	Fence
PointNet++	91.4	7.6	89.8	74.0	68.6	59.5	54.0	7.5	56.6	91.2
PointNet++ (MSG)	90.7	0.0	86.7	75.8	56.2	60.9	44.5	10.2	53.1	90.6
DGCNN	90.6	0.4	81.3	64.0	47.1	56.9	49.3	7.3	49.6	89.0
KPFCNN	90.2	0.0	86.8	86.8	81.1	73.1	42.9	21.6	60.3	91.7
MS-PCNN	91.0	3.5	90.5	77.3	62.3	68.5	53.6	17.1	58.0	91.5
TGNet	91.4	10.6	91.0	76.9	68.3	66.3	54.1	8.2	58.3	91.6
MS-TGNet	90.9	18.8	92.2	80.6	69.4	71.2	51.1	13.6	61.0	91.7
RandLA-Net	96.6	66.7	96.2	89.3	85.9	81.0	78.8	29.5	78.0	96.6
Point Transformer	96.7	64.6	95.9	91.0	87.6	79.0	87.5	36.9	79.9	96.8
ours	98.1	75.7	98.5	96.4	90.5	86.7	96.5	69.0	88.9	98.4

shows the semantic segmentation results of different methods on the L002 region of the Toronto-3D dataset. The results demonstrate our method’s superior performance, achieving a SOTA performance with 98.4% OA and 88.9% mIoU, representing significant improvements of 1.6% and 9.0% over Point Transformer, respectively. Particularly noteworthy are the dramatic gains in challenging categories: In the road marking (75.7% IoU) category, compared with Point Transformer (64.6%), PSNet achieved an IoU increase of +11.1%. This stems from our patch-based attention mechanism’s ability to preserve fine and small structures that typically get lost during conventional downsampling, underscoring how traditional approaches struggle with such fine-scale elements. For the fence (69.0% IoU, +32.1%) category, this remarkable enhancement demonstrates our method’s proficiency in handling elongated, discontinuous objects. The common point feature aggregation (CPFA) mechanism effectively connects spatially separated fence segments that would be processed independently in other frameworks.

Unlike methods that achieve strong performance on certain object categories at the expense of others (e.g., RandLA-Net, which attains a high IoU of 96.6% on the road category but performs poorly on the fence category, with only 29.5%), our approach consistently improves performance across all object types. The significant 9% gain in mIoU over Point Transformer can be attributed to our method’s superior preservation of local structures through intersecting patch generation and the effective prevention of feature dilution via CPFA. These results collectively validate our method’s ability to overcome three key limitations of existing approaches, information loss during downsampling, restricted receptive fields, and feature misalignment, while demonstrating robust performance across diverse urban objects in complex outdoor scenarios.

The experimental results on the CSPC Scene2 dataset (

Table 2. Semantic segmentation performance comparison on the Scene2 component of the CSPC dataset.

Methods	IoU						mIoU	OA
	Ground	Building	Car	Vegetation	Pole	Bridge
SnapNet	42.8	43.9	6.0	10.8	0.0	0.0	17.3	54.8
PointNet++	92.8	90.5	65.6	72.5	26.4	69.6	69.6	94.1
3D CNN	78.2	90.5	1.3	5.4	0.5	0.2	19.2	58.4
DeepNet	79.9	35.3	8.7	8.6	0.3	0.0	22.2	61.2
KPConv	94.1	87.8	66.6	77.5	0.0	0.0	54.3	93.6
RandLA-Net	92.0	87.9	79.9	67.3	17.0	6.0	58.3	93.3
Point Transformer	93.0	92.8	74.9	93.8	22.1	49.8	71.0	95.4
ours	95.8	95.1	88.9	98.6	44.5	58.9	80.3	97.2

) demonstrate that our method achieves superior performance, with PSNet attaining an OA of 97.2% and an mIoU of 80.3%. These results represent substantial improvements of 1.8% in OA and 9.3% in mIoU over Point Transformer, a SOTA model. One particularly compelling case underscores the architectural advantages of our approach. On the pole category, which presents a challenging class due to its slender and vertically oriented structure, our method achieves an IoU of 44.5%, surpassing Point Transformer by a significant margin of 22.4% (Point Transformer: 22.1%). This improvement can be attributed to the synergistic combination of our position encoding scheme and patch-based processing strategy. Specifically, the explicit encoding of relative heights and geometric characteristics unique to thin structures enables more accurate localization and classification, while the patch-based attention mechanism preserves fine-grained spatial details that are often lost during conventional downsampling procedures. This demonstrates the superior capability of our architecture in modeling complex, geometry-sensitive object categories. Notably, the CPFA module’s demonstrated capability across overlapping patches suggests strong potential for instance segmentation tasks, where precise object boundary preservation is paramount. Furthermore, our quantitative results on slender pole detection indicate particular promise for challenging object detection scenarios, as the architecture inherently addresses key limitations in current detection frameworks regarding elongated structures. This demonstrates the superior capability of our architecture in modeling complex, geometry-sensitive object categories, while simultaneously revealing its adaptability to broader 3D understanding tasks beyond semantic segmentation.

The experimental results presented in

Table 3. Semantic segmentation performance comparison on the Scene5 component of the CSPC (%) dataset.

Methods	IoU						mIoU	OA
	Ground	Building	Car	Vegetation	Pole	Bridge
SnapNet	40.2	38.4	0.2	8.4	0.0	-	17.5	52.3
PointNet++	89.8	87.2	25.1	34.5	22.8	-	51.9	91.2
3D CNN	71.0	56.5	1.3	9.1	1.5	-	27.9	69.9
DeepNet	71.3	44.9	0.9	10.6	0.5	-	25.6	63.3
KPConv	87.5	88.7	63.2	54.8	0.5	-	58.8	92.4
RandLA-Net	90.2	90.3	54.5	48.0	34.4	-	63.5	93.4
Point Transformer	88.2	90.2	54.1	56.5	40.5	-	65.9	94.6
ours	93.7	94.6	69.6	68.6	46.5	-	74.6	96.2

demonstrate that our proposed method achieves advanced performance on the CSPC Scene5 dataset, with significant improvements in both overall accuracy (OA) and mean Intersection-over-Union (mIoU) metrics. The superior performance (OA of 96.2%, mIoU of 74.6%) can be primarily attributed to our novel patch-based point cloud processing paradigm, which fundamentally differs from conventional multi-scale downsampling approaches. By replacing the conventional hierarchical downsampling strategy with our patch-based input generation, we effectively eliminate the feature distortion that typically occurs during repeated downsampling operations, thereby preserving more discriminative geometric information throughout the network. Notably, significant improvements are observed in challenging object categories, particularly those involving fine structures and small objects. For instance, our method achieves 46.5% mIoU for poles, a 6.0% improvement over Point Transformer, demonstrating enhanced capability in capturing slender and sparse structures. Similarly, we obtain 69.6% mIoU for cars, which represents a 6.4% gain over KPConv, indicating superior performance in segmenting compact yet discriminative regions. A potential explanation for these improvements may lie in the patch-based approach’s ability to preserve the resolution and geometric integrity of dense objects and slender structures, which would otherwise be degraded through conventional downsampling operations. At the same time, the model maintains strong performance on large-scale semantic categories such as the ground (93.7%) and buildings (94.6%), highlighting its effectiveness across diverse geometric scales.

The quantitative experimental results of the Toronto-3D and CSPC datasets show that our patching-based self-attention method has better prediction results for all types of features in complex scenes than other methods, and the IoU of some categories is significantly improved compared with existing methods. By abandoning the upsampling and downsampling operations and adopting the new patching-aggregation paradigm, the model can learn the local and long-range details more comprehensively and accurately, which further improves the prediction ability of the model for various ground objects in complex scenes.

To further evaluate the generalizability and scalability of our proposed method in indoor scenarios, we conducted comprehensive experiments on the S3DIS Area5 dataset, comparing PSNet with several SOTA approaches. As shown in

Table 4. Semantic segmentation performance comparison on the Area5 component of the S3DIS dataset.

Method	mAcc	mIoU	Params (M)	Latency (s)
KPConv	72.8	67.1	14.9	105.15
PAConv	73.0	66.6	90.1	28.13
Point Transformer	76.5	70.4	12.8	18.07
Fast Point Transformer	77.3	70.1	37.9	1.13
Stratified Transformer	78.1	72.0	92.0	43.02
PointNeXt-XL	83.0	74.9	41.6	38.16
PSNet (ours)	77.8	71.2	21.87	7.03

, our method achieves competitive performance, with 71.2% mIoU and 77.8% mAcc, while maintaining superior efficiency—requiring only 21.87M parameters and an average latency of 7.03 s. This represents a good balance between accuracy and computational cost. Quantitatively, compared to the SOTA model PointNeXt-XL, PSNet improves inference speed by a factor of 5.43, albeit with a 5.2% drop in mAcc and a 3.7% drop in mIoU. In contrast to the fastest method, Fast Point Transformer (1.13s of inference latency), PSNet improves the mAcc by 0.5% and the mIoU by 1.1%, but at the cost of a 6.22× increase in inference time. Specifically, PSNet replaces traditional multi-stage downsampling with a patch-based feature extraction paradigm, significantly reducing model complexity compared to PointNeXt-XL. Furthermore, the incorporation of a common point feature aggregation component enhances local topological modeling, enabling PSNet to surpass conventional convolution-based methods such as KPConv (+4.1% in mIoU) and PAConv (+4.6% in mIoU), while preserving its lightweight nature. Nonetheless, PSNet exhibits limitations in capturing the global context compared to attention-based models such as Stratified Transformer (78.1% mAcc and 72.0% mIoU) and PointNeXt-XL. The patch-based local interaction mechanism introduces noticeable information decay when modeling large-scale semantic relationships, which constrains segmentation accuracy on complex indoor scene datasets like S3DIS. Therefore, future work should focus on developing lightweight global modeling strategies to overcome the current accuracy bottleneck. Overall, the proposed method demonstrates competitive accuracy and efficiency on the S3DIS dataset. Although the performance gains are not as pronounced as those observed in outdoor scenarios, the method still exhibits strong scalability and effectiveness in indoor point cloud scenes.

4.5. Result Visualization

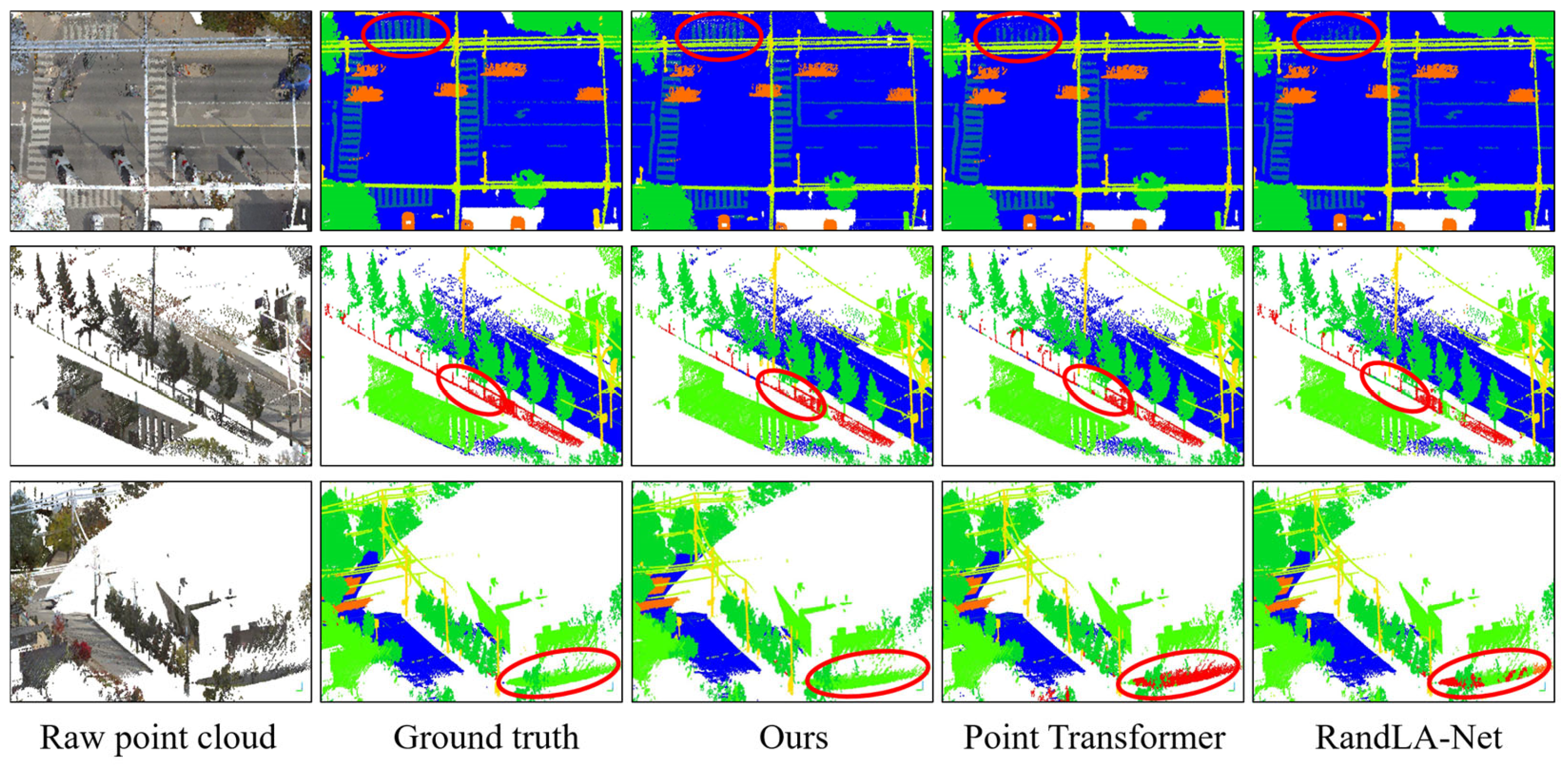
To compare the prediction results of the models more visually, the prediction results of the classical Point Transformer, RandLA-Net, and our method are visualized on the Toronto-3D and CSPC datasets. Figure 5 shows the prediction results of each method on the ROI of the Toronto-3D dataset. The three rows from top to bottom represent the three test examples in turn, and each column from left to right represents the raw point cloud in natural color (RGB), the label of the point cloud, and the prediction results of our method, Point Transformer, and RandLA-Net, in turn.

As shown in Example 1 (Figure 5), the prediction results of Point Transformer and RandLA-Net methods are not satisfactory for some of the dense road markings, and they can only predict some of the road markings in the highlighted part circled in the figure. Comparing the RGB point clouds, we can know that the misclassification of roads and road markings mainly exists in the boundary areas of the two classes. In contrast, our method has a smoother and more complete prediction of road markings. From the prediction results of Example 2, we can find that for a long strip of fence spanning a large spatial extent, each method misclassifies part of its area into the case of natural (trees and shrubs) or roads. For the highlighted part, the results obtained by our method are closer to the ground truth than the other methods. From the prediction results of Example 3, it can be observed that our method accurately identifies all the highlighted natural areas. In contrast, the Point Transformer and RandLA-Net methods exhibit significant misclassification between natural areas and fences. Analysis of RGB point clouds reveals that the misclassification phenomenon of other methods mainly occurs for two ground objects with close spatial relationships in the real world. This is because it is difficult for the model to learn the global features of large-scale ground objects from a macroscopic view under the restricted receptive field. The feature learning process is susceptible to interference from other ground objects in close proximity. The visualization results of each method on the Toronto-3D dataset show that the prediction results of the Point Transformer and RandLA-Net methods are misclassified in some regions. Compared with them, our method has fewer misclassifications, more complete and accurate prediction results, and better ability to capture a large range of spatial relationships.

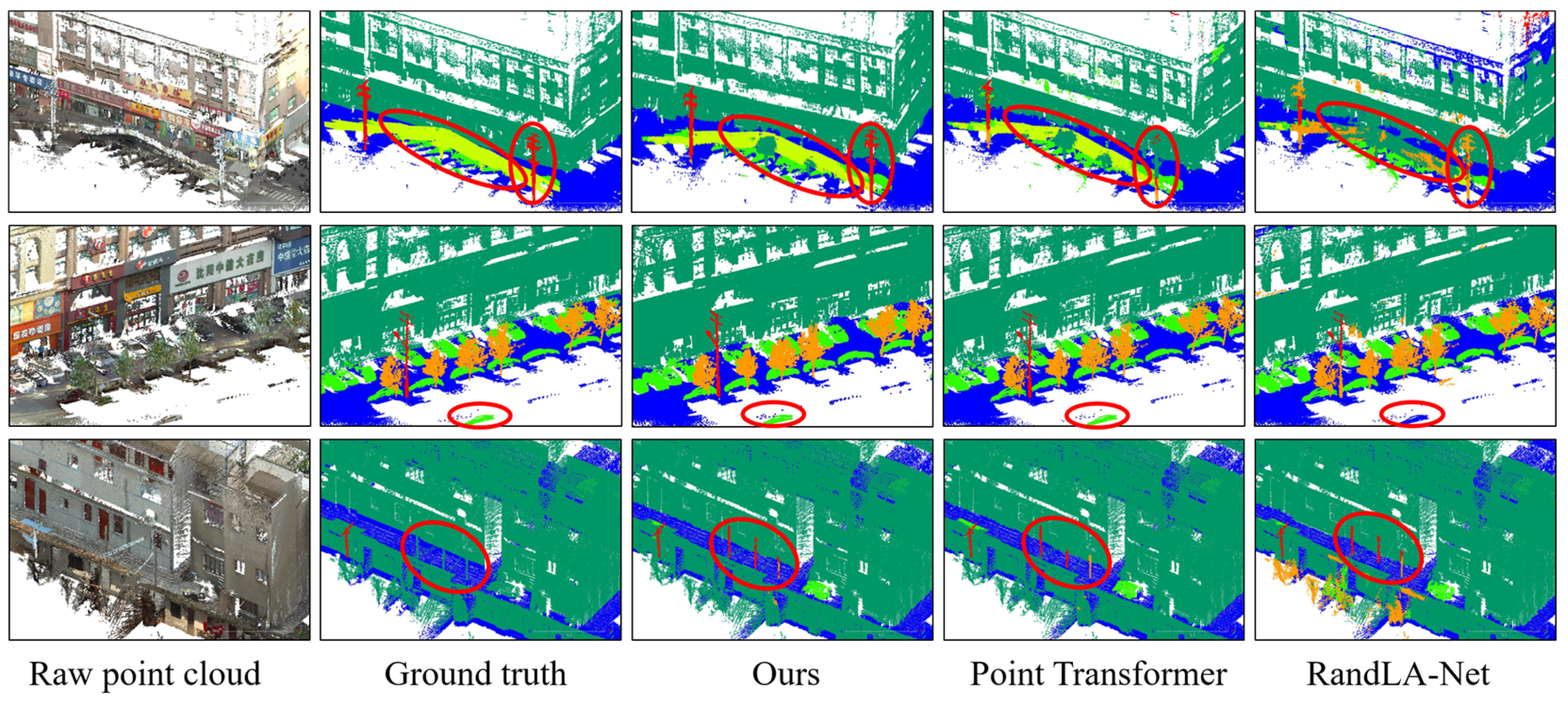
Figure 6 shows the prediction results of our method with Point Transformer and RandLA-Net on CSPC. In the prediction result of Example 1, the prediction result of the RandLA-Net method incorrectly predicts the whole bridge area into building and vegetation categories. In contrast, the prediction results of our method and Point Transformer only misclassify the bridge piers into building categories. Comparing the RGB point clouds, we can find that the color and shape features of the bridge piers are too similar to those of the buildings, resulting in poor feature differentiation, so there may be misclassification due to inaccurate localization of edge regions. In Example 2, Point Transformer and our method achieve good predictions on the highlighted car region, while the RandLA-Net method predicts the whole region as a ground class. These two examples above demonstrate the advantages of self-attention models over convolutional models for feature extraction. For the prediction results of Example 1 and Example 3, the Point Transformer and RandLA-Net methods easily predict tall utility poles with a similar shape to vegetation as vegetation. In contrast, our method correctly and completely predicts such long utility poles even if they are labeled as buildings in the ground truth labels. Visual comparison of RGB point clouds can confirm that these ground objects are more appropriately classified as utility poles. In conclusion, the visual comparison of prediction results on CSPC shows that the prediction results of our method are closer to the ground truth than Point Transformer and RandLA-Net methods. It is experimentally demonstrated that our method can capture long-range information by further expanding the receptive field and has more accurate prediction results on large-scale ground objects. It can significantly improve the model performance, and some of its prediction results are even better than the ground truth in terms of reasonableness.

The expanded receptive field enables PSNet to capture long-range context, as evidenced by the coverage in Figure 7. Figure 7 shows the range of receptive fields in different methods with multiple ROI examples. Each row represents one example, and each column from left to right represents the raw point cloud, the label of the point cloud, the receptive field of our method, and the receptive field of the Point Transformer. The red area indicates the range of the receptive field, and the blue area indicates the background. Unlike conventional architectures that progressively enlarge the receptive field through repeated downsampling, this study replaces this mechanism with a patch-based strategy where the receptive field size is determined by the number of neighboring points within each patch. This design ensures that PSNet’s receptive field remains consistent across all feature extraction layers, independent of network depth. Comparing the receptive field distribution of multiple examples, it is obvious that our method establishes larger receptive fields of the neural network. Comparing the receptive field of our method with the ground truth labels, it can be seen that the receptive field of our method covers a wide range of different classes of ground objects in the surrounding area, which allows the model to capture a larger range of spatial relationships and thus achieve a scene-level understanding of the input point cloud.

4.6. Ablation Study

To investigate the impact of different patch configurations on model performance, we conduct an ablation study on the number of center points/patches (${\mathrm{N}}_{\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}$) and neighbor points (${\mathrm{N}}_{\mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}}$) in the patch partitioning strategy. This study has conducted a detailed comparison of the different combinations of ${\mathrm{N}}_{\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}$ = [128, 256, 512] and ${\mathrm{N}}_{\mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}}$ = [200, 400, 800]. The results (

Table 5. Partition strategy ablation on the L002 region of Toronto-3D.

ID	${\mathbf{N}}_{\mathbf{s}\mathbf{a}\mathbf{m}\mathbf{p}\mathbf{l}\mathbf{e}}$	${\mathbf{N}}_{\mathbf{n}\mathbf{e}\mathbf{i}\mathbf{g}\mathbf{h}}$	mIoU (%)
1	128	200	63.5
2	128	400	72.2
3	128	800	85.9
4	256	200	76.7
5	256	400	88.9
6	256	800	87.5
7	512	200	86.3
8	512	400	88.7
9	512	800	87.8

) reveal several key observations regarding patch overlap and receptive field size. The ablation study on patch partitioning strategies reveals a critical trade-off between receptive field size and patch overlap. When the number of center points (${\mathrm{N}}_{\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}$) and neighbors (${\mathrm{N}}_{\mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}}$) are both too small (e.g., 128/200), the model suffers from insufficient point coverage and limited contextual understanding, resulting in poor performance (63.5% mIoU). Expanding the receptive field by increasing ${\mathrm{N}}_{\mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}}$ (e.g., 128/800) significantly improves accuracy (85.9% mIoU) by enhancing local geometric modeling. The optimal balance is achieved with moderate settings (256/400, 88.9% mIoU), where patch coverage slightly exceeds the input point count to ensure comprehensive sampling without excessive redundancy. However, overly dense partitioning (e.g., 512/800) leads to performance degradation (82.6% mIoU) due to feature overfitting and computational redundancy from extreme patch overlap. These findings demonstrate that effective point cloud segmentation requires careful calibration of patch density to maximize receptive field benefits while minimizing overlap-induced inefficiencies.

To further evaluate the effectiveness and contributions of each proposed component, we conducted an ablation study. This study compares different combinations of our key design elements: intersecting patch generation (IPG), position encoding (PE), self-attention feature encoding (SFE), and common point feature aggregation (CPFA). As shown in

Table 6. Module design ablation on the L002 region of Toronto-3D.

ID	IPG	SFE	PE	CPFA	mIoU (%)
1	-	-	-	-	79.9
2	√	√	-	-	85.6
3	√	√	√	-	86.8
4	√	√	√	√	88.9

, compared with the baseline Point Transformer (ID 1, mIoU = 79.9%), our full model (ID 4) achieved the highest performance (88.9% mIoU) by integrating all components. The intersecting patch generation (IPG) and self-attention feature encoding (SFE) combination establishes fundamental improvements (+5.7% mIoU) through adaptive point cloud partitioning and long-range dependency capture within patches. Position encoding (PE) further enhances geometric awareness (+1.2%) by explicitly modeling spatial relationships, particularly benefiting complex structural regions. The critical 2.1% improvement from common point feature aggregation (CPFA) highlights the importance of resolving feature conflicts in overlapping patches through scatter-reduce-based consolidation. These components collectively address four key challenges: IPG ensures comprehensive patch coverage, SFE enables contextual modeling, PE strengthens geometric sensitivity, and CPFA maintains feature consistency across patches. While the current IPG and PE design enhances geometric sensitivity, the fixed encoding strategy may struggle with highly irregular structures. In the future, we will consider designing adaptive patch partitioning and position encoding strategies to further enhance the generalization capability of this component.

5. Discussion

The experimental results demonstrate that our proposed patch-based self-attention network (PSNet) achieves advanced performance across multiple large-scale 3D point cloud datasets, including urban outdoor (Toronto-3D, CSPC) and indoor (S3DIS) environments. The key advantage of PSNet lies in its ability to address three fundamental limitations of existing point cloud segmentation methods: (1) restricted receptive fields due to hierarchical downsampling, (2) progressive information loss during feature propagation, and (3) feature misalignment caused by inconsistent local aggregation.

On the Toronto-3D dataset, PSNet outperforms strong baselines such as Point Transformer and RandLA-Net by significant margins (e.g., +9.0% mIoU and +1.6% OA over Point Transformer). The most notable improvements occur in geometrically challenging categories such as road markings (+11.1% IoU) and fences (+32.1% IoU), where conventional methods struggle due to their reliance on fixed-grid downsampling or limited receptive fields. This underscores the effectiveness of our intersecting patch generation (IPG) strategy, which ensures comprehensive spatial coverage while preserving fine-grained structures. Similarly, on the CSPC dataset, PSNet achieves a 22.4% IoU improvement for utility poles, demonstrating its superiority in modeling slender and sparse objects—a task where local geometric awareness and long-range context integration are critical. The success of PSNet can be attributed to two core innovations: Patch-based self-attention with CPFA: By replacing traditional downsampling with patchwise feature extraction and common point aggregation, PSNet mitigates information loss and maintains feature consistency across overlapping regions. The ablation study (Table 6) confirms that CPFA contributes a 2.1% mIoU gain by resolving feature conflicts in patch intersections. Expanded receptive fields: As visualized in Figure 7, PSNet’s patch partitioning enables scene-level context modeling, reducing misclassification in spatially extended objects (e.g., fences, bridges) that require long-range dependency capture.

While PSNet excels in outdoor scenes, its performance on fine-grained indoor objects (e.g., furniture in S3DIS) is slightly inferior to specialized architectures like PointNeXt-XL. This suggests that static patch sizing may not optimally adapt to highly variable indoor object scales. Future work could explore dynamic patch partitioning and hierarchical patch fusion to enhance multi-scale reasoning. Additionally, integrating lightweight global attention mechanisms could further bridge the gap between local detail preservation and scene-wide coherence.

6. Conclusions

In this work, we present PSNet, a novel patch-based self-attention network for large-scale 3D point cloud semantic segmentation. Departing from conventional downsampling paradigms, this study introduces a novel point cloud patch-aggregation framework to address the challenges of limited receptive fields and feature misalignment. Our approach leverages intersecting patch generation (IPG) to enable lossless partitioning of input point clouds into spatially overlapping patches, ensuring comprehensive coverage while preserving fine-grained structural details. To enhance geometric sensitivity, we incorporate explicit position encoding (PE) that captures spatial relationships, essential for accurately segmenting complex urban objects such as poles and road markings. Within each patch, local features are extracted through self-attention feature encoding (SFE), while common point feature aggregation (CPFA) synergistically integrates localized attention with long-range contextual modeling, enabling robust feature consolidation and preventing feature misalignment.

Extensive experiments on three large-scale benchmarks (Toronto-3D, CSPC Scene2, and S3DIS) demonstrate that PSNet achieves advanced performance, setting new benchmarks with 88.9% mIoU on Toronto-3D and 80.3% mIoU on CSPC, surpassing prior advanced models by up to 9.3% in mIoU. Qualitative visual comparisons further highlight its superior robustness in segmenting challenging object categories (such as fences and utility poles) with minimal misclassification. In terms of computational efficiency, PSNet strikes an effective balance between accuracy and speed. Compared to global attention-based methods, PSNet achieves competitive accuracy (1.1% higher mIoU than Fast Point Transformer) while offering significantly faster inference latency (5.43× faster than PointNeXt-XL).

This work effectively bridges the gap between local geometric precision and long-range contextual modeling, providing a scalable and efficient solution for real-world applications including autonomous driving, urban mapping, and indoor navigation. Future research will focus on adaptive patch optimization, enhanced position encoding strategies, and cross-dataset generalization to further advance large-scale and fine-grained 3D scene understanding. Additionally, future work could explore temporal encoding schemes based on LSTM or Transformer networks for processing time-sequential point clouds, enabling dynamic object tracking and trajectory prediction in applications such as autonomous driving.