Reconstruction of Three-Dimensional Temperature and Salinity in the Equatorial Ocean with Deep-Learning
Abstract
1. Introduction
2. Study Area and Data
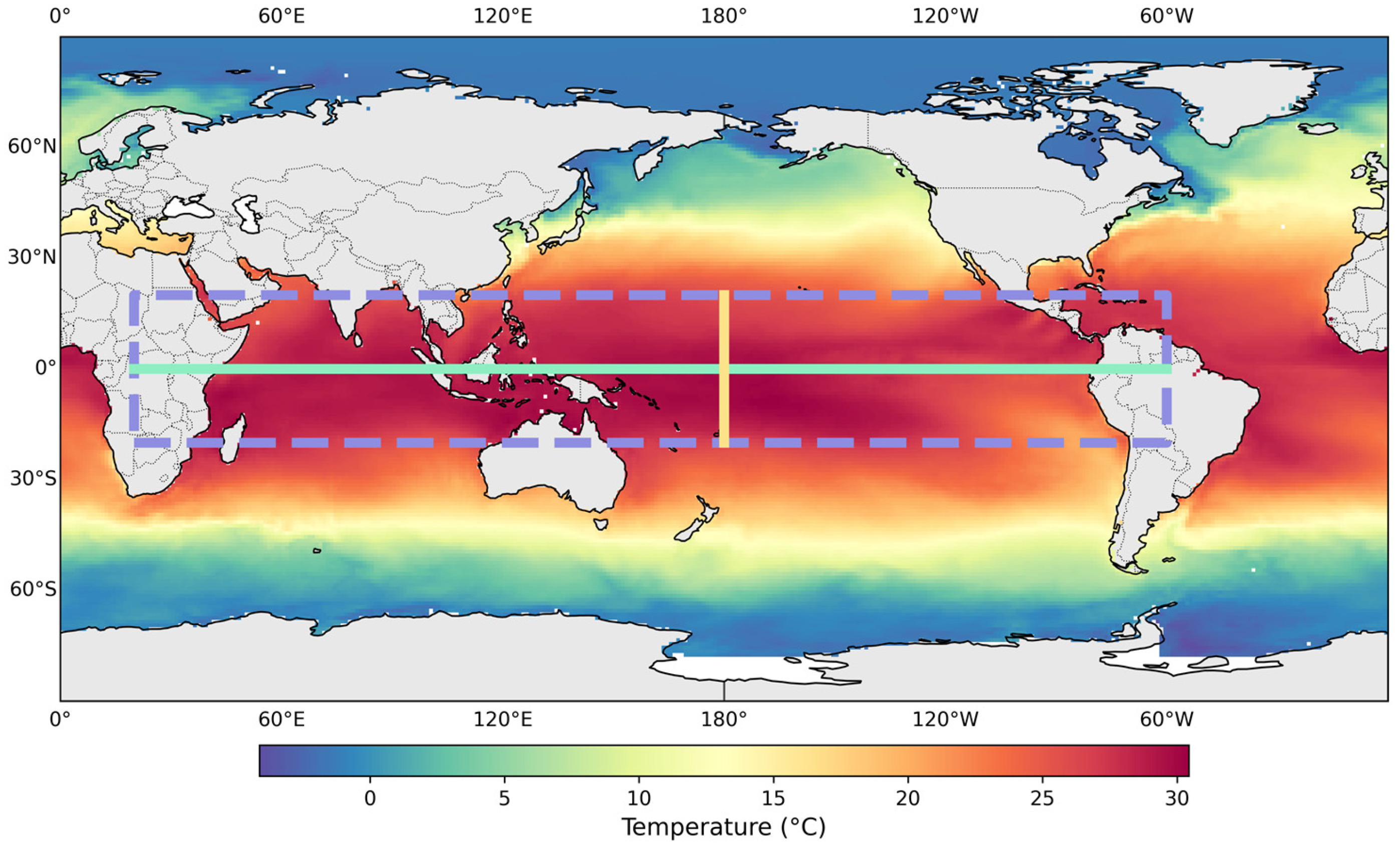
2.1. Study Area
2.2. Data
3. Model Architecture and Configuration
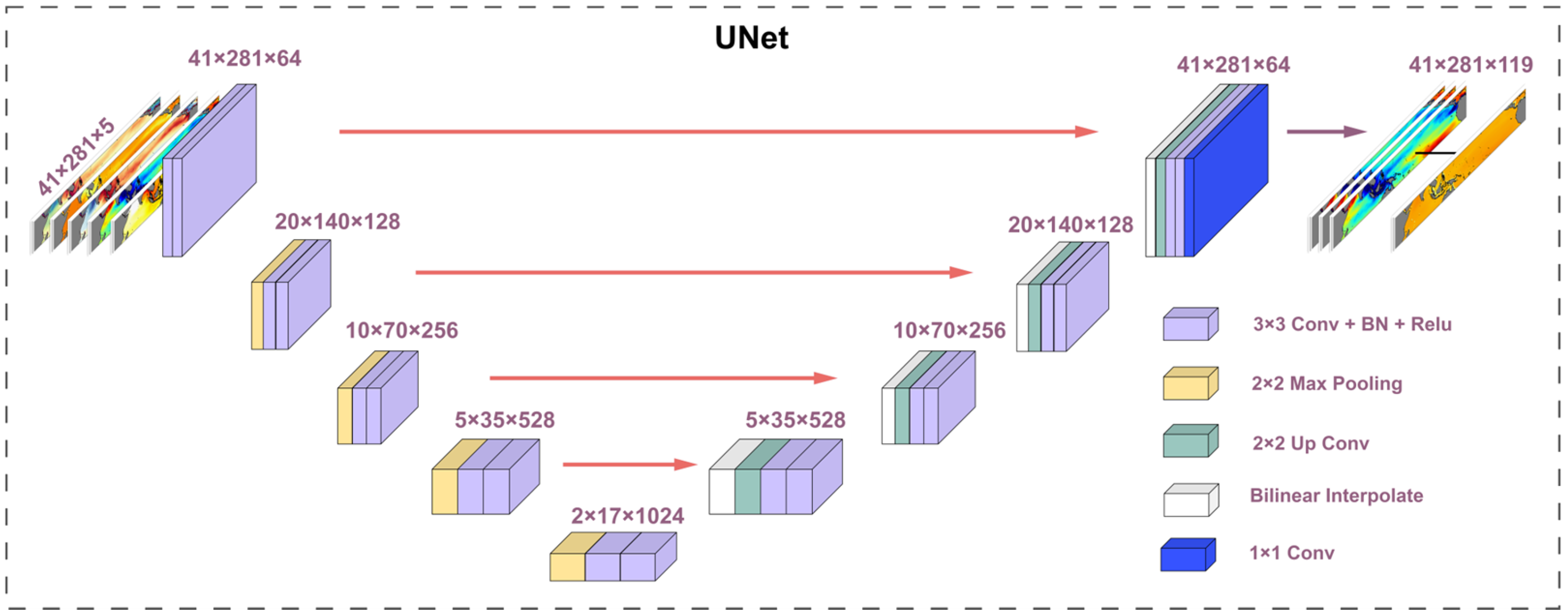
3.1. UNet
3.2. Vision Transformer
3.3. VI-UNet
3.4. Loss Function and Experimental Configuration
3.5. Experimental Design
4. Results
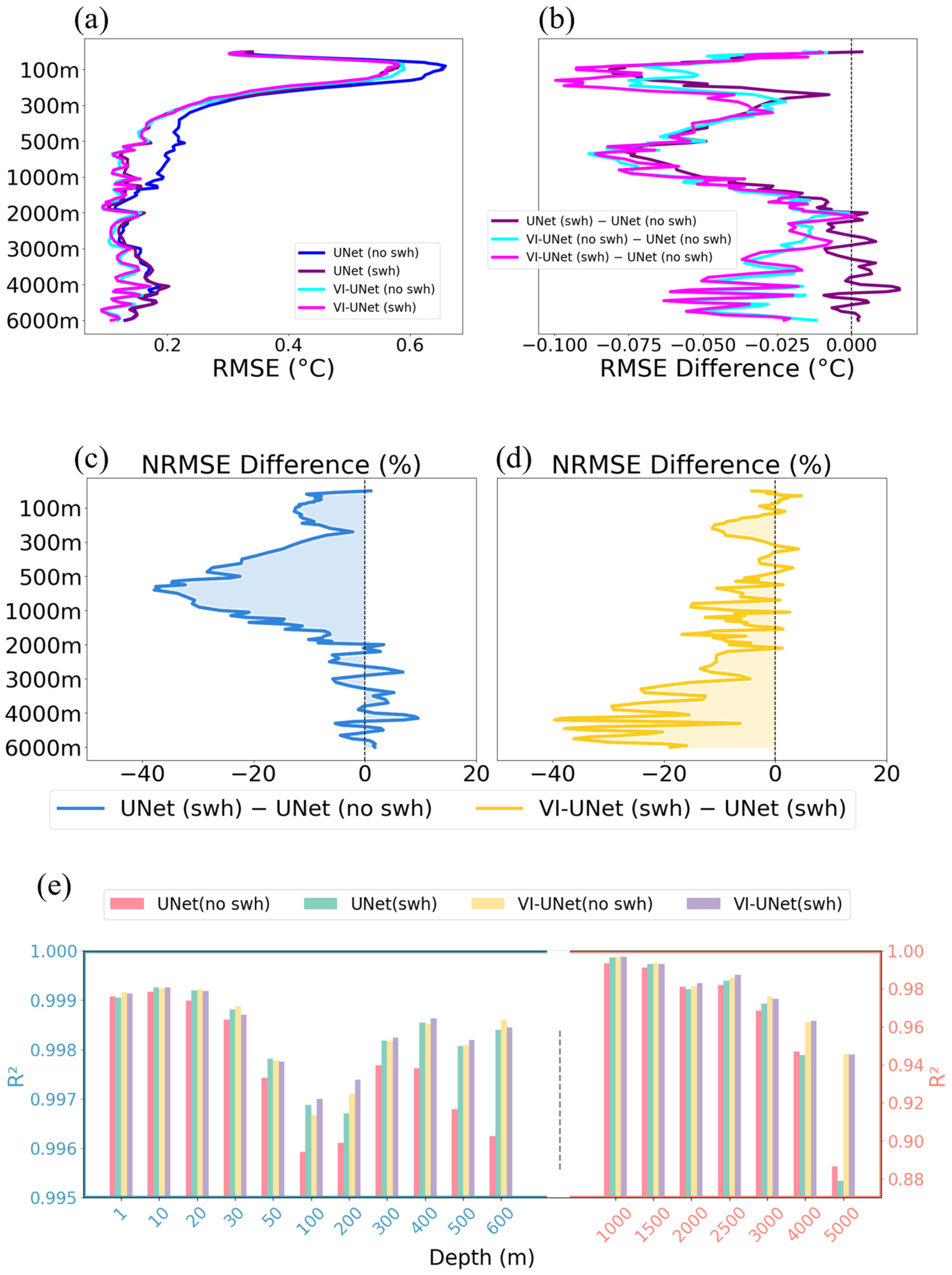
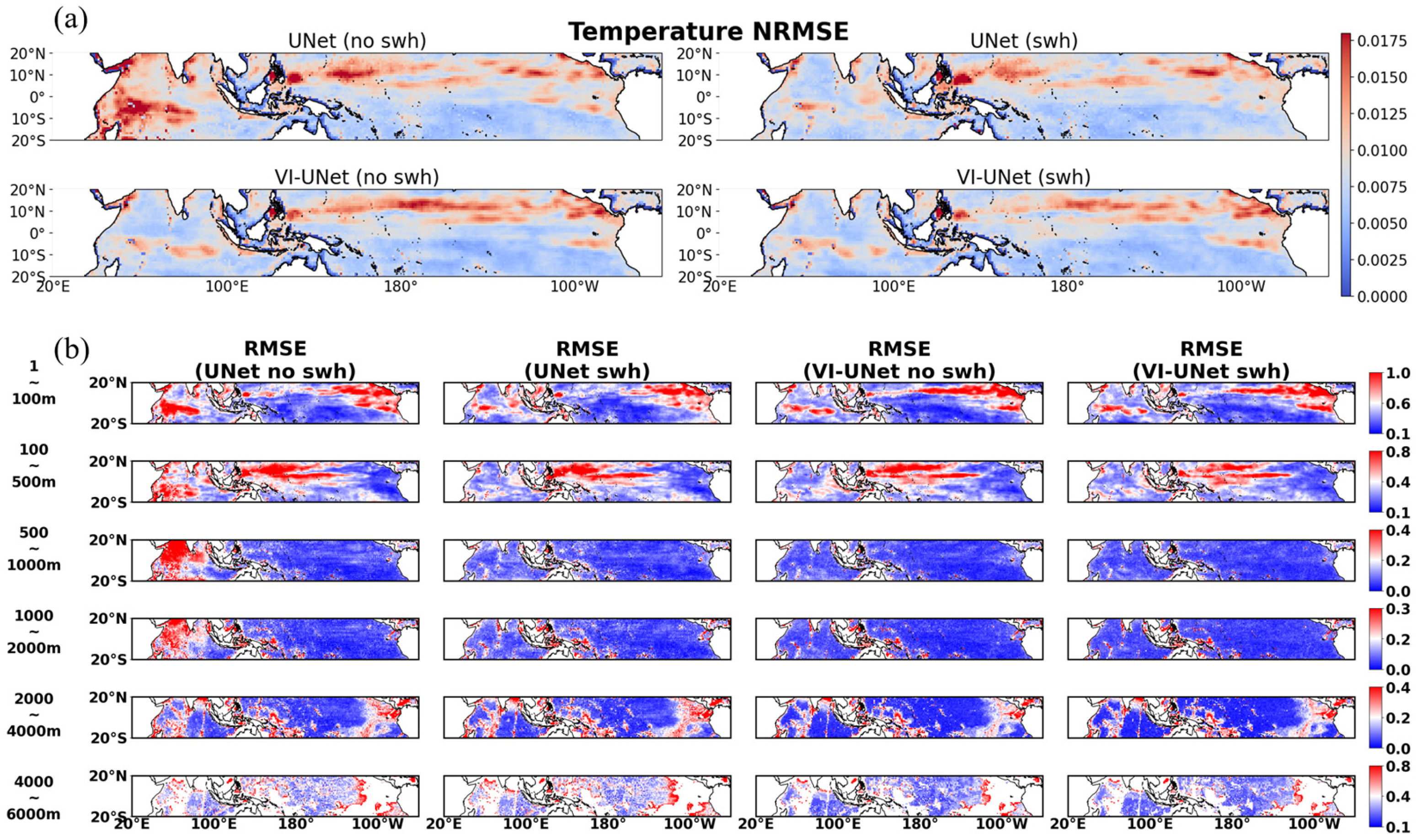
4.1. Temperature
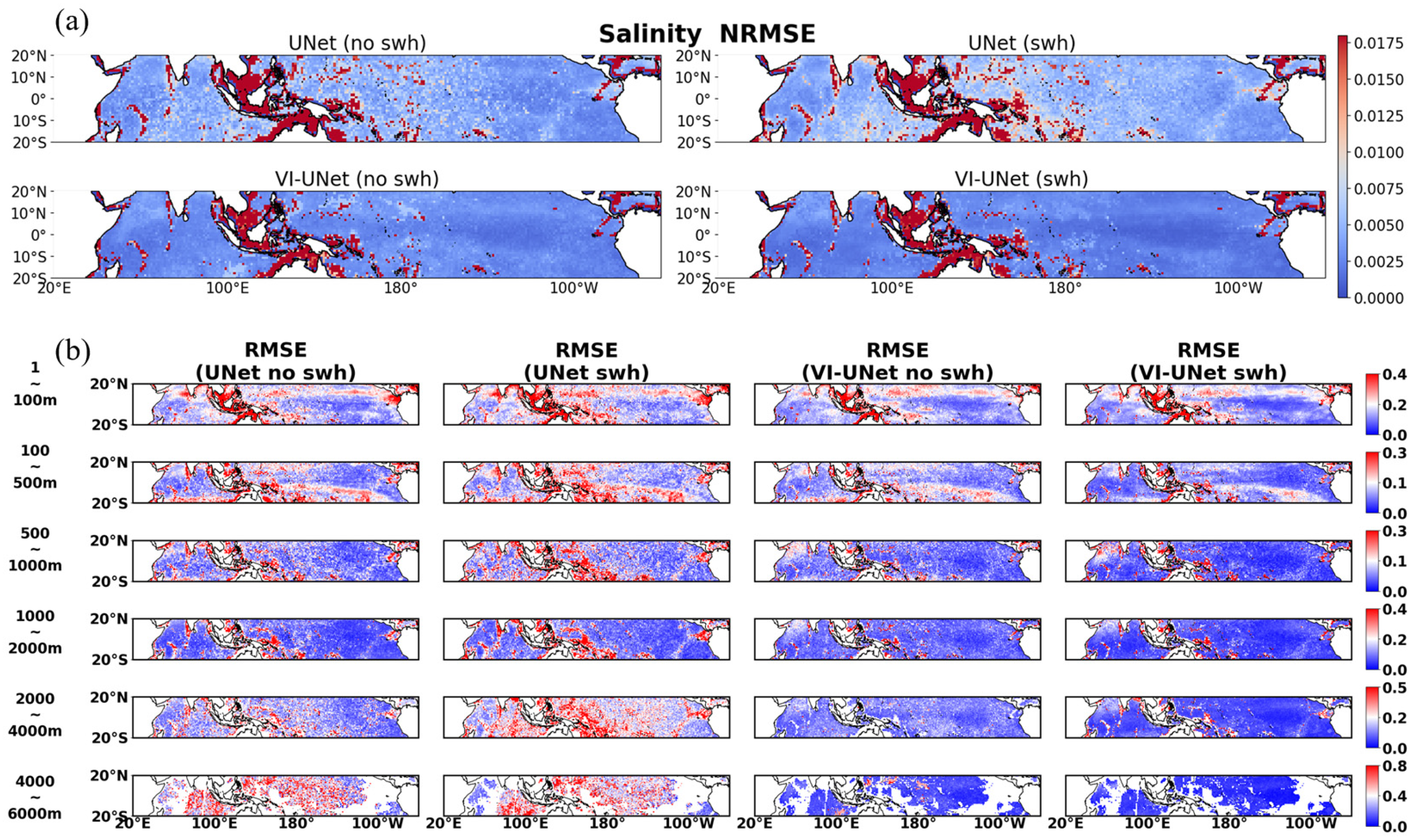
4.2. Salinity
5. Discussion
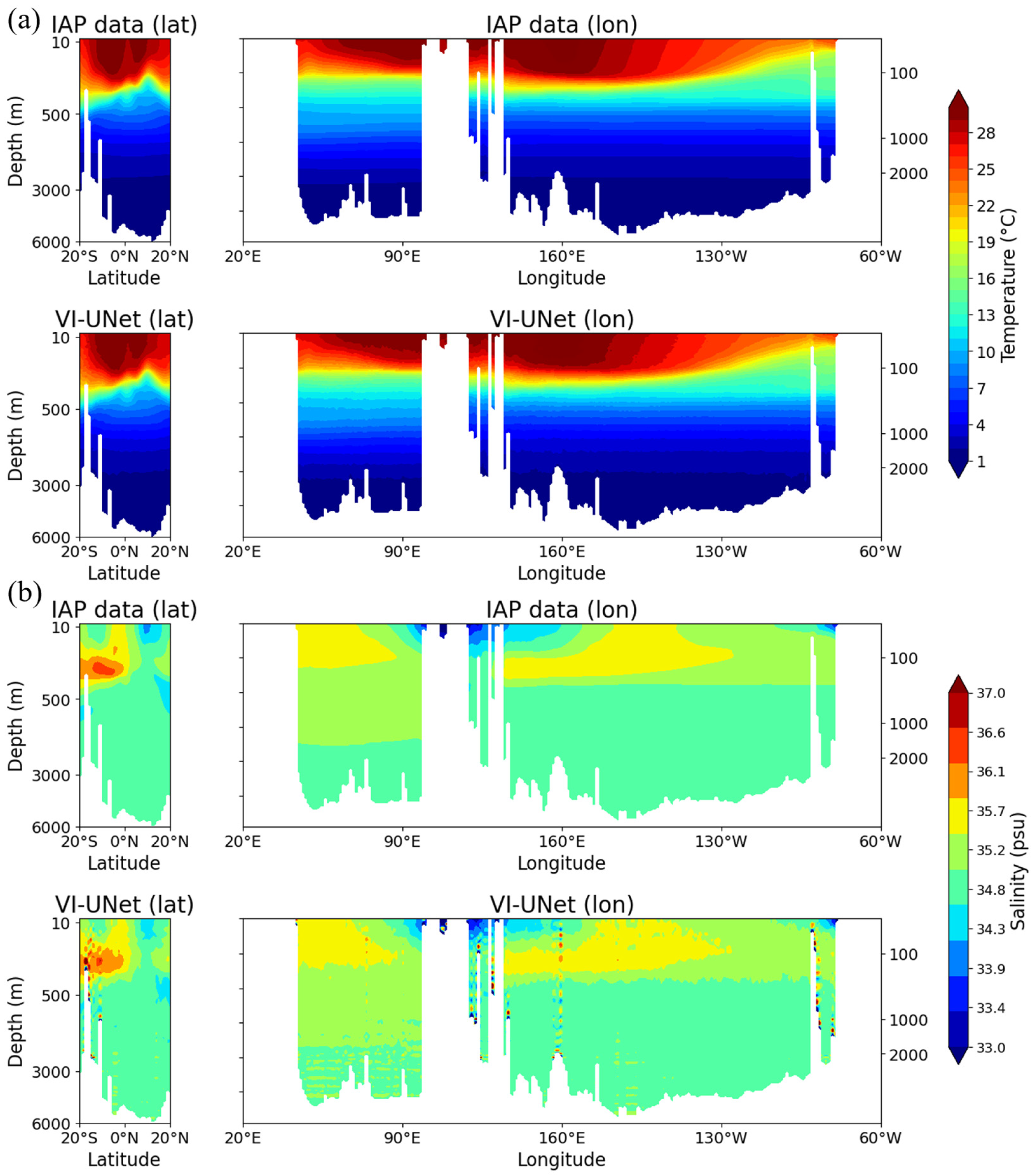
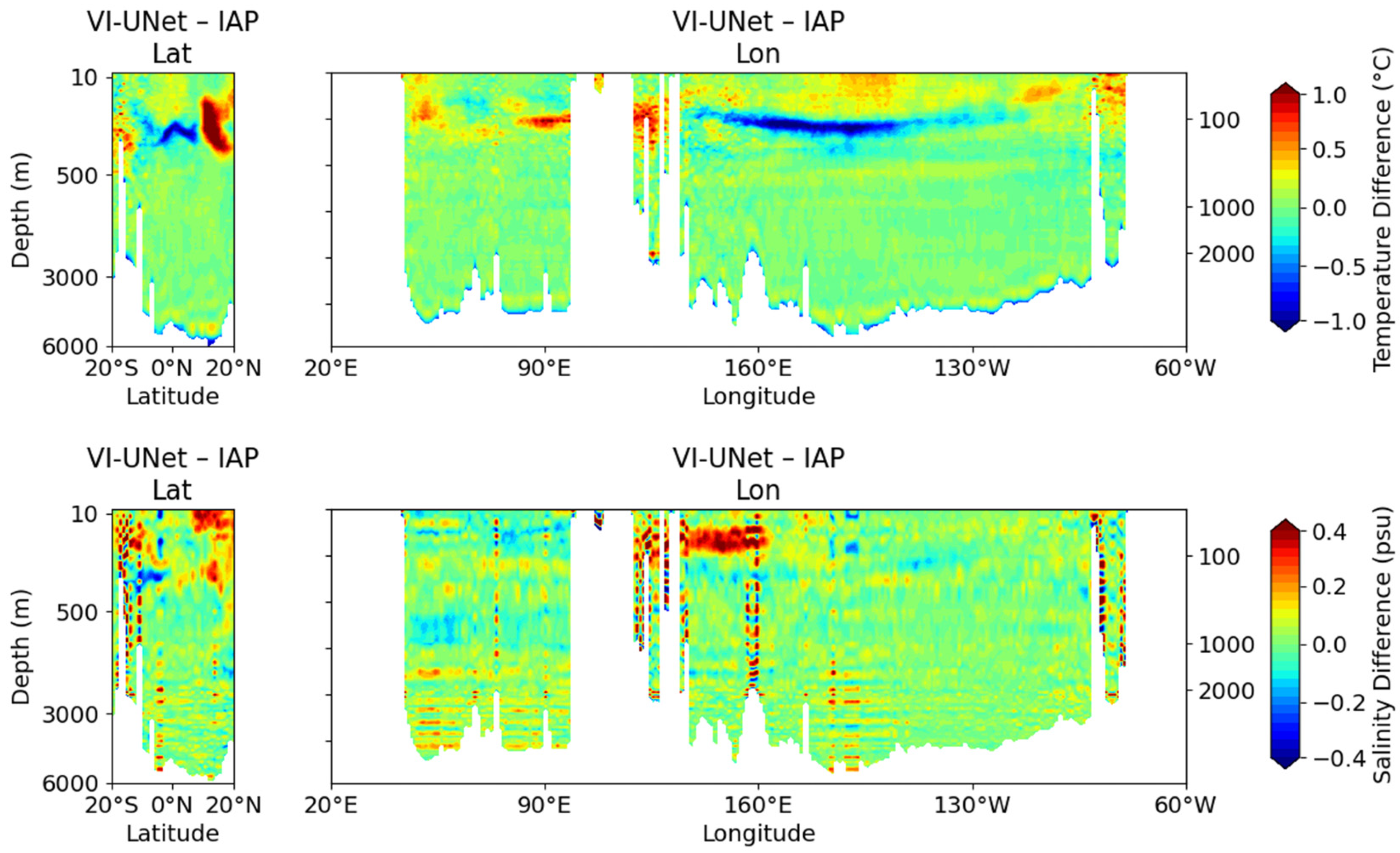
5.1. Profiles at Longitudinal and Zonal Sections
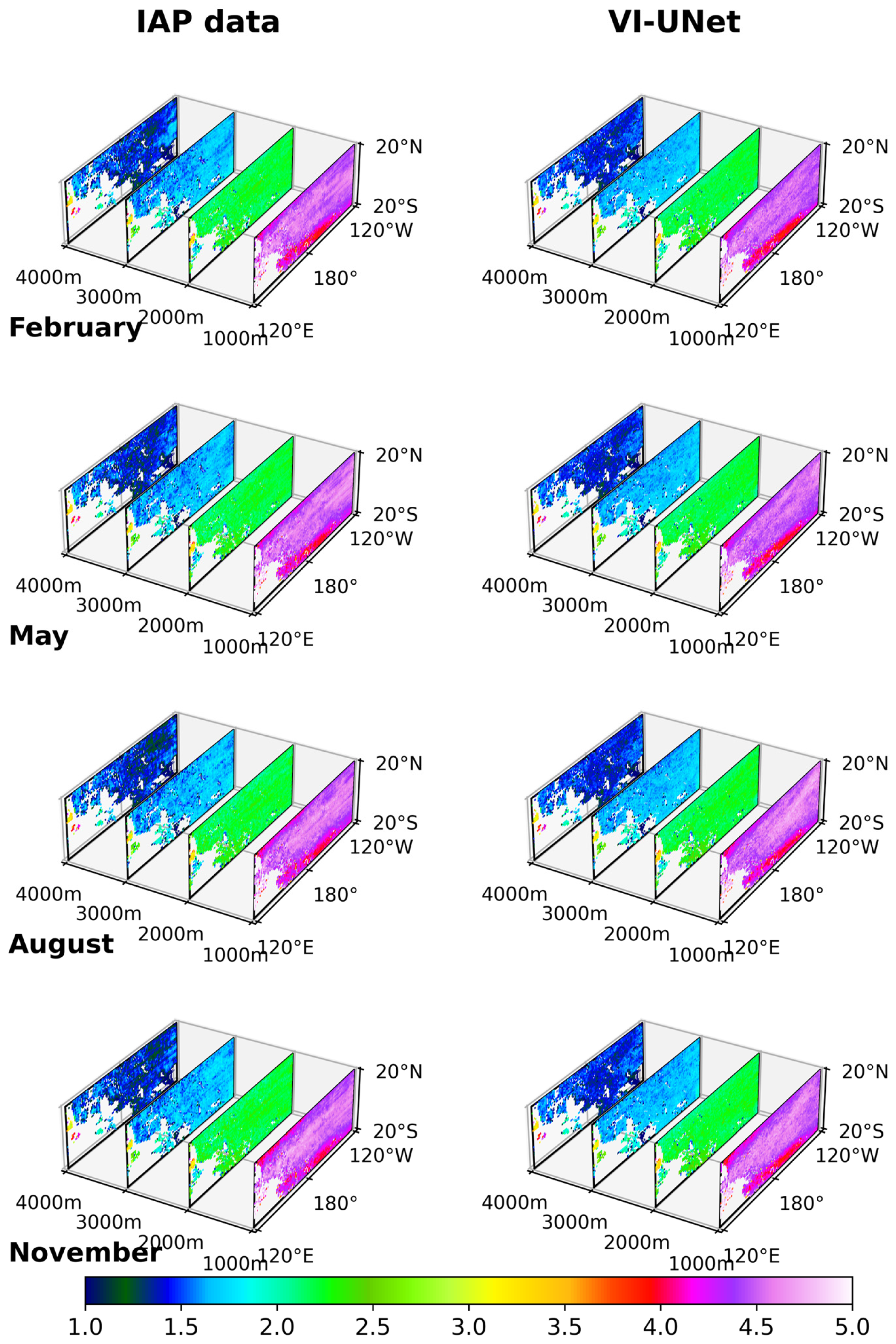
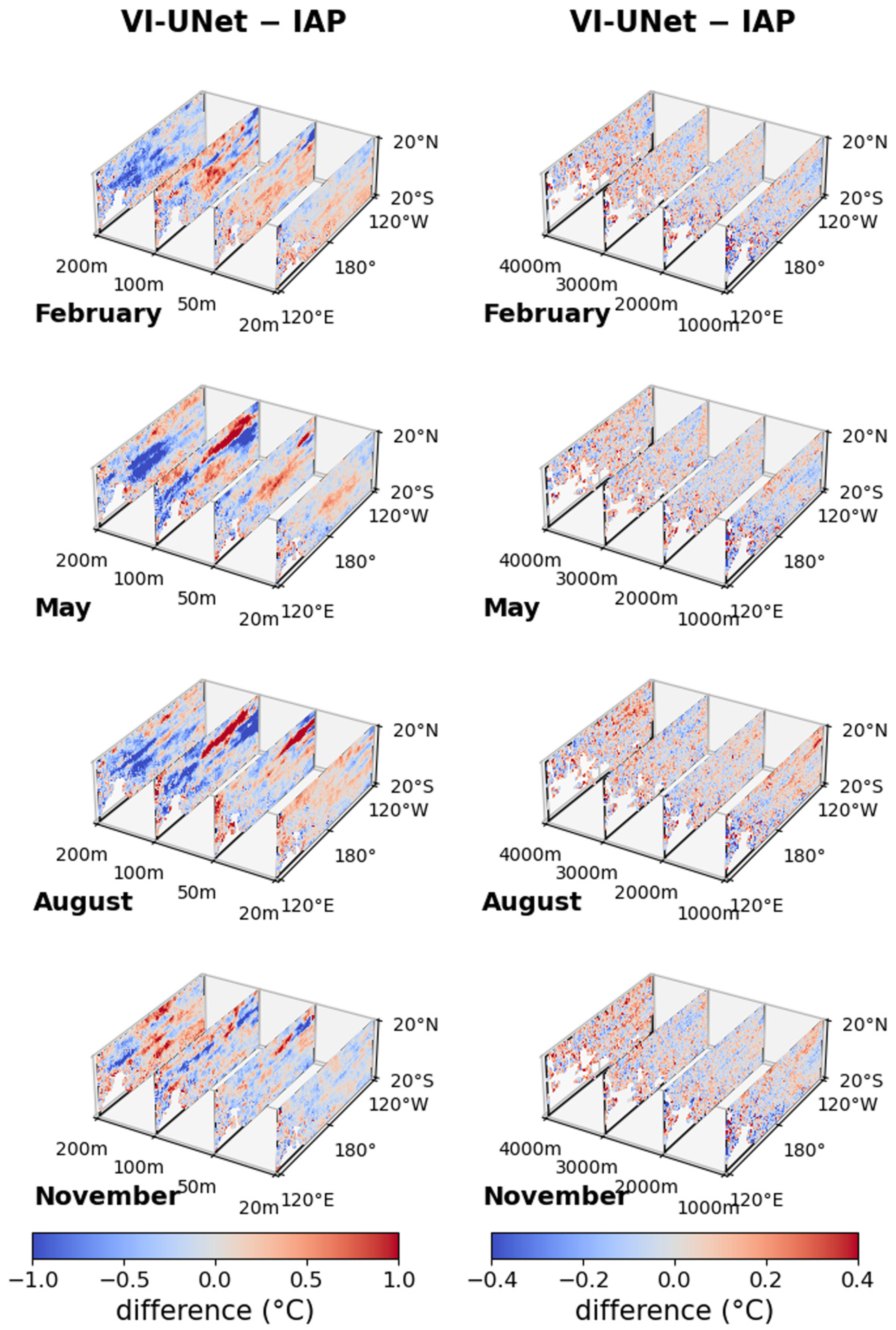
5.2. Seasonal Variations
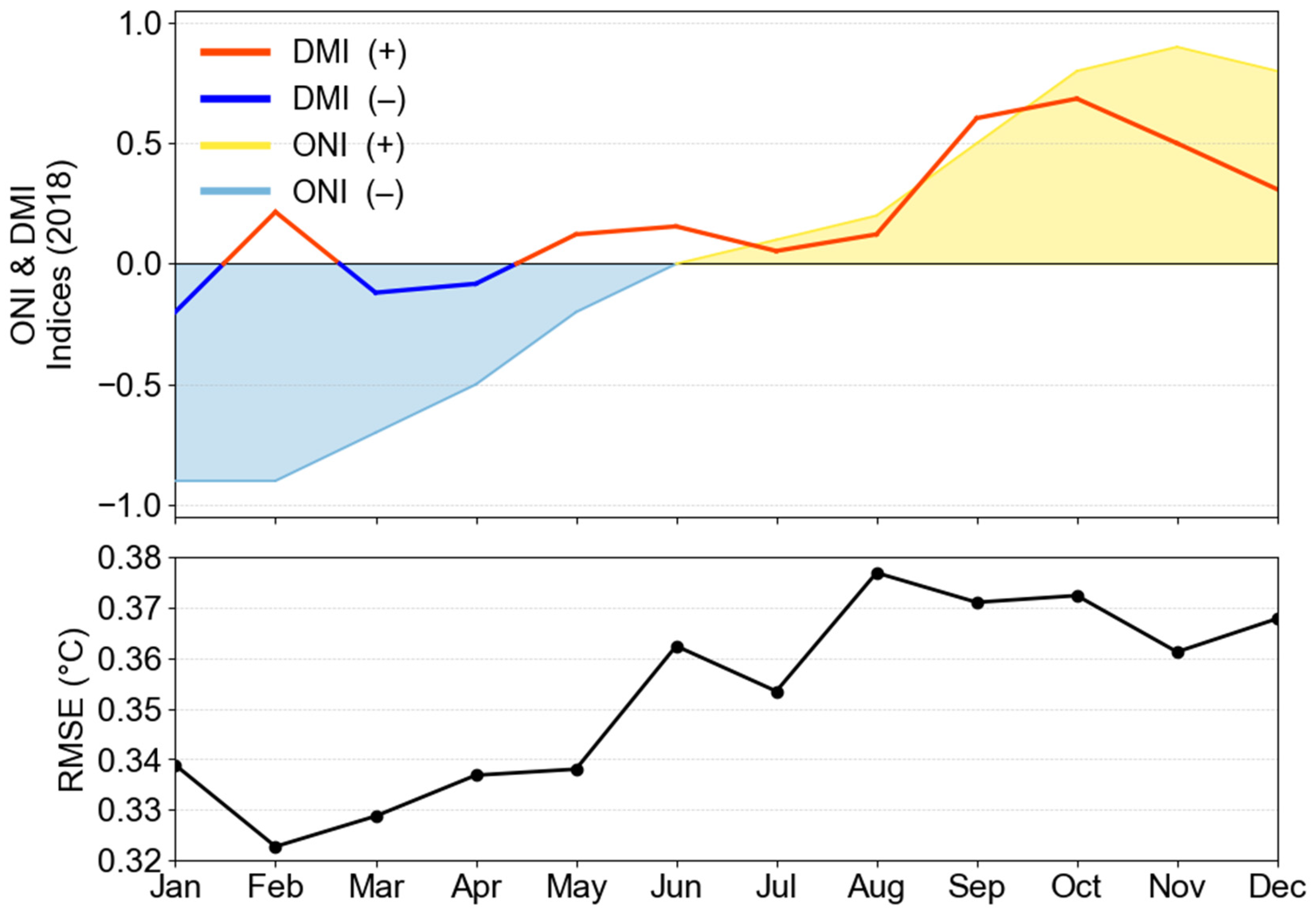
5.3. Evaluation During Climate Phenomena
5.4. Multi-Scale Self-Attention and Wave Physical Constraints
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, B.; Hua, L.; Mei, H.; Wu, X.; Kang, Y.; Zhao, N. Impact of Climate Change on the Dynamic Processes of Marine Environment and Feedback Mechanisms: An Overview. Arch. Comput. Methods Eng. 2024, 31, 3377–3408. [Google Scholar] [CrossRef]
- Ren, J.; Wang, C.; Sun, L.; Huang, B.; Zhang, D.; Mu, J.; Wu, J. Prediction of Sea Surface Temperature Using U-Net Based Model. Remote Sens. 2024, 16, 1205. [Google Scholar] [CrossRef]
- Webster, P.J. The Role of Hydrological Processes in Ocean-Atmosphere Interactions. Rev. Geophys. 1994, 32, 427–476. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, T.; Zhang, L.; Chen, X.; Zhang, W.; Jiang, J. Global Land Monsoon Precipitation Changes in CMIP6 Projections. Geophys. Res. Lett. 2020, 47, e2019GL086902. [Google Scholar] [CrossRef]
- Planton, Y.Y.; Vialard, J.; Guilyardi, E.; Lengaigne, M.; McPhaden, M.J. The Asymmetric Influence of Ocean Heat Content on ENSO Predictability in the CNRM-CM5 Coupled General Circulation Model. J. Clim. 2021, 34, 5775–5793. [Google Scholar] [CrossRef]
- Roemmich, D.; Gilson, J.; Wijesekera, H.; Wong, A.P.; Wijffels, S.E.; Riser, S.C.; Pouliquen, S.; Hosoda, S.; Poffa, N.; Park, H.M.; et al. Argo Data 1999–2019: Two Million Temperature-Salinity Profiles and Subsurface Velocity Observations from a Global Array of Profiling Floats. Front. Mar. Sci. 2020, 7, 700. [Google Scholar] [CrossRef]
- Dickey, T.; Lewis, M.; Chang, G. Optical Oceanography: Recent Advances and Future Directions Using Global Remote Sensing and In Situ Observations. Rev. Geophys. 2006, 44, RG000148. [Google Scholar] [CrossRef]
- Li, D.; Wang, P. Global Wavenumber Spectra of Sea Surface Salinity in the Mesoscale Range Using Satellite Observations. Remote Sens. 2024, 16, 1753. [Google Scholar] [CrossRef]
- Dubovik, O.; Schuster, G.L.; Xu, F.; Hu, Y.; Bösch, H.; Landgraf, J.; Li, Z. Grand Challenges in Satellite Remote Sensing. Front. Remote Sens. 2021, 2, 619818. [Google Scholar] [CrossRef]
- Meng, L.; Yan, X. Remote Sensing for Subsurface and Deeper Oceans: An Overview and a Future Outlook. IEEE Geosci. Remote Sens. Mag. 2022, 10, 72–92. [Google Scholar] [CrossRef]
- Schuster, G.T.; Chen, Y.; Feng, S. Review of Physics-Informed Machine-Learning Inversion of Geophysical Data. Geophysics 2024, 89, 1ND–V667. [Google Scholar] [CrossRef]
- Weglein, A.B.; Zhang, H.; Ramírez, A.C.; Liu, F.; Lira, J.E. Clarifying the Underlying and Fundamental Meaning of the Approximate Linear Inversion of Seismic Data. Geophysics 2009, 74, 1ND–Z107. [Google Scholar] [CrossRef][Green Version]
- Hu, L.Y.; Chugunova, T. Multiple-Point Geostatistics for Modeling Subsurface Heterogeneity: A Comprehensive Review. Water Resour. Res. 2008, 44, W11410. [Google Scholar] [CrossRef]
- Haines, K. A Direct Method for Assimilating Sea Surface Height Data into Ocean Models with Adjustments to the Deep Circulation. J. Phys. Oceanogr. 1991, 21, 843–868. [Google Scholar] [CrossRef]
- Wong, M.S.; Jin, X.; Liu, Z.; Nichol, J.E.; Ye, S.; Jiang, P.; Chan, P.W. Geostationary Satellite Observation of Precipitable Water Vapor Using an Empirical Orthogonal Function (EOF) Based Reconstruction Technique over Eastern China. Remote Sens. 2015, 7, 5879–5900. [Google Scholar] [CrossRef]
- Cassou, C.; Minvielle, M.; Terray, L.; Pérrigaud, C. A Statistical–Dynamical Scheme for Reconstructing Ocean Forcing in the Atlantic. Part I: Weather Regimes as Predictors for Ocean Surface Variables. Clim. Dyn. 2011, 36, 19–39. [Google Scholar] [CrossRef]
- Sun, G.; Huang, H.; Zhang, A.; Li, F.; Zhao, H.; Fu, H. Fusion of Multiscale Convolutional Neural Networks for Building Extraction in Very High-Resolution Images. Remote Sens. 2019, 11, 227. [Google Scholar] [CrossRef]
- Suárez Gómez, S.L.; García Riesgo, F.; Pérez Fernández, S.; Iglesias Rodríguez, F.J.; Díez Alonso, E.; Santos Rodríguez, J.D.; De Cos Juez, F.J. Wavefront Recovery for Multiple Sun Regions in Solar SCAO Scenarios with Deep Learning Techniques. Mathematics 2023, 11, 1561. [Google Scholar] [CrossRef]
- Xie, H.; Xu, Q.; Cheng, Y.; Yin, X.; Fan, K. Reconstructing Three-Dimensional Salinity Field of the South China Sea from Satellite Observations. Front. Mar. Sci. 2023, 10, 1168486. [Google Scholar] [CrossRef]
- Li, W.; Qi, F.; Tang, M.; Yu, Z. Bidirectional LSTM with Self-Attention Mechanism and Multi-Channel Features for Sentiment Classification. Neurocomputing 2020, 387, 63–77. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z. A Survey on Vision Transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 87–110. [Google Scholar] [CrossRef] [PubMed]
- Wei, M.; Shao, W.; Shen, W.; Hu, Y.; Zhang, Y.; Zuo, J. Contribution of Surface Waves to Sea Surface Temperatures in the Arctic Ocean. J. Ocean Univ. China Ocean. Coast. Sea Res. 2024, 23, 1151–1162. [Google Scholar] [CrossRef]
- Godfrey, J.S. The Effect of the Indonesian Throughflow on Ocean Circulation and Heat Exchange with the Atmosphere: A Review. J. Geophys. Res. Oceans 1996, 101, 12217–12237. [Google Scholar] [CrossRef]
- Lübbecke, J.F.; Böning, C.W.; Biastoch, A. Variability in the Subtropical-Tropical Cells and Its Effect on Near-Surface Temperature of the Equatorial Pacific: A Model Study. Ocean Sci. 2008, 4, 73–88. [Google Scholar] [CrossRef]
- Schott, F.A.; Xie, S.-P.; McCreary, J.P. Indian Ocean Circulation and Climate Variability. Rev. Geophys. 2009, 47, RG000245C. [Google Scholar] [CrossRef]
- Lumpkin, R.; Johnson, G.C. Global Ocean Surface Velocities from Drifters: Mean, Variance, El Niño–Southern Oscillation Response, and Seasonal Cycle. J. Geophys. Res. Oceans 2013, 118, 2992–3006. [Google Scholar] [CrossRef]
- Kiladis, G.N.; Weickmann, K.M. Horizontal Structure and Seasonality of Large-Scale Circulations Associated with Submonthly Tropical Convection. Mon. Weather Rev. 1997, 125, 1997–2013. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04599. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16×16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar] [CrossRef]
- Liu, F.; Ren, X.; Zhang, Z.; Sun, X.; Zou, Y. Rethinking Skip Connection with Layer Normalization in Transformers and ResNets. arXiv 2021, arXiv:2105.07205. [Google Scholar] [CrossRef]
- Xie, H.; Xu, Q.; Dong, C. Deep Learning for Mesoscale Eddy Detection with Feature Fusion of Multisatellite Observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 18351–18364. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2019, arXiv:1711.05101. [Google Scholar] [CrossRef]
- Ye, X.; Wu, Y.; Zhang, W.; Li, X.; Chen, Y.; Jin, C. Optimized Gradient Clipping for Noisy Label Learning. arXiv 2024, arXiv:2412.08941. [Google Scholar] [CrossRef]
- Gray, L.J.; Beer, J.; Geller, M.; Haigh, J.D.; Lockwood, M.; Matthes, K.; Cubasch, U.; Fleitmann, D.; Harrison, G.; Hood, L.; et al. Solar Influences on Climate. Rev. Geophys. 2010, 48, RG000282. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Ho, C.-R.; Zheng, Q.; Huang, S.-J.; Kuo, N.-J. Variability of Sea Surface Temperature and Warm Pool Area in the South China Sea and Its Relationship to the Western Pacific Warm Pool. J. Oceanogr. 2011, 67, 719–724. [Google Scholar] [CrossRef]
- Chand Reddy, P.R.; Salvekar, P.S. Equatorial East Indian Ocean Sea Surface Temperature: A New Predictor for Seasonal and Annual Rainfall. Curr. Sci. 2003, 85, 1600–1604. [Google Scholar]
- Smith, R.L. Poleward Propagating Perturbations in Currents and Sea Levels along the Peru Coast. J. Geophys. Res. Oceans 1978, 83, 6083–6092. [Google Scholar] [CrossRef]
- Woodberry, K.E.; Luther, M.E.; O’Brien, J.J. The Wind-Driven Seasonal Circulation in the Southern Tropical Indian Ocean. J. Geophys. Res. Oceans 1989, 94, 17985–18002. [Google Scholar] [CrossRef]
- Hagen, E. Northwest African Upwelling Scenario. Oceanol. Acta 2001, 24, 113–128. [Google Scholar] [CrossRef]
- Ouellet, V.; Secretan, Y.; St-Hilaire, A.; Morin, J. Daily Averaged 2D Water Temperature Model for the St. Lawrence River. River Res. Appl. 2014, 30, 733–744. [Google Scholar] [CrossRef]
- Grenier, M.; Cravatte, S.; Blanke, B.; Menkes, C.; Koch-Larrouy, A.; Durand, F.; Melet, A.; Jeandel, C. From the Western Boundary Currents to the Pacific Equatorial Undercurrent: Modeled Pathways and Water Mass Evolutions. J. Geophys. Res. Oceans 2011, 116, C12044. [Google Scholar] [CrossRef]
- McWilliams, J.C.; Sullivan, P.P.; Moeng, C.-H. Langmuir Turbulence in the Ocean. J. Fluid Mech. 1997, 334, 1–30. [Google Scholar] [CrossRef]
- Wang, P.; Özgökmen, T.M. Langmuir Circulation with Explicit Surface Waves from Moving-Mesh Modeling. Geophys. Res. Lett. 2018, 45, 216–226. [Google Scholar] [CrossRef]
- Wang, P.; McWilliams, J.C.; Yuan, J.; Liang, J.-H. Langmuir mixing schemes based on a modified K-Profile Parameterization. J. Adv. Model. Earth Syst. 2025, 17, e2024MS004729. [Google Scholar] [CrossRef]
- Karato, S.-I.; Karki, B.; Park, J. Deep Mantle Melting, Global Water Circulation and Its Implications for the Stability of the Ocean Mass. Prog. Earth Planet. Sci. 2020, 7, 76. [Google Scholar] [CrossRef]
- Schott, F.A.; McCreary, J.P., Jr. The Monsoon Circulation of the Indian Ocean. Prog. Oceanogr. 2001, 51, 1–123. [Google Scholar] [CrossRef]
- Rodrigues, R.R.; Rothstein, L.M.; Wimbush, M. Seasonal Variability of the South Equatorial Current Bifurcation in the Atlantic Ocean: A Numerical Study. J. Phys. Oceanogr. 2007, 37, 16–30. [Google Scholar] [CrossRef]
- Wang, P.; McWilliams, J.C.; Uchiyama, Y. A Nearshore Oceanic Front Induced by Wave Streaming. J. Phys. Oceanogr. 2021, 51, 1967–1984. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, C. Ocean Temperature and Color Frontal Zones in the Gulf of Mexico: Where, When, and Why. J. Geophys. Res. Oceans 2021, 126, e2021JC017544. [Google Scholar] [CrossRef]
- Yang, S.; Li, Z.; Yu, J.-Y.; Hu, X.; Dong, W.; He, S. El Niño–Southern Oscillation and Its Impact in the Changing Climate. Nat. Sci. Rev. 2018, 5, 840–857. [Google Scholar] [CrossRef]
- Claar, D.C.; Szostek, L.; McDevitt-Irwin, J.M.; Schanze, J.J.; Baum, J.K. Global Patterns and Impacts of El Niño Events on Coral Reefs: A Meta-Analysis. PLoS ONE 2018, 13, e0190957. [Google Scholar] [CrossRef] [PubMed]
- Glantz, M.H.; Ramirez, I.J. Reviewing the Oceanic Niño Index (ONI) to Enhance Societal Readiness for El Niño’s Impacts. Int. J. Disaster Risk Sci. 2020, 11, 394–403. [Google Scholar] [CrossRef]
- Nuttle, W.K.; Fourqurean, J.W.; Cosby, B.J.; Zieman, J.C.; Robblee, M.B. Influence of Net Freshwater Supply on Salinity in Florida Bay. Water Resour. Res. 2000, 36, 1805–1822. [Google Scholar] [CrossRef]
- Parampil, S.R.; Gera, A.; Ravichandran, M.; Sengupta, D. Intraseasonal Response of Mixed Layer Temperature and Salinity in the Bay of Bengal to Heat and Freshwater Flux. J. Geophys. Res. Oceans 2010, 115, C05002. [Google Scholar] [CrossRef]
- Justić, D.; Kourafalou, V.; Mariotti, G.; He, S.; Weisberg, R.; Androulidakis, Y.; Barker, C.; Bracco, A.; Dzwonkowski, B.; Hu, C.; et al. Transport Processes in the Gulf of Mexico Along the River Estuary Shelf Ocean Continuum: A Review of Research from the Gulf of Mexico Research Initiative. Estuaries Coasts 2022, 45, 621–657. [Google Scholar] [CrossRef]
- Dzwonkowski, B.; Fournier, S.; Reager, J.T.; Milroy, S.; Park, K.; Shiller, A.M.; Greer, A.T.; Soto, I.; Dykstra, S.L.; Sanial, V. Tracking Sea Surface Salinity and Dissolved Oxygen on a River-Influenced, Seasonally Stratified Shelf, Mississippi Bight, Northern Gulf of Mexico. Cont. Shelf Res. 2018, 169, 25–33. [Google Scholar] [CrossRef]
- Jensen, T.G. Arabian Sea and Bay of Bengal Exchange of Salt and Tracers in an Ocean Model. Geophys. Res. Lett. 2001, 28, 3967–3970. [Google Scholar] [CrossRef]
- Coachman, L.K. Circulation, Water Masses, and Fluxes on the Southeastern Bering Sea Shelf. Cont. Shelf Res. 1986, 5, 23–108. [Google Scholar] [CrossRef]
- Kashino, Y.; Hasegawa, T.; Syamsudin, F.; Ueki, I. Temperature and Salinity Variability at Intermediate Depths in the Western Equatorial Pacific Revealed by TRITON Buoy Data. J. Oceanogr. 2020, 76, 121–139. [Google Scholar] [CrossRef]
- He, Z.; Qiao, S.; Jin, L.; Shen, W.; Wu, B.; Sheng, J.; Fang, X.; Chen, L.; Yin, Z. Clay Mineralogy and Geochemistry of Surface Sediments in the Equatorial Western Indian Ocean and Implications for Sediment Sources and the Antarctic Bottom Water Inputs. J. Asian Earth Sci. 2023, 254, 105741. [Google Scholar] [CrossRef]
- Budillon, G.; Castagno, P.; Aliani, S.; Spezie, G.; Padman, L. Thermohaline Variability and Antarctic Bottom Water Formation at the Ross Sea Shelf Break. Deep Sea Res. Part I Oceanogr. Res. Pap. 2011, 58, 1002–1018. [Google Scholar] [CrossRef]
- Susanto, R.D.; Ray, R.D. Seasonal and Interannual Variability of Tidal Mixing Signatures in Indonesian Seas from High-Resolution Sea Surface Temperature. Remote Sens. 2022, 14, 1934. [Google Scholar] [CrossRef]
- Castruccio, F.S.; Curchitser, E.N.; Kleypas, J.A. A Model for Quantifying Oceanic Transport and Mesoscale Variability in the Coral Triangle of the Indonesian/Philippines Archipelago. J. Geophys. Res. Oceans 2013, 118, 6123–6144. [Google Scholar] [CrossRef]
- Montes, I.; Schneider, W.; Colas, F.; Blanke, B.; Echevin, V. Subsurface Connections in the Eastern Tropical Pacific during La Niña 1999–2001 and El Niño 2002–2003. J. Geophys. Res. Oceans 2011, 116, C12045. [Google Scholar] [CrossRef]
- Mercier, H.; Arhan, M.; Lutjeharms, J.R.E. Upper-Layer Circulation in the Eastern Equatorial and South Atlantic Ocean in January–March 1995. Deep Sea Res. Part I Oceanogr. Res. Pap. 2003, 50, 863–887. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, F.; He, X.; Wang, W.; Chang, L.; Kang, J. Latitudinal and Meridional Patterns of Picophytoplankton Variability Are Contrastingly Associated with Ekman Pumping and the Warm Pool in the Tropical Western Pacific. Ecol. Evol. 2023, 13, e10589. [Google Scholar] [CrossRef]
- Wang, F.; Li, Y.; Zhang, Y.; Hu, D. The Subsurface Water in the North Pacific Tropical Gyre. Deep Sea Res. Part I Oceanogr. Res. Pap. 2013, 75, 78–92. [Google Scholar] [CrossRef]
- Hayashi, M.; Jin, F.-F.; Stuecker, M.F. Dynamics for El Niño-La Niña Asymmetry Constrain Equatorial-Pacific Warming Pattern. Nat. Commun. 2020, 11, 4230. [Google Scholar] [CrossRef]
- Chen, Y.-Y.; Jin, F.-F. Dynamical Diagnostics of the SST Annual Cycle in the Eastern Equatorial Pacific: Part I A Linear Coupled Framework. Clim. Dyn. 2018, 50, 1841–1862. [Google Scholar] [CrossRef]
- Matsuura, T.; Iizuka, S. Zonal Migration of the Pacific Warm-Pool Tongue during El Niño Events. J. Phys. Oceanogr. 2000, 30, 1582–1600. [Google Scholar] [CrossRef]
- Lukas, R. The Termination of the Equatorial Undercurrent in the Eastern Pacific. Prog. Oceanogr. 1986, 16, 63–90. [Google Scholar] [CrossRef]
- Wu, S.; Bao, S.; Dong, W.; Wang, S.; Zhang, X.; Shao, C.; Zhu, J.; Li, X. Corrigendum: PGTransNet: A physics-guided transformer network for 3D ocean temperature and salinity predicting in tropical Pacific. Front. Mar. Sci. 2025, 12, 1548441. [Google Scholar] [CrossRef]
- Tian, T.; Cheng, L.; Wang, G.; Abraham, J.; Wei, W.; Ren, S.; Zhu, J.; Song, J.; Leng, H. Reconstructing ocean subsurface salinity at high resolution using a machine learning approach. Earth Syst. Sci. Data 2022, 14, 5037–5060. [Google Scholar] [CrossRef]
- Fu, L.-L.; Morrow, R. Chapter 4—Remote Sensing of the Global Ocean Circulation. Int. Geophys. 2013, 103, 83–111. [Google Scholar] [CrossRef]




| Experiments | Inputs | Outputs |
|---|---|---|
| UNet/VI-UNet (no swh) | SST, SSS, SSW, SSH | 3D Temperature/Salinity |
| UNet/VI-UNet (swh) | SST, SSS, SSW, SSH, SWH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Yi, D.L.; Wang, P. Reconstruction of Three-Dimensional Temperature and Salinity in the Equatorial Ocean with Deep-Learning. Remote Sens. 2025, 17, 2005. https://doi.org/10.3390/rs17122005
Yu X, Yi DL, Wang P. Reconstruction of Three-Dimensional Temperature and Salinity in the Equatorial Ocean with Deep-Learning. Remote Sensing. 2025; 17(12):2005. https://doi.org/10.3390/rs17122005
Chicago/Turabian StyleYu, Xiaoyu, Daling Li Yi, and Peng Wang. 2025. "Reconstruction of Three-Dimensional Temperature and Salinity in the Equatorial Ocean with Deep-Learning" Remote Sensing 17, no. 12: 2005. https://doi.org/10.3390/rs17122005
APA StyleYu, X., Yi, D. L., & Wang, P. (2025). Reconstruction of Three-Dimensional Temperature and Salinity in the Equatorial Ocean with Deep-Learning. Remote Sensing, 17(12), 2005. https://doi.org/10.3390/rs17122005






