Multi-Attitude Hybrid Network for Remote Sensing Hyperspectral Images Super-Resolution
Abstract
1. Introduction
- This paper proposes a hybrid network, named MAHN, based on hypergraph learning for remote sensing HSI SR. This model can efficiently decouple and characterize complex scenes in multiple dimensions, thus realizing precise reconstruction of spatial texture and spectral signals. Extensive experiments demonstrate that our method outperforms other cutting-edge algorithms and effectively reduces the computational complexity;
- In order to effectively extract and utilize frequency characteristics, we construct SHCAM and SHSAM based on high- and low-frequency features in spectral and spatial dimensions, respectively. Hypergraph modules with attention mechanisms achieve detailed texture and spectrum reconstruction by capturing the main structure and detail changes within the image;
- To cope with the challenge of highly coupled information in HSI, we use the semantic information in the mixed pixel to construct the relational hypergraph and design SH3M. By mapping the complex information within pixels into the semantic space, the propagation and reconstruction of a high-level semantic feature is effectively enhanced;
- To reduce domain discrepancies and enhance the compatibility among features, we design the SBAM based on the maximum entropy principle, enabling effective cross-domain interaction and fusion.
2. Related Works
2.1. Image Fusion for HSI SR
2.2. Single HSI SR
2.3. Hypergraph Learning
3. Materials and Methods
3.1. Overall Framework
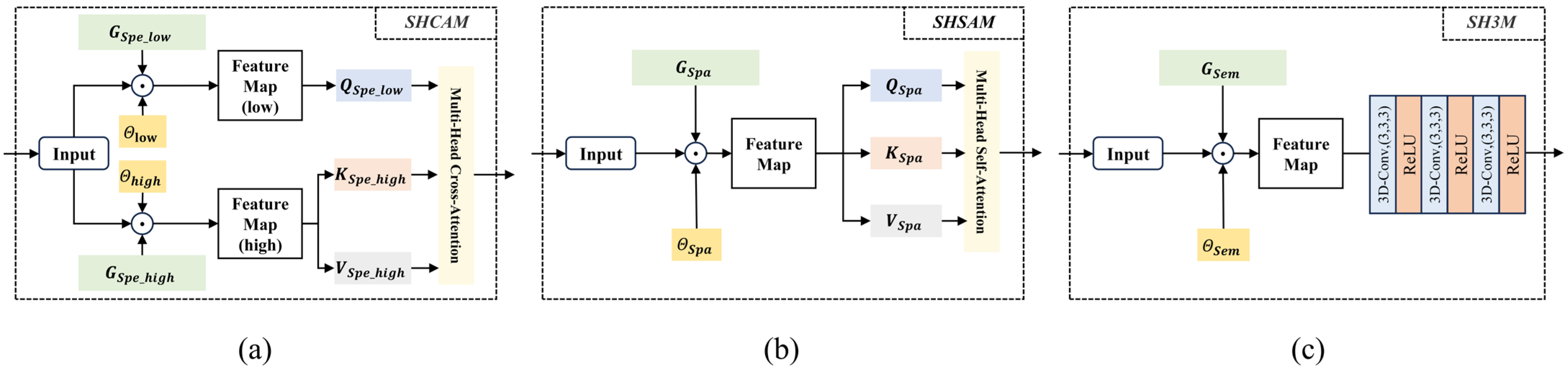
3.2. SHCAM
3.3. SHSAM
3.4. SH3M
3.5. SBAM
4. Results
4.1. Implementation Details
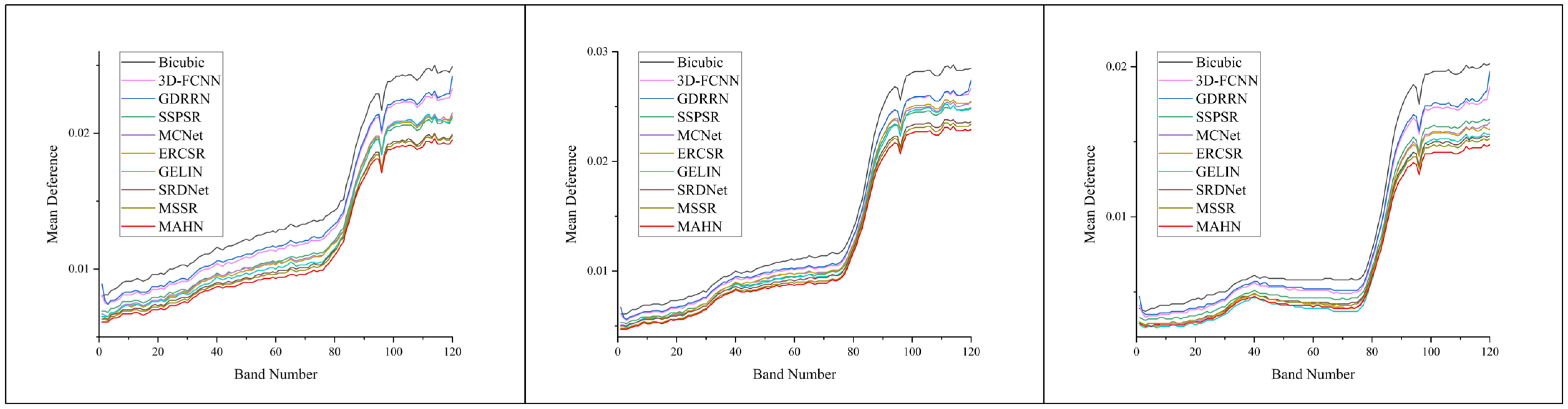
4.2. Results on MDAS
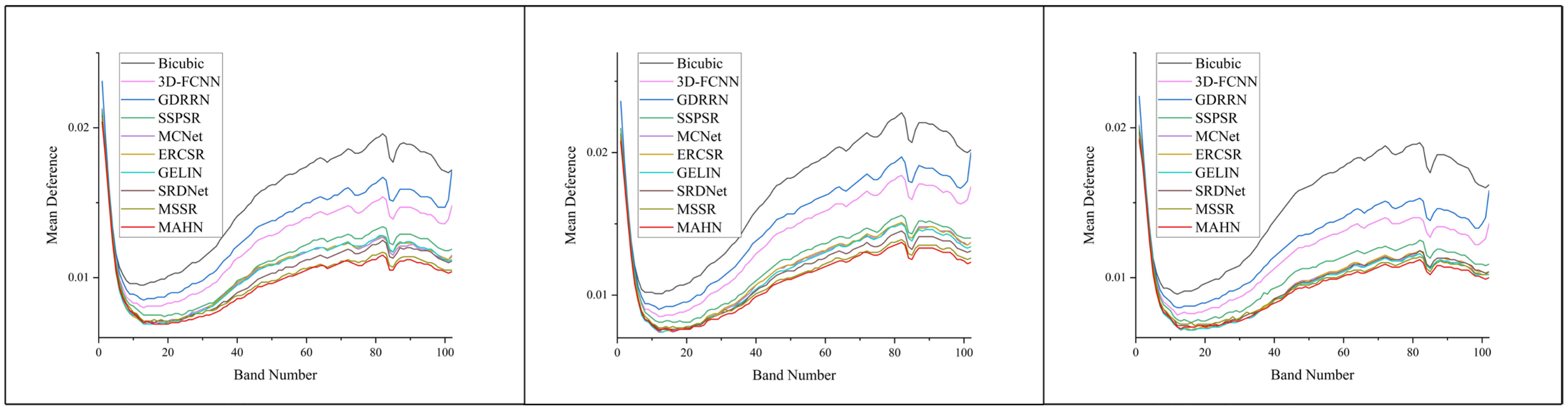
4.3. Results on Pavia Centre
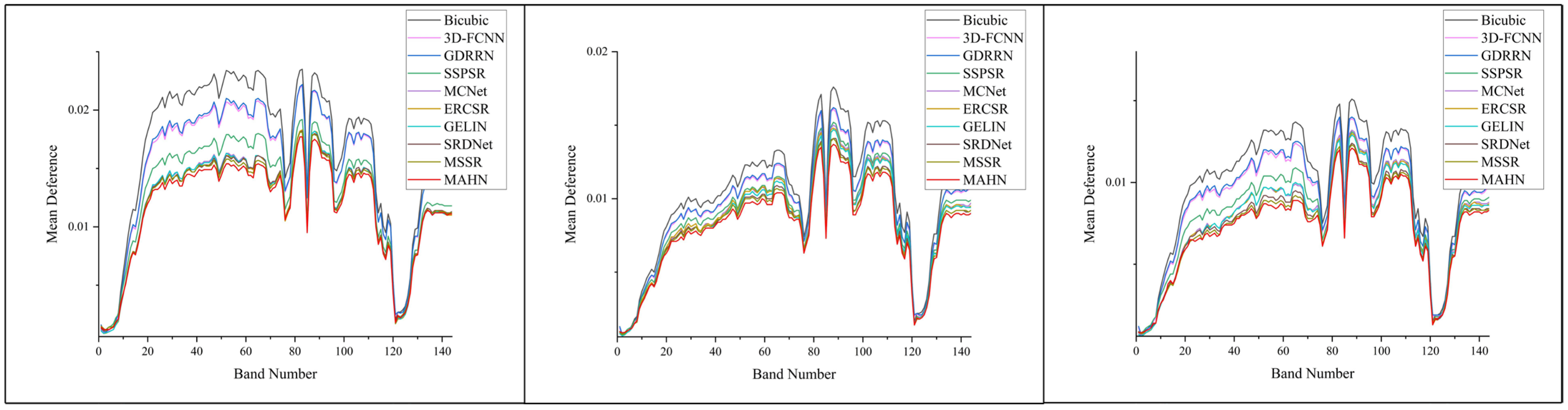
4.4. Results on Houston
5. Discussion
5.1. Parameters and Computational Cost
5.2. Ablation Study
5.3. SR for Real HSIs
6. Limitations
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, G.Y.; Al-qaness, M.A.A.; Al-Alimi, D.; Dahou, A.; Abd Elaziz, M.; Ewees, A.A. Hyperspectral image classification using graph convolutional network: A comprehensive review. Expert Syst. Appl. 2024, 257, 125106. [Google Scholar] [CrossRef]
- Wang, L.Q.; Zhu, T.C.; Kumar, N.; Li, Z.W.; Wu, C.L.; Zhang, P.Y. Attentive-adaptive network for hyperspectral images classification with noisy labels. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3254159. [Google Scholar] [CrossRef]
- Feng, H.; Wang, Y.C.; Chen, C.; Xu, D.D.; Zhao, Z.K.; Zhao, T.Q. Hyperspectral image classification framework based on multichannel graph convolutional networks and class-guided attention mechanism. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3388429. [Google Scholar] [CrossRef]
- Tu, B.; Yang, X.C.; He, W.; Li, J.; Plaza, A. Hyperspectral anomaly detection using reconstruction fusion of quaternion frequency domain analysis. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 8358–8372. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.F.; Liu, H.J.; Nie, J.; Zhou, X.C. Matrix factorization with framelet and saliency priors for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3248599. [Google Scholar] [CrossRef]
- Liu, S.H.; Song, M.P.; Xue, B.; Chang, C.; Zhang, M.J. Hyperspectral real-time local anomaly detection based on finite markov via line-by-line processing. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3345941. [Google Scholar] [CrossRef]
- Gomez, R.B.; Jazaeri, A.; Kafatos, M. Wavelet-based hyperspectral and multispectral image fusion. In Proceedings of the Conference on Geo-Spatial Image and Data Exploitation II, Orlando, FL, USA, 16 April 2001; pp. 36–42. [Google Scholar]
- Zhang, Y.F.; De Backer, S.; Scheunders, P. Noise-resistant wavelet-based bayesian fusion of multispectral and hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3834–3843. [Google Scholar] [CrossRef]
- Hardie, R.C.; Eismann, M.T.; Wilson, G.L. Map estimation for hyperspectral image resolution enhancement using an auxiliary sensor. IEEE Trans. Image Process. 2004, 13, 1174–1184. [Google Scholar] [CrossRef]
- Eismann, M.T.; Hardie, R.C. Application of the stochastic mixing model to hyperspectral resolution, enhancement. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1924–1933. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Bendoumi, M.A.; He, M.Y.; Mei, S.H. Hyperspectral image resolution enhancement using high-resolution multispectral image based on spectral unmixing. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6574–6583. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Liu, F.; Lyu, X.; Tong, Y.; Xu, Z.; Zhou, J. A synergistical attention model for semantic segmentation of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3243954. [Google Scholar] [CrossRef]
- Sun, Z.; Leng, X.; Zhang, X.; Zhou, Z.; Xiong, B.; Ji, K.; Kuang, G. Arbitrary-direction sar ship detection method for multiscale imbalance. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5208921. [Google Scholar] [CrossRef]
- Zhang, X.H.; Zhang, S.Q.; Sun, Z.Z.; Liu, C.F.; Sun, Y.L.; Ji, K.F.; Kuang, G.Y. Cross-sensor sar image target detection based on dynamic feature discrimination and center-aware calibration. IEEE Trans. Geosci. Remote Sens. 2025, 63, 3559618. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Liu, F.; Tong, Y.; Lyu, X.; Zhou, J. Semantic segmentation of remote sensing images by interactive representation refinement and geometric prior-guided inference. IEEE Trans. Geosci. Remote Sens. 2023, 62, 3339291. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Tao, F.F.; Tong, Y.; Gao, H.M.; Liu, F.; Chen, Z.Q.; Lyu, X. A cross-domain coupling network for semantic segmentation of remote sensing images. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3477609. [Google Scholar] [CrossRef]
- Xie, Q.; Zhou, M.H.; Zhao, Q.; Meng, D.Y.; Zuo, W.M.; Xu, Z.B.; Soc, I.C. Multispectral and hyperspectral image fusion by ms/hs fusion net. In Proceedings of the 32nd IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; IEEE Computer Soc: Long Beach, CA, USA, 2019; pp. 1585–1594. [Google Scholar]
- Dian, R.W.; Li, S.T.; Kang, X.D. Regularizing hyperspectral and multispectral image fusion by cnn denoiser. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1124–1135. [Google Scholar] [CrossRef]
- Zheng, Y.X.; Li, J.J.; Li, Y.S.; Guo, J.; Wu, X.Y.; Chanussot, J. Hyperspectral pansharpening using deep prior and dual attention residual network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8059–8076. [Google Scholar] [CrossRef]
- Dong, W.Q.; Yang, Y.F.; Qu, J.H.; Xie, W.Y.; Li, Y.S. Fusion of hyperspectral and panchromatic images using generative adversarial network and image segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3078711. [Google Scholar] [CrossRef]
- Wang, X.Y.; Ma, J.Y.; Jiang, J.J. Hyperspectral image super-resolution via recurrent feedback embedding and spatialspectral consistency regularization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3064450. [Google Scholar]
- Tang, Y.; Li, J.; Yue, L.W.; Liu, X.X.; Li, Y.J.; Xiao, Y.; Yuan, Q.Q. A cnn-transformer embedded unfolding network for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3431924. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Q.; Li, X.L. Mixed 2d/3d convolutional network for hyperspectral image super-resolution. Remote Sens. 2020, 12, 1660. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Q.; Li, X.L. Exploring the relationship between 2d/3d convolution for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8693–8703. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Yu, A.Z.; Lyu, X.; Gao, H.M.; Zhou, J. A frequency decoupling network for semantic segmentation of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2025, 63, 3531879. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Li, L.Y.; Xu, N.; Liu, F.; Yuan, C.; Chen, Z.Q.; Lyu, X. Aaformer: Attention-attended transformer for semantic segmentation of remote sensing images. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3397851. [Google Scholar] [CrossRef]
- Feng, Y.F.; You, H.X.; Zhang, Z.Z.; Ji, R.R.; Gao, Y. Hypergraph Neural Networks. In Proceedings of the 33rd AAAI Conference on Artificial Intelligence/31st Innovative Applications of Artificial Intelligence Conference/9th AAAI Symposium on Educational Advances in Artificial Intelligence, Honolulu, HI, USA, 27 Jan–1 February 2019; pp. 3558–3565. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Qu, J.H.; Shi, Y.Z.; Xie, W.Y.; Li, Y.S.; Wu, X.Y.; Du, Q. Mssl: Hyperspectral and panchromatic images fusion via multiresolution spatialspectral feature learning networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 318962. [Google Scholar] [CrossRef]
- Zhuo, Y.W.; Zhang, T.J.; Hu, J.F.; Dou, H.X.; Huang, T.Z.; Deng, L.J. A deep-shallow fusion network with multidetail extractor and spectral attention for hyperspectral pansharpening. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 7539–7555. [Google Scholar] [CrossRef]
- He, L.; Xie, J.H.; Li, J.; Plaza, A.; Chanussot, J.; Zhu, J.W. Variable subpixel convolution based arbitrary-resolution hyperspectral pansharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3189624. [Google Scholar] [CrossRef]
- Zhang, L.; Nie, J.T.; Wei, W.; Zhang, Y.N.; Liao, S.C.; Shao, L. Unsupervised adaptation learning for hyperspectral imagery super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 3070–3079. [Google Scholar]
- Guo, Z.L.; Xin, J.W.; Wang, N.N.; Li, J.; Gao, X.B. External-internal attention for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3207230. [Google Scholar] [CrossRef]
- Hong, D.F.; Yao, J.; Li, C.Y.; Meng, D.Y.; Yokoya, N.; Chanussot, J. Decoupled-and-coupled networks: Self-supervised hyperspectral image super-resolution with subpixel fusion. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3324497. [Google Scholar] [CrossRef]
- Zheng, K.; Gao, L.R.; Liao, W.Z.; Hong, D.F.; Zhang, B.; Cui, X.M.; Chanussot, J. Coupled convolutional neural network with adaptive response function learning for unsupervised hyperspectral super resolution. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2487–2502. [Google Scholar] [CrossRef]
- Sun, W.W.; Ren, K.; Meng, X.C.; Xiao, C.C.; Yang, G.; Peng, J.T. A band divide-and-conquer multispectral and hyperspectral image fusion method. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3046321. [Google Scholar] [CrossRef]
- Mei, S.H.; Yuan, X.; Ji, J.Y.; Zhang, Y.F.; Wan, S.; Du, Q. Hyperspectral image spatial super-resolution via 3d full convolutional neural network. Remote Sens. 2017, 9, 1139. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, L.; Ding, C.; Wei, W.; Zhang, Y.N. Single hyperspectral image super-resolution with grouped deep recursive residual network. In Proceedings of the 4th IEEE International Conference on Multimedia Big Data (BigMM), Xi’an, China, 13–16 September 2018; pp. 1–4. [Google Scholar]
- Dong, C.; Loy, C.C.G.; He, K.M.; Tang, X.O. Learning a deep convolutional network for image super-resolution. In Proceedings of the 13th European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; Springer International Publishing Ag: Zurich, Switzerland, 2014; pp. 184–199. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X.M. Image super-resolution via deep recursive residual network. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2790–2798. [Google Scholar]
- Li, J.J.; Cui, R.X.; Li, B.; Song, R.; Li, Y.S.; Dai, Y.C.; Du, Q. Hyperspectral image super-resolution by band attention through adversarial learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4304–4318. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Q.; Li, X.L. Hyperspectral image superresolution using spectrum and feature context. IEEE Trans. Ind. Electron. 2021, 68, 11276–11285. [Google Scholar] [CrossRef]
- Chen, C.; Wang, Y.C.; Zhang, Y.X.; Zhao, Z.K.; Feng, H. Remote sensing hyperspectral image super-resolution via multidomain spatial information and multiscale spectral information fusion. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3388531. [Google Scholar] [CrossRef]
- Liu, T.T.; Liu, Y.; Zhang, C.C.; Yuan, L.Y.; Sui, X.B.; Chen, Q. Hyperspectral image super-resolution via dual-domain network based on hybrid convolution. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3370107. [Google Scholar] [CrossRef]
- Liu, Y.T.; Hu, J.W.; Kang, X.D.; Luo, J.; Fan, S.S. Interactformer: Interactive transformer and cnn for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3183468. [Google Scholar] [CrossRef]
- Wu, Y.M.; Cao, R.H.; Hu, Y.K.; Wang, J.; Li, K.L. Combining global receptive field and spatial spectral information for single-image hyperspectral super-resolution. Neurocomputing 2023, 542, 126277. [Google Scholar] [CrossRef]
- Hu, Q.; Wang, X.Y.; Jiang, J.J.; Zhang, X.P.; Ma, J.Y. Exploring the spectral prior for hyperspectral image super-resolution. IEEE Trans. Image Process. 2024, 33, 5260–5272. [Google Scholar] [CrossRef]
- Yuan, Y.; Zheng, X.T.; Lu, X.Q. Hyperspectral image superresolution by transfer learning. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 1963–1974. [Google Scholar] [CrossRef]
- Cheng, Y.S.; Wang, X.Y.; Ma, Y.; Mei, X.G.; Wu, M.H.; Ma, J.Y. General hyperspectral image super-resolution via meta-transfer learning. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 6134–6147. [Google Scholar] [CrossRef] [PubMed]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 10674–10685. [Google Scholar]
- Pang, L.; Rui, X.; Cui, L.; Wang, H.; Meng, D.; Cao, X. HIR-Diff: Unsupervised hyperspectral image restoration via improved diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 17–18 June 2024; pp. 3005–3014. [Google Scholar] [CrossRef]
- Jiang, J.J.; Sun, H.; Liu, X.M.; Ma, J.Y. Learning spatial-spectral prior for super-resolution of hyperspectral imagery. IEEE Trans. Comput. Imaging 2020, 6, 1082–1096. [Google Scholar] [CrossRef]
- Wang, X.Y.; Hu, Q.; Jiang, J.J.; Ma, J.Y. A group-based embedding learning and integration network for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3217406. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Yuan, Y. Asymmetric dual-direction quasi-recursive network for single hyperspectral image super-resolution. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 6331–6346. [Google Scholar] [CrossRef]
- Zhao, M.H.; Ning, J.W.; Hu, J.; Li, T.T. Attention-driven dual feature guidance for hyperspectral super-resolution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3318013. [Google Scholar] [CrossRef]
- Mei, Z.Y.; Bi, X.; Li, D.G.; Xia, W.; Yang, F.; Wu, H. Dhhnn: A dynamic hypergraph hyperbolic neural network based on variational autoencoder for multimodal data integration and node classification. Inf. Fusion 2025, 119, 103016. [Google Scholar] [CrossRef]
- Ding, J.W.; Tan, Z.Y.; Lu, G.M.; Wei, J.S. Hypergraph denoising neural network for session-based recommendation. Appl. Intell. 2025, 55, 391. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (sips)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Wald, L. Quality of high resolution synthesised images: Is there a simple criterion? In Proceedings of the Third Conference Fusion of Earth Data: Merging Point Measurements, Raster Maps and Remotely Sensed Images, Cannes, France, 6 February 2000; pp. 99–103. [Google Scholar]
- Debes, C.; Merentitis, A.; Heremans, R.; Hahn, J.; Frangiadakis, N.; van Kasteren, T.; Liao, W.Z.; Bellens, R.; Pizurica, A.; Gautama, S.; et al. Hyperspectral and lidar data fusion: Outcome of the 2013 grss data fusion contest. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2405–2418. [Google Scholar] [CrossRef]





| S | Model | PSNR ↑ | SSIM ↑ | SAM ↓ | ERGAS ↓ |
|---|---|---|---|---|---|
| 2 | Bicubic | 32.348 | 0.8664 | 4.765 | 15.722 |
| 3D-FCNN [38] | 33.137 | 0.8941 | 4.473 | 14.317 | |
| GDRRN [39] | 33.034 | 0.8874 | 4.572 | 14.564 | |
| SSPSR [53] | 33.790 | 0.9101 | 4.166 | 13.169 | |
| MCNet [24] | 33.770 | 0.9097 | 4.271 | 12.959 | |
| ERCSR [25] | 33.788 | 0.9105 | 4.221 | 12.926 | |
| GELIN [54] | 33.921 | 0.9143 | 3.832 | 12.676 | |
| SRDNet [45] | 34.186 | 0.9186 | 3.678 | 12.479 | |
| MSSR [44] | 34.322 | 0.9215 | 3.325 | 12.295 | |
| MAHN | 34.364 | 0.9217 | 3.195 | 12.218 | |
| 3 | Bicubic | 30.308 | 0.7880 | 5.968 | 13.321 |
| 3D-FCNN [38] | 30.872 | 0.8208 | 5.742 | 12.415 | |
| GDRRN [39] | 30.866 | 0.8200 | 5.753 | 12.400 | |
| SSPSR [53] | - | - | - | - | |
| MCNet [24] | 31.135 | 0.8313 | 5.588 | 11.935 | |
| ERCSR [25] | 31.159 | 0.8328 | 5.569 | 11.900 | |
| GELIN [54] | 31.234 | 0.8366 | 5.151 | 11.775 | |
| SRDNet [45] | 31.430 | 0.8460 | 4.911 | 11.588 | |
| MSSR [44] | 31.451 | 0.8484 | 4.476 | 11.522 | |
| MAHN | 31.492 | 0.8513 | 4.291 | 11.498 | |
| 4 | Bicubic | 29.007 | 0.7120 | 7.190 | 11.501 |
| 3D-FCNN [38] | 29.389 | 0.7452 | 6.918 | 10.933 | |
| GDRRN [39] | 29.277 | 0.7221 | 6.986 | 11.101 | |
| SSPSR [53] | 29.722 | 0.7663 | 6.307 | 10.511 | |
| MCNet [24] | 29.604 | 0.7556 | 6.832 | 10.623 | |
| ERCSR [25] | 29.602 | 0.7574 | 6.887 | 10.619 | |
| GELIN [54] | 29.643 | 0.7610 | 6.410 | 10.541 | |
| SRDNet [45] | 29.791 | 0.7719 | 6.107 | 10.457 | |
| MSSR [44] | 29.808 | 0.7745 | 5.600 | 10.383 | |
| MAHN | 29.820 | 0.7756 | 5.445 | 10.381 |
| S | Model | PSNR ↑ | SSIM ↑ | SAM ↓ | ERGAS ↓ |
|---|---|---|---|---|---|
| 2 | Bicubic | 32.539 | 0.9085 | 4.615 | 7.820 |
| 3D-FCNN [38] | 34.251 | 0.9370 | 4.075 | 6.536 | |
| GDRRN [39] | 33.755 | 0.9240 | 4.258 | 6.944 | |
| SSPSR [53] | 35.314 | 0.9475 | 3.983 | 5.884 | |
| MCNet [24] | 35.587 | 0.9506 | 3.749 | 5.656 | |
| ERCSR [25] | 35.612 | 0.9509 | 3.726 | 5.635 | |
| GELIN [54] | 35.647 | 0.9513 | 3.668 | 5.614 | |
| SRDNet [45] | 35.842 | 0.9522 | 3.695 | 5.573 | |
| MSSR [44] | 36.236 | 0.9552 | 3.629 | 5.373 | |
| MAHN | 36.313 | 0.9561 | 3.541 | 5.320 | |
| 3 | Bicubic | 29.223 | 0.8062 | 5.692 | 7.385 |
| 3D-FCNN [38] | 30.410 | 0.8554 | 5.223 | 6.518 | |
| GDRRN [39] | 30.121 | 0.8365 | 5.463 | 6.853 | |
| SSPSR [53] | - | - | - | - | |
| MCNet [24] | 31.165 | 0.8753 | 5.064 | 5.999 | |
| ERCSR [25] | 31.168 | 0.8754 | 5.057 | 5.986 | |
| GELIN [54] | 31.160 | 0.8753 | 4.917 | 6.002 | |
| SRDNet [45] | 31.347 | 0.8793 | 4.907 | 5.917 | |
| MSSR [44] | 31.547 | 0.8836 | 4.768 | 5.792 | |
| MAHN | 31.718 | 0.8878 | 4.671 | 5.685 | |
| 4 | Bicubic | 27.284 | 0.7053 | 6.313 | 6.791 |
| 3D-FCNN [38] | 28.080 | 0.7580 | 6.082 | 6.242 | |
| GDRRN [39] | 27.955 | 0.7410 | 6.153 | 6.212 | |
| SSPSR [53] | 28.845 | 0.7968 | 5.681 | 5.739 | |
| MCNet [24] | 28.649 | 0.7867 | 6.018 | 5.864 | |
| ERCSR [25] | 28.644 | 0.7869 | 6.073 | 5.860 | |
| GELIN [54] | 28.630 | 0.7848 | 5.814 | 5.878 | |
| SRDNet [45] | 28.786 | 0.7913 | 5.918 | 5.817 | |
| MSSR [44] | 28.724 | 0.7881 | 5.678 | 5.843 | |
| MAHN | 28.866 | 0.7964 | 5.555 | 5.763 |
| S | Model | PSNR ↑ | SSIM ↑ | SAM ↓ | ERGAS ↓ |
|---|---|---|---|---|---|
| 2 | Bicubic | 35.854 | 0.9149 | 3.680 | 7.826 |
| 3D-FCNN [38] | 36.594 | 0.9303 | 3.391 | 7.235 | |
| GDRRN [39] | 36.532 | 0.9296 | 3.427 | 7.300 | |
| SSPSR [53] | 37.311 | 0.9396 | 3.140 | 6.647 | |
| MCNet [24] | 37.720 | 0.9437 | 2.980 | 6.284 | |
| ERCSR [25] | 37.724 | 0.9436 | 2.966 | 6.280 | |
| GELIN [54] | 37.764 | 0.9444 | 2.913 | 6.253 | |
| SRDNet [45] | 37.896 | 0.9464 | 2.720 | 6.180 | |
| MSSR [44] | 38.087 | 0.9490 | 2.572 | 6.058 | |
| MAHN | 38.119 | 0.9491 | 2.548 | 6.030 | |
| 3 | Bicubic | 33.388 | 0.8561 | 4.873 | 6.624 |
| 3D-FCNN [38] | 34.120 | 0.8785 | 4.448 | 6.118 | |
| GDRRN [39] | 33.961 | 0.8762 | 4.523 | 6.235 | |
| SSPSR [53] | - | - | - | - | |
| MCNet [24] | 34.718 | 0.8903 | 4.165 | 5.668 | |
| ERCSR [25] | 34.766 | 0.8913 | 4.137 | 5.633 | |
| GELIN [54] | 34.785 | 0.8920 | 4.067 | 5.631 | |
| SRDNet [45] | 34.932 | 0.8963 | 3.789 | 5.546 | |
| MSSR [44] | 34.938 | 0.8971 | 3.699 | 5.544 | |
| MAHN | 35.004 | 0.8985 | 3.605 | 5.512 | |
| 4 | Bicubic | 31.931 | 0.8026 | 6.169 | 5.907 |
| 3D-FCNN [38] | 32.587 | 0.8283 | 5.618 | 5.485 | |
| GDRRN [39] | 32.489 | 0.8267 | 5.677 | 5.552 | |
| SSPSR [53] | 33.124 | 0.8460 | 4.967 | 5.150 | |
| MCNet [24] | 32.977 | 0.8395 | 5.374 | 5.218 | |
| ERCSR [25] | 32.996 | 0.8399 | 5.367 | 5.206 | |
| GELIN [54] | 33.040 | 0.8413 | 5.246 | 5.186 | |
| SRDNet [45] | 33.165 | 0.8471 | 4.935 | 5.119 | |
| MSSR [44] | 33.145 | 0.8468 | 4.808 | 5.133 | |
| MAHN | 33.162 | 0.8473 | 4.735 | 5.132 |
| Model | PSNR ↑ | Parameters (M) | GFLOPs | Inference Time/Per Frame (s) |
|---|---|---|---|---|
| SSPSR [53] | 33.790 | 11.1 | 90.29 | 0.0348 |
| MCNet [24] | 33.770 | 1.9 | 236.61 | 0.0162 |
| ERCSR [25] | 33.788 | 1.3 | 178.84 | 0.0088 |
| GELIN [54] | 33.921 | 26.7 | 563.65 | 0.1305 |
| SRDNet [45] | 34.186 | 1.7 | 92.29 | 0.0162 |
| MSSR [44] | 34.322 | 24.5 | 49.64 | 0.0116 |
| MAHN | 34.364 | 4.3 | 14.72 | 0.0136 |
| SBAM | SHCAM | SHSAM | SH3M | PSNR ↑ | SSIM ↑ | SAM ↓ | ERGAS ↓ |
|---|---|---|---|---|---|---|---|
| 34.107 | 0.9155 | 3.523 | 12.668 | ||||
| √ | √ | 34.156 | 0.9170 | 3.472 | 12.549 | ||
| √ | √ | 34.144 | 0.9167 | 3.480 | 12.600 | ||
| √ | √ | 34.174 | 0.9181 | 3.453 | 12.531 | ||
| √ | √ | √ | 34.235 | 0.9195 | 3.422 | 12.476 | |
| √ | √ | √ | 34.216 | 0.9189 | 3.441 | 12.503 | |
| √ | √ | √ | 34.271 | 0.9204 | 3.371 | 12.421 | |
| √ | √ | √ | 34.296 | 0.9211 | 3.356 | 12.356 | |
| √ | √ | √ | √ | 34.364 | 0.9217 | 3.195 | 12.218 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Sun, Y.; Hu, X.; Zhang, N.; Feng, H.; Li, Z.; Wang, Y. Multi-Attitude Hybrid Network for Remote Sensing Hyperspectral Images Super-Resolution. Remote Sens. 2025, 17, 1947. https://doi.org/10.3390/rs17111947
Chen C, Sun Y, Hu X, Zhang N, Feng H, Li Z, Wang Y. Multi-Attitude Hybrid Network for Remote Sensing Hyperspectral Images Super-Resolution. Remote Sensing. 2025; 17(11):1947. https://doi.org/10.3390/rs17111947
Chicago/Turabian StyleChen, Chi, Yunhan Sun, Xueyan Hu, Ning Zhang, Hao Feng, Zheng Li, and Yongcheng Wang. 2025. "Multi-Attitude Hybrid Network for Remote Sensing Hyperspectral Images Super-Resolution" Remote Sensing 17, no. 11: 1947. https://doi.org/10.3390/rs17111947
APA StyleChen, C., Sun, Y., Hu, X., Zhang, N., Feng, H., Li, Z., & Wang, Y. (2025). Multi-Attitude Hybrid Network for Remote Sensing Hyperspectral Images Super-Resolution. Remote Sensing, 17(11), 1947. https://doi.org/10.3390/rs17111947







