Estimation of Atmospheric Boundary Layer Turbulence Parameters over the South China Sea Based on Multi-Source Data
Abstract
1. Introduction
2. Instrumentation and Data
2.1. Site Description
2.2. Instrumentation and Overview of the Data
3. Principle of Measurement and Methods
3.1. Principle of Measurement
3.2. Tatarski Model
3.3. Estimating Atmospheric Turbulence Parameters
3.4. Estimation of Near-Surface Based on CSAT3
4. Results and Discussion
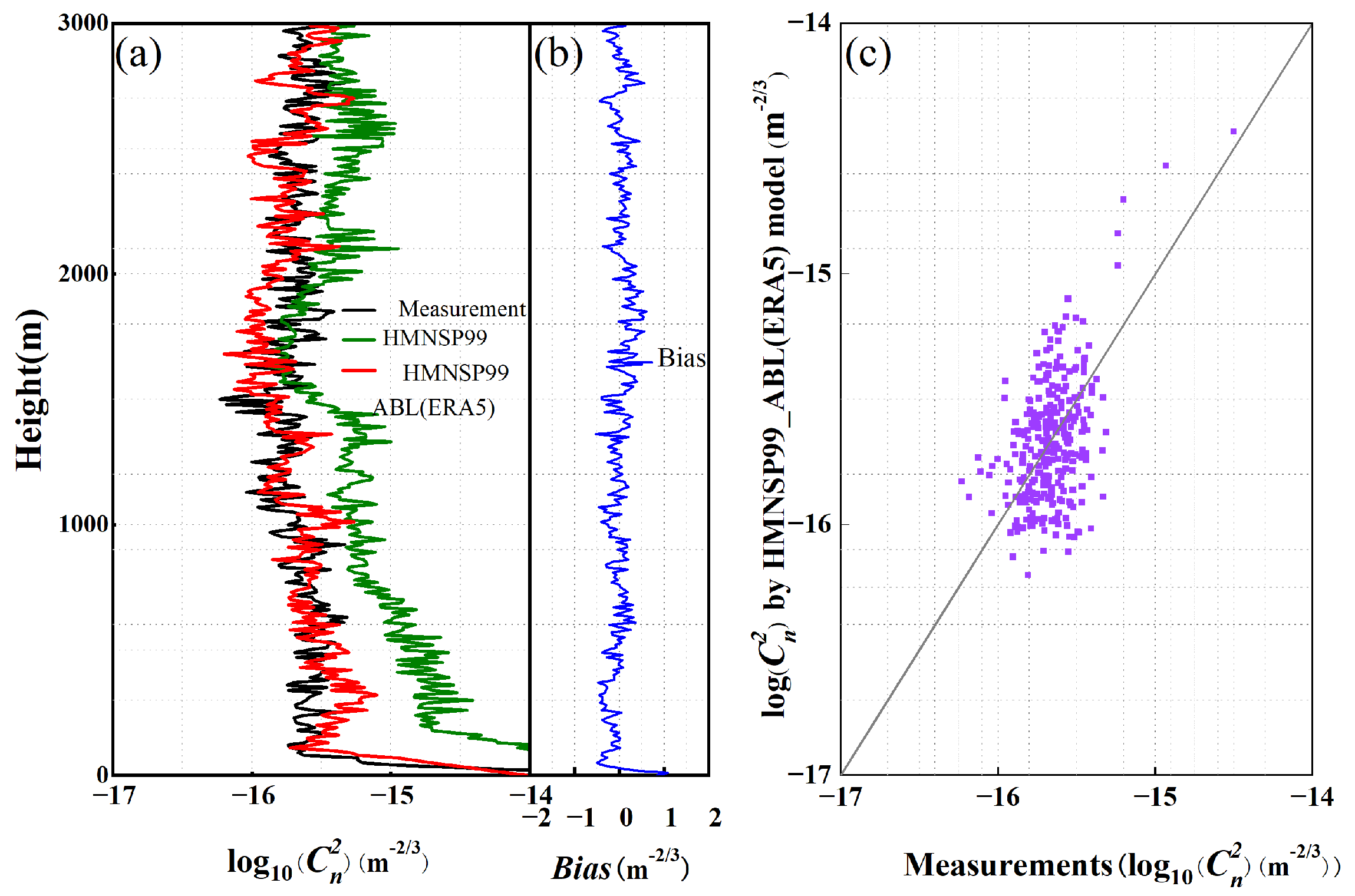
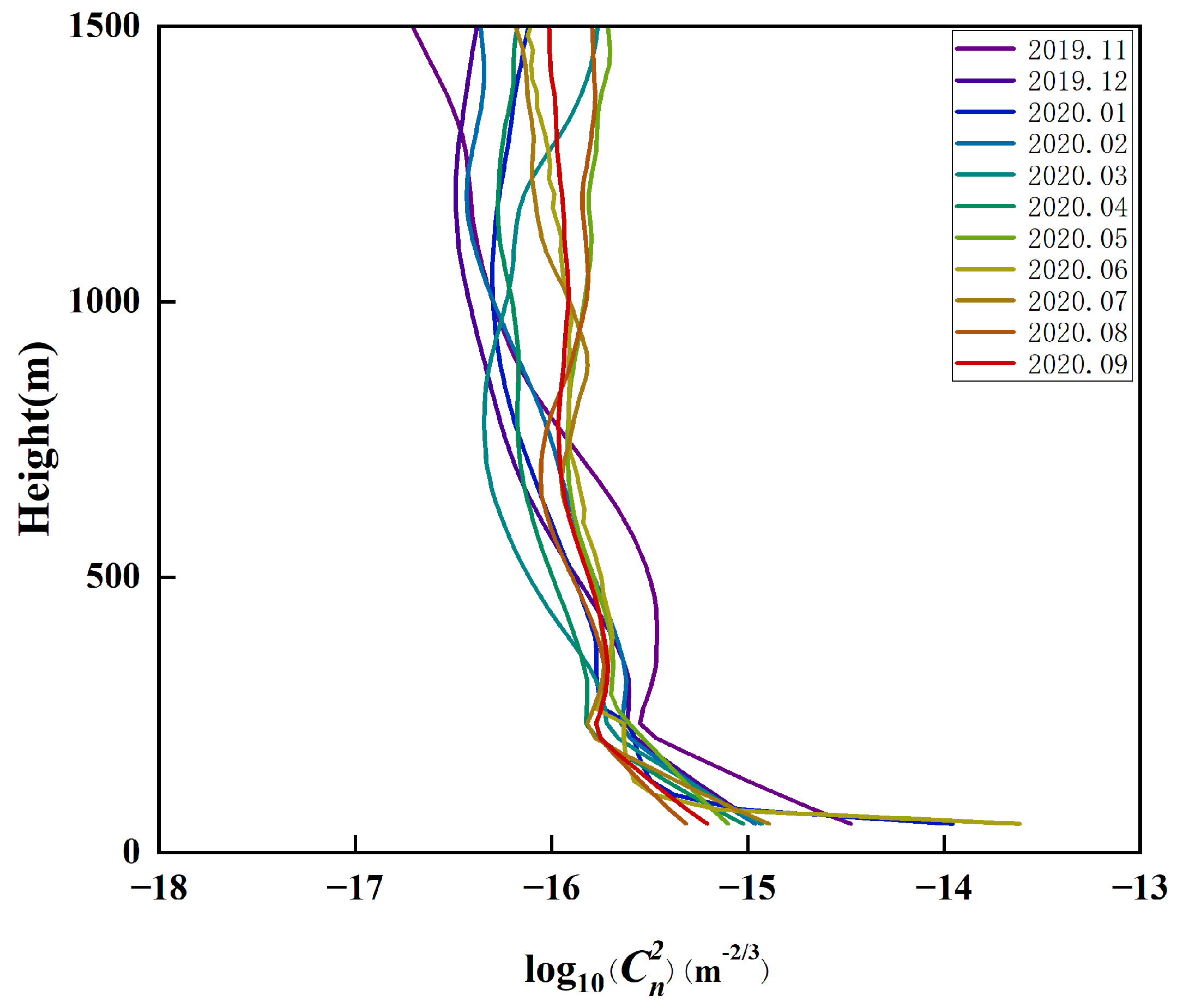
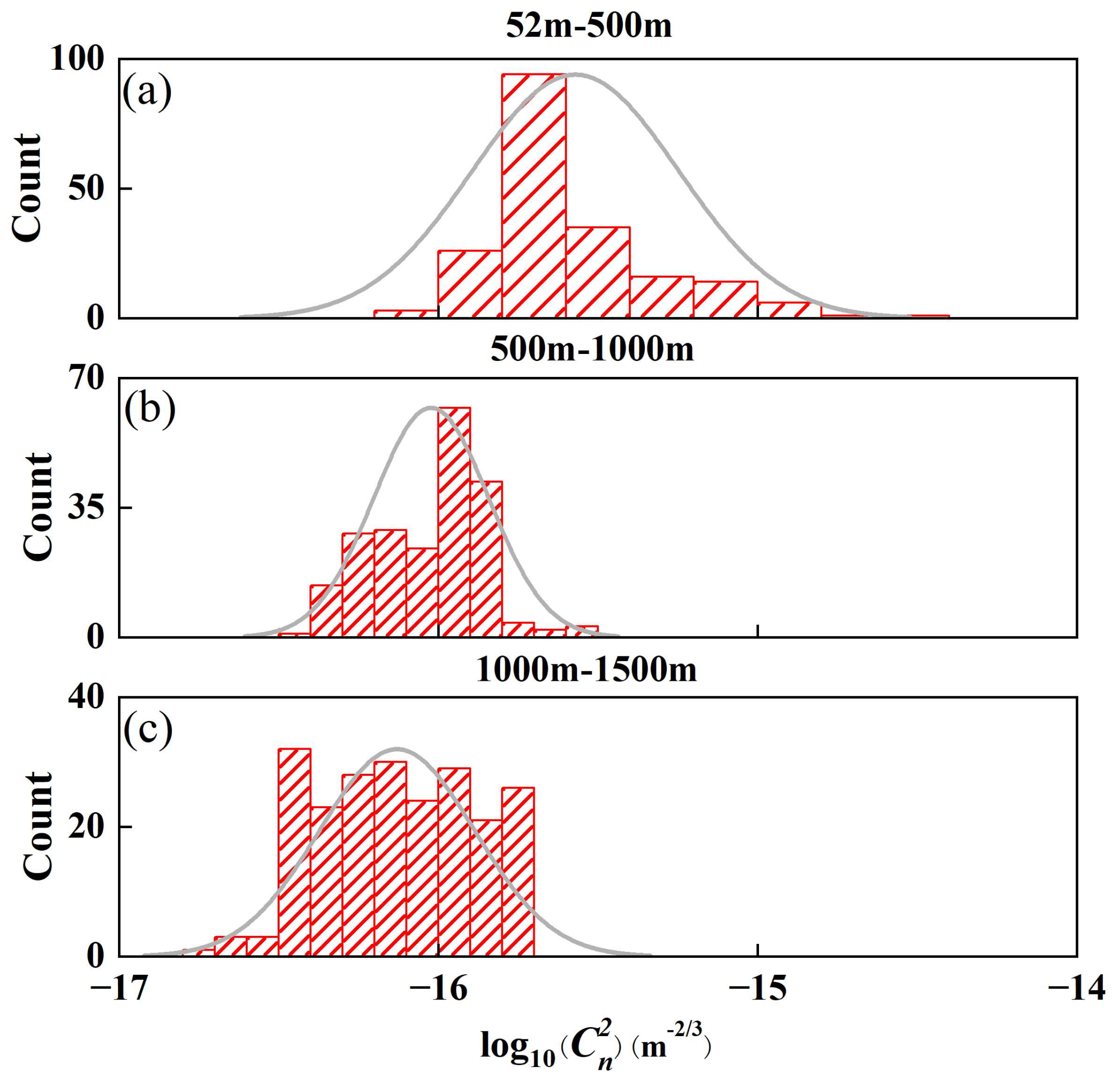
4.1. New Statistical Model of the Marine Atmospheric Boundary Layer
4.2. Error Analysis
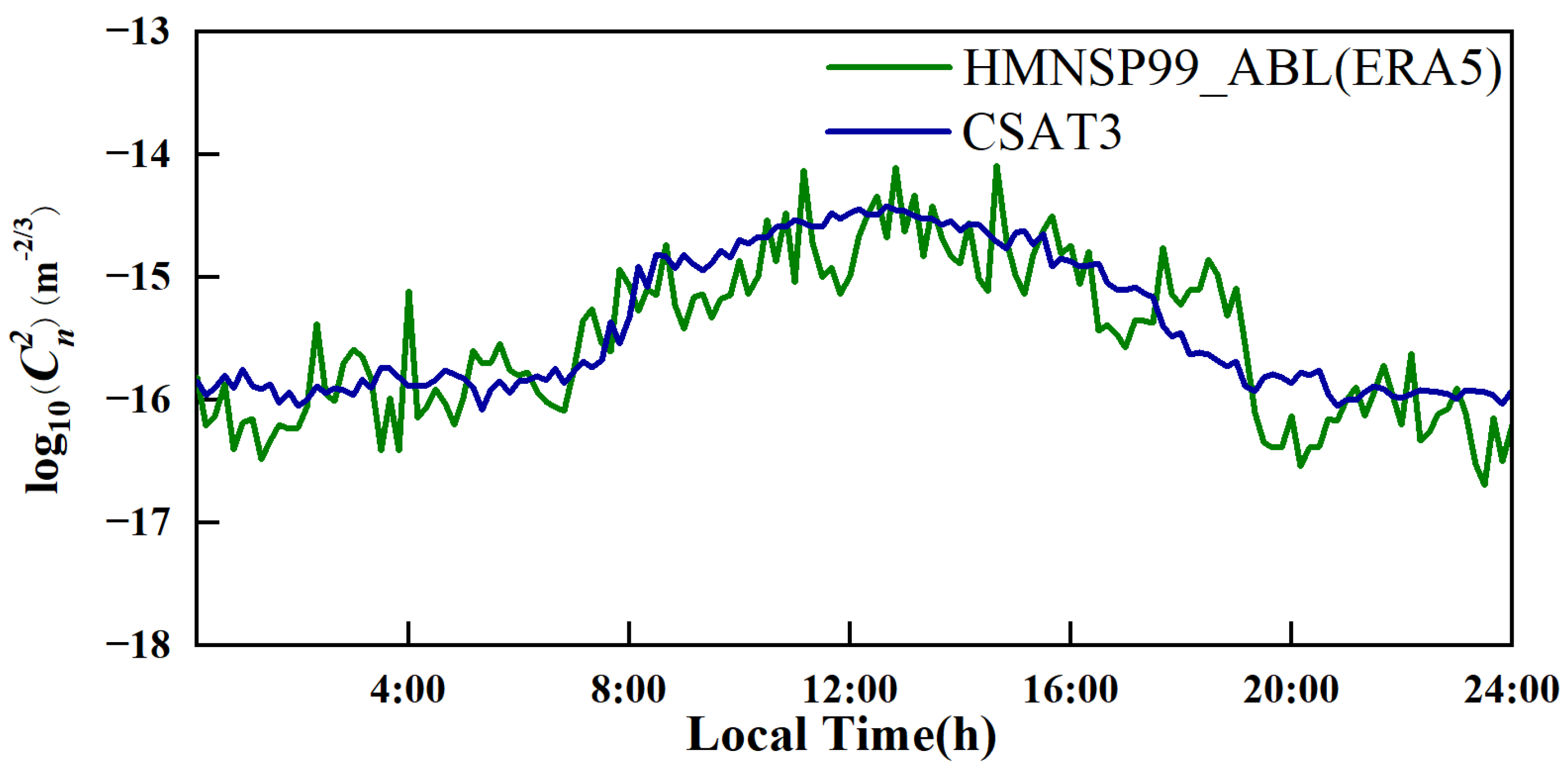
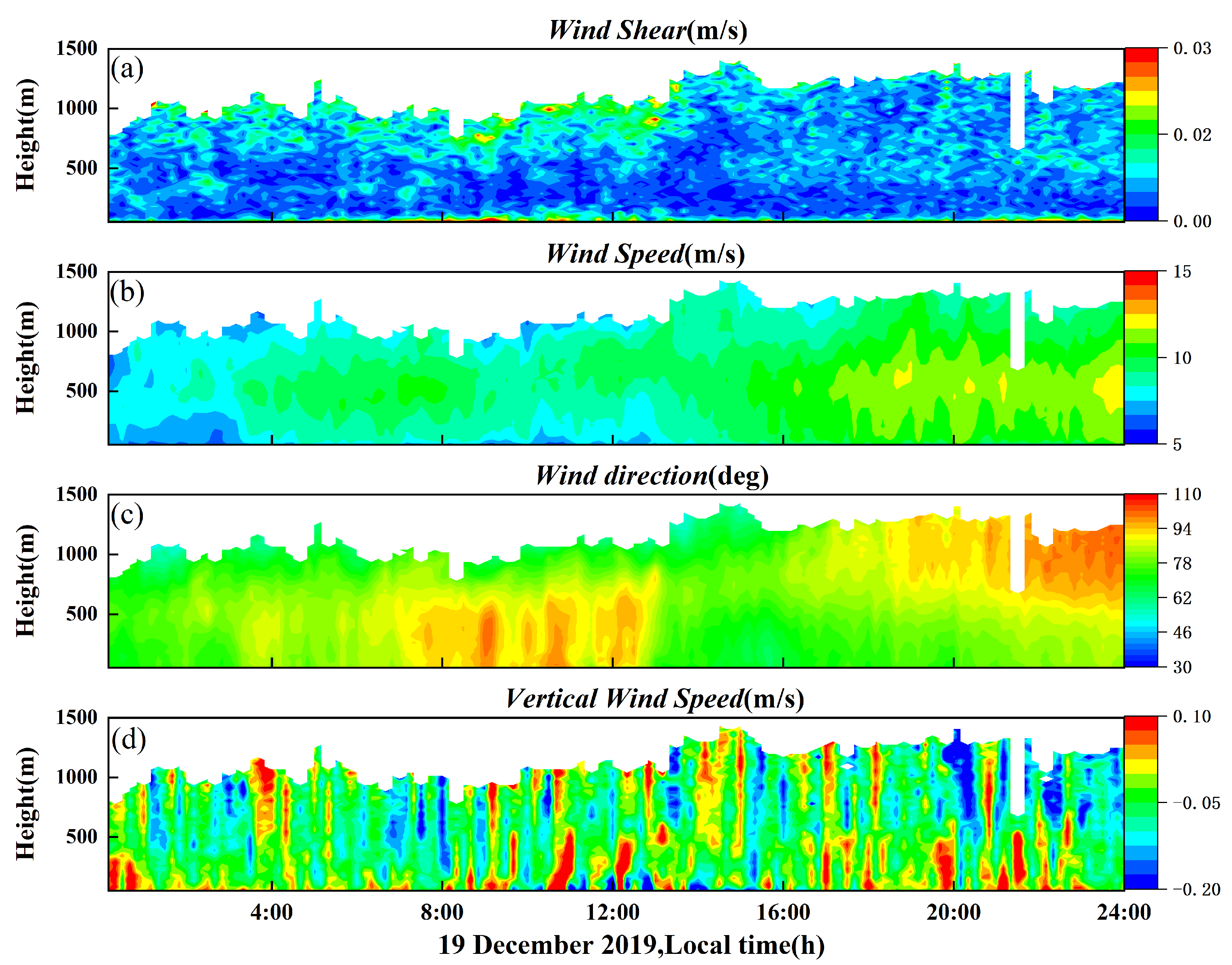
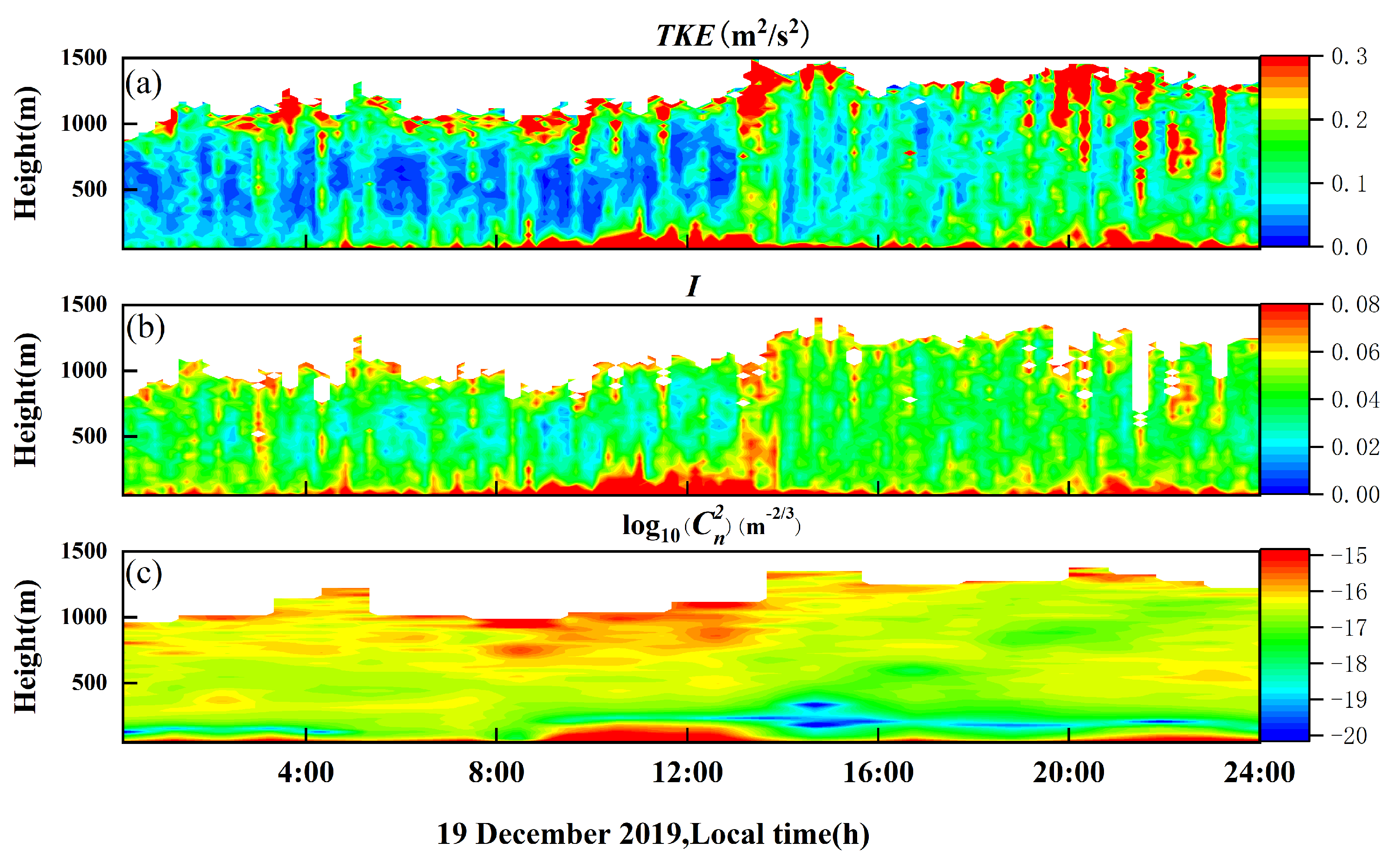
4.3. Characteristics of Turbulent Parameters in the MABL by Combining CDWL and HMNSP99_ABL (ERA5) Models
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABL | Atmospheric boundary layer |
| SCS | South China Sea |
| Atmospheric refractive index structure constant | |
| CDWL | Coherent Doppler wind lidar |
| MOST | Monin–Obukohov Similarity Theory |
| AIOFM | Anhui Institute of Optics and Fine Mechanics |
| ECMWF | European Center for Medium-Range Weather Forecasts |
| BLH | Boundary layer height |
| TKE | Turbulent kinetic energy |
| I | Turbulence intensity |
| RMSE | Root mean square error |
| MRE | Mean relative error |
| MABL | Marine atmospheric boundary layer |
| SNR | Signal-to-noise ratio |
References
- Tatarski, V.I. Wave Propagation in a Turbulent Medium; McGraw-Hill: New York, NY, USA, 1961; Volume 14, 285p. [Google Scholar] [CrossRef]
- Good, R.E.; Beland, R.R.; Murphy, E.A.; Brown, J.H.; Dewan, E.M. Atmospheric Models Of Optical Turbulence. Proc. SPIE 1988, 928, 165–186. [Google Scholar]
- Ata, Y.; Baykal, Y.; Gke, M.C. Average channel capacity in anisotropic atmospheric non-Kolmogorov turbulent medium. Opt. Commun. 2019, 451, 129–135. [Google Scholar] [CrossRef]
- Kim, S.H.; Chun, H.Y.; Lee, D.B.; Kim, J.H.; Sharman, R.D. Improving Numerical Weather Prediction-Based Near-Cloud Aviation Turbulence Forecasts by Diagnosing Convective Gravity Wave Breaking. Weather Forecast. 2021, 36, 1735–1757. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, H.S.; Wei, W.; Wu, B.G.; Cai, X.H.; Song, Y. Effects of turbulence structure and urbanization on the heavy haze pollution process. Atmos. Chem. Phys. 2019, 19, 1041–1057. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, H.S.; Wei, W.; Cai, X.H.; Song, Y.; Kang, L. A study on atmospheric turbulence structure and intermittency during heavy haze pollution in the Beijing area. Sci. China Earth Sci. 2019, 62, 2058–2068. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, J.; Qiao, J.; Wang, S. Relationship of atmospheric boundary layer depth with thermodynamic processes at the land surface in arid regions of China. Sci. China Earth Sci. 2011, 54, 1586–1594. [Google Scholar] [CrossRef]
- Bi, C.C.; Qing, C.; Wu, P.F.; Jin, X.M.; Liu, Q.; Qian, X.M.; Zhu, W.Y.; Weng, N.Q. Optical Turbulence Profile in Marine Environment with Artificial Neural Network Model. Remote Sens. 2022, 14, 2267. [Google Scholar] [CrossRef]
- Eaton, F.D. Recent developments of optical turbulence measurement techniques (Invited Paper). Proc. SPIE 2005, 5793. [Google Scholar]
- Shelekhov, A.; Afanasiev, A.; Shelekhova, E.; Kobzev, A.; Tel’minov, A.; Molchunov, A.; Poplevina, O. High-Resolution Profiling of Atmospheric Turbulence Using UAV Autopilot Data. Drones 2023, 7, 412. [Google Scholar] [CrossRef]
- Qian, X.; Yao, Y.Q.; Zou, L.; Wang, H.S.; Li, J.W. Optical turbulence in the atmospheric surface layer at the Ali Observatory, Tibet. Mon. Not. R. Astron. Soc. 2022, 510, 5179–5186. [Google Scholar] [CrossRef]
- Hufnagel, R.E.; Stanley, N.R. Modulation transfer function associated with image transmission through turbulent media. J. Opt. Soc. Am. 1964, 54, 52. [Google Scholar] [CrossRef]
- Thorpe, S.A. Turbulence and Mixing in a Scottish Loch. Philos. Trans. R. Soc. A 1977, 286. [Google Scholar]
- Banakh, V.A.; Smalikho, I.N.; Falits, A.V.; Sherstobitov, A.M. Estimating the Parameters of Wind Turbulence from Spectra of Radial Velocity Measured by a Pulsed Doppler Lidar. Remote Sens. 2021, 13, 2071. [Google Scholar] [CrossRef]
- Smalikho, I.N.; Banakh, V.A. Effect of Wind Transport of Turbulent Inhomogeneities on Estimation of the Turbulence Energy Dissipation Rate from Measurements by a Conically Scanning Coherent Doppler Lidar. Remote Sens. 2020, 12, 2802. [Google Scholar] [CrossRef]
- Yuan, J.; Xia, H.; Wei, T.; Wang, L.; Wu, Y. Identifying cloud, precipitation, windshear, and turbulence by deep analysis of the power spectrum of coherent Doppler wind lidar. Opt. Express 2020, 28, 37406. [Google Scholar] [CrossRef]
- Wang, C.; Jia, M.J.; Xia, H.Y.; Wu, Y.B.; Wei, T.W.; Shang, X.; Yang, C.Y.; Xue, X.H.; Dou, X.K. Relationship analysis of PM2.5 and boundary layer height using an aerosol and turbulence detection lidar. Atmos. Meas. Tech. 2019, 12, 3303–3315. [Google Scholar] [CrossRef]
- Zhang, H.J.; Zhu, L.M.; Sun, G.; Zhang, K.; Xu, M.M.; Liu, N.A.; Chen, D.L.; Wu, Y.; Cui, S.C.; Luo, T.; et al. Estimation and characterization of the refractive index structure constant within the marine atmospheric boundary layer. Appl. Opt. 2022, 61, 9762–9772. [Google Scholar] [CrossRef]
- Zhu, L.; Sun, G.; Zhang, H.; Xu, M.; Chen, D.; Shao, S.; Wu, P.; Li, X. Study on High Resolution Optical Turbulence Estimation Model of Marine Atmospheric Boundary Layer Using Lidar. Acta Opt. Sin. 2022, 42, 1201004. [Google Scholar]
- Jiang, P.; Yuan, J.L.; Wu, K.N.; Wang, L.; Xia, H.Y. Turbulence Detection in the Atmospheric Boundary Layer Using Coherent Doppler Wind Lidar and Microwave Radiometer. Remote Sens. 2022, 14, 2951. [Google Scholar] [CrossRef]
- Qing, H.Y.; Zhang, Y.N.; Zhou, C.; Zhao, Z.Y.; Chen, G. Atmospheric temperature profiles estimated by the vertical wind speed observed by MST radar. Acta Phys. Sin. 2014, 63, 094301. [Google Scholar] [CrossRef]
- Xu, M.M.; Zhou, L.P.; Shao, S.Y.; Weng, N.Q.; Liu, Q. Analyzing the Effects of a Basin on Atmospheric Environment Relevant to Optical Turbulence. Photonics 2022, 9, 235. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, K.; Sun, G.; Liu, Q.; Li, X.; Luo, T. Study of the Model through the New Dimensionless Temperature Structure Function near the Sea Surface in the South China Sea. Remote Sens. 2023, 15, 631. [Google Scholar] [CrossRef]
- Liu, N.; Luo, T.; Han, Y.; Yang, K.; Wu, Y.; Zhang, K.; Weng, N.; Li, X. Influence of Typhoon Peripheral Circulation on the Atmospheric Boundary Layer Structure in Coastal Areas. Acta Opt. Sin. 2021, 41, 041. [Google Scholar]
- Kuo, C.L. Assessments of Ali, Dome A, and Summit Camp for mm-wave Observations Using MERRA-2 Reanalysis. Astrophys. J. 2017, 848, 64. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Jpn. 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.R.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.Y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Kolmogoroff, A. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. C. R. Acad. Sci. URSS 1941, 30, 301–305. [Google Scholar]
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef]
- Coulman, C.E.; Vernin, J.; Coqueugniot, Y.; Caccia, J.L. Outer scale of turbulence appropriate to modeling refractive-index structure profiles. Appl. Opt. 1988, 27, 155–160. [Google Scholar] [CrossRef]
- Masciadri, E.; Vernin, J.; Bougeault, P. 3D mapping of optical turbulence using an atmospheric numerical model I. A useful tool for the ground-based astronomy. Astron. Astrophys. Suppl. Ser. 1999, 137, 185–202. [Google Scholar] [CrossRef]
- Chowdhuri, S.; Banerjee, T. Quantifying small-scale anisotropy in turbulent flows. Phys. Rev. Fluids 2024, 9, 074604. [Google Scholar] [CrossRef]
- Dewan, E.M.; Good, R.E.; Beland, R.; Brown, J. A Model for Cn2(Optical Turbulence) Profiles Using Radiosonde Data, Directorate of Geophysics, Air Force Materiel Command. 1993.
- Ruggiero, F.H.; DeBenedictis, D.A. Forecasting optical turbulence from mesoscale numerical weather prediction models. In Proceedings of the DoD High Performance Modernization Program Users Group Conference, Austin, TX, USA, 2007; pp. 10–14. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Meteorological Press: Beijing, China, 1991. [Google Scholar]
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the ground layer of the atmosphere. Dokl. Akad. Nauk SSSR 1954, 24, 163–187. [Google Scholar]
- Foken, T. 50 Years of the Monin–Obukhov Similarity Theory. Bound.-Layer Meteorol. 2006, 119, 431–447. [Google Scholar] [CrossRef]
- Hill, R.J.; Ochs, G.R.; Wilson, J.J. Measuring surface-layer fluxes of heat and momentum using optical scintillation. Bound.-Layer Meteorol. 1992, 58, 391–408. [Google Scholar] [CrossRef]
- Wyngaard, J.C. On surface layer turbulence. In Workshop on Micrometeorology; American Meteorological Society: Boston, MA, USA, 1973. [Google Scholar]
- Yang, Q.K.; Wu, X.Q.; Luo, T.; Qing, C.; Yuan, R.M.; Su, C.D.; Xu, C.S.; Wu, Y.; Ma, X.B.; Wang, Z.Y. Forecasting surface-layer optical turbulence above the Tibetan Plateau using the WRF model. Opt. Laser Technol. 2022, 153, 108217. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, J.; Lu, S. From the classic theory of turbulence to the nonequilibrium thermodynamic theory of atmospheric turbulence. Plateau Meteorol. 2012, 31, 1–27. [Google Scholar]
- Turchi, A.; Masciadri, E.; Lascaux, F.; Fini, L. Optical turbulence forecast: Ready for an operational application. Mon. Not. R. Astron. Soc. 2016, 466, 520–539. [Google Scholar]
- Wu, S.; Wu, X.; Su, C.; Yang, Q.; Qing, C. A reliable model to estimate the profile of the refractive index structure parameter () and integrated astroclimatic parameters in the atmosphere. Opt. Express 2021, 29, 12454–12470. [Google Scholar] [CrossRef]
- Masciadri, E.; Vernin, J.; Bougeault, P. 3D mapping of optical turbulence using an atmospheric numerical model—II. First results at Cerro Paranal. Astron. Astrophys. Suppl. Ser. 1999, 137, 203–216. [Google Scholar] [CrossRef]
- Jin, X.; Song, X.; Yang, Y.; Wang, M.; Shao, S.; Zheng, H. Estimation of turbulence parameters in atmospheric boundary layer based on Doppler lidar. Opt. Express 2022, 30, 13263–13277. [Google Scholar]
- Wang, L.; Yuan, J.L.; Xia, H.Y.; Zhao, L.J.; Wu, Y.B. Marine Mixed Layer Height Detection Using Ship-Borne Coherent Doppler Wind Lidar Based on Constant Turbulence Threshold. Remote Sens. 2022, 14, 745. [Google Scholar] [CrossRef]




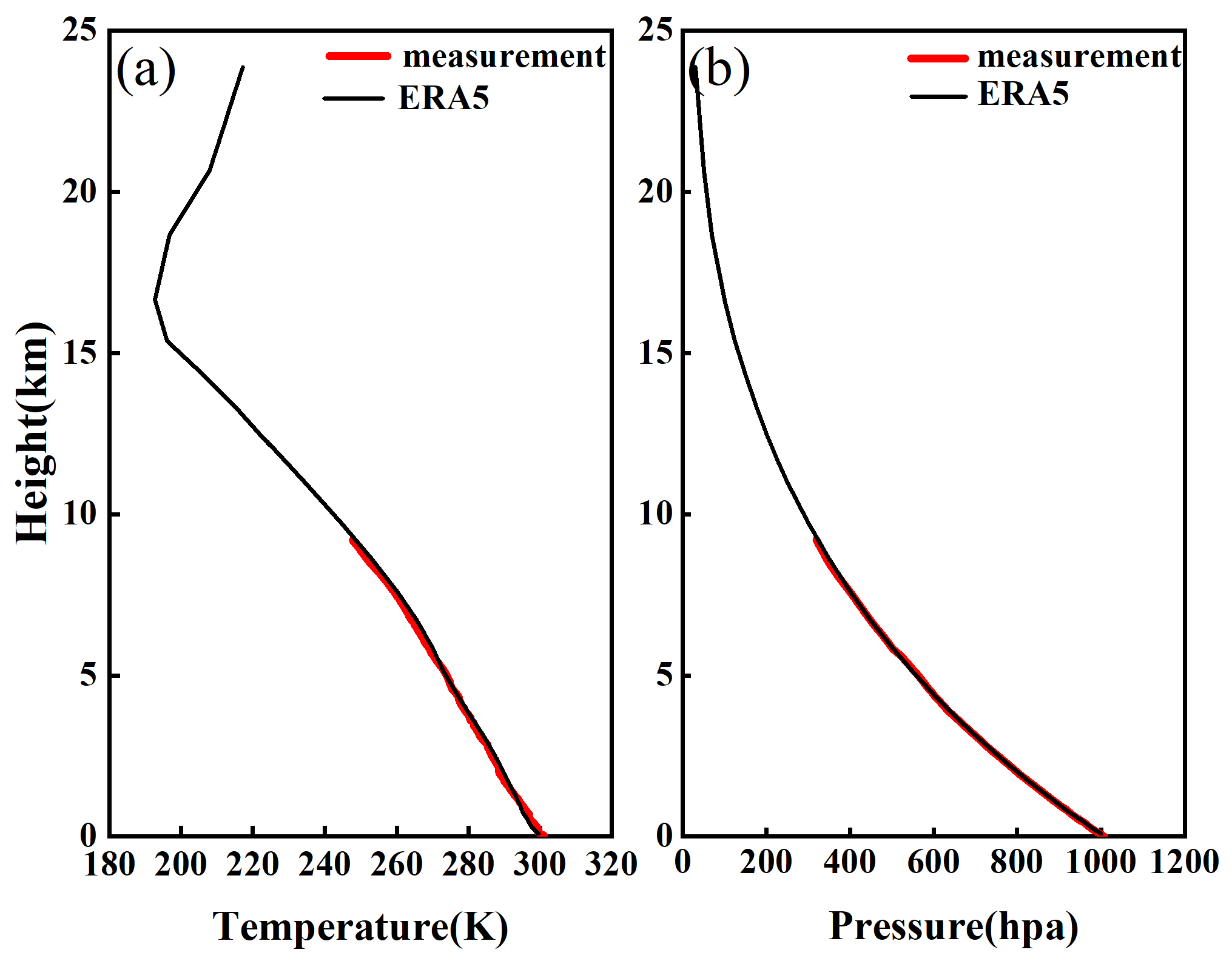
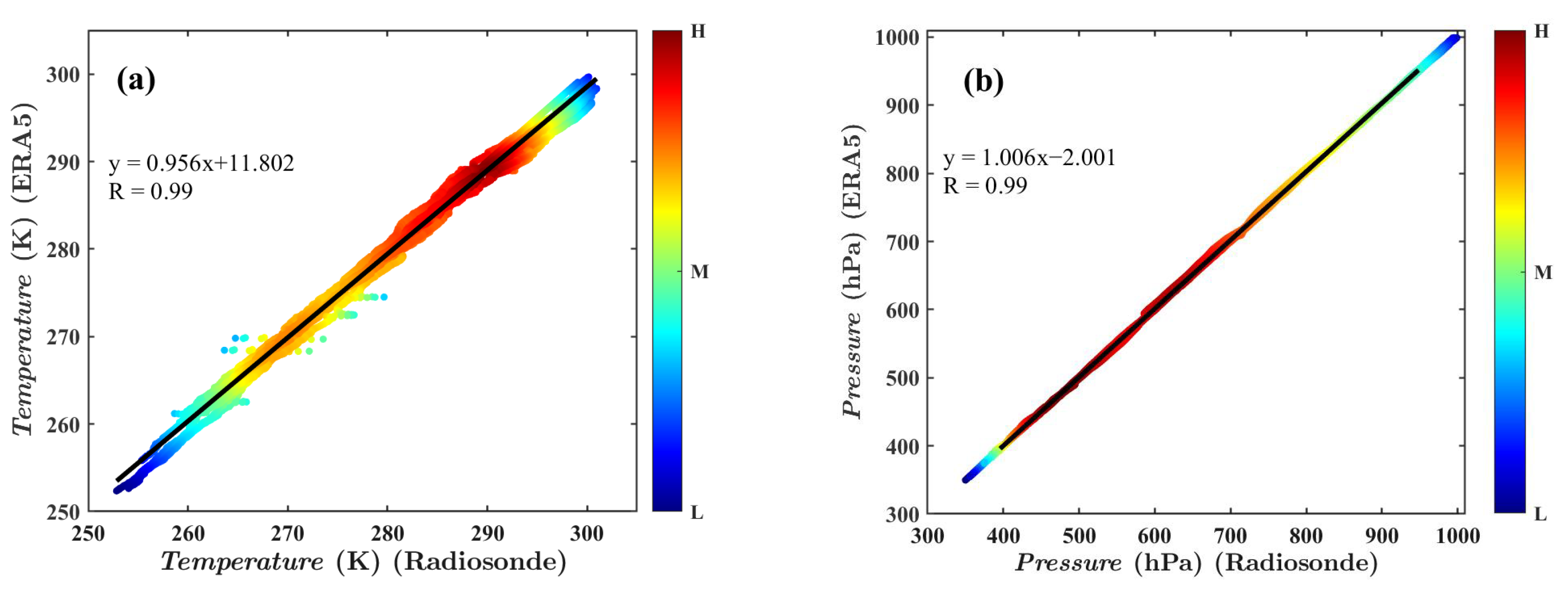
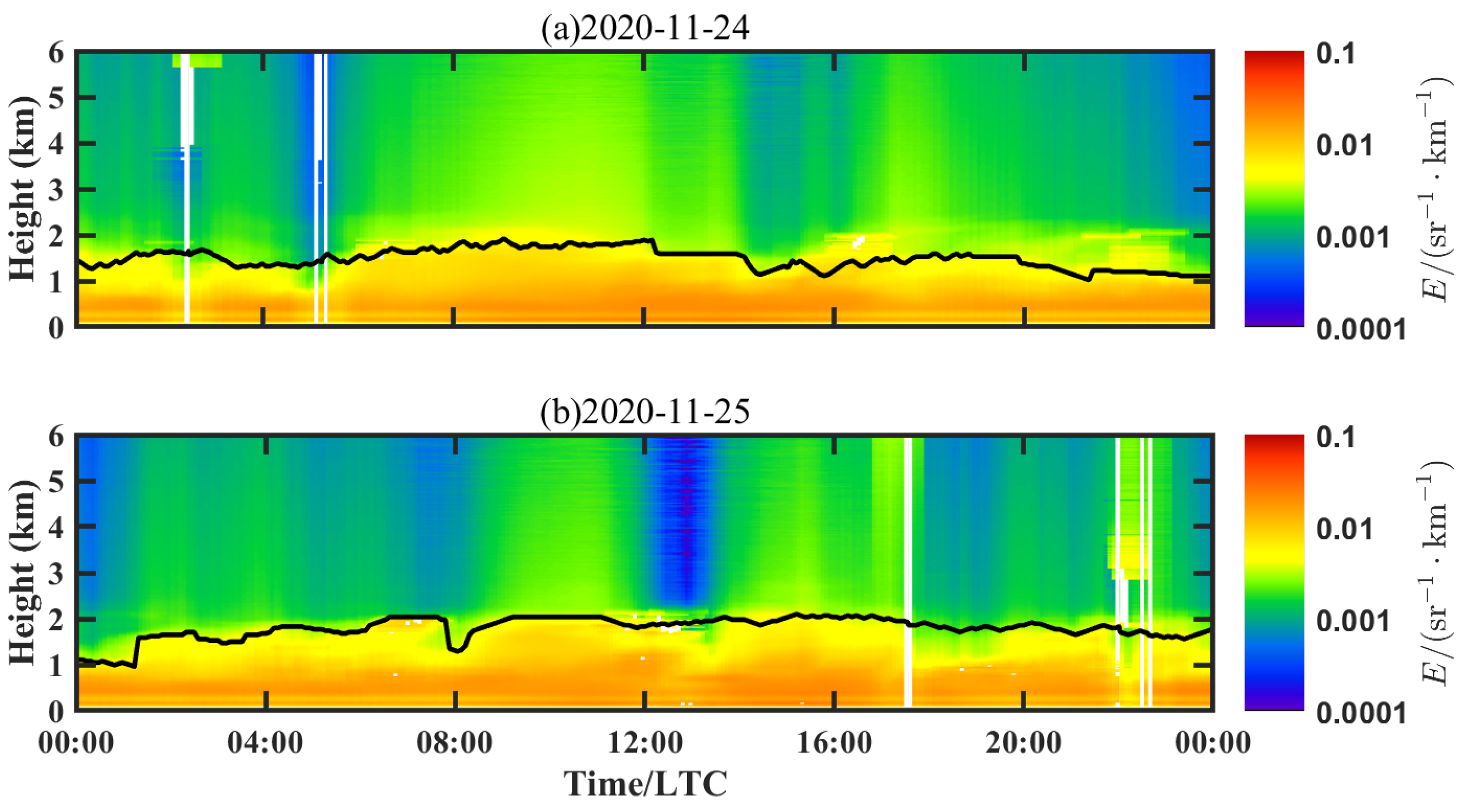
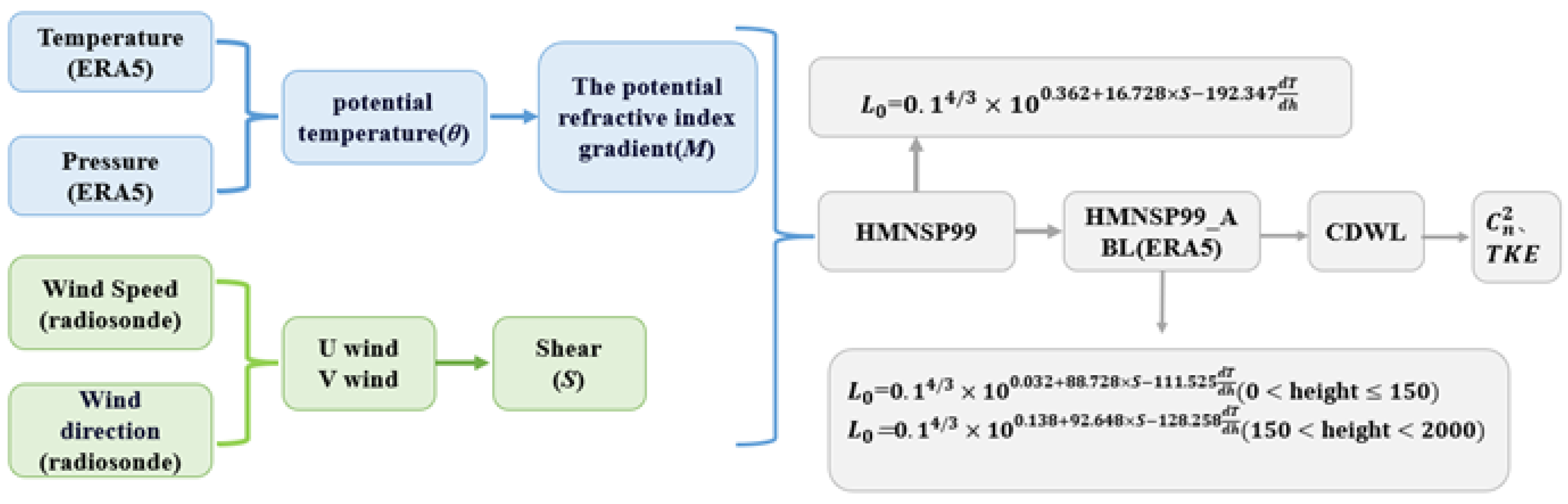


| Technical Specification | Parameters |
|---|---|
| Wavelength | 1550 nm |
| Pulse width | 100–400 ns |
| Single-pulse energy | ≥150 J |
| Radial detection range | 0–75 m/s |
| Speed measurement accuracy | <±0.1 m/s |
| Radial detection range | 50–6000 m |
| Balloon Number | Experimental Date | Release Time (LT) | Terminal Time (LT) | Ultimate Altitude (m) |
|---|---|---|---|---|
| 1 | 2020/10/17 | 15:56 | 17:30 | 15,620 |
| 2 | 2020/10/17 | 22:04 | 23:49 | 23,905 |
| 3 | 2020/10/18 | 18:29 | 20:16 | 30,968 |
| 4 | 2020/10/23 | 08:43 | 10:17 | 30,766 |
| 5 | 2020/10/25 | 08:52 | 10:32 | 31,702 |
| 6 | 2020/10/26 | 08:40 | 10:27 | 31,290 |
| 7 | 2020/11/02 | 19:23 | 21:33 | 31,690 |
| 8 | 2020/11/03 | 16:29 | 18:00 | 29,878 |
| 9 | 2020/11/04 | 16:53 | 18:34 | 28,797 |
| 10 | 2020/11/04 | 20:24 | 21:28 | 19,210 |
| 11 | 2020/11/12 | 16:27 | 17:59 | 30,030 |
| 12 | 2020/11/12 | 19:20 | 20:49 | 28,992 |
| RMSE | MRE | Bias | |
|---|---|---|---|
| 0.67 | 0.92 | 0.59 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Luo, T.; Yang, K.; Zhang, H.; Zhu, L.; Shao, S.; Cui, S.; Li, X.; Weng, N. Estimation of Atmospheric Boundary Layer Turbulence Parameters over the South China Sea Based on Multi-Source Data. Remote Sens. 2025, 17, 1929. https://doi.org/10.3390/rs17111929
Liu Y, Luo T, Yang K, Zhang H, Zhu L, Shao S, Cui S, Li X, Weng N. Estimation of Atmospheric Boundary Layer Turbulence Parameters over the South China Sea Based on Multi-Source Data. Remote Sensing. 2025; 17(11):1929. https://doi.org/10.3390/rs17111929
Chicago/Turabian StyleLiu, Ying, Tao Luo, Kaixuan Yang, Hanjiu Zhang, Liming Zhu, Shiyong Shao, Shengcheng Cui, Xuebing Li, and Ningquan Weng. 2025. "Estimation of Atmospheric Boundary Layer Turbulence Parameters over the South China Sea Based on Multi-Source Data" Remote Sensing 17, no. 11: 1929. https://doi.org/10.3390/rs17111929
APA StyleLiu, Y., Luo, T., Yang, K., Zhang, H., Zhu, L., Shao, S., Cui, S., Li, X., & Weng, N. (2025). Estimation of Atmospheric Boundary Layer Turbulence Parameters over the South China Sea Based on Multi-Source Data. Remote Sensing, 17(11), 1929. https://doi.org/10.3390/rs17111929









