Multi-Sensor Fusion and Machine Learning for Forest Age Mapping in Southeastern Tibet
Abstract
1. Introduction
2. Materials and Methods
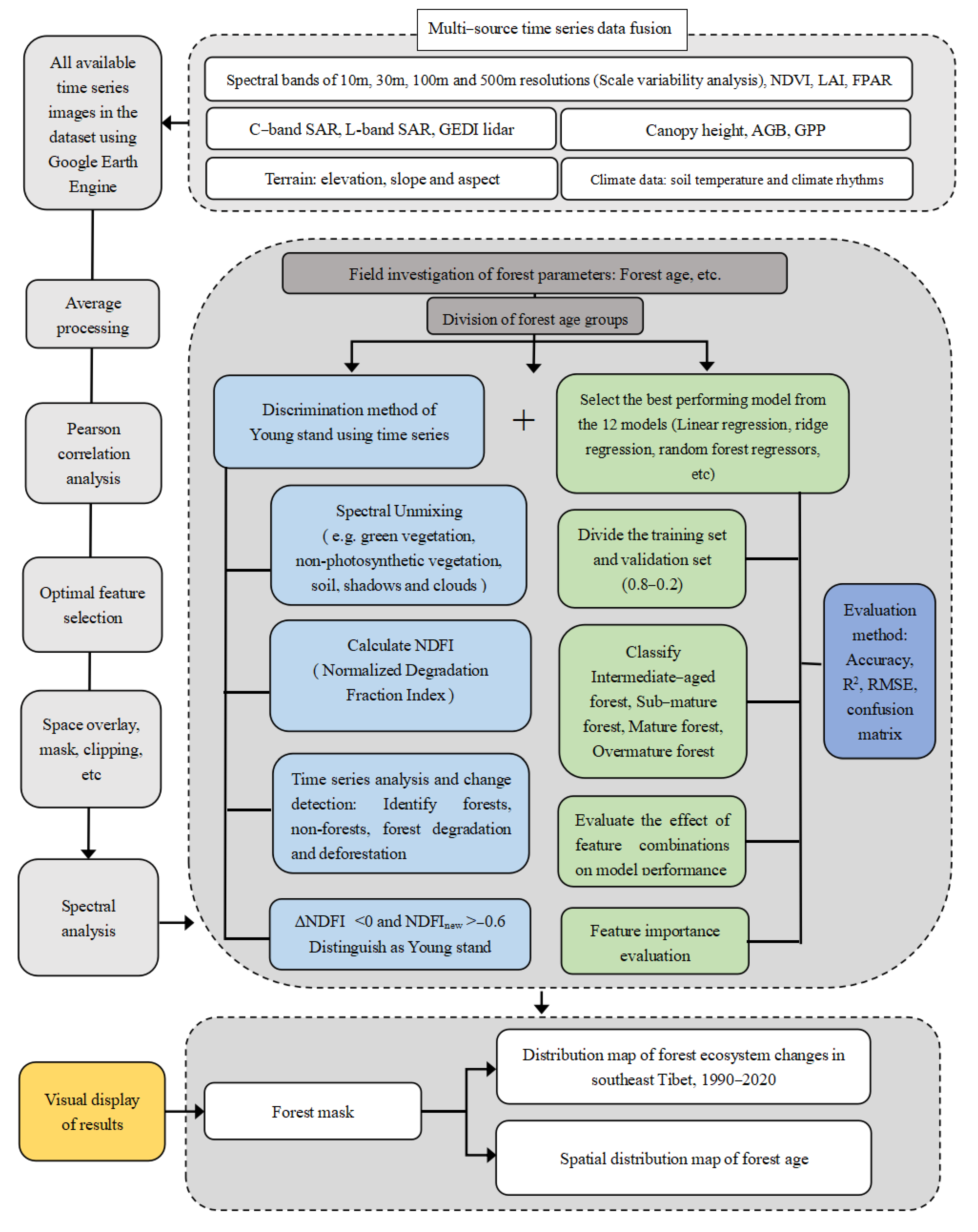
2.1. Research Strategy
- Data Collection
- Data Fusion and Preprocessing
- Field Surveys and Target Analysis
- Model Selection and Evaluation
- Detailed Classification Using the CODED Algorithm
- Feature Combination and Model Performance Analysis
- Results Visualization and Systematic Evaluation
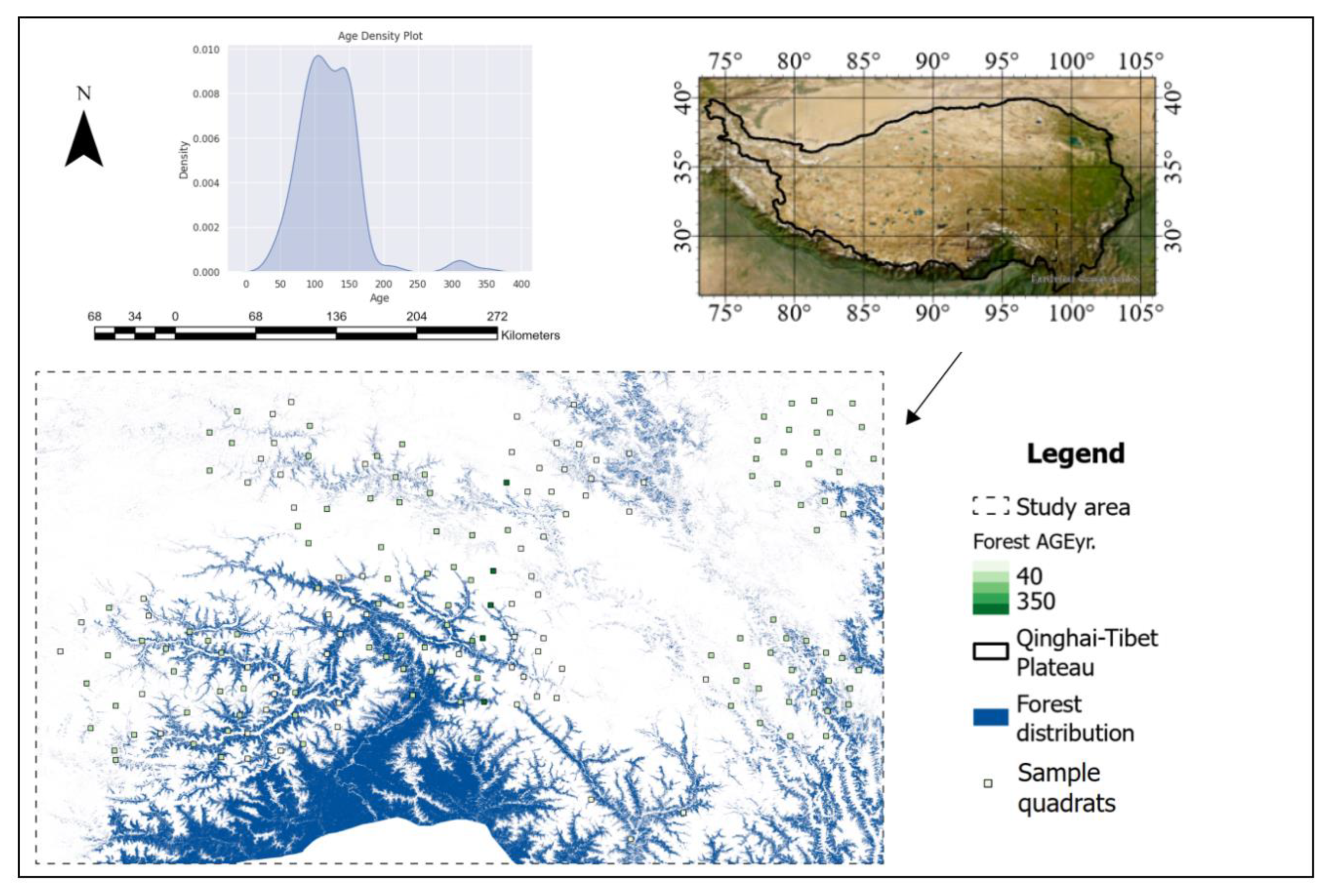
2.2. Research Area
2.3. Field Data and Forest Age Groups
2.4. Multi-Source Time-Series Remote-Sensing Data Fusion
- Spectroscopy, vegetation indices, and ecological remote-sensing product data:
- LiDAR forest structure and biomass data
- Climate and Soil Data
- SAR Data
- Topographic data:
2.5. Forest Change Detection and Age Identification
- Change Detection
- Classification of Disturbances
- Age Inference
2.6. Model Selection and Evaluation
2.7. Methods of Evaluation
3. Results
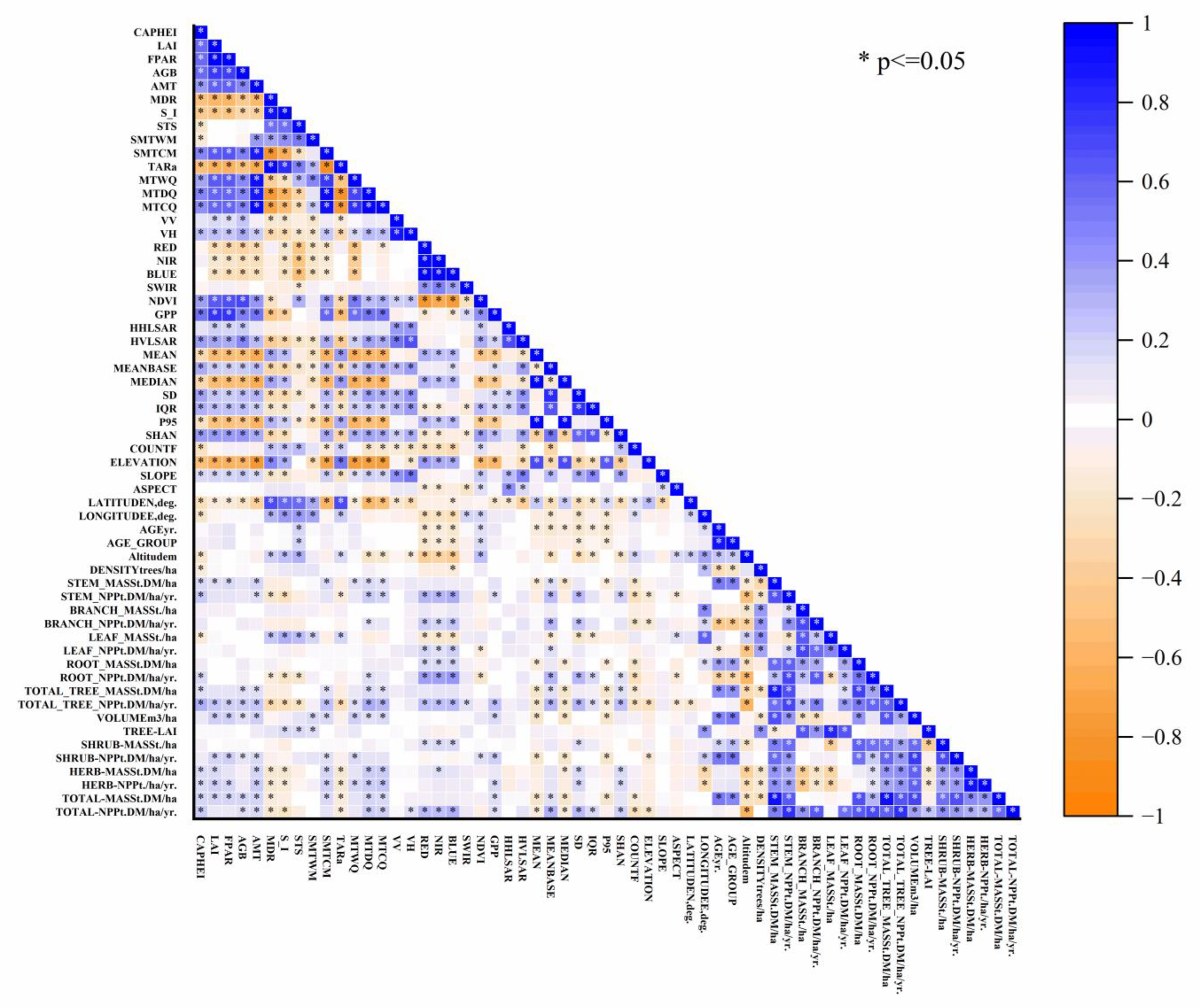
3.1. Correlation Analysis of Forest Age with Biomass and Ecological Variables
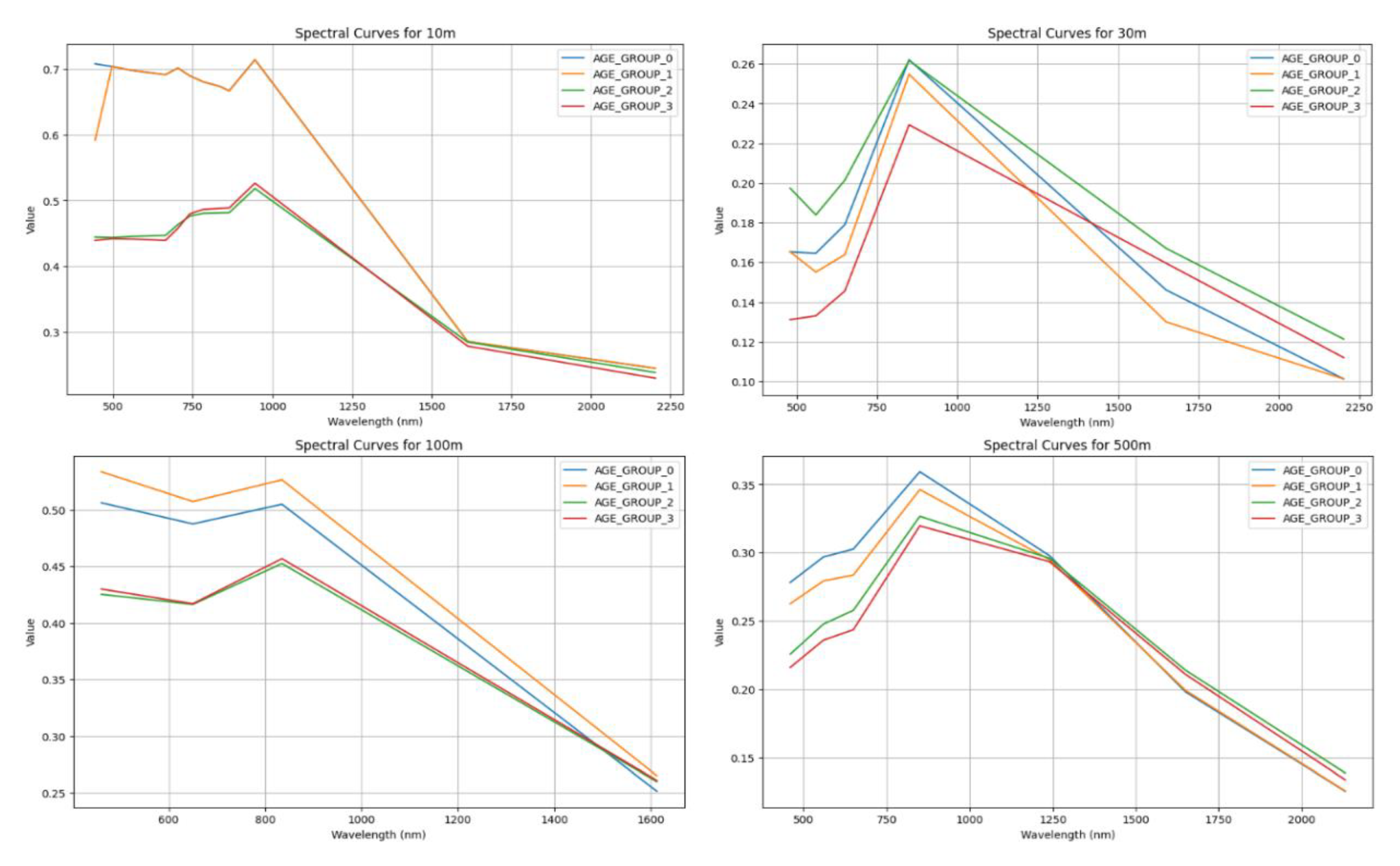
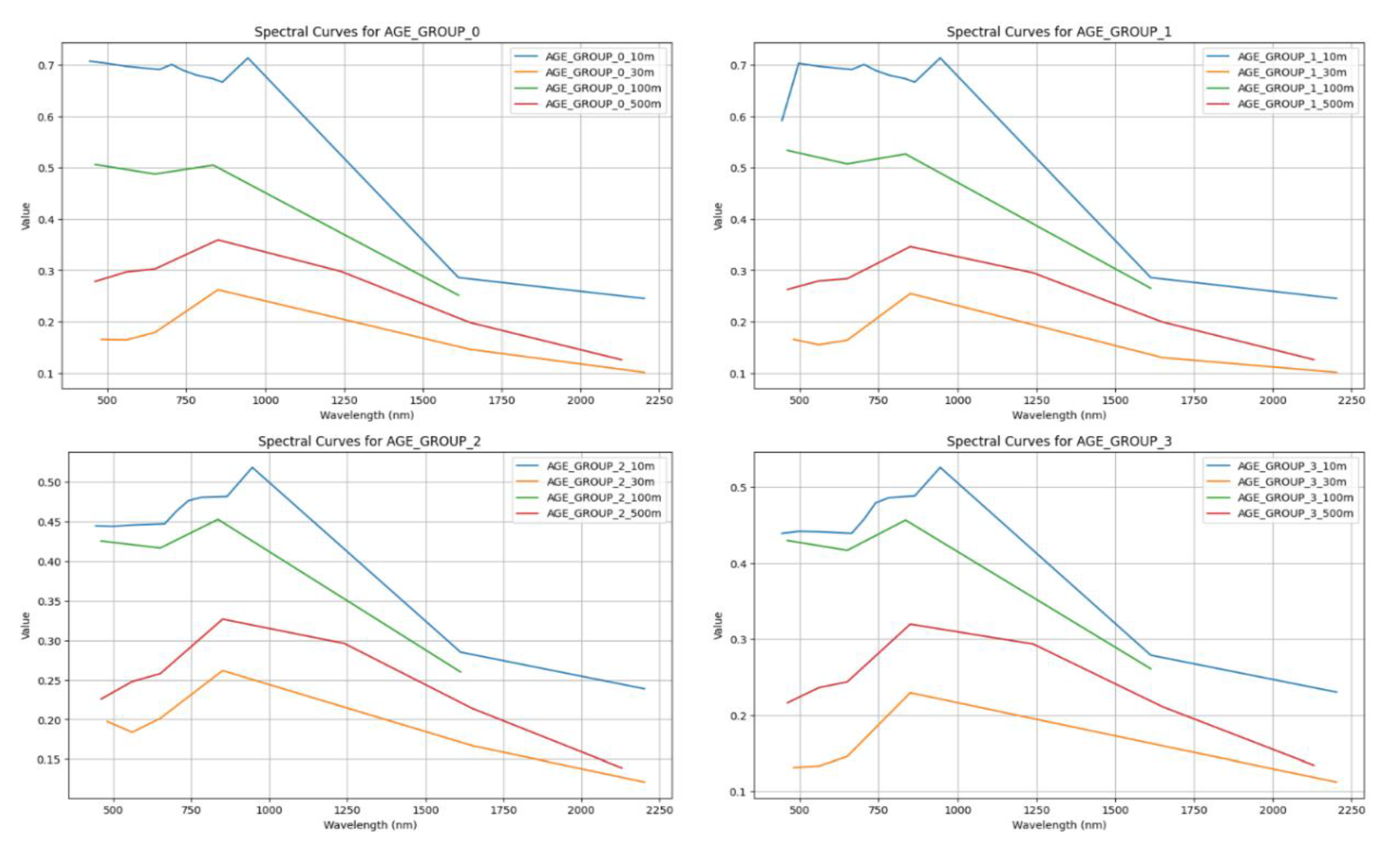
3.2. Forest Age Group—Scale Variability Relationship of Remote Sensing Spectroscopy
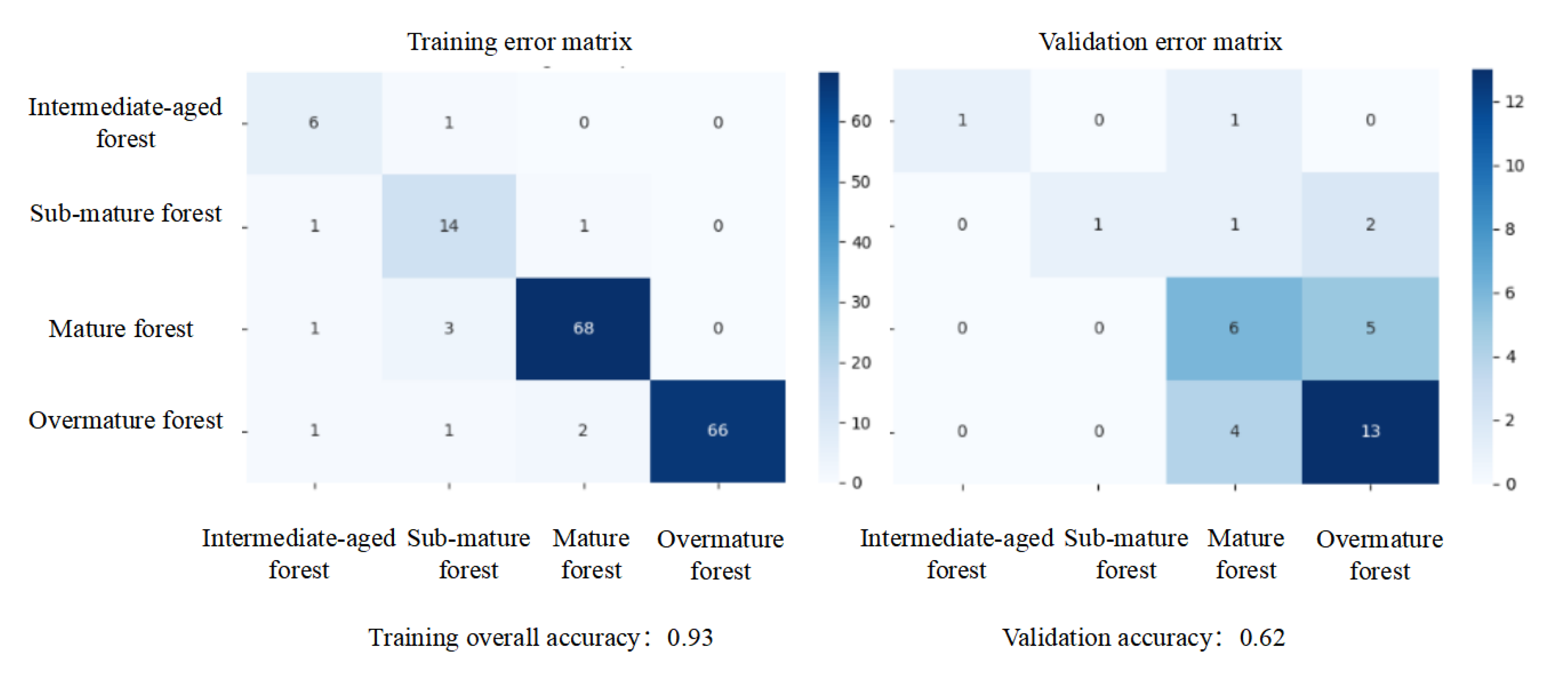
3.3. Model Performance
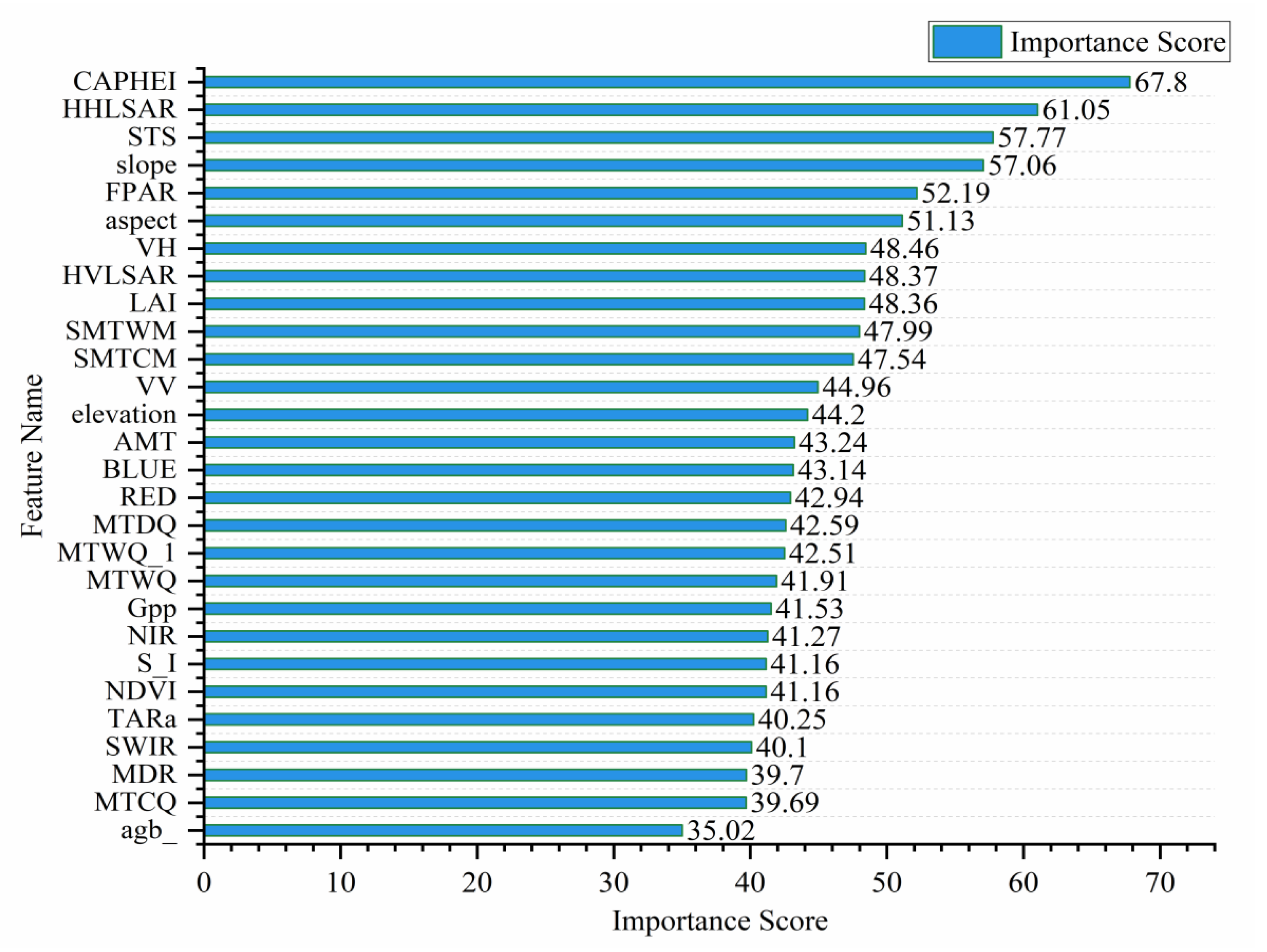
3.4. Evaluation of Forest Age Group Classification Results and Analysis of Characteristics of Predictors
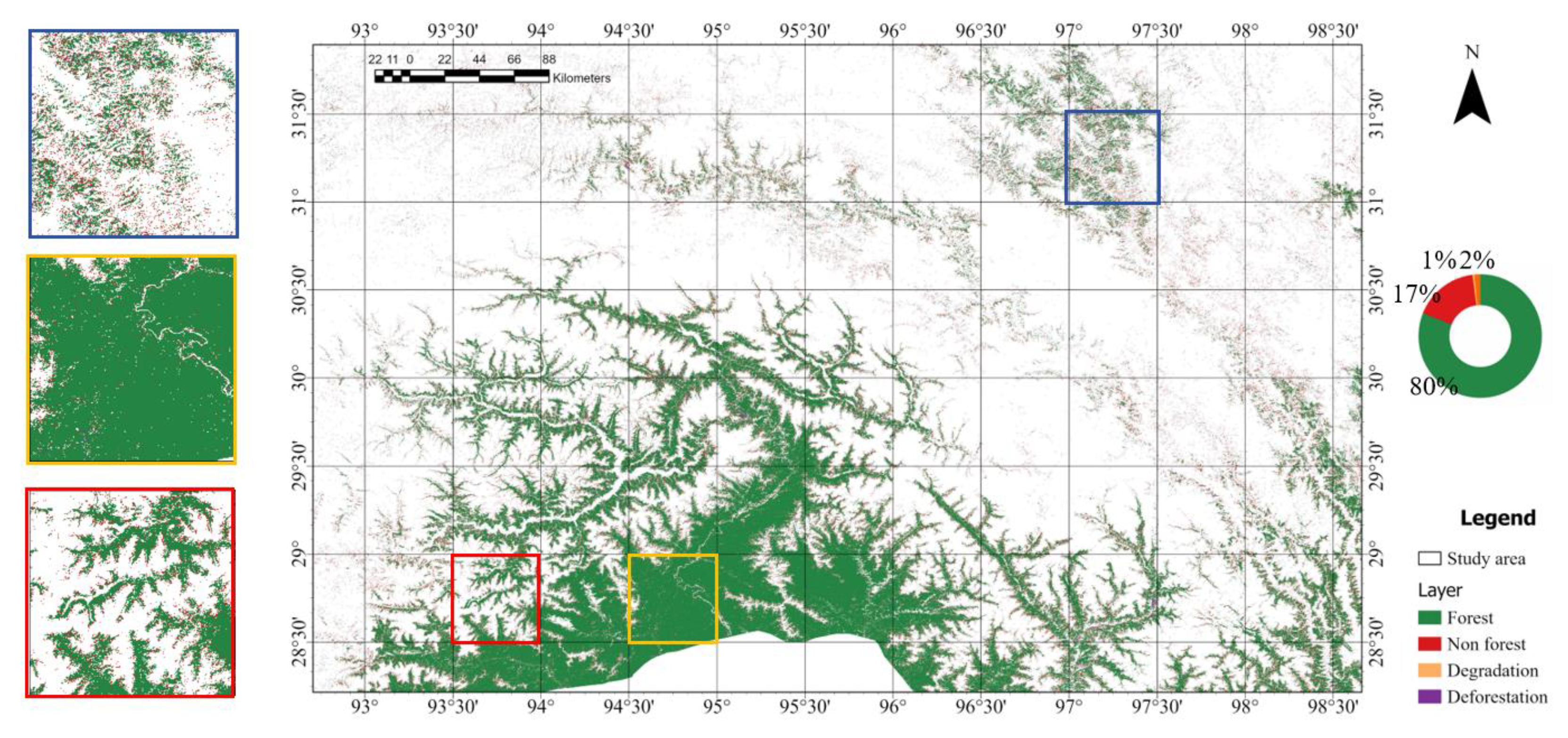
3.5. Spatial Distribution of Forest Age
4. Discussion
4.1. Ecological Characteristics of Forest Age
4.2. The Influence of Forest Age on Spectral Reflectance Characteristics
4.3. Spectral Reflectivity Characteristics Depend on the Scale Variability of Spatial Resolution
4.4. Error Sources and Model Generalizability Discussion
4.5. Limitations of the Study and Future Outlook
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Classification of Forest Parameters | Parameter Name | Describe |
|---|---|---|
| Age | AGEyr. | Forest age (years) is the average age of the dominant tree species. |
| Leaf area | TREE-LAI | Tree leaf-area index |
| Volume | VOLUMEm3/ha | Volume of wood per hectare |
| Tree Density | DENSITYtrees/ha | Density of trees per hectare |
| Biomass | STEM_MASSt.DM/ha | Biomass per hectare of tree trunk (dry matter) |
| BRANCH_MASSt./ha | Biological number of branches per hectare | |
| LEAF_MASSt./ha | Leaf biomass per hectare | |
| ROOT_MASSt.DM/ha | Root biomass (dry matter) per hectare | |
| TOTAL_TREE_MASSt.DM/ha | Total tree biomass per hectare | |
| HERB-MASSt.DM/ha | Herbaceous biomass per hectare | |
| SHRUB-MASSt./ha | Shrub biomass per hectare | |
| TOTAL-MASSt.DM/ha | Total biomass per hectare (trees, shrubs, herbs) | |
| Primary productivity | STEM_NPPt.DM/ha/yr. | Primary productivity per hectare of tree trunk (dry matter) |
| BRANCH_NPPt.DM/ha/yr. | Primary productivity per hectare of branches | |
| LEAF_NPPt.DM/ha/yr. | Primary productivity per hectare of leaves | |
| ROOT_NPPt.DM/ha/yr. | Primary productivity per hectare of roots | |
| TOTAL_TREE_NPPt.DM/ha/yr. | Total tree primary productivity per hectare | |
| HERB-NPPt./ha/yr. | Primary productivity per hectare of herbs | |
| SHRUB-NPPt.DM/ha/yr. | Primary productivity per hectare of shrub | |
| TOTAL-NPPt.DM/ha/yr. | Total primary productivity per hectare | |
| Geographic information | Altitude | Altitude |
| LATITUDE,deg. | North latitude | |
| LONGITUDEE,deg. | East longitude |
| Data Set | Abbreviated Name | Describe | Dataset Id (GEE) |
|---|---|---|---|
| ETH Global Sentinel-2 10 m Canopy Height (2020) | CAPHEI | Fusing GEDI with Sentinel-2 to generate probabilistic deep learning models for global retrieval of canopy height [83]. | users/nlang/ETH_GlobalCanopyHeight_2020_10m_v1 |
| Sensor-Independent MODIS and VIIRS LAI/FPAR CDR 2000 to 2022 (8d500m) | LAI | Leaf-Area Index (LAI), used to characterize the state of terrestrial ecosystems [84]. | projects/sat-io/open-datasets/BU_LAI_FPAR/wgs_500m_8d |
| Sensor-Independent MODIS & VIIRS LAI/FPAR CDR 2000 to 2022 (8d500m) | FPAR | Fraction of Photosynthetically Active Radiation (FPAR), used to characterize terrestrial ecosystem states. | projects/sat-io/open-datasets/BU_LAI_FPAR/wgs_500m_8d |
| Global Aboveground and Belowground Biomass Carbon Density Maps at 300 m Resolution (2010) | AGB | Living biomass carbon reserve density on wood and grassy vegetation in 2010. This includes the carbon stored in the living plant tissue (stems, bark, branches, twigs) located above the surface. This does not include fallen leaves or rough woody fragments that once attached to living plants but were later deposited and are no longer viable [85]. | NASA/ORNL/biomass_carbon_density/v1 |
| MOD17A3HGF.061: Terra Net Primary Production Gap-Filled Yearly Global 500 m (2001–2023) | GPP | Gross primary productivity [86]. | MODIS/061/MOD17A3HGF |
| SBIO1_Annual_Mean_Temperature (1000 m) | AMT | Average annual temperature, which indicates the average temperature at soil depth of 0–5 cm during the year (ecosystem conditions below the vegetation crown and near the surface) [87]. | projects/crowtherlab/soil_bioclim/SBIO_v2_0_5cm |
| SBIO2_Mean_Diurnal_Range (1000 m) | MDR | Mean daily range of temperature, i.e., –5 cm of soil depth. The average difference between the highest and lowest temperatures on a day. | projects/crowtherlab/soil_bioclim/SBIO_v2_0_5cm |
| SBIO3_Isothermality (1000 m) | S_I | The isotherm of soil depth of 0–5 cm, the formula is BIO2/BIO7 × 100, which reflects the uniformity of temperature change. | projects/crowtherlab/soil_bioclim/SBIO_v2_0_5cm |
| SBIO4_Temperature_Seasonality (1000 m) | STS | The seasonal temperature change of 0–5 cm soil depth, measured as a standard deviation, indicates the dispersion of temperature changes over a year. | projects/crowtherlab/soil_bioclim/SBIO_v2_0_5cm |
| SBIO5_Max_Temperature_of_Warmest_Month (1000 m) | SMTWM | The hottest monthly maximum temperature of 0–5 cm of soil depth indicates the maximum temperature in the hottest month of the year. | projects/crowtherlab/soil_bioclim/SBIO_v2_0_5cm |
| SBIO6_Min_Temperature_of_Coldest_Month (1000 m) | SMTCM | The coldest monthly minimum temperature of 0–5 cm of soil depth indicates the lowest temperature in the coldest month of the year. | projects/crowtherlab/soil_bioclim/SBIO_v2_0_5cm |
| SBIO7_Temperature_Annual_Range (1000 m) | TARa | The annual temperature range of 0–5 cm soil depth, the formula BIO5-BIO6, that is, the difference between the highest temperature of the hottest month and the lowest temperature of the coldest month. | projects/crowtherlab/soil_bioclim/SBIO_v2_0_5cm |
| SBIO8_Mean_Temperature_of_Wettest_Quarter (1000 m) | MTWQ | The wettest quarterly mean temperature of 0–5 cm of soil depth indicates the average temperature of the wettest quarter of the year. | projects/crowtherlab/soil_bioclim/SBIO_v2_0_5cm |
| SBIO9_Mean_Temperature_of_Driest_Quarter (1000 m) | MTDQ | The driest quarterly mean temperature of 0–5 cm of soil depth indicates the average temperature of the driest quarter of the year. | projects/crowtherlab/soil_bioclim/SBIO_v2_0_5cm |
| SBIO10_Mean_Temperature_of_Warmest_Quarter (1000 m) | MTWQ_1 | The warmest quarterly mean temperature of 0–5 cm of soil depth indicates the average temperature of the warmest quarter of the year. | projects/crowtherlab/soil_bioclim/SBIO_v2_0_5cm |
| SBIO11_Mean_Temperature_of_Coldest_Quarter (1000 m) | MTCQ | The coldest quarterly mean temperature of 0–5 cm of soil depth indicates the average temperature of the coldest quarter of the year. | projects/crowtherlab/soil_bioclim/SBIO_v2_0_5cm |
| Sentinel-1 SAR GRD: C-band Synthetic Aperture Radar Ground Range Detected, log scaling (2015–2023) | VV | Single-covalent polarization, vertical emission/vertical reception | COPERNICUS/S1_GRD |
| Sentinel-1 SAR GRD: C-band Synthetic Aperture Radar Ground Range Detected, log scaling (2015–2023) | VH | Two-band cross polarization, vertical emission/horizontal reception | COPERNICUS/S1_GRD |
| Global PALSAR-2/PALSAR Yearly Mosaic, version 1 | HHLSAR | HH polarization backscattering coefficient, 16-bit DN [88]. | JAXA/ALOS/PALSAR/YEARLY/SAR |
| Global PALSAR-2/PALSAR Yearly Mosaic, version 1 | HVLSAR | HV polarization backscattering coefficient, 16-bit DN. | JAXA/ALOS/PALSAR/YEARLY/SAR |
| Gridded GEDI Vegetation Structure Metrics and Biomass Density, 1 km pixel size (2019–2023) | MEAN | The mean of GEDI shot metric values within a pixel [89]. | LARSE/GEDI/GRIDDEDVEG_002/V1/1KM |
| Gridded GEDI Vegetation Structure Metrics and Biomass Density, 1 km pixel size (2019–2023) | MEANBASE | Standard error of the mean calculated using bootstrap resampling. | LARSE/GEDI/GRIDDEDVEG_002/V1/1KM |
| Gridded GEDI Vegetation Structure Metrics and Biomass Density, 1 km pixel size (2019–2023) | MEDIAN | The median value (50th percentile) of GEDI shot metric values within a pixel. | LARSE/GEDI/GRIDDEDVEG_002/V1/1KM |
| Gridded GEDI Vegetation Structure Metrics and Biomass Density, 1 km pixel size (2019–2023) | SD | The standard deviation of GEDI shot metric values within a pixel. | LARSE/GEDI/GRIDDEDVEG_002/V1/1KM |
| Gridded GEDI Vegetation Structure Metrics and Biomass Density, 1 km pixel size (2019–2023) | IQR | The interquartile range (75th percentile minus 25th percentile) of GEDI shot metric values within a pixel. | LARSE/GEDI/GRIDDEDVEG_002/V1/1KM |
| Gridded GEDI Vegetation Structure Metrics and Biomass Density, 1 km pixel size (2019–2023) | P95 | The 95th percentile value of GEDI shot-metric values within a pixel. | LARSE/GEDI/GRIDDEDVEG_002/V1/1KM |
| Gridded GEDI Vegetation Structure Metrics and Biomass Density, 1 km pixel size (2019–2023) | Mountain | Shannon’s diversity index (H) of GEDI shot metric values within a pixel. Calculated as:-1(sum(plog(p))) where p is the proportion of GEDI shot values per bin. | LARSE/GEDI/GRIDDEDVEG_002/V1/1KM |
| Gridded GEDI Vegetation Structure Metrics and Biomass Density, 1 km pixel size (2019–2023) | COUNTF | The count of GEDI shot metric values within a pixel. | LARSE/GEDI/GRIDDEDVEG_002/V1/1KM |
| PROBA-V C1 Top Of Canopy Daily Synthesis 100 m (2013-) | RED | Top of canopy reflectance RED channel | VITO/PROBAV/C1/S1_TOC_100M |
| PROBA-V C1 Top Of Canopy Daily Synthesis 100 m (2013-) | NIR | Top of canopy reflectance NIR channel | VITO/PROBAV/C1/S1_TOC_100M |
| PROBA-V C1 Top Of Canopy Daily Synthesis 100 m (2013-) | BLUE | Top of canopy reflectance BLUE channel | VITO/PROBAV/C1/S1_TOC_100M |
| PROBA-V C1 Top Of Canopy Daily Synthesis 100 m (2013-) | SWIR | Top of canopy reflectance SWIR channel | VITO/PROBAV/C1/S1_TOC_100M |
| PROBA-V C1 Top Of Canopy Daily Synthesis 100 m (2013-) | NDVI | Normalized Difference Vegetation Index | VITO/PROBAV/C1/S1_TOC_100M |
| Harmonized Sentinel-2 MSI: MultiSpectral Instrument, Level-2A (2017–2024) | “B1”, “B2”, “B3”, “B4”, “B5”, “B6”, “B7”, “B8”, “B8A”, “B9”, “B11”, “B12” | COPERNICUS/S2_SR_HARMONIZED | |
| Landsat Collection 2 (1990–2020) | “blue”, “green”, “red”, “nir”, “swir1”, “swir2” [90] | ||
| MOD09A1.061 Terra Surface Reflectance 8-Day Global 500 m (2000–2024) | "sur_refl_b01", "sur_refl_b02", "sur_refl_b03", "sur_refl_b04", "sur_refl_b05", "sur_refl_b06", "sur _ refl _ b07" [91] | MODIS/061/MOD09A1 | |
| NASADEM: NASA 30 m Digital Elevation Model | ELEVATION | Altitude [92] | NASA/NASADEM_HGT/001 |
| NASADEM: NASA NASADEM Digital Elevation 30 m | SLOPE | Slope | NASA/NASADEM_HGT/001 |
| NASADEM: NASA NASADEM Digital Elevation 30 m | ASPECT | The slopes are sloped | NASA/NASADEM_HGT/001 |
| Model Name | Description |
|---|---|
| Linear regression | Linear regression [93] models the relationship between the dependent variable (forest age) and the independent variables using a linear equation. |
| Ridge regression | Predicts forest age by shrinking coefficients with L2 regularization [94], suitable for handling multicollinearity. |
| Lasso regression | Predicts forest age by selecting important features with L1 regularization [95], suitable for high-dimensional data. |
| ElasticNet Regression | Predicts forest age by combining L1 and L2 regularization [96], suitable for high-dimensional data with multicollinearity. |
| Decision Tree Regression | Predicts forest age by recursively splitting data based on a forest structure [97], suitable for nonlinear relationships. |
| Random Forest Regression | Predicts forest age by averaging results from multiple decision forests [98], suitable for high-dimensional data requiring high accuracy. |
| Gradient Boosting Regression | Predicts forest age by sequentially adding weak learners to optimize the loss function [99], suitable for complex nonlinear relationships. |
| Extra forests Regression | Predicts forest age using random thresholds for splitting data [100], with faster training speed. |
| K-Nearest Neighbor Regression | Predicts forest age by averaging the values of the K nearest neighbors [101], suitable for low-dimensional data. |
| Support vector regression | Predicts forest age using a hyperplane and kernel functions [102], suitable for high-dimensional data. |
| Multilayer Perceptron Regression | Predicts forest age by fitting complex relationships with a neural network [103], suitable for large-scale data. |
| AdaBoost Regressor | Predicts forest age by training multiple weak learners with adjusted sample weights [104], suitable for improving model performance. |
References
- Xiao, Y.; Wang, Q.; Tong, X.; Atkinson, P.M. Thirty-meter map of young forest age in China. Earth Syst. Sci. Data 2023, 15, 3365–3386. [Google Scholar] [CrossRef]
- Shang, R.; Chen, J.M.; Xu, M.; Lin, X.; Li, P.; Yu, G.; He, N.; Xu, L.; Gong, P.; Liu, L.; et al. China’s current forest age structure will lead to weakened carbon sinks in the near future. Innovation 2023, 4, 100515. [Google Scholar] [CrossRef] [PubMed]
- Cheng, K.; Chen, Y.; Xiang, T.; Yang, H.; Liu, W.; Ren, Y.; Guan, H.; Hu, T.; Ma, Q.; Guo, Q. A 2020 forest age map for China with 30 m resolution. Earth Syst. Sci. Data 2024, 16, 803–819. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, D.; Zhu, Y.; Peng, H.; Xie, H. A review of forest carbon cycle models on spatiotemporal scales. J. Clean. Prod. 2022, 339, 130692. [Google Scholar] [CrossRef]
- Zhou, T.; Shi, P.; Jia, G.; Dai, Y.; Zhao, X.; Shangguan, W.; Du, L.; Wu, H.; Luo, Y. Age-dependent forest carbon sink: Estimation via inverse modeling. J. Geophys. Res. Biogeosci. 2015, 120, 2473–2492. [Google Scholar] [CrossRef]
- Yang, M.; Zhou, X.; Liu, Z.; Li, P.; Tang, J.; Xie, B.; Peng, C. A Review of General Methods for Quantifying and Estimating Urban Trees and Biomass. Forests 2022, 13, 616. [Google Scholar] [CrossRef]
- Maltman, J.C.; Hermosilla, T.; Wulder, M.A.; Coops, N.C.; White, J.C. Estimating and mapping forest age across Canada’s forested ecosystems. Remote Sens. Environ. 2023, 290, 113529. [Google Scholar] [CrossRef]
- Tian, L.; Wu, X.; Tao, Y.; Li, M.; Qian, C.; Liao, L.; Fu, W. Review of Remote Sensing-Based Methods for Forest Aboveground Biomass Estimation: Progress, Challenges, and Prospects. Forests 2023, 14, 1086. [Google Scholar] [CrossRef]
- Lin, X.; Shang, R.; Chen, J.M.; Zhao, G.; Zhang, X.; Huang, Y.; Yu, G.; He, N.; Xu, L.; Jiao, W. High-resolution forest age mapping based on forest height maps derived from GEDI and ICESat-2 space-borne lidar data. Agric. For. Meteorol. 2023, 339, 109592. [Google Scholar] [CrossRef]
- Xie, D.; Huang, H.; Feng, L.; Sharma, R.P.; Chen, Q.; Liu, Q.; Fu, L. Aboveground Biomass Prediction of Arid Shrub-Dominated Community Based on Airborne LiDAR through Parametric and Nonparametric Methods. Remote Sens. 2023, 15, 3344. [Google Scholar] [CrossRef]
- Thenkabail, P.S. Remote sensing of land resources: Monitoring, modeling, and mapping advances over the last 50 years and a vision for the future. In Remote Sensing Handbook—Three Volume Set; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Nilson, T.; Peterson, U. Age dependence of forest reflectance: Analysis of main driving factors. Remote Sens. Environ. 1994, 48, 319–331. [Google Scholar] [CrossRef]
- Baret, F.; Buis, S. Estimating Canopy Characteristics from Remote Sensing Observations: Review of Methods and Associated Problems. In Advances in Land Remote Sensing: System, Modeling, Inversion and Application; Liang, S., Ed.; Springer: Dordrecht, The Netherlands, 2008; pp. 173–201. [Google Scholar]
- Kayitakire, F.; Hamel, C.; Defourny, P. Retrieving forest structure variables based on image texture analysis and IKONOS-2 imagery. Remote Sens. Environ. 2006, 102, 390–401. [Google Scholar] [CrossRef]
- Tang, S.; Tian, Q.; Xu, K.; Xu, N.; Yue, J. Age informa-tion retrieval of Larix gmelinii forest using Sentinel-2 data. J. Remote Sens. 2020, 24, 1511–1524. (In Chinese) [Google Scholar] [CrossRef]
- Gao, S.; Zhong, R.; Yan, K.; Ma, X.; Chen, X.; Pu, J.; Gao, S.; Qi, J.; Yin, G.; Myneni, R.B. Evaluating the saturation effect of vegetation indices in forests using 3D radiative transfer simulations and satellite observations. Remote Sens. Environ. 2023, 295, 113665. [Google Scholar] [CrossRef]
- Donovan, G.H.; Gatziolis, D.; Derrien, M.; Michael, Y.L.; Prestemon, J.P.; Douwes, J. Shortcomings of the normalized difference vegetation index as an exposure metric. Nat. Plants 2022, 8, 617–622. [Google Scholar] [CrossRef]
- Mercier, A.; Myllymäki, M.; Hovi, A.; Schraik, D.; Rautiainen, M. Exploring the potential of SAR and terrestrial and airborne LiDAR in predicting forest floor spectral properties in temperate and boreal forests. Remote Sens. Environ. 2025, 316, 114486. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Jones, J.; Lucas, R.M.; Shimabukuro, Y.E. Mapping major land cover types and retrieving the age of secondary forests in the Brazilian Amazon by combining single-date optical and radar remote sensing data. Remote Sens. Environ. 2017, 194, 16–32. [Google Scholar] [CrossRef]
- Bolton, D.K.; Tompalski, P.; Coops, N.C.; White, J.C.; Wulder, M.A.; Hermosilla, T.; Queinnec, M.; Luther, J.E.; van Lier, O.R.; Fournier, R.A.; et al. Optimizing Landsat time series length for regional mapping of lidar-derived forest structure. Remote Sens. Environ. 2020, 239, 111645. [Google Scholar] [CrossRef]
- Torabzadeh, H.; Morsdorf, F.; Schaepman, M.E. Fusion of imaging spectroscopy and airborne laser scanning data for characterization of forest ecosystems—A review. ISPRS J. Photogramm. Remote Sens. 2014, 97, 25–35. [Google Scholar] [CrossRef]
- Toivonen, J.; Kangas, A.; Maltamo, M.; Kukkonen, M.; Packalen, P. Assessing biodiversity using forest structure indicators based on airborne laser scanning data. For. Ecol. Manag. 2023, 546, 121376. [Google Scholar] [CrossRef]
- Martin, M.; Valeria, O. “Old” is not precise enough: Airborne laser scanning reveals age-related structural diversity within old-growth forests. Remote Sens. Environ. 2022, 278, 113098. [Google Scholar] [CrossRef]
- Gazzea, M.; Solheim, A.; Arghandeh, R. High-resolution mapping of forest structure from integrated SAR and optical images using an enhanced U-net method. Sci. Remote Sens. 2023, 8, 100093. [Google Scholar] [CrossRef]
- Tian, L.; Liao, L.; Tao, Y.; Wu, X.; Li, M. Forest Age Mapping Using Landsat Time-Series Stacks Data Based on Forest Disturbance and Empirical Relationships between Age and Height. Remote Sens. 2023, 15, 2862. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, H.; Liu, A.; Qi, S.; Hu, B.; Huang, M.; Luo, J. Mapping of secondary forest age in China using stacked generalization and Landsat time series. Sci. Data 2024, 11, 302. [Google Scholar] [CrossRef] [PubMed]
- Véga, C.; St-Onge, B. Mapping site index and age by linking a time series of canopy height models with growth curves. For. Ecol. Manag. 2009, 257, 951–959. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, J.M.; Birdsey, R.; McCullough, K.; He, L.; Deng, F. Age structure and disturbance legacy of North American forests. Biogeosciences 2011, 8, 715–732. [Google Scholar] [CrossRef]
- Peng, D.; Zhang, H.; Liu, L.; Huang, W.; Huete, A.R.; Zhang, X.; Wang, F.; Yu, L.; Xie, Q.; Wang, C.; et al. Estimating the Aboveground Biomass for Planted Forests Based on Stand Age and Environmental Variables. Remote Sens. 2019, 11, 2270. [Google Scholar] [CrossRef]
- Huang, Z.; Li, X.; Du, H.; Zou, W.; Zhou, G.; Mao, F.; Fan, W.; Xu, Y.; Ni, C.; Zhang, B.; et al. An Algorithm of Forest Age Estimation Based on the Forest Disturbance and Recovery Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3322163. [Google Scholar] [CrossRef]
- Huang, C.; Goward, S.N.; Masek, J.G.; Thomas, N.; Zhu, Z.; Vogelmann, J.E. An automated approach for reconstructing recent forest disturbance history using dense Landsat time series stacks. Remote Sens. Environ. 2010, 114, 183–198. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Bullock, E.L.; Woodcock, C.E.; Olofsson, P. Monitoring tropical forest degradation using spectral unmixing and Landsat time series analysis. Remote Sens. Environ. 2020, 238, 110968. [Google Scholar] [CrossRef]
- Ma, Q.; Zhang, X.; Yuan, J.; Gong, Z.; Shang, R.; Cheng, K.; Chen, M.; Tan, Q.; Ju, W. Advancements in remote sensing based forest age estimation and its applications. Natl. Remote Sens. Bull. 2025, 29, 70–82. (In Chinese) [Google Scholar] [CrossRef]
- Li, X.; Dunkin, F.; Dezert, J. Multi-source information fusion: Progress and future. Chin. J. Aeronaut. 2024, 37, 24–58. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, T.; Zeng, J.; Luo, H.; Zhang, Y.; Liu, X.; Lin, Q.; Zhang, J. Spatial Pattern of Forest Age in China Estimated by the Fusion of Multiscale Information. Forests 2024, 15, 1290. [Google Scholar] [CrossRef]
- Balestra, M.; Marselis, S.; Sankey, T.T.; Cabo, C.; Liang, X.; Mokroš, M.; Peng, X.; Singh, A.; Stereńczak, K.; Vega, C.; et al. LiDAR Data Fusion to Improve Forest Attribute Estimates: A Review. Curr. For. Rep. 2024, 10, 281–297. [Google Scholar] [CrossRef]
- Schumacher, J.; Hauglin, M.; Astrup, R.; Breidenbach, J. Mapping forest age using National Forest Inventory, airborne laser scanning, and Sentinel-2 data. For. Ecosyst. 2020, 7, 60. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Wu, Z.; Yu, Y.; Li, F.; Fan, W. Forest age mapping based on multiple-resource remote sensing data. Environ. Monit. Assess. 2020, 192, 734. [Google Scholar] [CrossRef]
- Guan, X.; Yang, X.; Yu, Y.; Pan, Y.; Dong, H.; Yang, T. Canopy-Height and Stand-Age Estimation in Northeast China at Sub-Compartment Level Using Multi-Resource Remote Sensing Data. Remote Sens. 2023, 15, 3738. [Google Scholar] [CrossRef]
- Wang, Q.; Moreno-Martínez, Á.; Muñoz-Marí, J.; Campos-Taberner, M.; Camps-Valls, G. Estimation of vegetation traits with kernel NDVI. ISPRS J. Photogramm. Remote Sens. 2023, 195, 408–417. [Google Scholar] [CrossRef]
- Filella, I.; Penuelas, J. The red edge position and shape as indicators of plant chlorophyll content, biomass and hydric status. Int. J. Remote Sens. 1994, 15, 1459–1470. [Google Scholar] [CrossRef]
- Besnard, S.; Koirala, S.; Santoro, M.; Weber, U.; Nelson, J.; Gütter, J.; Herault, B.; Kassi, J.; N’Guessan, A.; Neigh, C.; et al. Mapping global forest age from forest inventories, biomass and climate data. Earth Syst. Sci. Data 2021, 13, 4881–4896. [Google Scholar] [CrossRef]
- Wu, T. The Qinghai–Tibetan Plateau: How High Do Tibetans Live? High Alt. Med. Biol. 2001, 2, 489–499. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Zhang, Y.; Xu, Z.; Teng, J.; Liu, C.; Liu, W.; Mpelasoka, F. The impact of climate change on runoff in the southeastern Tibetan Plateau. J. Hydrol. 2013, 505, 188–201. [Google Scholar] [CrossRef]
- Ma, S.; Zhou, Z.; Zhang, Y.; An, Y.; Yang, G. Identification of forest disturbance and estimation of forest age in subtropical mountainous areas based on Landsat time series data. Earth Sci. Inform. 2022, 15, 321–334. [Google Scholar] [CrossRef]
- Yang, K.; Chen, J.; Zhao, T.; Lu, C.; Xu, X.; Luo, Y.; Yang, Q.; Tan, C.; Fu, W.; Wang, Z. Effects of fine terrain complexity on cloud and precipitation changes over the Tibetan Plateau: A modeling study. npj Clim. Atmos. Sci. 2025, 8, 22. [Google Scholar] [CrossRef]
- Li, J.; Lu, C.; Chen, J.; Zhou, X.; Yang, K.; Li, J.; Wu, X.; Xu, X.; Wu, S.; Hu, R.; et al. The influence of complex terrain on cloud and precipitation on the foot and slope of the southeastern Tibetan Plateau. Clim. Dyn. 2024, 62, 3143–3163. [Google Scholar] [CrossRef]
- Souza, C.M.; Roberts, D.A.; Cochrane, M.A. Combining spectral and spatial information to map canopy damage from selective logging and forest fires. Remote Sens. Environ. 2005, 98, 329–343. [Google Scholar] [CrossRef]
- Pandit, M.K.; Manish, K.; Koh, L.P. Dancing on the roof of the world: Ecological transformation of the Himalayan landscape. BioScience 2014, 64, 980–992. [Google Scholar] [CrossRef]
- Tang, Y.; Wan, S.; He, J.; Zhao, X. Foreword to the special issue: Looking into the impacts of global warming from the roof of the world. J. Plant Ecol. 2009, 2, 169–171. [Google Scholar] [CrossRef]
- Wang, Q.; Hong, D. Understanding the plant diversity on the roof of the world. Innovation 2022, 3, 100215. [Google Scholar] [CrossRef] [PubMed]
- Roerink, G.J.; Menenti, M.; Soepboer, W.; Su, Z. Assessment of climate impact on vegetation dynamics by using remote sensing. Phys. Chem. Earth Parts A/B/C 2003, 28, 103–109. [Google Scholar] [CrossRef]
- Xu, X.; Chen, H.; Levy, J.K. Spatiotemporal vegetation cover variations in the Qinghai-Tibet Plateau under global climate change. Chin. Sci. Bull. 2008, 53, 915–922. [Google Scholar] [CrossRef]
- Cui, X.; Graf, H.-F. Recent land cover changes on the Tibetan Plateau: A review. Clim. Change 2009, 94, 47–61. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, H.; Guo, W.; Li, S.; Zhang, Q. Unexpectedly high nitrate levels in a pristine forest river on the Southeastern Qinghai-Tibet Plateau. J. Hazard. Mater. 2023, 458, 132047. [Google Scholar] [CrossRef]
- Clark, M.K.; House, M.; Royden, L.; Whipple, K.; Burchfiel, B.; Zhang, X.; Tang, W. Late Cenozoic uplift of southeastern Tibet. Geology 2005, 33, 525–528. [Google Scholar] [CrossRef]
- Opgenoorth, L.; Vendramin, G.G.; Mao, K.; Miehe, G.; Miehe, S.; Liepelt, S.; Liu, J.; Ziegenhagen, B. Tree endurance on the Tibetan Plateau marks the world’s highest known tree line of the Last Glacial Maximum. New Phytol. 2010, 185, 332–342. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, X.-M.; Zhu, H.-Z.; Gao, S.; Sun, J.; Zhu, H.-F.; Fang, J.-P.; Camarero, J.J.; Liang, E.-Y. A rapid transition from spruce-fir to pine-broadleaf forests in response to disturbances and climate warming on the southeastern qinghai-Tibet plateau. Plant Divers. 2023. [Google Scholar] [CrossRef]
- LY/T 2908-2017; Regulations for Age-Class and Age-Group Division of Main Tree-Species. China Forestry Industry: Beijing, China, 2018.
- Xia, J.; Xia, X.; Chen, Y.; Shen, R.; Zhang, Z.; Liang, B.; Wang, J.; Yuan, W. Reconstructing Long-Term Forest Age of China by Combining Forest Inventories, Satellite-Based Forest Age and Forest Cover Data Sets. J. Geophys. Res. Biogeosci. 2023, 128, e2023JG007492. [Google Scholar] [CrossRef]
- Bullock, E.L.; Woodcock, C.E.; Souza, C., Jr.; Olofsson, P. Satellite-based estimates reveal widespread forest degradation in the Amazon. Glob. Change Biol. 2020, 26, 2956–2969. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Aryal, R.R.; Wespestad, C.; Kennedy, R.; Dilger, J.; Dyson, K.; Bullock, E.; Khanal, N.; Kono, M.; Poortinga, A.; Saah, D.; et al. Lessons Learned While Implementing a Time-Series Approach to Forest Canopy Disturbance Detection in Nepal. Remote Sens. 2021, 13, 2666. [Google Scholar] [CrossRef]
- Bullock, E. Background and Motivation—CODED 0.2 Documentation. Available online: https://coded.readthedocs.io/en/latest/ (accessed on 1 January 2025).
- Souza, C.; Tenneson, K.; Dilger, J.; Wespestad, C.; Bullock, E. Forest Degradation and Deforestation. In Cloud-Based Remote Sensing with Google Earth Engine: Fundamentals and Applications; Cardille, J.A., Crowley, M.A., Saah, D., Clinton, N.E., Eds.; Springer International Publishing: Cham, Switzerland, 2024; pp. 1061–1091. [Google Scholar]
- Du, K.L.; Swamy, M.N.S. Neural Networks and Statistical Learning; Springer: London, UK, 2013. [Google Scholar]
- Lv, Z.; Duan, A.; Zhang, J. Influence of forest age, tree size, and climate factors on biomass and carbon storage allocation in Chinese fir forests. Ecol. Indic. 2024, 163, 112096. [Google Scholar] [CrossRef]
- Zhang, Y.; Yao, Y.; Wang, X.; Liu, Y.; Piao, S. Mapping spatial distribution of forest age in China. Earth Space Sci. 2017, 4, 108–116. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.M.; Wang, R.; Mo, G.; Luo, S.; Luo, X.; He, L.; Gonsamo, A.; Arabian, J.; Zhang, Y.; et al. The global distribution of leaf chlorophyll content. Remote Sens. Environ. 2020, 236, 111479. [Google Scholar] [CrossRef]
- Castro, K.L.; Sanchez-Azofeifa, G.A. Changes in Spectral Properties, Chlorophyll Content and Internal Mesophyll Structure of Senescing Populus balsamifera and Populus tremuloides Leaves. Sensors 2008, 8, 51–69. [Google Scholar] [CrossRef]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy near-infrared reflectance and terrestrial photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef]
- Lin, S.; Coops, N.C.; Tortini, R.; Jia, W.; Nesic, Z.; Beamesderfer, E.; Arain, M.A.; Li, J.; Liu, Q. Species and stand-age driven differences in photochemical reflectance index and light use efficiency across four temperate forests. Int. J. Appl. Earth Obs. Geoinf. 2021, 98, 102308. [Google Scholar] [CrossRef]
- Rautiainen, M.; Lukeš, P. Spectral contribution of understory to forest reflectance in a boreal site: An analysis of EO-1 Hyperion data. Remote Sens. Environ. 2015, 171, 98–104. [Google Scholar] [CrossRef]
- Gold, K.M.; Townsend, P.A.; Herrmann, I.; Gevens, A.J. Investigating potato late blight physiological differences across potato cultivars with spectroscopy and machine learning. Plant Sci. 2020, 295, 110316. [Google Scholar] [CrossRef]
- Liu, Y.; Ju, W.; Chen, J.; Zhu, G.; Xing, B.; Zhu, J.; He, M. Spatial and temporal variations of forest LAI in China during 2000–2010. Chin. Sci. Bull. 2012, 57, 2846–2856. [Google Scholar] [CrossRef]
- Ehbrecht, M.; Seidel, D.; Annighöfer, P.; Kreft, H.; Köhler, M.; Zemp, D.C.; Puettmann, K.; Nilus, R.; Babweteera, F.; Willim, K.; et al. Global patterns and climatic controls of forest structural complexity. Nat. Commun. 2021, 12, 519. [Google Scholar] [CrossRef]
- Song, G.; Wang, J.; Zhao, Y.; Yang, D.; Lee, C.K.F.; Guo, Z.; Detto, M.; Alberton, B.; Morellato, P.; Nelson, B.; et al. Scale matters: Spatial resolution impacts tropical leaf phenology characterized by multi-source satellite remote sensing with an ecological-constrained deep learning model. Remote Sens. Environ. 2024, 304, 114027. [Google Scholar] [CrossRef]
- Li, Y.; Lu, B.; Zhou, H.; Zhang, Y.; Zhao, Z.; Chen, W.; Wu, Y.; Guo, Z.; Jiang, J.; Xue, S. Effects of degradation level and vegetation recovery age on soil erodibility of alpine grasslands on the Qinghai−Tibetan Plateau. J. Soils Sediments 2024, 24, 294–306. [Google Scholar] [CrossRef]
- Marziliano, P.A.; Tognetti, R.; Lombardi, F. Is tree age or tree size reducing height increment in Abies alba Mill. at its southernmost distribution limit? Ann. For. Sci. 2019, 76, 17. [Google Scholar] [CrossRef]
- Kobayashi, S.; Fujita, M.S.; Yoshiharu, O.; Matthews, J.P. Analysis of the relationship between L-band SAR backscatter and understory weed density in eucalyptus plantation forests. GIScience Remote Sens. 2024, 61, 2360771. [Google Scholar] [CrossRef]
- Lang, N.; Jetz, W.; Schindler, K.; Wegner, J.D. A high-resolution canopy height model of the Earth. Nat. Ecol. Evol. 2023, 7, 1778–1789. [Google Scholar] [CrossRef] [PubMed]
- Pu, J.; Yan, K.; Roy, S.; Zhu, Z.; Rautiainen, M.; Knyazikhin, Y.; Myneni, R.B. Sensor-independent LAI/FPAR CDR: Reconstructing a global sensor-independent climate data record of MODIS and VIIRS LAI/FPAR from 2000 to 2022. Earth Syst. Sci. Data 2024, 16, 15–34. [Google Scholar] [CrossRef]
- Spawn, S.A.; Gibbs, H.K. Global Aboveground and Belowground Biomass Carbon Density Maps for the Year 2010; ORNL DAAC: Oak Ridge, TN, USA, 2020. [Google Scholar] [CrossRef]
- Running, S.; Zhao, M. MODIS/Terra Net Primary Production Gap-Filled Yearly L4 Global 500m SIN Grid V061. 2021. Available online: https://lpdaac.usgs.gov/products/mod17a3hgfv061/ (accessed on 27 March 2025).
- Lembrechts, J.J.; van den Hoogen, J.; Aalto, J.; Ashcroft, M.B.; De Frenne, P.; Kemppinen, J.; Kopecký, M.; Luoto, M.; Maclean, I.M.D.; Crowther, T.W.; et al. Global maps of soil temperature. Glob. Change Biol. 2022, 28, 3110–3144. [Google Scholar] [CrossRef]
- Shimada, M.; Itoh, T.; Motooka, T.; Watanabe, M.; Shiraishi, T.; Thapa, R.; Lucas, R. New global forest/non-forest maps from ALOS PALSAR data (2007–2010). Remote Sens. Environ. 2014, 155, 13–31. [Google Scholar] [CrossRef]
- Burns, P.; Hakkenberg, C.R.; Goetz, S.J. Multi-resolution gridded maps of vegetation structure from GEDI. Sci. Data 2024, 11, 881. [Google Scholar] [CrossRef] [PubMed]
- Earth Resources Observation and Science (EROS) Center. Landsat 8–9 Operational Land Imager/Thermal Infrared Sensor Level-2, Collection 2 [Dataset]. 2020. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-landsat-archives-landsat-8-9-olitirs-collection-2-level-2 (accessed on 1 January 2025).
- Vermote, E. MODIS/Terra Surface Reflectance 8-Day L3 Global 500 m SIN Grid V061 [Data Set]. 2021. Available online: https://lpdaac.usgs.gov/products/mod09a1v061/ (accessed on 27 March 2025).
- NASA JPL. NASADEM Merged DEM Global 1 Arc Second V001 [Data Set]. 2020. Available online: https://doi.org/10.5067/MEaSUREs/NASADEM/NASADEM_HGT.001 (accessed on 27 March 2025).
- Montgomery, D.C.; Peck, E.A. Introduction to Linear Regression Analysis. Appl. Stat. 1992, 32. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 2000, 42, 80–86. [Google Scholar] [CrossRef]
- Ranstam, J.; Cook, J.A. LASSO regression. Br. J. Surg. 2018, 105, 1348. [Google Scholar] [CrossRef]
- Hans, C. Elastic Net Regression Modeling With the Orthant Normal Prior. Publ. Am. Stat. Asso-Ciation 2011, 106, 1383–1393. [Google Scholar] [CrossRef]
- Tsai, H.H.; Chang, B.M.; Lin, X.P. Using decision tree, particle swarm optimization, and support vector regression to design a median-type filter with a 2-level impulse detector for image enhancement. Information Sciences 2012, 195, 103–123. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zemel, R.S.; Pitassi, T. A Gradient-Based Boosting Algorithm for Regression Problems. In Proceedings of the Neural In-formation Processing Systems, Vancouver, BC, Canada, 6–12 December 2000. [Google Scholar]
- Criminisi, A.; Robertson, D.; Konukoglu, E.; Shotton, J.; Pathak, S.; White, S.; Siddiqui, K. Regression forests for efficient anatomy detection and localization in computed tomography scans. Med. Image Anal. 2013, 17, 1293–1303. [Google Scholar] [CrossRef]
- Maltamo, M.; Kangas, A. Methods based on k-nearest neighbor regression in the prediction of basal area diameter distribution. Can. J. For. Res. 1998, 28, 1107–1115. [Google Scholar] [CrossRef]
- Wang, J.; Li, L.; Niu, D.; Tan, Z. An annual load forecasting model based on support vector regression with differential evolution algorithm. Appl. Energy 2012, 94, 65–70. [Google Scholar] [CrossRef]
- Agirre-Basurko, E.; Ibarra-Berastegi, G.; Madariaga, I. Regression and multilayer perceptron-based models to forecast hourly O3 and NO2 levels in the Bilbao area. Environ. Model. Softw. 2006, 21, 430–446. [Google Scholar] [CrossRef]
- Patil, S.; Patil, A.; Phalle, V.M. Life Prediction of Bearing by Using Adaboost Regressor; Social Science Electronic Publishing: Rochester, NY, USA, 2018. [Google Scholar]

| Age Groups | Age Range | Description |
|---|---|---|
| Young forest | <40 years | Trees in early growth stage with underdeveloped canopies and unstable stand structure. |
| Intermediate-aged forest | 40–60 years | Vigorously growing trees forming closed canopies with rapid height and diameter increases. |
| Sub-mature forest | 60–80 years | Trees approaching physiological maturity with slowing growth but accumulating economic value. |
| Mature forest | 80–120 years | Trees at peak utilization stage with optimal timber quality and ecological functions. |
| Overmature forest | >120 years | Declining trees with stagnant growth, increased vulnerability to pests and diseases. |
| Model Name | RMSE | R2 |
|---|---|---|
| Linear Regression | 24.77 | 0.444 |
| Ridge Regression | 25.26 | 0.422 |
| Lasso Regression | 26.44 | 0.366 |
| ElasticNet Regression | 29.28 | 0.223 |
| Decision Tree Regression | 24.77 | 0.444 |
| Random Forest Regression | 25.39 | 0.466 |
| Gradient Boosting Regression | 24.77 | 0.444 |
| Extra Forests Regression | 24.77 | 0.444 |
| K-Nearest Neighbor Regression | 24.41 | 0.410 |
| Support Vector Regression | 34.13 | −0.056 |
| Multilayer Perceptron Regression | 59.15 | −2.171 |
| AdaBoost Regressor | 29.81 | 0.195 |
| Feature Combination | Validation Accuracy |
|---|---|
| C-band radar band: VV, VH | 0.45 |
| L-band radar and GEDI feature combinations: HHLSAR, HVLSAR, mean, meanbase, median, sd, iqr, p95, shan, countf | 0.42 |
| Optical feature combinations: RED, NIR, BLUE, SWIR, NDVI | 0.28 |
| Radar and terrain feature combinations: VV, VH, HHLSAR, HVLSAR, mean, meanbase, median, sd, iqr, p95, shan, countf, elevation, slope, aspect | 0.57 |
| Ecological characteristics combination: CAPHEI, LAI, FPAR, Agb _, Gpp, AMT, MDR, S _ I, STS, SMTWM, SMTCM, TARa, MTWQ, MTDQ, MTWQ _ 1, MTCQ | 0.55 |
| Comprehensive combination of characteristics1 (Includes GEDI Data): CAPHEI, LAI, FPAR, agb_, AMT, MDR, S_I, STS, SMTWM, SMTCM, TARa, MTWQ, MTDQ, MTWQ_1, MTCQ, VV, VH, RED, NIR, BLUE, SWIR, NDVI, HHLSAR, HVLSAR, mean, meanbase, median, sd, iqr, p95, shan, countf, elevation, slope, aspect | 0.65 |
| Comprehensive combination of characteristics2 (Not including GEDI data)CAPHEI, LAI, FPAR, Agb_, AMT, MDR, S _ I, STS, SMTWM, SMTCM, TARa, MTWQ, MTDQ, MTWQ_1, MTCQ, VV, VH, RED, NIR, Blue, SWIR, NDVI, Gpp, HHLSAR,HVLSAR,elevation,slope,aspect | 0.62 |
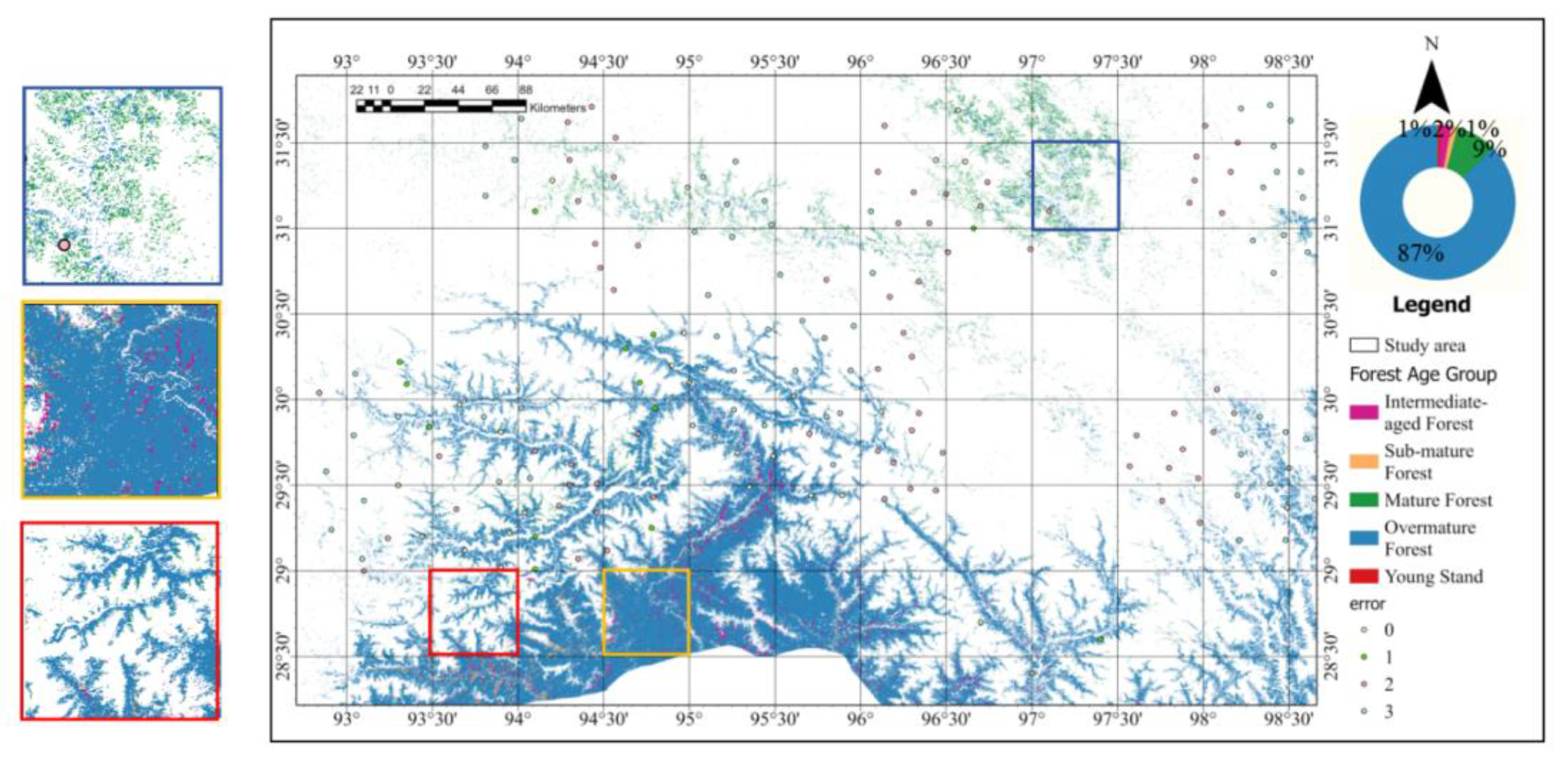
| Forest Age Group | Total Area (m2) | Percentage of Total Area |
|---|---|---|
| Young forest | 233,797,514.40 | 1% |
| Intermediate-aged forest | 833,776,911.90 | 2% |
| Sub-mature forest | 492,678,667.95 | 1% |
| Mature forest | 3,275,570,584.65 | 9% |
| Overmature forest | 33,472,546,497.30 | 87% |
| Total | 38,308,370,176.20 | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, Z.; Xu, K. Multi-Sensor Fusion and Machine Learning for Forest Age Mapping in Southeastern Tibet. Remote Sens. 2025, 17, 1926. https://doi.org/10.3390/rs17111926
Chi Z, Xu K. Multi-Sensor Fusion and Machine Learning for Forest Age Mapping in Southeastern Tibet. Remote Sensing. 2025; 17(11):1926. https://doi.org/10.3390/rs17111926
Chicago/Turabian StyleChi, Zelong, and Kaipeng Xu. 2025. "Multi-Sensor Fusion and Machine Learning for Forest Age Mapping in Southeastern Tibet" Remote Sensing 17, no. 11: 1926. https://doi.org/10.3390/rs17111926
APA StyleChi, Z., & Xu, K. (2025). Multi-Sensor Fusion and Machine Learning for Forest Age Mapping in Southeastern Tibet. Remote Sensing, 17(11), 1926. https://doi.org/10.3390/rs17111926






