Infrared Small Target Detection Using Directional Derivative Correlation Filtering and a Relative Intensity Contrast Measure
Abstract
1. Introduction
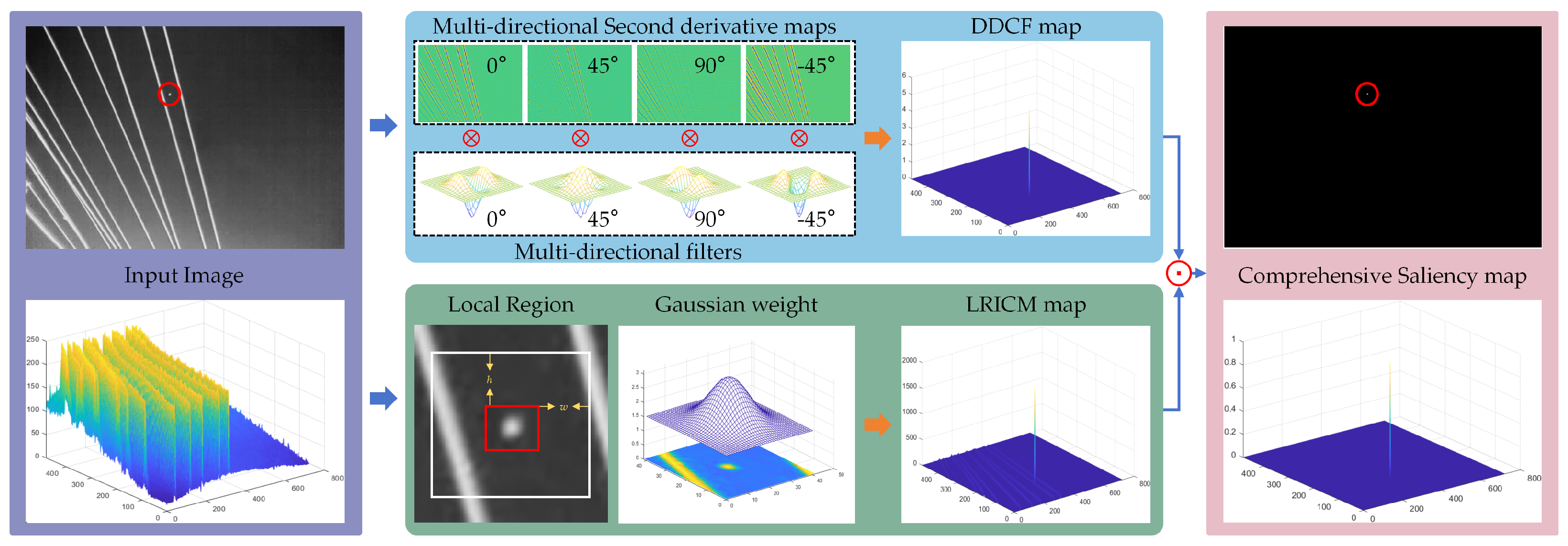
- A novel directional derivative correlation filtering (DDCF) method is proposed by thoroughly analyzing the differences in second-order derivative variations between small targets and background clutter. This method constructs four filters to process the second-order derivative maps of the image in different directions (0°, 45°, 90°, and −45°), generating a gradient saliency map that effectively eliminates edge clutter while enhancing the target signal.
- A new local relative intensity contrast measure (LRICM) method is introduced to improve the robustness of infrared small target detection. The LRICM method exploits the high contrast between small targets and their surroundings, addressing the limitations of DDCF in suppressing structural clutter such as corner interference.
- An effective small target detection scheme is proposed by fusing the response maps of DDCF and LRICM for mutual compensation. The fused map ensures that the target intensity is fully enhanced while significantly suppressing background clutter, including edges and corners.
2. Methodology
2.1. Directional Derivative Computation Based on Facet Model
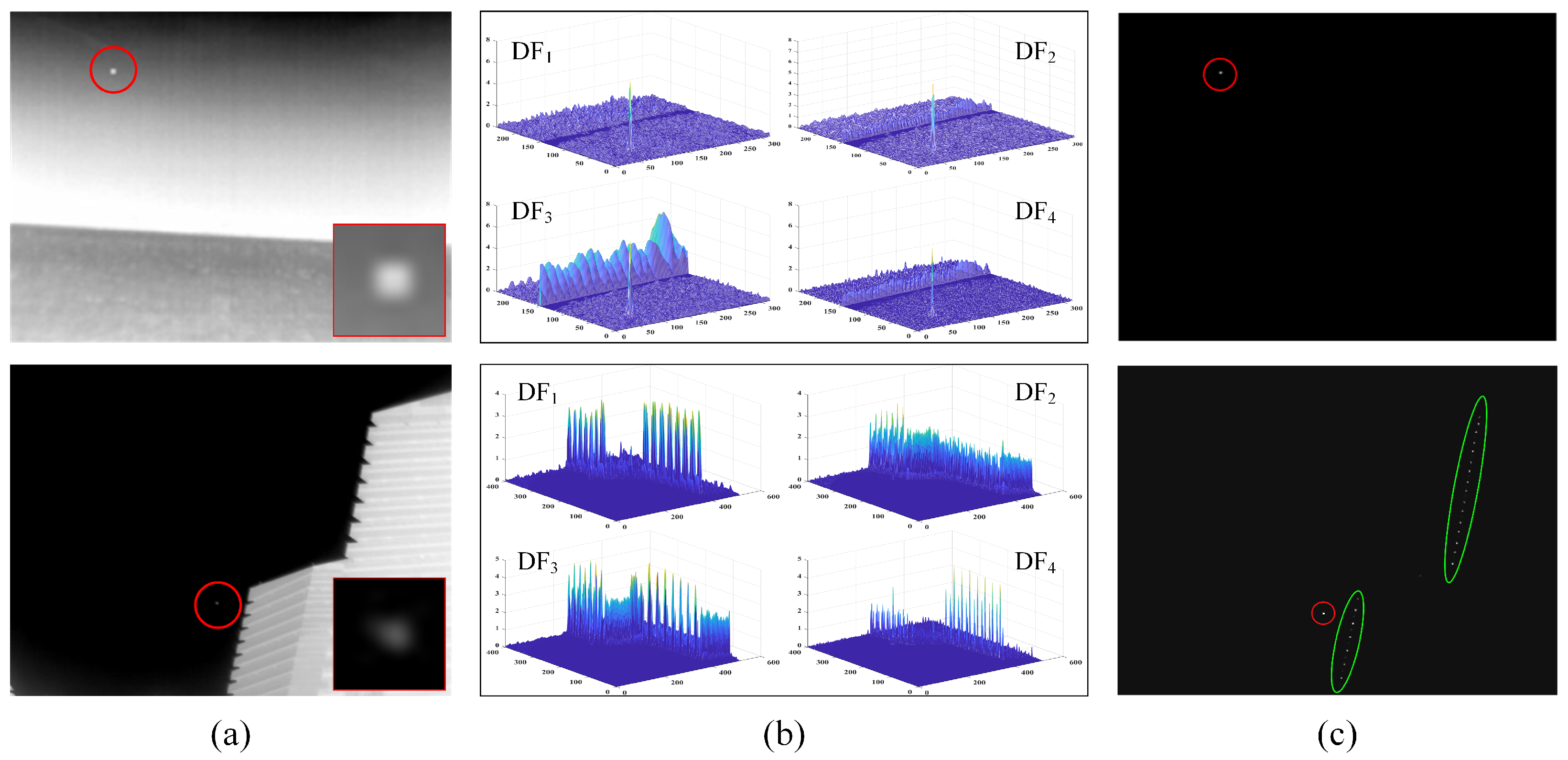
2.2. Directional Derivative Correlation Filtering
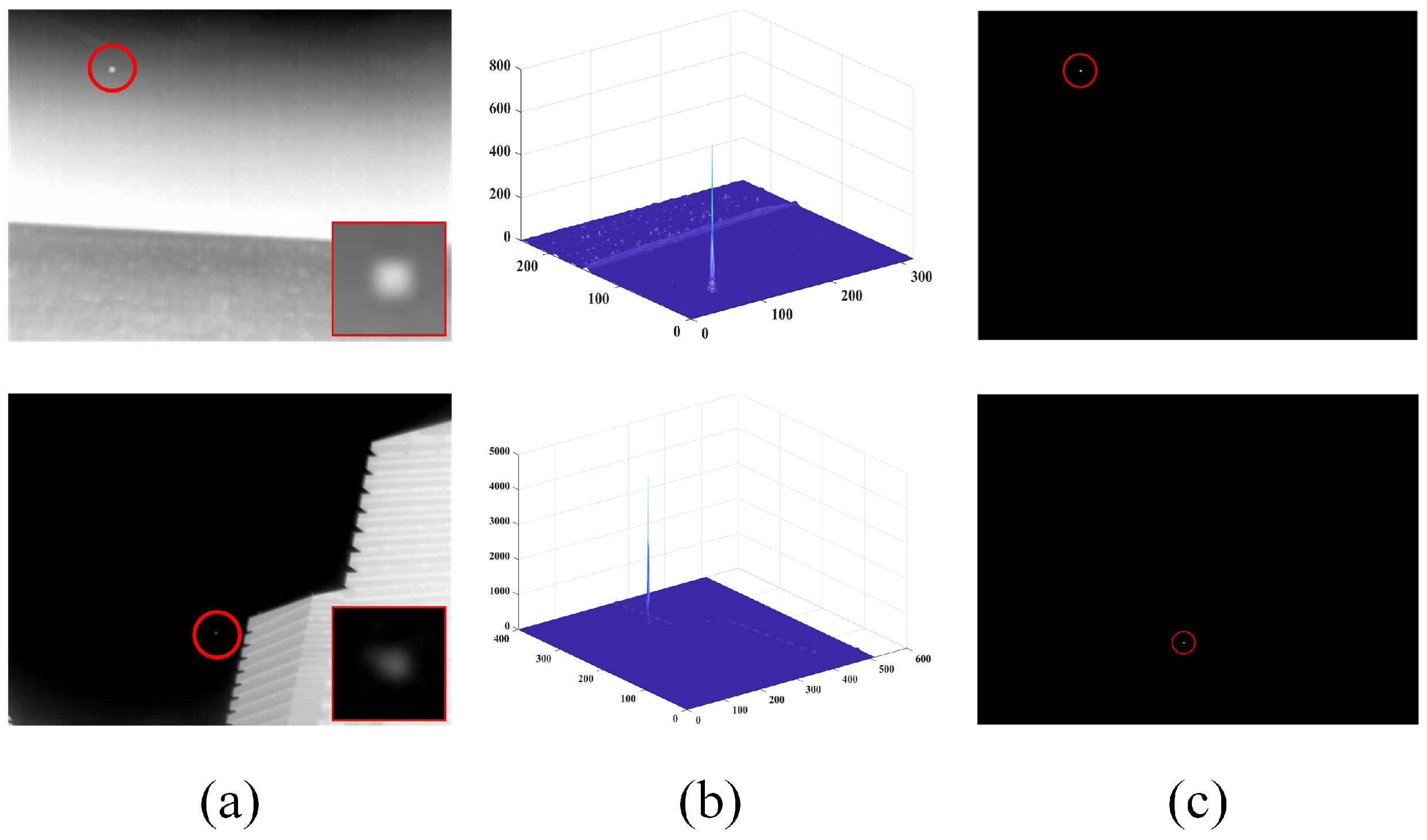
2.3. Local Relative Intensity Contrast Measure
- r is a non-negative value, with .
- When the center region represents the target, its intensity is greater than that of the surrounding region , so and . This implies that , indicating that the relative contrast has stronger target enhancement capabilities than the traditional contrast C.
- When the center region represents the local background, its intensity is typically less than or equal to that of the surrounding region . If , then and . If , then , which results in . In this case, , demonstrating that the relative contrast provides better background suppression than the traditional contrast C.
2.4. Target Detection Using DDCF and LRICM
| Algorithm 1 Infrared Small Target Detection Using DDCF and LRICM. |
| Input: An infrared image, , , , and Output: The segmented target image
|
3. Experiments
3.1. Experimental Setup
3.1.1. Dataset
3.1.2. Baseline Methods
3.1.3. Evaluation Metrics
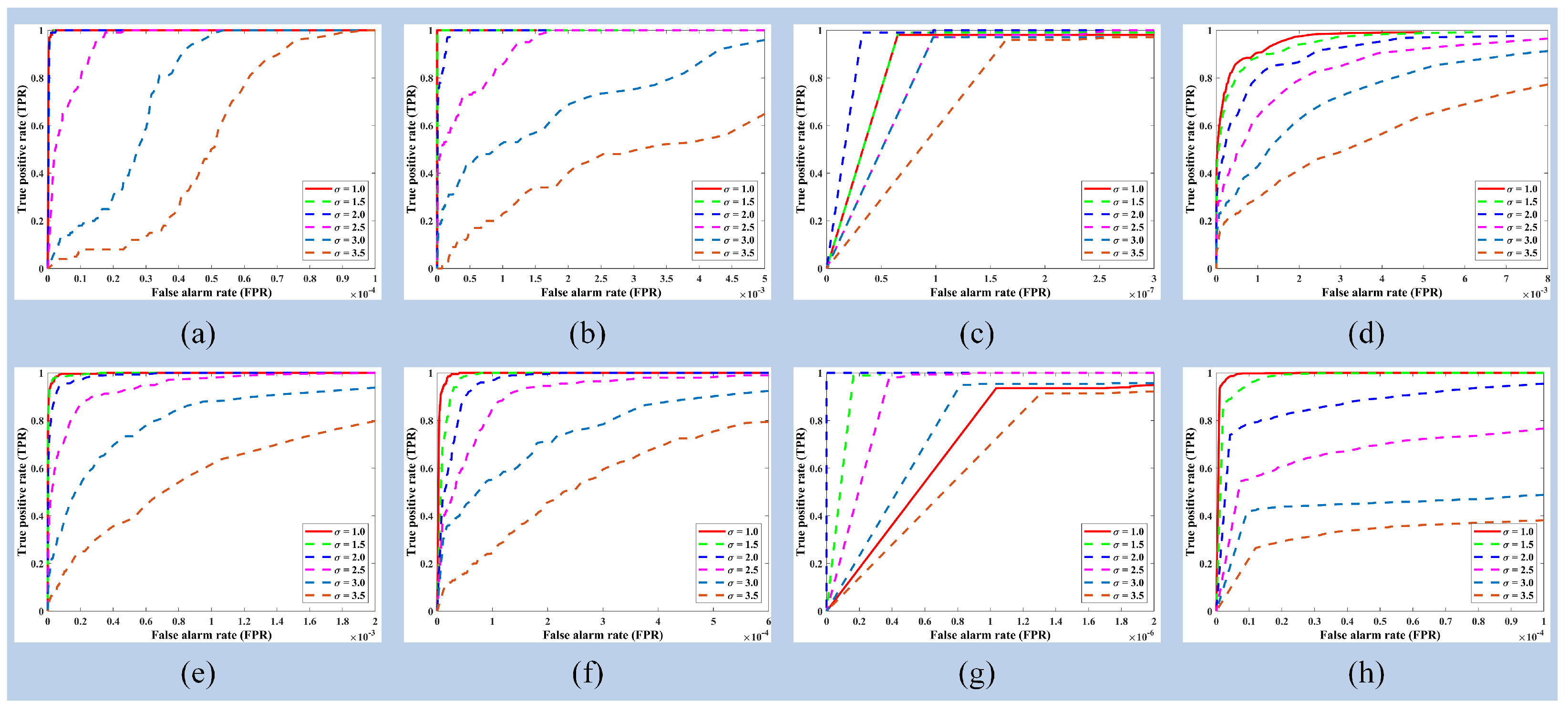
3.2. Parameter Configurations
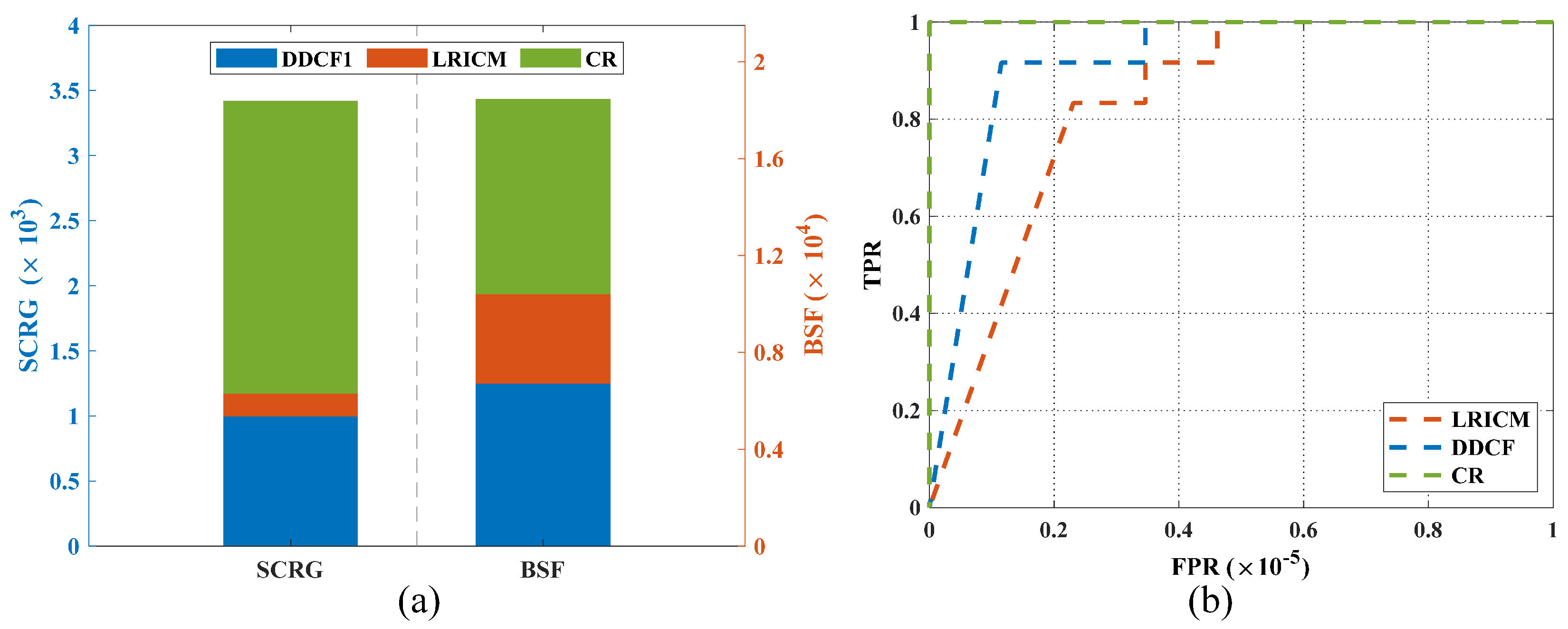
3.3. Ablation Experiments
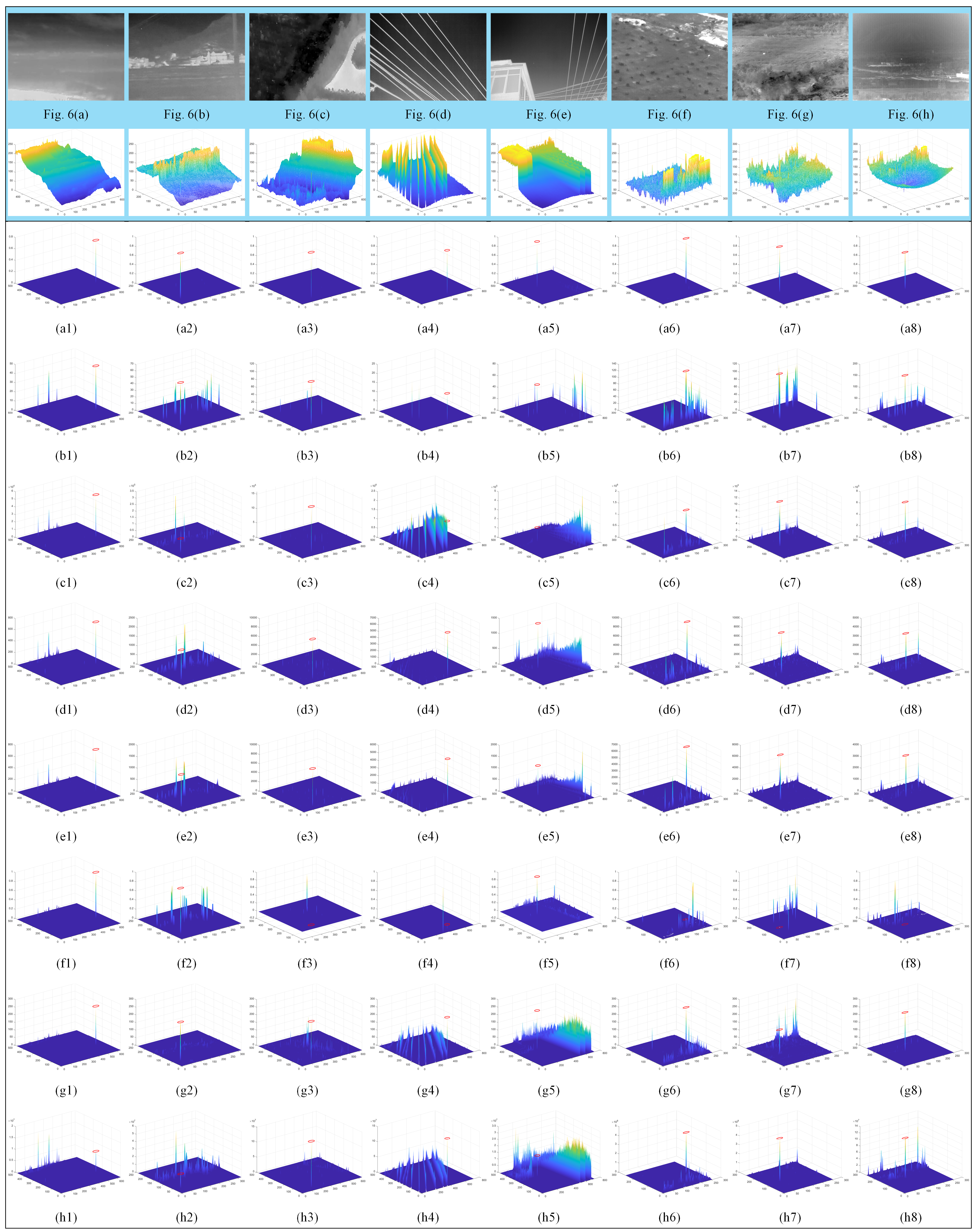
3.4. Visual Comparisons
3.5. Quantitative Comparisons
3.6. Computational Efficiency
- Second-order directional derivative computation: The algorithm uses a facet model to estimate second-order derivatives at each pixel. Each computation involves fitting a local window to obtain 10 Chebyshev polynomial coefficients. The complexity for this step is .
- Directional correlation filtering: Filtering is applied in four orientations (0°, 45°, 90°, and −45°), with each operation involving a convolution between the second-order derivative map and a filter of size . The complexity per direction is , and considering four directions, the total complexity becomes .
- Computation of local mean, minimum, and enhancement factor: For each pixel, a local processing window of size is analyzed to compute the mean and minimum intensity values. This leads to a complexity of .
- LRICM map computation: The local enhancement factor is computed for each pixel using a Gaussian-weighted sum over the local neighborhood, resulting in a complexity of .
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, F.; Dong, M.; Wang, X.; Yan, J. Infrared small-target detection using multiscale local average gray difference measure. Electronics 2022, 11, 1547. [Google Scholar] [CrossRef]
- Wang, X.; Xie, F.; Liu, W.; Tang, S.; Yan, J. Robust small infrared target detection using multi-scale contrast fuzzy discriminant segmentation. Expert Syst. Appl. 2023, 212, 118813. [Google Scholar] [CrossRef]
- Cui, Y.; Lei, T.; Chen, G.; Zhang, Y.; Peng, L.; Hao, X.; Zhang, G. Hollow side window filter with saliency prior for infrared small target detection. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Zhao, E.; Zheng, W.; Li, M.; Sun, H.; Wang, J. Infrared small target detection using local component uncertainty measure with consistency assessment. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Pitas, I.; Venetsanopoulos, A. Nonlinear mean filters in image-processing. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 573–584. [Google Scholar] [CrossRef]
- Barnett, J. Statistical analysis of median subtraction filtering with application to point target detection in infrared backgrounds. In Infrared Systems and Components III; SPIE: Bellingham, WA, USA, 1989; Volume 1050, pp. 10–18. [Google Scholar] [CrossRef]
- Deshpande, S.D.; Er, M.H.; Venkateswarlu, R.; Chan, P. Max-mean and max-median filters for detection of small targets. In Signal and Data Processing of Small Targets 1999; SPIE: Bellingham, WA, USA, 1999; Volume 3809, pp. 74–83. [Google Scholar] [CrossRef]
- Kim, S.; Yang, Y.; Lee, J.; Park, Y. Small target detection utilizing robust methods of the human visual system for irst. J. Infrared Millim. Terahertz Waves 2009, 30, 994–1011. [Google Scholar] [CrossRef]
- Wang, X.; Lv, G.; Xu, L. Infrared dim target detection based on visual attention. Infrared Phys. Technol. 2012, 55, 513–521. [Google Scholar] [CrossRef]
- Han, J.; Ma, Y.; Huang, J.; Mei, X.; Ma, J. An infrared small target detecting algorithm based on human visual system. IEEE Geosci. Remote Sens. Lett. 2016, 13, 452–456. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, T.; Wei, L.; Sang, N. Efficient method for multiscale small target detection from a natural scene. Opt. Eng. 1996, 35, 761–768. [Google Scholar] [CrossRef]
- Deng, H.; Sun, X.; Liu, M.; Ye, C.; Zhou, X. Infrared small-target detection using multiscale gray difference weighted image entropy. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 60–72. [Google Scholar] [CrossRef]
- Deng, H.; Sun, X.; Liu, M.; Ye, C.; Zhou, X. Small infrared target detection based on weighted local difference measure. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4204–4214. [Google Scholar] [CrossRef]
- Moradi, S.; Moallem, P.; Sabahi, M.F. Fast and robust small infrared target detection using absolute directional mean difference algorithm. Signal Process. 2020, 177, 107727. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Shen, Y.; Guo, Z. Infrared small target detection via center-surround gray difference measure with local image block analysis. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 63–81. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A local contrast method for small infrared target detection. IEEE Trans. Geosci. Remote Sens. 2014, 52, 574–581. [Google Scholar] [CrossRef]
- Han, J.; Ma, Y.; Zhou, B.; Fan, F.; Liang, K.; Fang, Y. A robust infrared small target detection algorithm based on human visual system. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2168–2172. [Google Scholar] [CrossRef]
- Chen, Y.; Xin, Y. An efficient infrared small target detection method based on visual contrast mechanism. IEEE Geosci. Remote Sens. Lett. 2016, 13, 962–966. [Google Scholar] [CrossRef]
- Wei, Y.; You, X.; Li, H. Multiscale patch-based contrast measure for small infrared target detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Han, J.; Liang, K.; Zhou, B.; Zhu, X.; Zhao, J.; Zhao, L. Infrared small target detection utilizing the multiscale relative local contrast measure. IEEE Geosci. Remote Sens. Lett. 2018, 15, 612–616. [Google Scholar] [CrossRef]
- Shi, Y.; Wei, Y.; Yao, H.; Pan, D.; Xiao, G. High-boost-based multiscale local contrast measure for infrared small target detection. IEEE Geosci. Remote Sens. Lett. 2018, 15, 33–37. [Google Scholar] [CrossRef]
- Qin, Y.; Bruzzone, L.; Gao, C.; Li, B. Infrared small target detection based on facet kernel and random walker. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7104–7118. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Zhang, H.; Zhao, Q.; Zhang, X.; Li, N. Infrared small target detection based on the weighted strengthened local contrast measure. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1670–1674. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, X. Robust infrared small target detection using a novel four-leaf model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 1462–1469. [Google Scholar] [CrossRef]
- Ye, L.; Liu, J.; Zhang, J.; Ju, J.; Wang, Y. A novel size-aware local contrast measure for tiny infrared target detection. IEEE Geosci. Remote Sens. Lett. 2025, 22, 1–5. [Google Scholar] [CrossRef]
- Qi, S.; Ma, J.; Tao, C.; Yang, C.; Tian, J. A robust directional saliency-based method for infrared small-target detection under various complex backgrounds. IEEE Geosci. Remote Sens. Lett. 2013, 10, 495–499. [Google Scholar] [CrossRef]
- Bai, X.; Bi, Y. Derivative entropy-based contrast measure for infrared small-target detection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2452–2466. [Google Scholar] [CrossRef]
- Liu, D.; Cao, L.; Li, Z.; Liu, T.; Che, P. Infrared small target detection based on flux density and direction diversity in gradient vector field. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2528–2554. [Google Scholar] [CrossRef]
- Cao, X.; Rong, C.; Bai, X. Infrared small target detection based on derivative dissimilarity measure. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3101–3116. [Google Scholar] [CrossRef]
- Zhang, X.; Ru, J.; Wu, C. Infrared small target detection based on gradient correlation filtering and contrast measurement. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5603012. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Li, W.; Liu, Y. Infrared small target detection based on gradient-intensity joint saliency measure. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7687–7699. [Google Scholar] [CrossRef]
- Wang, W.; Li, Z.; Siddique, A. Infrared maritime small-target detection based on fusion gray gradient clutter suppression. Remote Sens. 2024, 16, 1255. [Google Scholar] [CrossRef]
- Hao, C.; Li, Z.; Zhang, Y.; Chen, W.; Zou, Y. Infrared small target detection based on adaptive size estimation by multidirectional gradient filter. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Xi, Y.; Liu, D.; Kou, R.; Zhang, J.; Yu, W. Gradient-enhanced feature pyramid network for infrared small target detection. IEEE Geosci. Remote Sens. Lett. 2025, 22, 1–5. [Google Scholar] [CrossRef]
- Zhang, L.; Luo, J.; Huang, Y.; Wu, F.; Cui, X.; Peng, Z. Mdigcnet: Multidirectional information-guided contextual network for infrared small target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 2063–2076. [Google Scholar] [CrossRef]
- Ma, T.; Yang, Z.; Ren, X.; Wang, J.; Ku, Y. Infrared small target detection based on smoothness measure and thermal diffusion flowmetry. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7002505. [Google Scholar] [CrossRef]
- Haralick, R. Digital step edges from zero crossing of 2nd directional-derivatives. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 58–68. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Yang, Z.; Shi, F.; Yang, Y.; Zhao, M. Infrared small target detection based on singularity analysis and constrained random walker. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 2050–2064. [Google Scholar] [CrossRef]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared patch-image model for small target detection in a single image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef]
- Wu, F.; Yu, H.; Liu, A.; Luo, J.; Peng, Z. Infrared small target detection using spatiotemporal 4-D tensor train and ring unfolding. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–22. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Li, J.; Yang, J.; Siddique, A. Robust small infrared target detection using weighted adaptive ring top-hat transformation. Signal Process. 2024, 217, 109339. [Google Scholar] [CrossRef]
- Sun, H.; Bai, J.; Yang, F.; Bai, X. Receptive-field and direction induced attention network for infrared dim small target detection with a large-scale dataset irdst. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–13. [Google Scholar] [CrossRef]
- Hui, B.; Song, Z.; Fan, H.; Zhong, P.; Hu, W.; Zhang, X.; Ling, J.; Su, H.; Jin, W.; Zhang, Y.; et al. A dataset for infrared detection and tracking of dim-small aircraft targets under ground/air background. China Sci. Data 2020, 5, 291–302. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, Z. Infrared small target detection based on partial sum of the tensor nuclear norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef]
- Aghaziyarati, S.; Moradi, S.; Talebi, H. Small infrared target detection using absolute average difference weighted by cumulative directional derivatives. Infrared Phys. Technol. 2019, 101, 78–87. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Zhou, F.; Barnard, K. Asymmetric contextual modulation for infrared small target detection. In Proceedings of the 2021 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2021; pp. 949–958. [Google Scholar] [CrossRef]






| Sequences | Frames | Resolutions | Target Size and Shape | Background Description |
|---|---|---|---|---|
| Seq_1 | 100 | 640 × 480 | • ∼ | • Heavy clouds |
| • Triangle shaped | • High-intensity lake interference | |||
| Seq_2 | 100 | 320 × 240 | • ∼ | • Intense building interference |
| • From point to triangle shape | • Heavy edges and corners | |||
| Seq_3 | 100 | 640 × 480 | • ∼ | • High-intensity bushes |
| • Variable shape | • Shrub clutter of different scales | |||
| Seq_4 | 250 | 720 × 480 | • ∼ | • High-brightness wires |
| • Point shape | • Heavy edges | |||
| Seq_5 | 275 | 720 × 480 | • ∼ | • Intense building interference |
| • Point shape | • High-brightness wires | |||
| Seq_6 | 200 | 256 × 256 | • ∼ | • High-intensity stones |
| • Ellipse shape | • Dense Forest interference | |||
| Seq_7 | 280 | 256 × 256 | • ∼ | • Shrub clutter |
| • Circular shape | • Scattered stones | |||
| Seq_8 | 1200 | 256 × 256 | • ∼ | • Intense building interference |
| • Point shape | • Thick forest interference |
| Metrics | Parameter | Sq_1 | Sq_2 | Sq_3 | Sq_4 | Sq_5 | Sq_6 | Sq_7 | Sq_8 |
|---|---|---|---|---|---|---|---|---|---|
| SCRG | 1118.58 | 257.756 | 5743.40 | 53.8909 | 541.623 | 378.040 | 932.966 | 503.552 | |
| 634.270 | 158.668 | 8370.83 | 50.4575 | 436.577 | 273.071 | 1102.96 | 332.623 | ||
| 381.609 | 77.0201 | 9870.55 | 39.1242 | 266.048 | 149.595 | 1006.53 | 184.651 | ||
| 180.754 | 32.0840 | 8600.44 | 26.6670 | 138.703 | 64.8665 | 679.658 | 91.0055 | ||
| 78.2715 | 12.0105 | 6294.97 | 16.5672 | 67.0746 | 28.9064 | 386.735 | 42.6790 | ||
| 38.6712 | 4.19143 | 4277.85 | 9.60601 | 31.3070 | 17.0965 | 194.779 | 19.5860 | ||
| BSF | 17,951.4 | 7106.61 | 12,733.8 | 8896.81 | 17,462.9 | 3495.58 | 6789.94 | 5783.71 | |
| 15,568.2 | 5666.59 | 11,984.6 | 8223.98 | 14,836.0 | 3149.57 | 6449.29 | 5187.79 | ||
| 12,907.6 | 4102.07 | 11,286.9 | 8130.35 | 11,140.2 | 2825.26 | 5955.27 | 4493.41 | ||
| 10,480.9 | 2845.80 | 10,569.4 | 7291.23 | 8489.69 | 2390.03 | 5339.90 | 3603.10 | ||
| 10,309.4 | 2279.07 | 9698.69 | 5720.58 | 7294.63 | 1731.09 | 4735.32 | 3048.38 | ||
| 9942.20 | 2273.83 | 8807.85 | 6002.19 | 6974.20 | 1498.81 | 4029.35 | 2636.22 |
| Metrics | Parameter | Seq_1 | Seq_2 | Seq_3 | Seq_4 | Seq_5 | Seq_6 | Seq_7 | Seq_8 |
|---|---|---|---|---|---|---|---|---|---|
| SCRG | Ours | 5327.23 | 2161.24 | 152,881 | 765.581 | 5317.51 | 4701.86 | 11,838.7 | 14,188.2 |
| PSTNN | 118.056 | 25.4970 | 809.482 | 18.0156 | 183.449 | 33.7244 | 55.7637 | 31.8761 | |
| ADDGD | 187.299 | 21.9029 | 1237.00 | 4.66084 | 111.812 | 73.0348 | 125.696 | 130.914 | |
| MPCM | 116.611 | 20.4532 | 285.355 | 16.9110 | 225.730 | 47.2806 | 69.8973 | 67.2748 | |
| ADMD | 164.246 | 26.2851 | 332.135 | 17.4413 | 349.424 | 51.7063 | 92.8936 | 76.2349 | |
| FKRW | 385.183 | 175.569 | 281.145 | 92.2765 | 764.785 | 32.8007 | 38.8072 | 232.315 | |
| ELUM | 430.034 | 98.9511 | 88.0780 | 6.31599 | 115.720 | 66.0011 | 39.9629 | 125.680 | |
| HBMLCM | 73.3710 | 12.9106 | 748.422 | 2.36939 | 24.3549 | 58.7251 | 199.192 | 58.8405 | |
| BSF | Ours | 20,522.0 | 8685.67 | 13,784.1 | 17,645.5 | 29,336.8 | 4002.49 | 7210.42 | 6836.73 |
| PSTNN | 6178.88 | 1940.94 | 5295.24 | 4366.78 | 6842.73 | 1203.36 | 2259.84 | 2123.18 | |
| ADDGD | 10,379.0 | 2711.69 | 9082.53 | 3096.04 | 5965.53 | 2513.48 | 4564.98 | 4345.26 | |
| MPCM | 7243.25 | 1978.23 | 6975.03 | 2679.28 | 9089.19 | 1997.54 | 3731.93 | 3321.58 | |
| ADMD | 9490.52 | 2192.33 | 8047.79 | 4593.21 | 10,995.6 | 2252.68 | 4383.71 | 3545.21 | |
| FKRW | 9262.52 | 4999.54 | 7208.32 | 9311.87 | 12266.8 | 1540.51 | 3520.87 | 3252.49 | |
| ELUM | 12,721.3 | 5153.07 | 6497.50 | 1384.51 | 3030.48 | 2399.49 | 2986.55 | 5138.71 | |
| HBMLCM | 7029.30 | 1896.11 | 9162.27 | 1188.53 | 2035.65 | 2154.98 | 5025.96 | 2969.10 |
| Methods | Ours | PSTNN | ADDGD | MPCM | ADMD | FKRW | ELUM | HBMLCM | |
|---|---|---|---|---|---|---|---|---|---|
| Complexity | |||||||||
| Time (s) | Seq_1 | 0.0615 | 0.4992 | 0.0572 | 0.0835 | 0.0139 | 0.1438 | 0.0118 | 0.0270 |
| Seq_2 | 0.0131 | 0.1355 | 0.0119 | 0.0178 | 0.0029 | 0.0561 | 0.0019 | 0.0063 | |
| Seq_4 | 0.0715 | 0.6022 | 0.0607 | 0.0950 | 0.0143 | 0.1504 | 0.0122 | 0.0280 | |
| Seq_6 | 0.0118 | 0.0511 | 0.0105 | 0.0167 | 0.0024 | 0.0323 | 0.0017 | 0.0053 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, F.; Yang, D.; Yang, Y.; Wang, T.; Zhang, K. Infrared Small Target Detection Using Directional Derivative Correlation Filtering and a Relative Intensity Contrast Measure. Remote Sens. 2025, 17, 1921. https://doi.org/10.3390/rs17111921
Xie F, Yang D, Yang Y, Wang T, Zhang K. Infrared Small Target Detection Using Directional Derivative Correlation Filtering and a Relative Intensity Contrast Measure. Remote Sensing. 2025; 17(11):1921. https://doi.org/10.3390/rs17111921
Chicago/Turabian StyleXie, Feng, Dongsheng Yang, Yao Yang, Tao Wang, and Kai Zhang. 2025. "Infrared Small Target Detection Using Directional Derivative Correlation Filtering and a Relative Intensity Contrast Measure" Remote Sensing 17, no. 11: 1921. https://doi.org/10.3390/rs17111921
APA StyleXie, F., Yang, D., Yang, Y., Wang, T., & Zhang, K. (2025). Infrared Small Target Detection Using Directional Derivative Correlation Filtering and a Relative Intensity Contrast Measure. Remote Sensing, 17(11), 1921. https://doi.org/10.3390/rs17111921





