Abstract
The effective management of landfills requires advancements in techniques for rapid data collection and analysis of gas emissions. This work aims to refine methane (CH4) emission data acquired from landfills by applying a robust geostatistical method to drone-collected measurements. Specifically, we use UAV-mounted laser spectrophotometer technology (TDLAS-UAV) to gather rapid, high-resolution data, which can sometimes be noisy due to atmospheric variations and sensor drift. For data handling, the key innovation is the application of the local indicator of spatial association (LISA), a technique that typically provides p-values to assess the statistical significance of observed spatial clusters. This approach was applied both on an areal basis and on a linear basis, following the order of data acquisition, and it produced comparable results. Very low p-values are considered indicative of non-random clustering, suggesting the influence of an underlying spatial control factor. These results were subsequently validated through independent flux chamber surveys. This validation confirms the reliability and objectivity of our geostatistical method in improving drone-based methane emission assessments. The research highlights the need to optimize drone flight paths to ensure a uniform spatial distribution of data and reduce edge effects. It notes that many CH4 flux measurements often yield non-detectable results, suggesting a review of detection limits. Future work should refine UAV flight patterns and data processing with semi-controlled experiments—using known methane sources—to determine optimal acquisition parameters, such as flight height, sampling frequency, grid resolution, and wind influence.
1. Introduction
In recent years, great attention has been paid to monitoring gas emissions from landfills and detecting leaks in natural gas distribution networks. In landfills, the rate and type of gas production vary over time. Shortly after closure of a landfill (months to years), when gas production is greatest, methane (CH4) is the primary component of the gas, typically accounting for 55% by volume, and carbon dioxide (CO2) accounts for most of the remaining volume [1,2,3,4,5]. These components are produced from the anaerobic decomposition of biodegradable organic material. The detection of methane leakage is an environmental issue for the following reasons: (i) methane escaping into the atmosphere can lead to potential hazards, including the risk of explosion [6], and it constitutes an important greenhouse gas; (ii) methane leakage lowers the yield of gas collection and distribution systems and thus represents a wasted source of energy; (iii) the presence of emission points within the landfill may highlight portions of the landfill’s impermeable waterproofing cover that are flawed and could constitute preferential pathways for meteoric water infiltration, resulting in increased leachate production and the associated costs of disposal and potential groundwater pollution. Hence, the mitigation of methane emission to the atmosphere from landfill gas is targeted as a relevant issue in the European Commission Guidance on landfill gas [7].
Gas emission monitoring can be conducted in several ways: soil gas, near-surface gases, emissions, ambient air, and indoor air [8,9,10,11]. On the ground, probes can be used to sample soil gas topping the landfill, even at different depths (taking care not to intercept the cover sheet, if present) to determine the soil-pore gas concentration, and then using migration (diffusion) models, the flow of gas at the soil–atmosphere interface is inferred [12]. Flux chambers, static or dynamic, allow a direct measurement of flux to be determined [13,14,15]. In recent years, flux measurement techniques with flux chambers have developed in the direction of a rather rapid response [16,17,18].
Other methods of measuring CH4 concentrations at the soil–atmosphere interface, or in the first few meters of the atmosphere, related to possible landfill gas emissions, involve the use of portable analyzers based on infrared detectors [19,20], absorption spectroscopy (TDLAS) [21,22], and interferometry [23,24,25]. Clearly, the methodological approach, e.g., the spatial density of sampling, the gaseous species of interest, and the complementary acquisition of ground-based data, largely depends on the purposes of the study. However, due to a pronounced “nugget effect”—often resulting from localized gas exhalation—survey campaigns require a very large number of observations to identify exhalation/emission “hot spots” [26,27].
In order to reduce both the time and cost of acquisition campaigns—and to enable data collection in inaccessible areas [28]—UAV-mounted sensors offer significant improvements in acquisition speed and study-area coverage [29,30]. After data collection, the processing phase becomes critical. Depending on the measurement method, it may be necessary to filter out noise (such as false positives) before identifying points or areas with fluxes or concentrations that exceed the local background [31,32]. Typically, detecting these spatial “hot spots” requires geostatistical techniques. This can involve building a two-dimensional model of the spatial distribution through interpolation techniques (e.g., kriging in [33]; Delaunay tessellation in [34]), or applying the local indicator of spatial association (LISA) analysis [35,36].
In environments such as landfills, the preferential route through which methane-containing biogas emissions occur is precisely the interface surface between soil and the atmosphere [37]. In this regard, several experimental studies have led to very interesting application results, aimed at implementing SEM (surface emission monitoring) protocols, based on measurements via sensors mounted on drones. A survey carried out via drone can sometimes be integrated with ground measurements [29] or supported by interpolation techniques that take into strict consideration the characteristics of the wind (speed and direction) at the time of the survey [38].
This work aims to verify a new statistical approach that is useful to identify gaseous emissions from both capped and uncapped landfill sectors through UAV surveys. Accurate identification requires proper data handling to overcome the uncertainties inherent in ambient air measurements—taken over an air column of about 10 m—which are affected by factors such as methane background variability, variations in wind speed and direction, atmospheric pressure variations, changes in both the morphology of the landfill site and the type of surface layer present at ground level (grass, HDPE cover, rock granulate cover, etc.), or instrumental error [39].
The UAV-mounted TDLAS sensor generates a vast number of observations, resulting in a distribution of values that can be challenging to interpret. Therefore, this study focuses on advanced statistical processing of the data to identify significant clusters of high CH₄ values that are unlikely to occur by chance.
To assess the performance of the UAV-based surveys and our statistical approach, the results were compared with landfill gas flux measurements obtained via flux chambers at the soil–atmosphere interface. Although these flux chamber measurements carry their own uncertainties, they provide gas flux values that are less influenced by air column averaging and wind effects.
2. Materials and Methods
2.1. Equipment
2.1.1. Sensor for CH4 UAV Monitoring
A Pergam Laser Falcon sensor (Pergam Ltd., London, UK) based on tunable diode laser absorption spectroscopy (TDLAS), also known as a laser spectrometer, was used to measure methane (CH4) concentrations. This sensor utilizes a laser source that emits a precisely tuned beam at a specific frequency set at 1650 nm. This frequency is chosen to be readily absorbed by methane gas molecules while minimizing interference from other airborne compounds. The sensor then detects the returning laser beam with a receiving device.
The instrument has several ports for connection and communication with other systems (a micro USB port that provides the power supply, a standard USB port that enables bi-directional data transfer with a data logger and the drone itself, and a microSD card slot for storing hardware upgrade files). For easy integration onto the drone, the equipment features pre-drilled holes in its casing. Lightweight yet robust, custom-molded brackets are securely fastened to these holes using mechanical systems.
The sensor system also includes a data logger that has the role of acquiring information from the TDLAS, RTK (real-time kinematic) system, and altimeter, coupling methane measurement with the coordinates and height data. The data logger also exchanges important information to and from the UAV system, such as flight telemetry, loading of preset routes for automatic mode flight activities, and sensor control. With the TDLAS technology, the CH4 concentration (ppm * m) is determined over the distance between the sensor and the ground, i.e., the height above the ground. Therefore, it is necessary for the system to accurately scan and keep constant the flight elevation, as far as possible, to make observations comparable. The UAV system is equipped with its own autonomous height assessment system, described below, to avoid relying on pre-loaded maps (which were found to be prone to significant errors). This part of the system consists of an additional radar altimeter that directly measures the UAV–ground distance and allows the UAV to fly in a “terrain following” mode. Thus, even when flying over jagged planes, the distance between the ground plane and the UAV always remains constant.

Table 1.
Sensor specifications.

Table 2.
Radar altimeter specifications.

Table 3.
Data logger specifications.
2.1.2. UAV Platform
The TDLAS sensor was mounted on a quadcopter (Matrice 350, DJI) with a weight of 4 kg and a maximum takeoff weight of 6.14 kg. The quadcopter system represented the best choice for reliability, in-flight stability, payload portability, and maximization of flight time. The chosen system was then equipped with the above-mentioned RTK system, which provides excellent precision for georeferencing. The power system, consisting of two batteries operating simultaneously, ensured flight times of about 30 min, taking into account the increased power consumption due to the presence of the sensor and the data logger. Additional plus values inherent in four-motor systems are in-flight maneuverability and precision of movement, both when used with manual flight and when operated by automatic flight. Table 4 summarizes the UAV system specifications.

Table 4.
UAV system specifications.
2.1.3. Flux Chamber and Flux Determination
Landfill gas emissions were estimated following the procedure illustrated in [40]. As provided for in the guideline, flux measurements were conducted using a static non-stationary measurement system [15,18,28,37,41,42,43,44,45,46] (this type of system is defined as "non-stationary" because, assuming a constant emission flow from the soil, the concentration of analytes in the gas mixture within the chamber increases over time without remaining constant at any point in the chamber; it is termed “static” because, unlike dynamic chambers where an inert gas flows through the chamber, this system recirculates the gas without any treatment and analyzes it directly in the field) consisting of a handheld chamber connected to the sensor box. In particular, the capacity of the chamber is 2.76 liters, and it is made of steel and Teflon. Inside the chamber, a mixing device and sensors for pressure, humidity, and temperature are installed. Finally, its circular base area is 0.031 m2. The system is equipped with the following sensors (Table 5):
- PID (photo ionization detector): for measuring volatile organic compounds (VOCs) with a 10 eV PID lamp. Sensitive to a wide range of organic substances (and some inorganic substances, such as NH3, H2S); the reading is given as isobutylene equivalent (accuracy < 3% of the reading);
- NDIR (non-dispersive infrared absorption): for measuring CO2 (accuracy +/−2% of the reading);
- TDLAS (tunable diode laser absorption spectroscopy): for measuring CH4 (accuracy +/−2% of the reading);
- Ec (Electrochemical cell): for measuring H2S (accuracy < 3% of the reading).

Table 5.
Gas concentration ranges measurable by the sensors.
Table 5.
Gas concentration ranges measurable by the sensors.
| Sensor | Target | Measurable Range | Resolution (ppm) |
|---|---|---|---|
| TD LAS | CH4 | 0 ppm–10,000 ppm | 0.1 |
| IR | CO2 | 0–10,000 ppm | 1 |
| PID | VOCs | 0–50 ppm | 1 |
| EC | H2S | 0–100 ppm | 1 |
At each measurement point, data acquisition for flux calculation required approximately 3 to 5 min, that is the time span in which a linear increase of gas concentrations is generally observed. Curves of real-time concentration C(t) versus time were generated graphically by the bundled software, which is installed in the handheld computer, and the relative slope gradient for each compound was calculated. The equation that describes the interpolation curve is:
where:
C(t) = αt + β
- β is the y-intercept, corresponding to the expected value of C when t = 0;
- α is the slope of the regression line, i.e., the increasing rate of C with time (dC/dt).
The dimensions of the flux chamber barometric pressure data, air temperature, and the slope gradient of the curve (α ppm/s) were used for deriving the flux values in moles per square meter per day (mol∙m−2 d−1), as defined by the equation:
The Ack factor is related to the physical properties of the flux chamber and the environmental sampling parameters [40]:
where:
- 86,400 is the number of seconds in a day [s d−1];
- 106 is the conversion factor from ppm (in α) to mol∙mol−1;
- Patm is the atmospheric pressure [Pa];
- Vc is the net volume of the chamber [m3];
- R = 8.314472 is the universal gas constant [ m3∙Pa∙K−1∙mol−1];
- T is the air temperature [°K];
- AC is the base area of the chamber [m2].
2.1.4. Weather Data Monitoring
Environmental conditions, including soil and atmospheric parameters, can greatly affect CH4 emission from soil [42,43] as well as CH4 detection along the air column [44,45]. Weather monitoring at the site was carried out during the survey and in the four days preceding it. This was necessary to contextualize the emission phenomena based on any meteorological phenomena that may have occurred. Monitoring in the days prior aimed to verify the absence of rainfall and/or meteorological events of an unusual magnitude for the period of the year and for the area of interest, thereby excluding the possibility of anomalous emission profiles induced by such events. Weather data were acquired by a weather station, mounted on tripods; technical specifications, as well as the data acquired during the survey, are provided in the Supplementary Materials.
3. Sampling Strategies
Data collection was carried out in four areas, as illustrated in Figure 1.
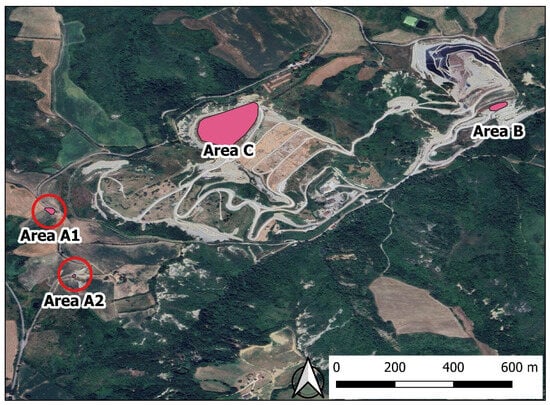
Figure 1.
Location of surveyed areas. Areas A1 and A2 are outside the landfill and are taken as the background area. Area B is active and not capped; in Area C, filling is over, and the area has been capped.
Areas A1 and A2 are two small plots located outside the main landfill body. Currently used for agricultural purposes (specifically for growing animal fodder), they serve as local reference sites for soil emissivity studies. The UAV flight over Area A1 yielded 469 methane (CH4) observations. Area A2, situated approximately 300 m south of Area A1, underwent two flux measurements using a flux chamber for CH4 and CO2.
Area B, approximately 60 × 20 m large, is located on a steep slope of the landfill where waste is still being disposed, and where a final cover (capping) has not yet been applied. In Area B, drone surveys yielded 658 CH4 measurements, and six points were measured for CH₄ and CO₂ flux using a flux chamber.
Area C is the main study area, with a surface of approximately 3 ha. Following the completion of landfill operations in 2021, a specialized plastic sheet, a high-density polyethylene (HDPE) geomembrane, was installed as a final cover (capping). A system of biogas wells and an active suction system are used in this area to collect the biogas and convert it into energy. The biogas wells are regularly inspected and cleaned to ensure they are working properly. A stabilized, unpaved track runs circularly throughout the site. Most of the biogas suction system is underground, except for some above-ground lines. Within the site, there are three collectors for the biogas capture lines, two located in the central area of the lot and the third positioned at the foot of the slope. Drone surveys in Area C yielded 2552 methane (CH4) measurements, and flux measurements (CH4 and CO2) were conducted at 37 points. In all areas, the acquisition parameters, including flight elevation (10 m agl), were the same. The data acquisition pattern is reported in Table 6.

Table 6.
Data acquisition pattern. Observations are provided by drone and flux chamber surveys, from investigated areas (A1, A2, B, C, see Figure 1).
4. Results
Data were acquired in the four areas illustrated in Figure 1, A1, A2, B, and C (where areas A1 and A2 are representative of the background scenario outside the landfill), with different expected emission characteristics.
The drone and flux chamber measurements were recorded via methods that do not return completely comparable results. Specifically, the CH4 observations acquired from the drone-mounted sensor return a concentration, expressed in ppmv * m, representing the CH4 concentration along the column of air (traversed by the TDLAS laser beam) between the ground and the sensor (at a height of approximately 10 m). With the flux chambers, the flux of CO2 and CH4, expressed as moles/m2/d−1, was measured directly at the soil–atmosphere interface.
A non-negligible disturbance component, related to different factors (e.g., ambient variability of the background, wind speed, and instrumental error), is expected for the measurements taken via drone in the above-mentioned terrain–drone air column, where the escaping gas from the surface mixes with the atmosphere. On the other hand, acquisition from drone-mounted sensors allows the acquisition of thousands of readings in a very brief time span at extremely low cost. In addition, it is important to highlight that the measurements taken with a flux chamber are point-specific and more representative of the actual emission “signal”; however, it is also known that the flux of volatiles is extremely variable in space and time.
Data processing included the following:
- Descriptive statistics of raw data obtained from the drone sensor (CH4) and flux chamber (CH4 and CO2) for each investigated area, and comparison between the datasets of each surveyed area;
- Spatial distribution of raw data;
- Organization of CH4 drone-derived data according to the following steps:
- Grouping of raw observations;
- Definition of the statistical indicator to assign to the grouped observations;
- Definition of the threshold value (TV);
- Contiguity analysis of grouped observations exceeding the TV (clustering);
- Calculation of the probabilities that the clustering is random;
- Comparison between non-random clustering and measurements from the flux chamber.
The following paragraphs describe in detail the results of the data processing.
4.1. Descriptive Statistics of Raw Data
Table 7 presents the descriptive statistics for drone and flux chamber measurements collected within the studied areas. As highlighted in Figure 2 (left and right), the distributions of CH4 (ppm * m) values in areas B and C largely fit, i.e., no significant difference in CH4 values is observed between capped and uncapped sections within the landfill. Instead, the background area (A1) located outside the landfill exhibits significantly lower values, particularly at higher percentiles. Specifically, CH4 values in A1 for >90 percentiles are approximately half of those observed in areas B and C.

Table 7.
Main statistics of data acquired by drone (ppm * m) and flux chamber (mol/m2/d). For CH4 and CO2 statistics, the number in parentheses in the “N_Obs” field refers to the number of observations greater than the detection limit. Out of 45 total CH4 flux measurements, only four were quantifiable. Therefore, for this entry, the statistics are unreliable. P10 to P99 are the respective percentiles.
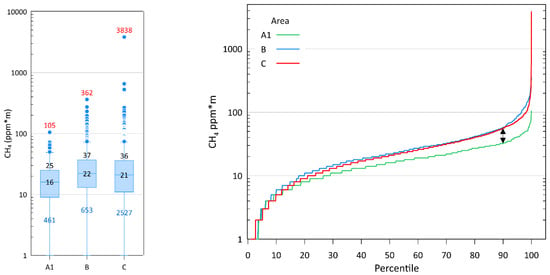
Figure 2.
(left) Distribution of CH4 values acquired by UAV (ppm * m) in the investigated areas (A1, B, C); (right) percentile distribution; the arrow marks the difference in distribution of A1 vs. B and C.
4.2. Spatial Distribution of Raw Data
The distribution of values acquired by the drone and flux chamber is represented in Figure 3 (areas A1 and B) and Figure 4 (Area C). To highlight the areas with higher values of drone surveys, the raw observations (ROs) were classified into three classes, as follows:
- Values below the 25th percentile (P25);
- Values between the 25th and 90th percentiles (P25-P90);
- Values between the 90th and 100th percentiles (P90-max).
In Area A1, RO values greater than P90 identify no spatial structures. No flux measurements were made with the flux chamber in this area.
In Area B, several observations exceeding P90 (i.e., values greater than 57 ppm * m) seem to be clustered in a small portion of the area, approximately in correspondence with the only two methane flux measurements exceeding the detection limit (Figure 3, bottom). It can be observed that the distance between the flux chamber measurement points and the point with the highest drone-measured values is only a few meters. However, within these few meters, there are also numerous observations with relatively low values; therefore, the relationships between the two types of measurements are not fully clear.
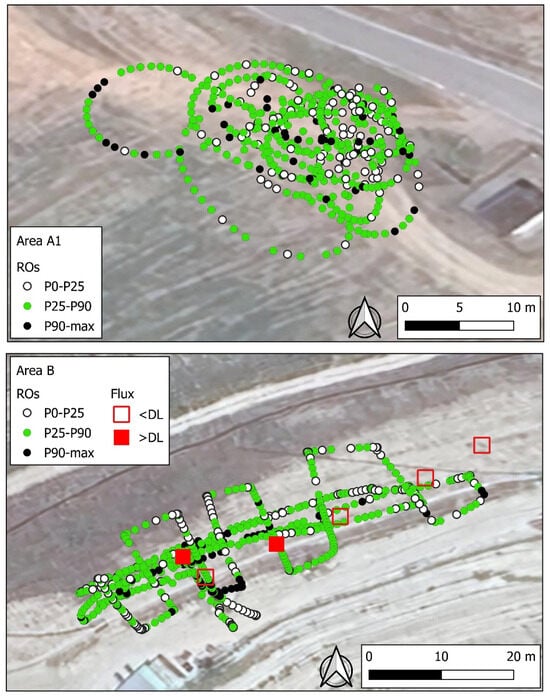
Figure 3.
Spatial distribution of CH4 (ppm * m) in Area A1 (top) and Area B (bottom). In Area B, the results of CH4 flux (mol/m2/d) measured by the flux chamber are also reported.
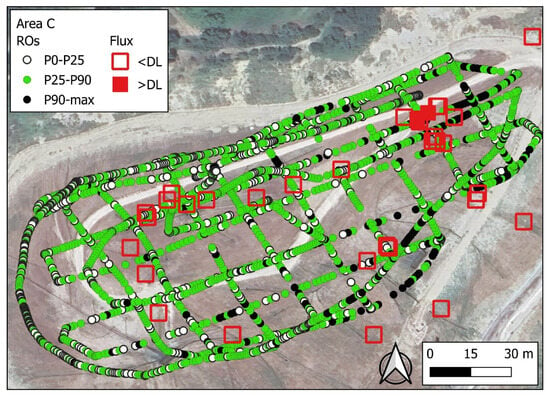
Figure 4.
Spatial distribution of CH4 (ppm * m) in Area C. The results of CH4 flux (mol/m2/d) measured by the flux chamber are also reported.
The situation is more complex in Area C, the main area of investigation (Figure 4). In the northern and western sectors, the values measured by the drone are relatively low. In other areas of the site, along the measurement acquisition path, the values are extremely variable over very small distances (about a few tens of centimeters). Overall, it is quite difficult to identify spatial structures in the CH4 distribution that can be correlated with the flux measurements. Out of 36 flux measurements, only two showed measurable values, while the rest were below the detection limit (DL).
4.3. Organization and Results of CH4 Drone-Derived Data
Individual raw observations (ROs) collected by the drone show a certain degree of randomness due to sensor errors and, mostly, complex acquisition conditions. To make the data informative and reliable, it is therefore necessary to develop a method of processing the data that highlights the spatial structure of CH4 distribution. The surveying of CH4 spatial structures of emission points/areas is based on two criteria, as follows:
- Spatial contiguity: the spatial structure is given by the contiguity of two or more points (or spatial elements) that show values above a certain threshold (binary approach);
- Low probability of randomness: the spatial contiguity of two or more elements exceeding the threshold must have a low probability of being random.
Ultimately, the probability of the contiguity of several points (or spatial elements) not being random regulates the identification of the threshold and the number of contiguous elements that define that structure.
These criteria were used to process the data, according to two different approaches: (i) a “linear” analysis between observations acquired at successive times and points of the drone’s trajectory, and (ii) a 2D “spatial” analysis, where raw observations were grouped in hexagonal cells (Figure 5).
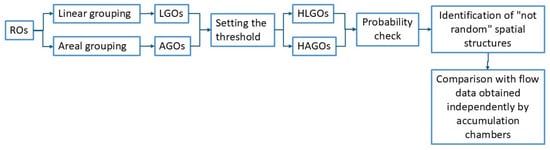
Figure 5.
General scheme of the processing of CH4 data acquired by drone. Two alternative processes are proposed. (i) The raw drone-acquired observations (ROs) are grouped on a linear basis: 11 ROs acquired consecutively form an LGO (linear grouped observation), which is assigned the 75th value of the 11 ROs; (ii) a variable number of ROs are grouped together, as they are included in the same areal unit and form an AGO (areal grouped observation), which is assigned the average of the values of the ROs enclosed in the area. A threshold value, TV (consisting of the 90th percentiles of the values of LGOs and AGOs), is established. Values exceeding the TVs are called HLGOs and HAGOs, respectively. The spatial contiguity is assessed, calculating the probabilities that adjacent groups of HLGOs and HAGOs may or may not be random. The results of this evaluation are compared with CH4 flux data acquired independently with the accumulation chambers.
The “linear” analysis: this method involves grouping ROs (taken in the same spatial and temporal order as detected) into sets of 11 and calculating the P75 for each group. Additionally, the coordinates of the central point within each group (i.e., the coordinates of the sixth observation) are assigned. The original number of n ROs is thus reduced to n/11 (which will be referred to herein as the “linear grouped observations”, LGOs). A threshold value (TV) is set; here, the TV is the P90 of the values (P75 of GOs) assigned to the LGOs. The TV splits the grouped observations into two sets: (i) grouped observations lower than the TV (90% of LGOs), and (ii) grouped observations higher than the TV (i.e., 10% of grouped observations, HLGOs).
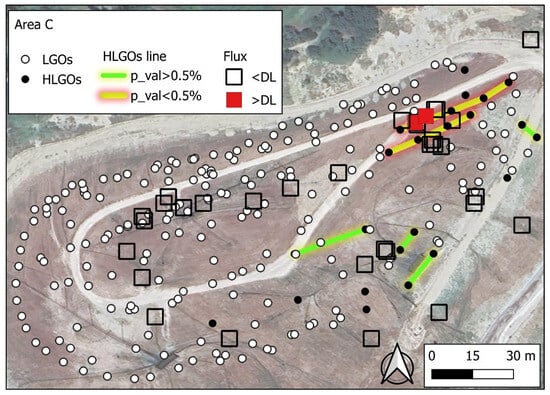
Figure 6.
CH4 distribution of LGOs and HLGOs (ppm * m) in Area C. There are two lineaments formed by four adjacent HLGOs (yellow line) and four lineaments formed by only two adjacent HLGOs (green lines). For the latter, the possibility that such structures are related to chance cannot be excluded. Results of CH4 flux (mol/m2/d) measured by the flux chamber are also reported.
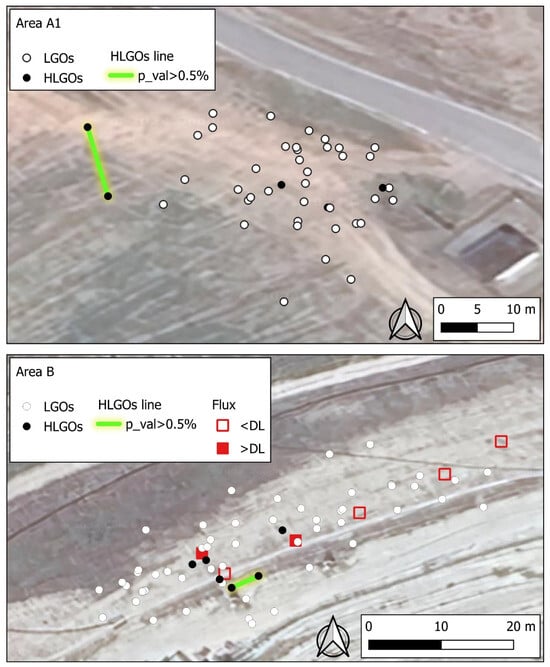
Figure 7.
CH4 distribution of LGOs and HLGOs (ppm * m) in areas A1 (top) and B (bottom). In each area, there is only one lineament formed by two adjacent HLGOs (green line). The possibility that such structures are related to chance cannot be excluded. In Area B, the results of CH4 flux (mol/m2/d) measured by the flux chamber are also reported.
According to combinatorial calculation, the probability of randomly obtaining a series x of consecutive (adjacent) HLGOs, given n as the total number of LGOs and h as the number of HLGOs, is given by:
Referring to the data from Area C, it can be seen that the approximately 2550 ROs (see Table 6) are reduced to 232 LGOs (2552/11). Assuming the TV is the P90 of the values assigned to all LGOs (i.e., the P75 value of the 11 ROs forming an LGO), 22 HLGOs are obtained. In the same area, the 22 HLGOs define two sets of four adjacent HLGOs and four sets of two adjacent HLGOs. In Figure 6, the adjacent HLGOs are connected by lines to better recognize them.
The next step is to evaluate if these “HLGO lineaments” may be due to chance. Applying equation [4], the following probability values (p_val%) are obtained (Table 8):

Table 8.
Calculation of the probability (p_val%) that x HLGOs are adjacent (i.e., form a cluster) by chance, in areas C, B, A1. n: number of LGOs; h: number of HLGOs; x: number of adjacent HLGOs.
The lower the p_val%, the lower the probability that the contiguity of x HLGOs will occur by chance. Contextually, the higher chance of the contiguity of x HLGOs is due to a spatial control factor. In Area C, the lowest values of p_val%, (0.0062%) are related to two sets of 4 adjacent HLGOs that therefore can rightly be considered correlated with an emissive source of CH4. This conclusion is supported by the flux measurements. In fact, the only two flux measures exceeding the DL (solid red squares, Figure 6) are situated near the linear structures identified by the proposed data processing. The spatial structure formed by only two adjacent HLGOs has a probability of being generated by chance greater than 0.5%. Consequently, there is lower confidence that these spatial structures could be linked to actual emissive phenomena.
The same procedure was applied to areas A1 and B. The results are shown in Figure 7. In each area, only one lineament formed by two adjacent HLGOs was found. These lineaments have a probability of being generated by chance greater than 0.5 (p_val% > 0.5); therefore, they are considered not fully reliable.
The “2D” spatial analysis: In this case, the grouping of ROs was related to a regular hexagonal grid. The hexagonal shape was selected as the most isotropic form. The entirety of Area C was subdivided into 104 hexagons with an apothem of approximately 9 m. The ROs included in each hexagon were grouped into an AGO (areal grouped observation). Unlike LGOs, each AGO consists of a different number of ROs, and its graphical representation consists of a hexagon and not a point.
Subsequently, various attributes were assigned to each AGO, as follows:
- ID number;
- num_obs: Number of ROs forming each AGO. Moreover, to ensure the reliability of the statistical attributes assigned to each AGO, a “percentage of coverage” was computed, given by the ratio between the number of ROs in the i-AGO and the maximum number of ROs in an AGO * 100. In Figure 8, the percentage of coverage for each AGO is reported. As can be observed, some AGOs consist of only two ROs, while others have up to a maximum of 90 ROs;
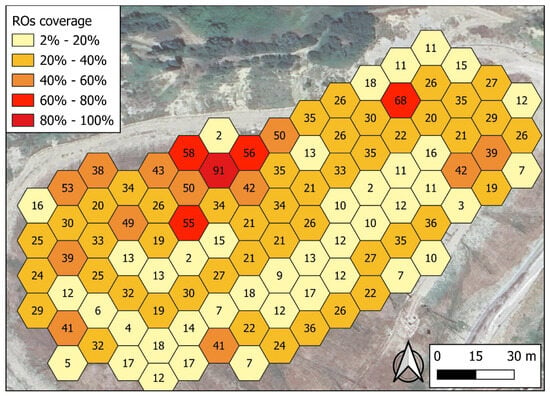 Figure 8. RO coverage for each AGO. The coverage is expressed as percentages related to the AGO with the highest number of ROs. The numbers inside the hexagons refer to the number of ROs detected by the drone in that hexagon.
Figure 8. RO coverage for each AGO. The coverage is expressed as percentages related to the AGO with the highest number of ROs. The numbers inside the hexagons refer to the number of ROs detected by the drone in that hexagon. - Main statistics of ROs falling in each single AGO (mean, st_dev, P25, median, P75, P95, max).
While the CH4 concentration value (ppm * m) assigned to each LGO is given by the P75 of the ROs forming that LGO, the value assigned to each AGO is given by the average of the ROs (this is because in some AGOs, the number of ROs is very small, so it would not be appropriate to refer to percentiles).
As in the linear analysis, the HAGOs are referenced as the AGOs exceeding the TV, which is set as the P90 of the values assigned to the AGOs (i.e., HAGOs are the top 10% of all AGOs).
In Figure 9, the outcomes of this processing are shown for Area C. Each hexagon was assigned the corresponding value of the AGOs. The TV is set as the P90 of all 104 AGO values. The AGOs exceeding the TV are referred to as HAGOs (in red). There are two clusters of HAGOs (n. 123-132-141-142-143 and 126-127-136). HAGOs n. 68, 145, and 164 are excluded from consideration, as they do not represent a cluster (they are not bordered by other HAGOs). The LISA (local indicator of spatial association; [36]) approach has been adopted to check if the observed clustering is casual or not. LISA provides a way to analyze spatial autocorrelation at the local level, allowing for the identification of local clusters, spatial outliers, and patterns that might not be apparent when examining the data globally. In particular, when a binary parameter is being investigated, the local joint count (LJC) indicator helps to understand how likely it is that the clustering occurred by chance. The evaluation of HAGO clustering involves the calculation of a pseudo-probability value, pp_val%, which is an estimate based on the number of random permutations rather than being calculated analytically. Therefore, pp_val% is not perfectly comparable to the p_val%, which is analytically calculated for assessing the HLGO clusters. The higher the number of permutations, the closer the pseudo-probability will be to a theoretical probability. In any case, similar to p_val, the lower pp_val is, the higher the chance that clustering around the ith element is due to a “control factor” governing the spatial distribution of the examined parameter. pp_val% calculations were made using the free and open-source software GeoDa 1.22.0.8 2024 version.
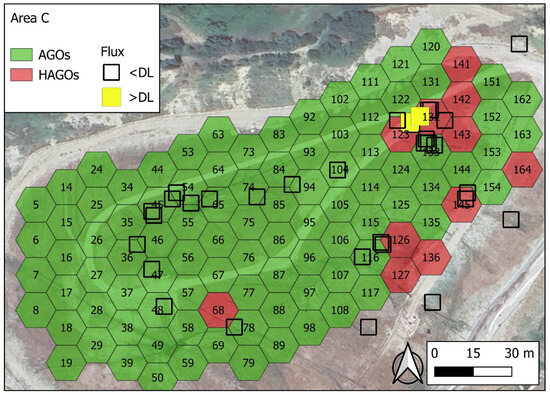
Figure 9.
Results of 2D analysis in Area C. Numbers inside the hexagons are their ID numbers. Red hexagons are the HAGOs. There are two clusters of HAGOs (n. 123-132-141-142-143 and n. 126-127-136). Squares are the points of CH4 flux measurements with the flux chamber. Full yellow squares represent points where CH4 flux was found to be greater than DL.
Table 9 reports the results of the LJC analysis for Area C.

Table 9.
Results of local joint count analysis, computed by GeoDa software. For each red hexagon in Figure 9 (i.e., hexagons where the mean value of observations detected by the drone exceeds the TV), the number of joints with other bordering red hexagons (JC) is counted. NN is the total number of joints with any other hexagon (the maximum value is 6, smaller for hexagons placed at the edges of the investigated area), pp-val% is the pseudo-probability that the JC configuration is random. pp-val% values less than 5% are marked in red.
In Figure 10, the hexagons indicating a JC number that is not attributable to random circumstances (i.e., with pp_val < 5%) are highlighted in yellow. Among these, hexagons 142 and 132 (pp_val near 1%) stand out, essentially coinciding with the area where a higher CH4 flux than the DL was measured. For hexagons 127 and 136, located in the southern margin of the investigated area, the pp_val% calculation is possibly affected by the edge effect, as discussed below.
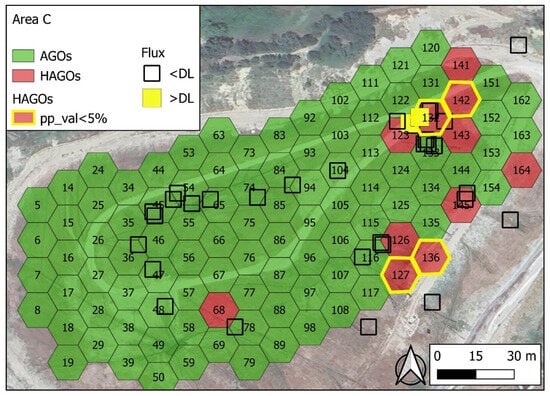
Figure 10.
Same as Figure 9; in addition, HAGOs whose clustering is poorly attributable to chance (pp_val < 5%) are marked in yellow.
Analogous data processing was conducted for Area B (the active filling area, without capping). In this case, since the area is quite small (approximately 60 × 30 m), it was necessary to resize the areal units (hexagons with an apothem of about 2.5 m). A total of 60 hexagons (and therefore 60 AGOs) were obtained. The mean of the CH4 values of the ROs was assigned to AGO. The clustering of HAGOs is shown in Figure 11. As can be seen in the figure, the only two CH4 flux values above the DL (which are also quite high, at 9.2 and 5.3 mol/m2/g, respectively) correspond to, or are in the immediate vicinity of (with distances less than 1.5 m), the HAGOs. Similar considerations apply to CO2 fluxes (the two highest CO2 values correspond to the points with the highest CH4 flux).
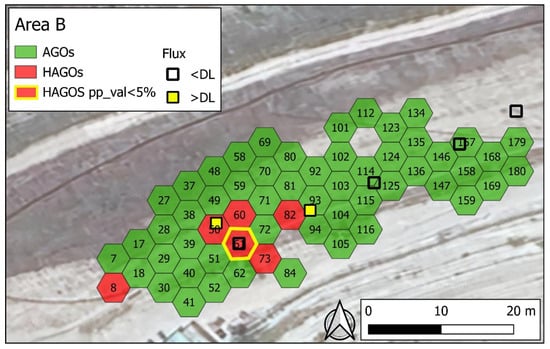
Figure 11.
Results of 2D analysis in Area B. Numbers inside the hexagons are their ID numbers. Red hexagons localize the HAGOs. A cluster of four HAGOs (n. 50-60-61-73) was tested for statistical significance. The clustering around element 61 (yellow circle) is not thought to be random but related to an emissive structure. This element is also very close (a few meters) to a measurement point where CH4 flux was clearly discernible.
Also in Area B, for each HAGO bordered by one or more HAGOs, the probabilities were calculated for the clustering to be a random result. Values of pp_val less than 5% were found in HAGO n. 61 (i.e., clustering around this hexagon was supposed to be non-random). The flux measurement inside this hexagon was lower than the DL; however, another flux measurement 3–4 m from hexagon 61 exceeded the DL.
In the background Area A1 (not represented in the figure), only three non-clustered HAGOs were found. This result is possibly due to a) a poor dataset, b) the limited area investigated, and c) the lack of a CH4 emission “structure”. In the A1 area, no CH4 flux measurements are available.
5. Discussion
5.1. Field Results
CH4 data acquired via UAVs show similar values in areas A1, B, and C in terms of absolute values (Figure 2); however, areas B and C show a higher frequency of potential outliers (i.e., values exceeding the inner fence at 75 P + 1.5 IQR) than values in background Area A1.
Areas B and C show different characteristics. In Area C (capped), it can be assumed that CH4 production processes are already active (with the maximum CH4 production rate expected within 10 years after capping; IPPC, 2006). In this area, the CH4 signal detected by the drone could be related to: (i) fluxes at the soil–atmosphere interface due to capping failures; or (ii) emissive sources located above the interface (e.g., wells/biogas collection lines). In Area B, which is still in the filling phase, it is possible that the methanogenic anaerobic phase has not yet reached its peak.
The main emission zones detected by UAV generally coincide with the few detectable flux measurements taken with the flux chambers (e.g., Area C: hexagons 123, 132, 141, 142, and 143 in Figure 9 and Figure 10, and Area B: hexagons 50, 60, 61, and 73 in Figure 11).
The observed coincidence between non-random HAGO clusters and locations identified by flux chambers as exhibiting higher CH4 (and CO2) fluxes is undoubtedly encouraging. However, perfect spatial alignment between the two measurement techniques could not be anticipated at a fine scale. This is because the sampling and analysis principles are different. The TDLAS-on-UAV method produces a weighted average of the CH4 concentration in free air along the vertical drone–ground axis (measured in ppm * m). Conversely, with the second approach, the rising over time of the CH4 concentration inside the flux chamber allows the calculation of a mass flux (mol/m2/d). The aforesaid differences between UAV and flux chamber measurement methods can lead to data discrepancies that may be difficult to interpret (Figure 12).
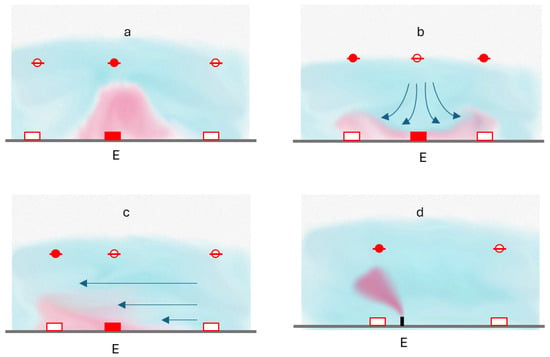
Figure 12.
Explanatory conceptual model of the relationships between the UAV sensor signal (CH4 measured in the soil–UAV column) and flux measured at the interface from the flux chambers. (a) Ideal conditions of no perturbation of the CH4 plume (the UAV signal and flux are consistent); (b) UAV-induced perturbation: the plume is displaced by downward air movement (the UAV signal and flux are inconsistent); (c) windiness: perturbation giving outcomes similar to case b; (d) above-ground emission sources: CH4 plume can be detected by UAV, flux is missed by chambers. E: emission area/point.
An idealized scenario would involve an undisturbed gas plume rising directly from the emission source to the soil–atmosphere interface (scenario “a” in Figure 12), leading to coincident signals from both acquisition methods. In the real-world scenario, factors like wind (scenario “c” in Figure 12) and/or the lateral displacement caused by the drone’s propellers (scenario “b” in Figure 12) can disrupt the plume, resulting in a “misalignment” between measurements taken at the soil–atmosphere interface and those within the overlying air column. Additionally, the presence of above-ground emission sources that generate atmospheric plumes but lack a corresponding flux at the soil–atmosphere interface (scenario “d” in Figure 12) must also be considered.
The measurements carried out with the flux chamber produce data that are more accurate because they are taken directly on the landfill surfaces. However, they offer discontinuous spatial data coverage that could lead to missing out small emission sources (e.g., a punctual failure of a landfill liner). Instead, TDLAS acquisition by UAV can produce thousands of affordable observations in a very short time. In fact, good flight planning allows excellent uniform coverage of the survey area. However, these measurements often suffer from the critical acquisition conditions of a UAV (the first 10 m of the air column). In this layer, the original gas flow in the atmosphere undergoes extremely fast and uncontrollable/unpredictable dispersion (dilution) in time and space.
Hence, there is a need for appropriate statistical techniques to filter the data and verify the existence of spatial structures related to the (higher) values of the observations.
5.2. Methods
The proposed processing of drone data ultimately consists of the following:
- The identification of spatial structures (i.e., clusters of spatial entities exceeding a threshold value, TV);
- The evaluation that such spatial structures are not randomly distributed (i.e., the probability that they are random is extremely low).
Once a non-random spatial structure is identified, it is compared with the outcome of the flux chambers.
The identification of a non-random spatial structure (linear or areal) includes the following steps:
- a.
- Grouping of raw observations (ROs);
- b.
- Selection of statistical indicators to assign to LGOs and AGOs;
- c.
- Setting the threshold value (TV);
- d.
- Contiguity analysis of grouped observations exceeding the TV (clustering);
- e.
- Calculating the probabilities that the observed clustering is random.
Within each stage of this process, various development options influence the final output. Nevertheless, these stages are interdependent and, to some extent, exhibit self-regulating characteristics, as follows:
- a.
- Grouping of ROs. The process of spatially aggregating ROs was implemented using two distinct methodologies: linear segmentation and areal unit (hexagonal grid) aggregation. Linear segmentation aggregates ROs acquired sequentially in time and space along the drone’s flight path, whereas areal unit aggregation uses hexagons to encompass all drone ROs acquired over a specific area. These two aggregation methods exhibit contrasting characteristics. Linear aggregation yields linear grouped observations (LGOs) with a uniform number of ROs (11 in this study) and is representative of the drone’s flight direction, translating to consistent statistical reliability. However, this method suffers from incomplete spatial coverage. Conversely, areal unit aggregation yields areal grouped observations (AGOs) that guarantee complete coverage of the survey area. However, the number of ROs within each AGO, and consequently the reliability of the derived statistical parameters, exhibits high variability contingent upon the drone’s flight paths. Ideally, each AGO should theoretically encompass a minimum of 20 ROs. In the present study, with 2550 ROs, 104 AGOs were established, resulting in an average of approximately 25 ROs/AGOs; nevertheless, the numbers of ROs vary between 2 and 90. Moreover, even if the number of ROs within each AGO is adequate, their distribution may still be uneven due to a high concentration of ROs along a preferred pathway, such as the UAV’s flight direction. Therefore, it is crucial to emphasize the importance of: (i) a UAV flight plan that ensures the most uniform areal coverage possible; and (ii) considering a reliability index (Figure 8).
- b.
- Selection of statistical indicators to assign to LGOs and AGOs. In this study, LGOs were assigned the P75 of aggregated ROs, while AGOs were assigned the mean of aggregated ROs. Other statistical indicators, such as the P50, P75, P90, etc., could also be assigned. However, the analysis of the available dataset revealed a slight influence of the chosen statistical indicator on the final spatial distribution of HLGOs and HAGOs. For example, see the distribution of HAGOs when mean, P50, P75, and max are assigned to AGOs and TV is set at the P90 of the chosen statistical indicator (Figure 13).
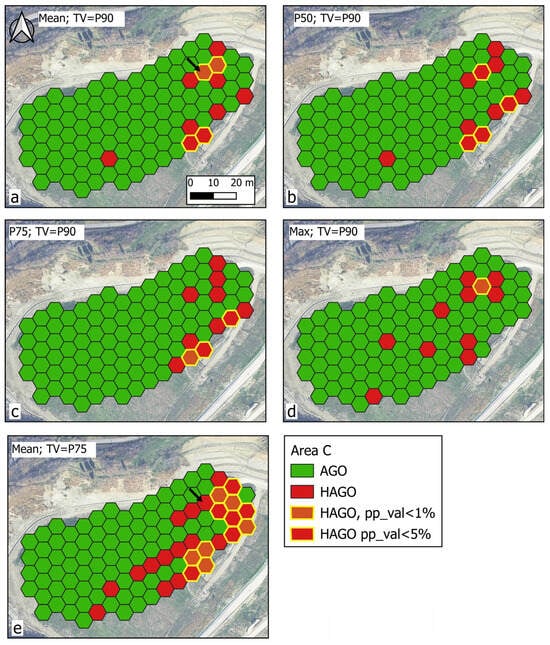
Figure 13.
Spatial distribution of AGOs and HAGOs in Area C when varying the statistical indicator and TV. In the plots (a–d), the statistical indicator of AGOs is respectively the mean, P50, P75, and max of ROs falling in each hexagon; the TV is set as the P90 of the respective indicator (i.e., green hexagons do not exceed the TV, red hexagons (HAGOs) do). With the same TV, the HAGO placement is roughly the same. When decreasing the TV (e.g., P90 to P75), the number of HAGOs obviously increases. The number of HAGOs with pp_val < 5% seems to increase at the edge of the investigated area. The clustering centered on HAGO n. 132 (arrow) has a pp_val < 5% when the TV is P90 (plot a); when the TV is set to P75 (plot (e)), the same clustering has a pp_val > 5% (as the number of HAGOS increases, the random formation of HAGO clusters is more likely).
- c.
- Setting the threshold value (TV). Selecting an appropriate threshold value (TV) is critical for interpreting the data. A higher TV results in a decrease in the number of HLGOs and HAGOs. Consequently, the likelihood of encountering random clusters of two or more adjacent HLGOs and HAGOs diminishes. In essence, increasing the TV reduces the overall number of clusters detected but strengthens the probability that identified clusters are non-random and attributable to underlying influencing factors (e.g., gas emissions). Conversely, employing a lower TV yields a greater number of HLGO and HAGO clusters, but generally, it elevates the probability that these clusters are random occurrences.
- d.
- Contiguity analysis of grouped observations exceeding the TV. This phase is the result of the choices made in the previous phases. The clusters of HLGOs and HAGOS are highlighted (consecutive HLGOs in the case of linear grouping, clustering of hexagons in the case of HAGOs).
- e.
- Calculating the probabilities that the clustering is random. Following the identification of HLGO or HAGO clusters, their statistical significance is evaluated using a p-value and pp-value. This value represents the probability that the clusters are merely random occurrences. For HLGO clusters, p-value calculation employs combinatorial methods. Although the underlying concept behind p-value calculation is straightforward, computational challenges may arise when dealing with large numbers of LGOs.
Based on the provided shapefile, the open-source software GeoDA is utilized to assess the pp_val of HAGO clusters. Given the total number of AGOs and the number of HAGOs, the software performs 10,000 simulations. In each simulation, HAGOs are randomly distributed across the study area. Subsequently, for each HAGO, GeoDA counts the number of neighboring HAGOs. For instance, if after 10,000 simulations, a HAGO is found adjacent to four other HAGOs in 23 simulations, the resulting pp_val% would be 23/10,000 × 100 = 0. 23%. At this stage, the problem of the “edge effect” may arise. Referring to Figure 13, normally, each HAGO borders six other elements, HAGOs, or AGOs (i.e., hexagons that exceed or do not exceed the TV). When the calculation involves HAGOs at the boundary of the area under investigation, the total number of shared boundaries is less than six (e.g., three or four). Therefore, the pp-value calculation could provide lower values (the probability of having one HAGO–HAGO border out of three or four total edges is lower than if the total number of edges is six).
As an example, in Figure 10, each n. 126, 127, and 136 HAGOs share two boundaries with the other HAGOs, but only HAGOs 127 and 136 have pp_val <5%. The edge effect can be a critical issue in data interpretation. For this reason, in planning the field activity, it would be advisable to extend the surveys in a small buffer around the target area. Another factor that influences the values of p_val and pp_val is the selection of the TV. As the TV decreases, the number of HLGOs and HAGOs increases, and, consequently, the probability of random clustering increases (see Figure 13, plots a and e).
6. Conclusions
The study focuses on the development and validation of a statistical method based on the local indicator of spatial association (LISA) for processing CH₄ data acquired via UAV. The innovation lies in the systematic grouping of thousands of raw observations to identify spatial structures—clusters of high methane values—that are unlikely to occur by chance. The analysis employs both a linear segmentation approach, which groups sequential observations along the drone’s flight path, and a two-dimensional areal aggregation using a hexagonal grid. In both cases, a threshold value is defined, and clusters exceeding this threshold are evaluated for randomness using combinatorial probability and LISA-derived pseudo-probabilities. Flux chamber measurements, which provide precise and localized methane and carbon dioxide flux data at the soil–atmosphere interface, were used as an independent reference to validate the identified statistical patterns. The encouraging correspondence between non-random clusters identified via LISA and the flux chamber data supports the reliability of the proposed method, even though perfect spatial alignment is not expected due to inherent differences in measurement principles.
The study also highlights areas for improvement in both UAV acquisition and flux measurement. In particular, it reveals the importance of an effective data acquisition strategy, including well-planned drone routes, to ensure: (i) a uniform areal distribution of observations across the study area; and (ii) a buffer zone around the target area to mitigate edge effects. Additionally, CH₄ flux measurements often did not yield detectable methane values, indicating a need to refine the detection limits of the method. Further research should include conducting data acquisition in semi-controlled conditions, where the methane source is known in terms of quantity and location, to determine optimal parameters such as flight height, sampling frequency, grid resolution, and the influence of wind.
Exploring the scalability of this approach to other gases and environmental contexts is also recommended. Despite some limitations, the experimental results from the landfill study are encouraging, demonstrating that the advanced statistical processing of drone data can effectively identify emission hotspots and be reliably validated by independent flux measurements.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs17111890/s1, Figures S1 and S2.
Author Contributions
Conceptualization, M.D.M., M.F. and A.V.; Data curation, M.D.M., A.D., C.F., L.L. and E.S.; Formal analysis, M.G.; Investigation, M.D.M., V.F. and M.T.; Methodology, M.G. and M.D.M.; Project administration, M.F. and N.T.; Visualization, C.F.; Writing–original draft, M.G., M.D.M., D.F. and L.L.; Writing–review & editing, M.G., M.D.M., A.D., M.F., V.F., D.F., L.L., B.N., P.A.R., E.S., M.T. and A.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets underlying this paper can be requested at maurizio.guerra@ispraambiente.it or maurizio.demolfetta@uniba.it.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allen, G.; Hollingsworth, P.; Kabbabe, K.; Pitt, J.R.; Mead, M.; Illingworth, S.; Roberts, G.; Bourn, M.; Shallcross, D.E.; Percival, C.J. The development and trial of an unmanned aerial system for the measurement of methane flux from landfill and greenhouse gas emission hotspots. Waste Manag. 2019, 87, 883–892. [Google Scholar] [CrossRef] [PubMed]
- Barchyn, T.; Hugenholtz, C.H.; Myshak, S.; Bauer, J. A UAV-based system for detecting natural gas leaks. J. Unmanned Veh. Syst. 2017, 6, 18–30. [Google Scholar] [CrossRef]
- Berisha, A.; Osmanaj, L. Determination of Methane Explosion Level in the Velekince Municipal Solid Waste Landfill. Ecol. Eng. Environ. Technol. 2021, 22, 82–88. [Google Scholar] [CrossRef]
- IPCC (Intergovernmental Panel on Climate Change)—National Greenhouse Gas Inventories Programme. 2006 IPCC Guidelines for National Greenhouse Gas Inventories: Waste. 5. In Proceedings of the Third Authors/Experts Meeting: Industrial Processes and Product Use, Washington, DC, USA, 27–29 July 2004. [Google Scholar]
- Mønster, J.; Kjeldsen, P.; Scheutz, C. Methodologies for measuring fugitive methane emissions from landfills—A review. Waste Manag. 2019, 87, 835–859. [Google Scholar] [CrossRef]
- Rusín, J.; Chamrádová, K.; Jastrzembski, T.; Skrínský, J. Explosion characteristics of a biogas/air mixtures. Chem. Eng. Trans. 2022, 90, 271–276. Available online: https://www.cetjournal.it/index.php/cet/article/view/12173 (accessed on 17 May 2025).
- European Commission. 2016. Available online: https://ec.europa.eu/environment/waste/landfill/pdf/guidance%20on%20landfill%20gas.pdf (accessed on 17 January 2025).
- Agency for Toxic Substances and Disease Registry. Landfill Gas Primer—An Overview for Environmental Health Professionals. Chapter 4: Monitoring of Landfill Gas. 2024. Available online: https://www.atsdr.cdc.gov/HAC/landfill/html/ch4.htm (accessed on 9 January 2025).
- Darynova, Z.; Blanco, B.; Juery, C.; Donnat, L.; Duclaux, O. Data assimilation method for quantifying controlled methane releases using a drone and ground-sensors. Atmos. Environ. X 2023, 17, 100210. [Google Scholar] [CrossRef]
- Karanjekar, R.V.; Bhatt, A.; Altouqui, S.; Jangikhatoonabad, N.; Durai, V.; Sattler, M.L.; Hossain, M.D.S.; Chen, V. Estimating methane emissions from landfills based on rainfall, ambient temperature, and waste composition: The CLEEN model. Waste Manag. 2015, 46, 389–398. [Google Scholar] [CrossRef]
- Scheutz, C.; Fredenslund, A.M.; Nedenskov, J.; Samuelsson, J.; Kjeldsen, P. Gas production, composition and emission at a modern disposal site receiving waste with a low-organic content. Waste Manag. 2011, 31, 946–955. [Google Scholar] [CrossRef]
- Randazzo, A.; Venturi, S.; Tassi, F. Soil processes modify the composition of volatile organic compounds (VOCs) from CO2- and CH4-dominated geogenic and landfill gases: A comprehensive study. Sci. Total Environ. 2024, 923, 171483. [Google Scholar] [CrossRef]
- Castro Gámez, A.F.; Rodríguez Maroto, J.M.; Vadillo Pérez, I. Quantification of methane emissions in a Mediterranean landfill (Southern Spain). A combination of flux chambers and geostatistical methods. Waste Manag. 2019, 87, 937–946. [Google Scholar] [CrossRef]
- Scheutz, C.; Cassini, F.; De Schoenmaeker, J.; Kjeldsen, P. Mitigation of methane emissions in a pilot-scale biocover system at the AV Miljø Landfill, Denmark: 2. Methane oxidation. Waste Manag. 2017, 63, 203–212. [Google Scholar] [CrossRef] [PubMed]
- Ngwabie, N.M.; Wirlen, Y.L.; Yinda, G.S.; VanderZaag, A.C. Quantifying greenhouse gas emissions from municipal solid waste dumpsites in Cameroon. Waste Manag. 2019, 87, 947–953. [Google Scholar] [CrossRef] [PubMed]
- Cassini, F.; Scheutz, C.; Skov, B.H.; Mou, Z.; Kjeldsen, P. Mitigation of methane emissions in a pilot-scale biocover system at the AV Miljø Landfill, Denmark: 1. System design and gas distribution. Waste Manag. 2017, 63, 213–225. [Google Scholar] [CrossRef]
- Jeong, S.; Park, J.; Kim, Y.M.; Park, M.H.; Kim, J.Y. Innovation of flux chamber network design for surface methane emission from landfills using spatial interpolation models. Sci. Total Environ. 2019, 688, 18–25. [Google Scholar] [CrossRef]
- Ishigaki, T.; Yamada, M.; Nagamori, M.; Ono, Y.; Inoue, Y. Estimation of methane emission from whole waste landfill site using correlation between flux and ground temperature. Environ. Geol. 2005, 48, 845–853. Available online: https://ui.adsabs.harvard.edu/link_gateway/2005EnGeo.48.845I/doi:10.1007/s00254-005-0008-0 (accessed on 17 May 2025). [CrossRef]
- Martin, C.R.; Zeng, N.; Karion, A.; Dickerson, R.R.; Ren, X.; Turpie, B.N.; Weber, K.J. Evaluation and environmental correction of ambient CO2 measurements from a low-cost NDIR sensor. Atmos. Meas. Tech. 2017, 10, 2383–2395. [Google Scholar] [CrossRef]
- Shi, J.; Jiang, Y.; Duan, Z.; Li, J.; Yuan, Z.; Tai, H. Designing an optical gas chamber with stepped structure for non-dispersive infrared methane gas sensor. Sens. Actuators A Phys. 2024, 367, 115052. [Google Scholar] [CrossRef]
- You, R.; Kang, H.; Zhang, X.; Zheng, S.; Shao, L.; Han, J.; Feng, G. Cubic nonlinear scanning for improved TDLAS-based methane concentration detection. Int. J. Hydrogen Energy 2024, 86, 14–23. [Google Scholar] [CrossRef]
- Zhu, H.; Letzel, M.O.; Reiser, M.; Kranert, M.; Bächlin, W.; Flassak, T. A new approach to estimation of methane emission rates from landfills. Waste Manag. 2013, 33, 2713–2719. [Google Scholar] [CrossRef]
- Dullo, F.T.; Lindecrantz, S.; Jágerská, J.; Hansen, J.H.; Engqvist, M.; Solbø, S.A.; Hellesø, O.G. Sensitive on-chip methane detection with a cryptophane-A cladded Mach-Zehnder interferometer. Opt. Express 2015, 23, 31564. [Google Scholar] [CrossRef]
- Fosco, D.; De Molfetta, M.; Renzulli, P.; Notarnicola, B. Progress in monitoring methane emissions from landfills using drones: An overview of the last ten years. Sci. Total Environ. 2024, 945, 173981. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chen, H.; Li, H.; Liu, C.; Li, J.; Chen, Q.; Li, K.; Zhang, S.; Gu, M. Ultra-high sensitivity methane gas sensor based on vernier effect in double D-shaped and cryptophane-A film-coated photonic crystal fiber: Design and FEM simulation. Results Phys. 2023, 52, 106840. [Google Scholar] [CrossRef]
- Pratt, C.; Walcroft, A.S.; Deslippe, J.; Tate, K.R. CH4/CO2 ratios indicate highly efficient methane oxidation by a pumice landfill cover-soil. Waste Manag. 2013, 33, 412–419. [Google Scholar] [CrossRef]
- Wong, C.L.Y. Analysis of the number of flux chamber samples and study area size on the accuracy of emission rate measurements. J. Air Waste Manag. Assoc. 2018, 68, 1103–1117. [Google Scholar] [CrossRef]
- Di Trapani, D.; Di Bella, G.; Viviani, G. Uncontrolled methane emissions from a MSW landfill surface: Influence of landfill features and side slopes. Waste Manag. 2013, 33, 2108–2115. [Google Scholar] [CrossRef]
- Abichou, T.; Bel Hadj Ali, N.; Amankwah, S.; Green, R.; Howarth, E.S. Using Ground- and Drone-Based Surface Emission Monitoring (SEM) Data to Locate and Infer Landfill Methane Emissions. Methane 2023, 2, 440–451. [Google Scholar] [CrossRef]
- Yong, H.; Allen, G.; Mcquilkin, J.; Ricketts, H.; Shaw, J.T. Lessons learned from a UAV survey and methane emissions calculation at a UK landfill. Waste Manag. 2024, 180, 47–54. [Google Scholar] [CrossRef]
- Barchyn, T.E.; Hugenholtz, C.H.; Fox, T.A. Plume detection modeling of a drone-based natural gas leak detection system. Elem. Sci. Anthr. 2019, 7, 41. [Google Scholar] [CrossRef]
- Emran, B.J.; Tannant, D.D.; Najjaran, H. Low-Altitude Aerial Methane Concentration Mapping. Remote Sens. 2017, 9, 823. [Google Scholar] [CrossRef]
- Morales, R.; Ravelid, J.; Vinkovic, K.; Korbeń, P.; Tuzson, B.; Emmenegger, L.; Chen, H.; Schmidt, M.; Humbel, S.; Brunner, D. Controlled-release experiment to investigate uncertainties in UAV-based emission quantification for methane point sources. Atmos. Meas. Tech. 2022, 15, 2177–2198. [Google Scholar] [CrossRef]
- Mackie, K.R.; Cooper, C.D. Landfill gas emission prediction using Voronoi diagrams and importance sampling. Environ. Model. Softw. 2009, 24, 1223–1232. [Google Scholar] [CrossRef]
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Anselin, L.; Xun, L. Operational local join count statistics for cluster detection. J. Geogr. Syst. 2019, 21, 189–210. [Google Scholar] [CrossRef]
- Obersky, L.; Rafiee, R.; Cabral, A.R.; Golding, S.D.; Clarke, W.P. Methodology to determine the extent of anaerobic digestion, composting and CH4 oxidation in a landfill environment. Waste Manag. 2018, 76, 364–373. [Google Scholar] [CrossRef]
- Souza, W.S.R.; Hart, A.J.; Fonseca, B.J.B.; Tahernezhadi, M.; Christensen, L.E. A Framework to Survey a Region for Gas Leaks Using an Unmanned Aerial Vehicle. IEEE Access 2023, 12, 1386–1407. [Google Scholar] [CrossRef]
- De Molfetta, M.; Fosco, D.; Renzulli, P.A.; Notarnicola, B. Identification and treatment of false methane values produced by the TDLAS technology equipped on UAVs. Integr. Environ. Assess. Manag. 2024, in press. [Google Scholar] [CrossRef]
- Sistema Nazionale per la Protezione dell’Ambiente. Progettazione del monitoraggio di vapori nei siti contaminati. In Linea Guida SNPA 15/2018; Appendix B.; SNPA: Rome, Italy, 2018; ISBN 978-88-448-0922-5. Available online: https://www.snpambiente.it/wp-content/uploads/2018/11/Appendice_B_linee_guida_snpa_15_2018.pdf (accessed on 14 February 2025).
- Lando, A.T.; Nakayama, H.; Shimaoka, T. Application of portable gas detector in point and scanning method to estimate spatial distribution of methane emission in landfill. Waste Manag. 2016, 59, 255–266. [Google Scholar] [CrossRef]
- Ozcan, H.K.; Borat, M.; Sezgin, N.; Nemlioglu, S.; Demir, G. Determination of seasonal variations of major landfill gas in Istanbul Kemerburgaz-Odayeri solid waste landfill. Fresenius Environ. Bull. 2006, 15, 272–276. Available online: https://avesis.iuc.edu.tr/yayin/31e91822-0f70-4955-8c2d-39f3566485db/determination-of-seasonal-variations-of-major-landfill-gas-in-istanbul-kemerburgaz-odayeri-solid-waste-landfill (accessed on 23 December 2024).
- Wu, T.; Cheng, J.; Wang, S.; He, H.; Chen, G.; Xu, H.; Wu, S. Hotspot Detection and Estimation of Methane Emissions from Landfill Final Cover. Atmosphere 2023, 14, 1598. [Google Scholar] [CrossRef]
- He, H.; Gao, S.; Hu, J.; Zhang, T.; Wu, T.; Qiu, Z.; Zhang, C.; Sun, Y.; He, S. In-Situ Testing of Methane Emissions from Landfills Using Laser Absorption Spectroscopy. Appl. Sci. 2021, 11, 2117. [Google Scholar] [CrossRef]
- Yang, H.; Bu, X.; Song, Y.; Shen, Y. Methane concentration measurement method in rain and fog coexisting weather based on TDLAS. Measurement 2022, 204, 112091. [Google Scholar] [CrossRef]
- Shah, A.; Pitt, J.; Kabbabe, K.; Allen, G. Suitability of a Non-Dispersive Infrared Methane Sensor Package for Flux Quantification Using an Unmanned Aerial Vehicle. Sensors 2019, 19, 4705. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).