Retrieving the Leaf Area Index of Dense and Highly Clumped Moso Bamboo Canopies from Sentinel-2 MSI Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Ground-Based Measurements of LAI
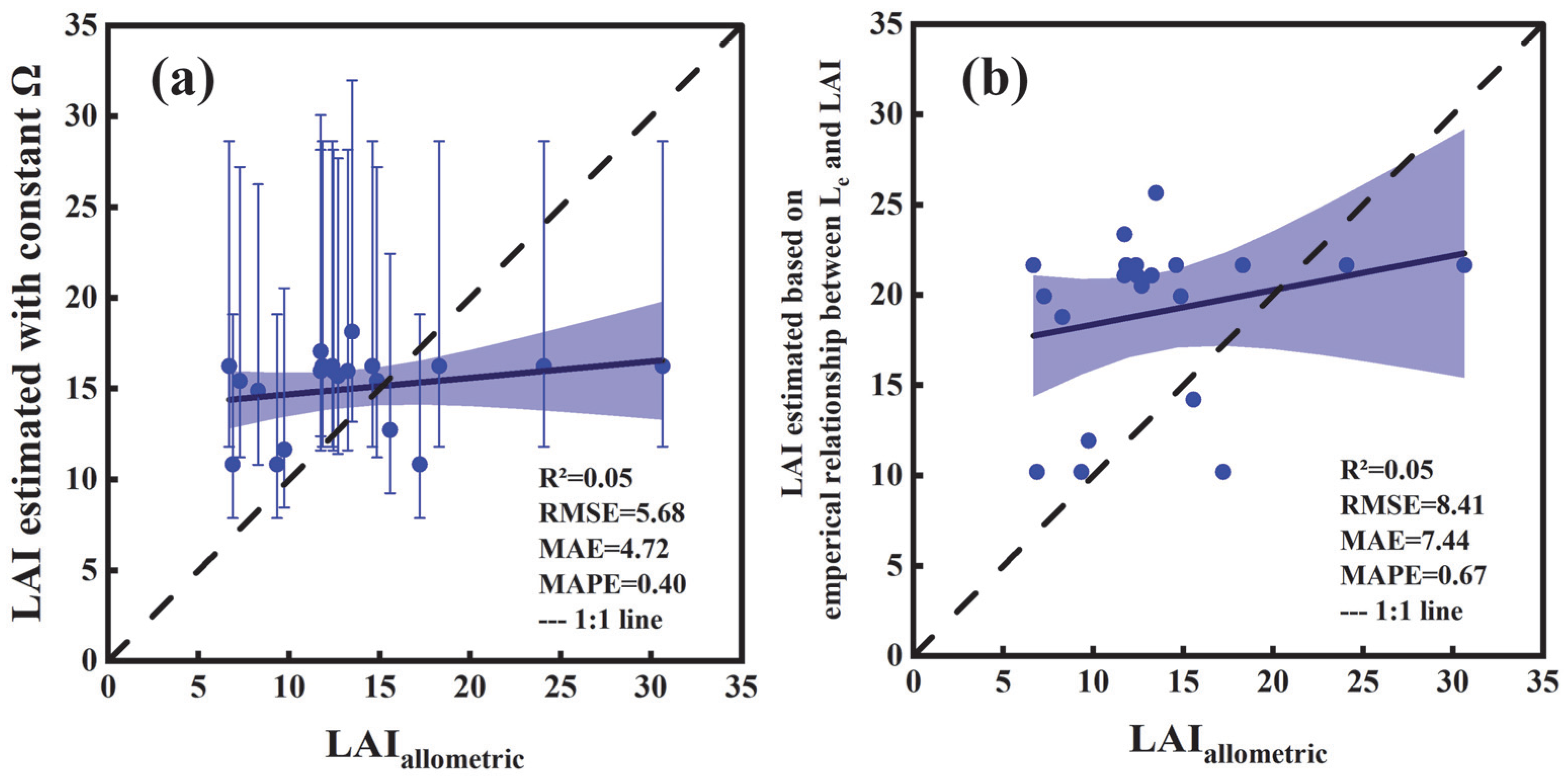
2.2.1. Determination of LAI from an Allometric Method
2.2.2. Determination of LAI from Ground-Based Gap Measurements
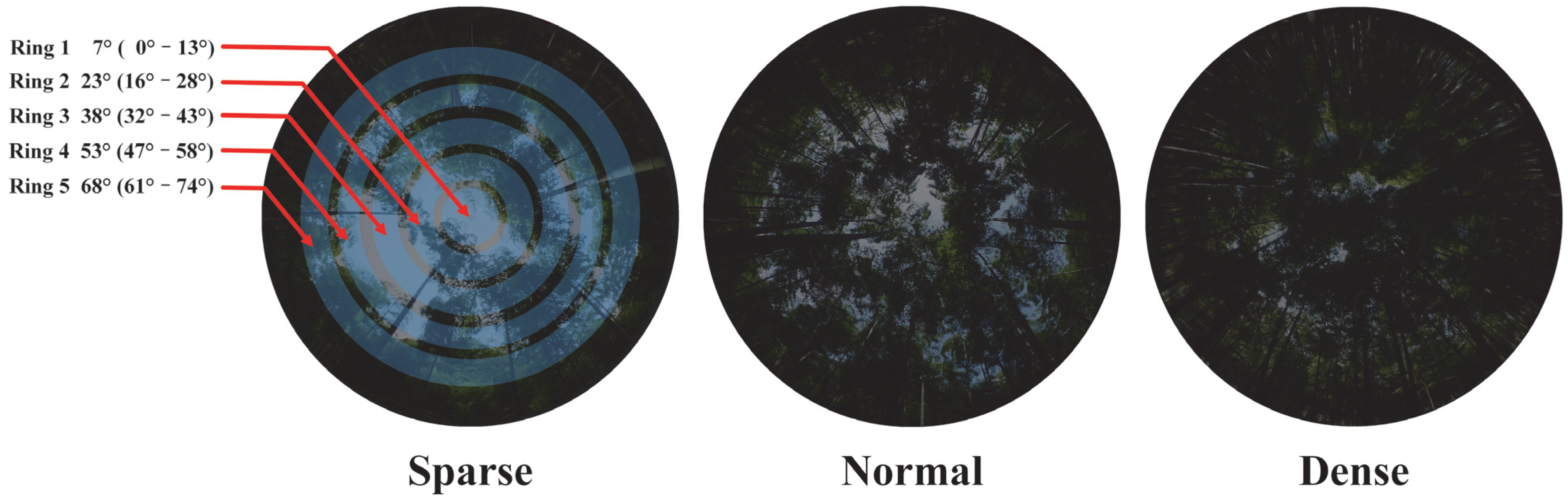
2.2.3. Field Measurements and Data Processing
2.3. Retrieving LAI from Satellite Remote Sensing Data
2.3.1. Physically Based LAI Retrieval Methods
2.3.2. Sentinel-2 MSI Images
2.4. Accuracy Assessment
3. Results
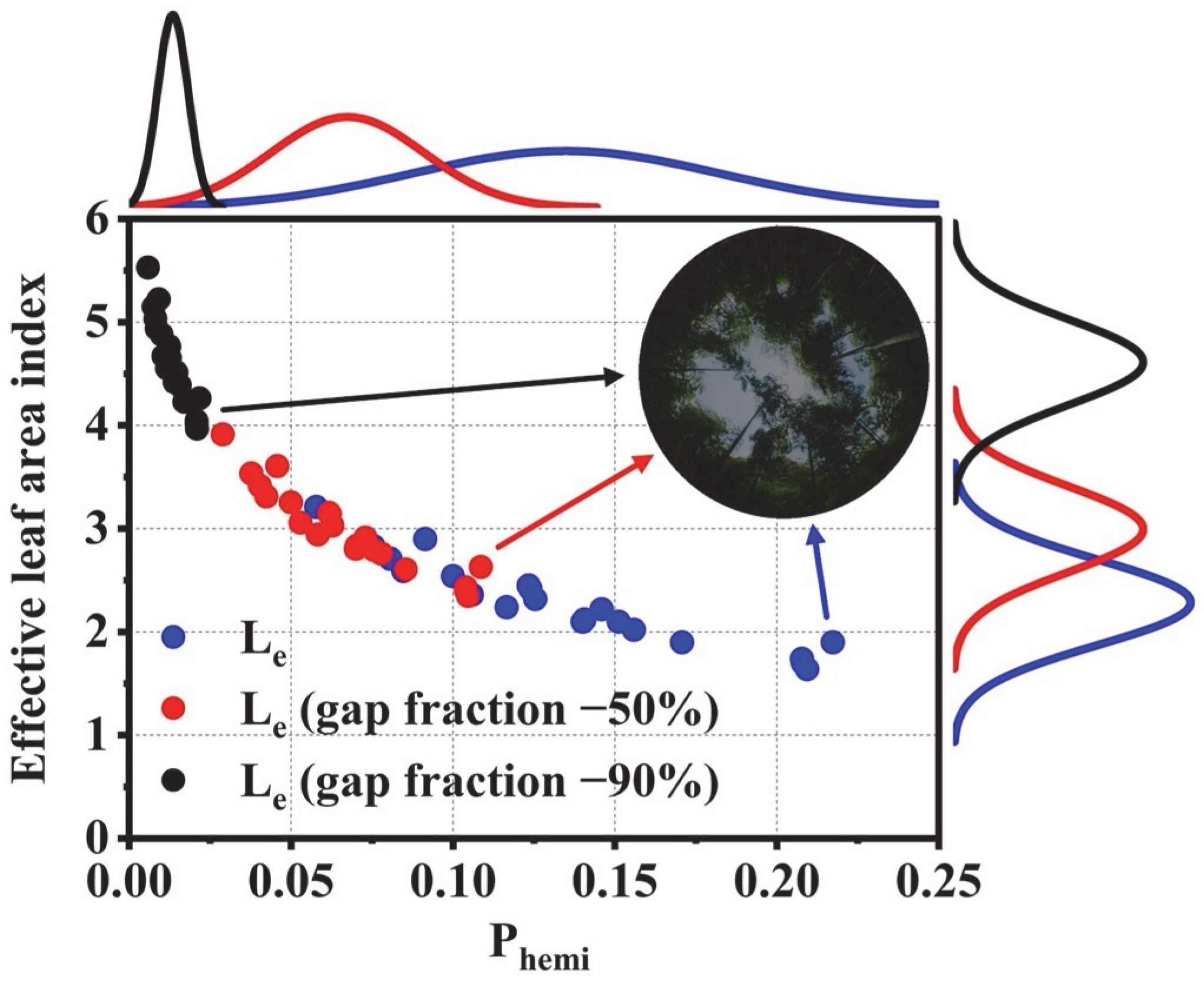
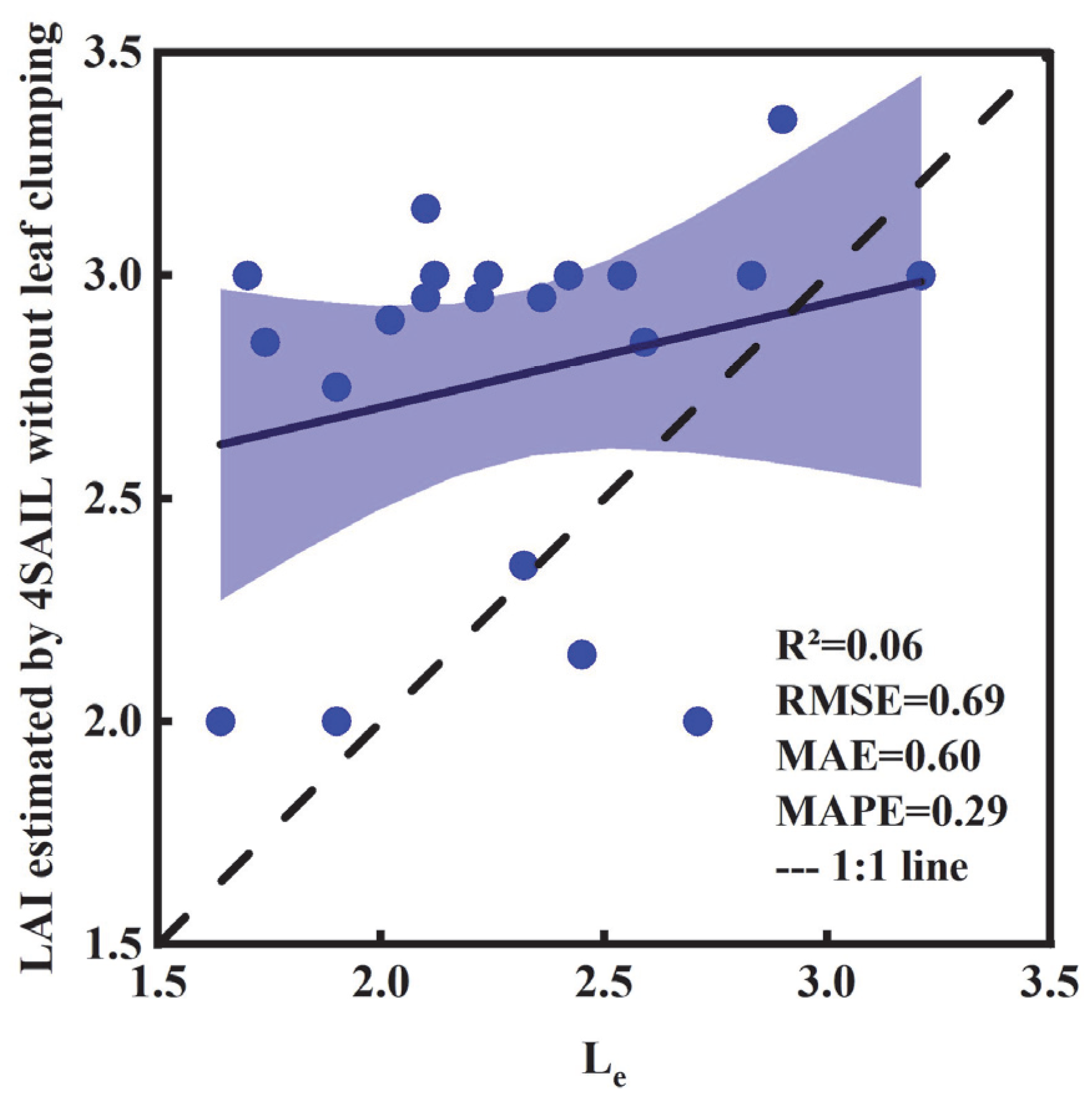
3.1. Le Estimated Based on the DHP Observations
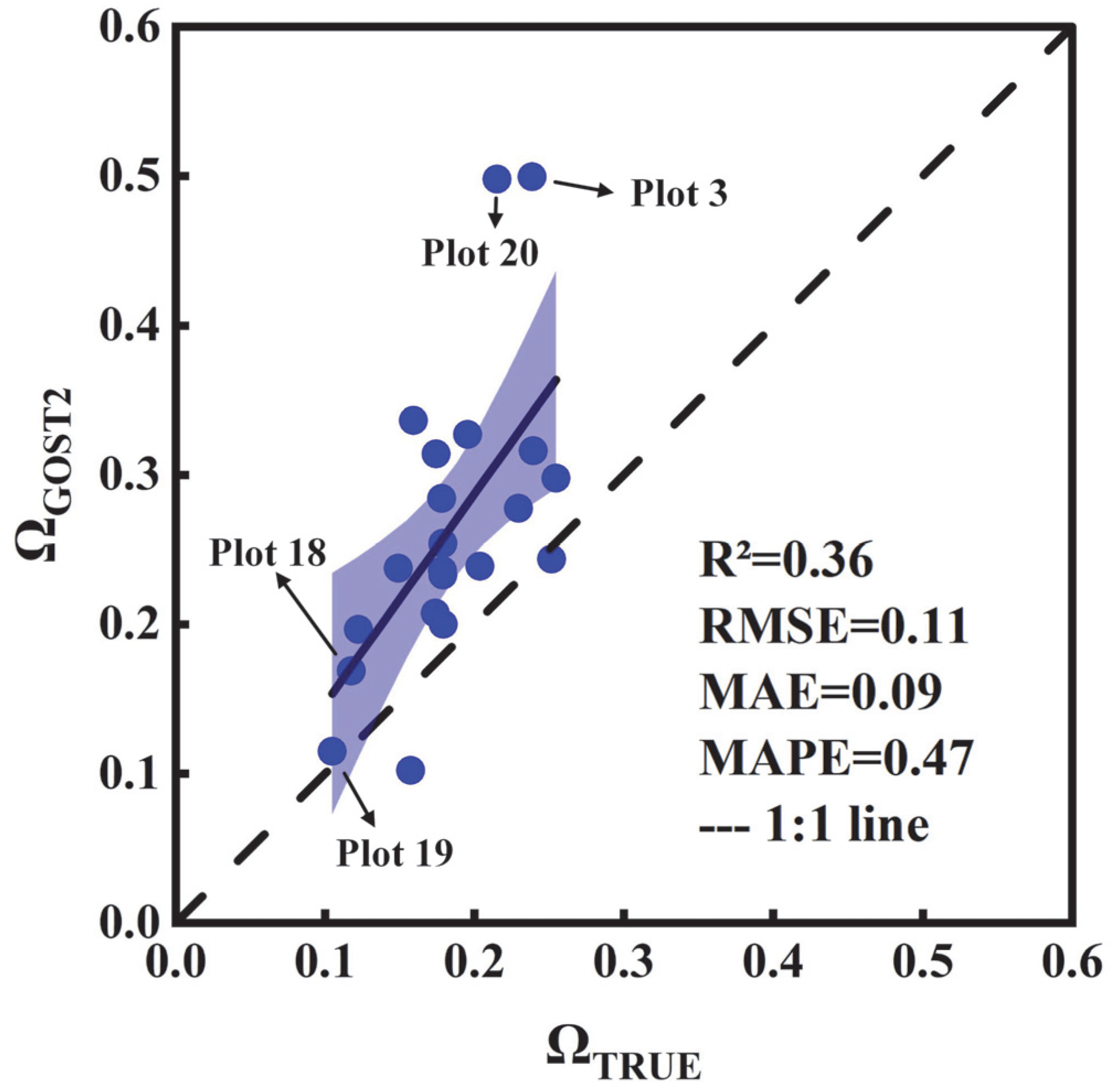
3.2. Ground-Based Clumping Index Estimations
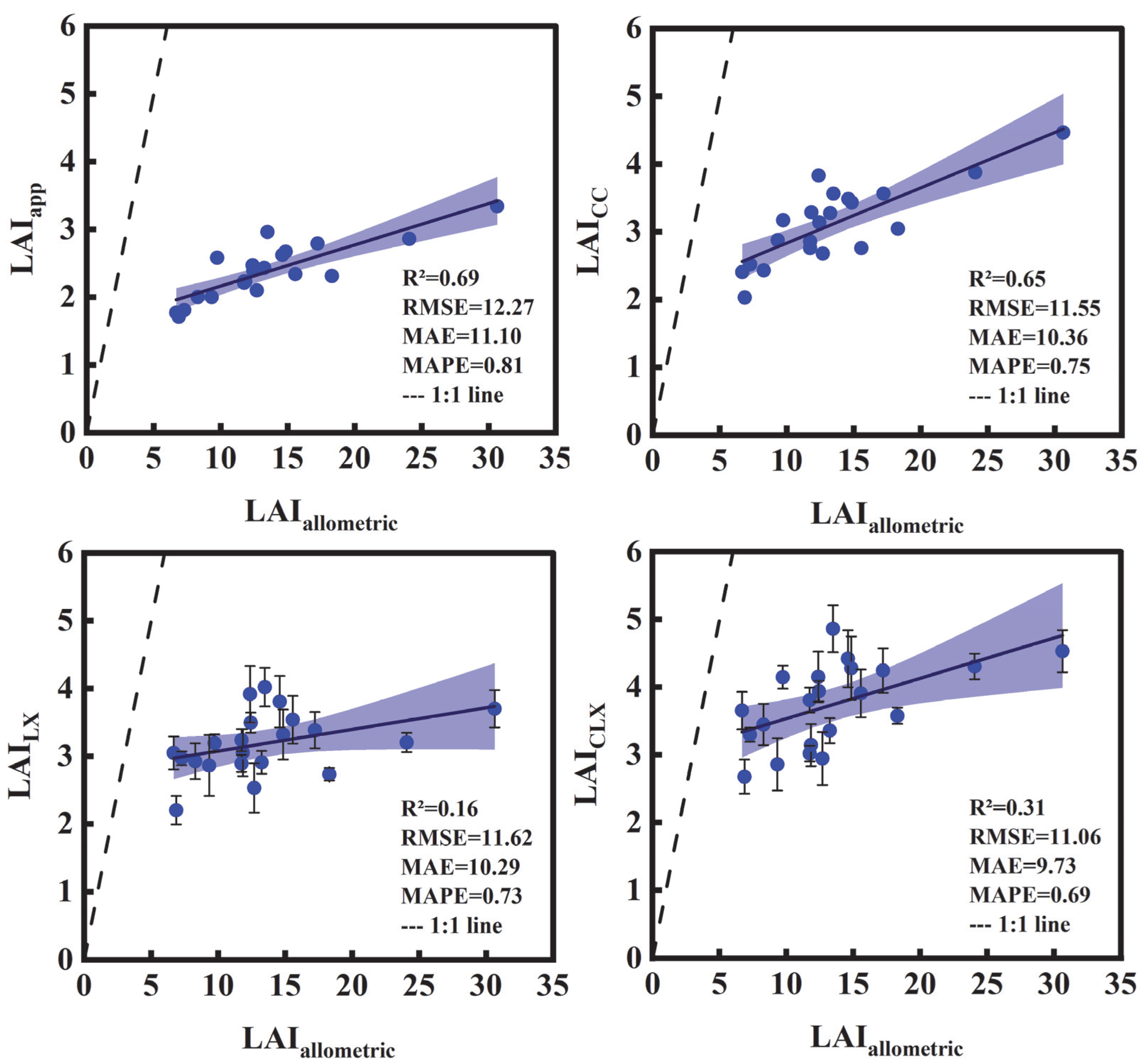
3.3. Ground-Based LAI Estimations
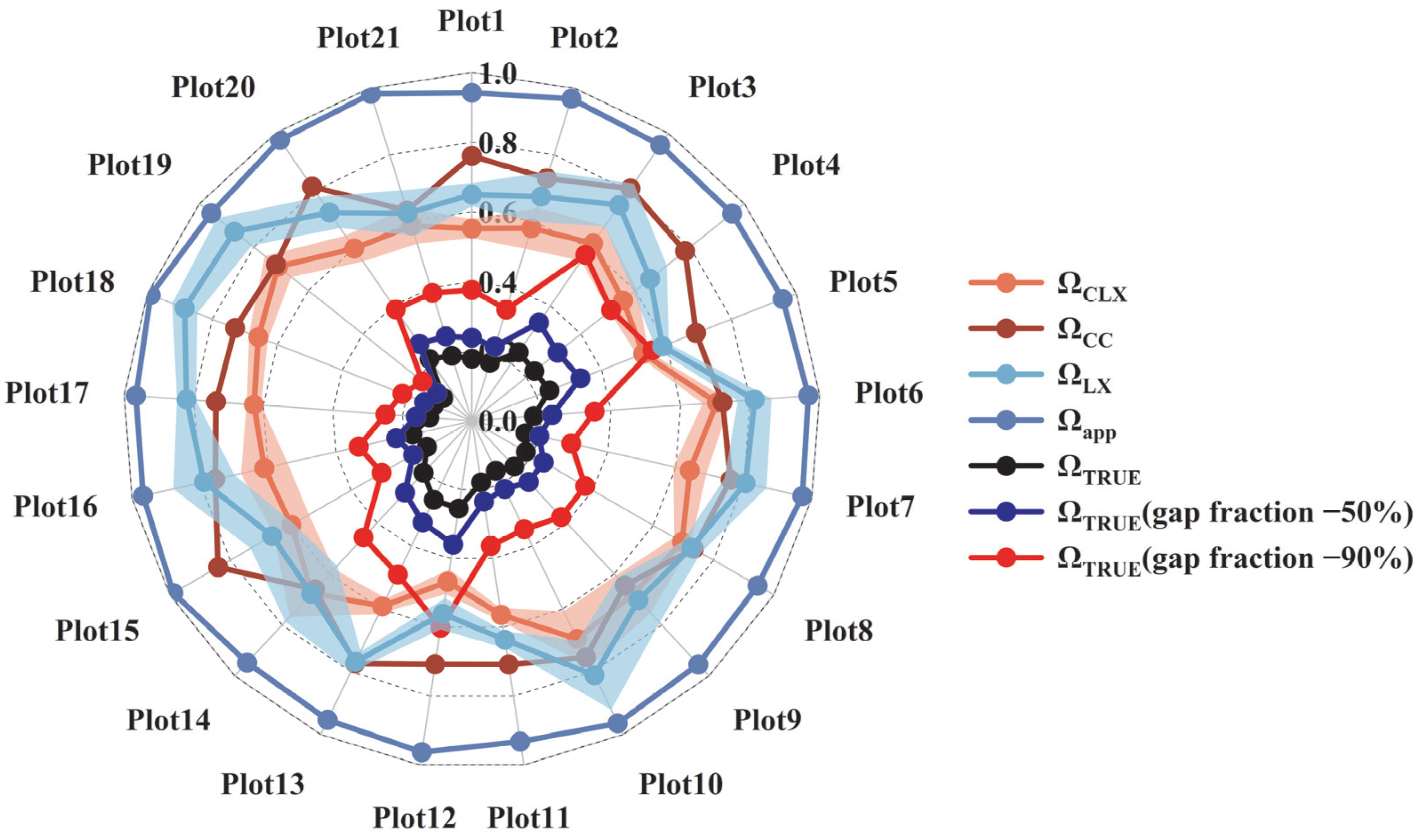
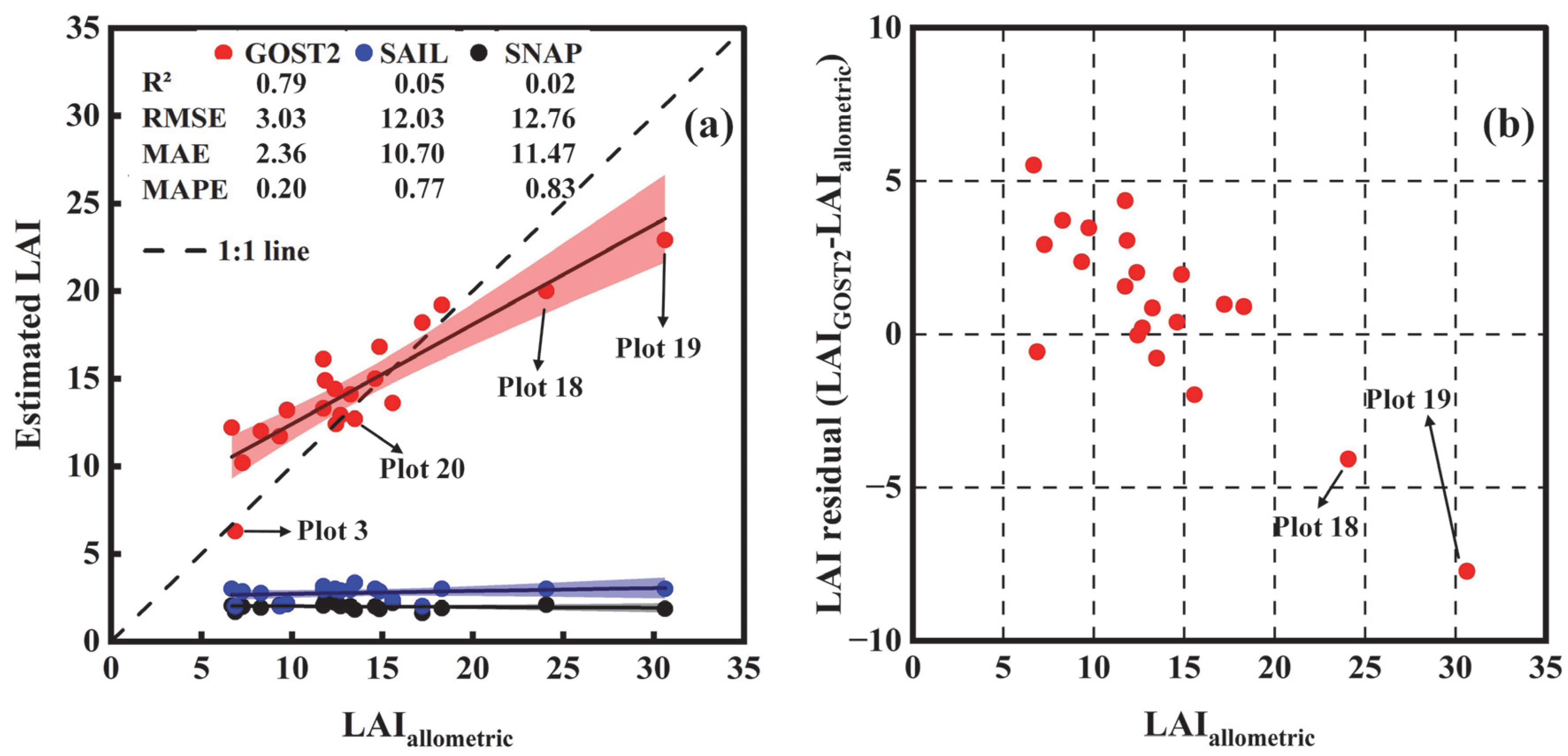
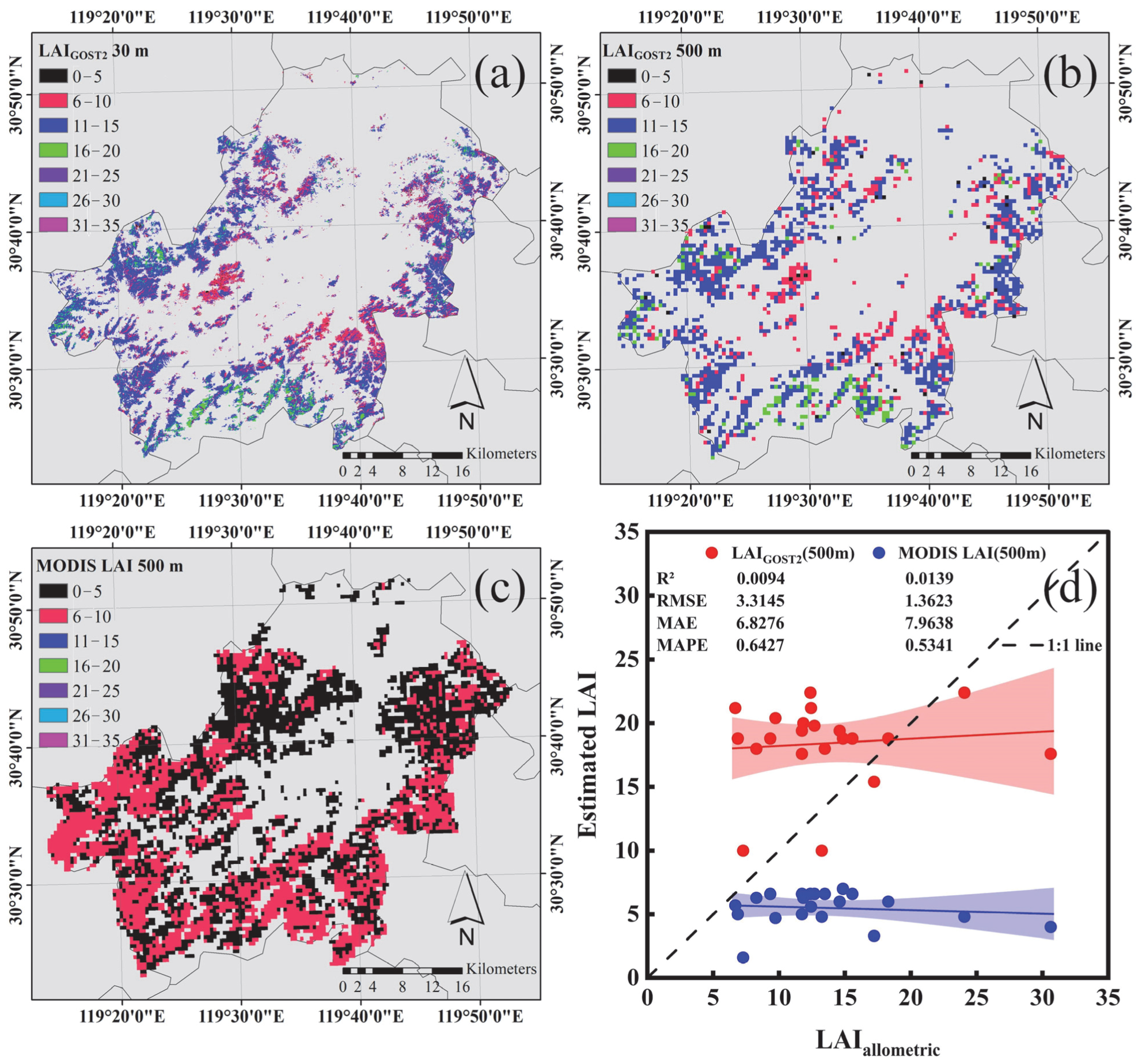
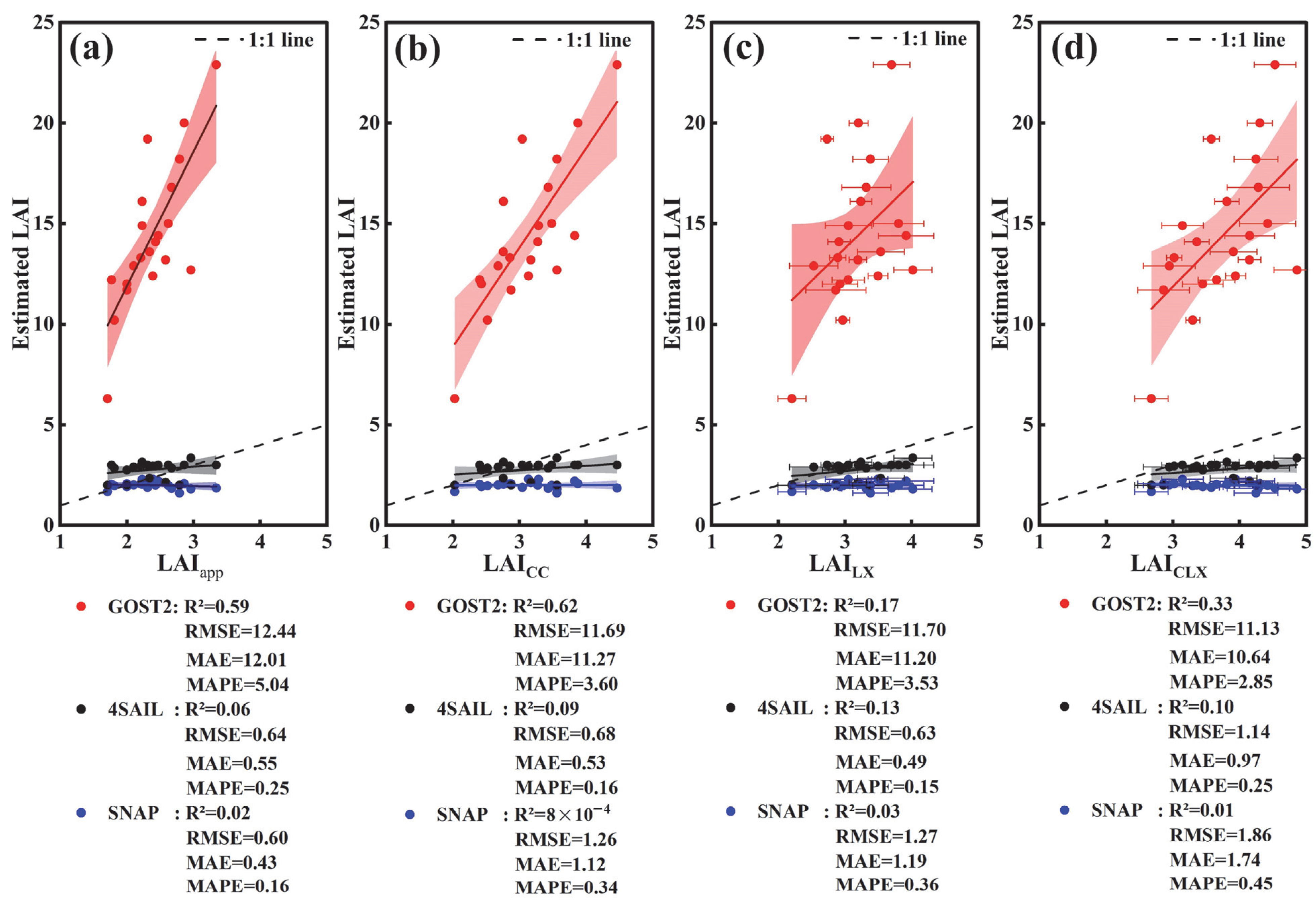
3.4. Satellite-Based LAI Estimations
4. Discussion
4.1. Why Do Gap Analysis-Based Methods Tend to Underestimate LAI?
4.2. Why Is LAI Underestimated by Satellite Remote Sensing Retrievals Without Leaf Clumping Consideration?
4.3. How Can We Validate LAI of Moso Bamboo Canopies Retrieved from Satellite Remote Sensing Data?
4.4. The Suggested Methods for Retrieving LAI of Moso Bamboo Canopies
4.5. Potential Ecological Implications of Applying the GOST2 Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baldocchi, D.; Wilson, K.; Gu, L. How the environment, canopy structure and canopy physiological functioning influence carbon, water and energy fluxes of a temperate broad-leaved deciduous forest—An assessment with the biophysical model CANOAK. Tree Physiol. 2002, 22, 1065–1077. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.M.; Chen, X.; Ju, W. Effects of vegetation heterogeneity and surface topography on spatial scaling of net primary productivity. Biogeosciences 2013, 10, 4879–4896. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F. Evaluation of canopy biophysical variable retrieval performances from the accumulation of large swath satellite data. Remote Sens. Environ. 1999, 70, 293–306. [Google Scholar] [CrossRef]
- Garrigues, S.; Lacaze, R.; Baret, F.J.T.M.; Morisette, J.T.; Weiss, M.; Nickeson, J.E.; Fernandes, R.; Plummer, S.; Shabanov, N.V.; Myneni, R.B.; et al. Validation and intercomparison of global Leaf Area Index products derived from remote sensing data. J. Geophys. Res. Biogeosci. 2008, 113, G02028. [Google Scholar] [CrossRef]
- Chen, J.M. Remote sensing of leaf area index and clumping index. Compr. Remote Sens. 2018, 3, 53–77. [Google Scholar]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An overview of global leaf area index (LAI): Methods, products, validation, and applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Xu, J.; Quackenbush, L.J.; Volk, T.A.; Im, J. Forest and crop leaf area index estimation using remote sensing: Research trends and future directions. Remote Sens. 2020, 12, 2934. [Google Scholar] [CrossRef]
- Fang, H. Canopy clumping index (CI): A review of methods, characteristics, and applications. Agric. For. Meteorol. 2021, 303, 108374. [Google Scholar] [CrossRef]
- Liang, S. Quantitative Remote Sensing of Land Surfaces; John Wiley & Sons, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; Francois, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; D’Urso, G.; Mauser, W.; Vuolo, F.; Hank, T. Evaluation of the PROSAIL model capabilities for future hyperspectral model environments: A review study. Remote Sens. 2018, 10, 85. [Google Scholar] [CrossRef]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niño, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION: Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E.; Jégo, G. Assessment of vegetation indices for regional crop green LAI estimation from Landsat images over multiple growing seasons. Remote Sens. Environ. 2012, 123, 347–358. [Google Scholar] [CrossRef]
- Ma, Q.; Li, Y.; Li, J.; Liu, Q. Modeling of Mixed-Pixel clumping Index from remote sensing data and its evaluation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2320–2331. [Google Scholar] [CrossRef]
- Claverie, M.; Vermote, E.F.; Weiss, M.; Baret, F.; Hagolle, O.; Demarez, V. Validation of coarse spatial resolution LAI and FAPAR time series over cropland in southwest France. Remote Sens. Environ. 2013, 139, 216–230. [Google Scholar] [CrossRef]
- García-Haro, F.J.; Campos-Taberner, M.; Muñoz-Marí, J.; Laparra, V.; Camacho, F.; Sanchez-Zapero, J.; Camps-Valls, G. Derivation of global vegetation biophysical parameters from EUMETSAT Polar System. ISPRS J. Photogramm. Remote Sens. 2018, 139, 57–74. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Efficient RTM-based training of machine learning regression algorithms to quantify biophysical & biochemical traits of agricultural crops. ISPRS J. Photogramm. Remote Sens. 2021, 173, 278–296. [Google Scholar]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of general regression neural networks for generating the GLASS leaf area index product from time-series MODIS surface reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Demarez, V.; Pinel, V.; Zagolski, F. Modeling radiative transfer in heterogeneous 3-D vegetation canopies. Remote Sens. Environ. 1996, 58, 131–156. [Google Scholar] [CrossRef]
- Chen, J.M.; Leblanc, S. A Four-scale bidirectional reflection model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]
- Banskota, A.; Serbin, S.P.; Wynne, R.H.; Thomas, V.A.; Falkowski, M.J.; Kayastha, N.; Gastellu-Etchegorry, J.P.; Townsend, P.A. An LUT-based inversion of DART model to estimate forest LAI from hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3147–3160. [Google Scholar] [CrossRef]
- Deng, F.; Chen, J.M.; Plummer, S.; Chen, M.; Pisek, J. Algorithm for global leaf area index retrieval using satellite imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2219–2229. [Google Scholar] [CrossRef]
- Chen, J.M.; Menges, C.H.; Leblanc, S.G. Global mapping of foliage clumping index using multi-angular satellite data. Remote Sens. Environ. 2005, 97, 447–457. [Google Scholar] [CrossRef]
- Leblanc, S.G.; Chen, J.M.; White, H.P.; Latifovic, R.; Lacaze, R.; Roujean, J.L. Canada-wide foliage clumping index mapping from multiangular POLDER measurements. Can. J. Remote Sens. 2005, 31, 364–376. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Pisek, J.; Schaaf, C.B.; Strahler, A.H. Global clumping index map derived from the MODIS BRDF product. Remote Sens. Environ. 2012, 119, 118–130. [Google Scholar] [CrossRef]
- Fan, W.; Chen, J.M.; Ju, W.; Zhu, G. GOST: A geometric-optical model for sloping terrains. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5469–5482. [Google Scholar]
- Fan, W.; Chen, J.M.; Ju, W.; Nesbitt, N. Hybrid geometric optical–radiative transfer model suitable for forests on slopes. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5579–5586. [Google Scholar]
- Fan, W.; Li, J.; Liu, Q. GOST2: The improvement of the canopy reflectance model GOST in separating the sunlit and shaded leaves. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1423–1431. [Google Scholar] [CrossRef]
- Stenberg, P.; Mõttus, M.; Rautiainen, M. Photon recollision probability in modelling the radiation regime of canopies—A review. Remote Sens. Environ. 2016, 183, 98–108. [Google Scholar] [CrossRef]
- Gu, C.; Clevers, J.G.; Liu, X.; Tian, X.; Li, Z.; Li, Z. Predicting forest height using the GOST, Landsat 7 ETM+, and airborne LiDAR for sloping terrains in the Greater Khingan Mountains of China. ISPRS J. Photogramm. Remote Sens. 2018, 137, 97–111. [Google Scholar] [CrossRef]
- Fan, W.; Li, J.; Liu, Q.; Zhang, Q.; Yin, G.; Li, A.; Zeng, Y.; Xu, B.; Xu, X.; Zhou, G.; et al. Topographic correction of forest image data based on the canopy reflectance model for sloping terrains in multiple forward mode. Remote Sens. 2018, 10, 717. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.M.; Qiu, F.; Fan, W.; Xu, M.; Wang, R. Simultaneous estimation of leaf directional-hemispherical reflectance and transmittance from multi-angular canopy reflectance. Remote Sens. Environ. 2024, 304, 114025. [Google Scholar] [CrossRef]
- Gower, S.T.; Kucharik, C.J.; Norman, J.M. Direct and indirect estimation of leaf area index, fAPAR, and net primary production of terrestrial ecosystems. Remote Sens. Environ. 1999, 70, 29–51. [Google Scholar] [CrossRef]
- Bréda, N.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef]
- Yan, G.; Hu, R.; Luo, J.; Weiss, M.; Jiang, H.; Mu, X.; Xie, D.; Zhang, W. Review of indirect optical measurements of leaf area index: Recent advances, challenges, and perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Fang, H.; Li, W.; Wei, S.; Jiang, C. Seasonal variation of leaf area index (LAI) over paddy rice fields in NE China: Intercomparison of destructive sampling, LAI-2200, digital hemispherical photography (DHP), and AccuPAR methods. Agric. For. Meteorol. 2014, 198, 126–141. [Google Scholar] [CrossRef]
- Baret, F.; de Solan, B.; Lopez-Lozano, R.; Ma, K.; Weiss, M. GAI estimates of row crops from downward looking digital photos taken perpendicular to rows at 57.5 zenith angle: Theoretical considerations based on 3D architecture models and application to wheat crops. Agric. For. Meteorol. 2010, 150, 1393–1401. [Google Scholar] [CrossRef]
- Nasahara, K.N.; Muraoka, H.; Nagai, S.; Mikami, H. Vertical integration of leaf area index in a Japanese deciduous broad-leaved forest. Agric. For. Meteorol. 2008, 148, 1136–1146. [Google Scholar] [CrossRef]
- Le Maire, G.; Marsden, C.; Verhoef, W.; Ponzoni, F.J.; Seen, D.L.; Bégué, A.; Stape, J.L.; Nouvellon, Y. Leaf area index estimation with MODIS reflectance time series and model inversion during full rotations of Eucalyptus plantations. Remote Sens. Environ. 2011, 115, 586–599. [Google Scholar] [CrossRef]
- Majasalmi, T.; Rautiainen, M.; Stenberg, P.; Lukeš, P. An assessment of ground reference methods for estimating LAI of boreal forests. For. Ecol. Manag. 2013, 292, 10–18. [Google Scholar] [CrossRef]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Review of methods for in situ leaf area index determination: Part I. Theories, sensors and hemispherical photography. Agric. For. Meteorol. 2004, 121, 19–35. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Smith, G.J.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination: Part II. Estimation of LAI, errors and sampling. Agric. For. Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
- Wilson, J.W. Incliend point quadrats (with appendix by J.E. Reeve). New Phytol. 1960, 59, 1–8. [Google Scholar] [CrossRef]
- Welles, J.M. Some indirect methods of estimating canopy structure. Remote Sens. Rev. 1990, 5, 31–43. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Plant canopy gap-size analysis theory for improving optical measurements of leaf-area index. Appl. Opt. 1995, 34, 6211–6222. [Google Scholar] [CrossRef] [PubMed]
- Leblanc, S.G.; Chen, J.M.; Fernandes, R.; Deering, D.W.; Conley, A. Methodology comparison for canopy structure parameters extraction from digital hemispherical photography in boreal forests. Agric. For. Meteorol. 2005, 129, 187–207. [Google Scholar] [CrossRef]
- Gower, S.T.; Norman, J.M. Rapid estimation of leaf area index in conifer and broad-leaf plantations. Ecology 1991, 72, 1896–1900. [Google Scholar] [CrossRef]
- Cutini, A.; Matteucci, G.; Mugnozza, G.S. Estimation of leaf area index with the Li-Cor LAI 2000 in deciduous forests. For. Ecol. Manag. 1998, 105, 55–65. [Google Scholar] [CrossRef]
- Gardingen, P.R.V.; Jackson, G.E.; Hernandez-Daumas, S.; Russell, G.; Sharp, L. Leaf area index estimates obtained for clumped canopies using hemispherical photography-sciencedirect. Agric. For. Meteorol. 1999, 94, 243–257. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J.M.; Miller, J.R. Determining digital hemispherical photograph exposure for leaf area index estimation. Agric. For. Meteorol. 2005, 133, 166–181. [Google Scholar] [CrossRef]
- Chianucci, F.; Cutini, A. Digital hemispherical photography for estimating forest canopy properties: Current controversies and opportunities. iForest 2012, 5, 290–295. [Google Scholar] [CrossRef]
- Kobayashi, H.; Ryu, Y.; Baldocchi, D.; Welles, J.; Norman, J. On the correct estimation of gap fraction: How to remove scattered radiation in gap fraction measurements? Agric. For. Meteorol. 2013, 174–175, 170–183. [Google Scholar] [CrossRef]
- Lang, A.R.G.; Xiang, Y. Estimation of leaf area index from transmission of direct sunlight in discontinuous canopies. Agric. For. Meteorol. 1986, 37, 229–243. [Google Scholar] [CrossRef]
- Leblanc, S.G.; Fournier, R.A. Hemispherical photography simulations with an architectural model to assess retrieval of leaf area index. Agric. For. Meteorol. 2014, 194, 64–76. [Google Scholar] [CrossRef]
- Xu, X.; Du, H.; Zhou, G.; Ge, H.; Shi, Y.; Zhou, Y.; Fan, W.; Fan, W. Estimation of aboveground carbon stock of Moso bamboo (Phyllostachys heterocycla var. pubescens) forest with a Landsat Thematic Mapper image. Int. J. Remote Sens. 2011, 32, 1431–1448. [Google Scholar] [CrossRef]
- Li, P.; Zhou, G.; Du, H.; Lu, D.; Mo, L.; Xu, X.; Shi, Y.; Zhou, Y. Current and potential carbon stocks in Moso bamboo forests in China. J. Environ. Manag. 2015, 156, 89–96. [Google Scholar] [CrossRef]
- Okutomi, K.; Shinoda, S.; Fukuda, H. Causal analysis of the invasion of broad-leaved forest by bamboo in Japan. J. Veg. Sci. 1996, 7, 723–728. [Google Scholar] [CrossRef]
- Li, R.; Werger, M.J.A.; De Kroon, H.; During, H.J.; Zhong, Z.C. Interactions between shoot age structure, nutrient availability and physiological integration in the giant bamboo Phyllostachys pubescens. Plant Biol. 2000, 2, 437–446. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, S.; Binkley, D.; Zhou, G.; Fang, F. The independence of clonal shoot’s growth from light availability supports moso bamboo invasion of closed-canopy forest. For. Ecol. Manag. 2016, 368, 105–110. [Google Scholar] [CrossRef]
- Xu, X.; Du, H.; Zhou, G.; Li, P. Method for improvement of MODIS leaf area index products based on pixel-to-pixel correlations. Eur. J. Remote Sens. 2016, 49, 57–72. [Google Scholar] [CrossRef]
- Mao, F.; Du, H.; Zhou, G.; Li, X.; Xu, X.; Li, P.; Sun, S. Coupled LAI assimilation and BEPS model for analyzing the spatiotemporal pattern and heterogeneity of carbon fluxes of the bamboo forest in Zhejiang Province, China. Agric. For. Meteorol. 2017, 242, 96–108. [Google Scholar] [CrossRef]
- Mao, F.; Li, X.; Du, H.; Zhou, G.; Han, N.; Xu, X.; Liu, Y.; Chen, L.; Cui, L. Comparison of two data assimilation methods for improving MODIS LAI time series for bamboo forests. Remote Sens. 2017, 9, 401. [Google Scholar] [CrossRef]
- Li, X.; Mao, F.; Du, H.; Zhou, G.; Xu, X.; Han, N.; Sun, S.; Gao, G.; Chen, L. Assimilating leaf area index of three typical types of subtropical forest in China from MODIS time series data based on the integrated ensemble Kalman filter and PROSAIL model. ISPRS J. Photogramm. Remote Sens. 2017, 126, 68–78. [Google Scholar] [CrossRef]
- Li, X.; Du, H.; Mao, F.; Zhou, G.; Chen, L.; Xing, L.; Fan, W.; Xu, X.; Liu, Y.; Cui, L.; et al. Estimating bamboo forest aboveground biomass using EnKF-assimilated MODIS LAI spatiotemporal data and machine learning algorithms. Agric. For. Meteorol. 2018, 256, 445–457. [Google Scholar] [CrossRef]
- Xing, L.; Li, X.; Du, H.; Zhou, G.; Mao, F.; Liu, T.; Zheng, J.; Dong, L.; Zhang, M.; Han, N.; et al. Assimilating multiresolution leaf area index of moso bamboo forest from MODIS time series data based on a Hierarchical Bayesian Network algorithm. Remote Sens. 2018, 11, 56. [Google Scholar] [CrossRef]
- Xu, X.; Du, H.; Zhou, G.; Mao, F.; Li, X.; Zhu, D.; Li, Y.; Cui, L. Remote estimation of canopy leaf area index and chlorophyll content in Moso bamboo (Phyllostachys edulis (Carrière) J. Houz.) forest using MODIS reflectance data. Ann. For. Sci. 2018, 75, 33. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Sun, Y.; Ruan, H.; Wang, G.; Dai, J.; She, G. Estimating canopy structure and biomass in bamboo forests using airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2019, 148, 114–129. [Google Scholar] [CrossRef]
- Ji, J.; Li, X.; Du, H.; Mao, F.; Fan, W.; Xu, Y.; Huang, Z.; Wang, J.; Kang, F. Multiscale leaf area index assimilation for Moso bamboo forest based on Sentinel-2 and MODIS data. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102519. [Google Scholar] [CrossRef]
- Wu, X.; Fan, W.; Du, H.; Ge, H.; Huang, F.; Xu, X. Estimating crown structure parameters of moso bamboo: Leaf area and leaf angle distribution. Forests 2019, 10, 686. [Google Scholar] [CrossRef]
- Huang, F.; Fan, W.; Du, H.; Xu, X.; Wu, J.; Zheng, M.; Du, Y. Estimation of Leaf Area Index of Moso Bamboo Canopies. J. Sustain. For. 2023, 42, 189–204. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T.; Adams, R. Evaluation of hemispherical photography for determining plant area index and geometry of a forest stand. Agric. For. Meteorol. 1991, 56, 129–143. [Google Scholar] [CrossRef]
- Kucharik, C.J.; Norman, J.M.; Gower, S.T. Characterization of radiation regimes in nonrandom forest canopies: Theory, measurements, and a simplified modeling approach. Tree Physiol. 1999, 19, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.B. A formula for average foliage density. Aust. J. Bot. 1967, 15, 141–144. [Google Scholar] [CrossRef]
- LI-COR Inc. LAI-2200 Plant Canopy Analyzer: Instruction Manual; LI-COR Inc.: Lincoln, NE, USA, 2010. [Google Scholar]
- Chen, J.M. Optically-based methods for measuring seasonal variation of leaf area index in boreal conifer stands. Agric. For. Meteorol. 1996, 80, 135–163. [Google Scholar] [CrossRef]
- Stroppiana, D.; Boschetti, M.; Confalonieri, R.; Bocchi, S.; Brivio, P.A. Evaluation of LAI-2000 for leaf area index monitoring in paddy rice. Field Crops Res. 2006, 99, 167–170. [Google Scholar] [CrossRef]
- Ryu, Y.; Sonnentag, O.; Nilson, T.; Vargas, R.; Kobayashi, H.; Wenk, R.; Baldocchi, D.D. How to quantify tree leaf area index in an open savanna ecosystem: A multi-instrument and multi-model approach. Agric. For. Meteorol. 2010, 150, 63–76. [Google Scholar] [CrossRef]
- Verhoef, W.; Jia, L.; Xiao, Q.; Su, Z. Unified optical-thermal four-stream radiative transfer theory for homogeneous vegetation canopies. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1808–1822. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F. Sentinel-2 ToolBox Level 2 Biophysical Product Algorithms, 2016, Scientific Toolbox Exploitation Platform. Available online: https://step.esa.int/docs/extra/ATBD_S2ToolBox_L2B_V1.1.pdf (accessed on 7 June 2022).
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Atzberger, C.; Darvishzadeh, R.; Immitzer, M.; Schlerf, M.; Skidmore, A.; Le Maire, G. Comparative analysis of different retrieval methods for mapping grassland leaf area index using airborne imaging spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 19–31. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, C.; Xiang, S.; Chen, L.; Yu, X.; Li, H.; Li, Z.; Guo, X.; Zhang, H.; Huang, X.; et al. A hybrid method of PROSAIL RTM for the retrieval canopy LAI and Chlorophyll Content of Moso bamboo (Phyllostachys pubescens) forests from Sentinel-2 MSI data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 18, 3125–3143. [Google Scholar] [CrossRef]
- Jonckheere, I.; Nackaerts, K.; Muys, B.; Coppin, P. Assessment of automaticgap fraction estimation of forests from digital hemispherical photography. Agric. For. Meteorol. 2005, 132, 96–114. [Google Scholar] [CrossRef]
- Hwang, Y.; Ryu, Y.; Kimm, H.; Jiang, C.; Lang, M.; Macfarlane, C.; Sonnentag, O. Correction for light scattering combined with sub-pixel classification improves estimation of gap fraction from digital cover photography. Agric. For. Meteorol. 2016, 222, 32–44. [Google Scholar] [CrossRef]
- Wei, S.; Fang, H. Estimation of canopy clumping index from MISR and MODIS sensors using the normalized difference hotspot and darkspot (NDHD) method: The influence of BRDF models and solar zenith angle. Remote Sens. Environ. 2016, 187, 476–491. [Google Scholar] [CrossRef]
- Pitman, A.; Noblet-Ducoudre, N.; Cruz, F.; Davin, T.; Bonan, G.; Brovkin, V.; Claussen, M.; Delire, C.; Ganzeveld, L.; Gayler, V.; et al. Uncertainties in climate responses to past land cover change: Firstresults from the LUCID intercomparison study. Geophys. Res. Lett. 2009, 36, L14814. [Google Scholar] [CrossRef]
- Li, X.; Du, H.; Mao, F.; Zhou, G.; Han, N.; Xu, X.; Liu, Y.; Zhu, D.; Zheng, J.; Dong, L.; et al. Assimilating spatiotemporal MODIS LAI data with a particle filter algorithm for improving carbon cycle simulations for bamboo forest ecosystems. Sci. Total Environ. 2019, 694, 133803. [Google Scholar] [CrossRef]
- Lai, Y.; Mu, X.; Li, W.; Zou, J.; Bian, Y.; Zhou, K.; Hu, R.; Li, L.; Xie, D.; Yan, G. Correcting for the clumping effect in leaf area index calculations using one-dimensional fractal dimension. Remote Sens. Environ. 2022, 281, 113259. [Google Scholar] [CrossRef]
- Stenberg, P. Correcting LAI-2000 estimates for the clumping of needles in shoots of conifers. Agric. For. Meteorol. 1996, 79, 1–8. [Google Scholar] [CrossRef]
- Woodgate, W.; Disney, M.; Armston, J.D.; Jones, S.D.; Suarez, L.; Hill, M.J.; Wilkes, P.; Soto-Berelov, M.; Haywood, A.; Mellor, A. An improved theoretical model of canopy gap probability for Leaf Area Index estimation in woody ecosystems. For. Ecol. Manag. 2015, 358, 303–320. [Google Scholar] [CrossRef]
- Yan, K.; Park, T.; Yan, G.; Liu, Z.; Yang, B.; Chen, C.; Nemani, R.; Knyazikhin, Y.; Myneni, R. Evaluation of MODIS LAI/FPAR product collection 6. Part 2: Validation and intercomparison. Remote Sens. 2016, 8, 460. [Google Scholar] [CrossRef]
- Yin, G.; Li, A.; Jin, H.; Zhao, W.; Bian, J.; Qu, Y.; Zeng, Y.; Xu, B. Derivation of temporally continuous LAI reference maps through combining the LAINet observation system with CACAO. Agric. For. Meteorol. 2017, 233, 209–221. [Google Scholar] [CrossRef]
- van Dijke, A.J.H.; Mallick, K.; Schlerf, M.; Machwitz, M.; Herold, M.; Teuling, A.J. Examining the link between vegetation leaf area and land-atmosphere exchange of water, energy, and carbon fluxes using FLUXNET data. Biogeosciences 2020, 17, 4443–4457. [Google Scholar] [CrossRef]
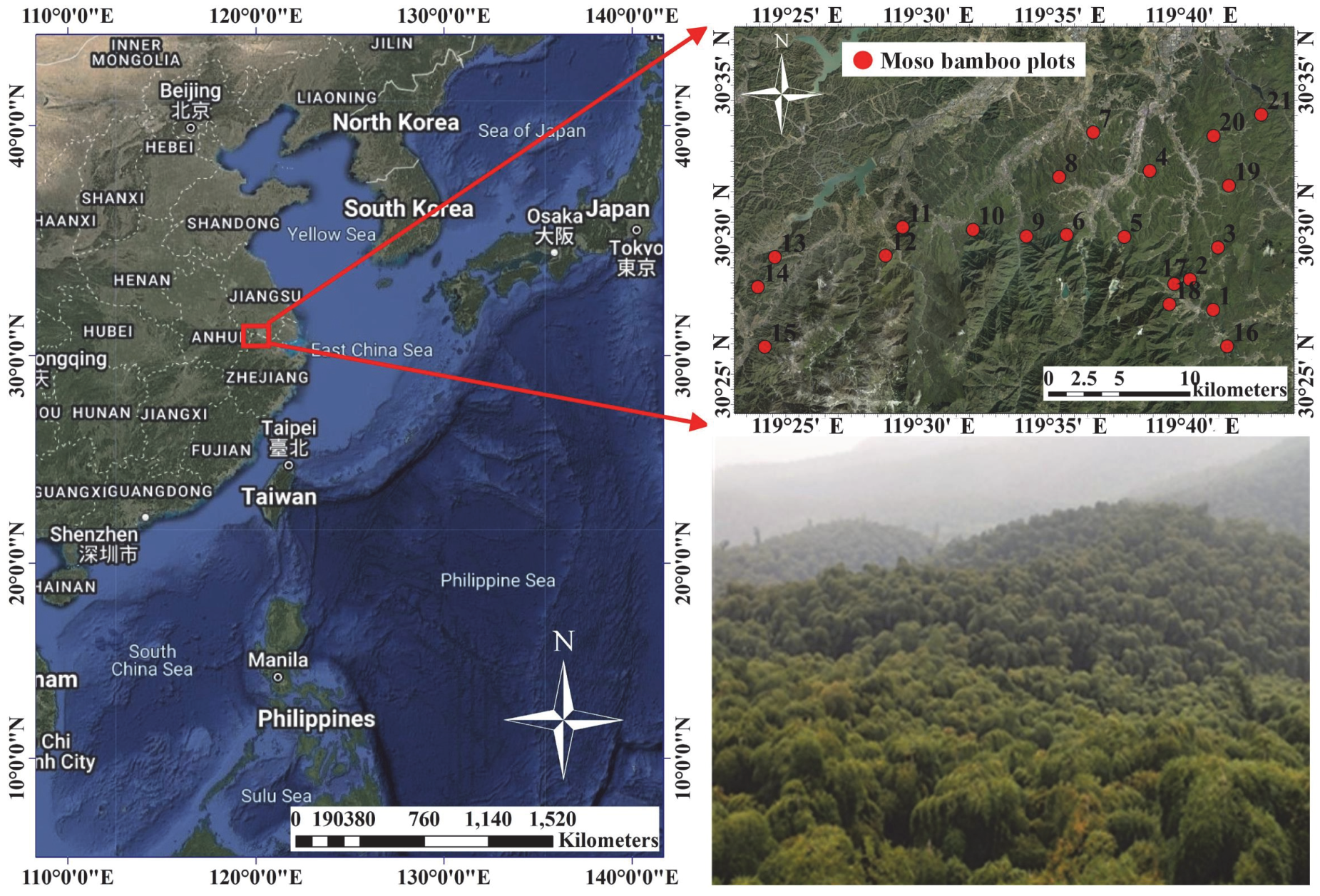

| Plots | Latitude | Longitude | DBH (cm) | CD (Crowns·ha−1) |
|---|---|---|---|---|
| 1 | 30°27′37′′ | 119°41′17″ | 9.83 ± 1.61 | 3178 |
| 2 | 30°28′37″ | 119°40′24″ | 10.56 ± 1.58 | 3533 |
| 3 | 30°29′40″ | 119°41′28″ | 9.84 ± 1.83 | 1856 |
| 4 | 30°30′01″ | 119°37′54″ | 9.50 ± 1.52 | 2367 |
| 5 | 30°32′11″ | 119°38′52″ | 11.35 ± 1.75 | 1578 |
| 6 | 30°30′05″ | 119°35′42″ | 10.00 ± 1.75 | 3489 |
| 7 | 30°33′27″ | 119°36′43″ | 10.23 ± 1.71 | 4378 |
| 8 | 30°31′59″ | 119°35′25″ | 8.94 ± 1.68 | 3711 |
| 9 | 30°30′02″ | 119°34′10″ | 11.40 ± 1.62 | 2556 |
| 10 | 30°30′15″ | 119°32′08″ | 10.28 ± 1.52 | 3200 |
| 11 | 30°30′20″ | 119°29′27″ | 10.19 ± 1.89 | 3178 |
| 12 | 30°29′24″ | 119°28′48″ | 10.01 ± 1.48 | 1756 |
| 13 | 30°29′21″ | 119°24′35″ | 9.99 ± 1.54 | 2567 |
| 14 | 30°28′22″ | 119°23′56″ | 10.56 ± 1.68 | 2256 |
| 15 | 30°26′24″ | 119°24′12″ | 11.16 ± 1.65 | 3467 |
| 16 | 30°26′25″ | 119°41′49″ | 10.93 ± 1.67 | 3411 |
| 17 | 30°28′28″ | 119°39′48″ | 11.16 ± 1.52 | 4067 |
| 18 | 30°27′48″ | 119°39′37″ | 11.16 ± 1.57 | 5356 |
| 19 | 30°31′42″ | 119°41′53″ | 11.38 ± 1.80 | 6622 |
| 20 | 30°33′20″ | 119°41′18″ | 10.87 ± 1.74 | 3122 |
| 21 | 30°34′02″ | 119°43′07″ | 10.45 ± 1.89 | 3044 |
| Model Parameters | Symbol | Units | Values | Model | References | |
|---|---|---|---|---|---|---|
| Leaf structure index | Ns | - | 1.1 | Both | [64] | |
| Leaf chlorophyll content | Cab | μg·cm−2 | 20:5:80 | Both | [64] | |
| Water thickness | EWT | μg·cm−2 | 0.003:0.001:0.008 | Both | [69] | |
| Dry matter content | Cm | g·cm−2 | 0.002:0.002:0.008 | Both | [69] | |
| Leaf area index | LAI | m2·m−2 | 1:1:35 | Both | [71] | |
| Leaf projection function | G(θ) | - | Planophile | Both | [70] | |
| Crown density | - | crowns·ha−1 | 1000:1000:7000 | GOST2 | [71] | |
| Crown radius | r | m | 1.5:0.5:5.0 | GOST2 | [70] | |
| Crown shape | - | - | Ellipsoid | GOST2 | [70] | |
| Height of trunk space | Ha | m | 7.5 | GOST2 | [70] | |
| Height of crown space | Hb | m | 5.5 | GOST2 | [70] | |
| Reflectance of the background | Rb | - | Measured | Both | - | |
| Sun zenith angle | θs | degree | 23 | Both | - | |
| View zenith angle | θv | degree | 5 | Both | - | |
| Solar azimuth angle | φs | degree | 124 | Both | - | |
| View azimuth angle | φv | degree | 89 | Both | - | |
| Model Parameters | Symbol | Units | Range or Fixed Value | Law |
|---|---|---|---|---|
| Leaf structure index | Ns | - | 1.20–2.20 | Gaussian |
| Leaf chlorophyll content | Cab | μg·cm−2 | 20–90 | Gaussian |
| Relative water content | Cw_Rel | - | 0.60–0.85 | Uniform |
| Dry matter content | Cm | g·cm−2 | 0.003:0.01 | Gaussian |
| Leaf area index | LAI | m2·m−2 | 0–15 | Gaussian |
| Average leaf angle | ALA | degree | 30–80 | Gaussian |
| Soil reflection coefficient | ρs | unitless | 0.5–3.5 | Gaussian |
| Band # | B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B8a | B9 | B10 | B11 | B12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Band center (nm) | 443 | 490 | 560 | 665 | 705 | 740 | 783 | 842 | 865 | 945 | 1375 | 1610 | 2190 |
| Band width (nm) | 20 | 65 | 35 | 30 | 15 | 15 | 20 | 115 | 20 | 20 | 30 | 90 | 180 |
| Spatial resolution (m) | 60 | 10 | 10 | 10 | 20 | 20 | 20 | 10 | 20 | 60 | 60 | 20 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, W.; Wu, J.; Zheng, G.; Zhang, Q.; Xu, X.; Du, H.; Zheng, M.; Zhang, K.; Zhang, F. Retrieving the Leaf Area Index of Dense and Highly Clumped Moso Bamboo Canopies from Sentinel-2 MSI Data. Remote Sens. 2025, 17, 1891. https://doi.org/10.3390/rs17111891
Fan W, Wu J, Zheng G, Zhang Q, Xu X, Du H, Zheng M, Zhang K, Zhang F. Retrieving the Leaf Area Index of Dense and Highly Clumped Moso Bamboo Canopies from Sentinel-2 MSI Data. Remote Sensing. 2025; 17(11):1891. https://doi.org/10.3390/rs17111891
Chicago/Turabian StyleFan, Weiliang, Jun Wu, Guang Zheng, Qian Zhang, Xiaojun Xu, Huaqiang Du, Mengxiang Zheng, Kexin Zhang, and Feng Zhang. 2025. "Retrieving the Leaf Area Index of Dense and Highly Clumped Moso Bamboo Canopies from Sentinel-2 MSI Data" Remote Sensing 17, no. 11: 1891. https://doi.org/10.3390/rs17111891
APA StyleFan, W., Wu, J., Zheng, G., Zhang, Q., Xu, X., Du, H., Zheng, M., Zhang, K., & Zhang, F. (2025). Retrieving the Leaf Area Index of Dense and Highly Clumped Moso Bamboo Canopies from Sentinel-2 MSI Data. Remote Sensing, 17(11), 1891. https://doi.org/10.3390/rs17111891






