Adaptive Multi-Radar Anti-Bias Track Association Algorithm Based on Reference Topology Features

Abstract

Accurate track association is essential for multi-radar fusion, since incorrect associations may result in significant errors in integrated information. To address the track association problem in multi-radar systems, particularly the challenges posed by offset bias, this paper proposes an adaptive multi-radar anti-bias track association algorithm based on reference topological features (RETs) that achieves accurate association despite offset bias and radar missed detections. The multi-radar adaptive RET algorithm employs the Optimal Sub-Pattern Assignment (OSPA) metric, which is corrected for offset bias, to measure the distance among RETs, thus generating an association cost matrix. The obtained distances among RETs follow a chi-squared distribution, thereby replacing the manually adjusted association threshold with an adaptive association threshold, enhancing robustness against offset bias and measurement noise. Subsequently, the multi-dimensional association cost matrix is filtered using threshold filtering to reduce erroneous associations caused by radar missed detections. Finally, the Lagrangian relaxation algorithm is applied to assign the association cost matrix and determine the final track association. The simulation results demonstrate that the multi-radar adaptive RET algorithm achieves accurate association results and exhibits considerable adaptability to radar offset bias and random noise errors.

1. Introduction

Track association aims to determine whether tracks from different radars correspond to the same target [1]. This is a core problem in multi-radar data fusion. In multi-radar multi-target tracking fusion systems, radars transmit the detected information to a fusion center, where the track association and fusion of the received radar data are performed [2].

Track association is a prerequisite for radar bias registration, and the presence of bias can affect the results of track association. Therefore, track association and bias estimation are mutually coupled [3], making the problem more difficult to solve. Prior methodologies predominantly decoupled association and bias estimation, resulting in suboptimal solutions due to their inherent interdependency. Stone [4] proposed a heuristic algorithm that first calculates the correlation of radar tracks and then estimates the relative translational bias, but it did not consider azimuth bias [5] introduced the Global Nearest Neighbor Pattern (GNP) algorithm, which accounts for radar bias in the association cost matrix, but GNP is a difficult mixed-integer nonlinear programming problem [6].

In addition, during the radar tracking and measurement process, due to the influence of random noise, offset bias, missed detections, and other factors, the radar measurements of the target’s position may deviate from its true value. Traditional track association algorithms [7,8] mainly rely on the absolute position information of the target, and the presence of bias significantly degrades the performance of these algorithms [9,10].

There are generally two approaches to addressing the track association problem in the presence of radar bias. The first approach involves joint bias estimation and data association [11,12,13]. A joint data association, registration, and fusion method based on the Expectation-Maximization (EM) algorithm was proposed in [14,15], which considers the impact of radar bias. The global nearest pattern matching (GNPM) method was introduced in [16], but GNPM is a challenging mixed-integer nonlinear programming problem. In [17], a multi-start local search (MSLS) method was proposed as a heuristic approach. However, due to the need to maintain a large number of initial bias estimates to achieve satisfactory performance, the computational cost of MSLS is high.

Another anti-bias approach is to select association statistics that are insensitive to offset bias, thereby reducing the impact of offset bias on the association results and ensuring the accuracy and reliability of the association. The authors of [18] proposed an algorithm that eliminates offset bias by constructing track vectors to achieve anti-bias. However, the performance of this algorithm depends on the tracking quality and is easily affected by unstable tracking. Tian W. et al. proposed an algorithm based on reference topological features (RETs), which employs the relative positional relationship between the target measurement and its neighboring measurements as the association metric [19]. Within the measurement domains of different radars, tracks corresponding to the same target and their adjacent tracks exhibit similar topological structures [20,21]. This algorithm employs the Optimal Sub-Pattern Assignment (OSPA) metric to calculate the distance between RETs, which adapts well to association in complex motion scenarios. However, the association threshold needs to be manually set based on experience, making it difficult to maintain stable track association accuracy.

When associating tracks from three or more radars, the resulting association cost matrix becomes multi-dimensional, necessitating the resolution of the s-D assignment problem, which is NP-hard [22]. Most anti-bias track association algorithms [23,24] are limited to dual-radar scenarios and are unable to address the track association problem among multiple radars [25] proposed a track association algorithm for multi-radar systems based on state estimation and vector decomposition cancellation. By constructing track distance vectors and defining a multi-radar association threshold using a chi-squared distribution test, the method achieves both system bias compensation and track association in environments involving three or more radars. However, the algorithm is relatively sensitive to the accuracy of target state estimation, which may lead to fluctuations in association accuracy. The Lagrangian relaxation algorithm can perform multi-dimensional matrix assignment [26,27]; however, in scenarios with missed detections, it attempts to assign all objects, thereby resulting in forced associations among different source objects.

The main contributions of this paper can be summarized as follows:

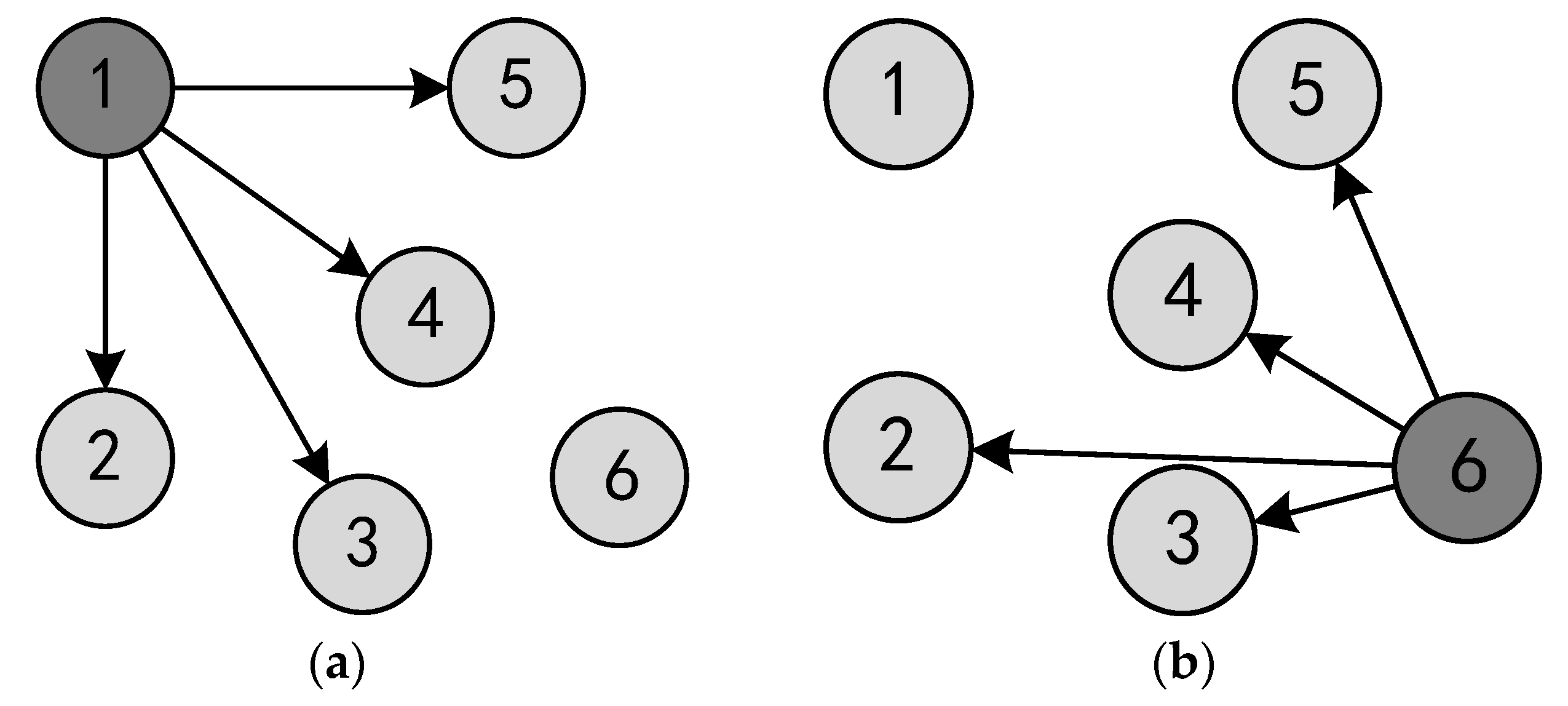
(a)

The multi-radar adaptive RET algorithm proposed in this paper addresses the instability caused by manually setting the association threshold in the OSPA metric. It improves the traditional OSPA metric and threshold by modifying the Mahalanobis distance to account for offset bias, and constructs a multi-dimensional association cost matrix. This modification replaces the fixed threshold with an adaptive one, which enhances robustness against offset bias and measurement noise.

(b)

To address the issue of incorrect associations caused by radar missed detections, we derived a threshold filtering method, which filters the association costs at the matrix dimension level to reduce the occurrence of forced associations between tracks from different sources. Subsequently, the Lagrangian relaxation algorithm was used to assign the association cost matrix and determine the final track association relationships.

(c)

The multi-radar adaptive RET algorithm achieves track association using only the radar’s position measurement information of the target, without the need for radar tracking or state estimation of the target. As a result, the algorithm is able to adapt to multi-radar track association problems in various complex motion scenarios, and simulation data have validated the effectiveness of the algorithm.

The overview of this paper is as follows: Section 2 introduces the composition of radar measurement bias and models it, studying and verifying the insensitivity of the RET metric to bias. The distance among RETs is calculated, and an association cost matrix is constructed. Section 3 improves the traditional OSPA metric solving method by modifying the Mahalanobis distance to include an offset bias-weighted distance, achieving adaptive association thresholds. Furthermore, it applies threshold filtering to the association cost matrix and uses the Lagrangian relaxation algorithm to perform s-D assignment and determine track association relationships. Section 4 presents simulation results to verify the performance of the proposed algorithm and compares it with the vector decomposition cancellation-based association algorithm. Section 5 summarizes the paper.

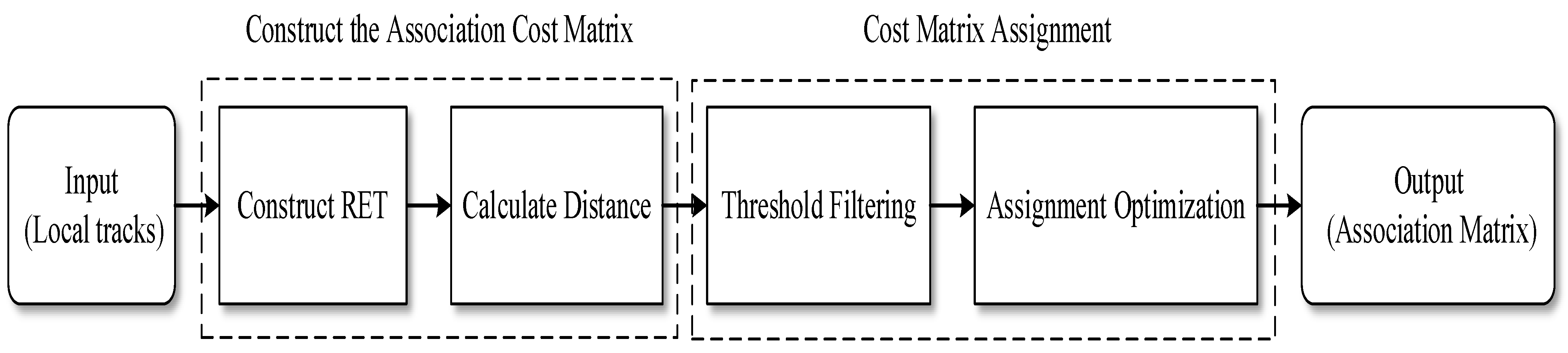
2. Track Association Problem Modeling

2.1. Target Measurement Modeling

Radar measures multiple targets in the detection area, and the measurement results consist of the true position of the target and measurement errors. These errors primarily arise from radar offset bias, platform installation bias, biased radar position measurements, and inaccurate radar timing, which are collectively referred to as radar offset bias in this paper [28,29]. Additionally, random noise during measurement is also a major source of measurement error, typically modeled as a Gaussian distribution with zero mean, independent of both the radar’s offset bias and the target’s position. Radar offset bias can be approximated as a fixed bias, manifesting as a constant offset across the measurement dimensions [30]. The radar measurements of a target are generally modeled as the sum of the target’s true state, radar offset bias, and random errors [31], and can be expressed in the global Cartesian coordinate system as:

$$Z_i^s=X_i^s+b_s+e_i^s$$

(1)

where $X_i^s$ is the true state vector, $b_s$ is the radar offset bias, and $e_i^s$ is the Gaussian random error with zero mean and covariance matrix $P_i^A$. The schematic diagram of the radar measurement is shown in Figure 1.

In the local polar coordinate system with the radar as the origin, as shown in Figure 1, the relative position of the target to the radar is represented by the measured range and azimuth. Due to the presence of radar offset bias and random noise errors, the radar’s measurement of the target’s position will deviate from its true position. The measurement results can be expressed as follows [32,33]:

$$\left[\begin{array}{c}{r}_i^s\\ {\theta }_i^s\end{array}\right]=\left[\begin{array}{c}{\widehat{r}}_i^s\\ {\widehat{\theta }}_i^s\end{array}\right]+\left[\begin{array}{c}\Delta r^s\\ \Delta {\theta }^s\end{array}\right]+\left[\begin{array}{c}{v}_r^s\\ v_{\theta }^s\end{array}\right]$$

(2)

where $r_i^s$ and ${\theta }_i^s$ represent the radar’s measured position of the target, ${\widehat{r}}_i^s$ and ${\widehat{\theta }}_i^s$ represent the true position of the target, $\Delta r^s$ and $\Delta {\theta }^s$ represent the radar’s range and azimuth bias, and $v_r^s$ and $v_{\theta }^s$ represent the random noise errors in range and azimuth, respectively.

$$\left[\begin{array}{c}{v}_r^s\\ v_{\theta }^s\end{array}\right]\sim \mathcal{N}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}{({\sigma }_r^s)}^2& 0\\ 0& {({\sigma }_{\theta }^s)}^2\end{array}\right]\right)$$

(3)

Track association means to find the matching tracks belonging to the same target among the radar measurements at that moment, i.e., to find the most probable association among them. In a multi-radar track association scenario, each radar measurement provides the target’s range and azimuth in the radar’s polar coordinate system, denoted as $Z_t^s=\left(r_t^s,{\theta }_t^s\right)$. The radar’s position coordinates in the Cartesian coordinate system are denoted as $S=\left(x_s,y_s\right)$. For uniform track association and fusion, it is necessary to transform the multi-radar track measurements to a global Cartesian coordinate system with the fusion center as the coordinate origin. The coordinate transformation formulas are as follows:

$$\left\{\begin{array}{c}{x}_t^s=r\cos \theta +x_s\\ y_t^s=r\sin \theta +y_s\end{array}\right.$$

(4)

After converting from polar to Cartesian coordinates, the offset caused by radar offset bias in the x- and y-directions varies with the target’s position in polar coordinates. In other words, the offset bias in the global Cartesian coordinate system is no longer a fixed spatial offset, but a target-dependent and spatially varying error pattern. The measurement noise covariance matrix $P$ will also undergo a rotation as the measurement coordinate system is transformed. The transformed matrix can be approximately expressed as:

$$P\left(Z_t^s\right)=JP{J}^T$$

(5)

where $J$ represents the Jacobian matrix expanded at the measurement point $Z_t^s=\left(r_t^s,{\theta }_t^s\right)$:

$$J\left(Z_t^s\right)=\left[\begin{array}{cc}\cos {\theta }_t^s& -r\sin {\theta }_t^s\\ \sin {\theta }_t^s& r\cos {\theta }_t^s\end{array}\right]$$

(6)

2.2. Definition of RETs

Traditional track association algorithms mostly use the absolute position information of the target for association, while the absolute position of the target will be affected by factors such as radar bias, which degrades the association accuracy, and the algorithms lack sufficient stability and robustness [34,35]. In a multi-target observation scenario, in addition to its own absolute position, the target also has a relative position relationship among other targets, and this relative position information among targets is called the target topology. Although the radar offset bias interferes with the measurement of the absolute position of the target, it has little effect on the relative position information among neighboring targets. For a single target under observation, the relative positional information derived from its spatial relationships with neighboring targets is defined as the reference topology feature (RET) of that target [36,37,38].

First, for the track measurement $Z_i^s$ of radar $S$, the set of its neighboring reference tracks is defined as:

$${\mathbb{R}}_i^s(R)=\left\{Z_j^s\right|\left|\right|Z_j^s-Z_i^s|{|}_2\le R,j\ne i\}=\{Z_{i,1}^s,Z_{i,2}^s,\dots ,Z_{i,n_i^s}^s\}$$

(7)

where $R$ is the topology radius, $Z_{i,k}^s$ is the k-th element of the set ${\mathbb{R}}_i^s(R)$, and $n_i^s$ represents the cardinality of the set ${\mathbb{R}}_i^s(R)$. The set ${\mathbb{R}}_i^s(R)$ denotes the collection of track measurements centered at the target track measurement $Z_i^s$ within a range defined by the topology radius $R$. This set contains a total of $n_i^s$ elements, including the target track and $n_i^s-1$ neighboring targets.

The reference topology feature (RET) of radar $S$’s track measurement $Z_i^s$ is defined as:

$${\mathbb{T}}_i^s(R)=\left\{t_{i,k}^s\mid t_{i,k}^s=Z_{i,k}^s-Z_i^s,Z_{i,k}^s\in {\mathbb{R}}_i^s(R)\right\}$$

(8)

As the topology radius $R$ increases, the number of targets in the neighboring reference track set of the track measurement increases, which leads to a significant increase in the structural information of the RET and the computational complexity of the association. To control the computation time, a cardinality constraint $n_i^s<n_t$ is introduced, considering only the $n_t$-nearest neighbors of the track.

As shown in Figure 2, the schematic of the RETs for Target 1 and Target 6 in a space containing six targets is illustrated when $n_t=4$. The arrow between the two targets in the figure represents the distance vector from one target to the other. It can be observed that the RETs of targets from different sources vary significantly, which aids in achieving accurate track association.

When the system satisfies $\Delta {\theta }^s+v_{\theta }^s\le 1$ and the mutually referenced targets have similar azimuth angles ${\widehat{\theta }}_i^s$ and ${\widehat{\theta }}_j^s$, we can derive:

$$Z_i^s-Z_j^s=\left[\begin{array}{c}{x}_i^s-x_j^s\\ y_i^s-y_j^s\end{array}\right]\simeq \left[\begin{array}{c}{\overline{x}}_i^s-{\overline{x}}_j^s\\ {\overline{y}}_i^s-{\overline{y}}_j^s\end{array}\right]=X_i^s-X_j^s$$

(9)

where ${\overline{x}}_i^s$ and ${\overline{y}}_i^s$ represent the true coordinates of the targets. In this case, the relative positions between target measurements are nearly insensitive to radar measurement biases. Therefore, in the presence of radar offset bias, the RET can be expressed as:

$$\begin{array}{cc}{\mathbb{T}}_i^s\left(b_s\right)& =\left\{\left(Z_{i,1}^s+b_s\right)-\left(Z_i^s+b_s\right),\left(Z_{i,2}^s+b_s\right) -\right.\left.\left(Z_i^s+b_s\right),\dots ,\left(Z_{i,n_t}^s+b_s\right)-\left(Z_i^s+b_s\right)\right\}\hfill \\ & =\left\{Z_{i,1}^s-Z_i^s,Z_{i,2}^s-Z_i^s,\dots ,Z_{i,n_t}^s-Z_i^s\right\}\hfill \\ & =\left\{t_{i,1}^s,t_{i,2}^s,\dots ,t_{i,n_t}^s\right\}\hfill \\ & ={\mathbb{T}}_i^s\left(b_s=0\right)\hfill \end{array}$$

(10)

Therefore, radar offset bias does not affect the RET. Using the RET of track measurements for track association can achieve anti-bias effects, effectively mitigating the impact of radar bias.

2.3. Track Association Metric from Multi-Radars

Based on the selection of RET as the reference unit for association, the core of the track association problem is to determine the cost calculation method for assessing whether different tracks are associated, which transforms the multi-target association decision problem into finding a local optimal solution to the association costs among different tracks [39]. Traditional track association algorithms typically employ the Mahalanobis distance between two measurement tracks to evaluate the proximity between them. A smaller Mahalanobis distance indicates a higher likelihood that the two measurement tracks originate from the same target.

This paper proposes the use of reference topology features as the association metric. However, it is important to note that the traditional association cost calculation cannot be directly applied to calculate the association cost among RETs [40]. Therefore, it is necessary to find an evaluation metric that can measure the degree of similarity among sets. The Optimal Sub-Pattern Assignment (OSPA) metric, which is derived from the Wasserstein distance, aims to identify the minimum conversion cost of the transformation between two distributions, i.e., the distance between two distributions [41,42]. In this paper, the OSPA metric was employed to quantify the distance among RETs. Considering the scenario of m radars observing multiple targets, the OSPA distance among ${\mathbb{T}}_{i_1}^{s_1},{\mathbb{T}}_{i_2}^{s_2},\dots ,{\mathbb{T}}_{i_m}^{s_m}$ is constructed as follows [32]:

$$\begin{array}{ll}D\left({\mathbb{T}}_{i_1}^{s_1},{\mathbb{T}}_{i_2}^{s_2},\dots ,{\mathbb{T}}_{i_m}^{s_m}\right)& =\{{\displaystyle \frac{1}{{\displaystyle \sum _{p=1}^m{n}_{i_p}^{s_p}}-(m-1)l_h}}{\mathrm{m}\mathrm{i}\mathrm{n}}_h\left[c^r\left({\displaystyle \sum _{p=1}^m{n}_{i_p}^{s_p}}-m{l}_h\right)\right.\hfill \\ & {\left.\left.+{\displaystyle \sum _{k_1=1}^{n_{i1}^{s_1}}{\displaystyle \sum _{k_2=1}^{n_{i2}^{s_2}}\dots }}{\displaystyle \sum _{k_m=1}^{n_{i_m}^{s_m}}{\left(d\left(t_{i_1,k_1}^{s_1},t_{i_2,k_2}^{s_2},\dots ,t_{i_m,k_m}^{s_m}\right)\right)}^r}{h}_{k_1,k_2,\dots ,k_m}\right]\right\}}^{(1/r)}\hfill \end{array}$$

(11)

where $s_1,s_2,\dots ,s_m$ represents the radar index, $k_1,k_2,\dots ,k_m$ represents the index of elements in the reference topology feature set, $n_{i_1}^{s_1},n_{i_2}^{s_2},\dots ,n_{i_m}^{s_m}$ is the number of targets in the reference topology feature set, and $1\le r<\infty$ is the order of the OSPA metric. $d\left(t_{i_1,k_1}^{s_1},t_{i_2,k_2}^{s_2},\dots ,t_{i_m,k_m}^{s_m}\right)$ represents the reference distance among $t_{i_1,k_1}^{s_1},t_{i_2,k_2}^{s_2},\dots ,t_{i_m,k_m}^{s_m}$, which is expressed using the Mahalanobis distance. When the distance exceeds the set threshold $c$, $d\left(t_{i_1,k_1}^{s_1},t_{i_2,k_2}^{s_2},\dots ,t_{i_m,k_m}^{s_m}\right)=c$.

$$d\left(t_{i_1,k_1}^{s_1},t_{i_2,k_2}^{s_2},\dots ,t_{i_m,k_m}^{s_m}\right)=\max \left\{\right||t_{i_p,k_p}^{s_p}-t_{i_q,k_q}^{s_q}|{|}_2|1\le p\le m,1\le q\le m,p\ne q\}$$

(12)

After calculating the Mahalanobis distance, it is necessary to solve the assignment relationship among $t_{i_1,k_1}^{s_1},t_{i_2,k_2}^{s_2},\dots ,t_{i_m,k_m}^{s_m}$. h represents the assignment matrix among $t_{i_1,k_1}^{s_1},t_{i_2,k_2}^{s_2},\dots ,t_{i_m,k_m}^{s_m}$, with dimensions $n_{i_1}^{s_1}*n_{i_2}^{s_2}*\dots *n_{i_m}^{s_m}$. $l_h={\displaystyle \sum _{k_1=1}^{n_{i_1}^{s_1}}{\displaystyle \sum _{k_2=1}^{n_{i_2}^{s_2}}\dots }}{\displaystyle \sum _{k_m=1}^{n_{i_m}^{s_m}}{h}_{k_1{k}_2\dots k_m}}$ denotes the number of matching pairs in the RET, ${\displaystyle \sum _{p=1}^m{n}_{i_p}^{s_p}}-m{l}_h$ represents the number of unpaired elements among the m $\mathrm{RETs}$, and ${\displaystyle \sum _{p=1}^m{n}_{i_p}^{s_p}}-(m-1)l_h$ is the total number of paired and unpaired elements in the m $\mathrm{RETs}$.

$$h_{k_1{k}_2\dots k_m}=\{\begin{array}{c}1,t_{i_1,k_1}^{s_1},t_{i_2,k_2}^{s_2},\dots ,t_{i_m,k_m}^{s_m}\mathrm{paired}\\ 0,\mathrm{otherwise}\end{array}$$

(13)

$${\displaystyle \sum _{k_p=1}^{n_{i_p}^{s_p}}{h}_{k_1{k}_2\dots k_m}}\le 1,k_q=1,\dots ,n_{i_p}^{s_p},q\ne p$$

(14)

3. Improved Adaptive Threshold and Cost Matrix Assignment

3.1. Improvement in Association Metric in the Presence of Radar Bias

The original OSPA algorithm involves the calculation of the distance among measurement tracks in a set using the Mahalanobis distance, with the association threshold set as a parameter that relies on empirical adjustment. However, the setting of the association threshold is influenced by factors such as target distribution and measurement noise, making it difficult to adapt to complex and dynamic track association scenarios using empirical threshold adjustment alone. Consequently, there is a necessity to enhance the calculation method of the OSPA distance based on the presence of radar bias.

The expression for calculating the Mahalanobis distance $d\left(t_{i,k}^{s_1},t_{j,l}^{s_2}\right)$ in the original OSPA distance is as follows:

$$d(t_{i,k}^{s_1},t_{j,l}^{s_2})={\left[t_{i,k}^{s_1}-t_{j,l}^{s_2}\right]}^T{P}_{ik,jl}^{-1}\left[t_{i,k}^{s_1}-t_{j,l}^{s_2}\right]$$

(15)

where $t_{i,k}^{s_1}$ represents the vector between track $Z_i^{s_1}$ and track $Z_k^{s_1}$ within the topology centered at radar $s_1$’s measurement $Z_i^{s_1}$, and $t_{j,l}^{s_2}$ is similarly defined. $P_{ik,jl}$ represents the estimated error covariance matrix between the two pairs of measurements. When the radar bias has been registered, $P_{ik,jl}$ includes only the measurement noise covariance matrix after target tracking. However, in the presence of radar bias, it must also incorporate the covariance matrix of the radar bias $R$, which is an empirical value derived from the prior knowledge of the radar bias distribution.

$$P_{ik,jl}=P_{ik}+P_{jl}+R_{ik}+R_{jl}$$

(16)

The radar measurement noise follows a Gaussian distribution $\mathcal{N}\left(0,P_S\right)$, and the Jacobian matrices for different measurement points vary after the coordinate transformation. Consequently, the measurement noise covariance matrix also differs and can be expressed as:

$$\begin{array}{cc}\left\{\begin{array}{c}{P}_i^{s_1}=J\left(Z_i^{s_1}\right)P_{s_1}J{\left(Z_i^{s_1}\right)}^T\\ P_k^{s_1}=J\left(Z_k^{s_1}\right)P_{s_1}J{\left(Z_k^{s_1}\right)}^T\end{array}\right.& \left\{\begin{array}{c}{P}_j^{s_2}=J\left(Z_j^{s_2}\right)P_{s_2}J{\left(Z_j^{s_2}\right)}^T\\ P_l^{s_2}=J\left(Z_l^{s_2}\right)P_{s_2}J{\left(Z_l^{s_2}\right)}^T\end{array}\right.\end{array}$$

(17)

The measurement noise of $t_{i,k}^{s_1}$ follows the distribution $\mathcal{N}\left(0,P_i^{s_1}+P_k^{s_1}\right)$, and the measurement noise of $t_{j,l}^{s_2}$ follows the distribution $\mathcal{N}\left(0,P_j^{s_2}+P_l^{s_2}\right)$. Therefore, the measurement noise of the corresponding track pair follows the distribution $\mathcal{N}\left(0,P_i^{s_1}+P_k^{s_1}+P_j^{s_2}+P_l^{s_2}\right)$, which can be expressed as:

$$P_{ik}+P_{jl}=P_i^{s_1}+P_k^{s_1}+P_j^{s_2}+P_l^{s_2}$$

(18)

Similarly, the covariance matrix of the radar bias can be expressed as:

$$\begin{array}{cc}\left\{\begin{array}{c}{R}_i^{s_1}=J\left(Z_i^{s_1}\right)R_{s_1}J{\left(Z_i^{s_1}\right)}^T\\ R_k^{s_1}=J\left(Z_k^{s_1}\right)R_{s_1}J{\left(Z_k^{s_1}\right)}^T\end{array}\right.& \left\{\begin{array}{c}{R}_j^{s_2}=J\left(Z_j^{s_2}\right)R_{s_2}J{\left(Z_j^{s_2}\right)}^T\\ R_l^{s_2}=J\left(Z_l^{s_2}\right)R_{s_2}J{\left(Z_l^{s_2}\right)}^T\end{array}\right.\end{array}$$

(19)

When calculating the covariance matrix of the radar bias, since the radar bias is an inherent property of the radar, measurements from the same radar exhibit certain correlations. Therefore, the covariance matrix needs to be corrected by incorporating the cross-covariance matrix between measurements from the same radar, as follows:

$$R_{ik}+R_{jl}=R_i^{s_1}+R_k^{s_1}-R_{ik}^{s_1}-R_{ki}^{s_1}+R_j^{s_2}+R_l^{s_2}-R_{jl}^{s_2}-R_{lj}^{s_2}$$

(20)

The Jacobian matrix for the cross-covariance of two target measurements has its expansion points determined by the respective measurement points of the two targets. The expression is as follows:

$$\left\{\begin{array}{c}{R}_{ik}^{s_1}=J\left(Z_i^{s_1}\right)R_{s_1}J{\left(Z_k^{s_1}\right)}^T\\ R_{ki}^{s_1}=J\left(Z_k^{s_1}\right)R_{s_1}J{\left(Z_i^{s_1}\right)}^T\end{array}\right.$$

(21)

According to properties of multivariate Gaussian distributions, a zero-mean Gaussian vector normalized by its covariance yields a squared Mahalanobis distance that follows a ${\chi }^2$ distribution with k degrees of freedom. Thus, when offset bias is incorporated into the covariance, the resulting weighted Mahalanobis distance strictly conforms to the ${\chi }^2$ distribution. The improved radar offset bias-weighted Mahalanobis distance $d\left(t_{i,k}^{s_1},t_{j,l}^{s_2}\right)$ follows ${\chi }^2$ distribution with degrees of freedom $n=2$. To achieve association, the ${\chi }^2$ distribution threshold condition must be satisfied. The threshold value can be set to the value corresponding to a 0.95 confidence level, enabling adaptive track association across different parameters and scenarios without the need for manual setting and adjustment of the track association threshold.

In this section, the original Mahalanobis distance and the association threshold that requires manual adjustment in the OSPA distance are enhanced to the bias-corrected Mahalanobis distance and adaptive association threshold. This adjustment is capable of adapting to a broader range of association scenarios and mitigates the instability of the association effect caused by unknown parameters.

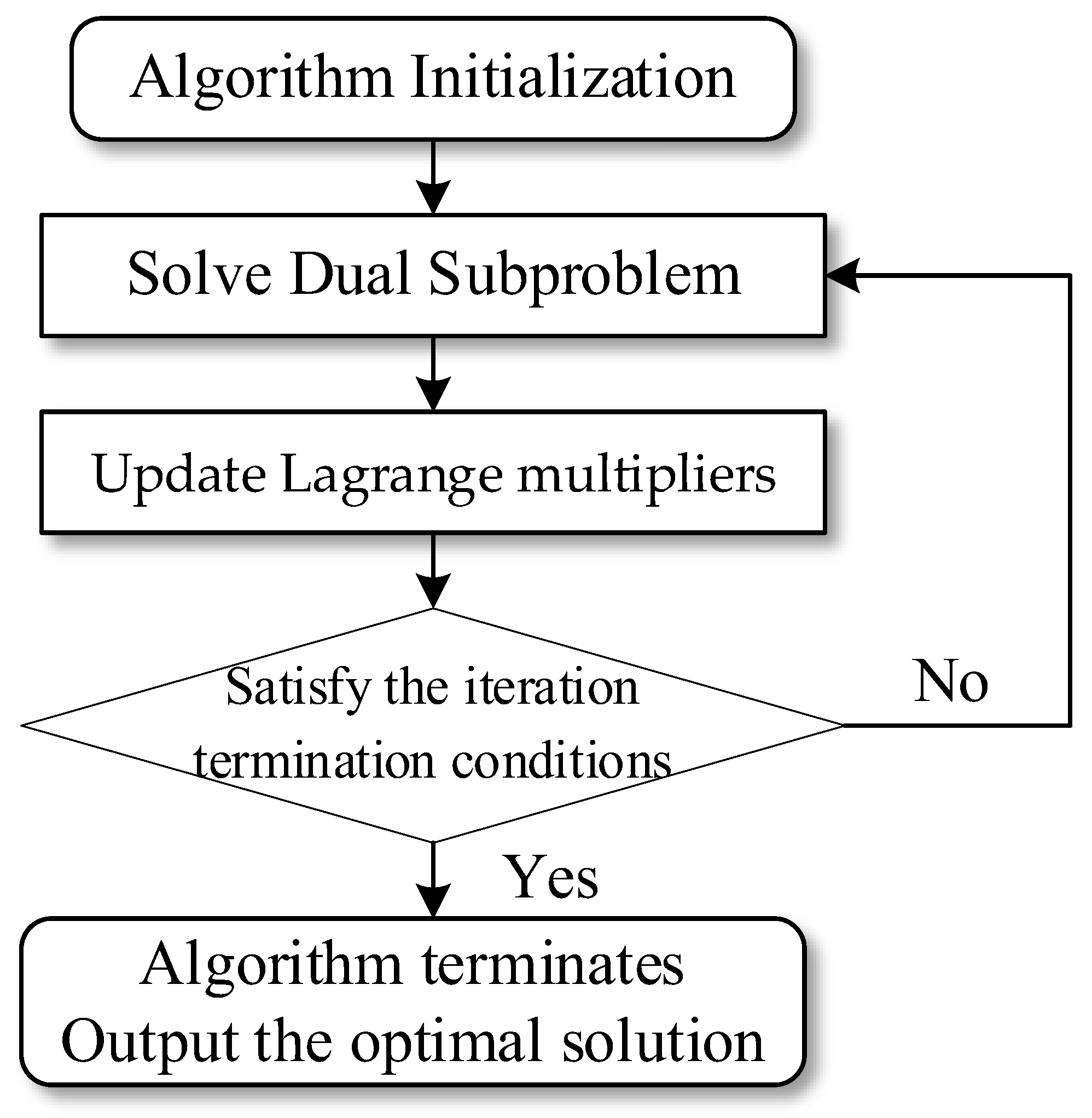
3.2. Assignment of Multi-Dimensional Association Cost Matrix

In this paper, we considered a multi-target track association problem for three radars, and the resulting assignment problem based on the 3D association cost matrix was a typical N-P hard combinatorial optimization problem [26], which can be sub-optimally solved by using the Lagrangian relaxation algorithm [27].

Since missed detections inevitably occur in practical measurement processes, the completeness of the matching between observed data and true targets is disrupted, introducing the risk of incorrect associations and resulting in an increase in association errors. Ideally, data association should be performed based on the optimal matching between targets and observations. However, when a target is not detected (i.e., a missed detection occurs), its corresponding dimension in the cost matrix lacks a valid matching candidate, forcing the allocation algorithm to assign the matching opportunity to other targets. Additionally, allocation algorithms (such as the Hungarian algorithm or Lagrangian relaxation algorithm) typically aim to maximize associations. As a result, even when some matches incur high costs, the algorithm may still attempt to establish associations, further increasing the likelihood of incorrect matches. Therefore, missed detections not only directly prevent targets from being correctly matched but also introduce false associations, exacerbating overall association errors.

To reduce incorrect associations, threshold filtering is applied to the association cost matrix. The fundamental principle of threshold filtering is that, if every element in a specific dimension of the association cost matrix exceeds a predefined threshold, it indicates that the target has excessively high association costs with all candidate matches. This suggests that the target in this dimension has not found a reasonable match and should therefore not be associated. To achieve this, all cost values in the corresponding dimension are set to infinity. When a matching cost is assigned an infinite value, that match will never be selected, thereby completely eliminating the possibility of associating the target during the optimization process.

The specific operation is as follows: Based on the OSPA metric, the association cost matrix $C$ among the RET sets can be obtained, where $C_{ijk}=d_{p,c}({\mathbb{T}}_i^{s_1},{\mathbb{T}}_j^{s_2},{\mathbb{T}}_k^{s_3})$. Process $C$ according to Equation (22): if all values in a certain dimension of the association cost matrix exceed the threshold $c$, then set all values in that dimension to infinity. This treatment facilitates identification and decision-making in the Lagrangian relaxation algorithm, effectively reducing the occurrence of different-source tracks being forcibly associated due to missed detections.

$$C\left(i,j,k\right)=\left\{\begin{array}{c}Inf,\forall C\left(i,:,:\right)=c\\ C\left(i,j,k\right)\end{array}\right.$$

(22)

In this paper, the three-dimensional association cost matrix was assumed to have dimensions n1 × n2 × n3. The Lagrangian algorithm relaxes some of the constraints and decomposes the three-dimensional allocation problem into a series of relaxed two-dimensional allocation problems for solving [43,44]. Lagrange multipliers $U=(u_1,u_2,\dots ,u_{n_3})$ are introduced and substituted into the cost function to minimize the cost of the relaxed problem. The solution obtained by this method represents the lower bound of the true solution, while the feasible solution forms the upper bound. The difference between the two is called the approximate dual gap. The algorithm iteratively adjusts the Lagrangian multipliers between the dual solution and the feasible solution, progressively bringing them into agreement. When the two are equal, the optimal solution is reached [45]. If a dual solution simultaneously satisfies feasibility, it can be directly determined as the optimal solution.

The mathematical model for the 3D assignment problem can be described as follows:

$$J=\underset{{\rho }_{i_1{i}_2{i}_3}}{\min }{\displaystyle \sum _{i_1=0}^{n_1}{\displaystyle \sum _{i_2=0}^{n_2}{\displaystyle \sum _{i_3=0}^{n_3}{c}_{i_1{i}_2{i}_3}\times }}}{\rho }_{i_1{i}_2{i}_3}$$

(23)

$$\begin{array}{ll}s.t& {\displaystyle \sum _{i_1=0}^{n_1}{\displaystyle \sum _{i_2=0}^{n_2}{\rho }_{i_1{i}_2{i}_3}}}=1,i_3=1,2,\dots ,n_3\hfill \\ & {\displaystyle \sum _{i_1=0}^{n_1}{\displaystyle \sum _{i_3=0}^{n_3}{\rho }_{i_1{i}_2{i}_3}}}=1,i_2=1,2,\dots ,n_2\hfill \\ & {\displaystyle \sum _{i_2=0}^{n_2}{\displaystyle \sum _{i_3=0}^{n_3}{\rho }_{i_1{i}_2{i}_3}}}=1,i_1=1,2,\dots ,n_1\hfill \end{array}$$

(24)

where $J$ is the objective function, and $c_{i_1{i}_2{i}_3}$ represents the cost of pairing the $i_m$-th element in the $m$-th dimension, ${\rho }_{i_1{i}_2{i}_3}=\left\{\begin{array}{c}1,if i_1,i_2,i_3 are assigned to a target\\ 0,otherwise\end{array}\right.$.

The steps for solving the 3D assignment problem using the Lagrangian relaxation algorithm are as follows:

(1)

Initialization: $u_{i_3}=0,\forall i_3=1,2,\dots ,n_3$, $f_{dual}=-\infty$, $f_{primal}=\infty$, and iteration count $iter=0$, with the maximum number of iterations set to $maxiter=100$.

(2)

Calculate the cost of the dual problem:

$$d_{i_1{i}_2}=\underset{i_3}{\min }(c_{i_1{i}_2{i}_3}-u_{i_3}),\forall i_1=1,2,\dots ,n_1,\forall i_2=1,2,\dots ,n_2$$

(25)

(3)

Solve the dual subproblem:

$$\{f_d,{\omega }_{i_1{i}_2}^{*}\}=\underset{{\omega }_{i_1{i}_2}}{\min }{\displaystyle \sum _{i_1=0}^{n_1}{\displaystyle \sum _{i_2=0}^{n_2}{d}_{i_1{i}_2}{\omega }_{i_1{i}_2}}}$$

(26)

$${\displaystyle \sum _{i_1=0}^{n_1}{\omega }_{i_1{i}_2}=1};\forall i_2=1,2,\dots ,n_2$$

(27)

$${\displaystyle \sum _{i_2=0}^{n_2}{\omega }_{i_1{i}_2}=1};\forall i_1=1,2,\dots ,n_1$$

(28)

If ${\omega }_{i_1{i}_2}^{*}=1$, let ${\eta }_{i_1}=i_2,\forall i_1=1,2,\dots ,n_1,\forall i_2=1,2,\dots ,n_2$. This is a generalized 2D assignment problem that can be solved using the Hungarian algorithm.

(4)

Update the Lagrange multipliers: To generate a series of dual vectors $u^{(0)}\to u^{(1)}\to \dots u^{(l)}\to \dots u^{(*)}$, with $l$ representing the iteration count, we have

$${\rho }_{i_1{i}_2{i}_3}^{*(l)}=\{\begin{array}{c}{\omega }_{i_1{i}_2}^{*},if i_3=\arg \underset{p}{\min }(c_{i_1{i}_{2}p}-u_p)\\ 0,otherwise\end{array}$$

(29)

$$g_{i_3}^{(l)}=1-{\displaystyle \sum _{i_1=0}^{n_1}{\displaystyle \sum _{i_2=0}^{n_2}{\rho }_{i_1{i}_2{i}_3}^{*(l)}},}\forall i_3=1,2,\dots ,n_3$$

(30)

Let $u^{(0)}=0$, $u_{i_3}^{(l+1)}=u_{i_3}^{(l)}+\left({\displaystyle \frac{\alpha +1}{\alpha }}\right)({\displaystyle \frac{q_{\alpha }-q{(u)}^{(l)}}{\left|\right|g|{|}_2^2}})P_{i_3}^{(l)},1⩽{\mathrm{i}}_3⩽{\mathrm{n}}_3$, where $p^{(l)}=H^{(l)}{g}^{(l)},p^{(l)}={[p_1^{(l)},p_2^{(l)},\dots ,p_{n_3}^{(l)}]}^T$, $H^{(l+1)}=H^{(l)}+{\displaystyle \frac{\left(1-{\alpha }^{-2}\right)p^{(l)}{p}^{(l)T}}{g^{(l)T}{p}^{(l)}}}$, and $H^{(0)}=I$. When $\alpha =2$, $u_{i_3}^{(l)}$ achieves the best iteration effect, while $q_{\alpha }=\left[1+{\displaystyle \frac{a}{{\beta }^b}}\right]q^{*(l)}$, where $q^{*(l)}$ is the optimal dual solution from the previous $l$ iterations, and parameters $a$ and $b$ satisfy $0.05\le a\le 0.3$, $1.1\le b\le 1.6$, and ${\beta }_{(l+1)}=\left\{\begin{array}{l}{\beta }_{(l)}+1,q{(u)}^{(l)}<q^{*(l-1)}\hfill \\ \max \left({\beta }_{(l)}-1,1\right),otherwise\hfill \end{array}\right.$ [44].

(5)

Construct feasible solutions: $\left\{f_P,{\rho }_{i_1{i}_2{i}_3}^{*}\right\}={\min }_{{\rho }_{i_1{i}_2{i}_3}}{\displaystyle \sum _{i_1=0}^{n_1}{\displaystyle \sum _{i_3=0}^{n_3}{c}_{i_1{\eta }_{i_1}}}}{\rho }_{i_1{\eta }_{i_1}{i}_3}$, where ${\rho }_{i_1{\eta }_{i_1}{i}_3}$ satisfies:

$${\displaystyle \sum _{i_1=0}^{n_1}{\rho }_{i_1{\eta }_{i_1}{i}_3}}=1,\forall \mathrm{i}3=1,2,\dots ,n_3$$

(31)

$${\displaystyle \sum _{i_2=0}^{n_2}{\rho }_{i_1{\eta }_{i_1}{i}_3}}=1,\forall i_1=1,2,\dots ,n_1$$

(32)

(6)

Iteration: Improve the quality of the solution.

$$f_{dual}=\max (f_{dual},f_d)$$

(33)

$$f_{primal}=\min (f_{primal},f_p)$$

(34)

$$gap=(f_{primal}-f_{dual})/\left|f_{primal}\right|$$

(35)

If the relative dual gap is less than 0.01 or the number of iterations exceeds the maximum iteration count, the algorithm ends; otherwise, proceed to step (2). This completes the allocation of the three-dimensional association cost matrix. For track association involving four or more radars, the allocation of four-dimensional or higher association cost matrices is required, which can be addressed by introducing additional Lagrange multipliers.

The flowchart of the Lagrangian relaxation algorithm is shown in Figure 3.

The algorithm flow chart is shown in Figure 4. The algorithm input is the measurement coordinates in the local polar coordinate system of each radar at each moment. The targets observed by all radars are traversed to obtain the corresponding RET of each target. The improved Mahalanobis distance among RET elements is calculated to obtain a multidimensional matrix $d\left(t_{i_1,k_1}^{s_1},t_{i_2,k_2}^{s_2},\dots ,t_{i_m,k_m}^{s_m}\right)$. The optimal matching relationship among RETs is then solved, and the matrix is preliminarily assigned to obtain the assignment relationship. Subsequently, the OSPA distance and association cost matrix among all targets’ corresponding RETs are computed. The association cost matrix is assigned to obtain the track association relationship.

The multi-radar track association algorithm based on RETs proposed in this paper mainly includes distance calculation and cost matrix assignment operations. The computational complexity of the algorithm is

$$T_{RET}=O\{n^{m}k(1+{(n_t)}^m)\}$$

(36)

where $n$ is the number of targets, $m$ is the number of radars, $k$ is the number of iterations of the Lagrangian relaxation algorithm, and $n_t$ is the number of elements in the neighboring reference track set in the radar measurement. Moreover, the computational complexity of the vector decomposition cancellation-based algorithm used for comparison is

$$T_{tt}=O\left\{(m-1)n^2+{\displaystyle \frac{(m-1)(m-2)n^3}{2}}\right\}$$

(37)

It can be observed that the two algorithms differ in computational complexity, and the choice between them can be made based on the specific requirements for association accuracy and computational performance.

As the number of radars increases, both the dimensionality of the association cost matrix and the scale of the Lagrangian relaxation iterations grow exponentially, leading to a significant rise in computational load and latency. At the same time, missed detections and measurement errors from different radars are more likely to accumulate during data fusion, which may in turn compromise the accuracy of association. Therefore, in practical applications, a balance must be struck among the number of radars, computational efficiency, and association accuracy.

4. Simulation Results and Discussion

This section presents the simulations and performance analysis for the proposed multi-radar adaptive track association algorithm based on RETs. Furthermore, a comparative analysis was conducted between the original RET algorithm and the improved adaptive threshold RET algorithm to illustrate the efficacy of the modified algorithm.

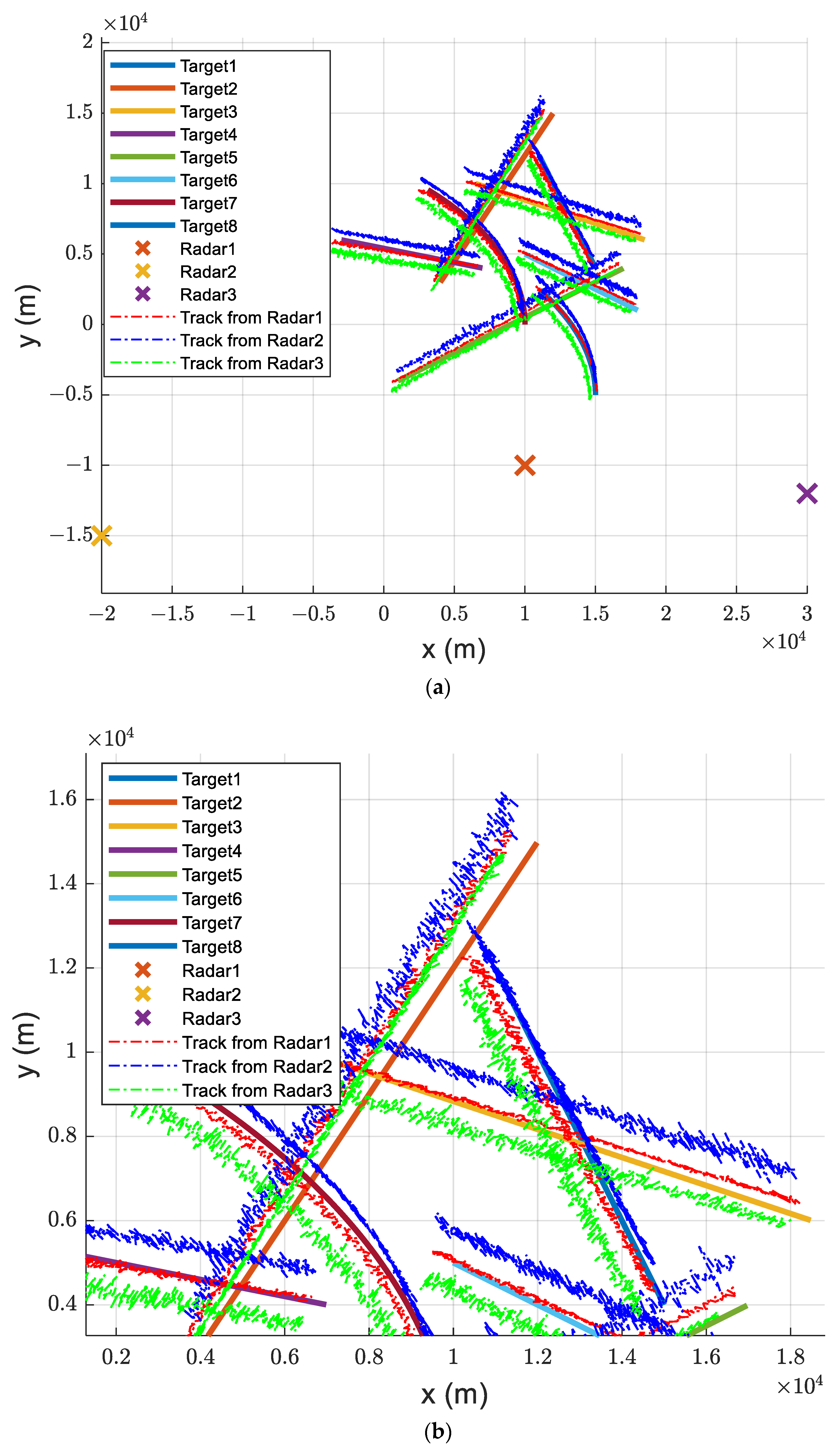
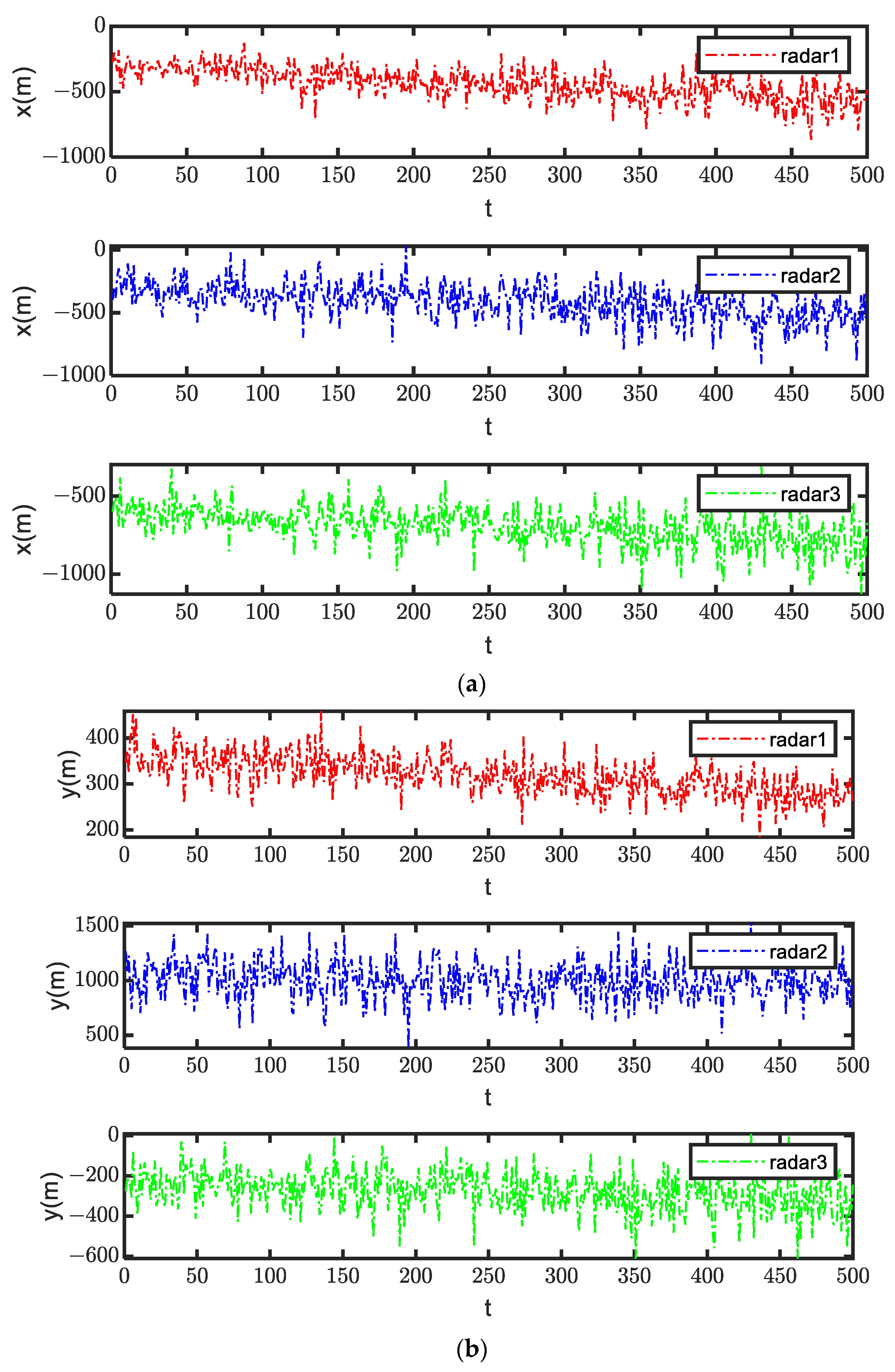
4.1. Simulation Environment

The simulation area was set with a range size of $\left[-5,20\right]\times \left[-5,15\right] {\mathrm{km}}^2$, and eight flying targets were distributed in formation, moving at a constant linear velocity. Three fixed radars were used to observe the targets, located at positions $\left[18 \mathrm{km},-10 \mathrm{km}\right]$, $\left[-20 \mathrm{km},30 \mathrm{km}\right]$, and $\left[30 \mathrm{km},30 \mathrm{km}\right]$. The sample interval of radars was $T_s=0.4 \mathrm{s}$, and the target positions were sampled synchronously. Radars reported the measured positions to the fusion center located at $(0,0)m$ in real time. Radar offset errors followed a Gaussian distribution with a mean of 0. The standard deviation of azimuth measurement noise was ${\sigma }_{\theta ,1}={\sigma }_{\theta ,2}={\sigma }_{\theta ,3}=0.3°$, and the standard deviation of range measurement noise was ${\sigma }_{r,1}={\sigma }_{r,2}={\sigma }_{r,3}=30 \mathrm{m}$. The missed detection probability for the radars was set to $P_{miss}=5\%$. To demonstrate the algorithm’s robustness, the simulation introduced a significant radar offset bias, greater than 5 times the measurement error. The azimuth radar bias was set to 1.5°, denoted as $\Delta {\theta }_1=\Delta {\theta }_2=\Delta {\theta }_3=1.5°$, and the range radar bias was denoted as $\Delta r_1=\Delta r_2=\Delta r_3=250 \mathrm{m}$.

The parameter that was utilized to evaluate the association algorithm in this section was the association accuracy. The association accuracy is defined as the ratio of the total number of correctly associated targets at each time step to the total number of targets observed at each measurement time. The association accuracy is:

$$R_c={\displaystyle \frac{n_c}{n}}$$

(38)

where $n$ denotes the total number of targets, and $n_c$ represents the number of correctly associated targets. To validate the performance superiority of the proposed algorithm, we conducted track association experiments in a simulated environment using both the proposed method and the vector decomposition cancellation-based association algorithm.

The simulation environment is shown in Figure 5.

The radar measurements of the targets and the true tracks of the targets, along with some details, are shown in Figure 6.

Taking Target 1 as an example, the errors between the radar’s position measurements and the target’s true position in the x- and y-directions are shown in Figure 7.

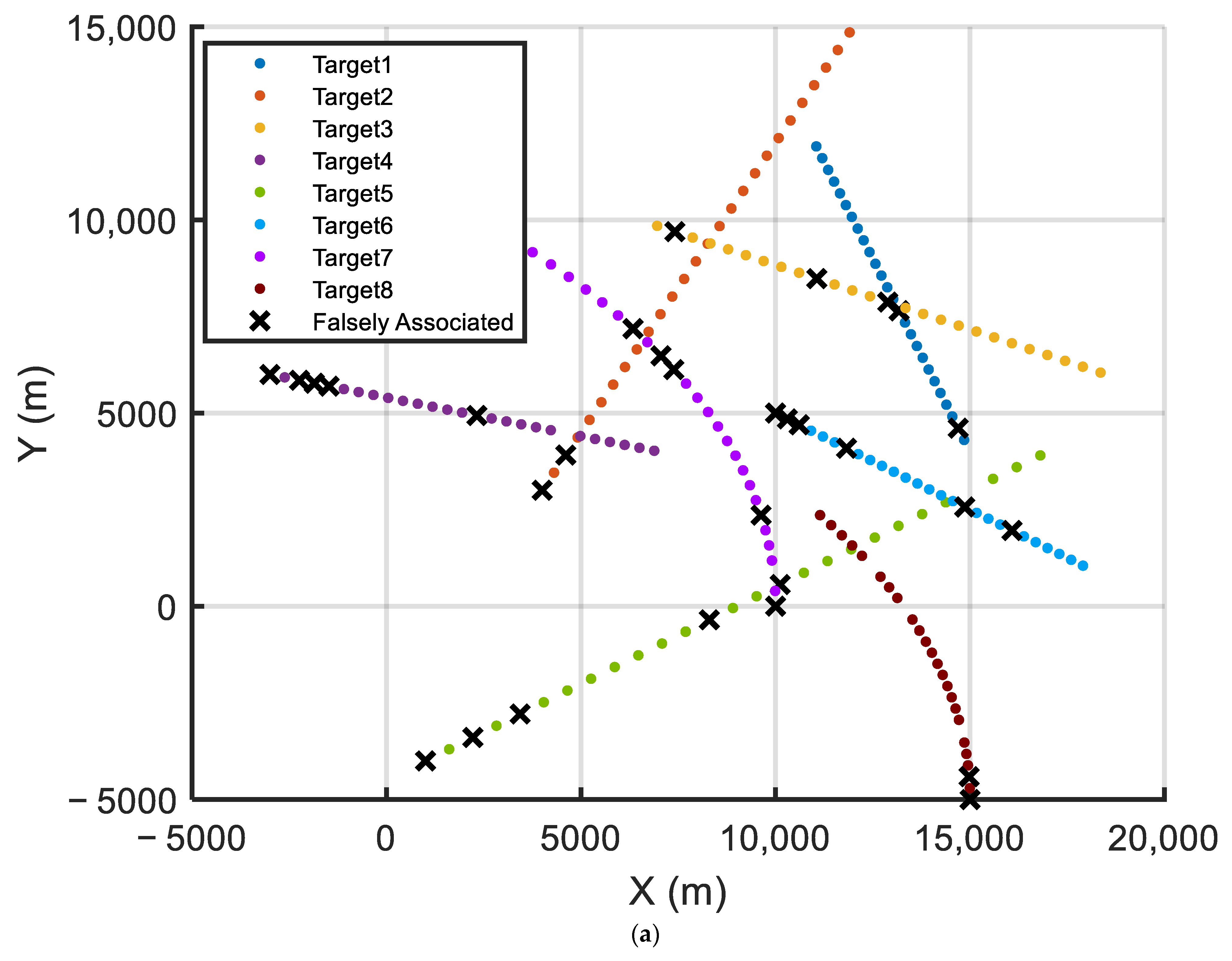
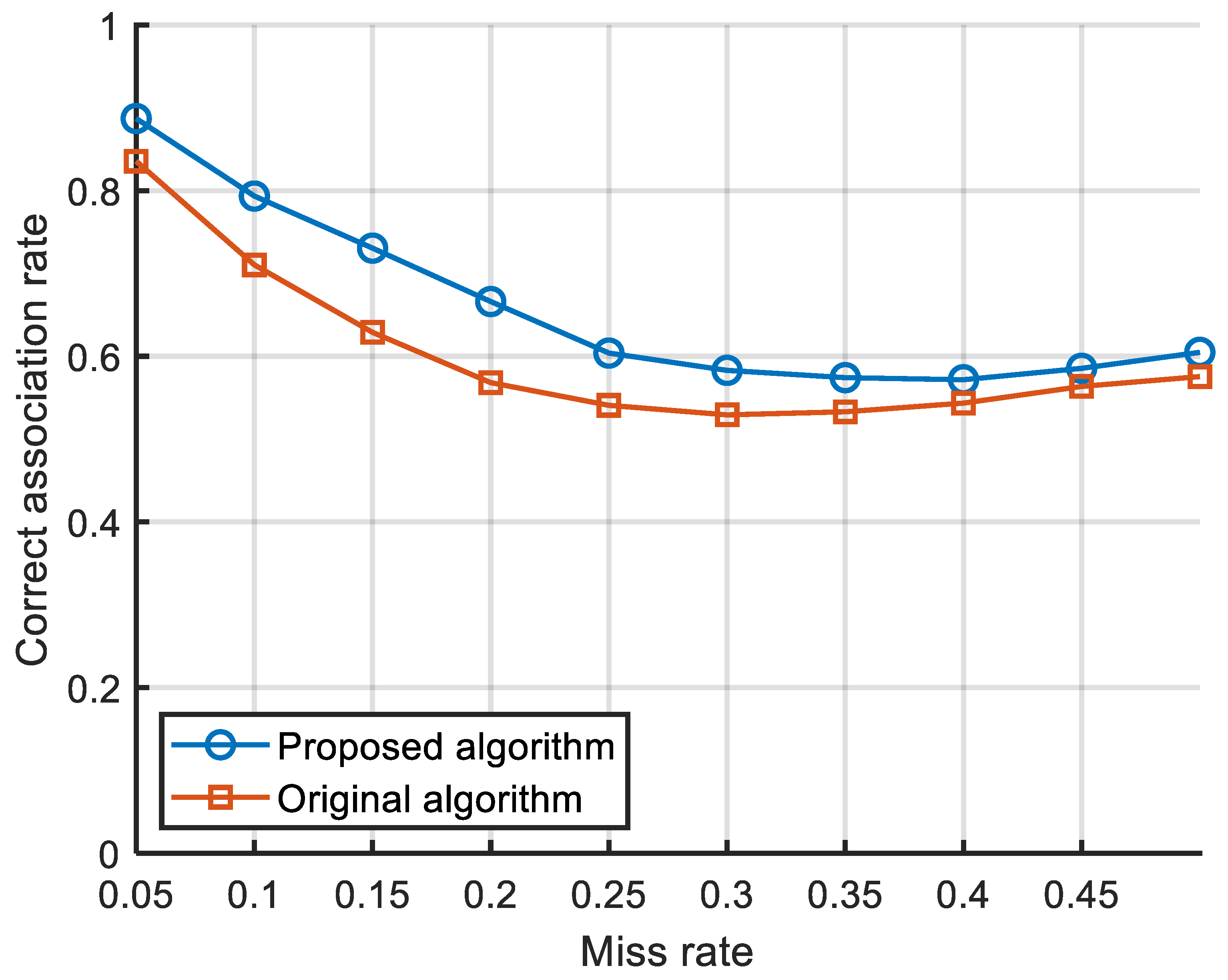
4.2. Track Association Performance

Firstly, to intuitively display the track association performance, the correctly associated track points for a single simulation trial were plotted, as shown in Figure 8. Under this radar bias, the proposed algorithm achieves an association accuracy of 0.9024 with a runtime of 1000 s, whereas the vector decomposition cancellation-based (VDC) association algorithm achieves an accuracy of 0.8176 with a runtime of 20 s. The overall computational complexity of the proposed algorithm primarily stems from two critical components: (1) the OSPA distance during the construction and matching processes of RET, and (2) the Lagrangian relaxation algorithm implemented in the cost matrix assignment step. Although these factors impose certain computational overheads, the proposed method demonstrates substantial practical value when considering its robustness, accuracy improvement, and adaptability. In particular, for scenarios involving high-precision target identification and heterogeneous radar cooperative systems, the algorithm effectively addresses the limitations of traditional methods in bias modeling and robustness.

Due to the over-sampling of the original data, only every 20th sampling point was plotted for ease of observation. Using radar 1 as the reference, the results of each moment association are matched; if the association is correct, it is plotted according to the color of the track to which the different targets belong and the coordinates of the original position; if the association is incorrect, it is indicated as a black cross; if the target is not detected by radar 1 at the current moment, it is not shown in the figure.

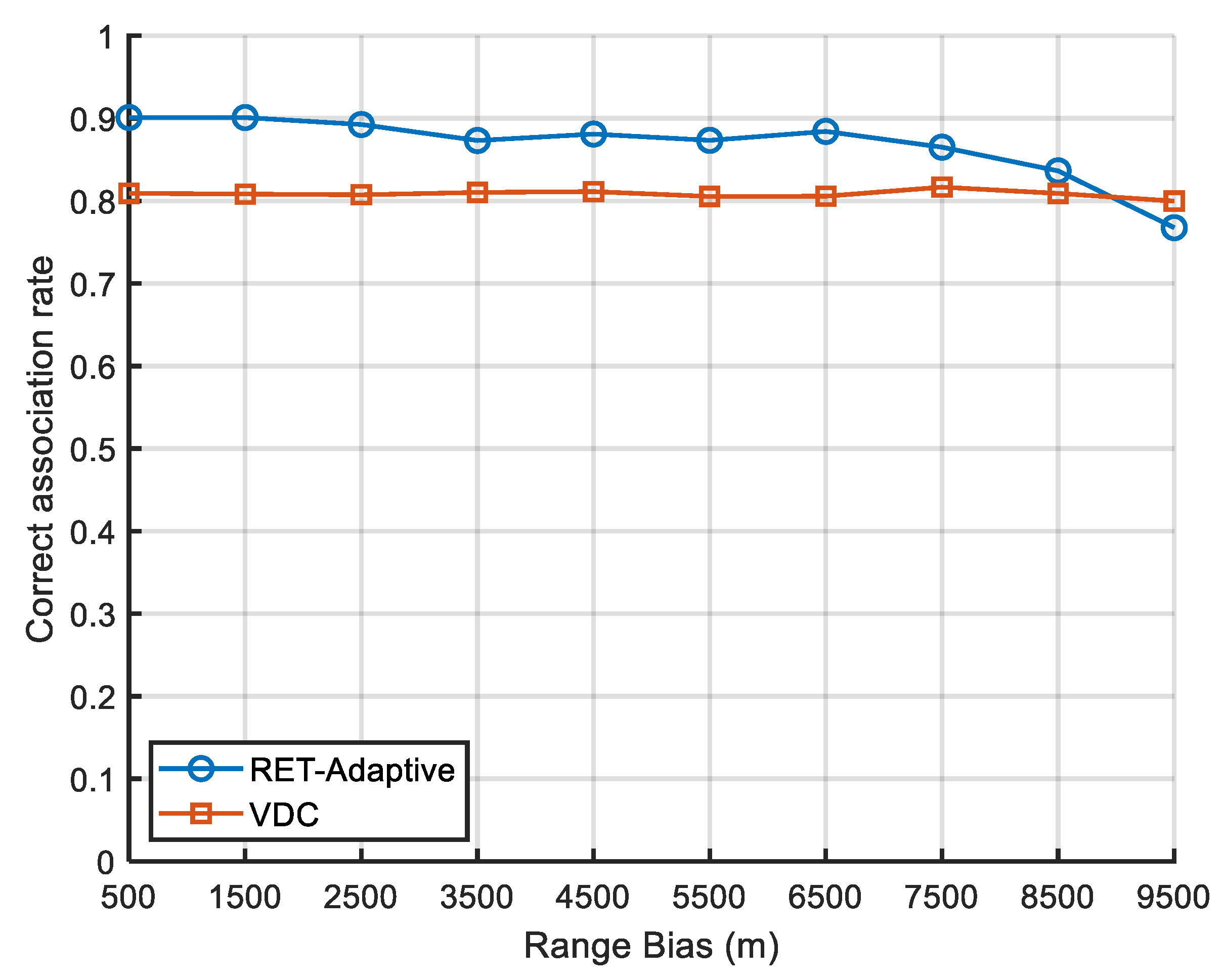
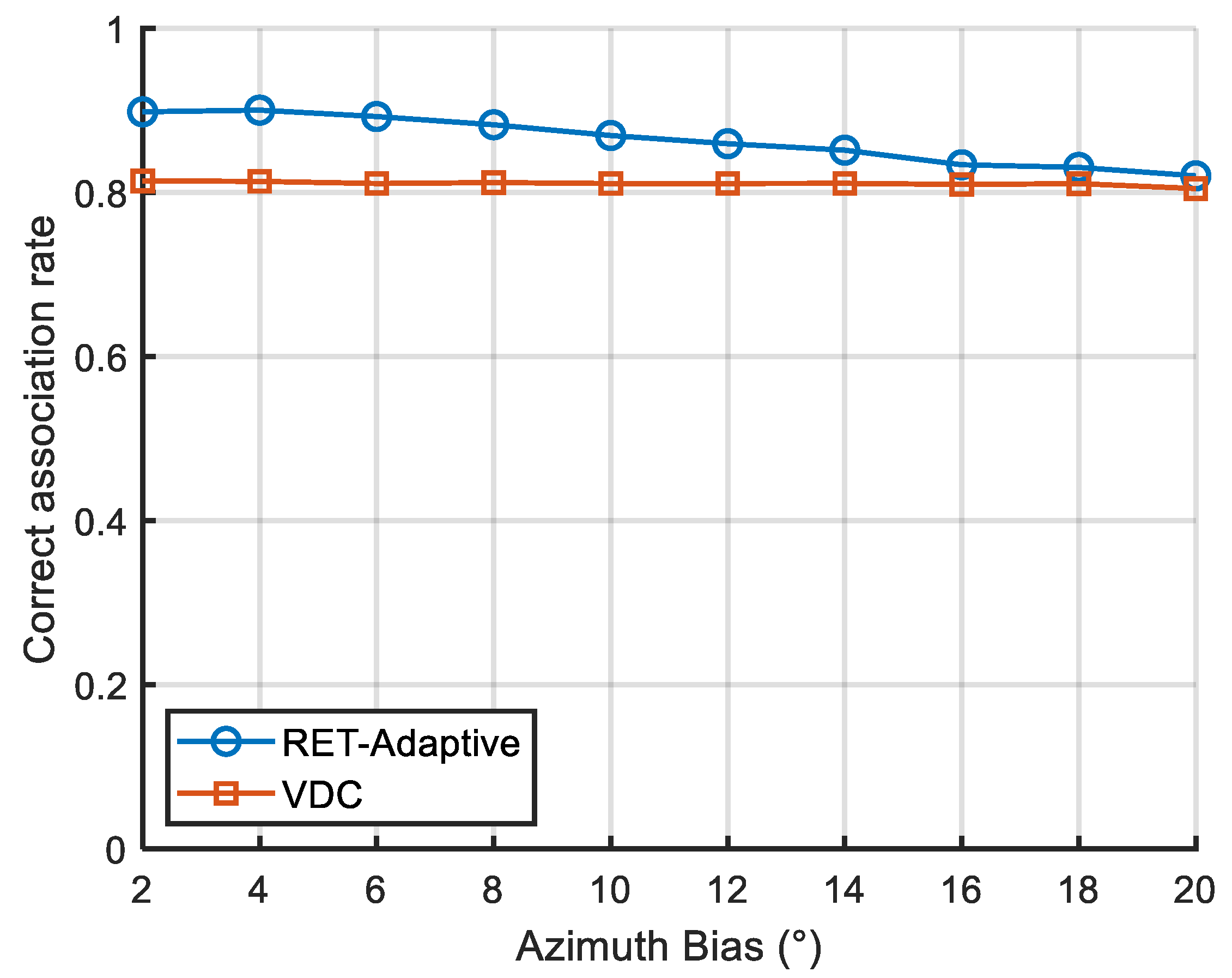
4.3. Influence of Radar Offset Bias on Algorithm Performance

In order to verify the ability of the track association algorithm against radar offset bias described in this paper, two groups of Monte Carlo experiments were designed, and the number of Monte Carlo simulations for each group of experiments was set to 50 times. Under the premise of controlled variables, ten sets of radar bias parameters were configured to investigate the relationship between the association accuracy of the improved RET algorithm and the vector decomposition cancellation-based association algorithm with variations in range measurement bias and azimuth measurement bias. The standard deviation of measurement noise errors ${\sigma }_{\theta ,1}={\sigma }_{\theta ,2}={\sigma }_{\theta ,3}=0.3°$ and ${\sigma }_{r,1}={\sigma }_{r,2}={\sigma }_{r,3}=30 \mathrm{m}$ were kept constant, and the specific parameter settings for the radar bias are shown in

Table 1. Design of parameters for the anti-bias experiments.

Experiment	$\Delta \mathit{\theta }\left(°\right)$	$\Delta \mathit{r}\left(\mathit{m}\right)$
Experiment 1	$1.5$	$[\underset{10 \mathrm{sets}}{\underbrace{500,1500,\dots ,9500}}]$
Experiment 2	$[\underset{10 \mathrm{sets}}{\underbrace{2,4,6,\dots ,20}}]$	$250$

.

Figure 9 and Figure 10 illustrate the influence of range offset bias and azimuth offset bias on the association accuracy of the algorithms. It can be observed that both algorithms exhibit strong robustness to radar offset bias. When the range bias increases, the association accuracy of the RET algorithm fluctuates around 90%, while the accuracy of vector decomposition cancellation-based algorithm fluctuates around 80%. However, when the range offset bias becomes excessively large, the conditions under which the RET structure remains insensitive to biases are no longer satisfied. As a result, the association performance of the RET algorithm may exhibit a certain degree of degradation. Meanwhile, an increase in azimuth bias can also violate these conditions, thereby reducing the association accuracy of the RET algorithm. When $\Delta \theta =16°$, the accuracy of the RET algorithm decreases to a level comparable to that of the vector decomposition-based algorithm. Therefore, when $\Delta \theta <16°$, the proposed algorithm outperforms the vector decomposition-based algorithm.

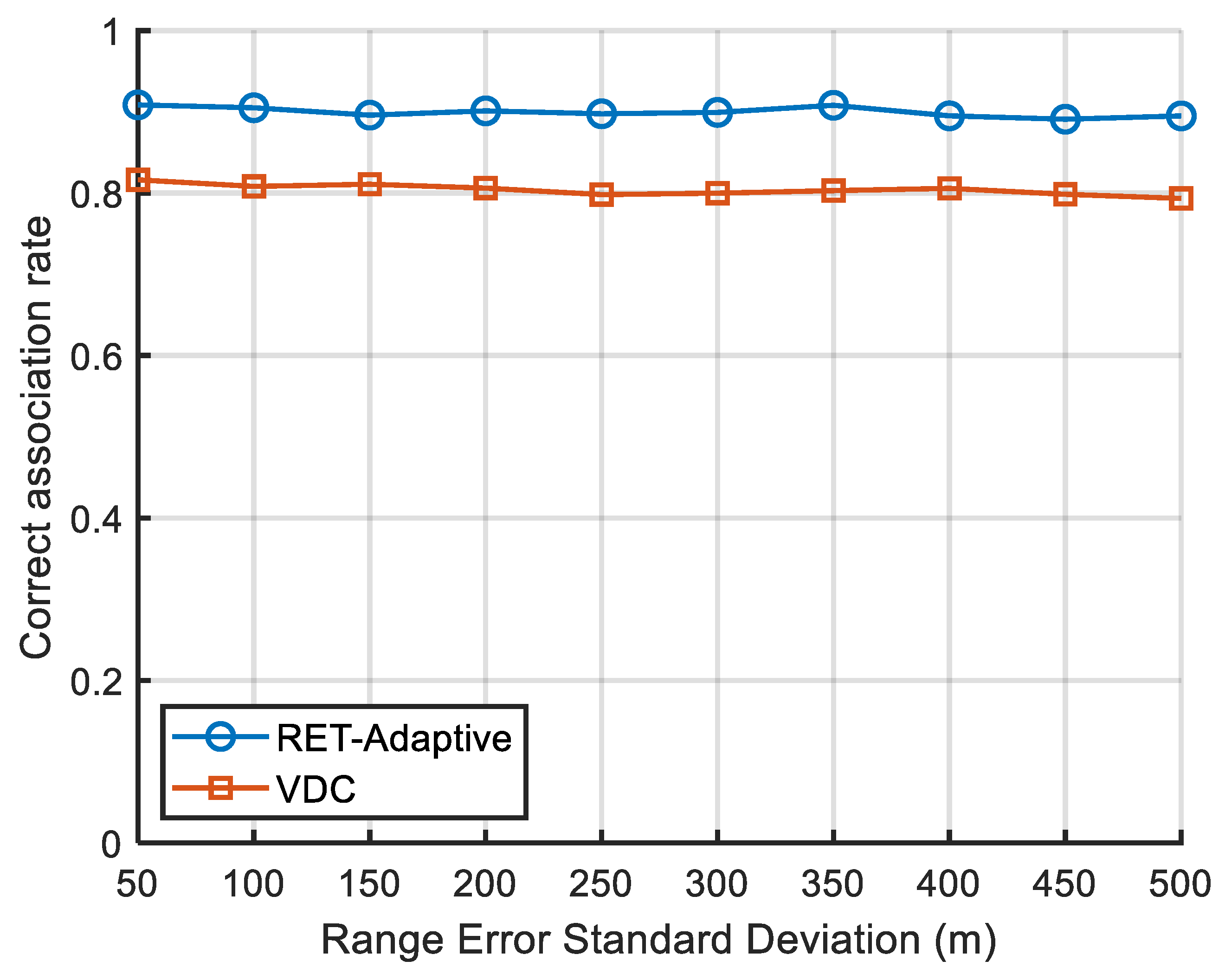
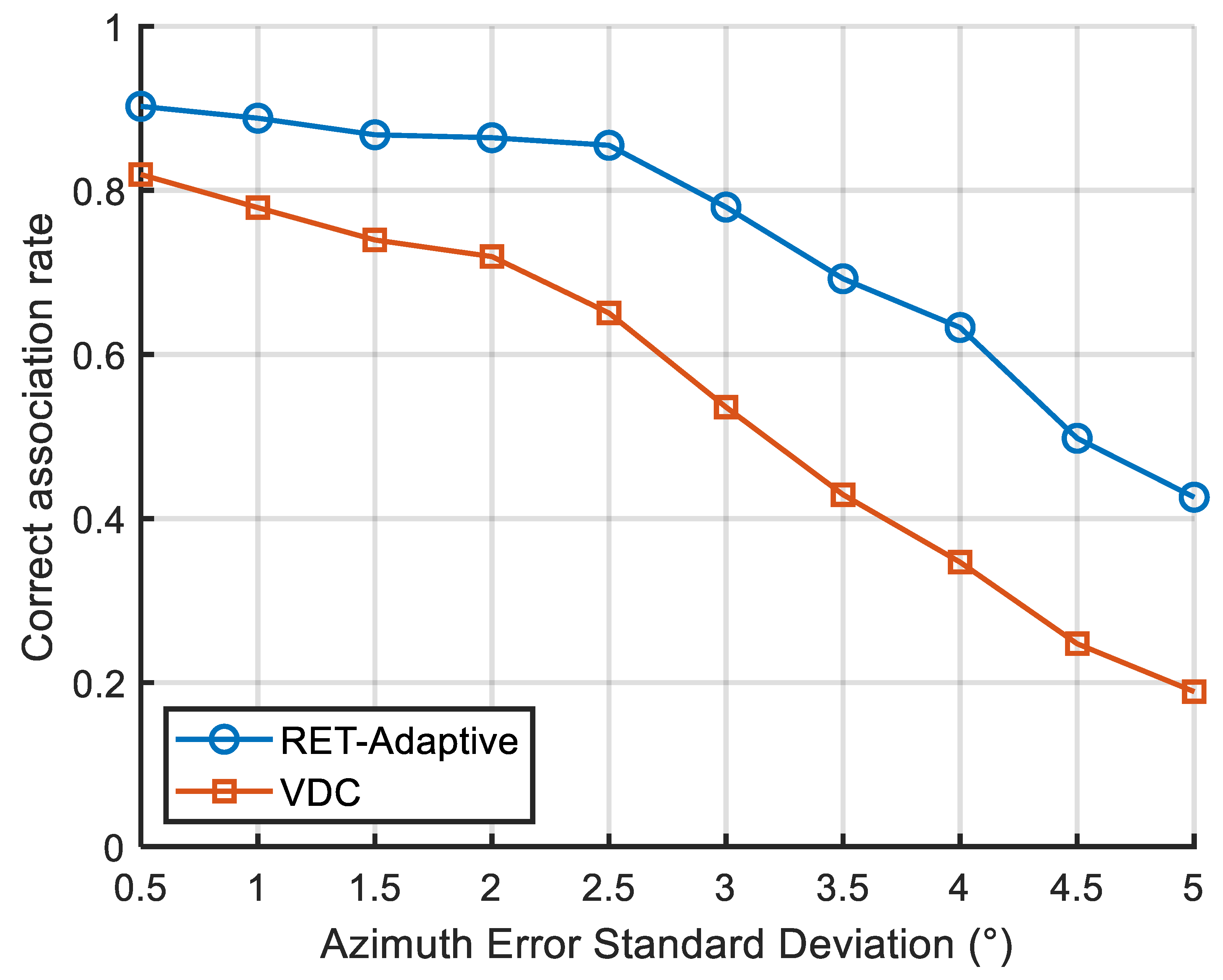
4.4. Influence of Measurement Noise on Algorithm Performance

Similarly, to investigate the influence of measurement noise error on the performance of the proposed algorithm, two sets of Monte Carlo experiments were designed, with 50 Monte Carlo runs each. The radar biases $\Delta {\theta }_1=\Delta {\theta }_2=\Delta {\theta }_3=1.5°$ and $\Delta r_1=\Delta r_2=\Delta r_3=250 \mathrm{m}$ were kept constant, and the specific parameter settings for the random measurement noise error standard deviations are shown in

Table 2. Design of parameters for anti-noise experiments.

Experiment	${\mathit{\sigma }}_{\mathit{\theta }}(°)$	${\mathit{\sigma }}_{\mathit{r}}(\mathit{m})$
Experiment 1	$0.3$	$[\underset{10 \mathrm{sets}}{\underbrace{50,100,\dots ,500}}]$
Experiment 2	$[\underset{10 \mathrm{sets}}{\underbrace{0.5,1,\dots ,5.0}}]$	$30$

.

Figure 11 and Figure 12 illustrate the influence of range noise error standard deviation and azimuth noise error standard deviation on the association accuracy of the algorithms. It can be observed that both algorithms exhibit strong robustness to the standard deviation of range noise error. As the range error standard deviation increases, the association accuracy remains relatively stable, with the RET algorithm achieving an accuracy of approximately 90% and the vector decomposition cancellation-based algorithm maintaining an accuracy of approximately 81%. However, as the azimuth error standard deviation increases, the association accuracy of both algorithms experiences a certain degree of decline. When ${\sigma }_{\theta }>2°$, the rate of decline in accuracy becomes more pronounced, indicating that the standard deviation of measurement azimuth error exerts a greater influence on algorithm performance. Given that the vector decomposition cancellation-based association algorithm relies on the precision of target state estimation, an excessively large azimuth error standard deviation significantly degrades the accuracy of state estimation, resulting in a more pronounced deterioration in algorithm performance. In contrast, the proposed algorithm outperforms the vector decomposition cancellation-based association algorithm.

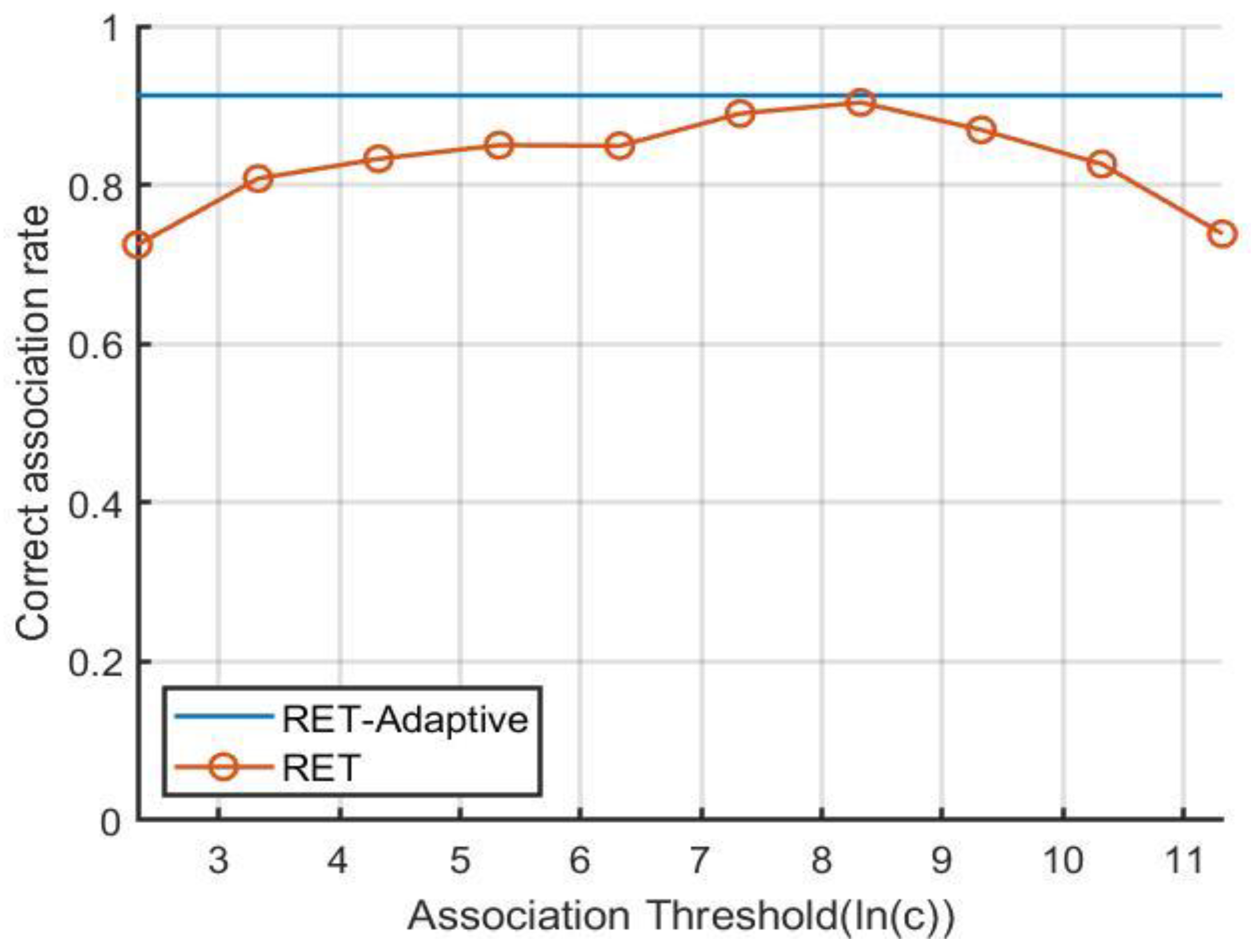
4.5. Performance Verification of Adaptive Threshold

To compare the performance of the improved adaptive threshold RET algorithm with the RET algorithm that requires manual threshold adjustment, a set of representative parameters was selected for a Monte Carlo comparison experiment. The radar azimuth bias was set to $\Delta {\theta }_1=\Delta {\theta }_2=\Delta {\theta }_3=3°$, and the range bias was set to $\Delta r_1=\Delta r_2=\Delta r_3=250 \mathrm{m}$. In this scenario, the threshold in the original RET algorithm increases geometrically, with a range of variation set to c = [5, 10, 20, 40, 80, 160, 320, 640, 1280, 2560]. For each fixed threshold, 50 Monte Carlo simulations were conducted, and the comparison of the association results is shown in Figure 13.

The orange line represents the association accuracy of the original RET algorithm as the threshold $\mathrm{c}$ continuously changes, while the blue line represents the association accuracy of the improved RET algorithm with the adaptive threshold. It can be observed that manually adjusting the threshold results in significant instability in the algorithm performance, with the association accuracy fluctuating depending on the selected threshold. Meanwhile, the orange line consistently lies below the blue line, indicating that manually setting the threshold makes it difficult to precisely select the threshold that yields the highest association accuracy. This verifies that the improved RET algorithm enhances the stability of the algorithm and improves association performance.

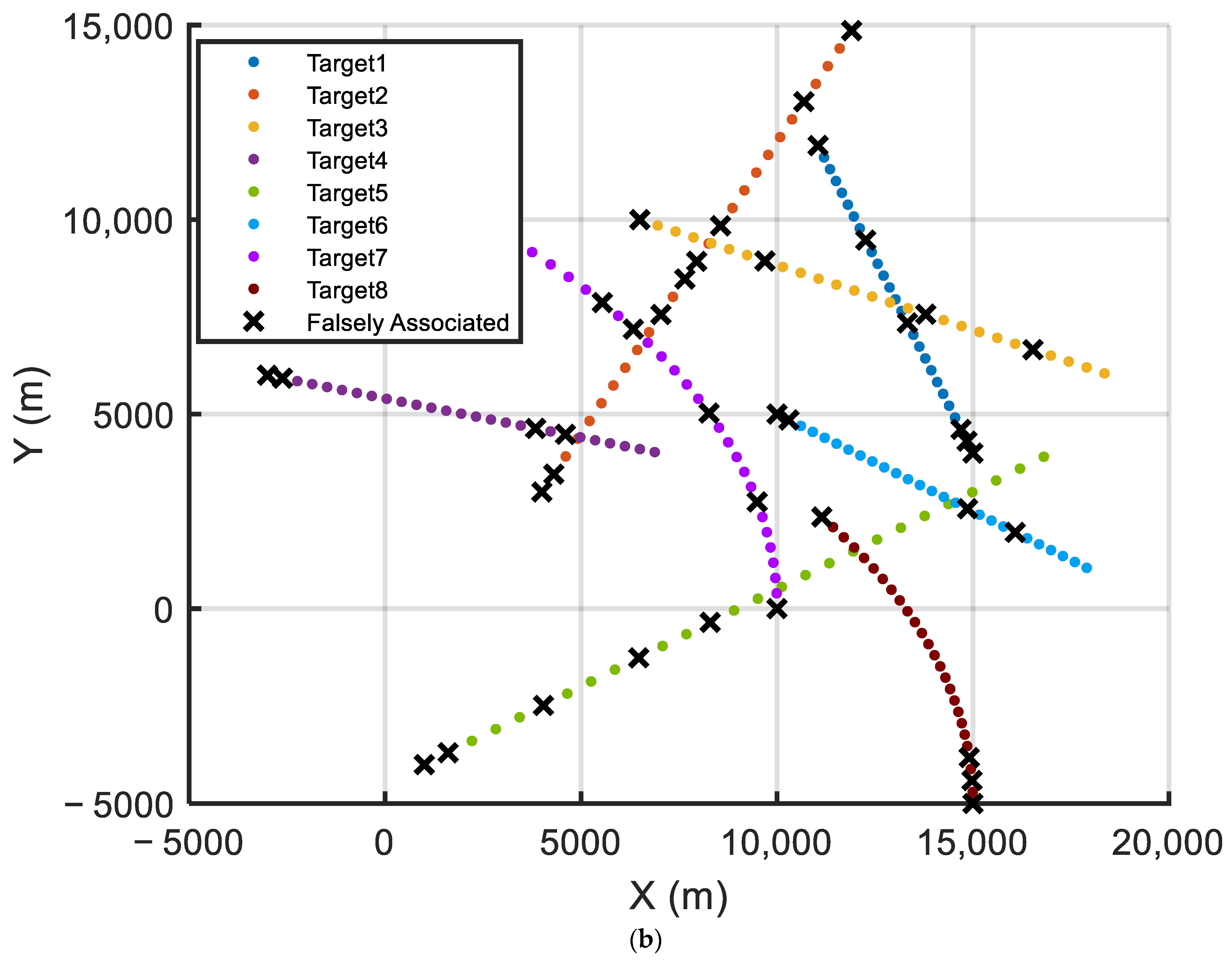
4.6. Performance Verification of the Improved Assignment Algorithm

To verify the performance of the proposed improved assignment algorithm under the conditions of missed detection, two sets of Monte Carlo experiments were conducted, each with 50 runs. The radar bias and the standard deviation of measurement noise error were kept constant, as $\Delta {\theta }_1=\Delta {\theta }_2=\Delta {\theta }_3=3°$, $\Delta r_1=\Delta r_2=\Delta r_3=250 \mathrm{m}$, ${\sigma }_{\theta ,1}={\sigma }_{\theta ,2}={\sigma }_{\theta ,3}=0.3°$, and ${\sigma }_{r,1}={\sigma }_{r,2}={\sigma }_{r,3}=30 \mathrm{m}$. The experiments were performed with missed detection rates set to $miss rate=[0.05,0.10,0.15,0.20,0.25,0.30,0.35,0.40,0.45,0.50]$.

As illustrated in Figure 14, a comparison of the association accuracy of the proposed algorithm and the original Lagrangian assignment algorithm is presented, with the analysis conducted under various missed detection rates. It is evident that the proposed algorithm attains superior association accuracy in comparison to the original multi-dimensional assignment algorithm, effectively mitigating erroneous matches of different source tracks resulting from missed detections. This validates the effectiveness of the proposed algorithm in improving track association accuracy under conditions of missed detection. Meanwhile, as the missed detection rate increases, the overall association accuracy declines, but exhibits a partial recovery once the rate exceeds 0.35. This trend can be attributed to two factors: first, the number of observable targets decreases under high missed detection conditions, leading to reduced association dimensionality and a lower probability of incorrect matching; second, the algorithm tends to adopt a more conservative matching strategy under sparse observations, proactively filtering out uncertain associations, which indirectly improves the accuracy of the confirmed matches. It is important to note that this recovery does not indicate a true performance improvement, but rather results from a simplification effect in the association process due to sparse observations. Therefore, an excessively high missed detection rate should be avoided in practical applications to ensure the integrity of the tracking system.

5. Conclusions

This paper proposes an adaptive multi-radar track association algorithm based on reference topological features. The simulation results demonstrate that the algorithm achieves high association accuracy and exhibits robust adaptability to radar offset bias and measurement noise errors under practical application conditions. The superiority of adaptive association thresholds over fixed thresholds is validated, eliminating the uncertainty and instability caused by manual parameter tuning in the original algorithm. The threshold filtering method significantly enhances association accuracy under missed detection conditions. Compared to the multi-radar track association algorithm based on vector decomposition cancellation, the proposed algorithm enhances association accuracy superiorly. Additionally, the association process does not rely on tracking and estimating target states, making it more suitable for track association in a variety of complex motion scenarios.