Next Article in Journal
Adaptive Multi-Radar Anti-Bias Track Association Algorithm Based on Reference Topology Features
Previous Article in Journal
Optimizing Camera Settings and Unmanned Aerial Vehicle Flight Methods for Imagery-Based 3D Reconstruction: Applications in Outcrop and Underground Rock Faces
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 17
Issue 11
10.3390/rs17111878
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Scalable Hyperspectral Enhancement via Patch-Wise Sparse Residual Learning: Insights from Super-Resolved EnMAP Data

by
Parth Naik
1,2,*,
Rupsa Chakraborty
1,2,
Sam Thiele
2 and
Richard Gloaguen
2
1
Center for Advanced Systems Understanding, Helmholtz-Zentrum Dresden-Rossendorf, 01328 Görlitz, Germany
2
Helmholtz-Institute Freiberg for Resource Technology, Helmholtz-Zentrum-Dresden Rossendorf, 09599 Freiberg, Germany
*
Author to whom correspondence should be addressed.
Remote Sens. 2025, 17(11), 1878; https://doi.org/10.3390/rs17111878
Submission received: 14 April 2025 / Revised: 19 May 2025 / Accepted: 20 May 2025 / Published: 28 May 2025
Browse Figures
Review Reports Versions Notes

Abstract

:
A majority of hyperspectral super-resolution methods aim to enhance the spatial resolution of hyperspectral imaging data (HSI) by integrating high-resolution multispectral imaging data (MSI), leveraging rich spectral information for various geospatial applications. Key challenges include spectral distortions from high-frequency spatial data, high computational complexity, and limited training data, particularly for new-generation sensors with unique noise patterns. In this contribution, we propose a novel parallel patch-wise sparse residual learning (P2SR) algorithm for resolution enhancement based on fusion of HSI and MSI. The proposed method uses multi-decomposition techniques (i.e., Independent component analysis, Non-negative matrix factorization, and 3D wavelet transforms) to extract spatial and spectral features to form a sparse dictionary. The spectral and spatial characteristics of the scene encoded in the dictionary enable reconstruction through a first-order optimization algorithm to ensure an efficient sparse representation. The final spatially enhanced HSI is reconstructed by combining the learned features from low-resolution HSI and applying an MSI-regulated guided filter to enhance spatial fidelity while minimizing artifacts. P2SR is deployable on a high-performance computing (HPC) system with parallel processing, ensuring scalability and computational efficiency for large HSI datasets. Extensive evaluations on three diverse study sites demonstrate that P2SR consistently outperforms traditional and state-of-the-art (SOA) methods in both quantitative metrics and qualitative spatial assessments. Specifically, P2SR achieved the best average PSNR (25.2100) and SAM (12.4542) scores, indicating superior spatio-spectral reconstruction contributing to sharper spatial features, reduced mixed pixels, and enhanced geological features. P2SR also achieved the best average ERGAS (8.9295) and Q2n (0.5156), which suggests better overall fidelity across all bands and perceptual accuracy with the least spectral distortions. Importantly, we show that P2SR preserves critical spectral signatures, such as Fe2+ absorption, and improves the detection of fine-scale environmental and geological structures. P2SR’s ability to maintain spectral fidelity while enhancing spatial detail makes it a powerful tool for high-precision remote sensing applications, including mineral mapping, land-use analysis, and environmental monitoring.

1. Introduction

Hyperspectral imaging data (HSI) capture detailed spectral information across a wide range of wavelengths, which inherently results in a trade-off between spatial and spectral resolution. A range of resolution enhancement methods have been developed to help mitigate resolution limitations, each with distinct approaches to improving spatial fidelity while preserving (hyper) spectral information. These HSI resolution enhancement methods can be broadly categorized into data fusion-based methods, model-based super-resolution techniques, regularization approaches, and hybrid methods that combine several solitary techniques. Understanding the taxonomy of these techniques and their fundamental differences is important for selecting the most suitable approach for specific applications. Data fusion-based enhancement methods integrate HSI with co-registered high-resolution datasets, such as panchromatic (Pan) or multispectral imaging data (MSI). Earlier studies, presented in [1,2], leveraged spectral unmixing and mixing models to integrate data from sensors with different resolutions, setting the stage for subsequent HSI enhancement methods. This led to classical fusion approaches, such as pan-sharpening techniques, which fuse a high-spatial resolution panchromatic band with a low-resolution HSI. There are several pan-sharpening techniques, among which the PCA-based component substitution approaches [3,4], the Gram–Schmidt spectral sharpening method [5], and guided filters [6,7] are classically used for HSI pansharpening. Multisensor fusion methods extend pan-sharpening approaches by combining data from multiple modalities, theoretically enabling more comprehensive resolution enhancement. Techniques such as coupled nonnegative matrix factorization (CNMF) [8] jointly decompose high-resolution MSI and low-resolution HSI into shared spectral and spatial components, effectively integrating their complementary information for enhanced spatio-spectral resolution. HySure [9] is another popular fusion-based method where the high-resolution data are reconstructed by exploiting a low-dimensional subspace representation of HSI. Subspace-based regularization ensures stability and preserves spectral integrity while incorporating prior knowledge for accurate reconstruction.
In contrast to pan-sharpening, model-based super-resolution techniques aim to generate high-resolution HSI from low-resolution inputs, either by enhancing individual images (single-image super-resolution) or combining multiple observations (multi-image super-resolution) through a feature learning mechanism. Traditional super-resolution methods like maximum a posteriori estimation (MAP) [10,11] and spectral reconstruction methods [12,13] rely on mathematical modeling and prior information to deliver high-resolution HSI and often suffer from computational inefficiencies. Some more advancements in model-based hyperspectral super-resolution were presented in [14,15,16] to resolve the problem of degraded spectral fidelity observed in earlier approaches. Specifically, the study in [14] proposed a super-resolution method incorporating low-rank and group-sparse modeling to handle unknown blurring in HSI data by leveraging the inherent low-rank structure of HSI and group-sparse constraints for effective reconstruction. Similarly, the study [15] introduced a joint spectral-spatial sub-pixel mapping model, which integrates spectral unmixing and spatial contextual information to maintain spectral fidelity of enhanced HSI.
Deep learning has significantly advanced HSI image super-resolution (HSI-SR) by offering models tailored to the unique challenges of spectral and spatial fidelity. Early models like FS-3DCNN [17] and SRCNN [18] adapted convolutional networks to HSI, leveraging 3D convolutions to capture spatio-spectral features. Deep Residual models [19,20,21] adapted residual learning for HSI-SR, enabling effective feature extraction across multiple spectral bands with improved reconstruction quality. GAN-based models like HS-SRGAN [22] and HyperGAN [23] incorporated adversarial and perceptual loss to generate visually realistic high-resolution HSIs, ensuring finer spatial details while preserving spectral integrity. Channel attention mechanisms were introduced in MPNet [24] and HSRnet [25], enabling models to focus on critical spectral features while maintaining enhanced spectral fidelity through neighbor-group integration. The latest advancements in this category include models like ESSAformer [26] and Interactformer [27], which integrate transformer and 3D convolution architectures to effectively balance global and local feature extraction. A few recently proposed unsupervised deep learning approaches [28,29] leverage attention-embedded degradation learning and spatio-spectral information disentanglement to conduct HIS enhancement with minimal data requirements. Similar advanced mechanisms, like spatial diffusion and cross-scale nonlocal attention, were used in [30,31] to improve feature extraction and achieve superior spatial detail reconstruction. These latest deep learning-based studies collectively highlight the trend toward unsupervised, attention-based, and fusion-driven deep learning techniques to overcome HSI sensor limitations.
Lastly, hybrid enhancement methods combine multiple approaches, e.g., fusing pan-sharpening with deep learning-based super-resolution, to leverage their respective strengths. In such a scenario, pan-sharpening methods excel in integrating spatial details from complementary sources, while super-resolution techniques focus on internal feature learning. Several earlier proposed hybrid methods, including the approach in [32], integrate spectral unmixing with data fusion techniques, wherein HSI is decomposed into endmembers and abundance maps that are subsequently refined using high-resolution MSI imagery. Similarly, [33,34] introduces a hybrid framework that couples sparse representation with convolutional neural networks (CNNs), where sparse coding provides an initial estimation, and the CNN predicts high-frequency spatial details for refinement. More recently, methods incorporating generative adversarial networks (GANs) have emerged, such as the work [35], which combines a GAN-based super-resolution model with a physical observation model to enhance both spatial quality and spectral accuracy. These examples illustrate how hybrid methods evolve by blending classical, physics-driven, and statistical techniques with capabilities of advanced machine learning approaches, leading to more robust and versatile solutions for HSI resolution enhancement. The taxonomy of these methods is shown in Figure 1 to underscore the diverse strategies available for enhancing HSI.
This paper presents a novel hybrid fusion-based process for enhancing HSI resolution by integrating high-resolution MSI through a multi-stage process that conducts feature decomposition, sparse coding, and parallel patch-wise refinement. Our method, Parallel Patch-wise Sparse Residual Learning (P2SR), offers a robust and efficient solution for hyperspectral resolution enhancement. P2SR tackles several critical challenges in existing HSI resolution enhancement techniques, including noise amplification, excessive computational demands, significant information loss, and the requirement for large training datasets. Traditional methods, such as CNMF, often rely on global assumptions about the data, making them highly sensitive to noise and prone to losing fine details during reconstruction. In contrast, P2SR employs a patch-wise processing strategy that focuses on local data structures, enabling adaptive feature decomposition and sparse coding. This localized approach minimizes noise amplification and enhances the reconstruction of intricate details, overcoming the limitations of global factorization methods. Additionally, P2SR addresses issues prevalent in single- and multi-image super-resolution techniques, such as over-smoothing and aliasing artifacts, which degrade image quality. Unlike deep learning-based methods that depend heavily on extensive training datasets and suffer from high inference latency, P2SR does not require large datasets, making it more practical for scenarios with limited training data. The method incorporates a distributed computation framework and parallel patch-wise processing, which significantly reduces computational overhead. By processing small spatial regions concurrently, P2SR leverages locally informative relationships rather than relying on generalizations across an entire dataset, a common drawback in both traditional iterative algorithms and deep learning models. This parallel processing approach not only improves computational efficiency but also ensures scalability for large datasets, making P2SR suitable for near-real-time applications. By combining the strengths of traditional analytical techniques with modern state-of-the-art processing concepts, P2SR provides a robust, efficient, and scalable solution for high-quality HSI resolution enhancement.

2. Study Areas and Dataset Description

2.1. Study Areas

A total of three study sites, including a benchmark site and two test sites with distinct geo-characteristics, were selected to evaluate the proposed method. The benchmark site covers an area in the city of Augsburg, Germany. The other two test sites are located in Spain and Namibia and have been previously studied from a geological and ecological perspective, allowing us to evaluate application-specific aspects of the proposed resolution enhancement approach [36,37].
Test site 1 is located in the Marinkas-Quellen region of Southern Namibia. The area has an arid environment with limited vegetation and extensive bedrock exposure. Combined with limited seasonal variation and low population density, Marinkas-Quellen is an ideal location for testing the proposed method for large-scale geological mapping. The area hosts significant critical raw materials, including geologically interesting Rare Earth Elements (REE) bearing carbonatites [38].
Test site 2 is located at Rio-Tinto, north of Huelva in the Iberian Pyrite Belt (IPB), Spain, a geologically significant region due to its endowment of massive sulphide copper ores and a mining history that dates back to pre-Roman times. The rocks of the Rio-Tinto area are intensely altered by low-grade hydrothermal activity associated with mineralization and regional metamorphism. These altered minerals provide distinct spectral signatures that can be effectively detected and analyzed using HSI to help locate previously undiscovered ore deposits. The area’s extensive mining history has also led to widespread anthropogenic land cover changes, including environmentally damaging disturbances and mine wastes [39]. Hyperspectral studies in this region can thus also help to effectively monitor and manage this legacy through the quantification of vegetation health and mapping of hazardous (acid-creating) mine wastes. The location and the extent of both the study areas are shown in Figure 2.

2.2. Multi-Modal Benchmark Dataset

We use a benchmark HSI-MSI dataset to ensure a standardized evaluation and comparison of results with state-of-the-art methods. We selected the benchmark MDAS dataset [40] for the city of Augsburg, Germany. The dataset was specially devised to test multiple remote sensing applications, including methods for hyperspectral resolution enhancement. The dataset is unique as compared to contemporary datasets, as most of them only emphasize spatial resolution, whereas MDAS claims to challenge the algorithms for spectral enhancement, instrumental effects, and environmental impact. The original dataset is constructed with multi-modality—SAR data, multispectral image, HSI, DSM, and geographic data. We used the HSI acquired by the German Aerospace Center (DLR) using the HySpex airborne imaging spectrometer system. The HySpex HSI covers a spectral range from 416 to 992 nm with 160 channels and 256 channels covering a spectral range from 968 to 2498 nm using the HySpex VNIR-1600 and SWIR-320m-e sensors (HySpex by neo, Oslo, Norway), respectively. We also used the MDAS MSI, which is the Sentinel-2 bottom of atmosphere (BOA) reflectance and geocoded in WGS 84/UTM zone 32 N. It has 12 spectral bands with wavelengths ranging from 440 to 2200 nm. The final image is cropped to the ROI, resulting in a size of 1371 × 888 pixels.

2.3. Satellite and Airborne Remote Sensing Datasets for the Test Sites

The tested satellite remote sensing datasets included co-registered HSI and MSI for the two test sites (Marinkas and Rio-Tinto). We used the EnMAP HSI with Sentinel-2 and PlanetScope MSI for the implementation of our proposed method. EnMAP captures HSI across visible, near-infrared (VNIR), and shortwave infrared (SWIR) ranges (420–2450 nm) with over 240 spectral bands. The ground sampling distance (GSD) is 30 m per pixel, with a 30 km swath width, enabling both broad and targeted data acquisition. The sensor achieves a signal-to-noise ratio (SNR) greater than 500 (VNIR) and 150 (SWIR) at reference radiance, ensuring high radiometric quality with an accuracy of ≤5% and a 14-bit dynamic range. We used the Level-2A (surface reflectance with atmospheric correction) data, although it is also delivered in Level-1B (at-sensor radiance) and Level-1C (orthorectified radiance).
The high-resolution airborne HSI data for the Rio-Tinto area were acquired using the HySpex sensor (as part of the EU Horizon project, INFACT under grant agreement nº 776487). An empirical line correction (ELC) was performed to convert the geo-rectified HySpex radiance data into relative reflectance, before resampling to 2 m spatial resolution. The ELC model was fit to target ground reflectance measurements acquired with a FieldSpec Spectral Evolution handheld spectroradiometer during the airborne acquisition. The airborne HSI for the Marinkas-Quellen area was acquired using the HyMap sensor from a height of 2000 m, resulting in a 5 m spatial sampling. Geometric and radiometric corrections were conducted by the HyVista Corporation, which acquired the data. Atmospheric correction was performed using a continental aerosol model and a mid-latitude summer atmospheric model, with an ozone count of 340 ppm and a 75 km visibility, to estimate ground reflectance. We used these high-resolution airborne data as a means to validate the satellite HSI resolution enhancement results.
The satellite MSI consists of Sentinel-2 data that include data across 13 spectral bands, ranging from the visible (VIS) and near-infrared (NIR) to the shortwave infrared (SWIR), with a GSD ranging between 10 m and 60 m. Out of the 13, we used 10 spectral bands at 10 m GSD (Visible, Red Edge, NIR, and SWIR). The high radiometric performance is ensured with a 12-bit dynamic range and is available at multiple processing levels, of which Level-2A (bottom-of-atmosphere reflectance with atmospheric correction) was used in the experiments. The Planetscope MSI was captured by Planet Labs with eight spectral bands (Visible, Red Edge, and NIR) at 3 m spatial resolution. We used the Level-3B ortho-rectified scaled surface reflectance 8-band image. Some key specifications and details of the HSI and MSI datasets used for this study are given in Table 1.

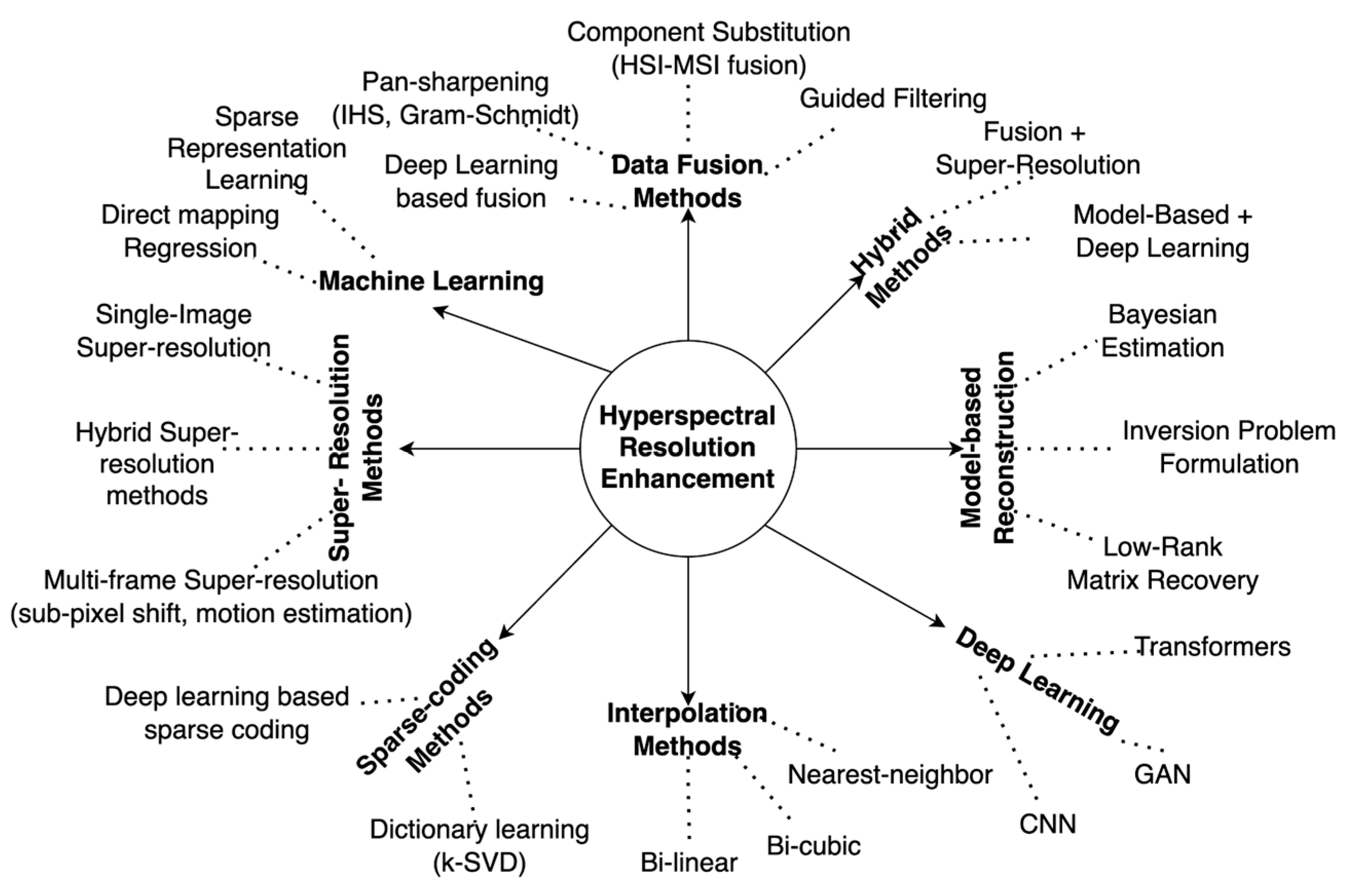
3. Proposed Method and Experimental Setup

3.1. Parallel Patch-Wise Sparse Residual Learning (P2SR) Method

The proposed P2SR method employs a multi-stage approach that combines sparse coding and residual learning to generate HSI with higher spatial resolution (i.e., GSD) by fusion of low-resolution HSI and high-resolution MSI. P2SR is an organized approach that sequentially ensures consistency of data (through systematic pre-processing), captures diverse spatio-spectral features (via multi-decomposition), effectively fuses spatio-spectral features (with dictionary learning and sparse coding), and reconstructs high-resolution HSI (using first order optimization and guided filtering) with easy and accelerated deployment (using parallel computing). These steps are described in detail in the following paragraphs of this subsection.
In the first stage, HSI and MSI data are preprocessed to address nan values, invalid bands, and data gaps to ensure overall data integrity. The MSI is downsampled to align with the HSI’s resolution, and adaptive patch sizes and strides are calculated based on data dimensions (height and width) to enable efficient regional processing. A set of selected decomposition techniques— 3D-wavelet transforms (3DWT), Independent component analysis (ICA), and Non-negative matrix factorization (NMF) are employed to extract spectral and spatial features from the HSI, creating a rich set of components that encapsulate the underlying data structure. The proposed P2SR method integrates these decomposition methods with their unique advantages: ICA isolates statistically independent spectral signatures and emphasizes variance, NMF enforces non-negativity for improved interpretability with localized features, and 3DWT isolates multi-scale spectral patterns in the HSI data. The method applies each decomposition separately to the low-resolution hyperspectral patches to effectively utilize these complementary strengths. These patches provide a robust representation of the spatial and spectral content, allowing the model to learn high-frequency spatial details effectively.
The spectral bases extracted through multi-decompositions are crucial in forming a sparse dictionary that encodes the locally relevant spectral information. In the second stage, a dictionary (see supervised dictionary learning [41]) is trained using a combination of downsampled MSI patches and spectral components extracted from the HSI through multiple decompositions. The goal of this dictionary is to capture the spectral characteristics of different materials present in the patch, while also accommodating the spatial details provided by the MSI. By leveraging both sources of information—low spatial resolution data from the HSI and relatively higher spatial resolution data from the MSI—the dictionary is constructed to be representative of the high-resolution hyperspectral space, enabling accurate super-resolution reconstruction. The next step is to utilize it for sparse coding, where each patch of the low-resolution HSI is represented as a linear combination of a few dictionary atoms. The patch-wise approach makes sparse coding faster and more accurate as each patch consists of only a few distinct materials. Sparse coding is based on the principle of sparsity, which assumes that natural signals can be efficiently represented using a small number of meaningful basis elements. It helps to suppress noise and irrelevant information while preserving the critical spectral structures necessary for reconstruction. However, the challenge in sparse coding is to determine the optimal sparse representation and optimally enforce sparsity constraints. Therefore, we employ the Fast Iterative Shrinkage-Thresholding Algorithm (FISTA) [42] to solve this optimization problem. FISTA accelerates sparse reconstruction due to its fast convergence and ensures that the learned dictionary is utilized effectively to recover high-resolution hyperspectral details while avoiding overfitting or introducing artefacts. As a result, the final sparse representation of each hyperspectral patch is well-structured, preserving the essential spectral characteristics of the original scene while benefiting from the enhanced spatial resolution provided by the MSI. This combination of dictionary learning and sparse coding enables a highly effective fusion of MSI and HSI, leading to superior resolution enhancement with minimal spectral distortion.
The final reconstruction stage integrates the estimated high-resolution hyperspectral features with the upsampled HSI. The last step produces a final reconstructed and enhanced HSI with guided filtering, applied to leverage the MSI bands as a structural reference to enhance spatial fidelity while minimizing artefacts. This step ensures that both fine spectral details extracted from the learned dictionary and the global spatial structure of the original HSI are retained. This systematic multi-stage process ensures that the resolution-enhanced HSI achieves an improved spatial resolution while preserving spectral integrity, making it suitable for high-precision remote sensing applications. These multiple stages are encapsulated in a parallel computing framework that enhances computational efficiency, especially given the high-dimensional nature of hyperspectral data. The method can be implemented on an HPC system, and the patch-wise computations scale across multiple processing cores. Some specific loop operations are compiled with JIT compiler for faster matrix operations within iterative loops. Additionally, efficient memory management techniques are employed to handle the substantial data load (e.g., use of early stopping in FISTA, log-based debugging, and preference for vectorized packages for implementation) while minimizing computational overhead. The flowchart for the implementation of the method is shown in Figure 3. Additionally, an algorithm table with a pseudo code is provided in Appendix A for a more detailed description of the method and key equations of integral components of the proposed method.

3.2. Experimental Setup and Evaluation Strategies

The experiments are organized to perform HSI resolution enhancement in diverse terrain conditions and at multiple spatial levels. The proposed P2SR method and a few selected state-of-the-art (SOA)/established methods are implemented for the enhancement of EnMAP data from 30 m to 10 m spatial resolution using Sentinel-2 data and to 3 m spatial resolution using PlanetScope data. The five selected methods for comparison include the following: (1) Bicubic interpolation (Bicubic) and (2) Custom Hyperspectral Super-resolution (c-HySure); c-Hysure is a custom Python implementation of the Hysure method [9] with original MATLAB (R2014b) code: https://github.com/alfaiate/HySure (accessed on 25 January 2025). (3) Coupled non-negative matrix factorization (CNMF) [8]; CNMF source code: https://naotoyokoya.com/assets/zip/CNMF_Python.zip (accessed on 25 January 2025). (4) Residual Two-stream Fusion Network (ResTFNet) [34]; ResTFNet source code: https://github.com/liouxy/tfnet_pytorch (accessed on 25 January 2025). (5) Spatial–Spectral Reconstruction Network (SSRNet) [43]; SSRNet source code: https://github.com/hw2hwei/SSRNET (accessed on 25 January 2025). These methods are prominently used for comparative evaluation and are reproducible with open-source codes. All methods (except bicubic) are based on HSI-MSI fusion, which makes them suitable for comparison with the proposed method.
The proposed P2SR method is evaluated using a combination of quantitative metrics and qualitative assessment. Quantitative metrics used for the evaluation of enhanced HSI are—Peak Signal-to-Noise Ratio (PSNR), Spectral Angle Mapper (SAM), Erreur Relative Globale Adimensionnelle de Synthèse (ERGAS), and Universal Image Quality Index for n-bands (Q2n). PSNR is a simple and widely used metric that measures reconstruction quality, but it is not always correlated with visual perception. SAM measures spectral distortion between the reference and reconstructed HSI. ERGAS measures global relative reconstruction error across all bands, and Q2n is a multi-band extension of the structural similarity measure (SSIM) that measures covariance between reference and reconstructed HSI, depicting preservation of structural information. Along with SOA methods, we also use a benchmark dataset (MDAS) with known high-resolution ground truth that allows for objective comparisons with other SOA methods (with open-source codes) and ensures generalization. The 10 m enhanced HSI products delivered from five SOA methods and the proposed method are evaluated using the assessment metrics for all three datasets. These metrics are computed for enhanced HSI against a high-resolution reference HSI captured with airborne sensors. The proposed method is then used to produce 3 m-enhanced HSI products for Marinkas-Quellen and Rio-Tinto to make a qualitative and application-oriented assessment. The qualitative assessment includes minimum wavelength maps, band-index inspection, spectral profile consistency checks, and identifying interesting geological enhanced structures.

4. Results

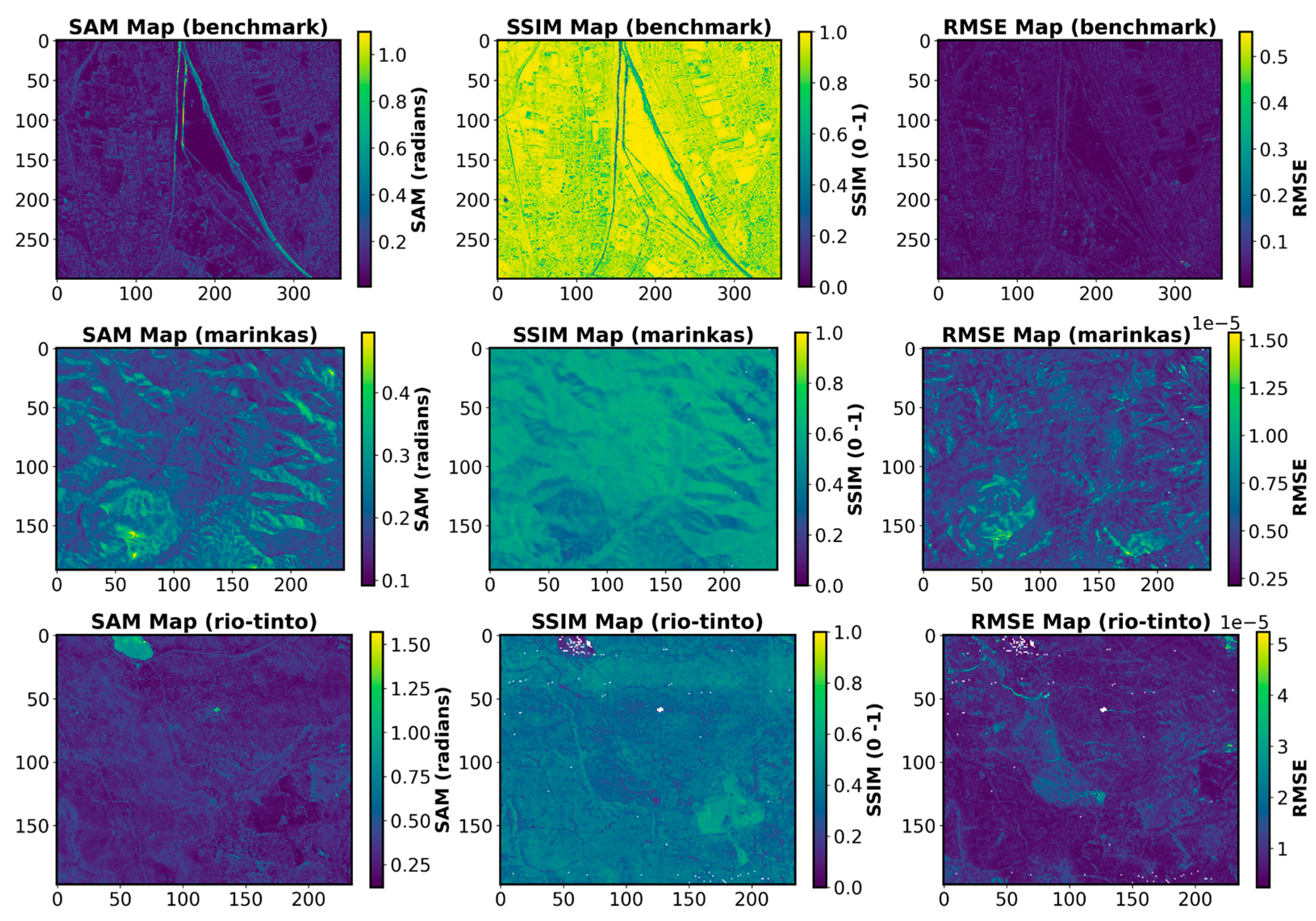
4.1. Metrics-Based Assessment of Enhanced Hyperspectral Products

The 10 m enhanced products were evaluated using PSNR, SAM, ERGAS, and Q2n metrics for all three study sites (Table 2). These scores indicate that the proposed P2SR method outperforms all considered SOA / established methods on all metrics for all datasets, except for the Q2n metric in Rio-Tinto, where SSR-Net has the highest Q2n score. This indicates the robust nature of P2SR when exposed to different terrain conditions and the accurate reconstruction of HSI across diverse land features. The fact that P2SR achieves the best PSNR and SAM scores for all datasets indicates a stable performance in simultaneously maintaining the spatial and spectral quality of enhanced HSI in diverse scenarios. A high PSNR does not always guarantee spectral fidelity, and this is distinctly observed for CNMF, which achieves high PSNR scores close to the P2SR method, but low SAM scores indicate inaccuracies in spectral reconstruction. Similarly, ResTFNet delivered better SAM scores as compared to CNMF, indicating better spectral reconstruction but lower PSNR, suggesting inaccuracies in spatial reconstruction.
The proposed P2SR method also outperforms all methods in terms of ERGAS score, indicating robustness in relative spatio-spectral reconstruction (not only pixel-wise errors) and independence on the intensity distribution of the original HSI. This difference can be observed between CNMF and deep learning methods (ResTFNet and SSR-NET), where there is a high difference in the average PSNR scores (dependent on reflectance distribution), but the difference reduces in average ERGAS scores, indicating compromised performance of deep learning methods due to high variations in HSI reflectance. Also, among the two deep learning models, SSR-NET achieves a better average ERGAS score than ResTFNet, indicating a better spatio-spectral reconstruction for uniform distributions of reflectance values, but, for non-uniform distributions (such as in most realistic scenarios), SSR-NET offers a better spatial reconstruction ability (better PSNR score) and ResTFNet has a better spectral reconstruction ability (better SAM score). In terms of universal image quality aspects, such as luminance and contrast (along with structural similarity), the P2SR method performs better than all methods, except for the Rio-Tinto area, where SSR-NET achieves a slightly better Q2n score. This could be attributed to the complex and dynamic features around mining areas.
The visual maps of SAM, SSIM, and RMSE metrics, as presented in Figure 4 for three distinct sites, provide a comprehensive evaluation of P2SR performance in enhancing EnMAP data. These metrics collectively assess the spectral fidelity, spatial quality, and pixel-wise accuracy of the enhanced imagery, offering insights into the method’s strengths and limitations. The SAM metric quantifies the angular difference between the spectral signatures of enhanced and reference pixels, with lower values indicating better preservation of spectral information. The SAM map’s localization of errors to specific features, such as water bodies and irregular topography, suggests that P2SR generally maintains high spectral fidelity across most of the scene but encounters challenges in areas with complex spectral or spatial characteristics. The higher SAM errors in water bodies could stem from their dynamic nature (e.g., varying water composition, surface reflections) or the low reflectance in certain spectral bands, which complicates accurate reconstruction. Errors in regions with rugged terrain likely arise from shadowing effects, mixed pixels, or rapid spatial–spectral transitions. Despite these localized errors, the overall low SAM values (implied by the method’s accuracy) suggest that P2SR effectively preserves the spectral integrity of most materials, enabling reliable downstream tasks.
The SSIM map’s high confidence in reconstructing diverse terrain features underscores P2SR’s ability to capture fine-scale structural details, such as edges, textures, and patterns. This is particularly significant for applications requiring precise delineation of environmental variables (e.g., vegetation boundaries, soil types) or structural features (e.g., urban infrastructure, geological formations). The ability to resolve these features at 10 m and 3 m resolutions facilitates finer detection of changes, such as urban expansion or land degradation, compared to the original 30 m EnMAP data. Moreover, the RMSE map’s high confidence in spatial reconstruction complements the SSIM results, confirming that P2SR accurately reconstructs pixel intensities across diverse terrains. This precision is critical for quantitative applications, such as biomass estimation or mineral mapping, where small errors in pixel values can significantly affect results. The consistency of RMSE performance across the three sites indicates that P2SR is robust to variations in scene content.

4.2. Qualitative Spatial Assessment of Enhanced Hyperspectral Products

The qualitative assessment suggests that the P2SR method produces compelling results, as demonstrated in the false color composite (FCC) patches presented in Figure 5 and Figure 6. In Figure 5, the original 30 m EnMAP data are compared with the 10 m enhanced output, revealing marked improvements in spatial clarity. Urban features, such as buildings and infrastructure, exhibit sharper edges and more defined boundaries, addressing the problem of mixed pixels, where multiple land cover types are blended within a single pixel at coarser resolutions. This enhanced delineation is particularly evident in complex urban environments, where fine-scale features, like roads, buildings, and vegetation patches, are resolved with greater precision. Similarly, water bodies and bridges show refined boundaries, with land–water interfaces appearing smoother yet distinctly separated, which is crucial for applications like coastal zone management or flood mapping.
Figure 6, focusing on the Marinkas site, extends the analysis to both 10 m and 3 m resolutions, showcasing the method’s scalability. The FCC patches at these higher resolutions maintain spectral consistency across spatial regions with uniform material composition, such as different mineral classes. This is a critical achievement, as it indicates that P2SR avoids introducing spectral distortions during the resolution enhancement process—a common pitfall in traditional super-resolution techniques. The visualization of SWIR wavelengths further highlights the method’s ability to control noise, producing smooth spatial transitions while preserving sharp edges. This noise suppression is particularly valuable in SWIR bands, which are sensitive to atmospheric and sensor noise but essential for identifying materials like minerals or vegetation health.

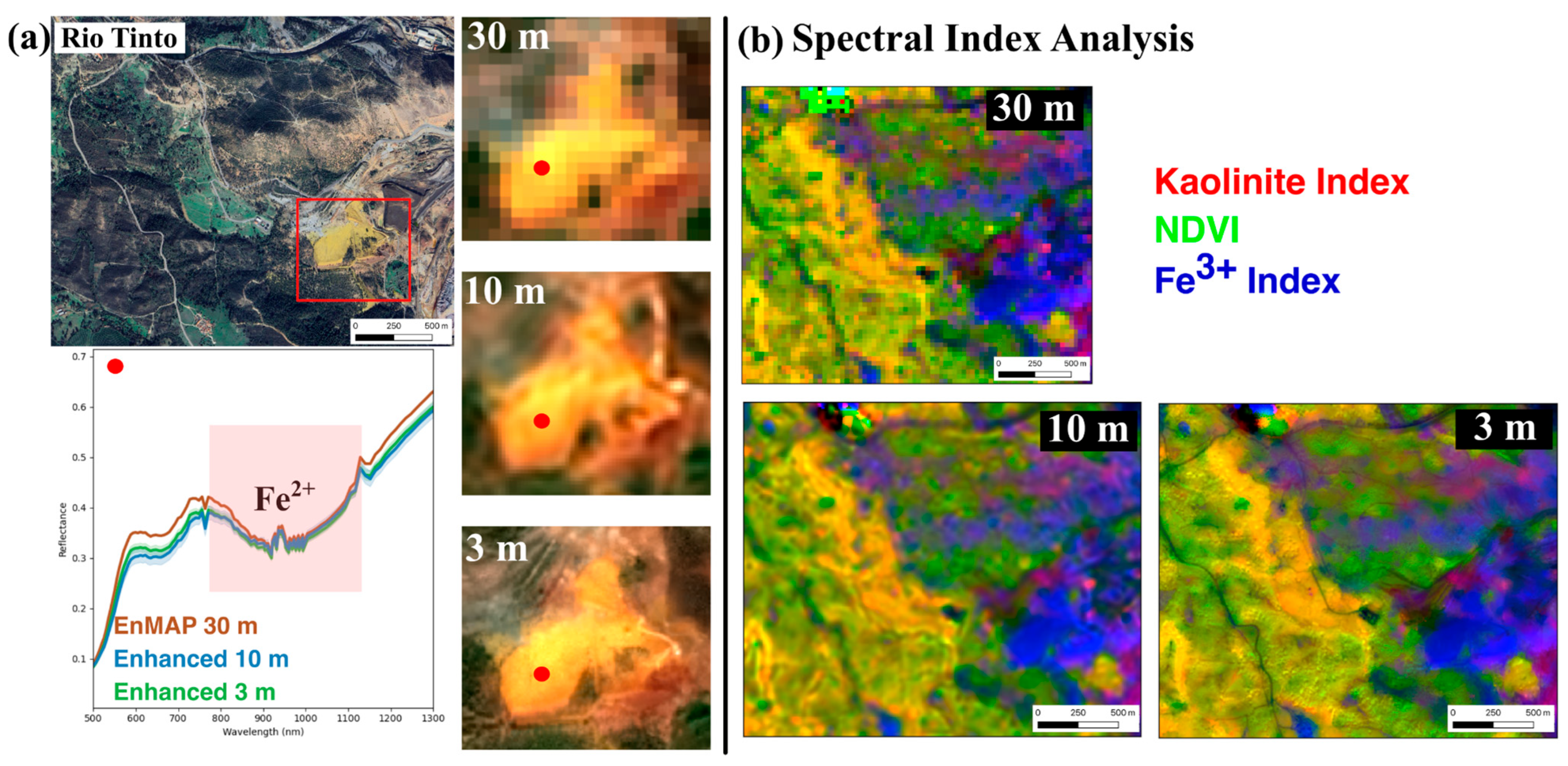
4.3. Application-Oriented Assessment of Enhanced HSI Products

The application-oriented assessment in Rio-Tinto is divided into two blocks, as shown in Figure 7. The prominent feature (highlighted in the red bounding box) in Figure 7a, identified as transported mine waste, exhibits well-defined and sharper boundaries in the enhanced HSI products. This region is also spectrally distinct due to its strong Fe2+ absorption feature between 800 nm and 1200 nm. Spectral analysis of the enhanced products confirms that they retain this spectral information with minimal variation. This site is particularly significant due to its diverse land cover and geologically important spectral features. A spectral index analysis was employed to evaluate the enhanced products further. Three spectral indices were considered: kaolinite ( R 1600 : 1700 R 2145 : 2185 ∗ R 2295 : 2365 R 2185 : 2225 ), NDVI ( N I R − R e d N I R + R e d ), and Fe3+ index ( R 600 R 570 ) and an RGB composite of the results was generated. In Figure 7b, sparse vegetation in kaolinite-rich soil appears yellow, while magenta spots indicate areas of bare soil with Fe-rich clay. The enhanced products preserve and effectively amplify these subtle spectral variations while spatially enhancing roads and other distinct features. An in-depth evaluation of the proposed method for mineral mapping is provided in the study presented in [44].
Marinkas-Quellen is a geologically complex site with minimal vegetation cover. Significantly, the enhanced HSI products reveal finer geological structures that are entirely absent in the original coarser 30 m HSI data. In the true-colour composite of the enhanced 3 m HSI product, distinct foliation and/or bedding patterns are clearly visible, as highlighted by the yellow bounding box in Figure 8a. The primary spectral signatures in this region are observed in the SWIR, particularly from carbonates and clays. Further analysis of the enhanced products using minimum wavelength mapping (MWL) in the SWIR domain shows significantly improved clarity in geological demarcations (Figure 8b). Broadly, shades ranging from green to cyan (from 2325 nm to 2335 nm) indicate carbonate-bearing lithotypes, while darker blue (~2340 nm) signifies the presence of Mg-OH in alteration. Additionally, a small dyke-like feature is apparent in the enhanced products (most prominent at 3 m), marked by reddish tones in the MWL, suggesting the presence of a Fe-OH absorption feature around 2250 nm.

5. Discussion

This study introduces P2SR, a novel multi-stage sparse residual learning framework designed for hyperspectral image (HSI) resolution enhancement, leveraging the computational efficiency of parallel processing architectures. By integrating patch-wise processing, sparse coding, and residual learning, P2SR achieves robust and consistent performance across benchmark datasets and real-world test scenarios, such as EnMAP products. The hybrid methodology synergistically combines the strengths of statistical techniques, such as guided filtering and FISTA, with select machine learning paradigms, including hierarchical feature extraction and local feature learning. This section discusses the theoretical underpinnings, empirical strengths, and limitations of P2SR, while situating it within the broader context of HSI enhancement and super-resolution research.

5.1. Significant Contributions to Hyperspectral Resolution Enhancement

The core innovation of P2SR lies in its patch-wise processing strategy, which enables the model to capture locally salient spatial–spectral relationships while mitigating the influence of globally irrelevant features. Unlike traditional global approaches that may struggle with high-dimensional HSI data due to computational complexity or overfitting, patch-wise processing decomposes the HSI into manageable sub-regions, allowing for efficient parallelization on multi-core processors or GPU architectures. This design aligns with the distributed computing paradigms observed in modern deep learning frameworks [45,46,47], but avoids the heavy reliance on large-scale annotated datasets, a common bottleneck in deep learning-based HSI enhancement.
The integration of sparse residual learning further enhances P2SR’s robustness. By employing FISTA for sparse coding, P2SR constrains noise propagation and spectral distortions, a critical challenge noted in prior HSI-MSI fusion studies [48,49,50]. These studies highlighted how high-frequency spatial information from auxiliary MSI can corrupt spectral fidelity, leading to artifacts in super-resolved outputs. P2SR mitigates this through a multi-stage regularization process, where guided filtering and iterative thresholding ensure that only relevant high-frequency details are incorporated into the enhanced HSI. Empirical results demonstrate that P2SR achieves superior performance in 3x and 10x super-resolution tasks for EnMAP datasets, with metrics such as average PSNR and SAM surpassing state-of-the-art methods by approximately 0.98–9.94 dB and 3.65–6.98, respectively.
Theoretically, P2SR bridges the gap between classical sparse coding and modern deep learning by adopting hierarchical feature extraction and residual learning, concepts popularized by convolutional neural networks (CNNs) [45] and transformers [47]. However, unlike deep architectures that require extensive training data to model complex spatio-spectral relationships, P2SR leverages dictionary learning to construct compact, data-driven representations. This reduces the computational overhead and mitigates the risk of overfitting, particularly for new-generation hyperspectral sensors (e.g., EnMAP, PRISMA) with unique spectral response characteristics or noise patterns.

5.2. Comparative Analysis with Deep Learning Based Approaches

Deep learning has significantly advanced HSI enhancement by capturing intricate spatial and spectral dependencies. Architectures such as 3D CNNs [45] exploit spatio-spectral correlations, recurrent neural networks (RNNs) [46] model sequential dependencies across spectral bands, and transformers [47] leverage self-attention mechanisms to learn global priors. However, these models face three critical challenges: (1) the need for massive, diverse training datasets, which are often unavailable for hyperspectral applications due to acquisition costs and sensor variability; (2) sensitivity to spectral misalignment and spatial resolution variability, which can degrade generalization to new sensors or environmental conditions; and (3) high computational complexity, limiting scalability for large-scale HSI datasets.
P2SR addresses these challenges by selectively incorporating robust mechanisms from deep learning while relying on sparse representations and dictionary learning. For instance, the patch-wise processing and sliding window operations mimic the local feature learning of CNNs, while multi-scale decomposition enables hierarchical feature extraction similar to deep architectures. Unlike data-intensive deep models, P2SR’s dictionary-based approach adapts to the intrinsic structure of the input HSI, reducing the dependency on external training data. Furthermore, the parallel computing framework ensures scalability, with extensive runtime improvements on high-performance computing systems.
However, P2SR has a few trade-offs with mechanisms in deep learning architectures. Deep learning models, particularly transformers, excel at modeling long-range dependencies across large HSI scenes, whereas P2SR’s patch-wise approach may struggle to capture global contextual information in highly heterogeneous environments. Future iterations of P2SR could explore hybrid attention mechanisms [47] to balance local and global feature learning, potentially improving performance in complex scenes without sacrificing computational efficiency.

5.3. Limitations and Future Scope

Despite its strong empirical performance, P2SR exhibits several limitations that require further investigation. First, the adaptive patch size and stride selection process, while effective in most cases, remains sensitive to parameter tuning. Small patches may fail to capture sufficient contextual information, leading to loss of fine spatial details, while large patches risk over-smoothing high-frequency features. This trade-off is particularly observed in scenes with diverse land cover types, where optimal patch sizes may vary spatially. A potential solution lies in dynamic patch size adaptation based on local entropy or texture analysis, which could enhance robustness across heterogeneous datasets.
Secondly, the dictionary learning component, while effective for sparse representation, introduces the risk of spectral distortions in regions with complex land feature distributions (e.g., urban–rural interfaces). Although FISTA mitigates these errors by regularizing sparse residuals, the construction of a single dictionary may not adequately represent multi-scale frequency components. A promising direction is the development of multi-dictionary learning frameworks [51], where separate dictionaries can be trained for low-, mid-, and high-frequency bands, potentially improving spectral fidelity in challenging scenarios. Also, P2SR’s temporal robustness remains untested. Hyperspectral datasets often exhibit temporal variability due to changes in illumination, atmospheric conditions, or land cover dynamics. The current dictionary learning approach assumes static spectral characteristics, which may limit performance on time-series data. Incorporating dynamic dictionary updates could enable P2SR to adapt to evolving environmental conditions, ensuring consistent performance in longitudinal studies.
Finally, while P2SR’s parallel computing framework enhances scalability, its performance on resource-constrained platforms (e.g., embedded systems for on-board satellite processing) remains unverified. Optimizing the algorithm for low-power computing systems, potentially through the quantization or pruning of dictionary elements, could broaden its applicability in real-time remote sensing applications.
To address the identified limitations and further advance P2SR, several research directions, such as developing frequency-specific dictionaries for multi-scale feature representation, can be considered to mitigate spectral distortions in complex scenes, improving generalization across diverse datasets. Implementing dynamic dictionary updates or learning strategies would enable P2SR to handle temporal variability, making it suitable for time-series HSI enhancement in dynamic environments. Incorporating sensor-specific calibration modules could improve P2SR’s performance on future-generation hyperspectral sensors with distinct spectral or noise characteristics. Adapting P2SR for resource-constrained platforms through techniques like model compression or multi-objective optimization would facilitate its deployment in on-board processing systems for real-time applications. Lastly, enhancing explainability and uncertainty quantification could provide confidence intervals for super-resolved outputs, improving interpretability and trustworthiness in critical applications like environmental monitoring.

6. Conclusions

The proposed P2SR method demonstrates a robust and effective approach for HSI enhancement, consistently outperforming SOA methods across multiple quantitative and qualitative evaluations. The metric-based assessment reveals that P2SR achieves superior performance in terms of PSNR, SAM, and ERGAS across diverse terrains, indicating its ability to balance spatial and spectral accuracy effectively. Although SSR-Net slightly surpasses P2SR on the Q2n metric in the Rio-Tinto dataset, the overall results confirm P2SR’s stability and precision in reconstructing HSI under varying terrain conditions. The qualitative spatial assessments further validate these findings, showing sharper spatial features, reduced mixed pixels, and improved structural integrity across different resolutions (10 m and 3 m). Moreover, the application-oriented assessment highlights P2SR’s ability to preserve and enhance critical spectral signatures in geologically complex regions, as seen in the identification of Fe2+ absorption features and the detection of fine-scale geological structures. The method’s ability to maintain spectral fidelity while enhancing spatial detail ensures its applicability in real-world scenarios, including mineral mapping, vegetation analysis, and land-use classification. With its efficient decomposition strategy and parallel processing framework, P2SR provides an advanced, scalable solution for enhancing HSI, bridging the gap between sensor limitations and the demand for high-resolution spectral data in remote sensing applications. However, P2SR’s adaptive patch size selection risks losing fine spatial details or oversmoothing high-frequency features, and dictionary learning may introduce spectral distortions in complex scenes. The performance on resource-constrained platforms also requires validation.

Author Contributions

Conceptualization, P.N.; Methodology, P.N. and S.T.; Validation, P.N. and R.C.; Formal analysis, P.N. and R.C.; Investigation, P.N. and R.C.; Data curation, P.N.; Writing—original draft, P.N. and R.C.; Writing—review & editing, P.N., R.C., S.T. and R.G.; Visualization, P.N. and R.C.; Supervision, S.T. and R.G.; Project administration, S.T. and R.G.; Funding acquisition, S.T. and R.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research is funded by Open projects at the Center for Advanced Systems Understanding under the Grant #1089999008 at Helmholtz Zentrum Dresden Rossendorf.

Data Availability Statement

The source code of the developed method is available on GitHub (https://github.com/naikp13/hsi_enhancement). All open-source data can also be accessed from the GitHub page. The raw and proprietary data of this article may be made available by the authors on request.

Acknowledgments

We are grateful to the Open Projects programme of the Center for Advanced Systems Understanding (Helmholtz-Zentrum Dresden-Rossendorf) for the support and funding of this project. The EnMAP Level 2A data were provided by the German Aerospace Center (DLR) under proposal number A00001-P00375. We also thank Planet Labs PBC [52] for providing the PlanetScope data accessed under the Education and Research Program—PlanID 748533.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Appendix A contains the algorithm for the implementation of the proposed P2SR method along with a pseudo-code of the implemented source code.
Algorithm A1 For parallel patchwise spare residual learning method (P2SR)
1. Input:
I M S I : Multispectral data,  I M S I ∈ R H m × W m × C m ,  I H S I : Hyperspectral data,  I H S I ∈ R H h × W h × C h
2. Pre-processing:
    Normalize each band to [0, 1]
    Set  I M S I [ i , j , k ] = N a N   i f , I M S I [ i , j , k ]   ≤ 0  
    Set  I H S I [ i , j , k ] = N a N   i f   I H S I [ i , j , k ]   ≤ 0  
    If  ∑ i , j i s n a n   ( I H S I [ i , j , c ] )   /   ( H h   ∗   W h ) > θ ,   E l i m i n a t e   b a n d   c  
         I H S I [ i , j , c ]   ←   m e d i a n   f i l t e r   i f   N a N ,   e l s e   u n c h a n g e d
3. Patch Processing:
    Compute Scaling factor f =  H m H h
    Downsample MSI by factor f,  I M S I − L R  = zoom( I M S I , f)
            ∀   x ,   y   ∈ { ( i , j )   |   i ,   j   ∈ [ 0 , H h − p   ] s t e p   s } :
     -
 Extract patches:
     -
  P H S I  =  I H S I [ x   :   x + p ,   y   :   y + p ,   : ]
     -
  P M S I − L R  =  I M S I − L R [ x   :   x + p ,   y   :   y + p ,   : ]
     -
  P M S I − H R  =  I M S I − H R [ x   :   x + p ,   y   :   y + p ,   : ]
    Feature Decomposition on  P H S I  for 5-components (K)
     -
  W w a v e l e t  = 3d-wavelet transform ( P H S I   ,   K 5   ) ,  W I C A  = FastICA ( P H S I   ,   K 5 ) ,  W N M F  = NMF ( P H S I ,   K 5   )
     -
  W c o m b i n e d  =  [ W w a v e l e t   ,   W I C A   ,   W N M F   ]
    Dictionary Learning with ‘ A ’ atoms
         D   ← D i c t i o n a r y L e a r n i n g ( [ P M S I − L R   ,   W c o m b i n e d   ] ,   A )  
    Sparse Coding using FISTA with ‘ λ ’ regularization
    Given a dictionary  D   ∈   R n   X   A , use FISTA iterations to minimize
     -
  m i n α   0.5   ∗ | | X − α D T | | 2 + λ | | α | |  
    Predict high-resolution residuals
     -
  R p r e d = r e s h a p e ( α D T ) → R H m × W m × C m
     -
  R r e s i d u a l = R p r e d − u p s a m p l e   ( m e a n   ( W c o m b i n e d ) )  
    Accumulate residuals from individual patches
     -
  I H S I − H R [ f x   :   f x + f p ,   f y   :   f y + f p ,   : ] + = R r e s i d u a l s
4. Normalization of aggregated residuals
               I H S I − H R   [ i ,   j ,   : ]     / = c o u n t s [ i ,   j ] ,   i f   c o u n t s > 0    
5. Selection of MSI-guide bands and injection of high-frequency details
    Select three suitable MSI-guide bands:  I M S I − g u i d e ∈   R H m × W m × C m
    Extract high-frequency details:  I H F = m e a n ( I M S I − g u i d e ) − G a u s s i a n ( m e a n ( I M S I − g u i d e ) ,   σ = 1 )
    Inject high-frequency details: For each band  b   ∈   [ 1 ,   C h ] ,
                   I H S I − H R   [ . . . , b ] + = I H F  
6. Guided Filtering with MSI-guide bands
     I H S I − e n h a n c e d [ . . . ,   b ] = G u i d e d . F i l t e r ( I M S I − g u i d e   ,   I H S I − H R )
7. Output:
     I H S I − e n h a n c e d  Enhanced Hyperspectral,  I H S I − e n h a n c e d ∈ R H m × W m × C h  
A pseudo-code that outlines the key steps, classes, and methods implemented in the actual source code can be accessed on the following GitHub link (https://github.com/naikp13/hsi_enhancement/blob/main/pseudo.txt). It preserves the logical flow and structure of the original source code.

References

  1. Zhukov, B.; Oertel, D.; Lanzl, F.; Reinhackel, G. Unmixing-Based Multisensor Multiresolution Image Fusion. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1212–1226. [Google Scholar] [CrossRef]
  2. Eismann, M.T.; Hardie, R.C. Application of the Stochastic Mixing Model to Hyperspectral Resolution Enhancement. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1924–1933. [Google Scholar] [CrossRef]
  3. Shah, V.P.; Younan, N.H.; King, R.L. An Efficient Pan-Sharpening Method via a Combined Adaptive PCA Approach and Contourlets. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1323–1335. [Google Scholar] [CrossRef]
  4. Jelének, J.; Kopačková, V.; Koucká, L.; Mišurec, J. Testing a Modified PCA-Based Sharpening Approach for Image Fusion. Remote Sens. 2016, 8, 794. [Google Scholar] [CrossRef]
  5. Dalla Mura, M.; Vivone, G.; Restaino, R.; Addesso, P.; Chanussot, J. Global and Local Gram-Schmidt Methods for Hyperspectral Pansharpening. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar] [CrossRef]
  6. Qu, J.; Li, Y.; Dong, W. A New Hyperspectral Pansharpening Method Based on Guided Filter. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5125–5128. [Google Scholar] [CrossRef]
  7. Dong, W.; Xiao, S.; Li, Y. Hyperspectral Pansharpening Based on Guided Filter and Gaussian Filter. J. Vis. Commun. Image Represent. 2018, 53, 171–179. [Google Scholar] [CrossRef]
  8. Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled Nonnegative Matrix Factorization Unmixing for Hyperspectral and Multispectral Data Fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
  9. Simoes, M.; Bioucas-Dias, J.; Almeida, L.B.; Chanussot, J. A Convex Formulation for Hyperspectral Image Superresolution via Subspace-Based Regularization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3373–3388. [Google Scholar] [CrossRef]
  10. Irmak, H.; Akar, G.B.; Yuksel, S.E. A MAP-Based Approach for Hyperspectral Imagery Super-Resolution. IEEE Trans. Image Process. 2018, 27, 2942–2951. [Google Scholar] [CrossRef]
  11. Irmak, H.; Akar, G.B.; Yuksel, S.E.; Aytaylan, H. Super-Resolution Reconstruction of Hyperspectral Images via an Improved MAP-Based Approach. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 7244–7247. [Google Scholar] [CrossRef]
  12. Akgun, T.; Altunbasak, Y.; Mersereau, R.M. Super-Resolution Reconstruction of Hyperspectral Images. IEEE Trans. Image Process. 2005, 14, 1860–1875. [Google Scholar] [CrossRef]
  13. Zhang, H.; Zhang, L.; Shen, H. A Super-Resolution Reconstruction Algorithm for Hyperspectral Images. Signal Process. 2012, 92, 2082–2096. [Google Scholar] [CrossRef]
  14. Huang, H.; Christodoulou, A.G.; Sun, W. Super-Resolution Hyperspectral Imaging with Unknown Blurring by Low-Rank and Group-Sparse Modeling. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 2155–2159. [Google Scholar] [CrossRef]
  15. Xu, X.; Tong, X.; Li, J.; Xie, H.; Zhong, Y.; Zhang, L.; Song, D. Hyperspectral Image Super Resolution Reconstruction with a Joint Spectral-Spatial Sub-Pixel Mapping Model. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6129–6132. [Google Scholar] [CrossRef]
  16. He, S.; Zhou, H.; Wang, Y.; Cao, W.; Han, Z. Super-Resolution Reconstruction of Hyperspectral Images via Low Rank Tensor Modeling and Total Variation Regularization. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6962–6965. [Google Scholar] [CrossRef]
  17. Wang, L.; Bi, T.; Shi, Y. A Frequency-Separated 3D-CNN for Hyperspectral Image Super-Resolution. IEEE Access 2020, 8, 86367–86379. [Google Scholar] [CrossRef]
  18. Ma, X.; Hong, Y.; Song, Y.; Chen, Y. A Super-Resolution Convolutional-Neural-Network-Based Approach for Subpixel Mapping of Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4930–4939. [Google Scholar] [CrossRef]
  19. Liu, W.; Lee, J. An Efficient Residual Learning Neural Network for Hyperspectral Image Superresolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1240–1253. [Google Scholar] [CrossRef]
  20. Wang, C.; Liu, Y.; Bai, X.; Tang, W.; Lei, P.; Zhou, J. Deep Residual Convolutional Neural Network for Hyperspectral Image Super-Resolution. In Image and Graphics, Proceedings of the 9th International Conference, ICIG 2017, Shanghai, China, 13–15 September 2017; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2017; pp. 370–380. [Google Scholar] [CrossRef]
  21. Zhu, Z.; Hou, J.; Chen, J.; Zeng, H.; Zhou, J. Hyperspectral Image Super-Resolution via Deep Progressive Zero-Centric Residual Learning. IEEE Trans. Image Process. 2021, 30, 1423–1438. [Google Scholar] [CrossRef] [PubMed]
  22. Wang, B.; Zhang, S.; Feng, Y.; Mei, S.; Jia, S.; Du, Q. Hyperspectral Imagery Spatial Super-Resolution Using Generative Adversarial Network. IEEE Trans. Comput. Imaging 2021, 7, 948–960. [Google Scholar] [CrossRef]
  23. Wang, J.; Zhu, X.; Jing, L.; Tang, Y.; Li, H.; Xiao, Z.; Ding, H. HyperGAN: A Hyperspectral Image Fusion Approach Based on Generative Adversarial Networks. Remote Sens. 2024, 16, 4389. [Google Scholar] [CrossRef]
  24. Hu, J.; Liu, Y.; Kang, X.; Fan, S. Multilevel Progressive Network with Nonlocal Channel Attention for Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5543714. [Google Scholar] [CrossRef]
  25. Hu, J.-F.; Huang, T.-Z.; Deng, L.-J.; Jiang, T.-X.; Vivone, G.; Chanussot, J. Hyperspectral Image Super-Resolution via Deep Spatiospectral Attention Convolutional Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 7251–7265. [Google Scholar] [CrossRef]
  26. Zhang, M.; Zhang, C.; Zhang, Q.; Guo, J.; Gao, X.; Zhang, J. ESSAformer: Efficient Transformer for Hyperspectral Image Super-Resolution. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023; pp. 23016–23027. [Google Scholar] [CrossRef]
  27. Liu, Y.; Hu, J.; Kang, X.; Luo, J.; Fan, S. Interactformer: Interactive Transformer and CNN for Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5531715. [Google Scholar] [CrossRef]
  28. Gao, L.; Li, J.; Zheng, K.; Jia, X. Enhanced Autoencoders with Attention-Embedded Degradation Learning for Unsupervised Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5509417. [Google Scholar] [CrossRef]
  29. Fang, Y.; Liu, Y.; Chi, C.-Y.; Long, Z.; Zhu, C. CS2DIPs: Unsupervised HSI Super-Resolution Using Coupled Spatial and Spectral DIPs. IEEE Trans. Image Process. 2024, 33, 3090–3101. [Google Scholar] [CrossRef] [PubMed]
  30. Jia, S.; Zhu, S.; Wang, Z.; Xu, M.; Wang, W.; Guo, Y. Diffused Convolutional Neural Network for Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5504615. [Google Scholar] [CrossRef]
  31. Li, S.; Tian, Y.; Wang, C.; Wu, H.; Zheng, S. Hyperspectral Image Super-Resolution Network Based on Cross-Scale Nonlocal Attention. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5509615. [Google Scholar] [CrossRef]
  32. Bieniarz, J.; Cerra, D.; Avbelj, J.; Reinartz, P.; Müller, R. Hyperspectral Image Resolution Enhancement Based On Spectral Unmixing and Information Fusion. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXVIII–4/W19, 33–37. [Google Scholar] [CrossRef]
  33. Li, L.; He, H.; Chen, N.; Kang, X.; Wang, B. SLRCNN: Integrating Sparse and Low-Rank with a CNN Denoiser for Hyperspectral and Multispectral Image Fusion. Int. J. Appl. Earth Obs. Geoinf. 2024, 134, 104227. [Google Scholar] [CrossRef]
  34. Liu, X.; Liu, Q.; Wang, Y. Remote Sensing Image Fusion Based on Two-Stream Fusion Network. Inf. Fusion 2020, 55, 1–15. [Google Scholar] [CrossRef]
  35. Xiao, J.; Li, J.; Yuan, Q.; Jiang, M.; Zhang, L. Physics-Based GAN With Iterative Refinement Unit for Hyperspectral and Multispectral Image Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6827–6841. [Google Scholar] [CrossRef]
  36. Booysen, R.; Jackisch, R.; Lorenz, S.; Zimmermann, R.; Kirsch, M.; Nex, P.A.; Gloaguen, R. Detection of REEs with lightweight UAV-based hyperspectral imaging. Sci. Rep. 2020, 10, 17450. [Google Scholar] [CrossRef]
  37. Thiele, S.T.; Lorenz, S.; Kirsch, M.; Acosta, I.C.C.; Tusa, L.; Herrmann, E.; Möckel, R.; Gloaguen, R. Multi-scale, multi-sensor data integration for automated 3-D geological mapping. Ore Geol. Rev. 2021, 136, 104252. [Google Scholar] [CrossRef]
  38. Smithies, R.H.; Marsh, J.S. The Marinkas Quellen Carbonatite Complex, southern Namibia; carbonatite magmatism with an uncontaminated depleted mantle signature in a continental setting. Chem. Geol. 1998, 148, 201–212. [Google Scholar] [CrossRef]
  39. Salkield, L.U. A Technical History of the Rio Tinto Mines: Some Notes on Exploitation from Pre-Phoenician Times to the 1950s; Cahalan, M.J., Ed.; Springer: Dordrecht, The Netherlands, 1987. [Google Scholar] [CrossRef]
  40. Hu, J.; Liu, R.; Hong, D.; Camero, A.; Yao, J.; Schneider, M.; Kurz, F.; Segl, K.; Zhu, X.X. MDAS: A New Multimodal Benchmark Dataset for Remote Sensing. Earth Syst. Sci. Data 2023, 15, 113–131. [Google Scholar] [CrossRef]
  41. Mairal, J.; Ponce, J.; Sapiro, G.; Zisserman, A.; Bach, F. Supervised Dictionary Learning. In Advances in Neural Information Processing Systems; Koller, D., Schuurmans, D., Bengio, Y., Bottou, L., Eds.; MIT Press: Cambridge, MA, USA, 2008; Volume 21. [Google Scholar]
  42. Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
  43. Zhang, X.; Huang, W.; Wang, Q.; Li, X. SSR-NET: Spatial–Spectral Reconstruction Network for Hyperspectral and Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5953–5965. [Google Scholar] [CrossRef]
  44. Chakraborty, R.; Thiele, S.; Naik, P.; Gloaguen, R. Evaluation of Spectral and Spatial Reconstruction in Resolution-Enhanced Hyperspectral Data for Effective Mineral Mapping. In Proceedings of the IGARSS 2025—2025 IEEE International Geoscience and Remote Sensing Symposium, Brisbane, Australia, 3–8 August 2025. [Google Scholar] [CrossRef]
  45. Liu, Z.; Wang, W.; Ma, Q.; Liu, X.; Jiang, J. Rethinking 3D-CNN in Hyperspectral Image Super-Resolution. Remote Sens. 2023, 15, 2574. [Google Scholar] [CrossRef]
  46. Fu, Y.; Liang, Z.; You, S. Bidirectional 3D Quasi-Recurrent Neural Network for Hyperspectral Image Super-Resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2674–2688. [Google Scholar] [CrossRef]
  47. Wu, H.; Wang, C.; Lu, C.; Zhan, T. HCT: A Hybrid CNN and Transformer Network for Hyperspectral Image Super-Resolution. Multimed. Syst. 2024, 30, 185. [Google Scholar] [CrossRef]
  48. Fotiadou, K.; Tsagkatakis, G.; Tsakalides, P. Spectral Super Resolution of Hyperspectral Images via Coupled Dictionary Learning. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2777–2797. [Google Scholar] [CrossRef]
  49. Li, J.; Yuan, Q.; Shen, H.; Meng, X.; Zhang, L. Hyperspectral Image Super-Resolution by Spectral Mixture Analysis and Spatial–Spectral Group Sparsity. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1250–1254. [Google Scholar] [CrossRef]
  50. PV, A.; Krishna Mohan, B.; Porwal, A. Spatial-Spectral Feature Based Approach towards Convolutional Sparse Coding of Hyperspectral Images. Comput. Vis. Image Underst. 2019, 188, 102797. [Google Scholar] [CrossRef]
  51. Chiang, C.-K.; Su, T.-F.; Yen, C.; Lai, S.-H. Multi-Attributed Dictionary Learning for Sparse Coding. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1137–1144. [Google Scholar] [CrossRef]
  52. Planet Team. Planet Application Program Interface: In Space for Life on Earth. San Francisco, CA, USA. 2025. Available online: https://api.planet.com (accessed on 24 January 2025).
Remotesensing 17 01878 g001
Figure 1. A sparse taxonomy of hyperspectral resolution enhancement methods.
Figure 1. A sparse taxonomy of hyperspectral resolution enhancement methods.
Remotesensing 17 01878 g001
Remotesensing 17 01878 g002
Figure 2. Map showing the location and extent of the study areas.
Figure 2. Map showing the location and extent of the study areas.
Remotesensing 17 01878 g002
Remotesensing 17 01878 g003
Figure 3. Implementation flowchart of the proposed enhancement method.
Figure 3. Implementation flowchart of the proposed enhancement method.
Remotesensing 17 01878 g003
Remotesensing 17 01878 g004
Figure 4. Metric maps of SAM, SSIM, and RMSE for all three study sites.
Figure 4. Metric maps of SAM, SSIM, and RMSE for all three study sites.
Remotesensing 17 01878 g004
Remotesensing 17 01878 g005
Figure 5. Resolution enhanced 10 m FCC (995, 735, 475 nm) patches from benchmark data.
Figure 5. Resolution enhanced 10 m FCC (995, 735, 475 nm) patches from benchmark data.
Remotesensing 17 01878 g005
Remotesensing 17 01878 g006
Figure 6. Resolution enhanced FCC (2045, 1995, and 1945 nm) patches at 10 m and 3 m from Marinkas’ data.
Figure 6. Resolution enhanced FCC (2045, 1995, and 1945 nm) patches at 10 m and 3 m from Marinkas’ data.
Remotesensing 17 01878 g006
Remotesensing 17 01878 g007
Figure 7. (a) Yellow transported mine waste with detailed boundaries in 10 m and the 3 m enhanced HSI with a consistent broad Fe2+ absorption feature between 800 nm and 1200 nm. (b) RGB composite of Kaolinite index, NDVI, and Fe3+ index at original 30 m HSI with 10 m and 3 m enhanced HSI for the same extent as shown in subfigure (a).
Figure 7. (a) Yellow transported mine waste with detailed boundaries in 10 m and the 3 m enhanced HSI with a consistent broad Fe2+ absorption feature between 800 nm and 1200 nm. (b) RGB composite of Kaolinite index, NDVI, and Fe3+ index at original 30 m HSI with 10 m and 3 m enhanced HSI for the same extent as shown in subfigure (a).
Remotesensing 17 01878 g007
Remotesensing 17 01878 g008
Figure 8. Patches from the Marinkas test site displaying the original (30 m) and enhanced HSI (10 m and 3 m). Yellow boxes indicate significant geological feature enhancements. Subfigure (a) shows a True color compositie of the area and Subfigure (b) shows a minimum wavelength map of the area.
Figure 8. Patches from the Marinkas test site displaying the original (30 m) and enhanced HSI (10 m and 3 m). Yellow boxes indicate significant geological feature enhancements. Subfigure (a) shows a True color compositie of the area and Subfigure (b) shows a minimum wavelength map of the area.
Remotesensing 17 01878 g008
Table 1. Specifications of HSI and MSI datasets used for the experiments.
Table 1. Specifications of HSI and MSI datasets used for the experiments.
DatasetsArea of AcquisitionSpatial Resolution (m)Spectral Range (nm)No. of Spectral Bands
HySpex (airborne HSI)Benchmark, Rio-Tinto2416–2498416
HyMap (airborne HSI)Marinkas5450–2480125
EnMAP (satellite HSI)All sites *30418–2445224
Sentinel-2 (satellite MSI)All sites10442–220210
PlanetScope (satellite MSI)Marinkas, Rio-Tinto3431–8858
* Benchmark site consists of simulated EnMAP data with identical EnMAP specifications captured with an airborne sensor.
Table 2. Assessment metrics for spectral and spatial assessment of enhanced HSI.
Table 2. Assessment metrics for spectral and spatial assessment of enhanced HSI.
MethodsDatasetPSNR ↑SAM ↓ERGAS ↓Q2n ↑
BicubicBenchmark27.57817.83888.02380.5161
Marinkas18.686616.21789.06650.4973
Rio-Tinto27.616219.707012.04460.4168
Average24.626914.58789.71160.4767
c-HysureBenchmark16.540361.151328.30780.3218
Marinkas9.980416.105318.50970.4786
Rio-Tinto19.307374.251327.31840.2615
Average15.276050.502624.71190.3539
CNMFBenchmark28.45357.37297.34670.6561
Marinkas17.439727.808327.80830.2932
Rio-Tinto26.810523.111721.77750.1504
Average24.234519.430918.97750.3665
ResTFNetBenchmark16.369018.949927.87680.5499
Marinkas8.958212.333125.58770.3832
Rio-Tinto23.927318.352915.68760.3935
Average16.418116.545323.05070.4422
SSR-NETBenchmark16.368921.829227.87700.3946
Marinkas8.934513.576625.44530.3681
Rio-Tinto25.254022.186914.88890.4647
Average16.852419.197422.73700.4091
P2SR (proposed)Benchmark28.75817.17876.99320.6670
Marinkas19.330212.10168.00170.5151
Rio-Tinto27.541818.082511.79360.3649
Average25.210012.45428.92950.5156
Best results are shown in bold.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Naik, P.; Chakraborty, R.; Thiele, S.; Gloaguen, R. Scalable Hyperspectral Enhancement via Patch-Wise Sparse Residual Learning: Insights from Super-Resolved EnMAP Data. Remote Sens. 2025, 17, 1878. https://doi.org/10.3390/rs17111878

AMA Style

Naik P, Chakraborty R, Thiele S, Gloaguen R. Scalable Hyperspectral Enhancement via Patch-Wise Sparse Residual Learning: Insights from Super-Resolved EnMAP Data. Remote Sensing. 2025; 17(11):1878. https://doi.org/10.3390/rs17111878

Chicago/Turabian Style

Naik, Parth, Rupsa Chakraborty, Sam Thiele, and Richard Gloaguen. 2025. "Scalable Hyperspectral Enhancement via Patch-Wise Sparse Residual Learning: Insights from Super-Resolved EnMAP Data" Remote Sensing 17, no. 11: 1878. https://doi.org/10.3390/rs17111878

APA Style

Naik, P., Chakraborty, R., Thiele, S., & Gloaguen, R. (2025). Scalable Hyperspectral Enhancement via Patch-Wise Sparse Residual Learning: Insights from Super-Resolved EnMAP Data. Remote Sensing, 17(11), 1878. https://doi.org/10.3390/rs17111878

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop