Meta-Features Extracted from Use of kNN Regressor to Improve Sugarcane Crop Yield Prediction †
Abstract
1. Introduction
2. Materials and Methods
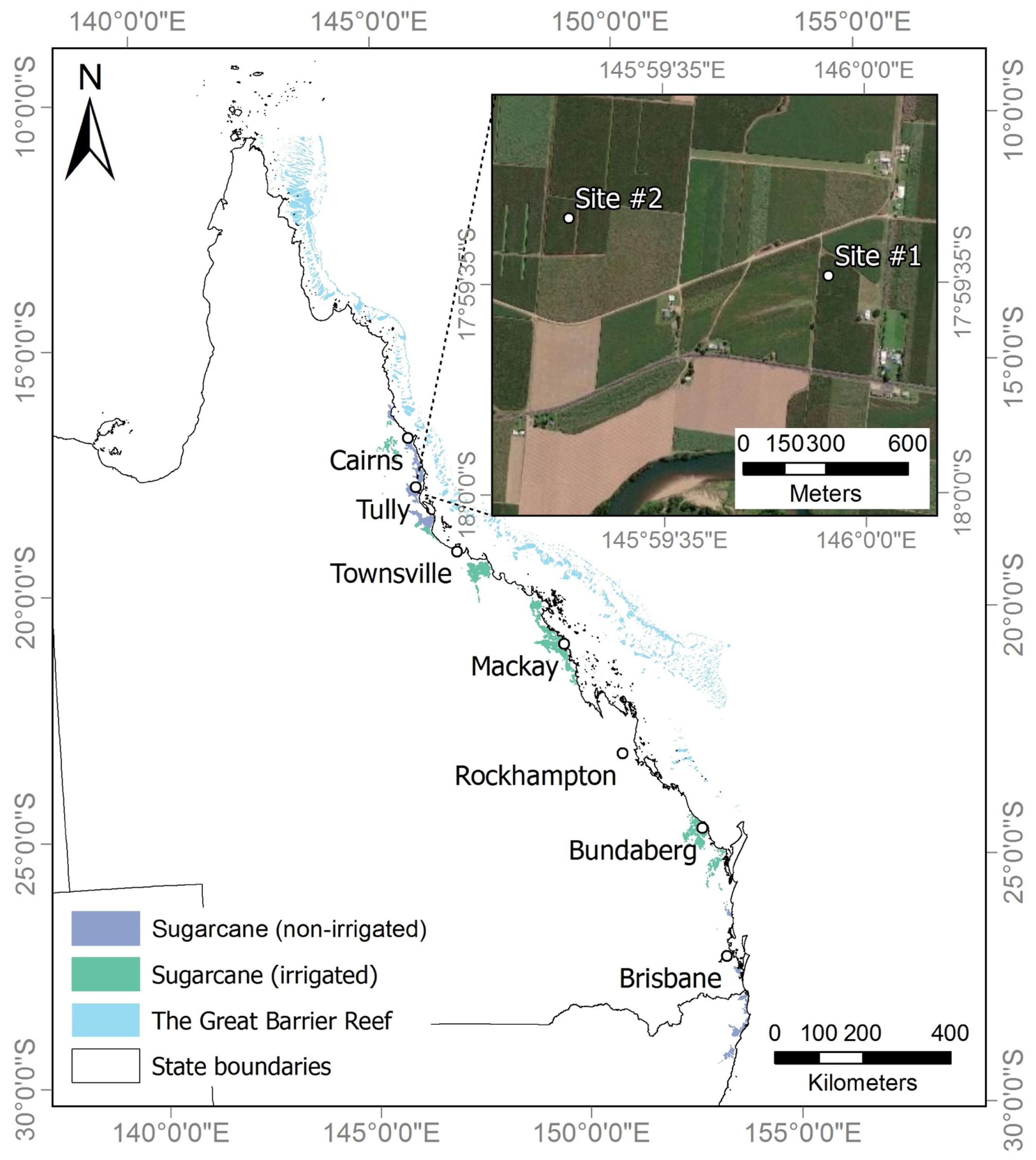
2.1. Study Area
2.2. Dataset
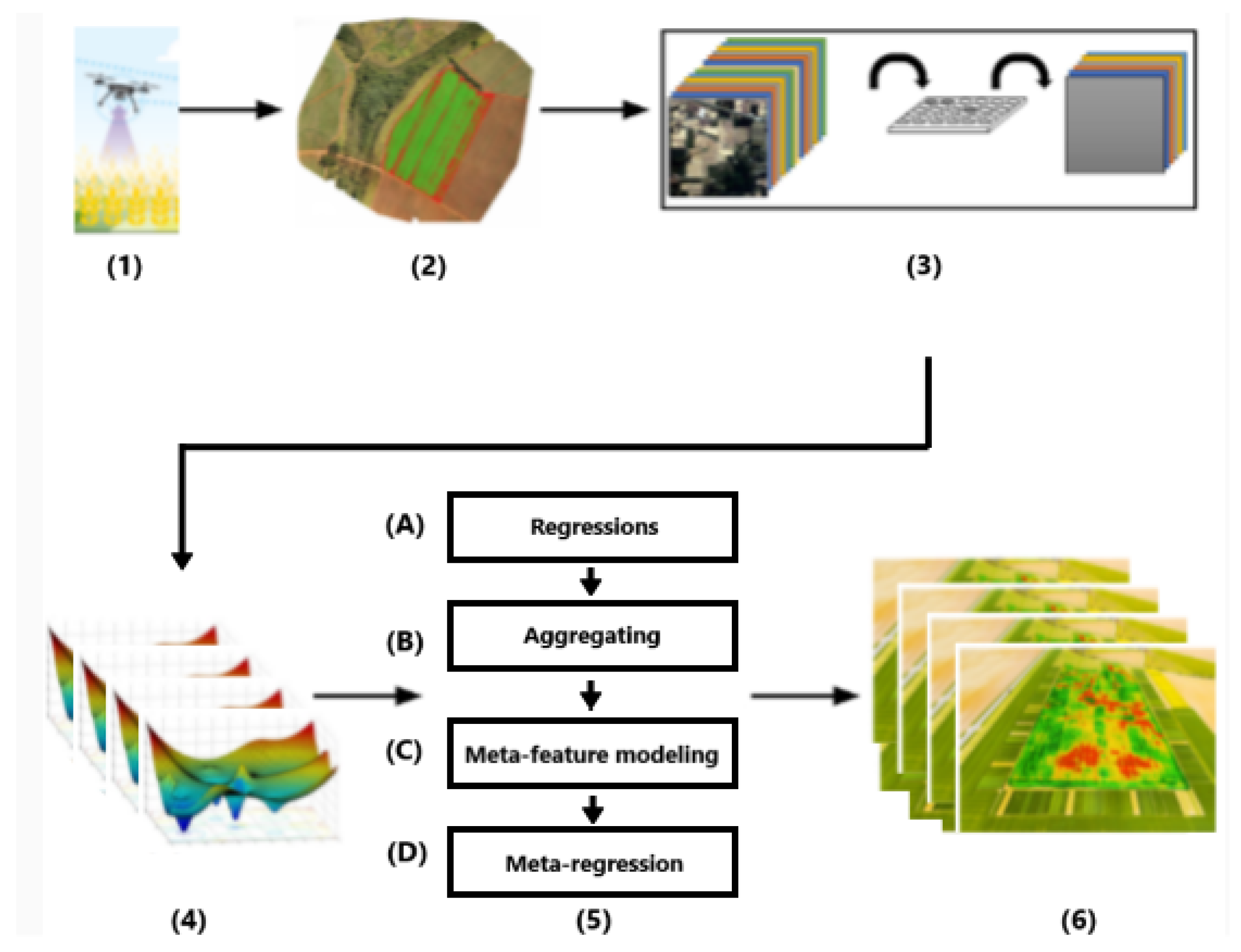
2.3. Proposed Approach
- SVR: a generalization of Support Vector Machine (SVM) obtained by introducing a -insensitive region around the function, called a tube. This tube reformulates the optimization problem to find the tube that best approximates the continuous-valued function while balancing model complexity and prediction error.
- RF regressor: a meta-estimator that fits some decision trees on multiple subsamples of the dataset and uses the average to improve predictive accuracy and control overfitting.
- GB regressor: estimator that builds an additive model progressively, allowing the optimization of arbitrary differentiable loss functions. At each stage, a regression tree is fitted on the negative gradient of the given loss function.
- AB regressor: is a meta-estimator that starts by fitting a regressor on the original dataset and then fits additional copies of the regressor on the same dataset, but where the weights of the instances are adjusted according to the error of the current prediction.
2.3.1. Crop Yield Prediction Workflow
2.3.2. Overview of Proposed Meta-Feature Approach
- is the meta-feature vector;
- d is the number of regressors;
- is the prediction of the i-th regressor for the input sample .
2.3.3. Meta-Feature Modeling
2.3.4. Meta-Regressor by kNN
2.3.5. Grid Search
2.4. Experimental Evaluation
2.4.1. Baseline Methods
2.4.2. Experimental Protocol
- R2: R-squared value for a linear regression (described in Equation (2));
- n: sample size used in regression;
- p: number of predictors used in the regression, including the constant.
- : observed value;
- : predicted value from the model;
- : mean of the observed values;
- n: total number of observations.
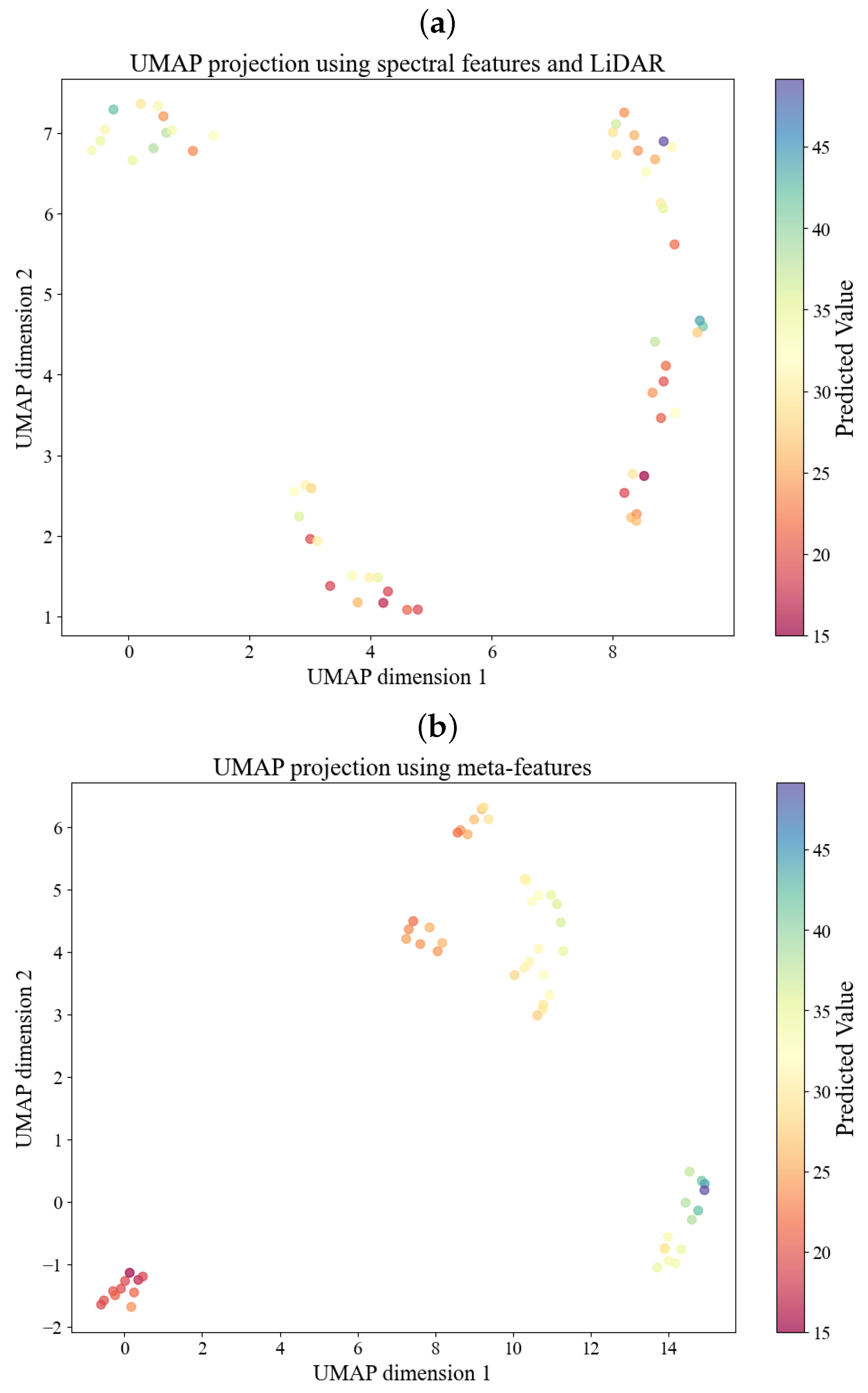
3. Results
3.1. Prelimenary Results
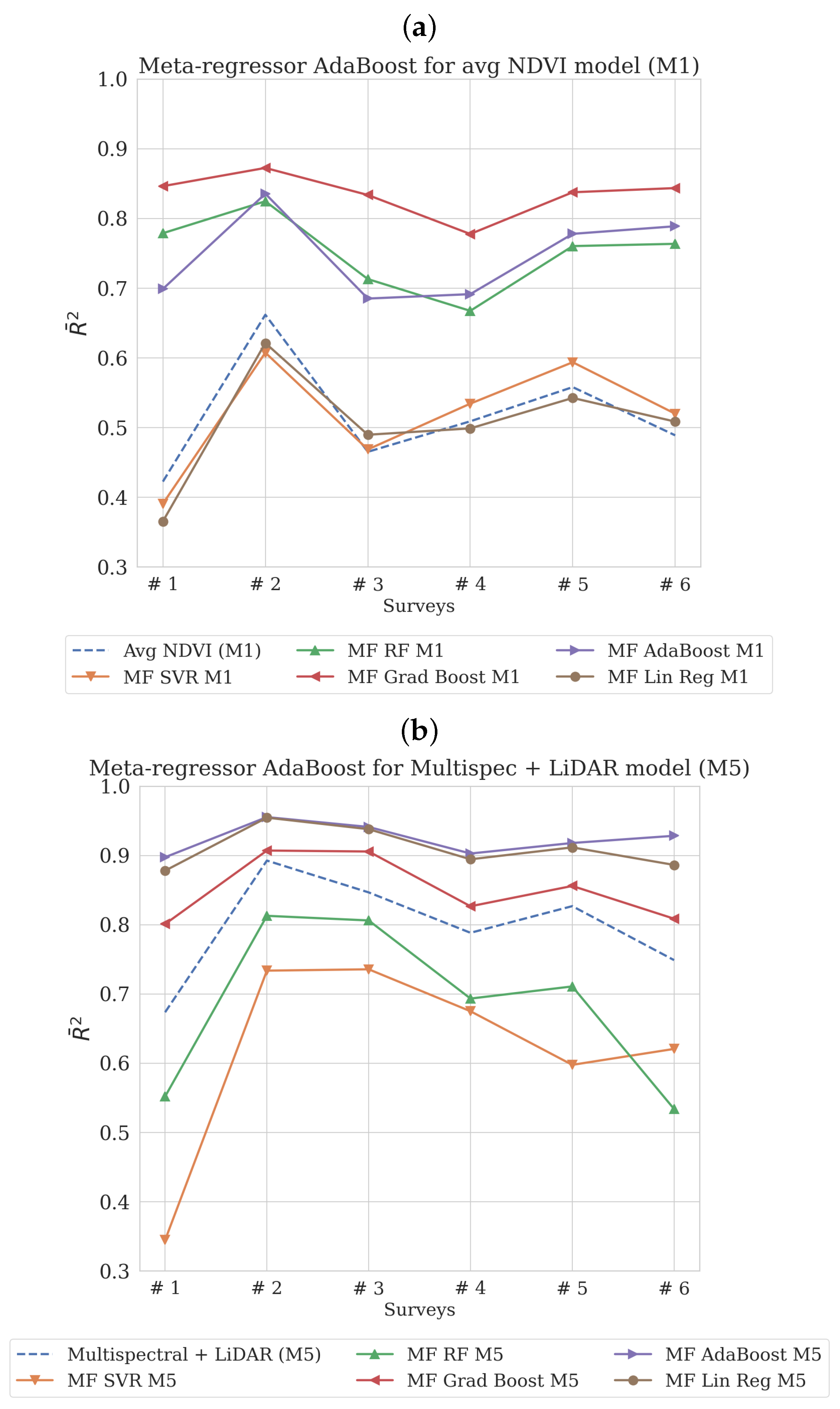
3.2. Results by Meta-Features Produced from kNN Meta-Regressor
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Klompenburg, T.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Amarasingam, N.; Salgadoe, A.S.A.; Powell, K.; Gonzalez, L.F.; Natarajan, S. A review of UAV platforms, sensors, and applications for monitoring of sugarcane crops. Remote Sens. Appl. Soc. Environ. 2022, 26, 100712. [Google Scholar] [CrossRef]
- Nogueira, E.A.; Felix, J.P.; Fonseca, A.U.; Vieira, G.; Ferreira, J.C.; Fernandes, D.S.; Oliveira, B.M.; Soares, F. Deep Learning for Super Resolution of Sugarcane Crop Line Imagery from Unmanned Aerial Vehicles. In Advances in Visual Computing, Proceedings of the 18th International Symposium, ISVC 2023, Lake Tahoe, NV, USA, 16–18 October 2023; Springer: Cham, Switzerland, 2023; pp. 597–609. [Google Scholar] [CrossRef]
- Ribeiro, J.B.; da Silva, R.R.; Dias, J.D.; Escarpinati, M.C.; Backes, A.R. Automated detection of sugarcane crop lines from UAV images using deep learning. Inf. Process. Agric. 2024, 11, 385–396. [Google Scholar] [CrossRef]
- De França e Silva, N.R.; Chaves, M.E.D.; Luciano, A.C.d.S.; Sanches, I.D.; de Almeida, C.M.; Adami, M. Sugarcane yield estimation using satellite remote sensing data in empirical or mechanistic modeling: A systematic review. Remote Sens. 2024, 16, 863. [Google Scholar] [CrossRef]
- Arakawa, K.; Shimizu, R.; Kikuchi, S.; Capi, G. Sugar Cane Yield Prediction Using Drone Data Processed by LSTM Algorithm. In Proceedings of the 2025 3rd International Conference on Mechatronics, Control and Robotics (ICMCR), Singapore, 14–16 February 2025; IEEE: Piscataway, NJ, USA, 2025; pp. 75–79. [Google Scholar] [CrossRef]
- Afraei, S.; Shahriar, K.; Madani, S.H. Statistical assessment of rock burst potential and contributions of considered predictor variables in the task. Tunn. Undergr. Space Technol. 2018, 72, 250–271. [Google Scholar] [CrossRef]
- Bessa, A.D. Explaining and Identifying Data to Support Data-Driven Analyses. Ph.D Thesis, Tandon School of Engineering, New York University, New York, NY, USA, 2020. Available online: https://www.proquest.com/openview/d114405d255b4cf22737514bb01ca748/1?cbl=18750&diss=y&pq-origsite=gscholar (accessed on 2 March 2025).
- Akbarian, S.; Xu, C.; Wang, W.; Ginns, S.; Lim, S. An investigation on the best-fit models for sugarcane biomass estimation by linear mixed-effect modelling on unmanned aerial vehicle-based multispectral images: A case study of Australia. Inf. Process. Agric. 2023, 10.3, 361–376. [Google Scholar] [CrossRef]
- Sarkar, S.; Dey, A.; Pradhan, R.; Sarkar, U.M.; Chatterjee, C.; Mondal, A.; Mitra, P. Crop Yield Prediction Using Multimodal Meta-Transformer and Temporal Graph Neural Networks. IEEE Trans. Agrifood Electron. 2024, 2, 545–553. [Google Scholar] [CrossRef]
- Bansal, Y.; Lillis, D.; Kechadi, M.T. A neural meta model for predicting winter wheat crop yield. Mach. Learn. 2024, 113, 3771–3788. [Google Scholar] [CrossRef]
- Ermolieva, T.; Havlik, P.; Lessa-Derci-Augustynczik, A.; Boere, E.; Frank, S.; Kahil, T.; Wang, G.; Balkovic, J.; Skalsky, R.; Folberth, C.; et al. A novel robust meta-model framework for predicting crop yield probability distributions using multisource data. Cybern. Syst. Anal. 2023, 59, 844–858. [Google Scholar] [CrossRef]
- Tunio, M.H.; Li, J.P.; Zeng, X.; Akhtar, F.; Shah, S.A.; Ahmed, A.; Yang, Y.; Heyat, M.B.B. Meta-knowledge guided Bayesian optimization framework for robust crop yield estimation. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 101895. [Google Scholar] [CrossRef]
- Anbananthen, K.S.M.; Subbiah, S.; Chelliah, D.; Sivakumar, P.; Somasundaram, V.; Velshankar, K.H.; Khan, M.A. An intelligent decision support system for crop yield prediction using hybrid machine learning algorithms. F1000Research 2021, 10, 1143. [Google Scholar] [CrossRef] [PubMed]
- Joshaghani, M.; Barak, S.; Asadi, A.; Mirafzali, E. Retail Time Series Forecasting Using An Automated Deep Meta-Learning Framework. SSRN Electron. J. 2023. [Google Scholar] [CrossRef]
- Shendryk, Y.; Sofonia, J.; Garrard, R.; Rist, Y.; Skocaj, D.; Thorburn, P. Fine-scale prediction of biomass and leaf nitrogen content in sugarcane using UAV LiDAR and multispectral imaging. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102177. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. An Introduction to Statistical Learning; Springer: Cham, Switzerland, 2023; Volume 112. [Google Scholar] [CrossRef]
- Barbosa, L.A.F.; Pedronette, D.C.G.; Guilherme, I.R. A Meta-Feature Model for Exploiting Different Regressors to Estimate Sugarcane Crop Yield. In Proceedings of the IGARSS 2023–2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 2030–2033. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 10–14 December 1973; NASA/Goddard Space Flight Center: Greenbelt, MD, USA, 1973; pp. 309–317. Available online: https://ntrs.nasa.gov/citations/19740022614 (accessed on 2 March 2025).
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a Green Channel in Remote Sensing of Global Vegetation From EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Evett, I.; Jackson, G.; Lambert, J.; McCrossan, S. The impact of the principles of evidence interpretation on the structure and content of statements. Sci. Justice 2000, 40, 233–239. [Google Scholar] [CrossRef] [PubMed]
- Steele, M.R.; Gitelson, A.A.; Rundquist, D.C.; Merzlyak, M.N. Nondestructive estimation of anthocyanin content in grapevine leaves. Am. J. Enol. Vitic. 2009, 60, 87–92. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of Soil-Adjusted Vegetation Indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Barnes, E.; Clarke, T.; Richards, S.; Colaizzi, P.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T.; et al. Coincident detection of crop water stress, nitrogen status and canopy density using ground based multispectral data. In Proceedings of the Fifth International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000; Volume 1619. Available online: https://www.tucson.ars.ag.gov/unit/Publications/PDFfiles/1356.pdf (accessed on 2 March 2025).
- Hess, K.W.; Schmalz, R.A.; Zervas, C.E.; Collier, W. Tidal Constituent and Residual Interpolation (TCARI): A New Method for the Tidal Correction of Bathymetric Data. 1999. Available online: https://repository.library.noaa.gov/view/noaa/1689/noaa_DS1_1689.pdf (accessed on 2 March 2025).
- Hunt, E.R., Jr.; Daughtry, C.; Eitel, J.U.; Long, D.S. Remote sensing leaf chlorophyll content using a visible band index. Agron. J. 2011, 103, 1090–1099. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Stark, R.; Grits, U.; Rundquist, D.; Kaufman, Y.; Derry, D. Vegetation and soil lines in visible spectral space: A concept and technique for remote estimation of vegetation fraction. Int. J. Remote Sens. 2002, 23, 2537–2562. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. Available online: https://www.jmlr.org/papers/volume12/pedregosa11a/pedregosa11a.pdf?source=post_page (accessed on 2 March 2025).
- Barbosa, L.A.F.; Pedronette, D.C.G.; Guilherme, I.R. Estudo comparativo entre diferentes regressores para estimar produtividade de cana-de-açúcar. SBSR-Simpósio Bras. Sensoriamento Remoto 2023, 20, 1020–1023. Available online: http://marte2.sid.inpe.br/col/sid.inpe.br/marte2/2023/04.30.20.56/doc/155771.pdf (accessed on 2 March 2025).
- Cosenza, D.N.; Korhonen, L.; Maltamo, M.; Packalen, P.; Strunk, J.L.; Næsset, E.; Gobakken, T.; Soares, P.; Tomé, M. Comparison of linear regression, k-nearest neighbour and random forest methods in airborne laser-scanning-based prediction of growing stock. For. Int. J. For. Res. 2020, 94, 311–323. [Google Scholar] [CrossRef]
- Malhotra, K.; Mishra, D.; Tumrate, C.S. Prediction of concrete compressive strength employing machine learning techniques. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- Venkatesh, T.; Livingston, J.; Rajkumar, S. A Predictive Model for Marine Debris Prediction (A Comparative Case Study). In Proceedings of the 2024 Second International Conference on Emerging Trends in Information Technology and Engineering (ICETITE), Vellore, India, 22–23 February 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Ippolito, P.P. Hyperparameter Tuning: The Art of Fine-Tuning Machine and Deep Learning Models to Improve Metric Results. In Applied Data Science in Tourism: Interdisciplinary Approaches, Methodologies, and Applications; Springer: Berlin/Heidelberg, Germany, 2022; pp. 231–251. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Shen, W. A review of ensemble learning algorithms used in remote sensing applications. Appl. Sci. 2022, 12, 8654. [Google Scholar] [CrossRef]
- Tahaseen, M.; Moparthi, N.R. An Assessment of the Machine Learning Algorithms Used in Agriculture. In Proceedings of the 2021 5th International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 2–4 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1579–1584. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar] [CrossRef]
- De Antonio, A.L.T.; Pedronette, D.C.G. Manifold Learning for Brain Tumor MRI Image Retrieval and Classification. In Proceedings of the 2023 IEEE 23rd International Conference on Bioinformatics and Bioengineering (BIBE), Dayton, OH, USA, 4–6 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 36–42. [Google Scholar] [CrossRef]
- Gonçalves, F.M.F.; Pedronette, D.C.G.; da Silva Torres, R. Regression by re-ranking. Pattern Recognit. 2023, 140, 109577. [Google Scholar] [CrossRef]





| Feature | Explanation |
|---|---|
| max | Maximum value of all pixels within each plot |
| min | Minimum value of all pixels within each plot |
| avg | Average value of all pixels within each plot |
| std | Standard deviation of all pixels within each plot |
| p25 | 25th percentile of all pixels within each plot |
| p50 | 50th percentile of all pixels within each plot |
| p75 | 75th percentile of all pixels within each plot |
| Name | Equation |
|---|---|
| Normalized Difference Vegetation Index (NDVI) [19] | (NIR − R)/(NIR + R) |
| Normalized Difference Red Edge Index (NDRE) [20] | (NIR − RE)/(NIR + RE) |
| Green NDVI (GNDVI) [21] | (NIR − G)/(NIR + G) |
| Enhanced Vegetation Index (EVI) [22] | 2.5(NIR − R)/(NIR + R) + 6R − 7.5B + 1 |
| Modified Anthocyanin Content Index (MACI) [23] | NIR/G |
| Optimized Soil Adjusted Vegetation Index (OSAVI) [24] | (1 + 0.16) (NIR − R)/(NIR + R + 0.16) |
| Simplified Canopy Chlorophyll Content Index (SCCCI) [25] | NDRE/NDVI |
| Transformed Chlorophyll Absorption and Reflectance Index (TCARI) [26] | 3[RE − R − 0.2(RE/G)(RE/R)]/OSAVI |
| Triangular Greenness Index (TGI) [27] | −0.5[(668 − 475)(R − G) − (668 − 560)(R − B)] |
| Visible Atmospherically Resistant Index (VARI) [28] | (G × R)/(G + R − B) |
| Feature | Explanation |
|---|---|
| max | maximum height |
| avg | average height |
| qav | quadratic average height |
| std | standard deviation of height |
| ske | height skewness |
| kur | height kurtosis |
| p05 to p95 | 5th to 95th height percentiles (increments of 5 percentiles) |
| b05 to b95 | 5th to 95th bicentiles a (increments of 5 percentiles) |
| d00 | number of points between 0 (i.e., ground) and 0.01 m divided by the total number of points |
| d01 b | the number of points between 0.01 and 0.5 m divided by the total number of points |
| d02 b | the number of points between 0.5 and 1 m divided by the total number of points |
| d03 b | the number of points between 1 and 10 m divided by the total number of points |
| Model | Features |
|---|---|
| M1 | average NDVI (avg NDVI) |
| M2 | maximum NDVI (max NDVI) |
| M3 | Multispectral principal components ( MultispecPCs) |
| M4 | LiDAR principal components (LiDARPCs) |
| M5 | Multispectral + LiDAR principal components (MultispecPCs + LiDARPCs) |
| MF SVR M1…M5 | Meta-feature extracted by SVR on M1…M5 |
| MF RF M1…M5 | Meta-feature extracted by RF on M1…M5 |
| MF Grad Boost M1…M5 | Meta-feature extracted by Gradient Boosting on M1…M5 |
| MF AdaBoost M1…M5 | Meta-feature extracted by AdaBoost on M1…M5 |
| MF Linear Regression M1…M5 | Meta-feature extracted by Linear Regression on M1…M5 |
| MF kNN M1…M5 | Meta-feature extracted by kNN on M1…M5 |
| Regressor | Hyperparameters |
|---|---|
| SVR | kernel = ’rbf’, C = 10, coef0 = 0.01, degree = 3, gamma = ’scale’ |
| Random Forest | n_estimators = 200, max_features = ’sqrt’, max_depth = 3, random_state = 18 |
| Gradient boosting | learning_rate = 0.01, max_depth = 4, n_estimators = 100, subsample = 0.5 |
| AdaBoost | learning_rate = 0.1, loss = ’exponential’, n_estimators = 50 |
| Regressors | avgNDVI | maxNDVI | LiDARPCs | MultispecPCs | MultispecPCs + LiDARPCs |
|---|---|---|---|---|---|
| LR | 0.17 | 0.18 | 0.40 | 0.42 | 0.39 |
| SVR | 0.52 | 0.48 | 0.63 | 0.64 | 0.39 |
| Random Forest | 0.52 | 0.48 | 0.63 | 0.62 | 0.30 |
| Gradient Boosting | 0.51 | 0.49 | 0.49 | 0.54 | 0.00 |
| Ada Boost | 0.51 | 0.50 | 0.64 | 0.65 | 0.50 |
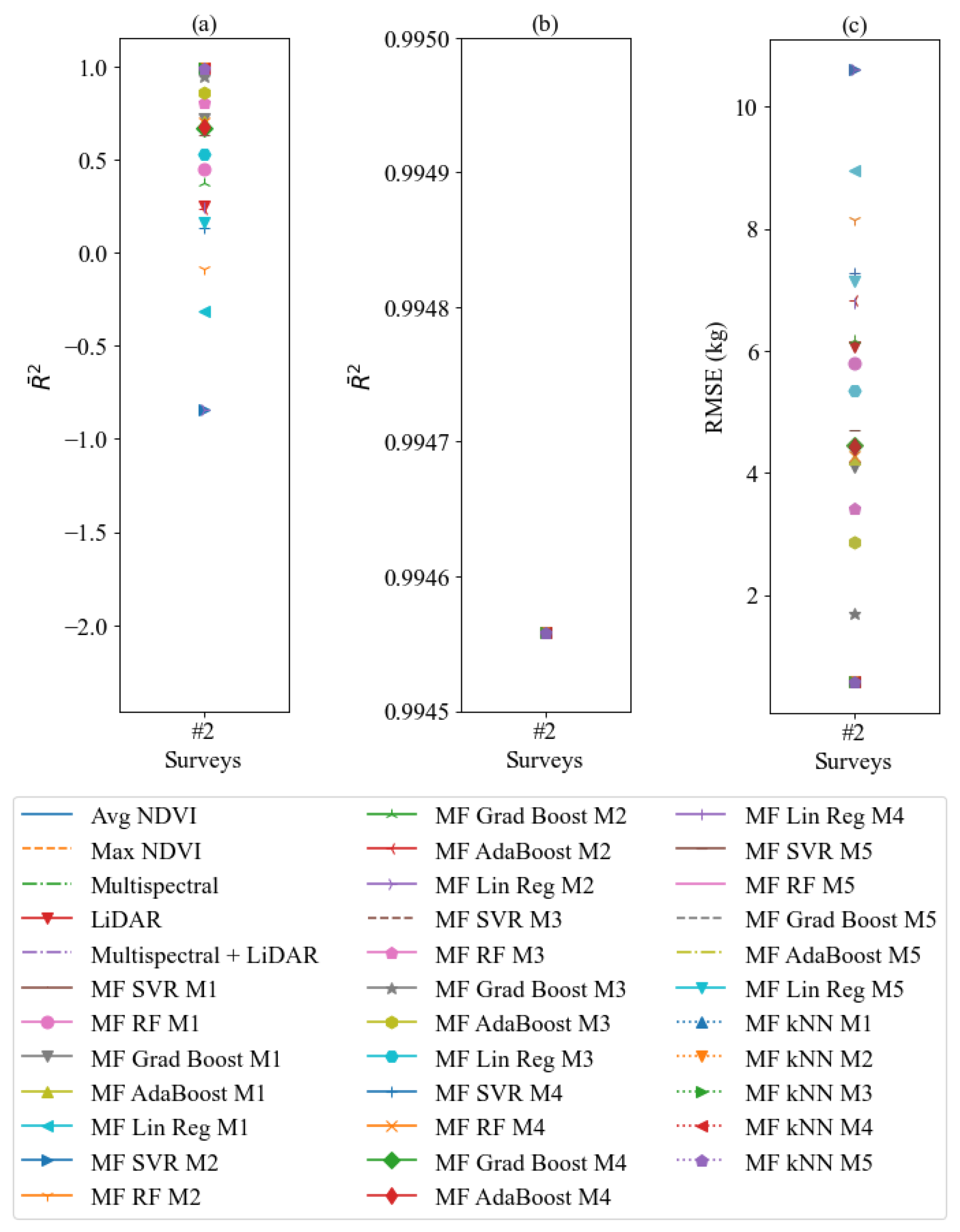
| Feature Model | kNN | AdaBoost | RMSE kNN | RMSE AdaBoost |
|---|---|---|---|---|
| Avg NDVI | −0.3135 | 0.2370 | 8.9590 | 6.8284 |
| Max NDVI | −0.8407 | −0.1465 | 10.6058 | 8.3700 |
| Multispectral | −0.1451 | 0.3187 | 6.9988 | 5.3984 |
| LiDAR | 0.2498 | 0.6571 | 6.0561 | 4.0943 |
| Multispectral + LiDAR | −2.2980 | 0.0281 | 8.9785 | 4.8742 |
| MF SVR M1 | −0.3135 | 0.1771 | 8.9590 | 7.0911 |
| MF RF M1 | 0.4488 | 0.5311 | 5.8035 | 5.3530 |
| MF Grad Boost M1 | 0.7252 | 0.7211 | 4.0977 | 4.1282 |
| MF AdaBoost M1 | 0.7076 | 0.7139 | 4.2273 | 4.1810 |
| MF Lin Reg M1 | −0.3135 | 0.1719 | 8.9590 | 7.1138 |
| MF SVR M2 | −0.8407 | −0.1821 | 10.6058 | 8.4991 |
| MF RF M2 | −0.0839 | 0.1841 | 8.1385 | 7.0612 |
| MF Grad Boost M2 | 0.3780 | 0.6091 | 6.1654 | 4.8876 |
| MF AdaBoost M2 | 0.2388 | 0.5683 | 6.8201 | 5.1362 |
| MF Lin Reg M2 | −0.8407 | −0.1776 | 10.6058 | 8.4831 |
| MF SVR M3 | 0.7272 | 0.8462 | 4.0833 | 3.0658 |
| MF RF M3 | 0.8081 | 0.9067 | 3.4245 | 2.3881 |
| MF Grad Boost M3 | 0.9528 | 0.9406 | 1.6985 | 1.9046 |
| MF AdaBoost M3 | 0.8651 | 0.9044 | 2.8710 | 2.4165 |
| MF Lin Reg M3 | 0.5331 | 0.5851 | 5.3413 | 5.0352 |
| MF SVR M4 | 0.1326 | 0.5767 | 7.2803 | 5.0857 |
| MF RF M4 | 0.7022 | 0.7868 | 4.2659 | 3.6096 |
| MF Grad Boost M4 | 0.6744 | 0.8037 | 4.4607 | 3.4634 |
| MF AdaBoost M4 | 0.6797 | 0.7692 | 4.4238 | 3.7558 |
| MF Lin Reg M4 | 0.2458 | 0.5674 | 6.7888 | 5.1414 |
| MF SVR M5 | 0.6388 | 0.8150 | 4.6980 | 3.3627 |
| MF RF M5 | 0.8183 | 0.8060 | 3.3323 | 3.4435 |
| MF Grad Boost M5 | 0.9452 | 0.9460 | 1.8294 | 1.8169 |
| MF AdaBoost M5 | 0.8701 | 0.9235 | 2.8171 | 2.1621 |
| MF Lin Reg M5 | 0.1682 | 0.5218 | 7.1294 | 5.4055 |
| MF kNN M1 | 0.9946 | 0.9906 | 0.5766 | 0.7575 |
| MF kNN M2 | 0.9946 | 0.9881 | 0.5766 | 0.8532 |
| MF kNN M3 | 0.9946 | 0.9884 | 0.5766 | 0.8436 |
| MF kNN M4 | 0.9946 | 0.9908 | 0.5766 | 0.7514 |
| MF kNN M5 | 0.9946 | 0.9852 | 0.5766 | 0.9502 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbosa, L.A.F.; Guilherme, I.R.; Pedronette, D.C.G.; Tisseyre, B. Meta-Features Extracted from Use of kNN Regressor to Improve Sugarcane Crop Yield Prediction. Remote Sens. 2025, 17, 1846. https://doi.org/10.3390/rs17111846
Barbosa LAF, Guilherme IR, Pedronette DCG, Tisseyre B. Meta-Features Extracted from Use of kNN Regressor to Improve Sugarcane Crop Yield Prediction. Remote Sensing. 2025; 17(11):1846. https://doi.org/10.3390/rs17111846
Chicago/Turabian StyleBarbosa, Luiz Antonio Falaguasta, Ivan Rizzo Guilherme, Daniel Carlos Guimarães Pedronette, and Bruno Tisseyre. 2025. "Meta-Features Extracted from Use of kNN Regressor to Improve Sugarcane Crop Yield Prediction" Remote Sensing 17, no. 11: 1846. https://doi.org/10.3390/rs17111846
APA StyleBarbosa, L. A. F., Guilherme, I. R., Pedronette, D. C. G., & Tisseyre, B. (2025). Meta-Features Extracted from Use of kNN Regressor to Improve Sugarcane Crop Yield Prediction. Remote Sensing, 17(11), 1846. https://doi.org/10.3390/rs17111846








