Sentinel-1 Noise Suppression Algorithm for High-Wind-Speed Retrieval in Tropical Cyclones
Abstract
1. Introduction
2. Data
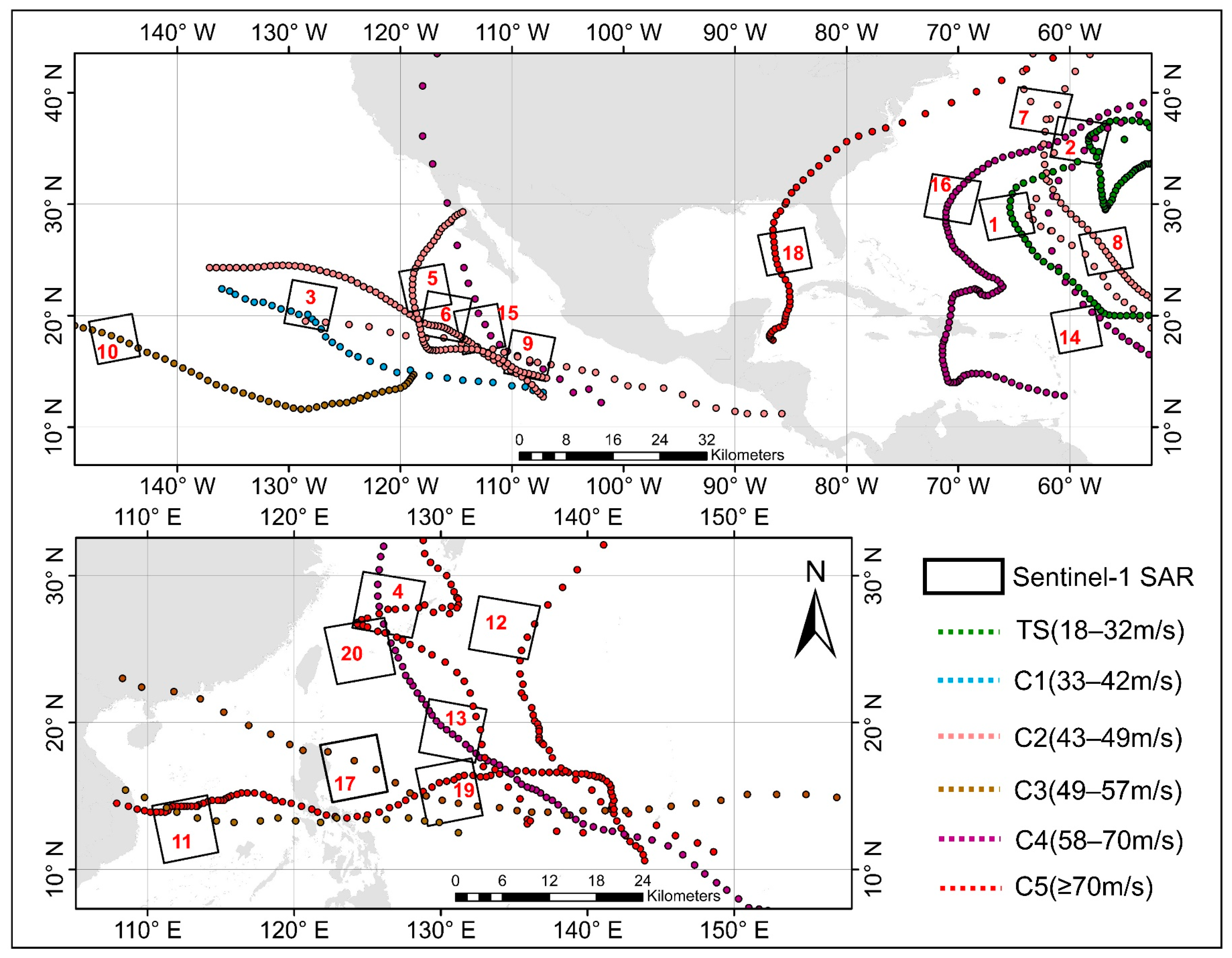
2.1. SAR Data
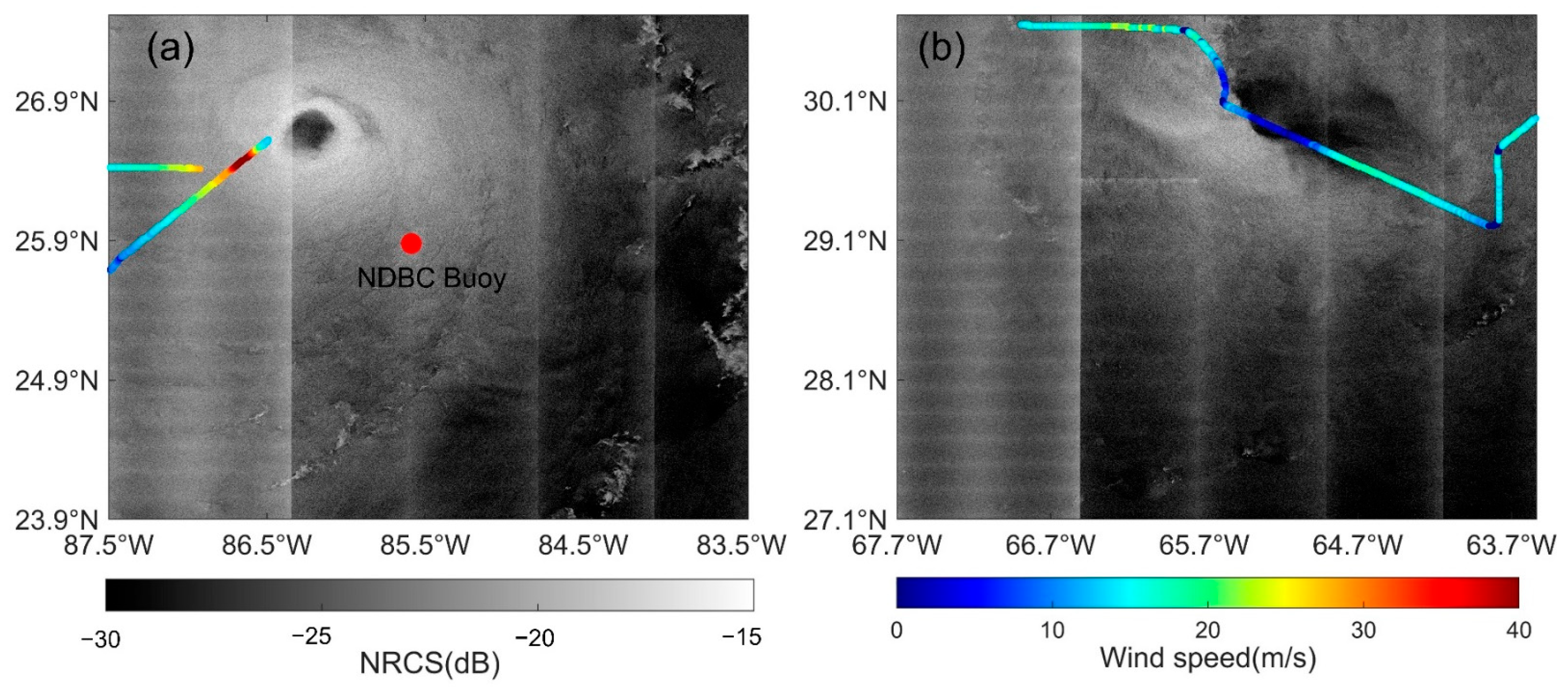
2.2. Validation Data
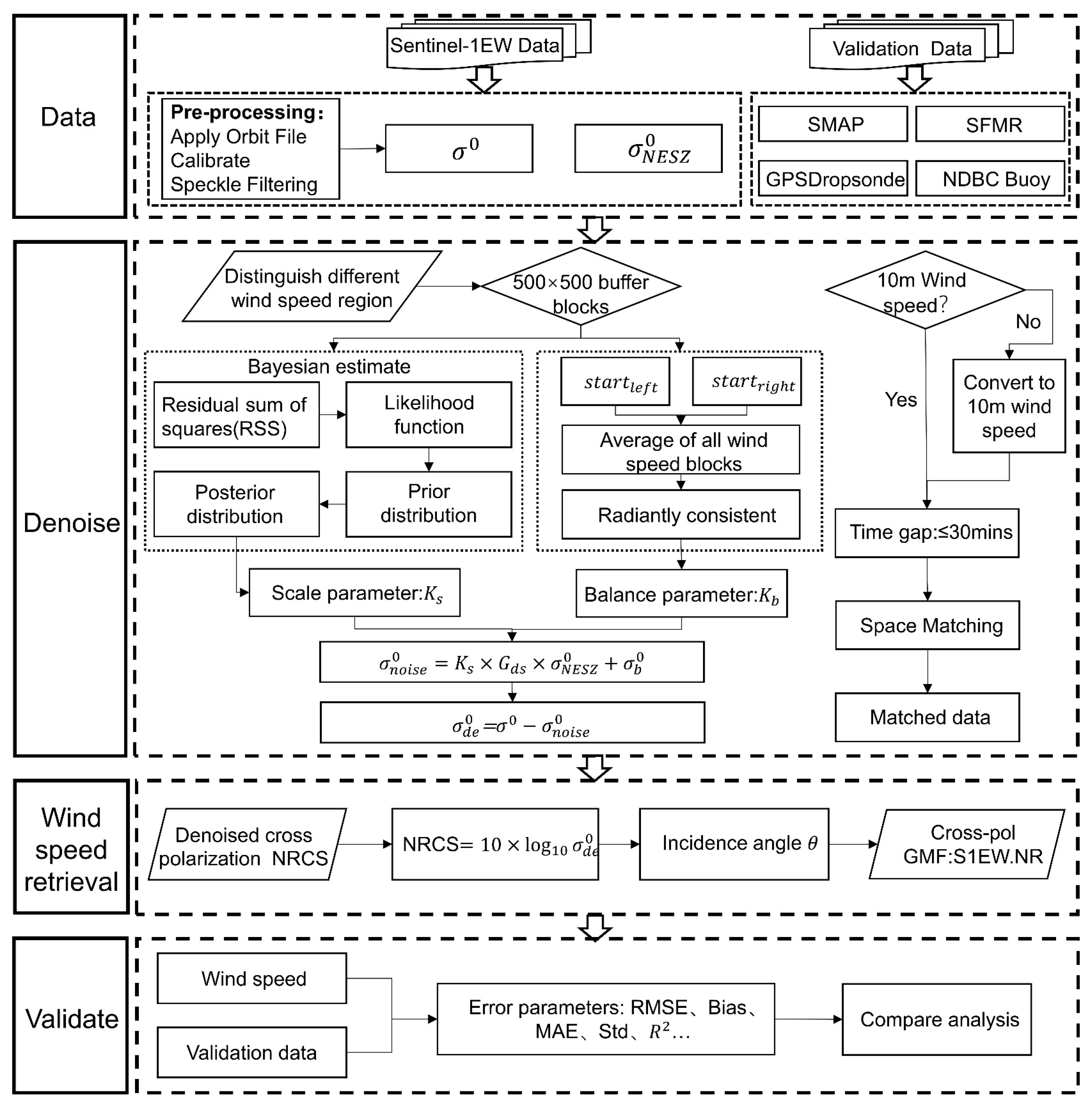
3. Method
3.1. Two-Dimensional Noise Field Reconstruction
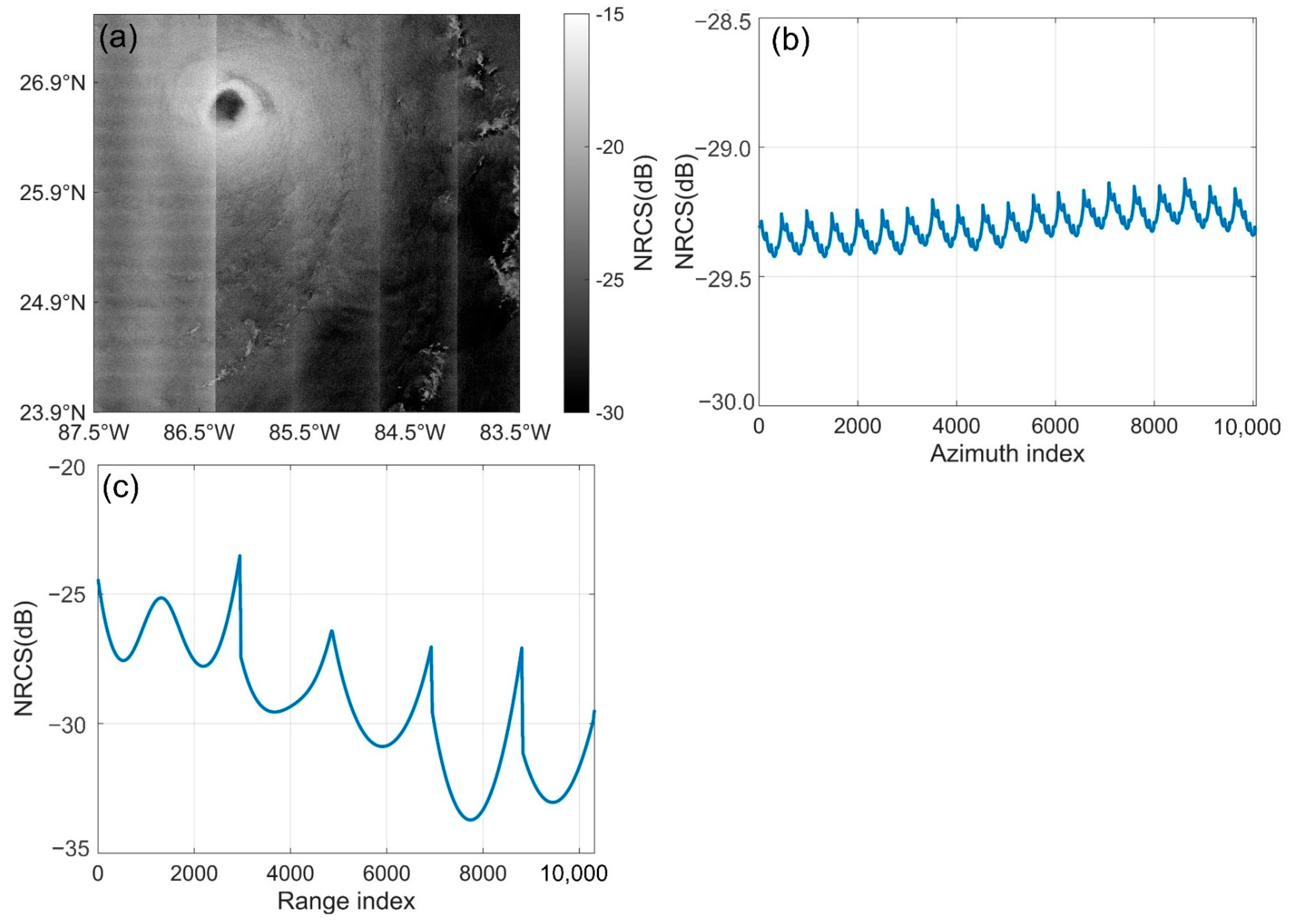
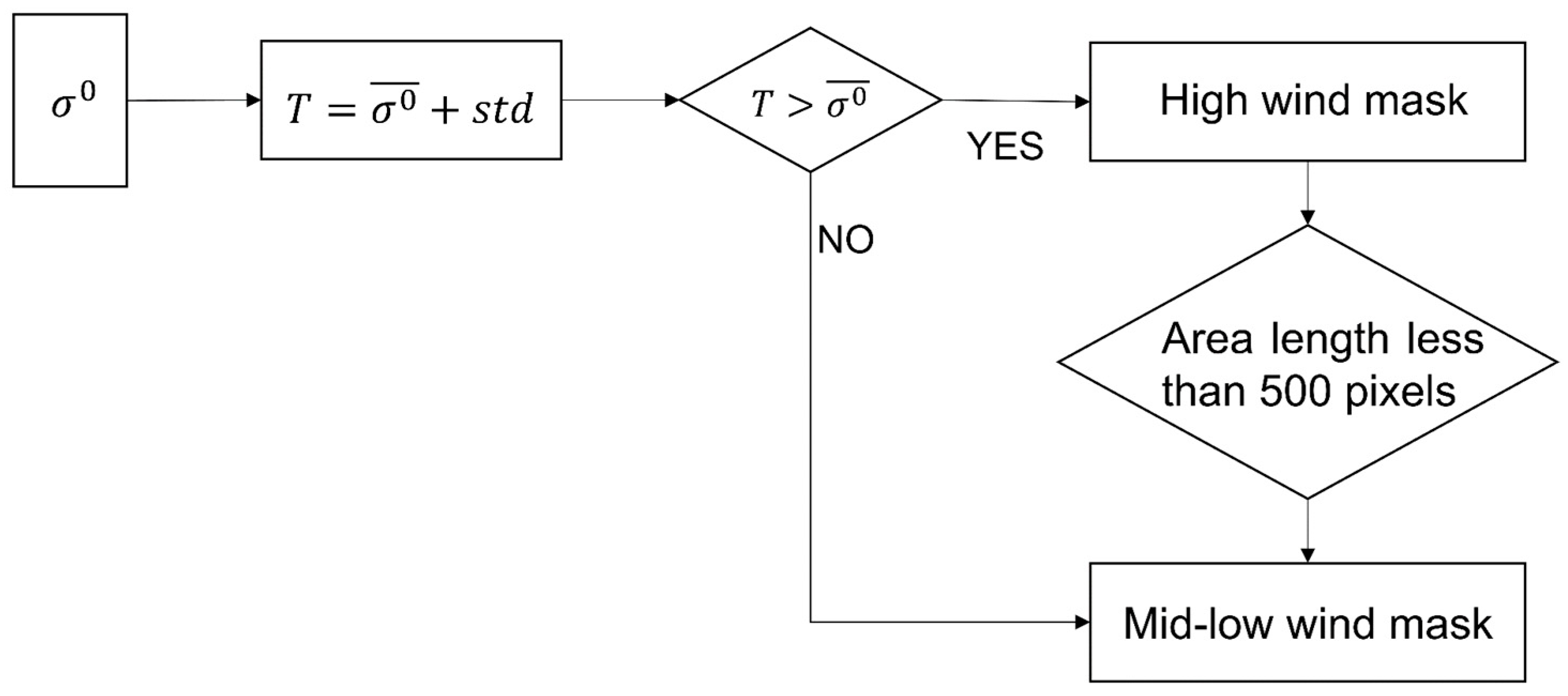
3.1.1. Mid–Low- and High-Wind-Speed Area Blocks
3.1.2. Optimal Noise-Scaling Factor Calculation
3.1.3. Optimal Power Balance Factor Calculate
3.2. Cross-Pol Wind Speed Retrieval Model
4. Results of Denoise and Wind Speed Retrieval
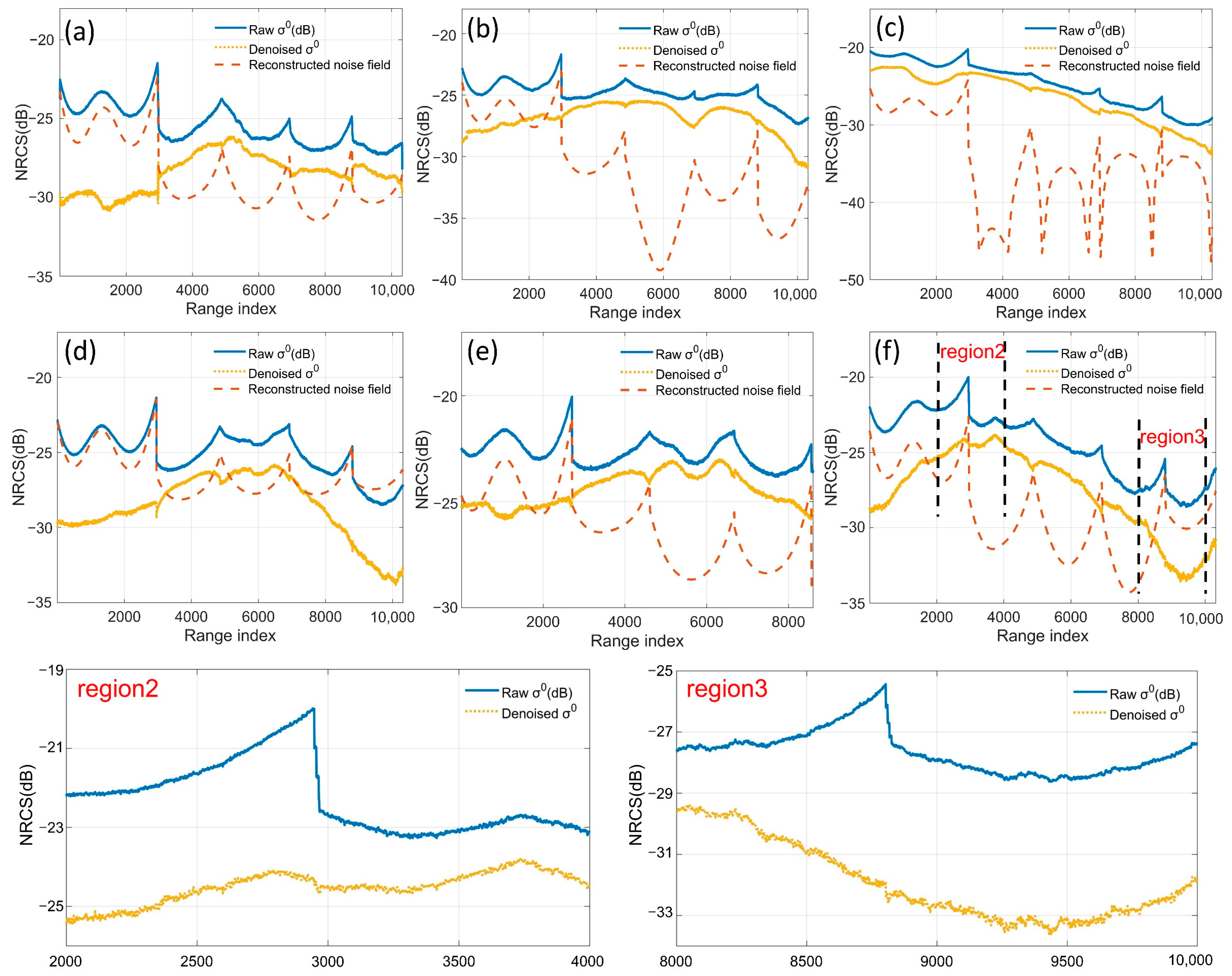
4.1. Noise Suppression Effect of Reconstructed 2D Noise Field
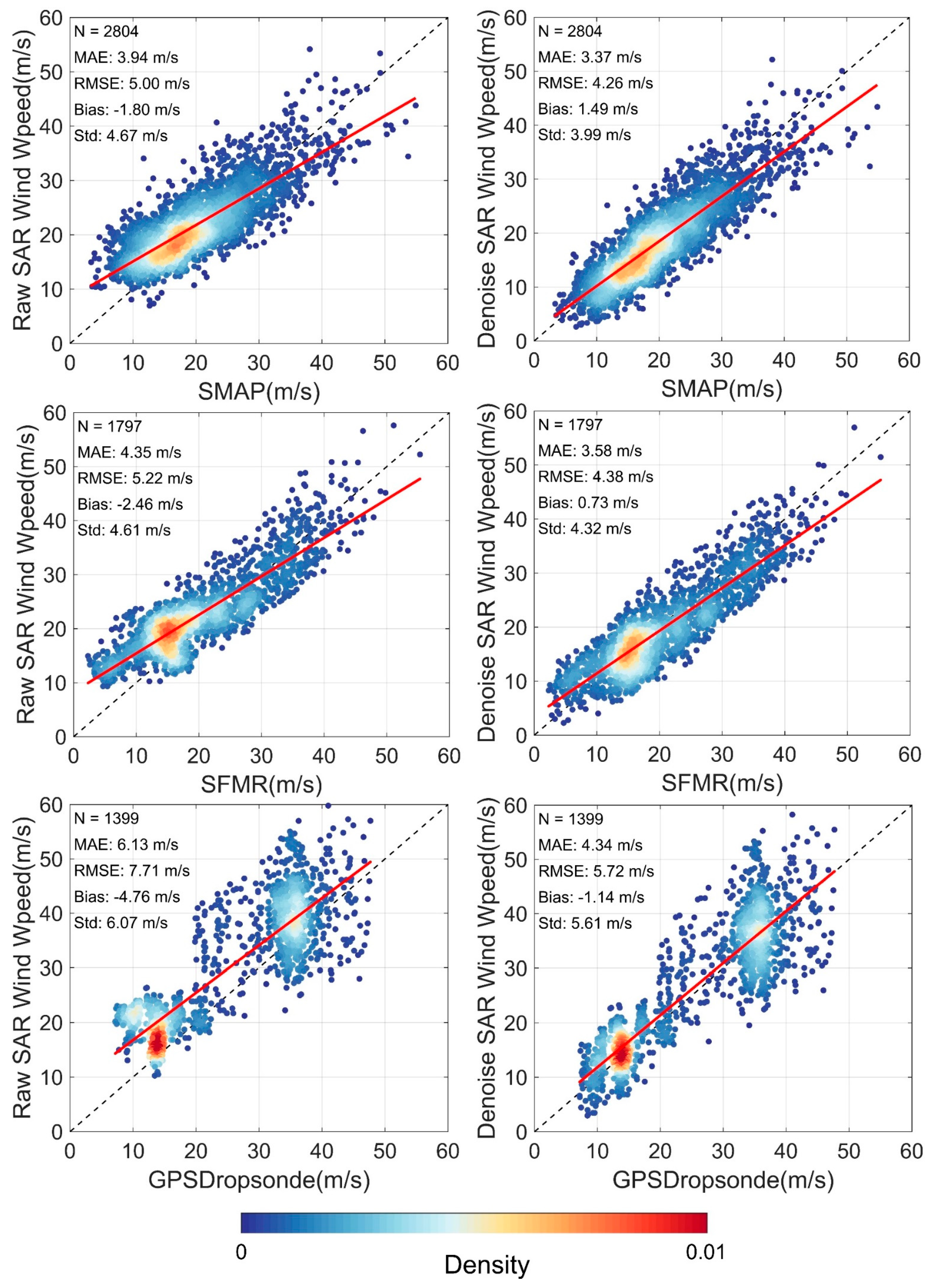
4.2. Results of Wind Speed Retrieval
5. Discussion
5.1. Noise Suppression Effect of 2D Noise Field Reconstruction
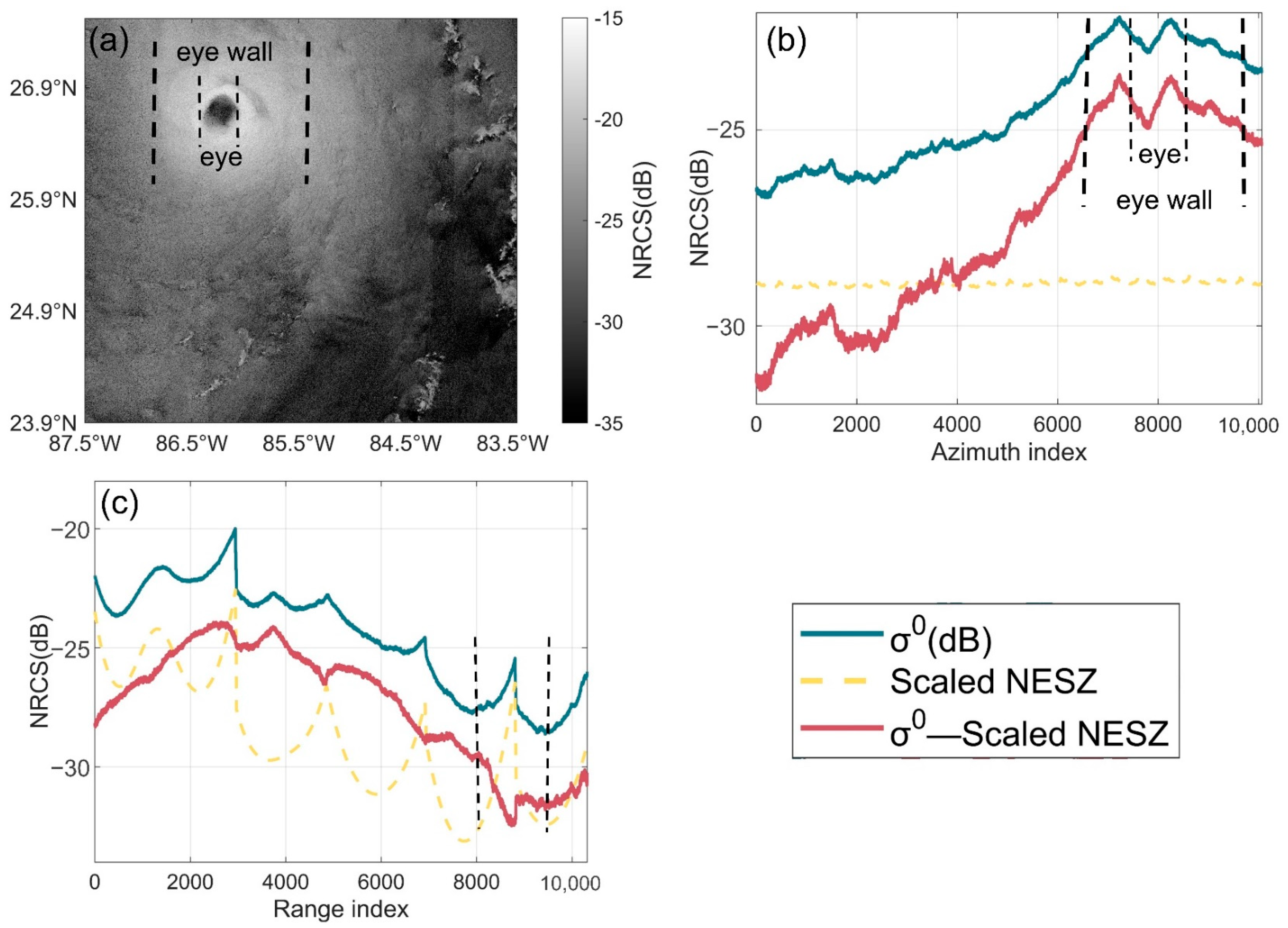
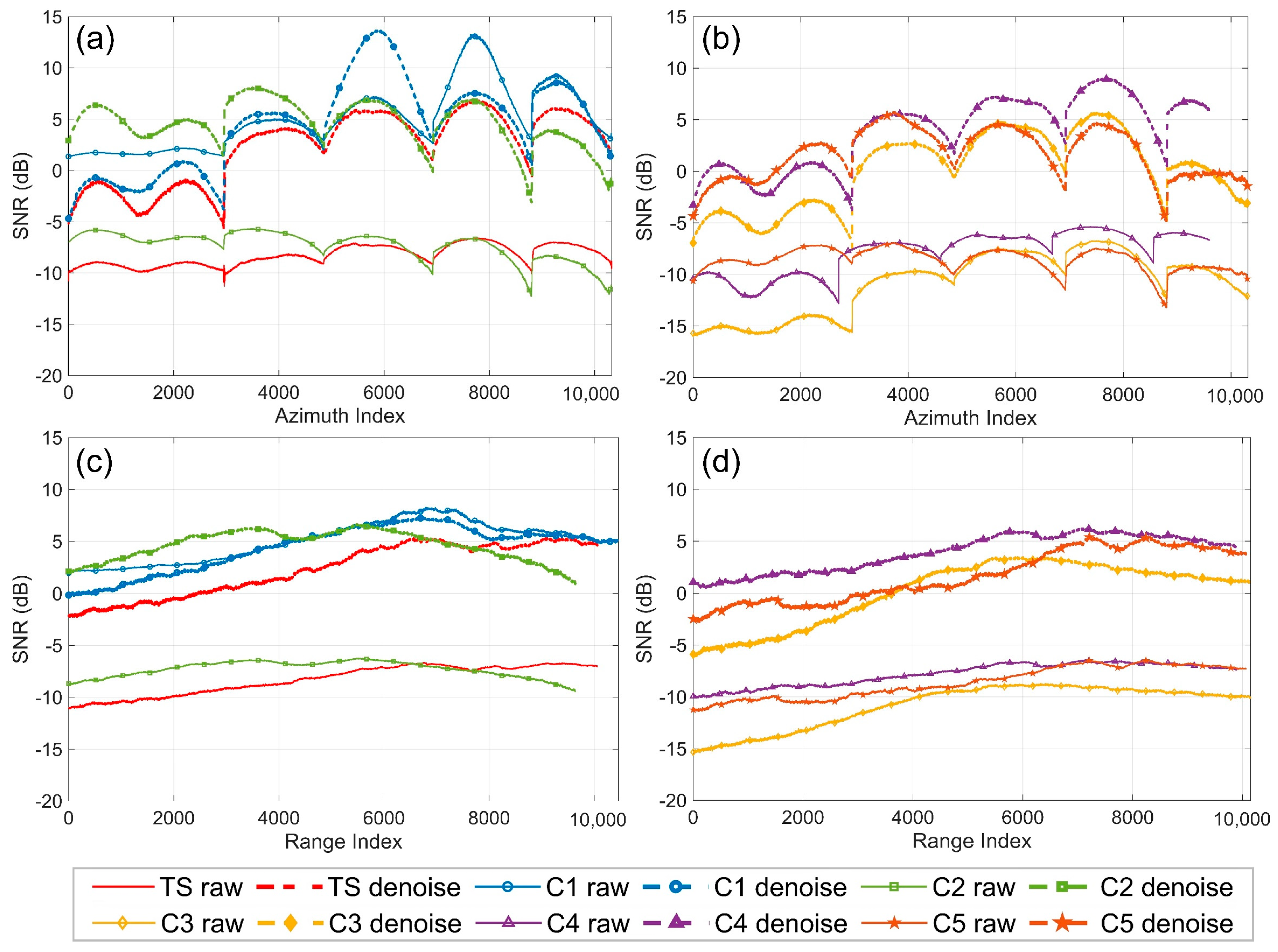
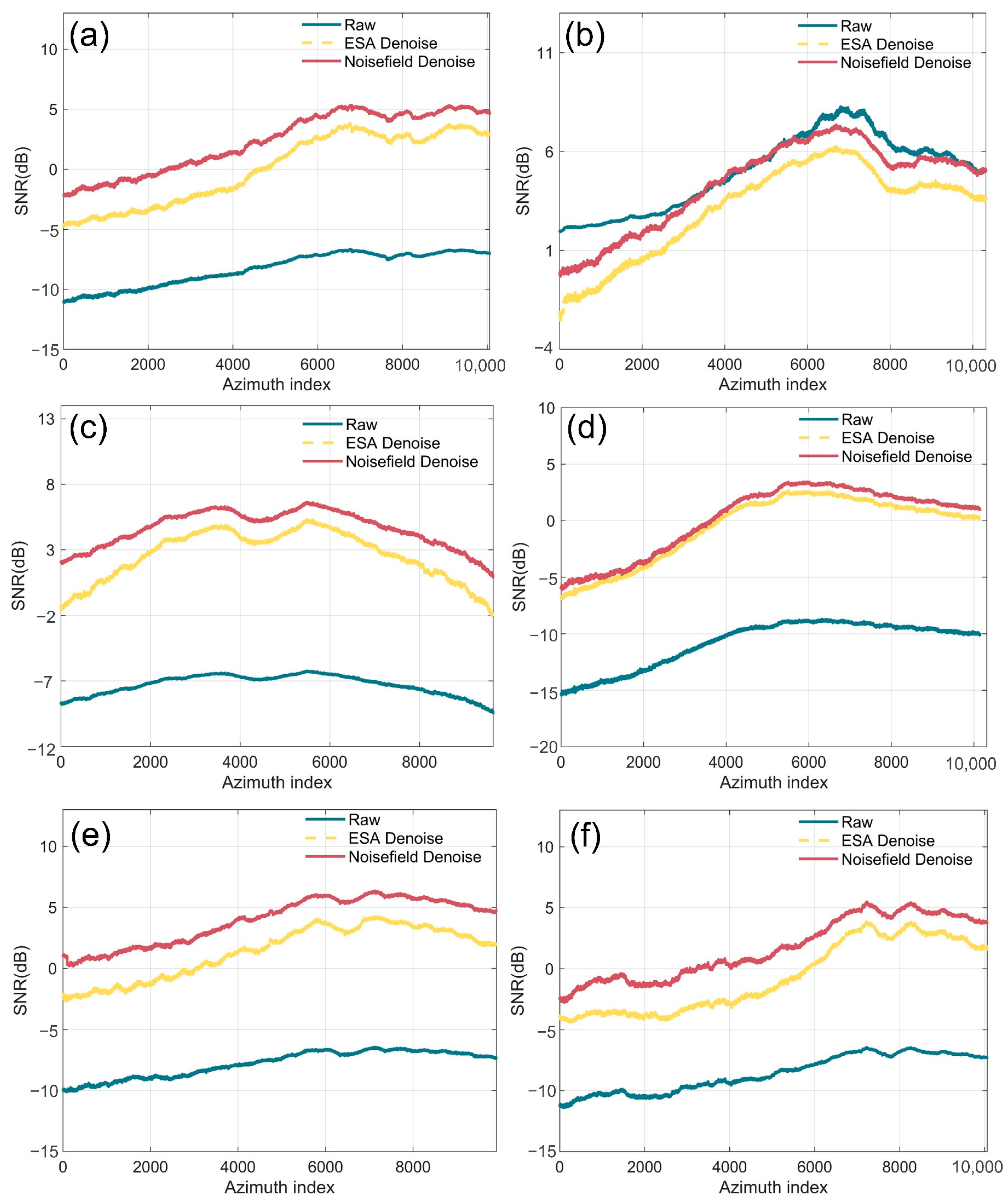
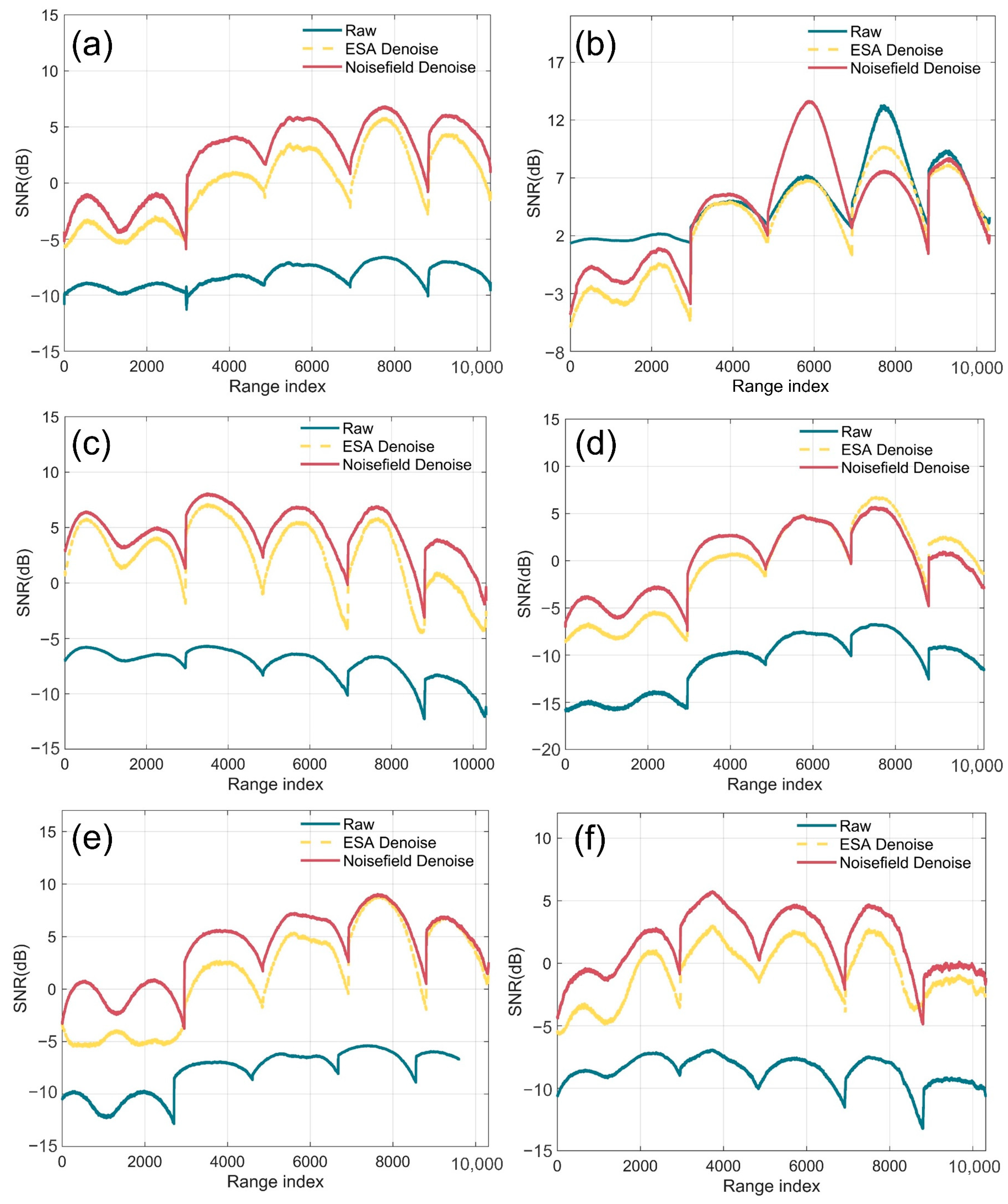
5.1.1. SNR Analysis of SAR Before and After Noise Removal
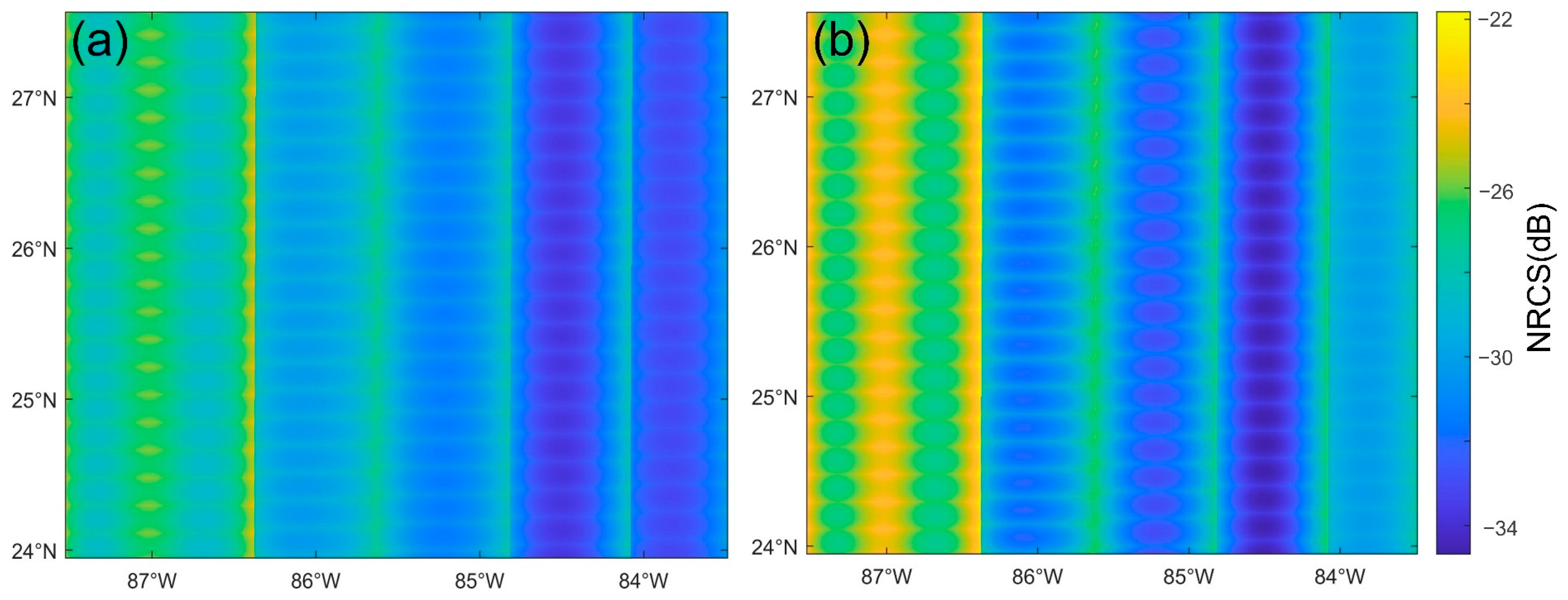
5.1.2. Comparative Analysis with ESA Noise Vectors
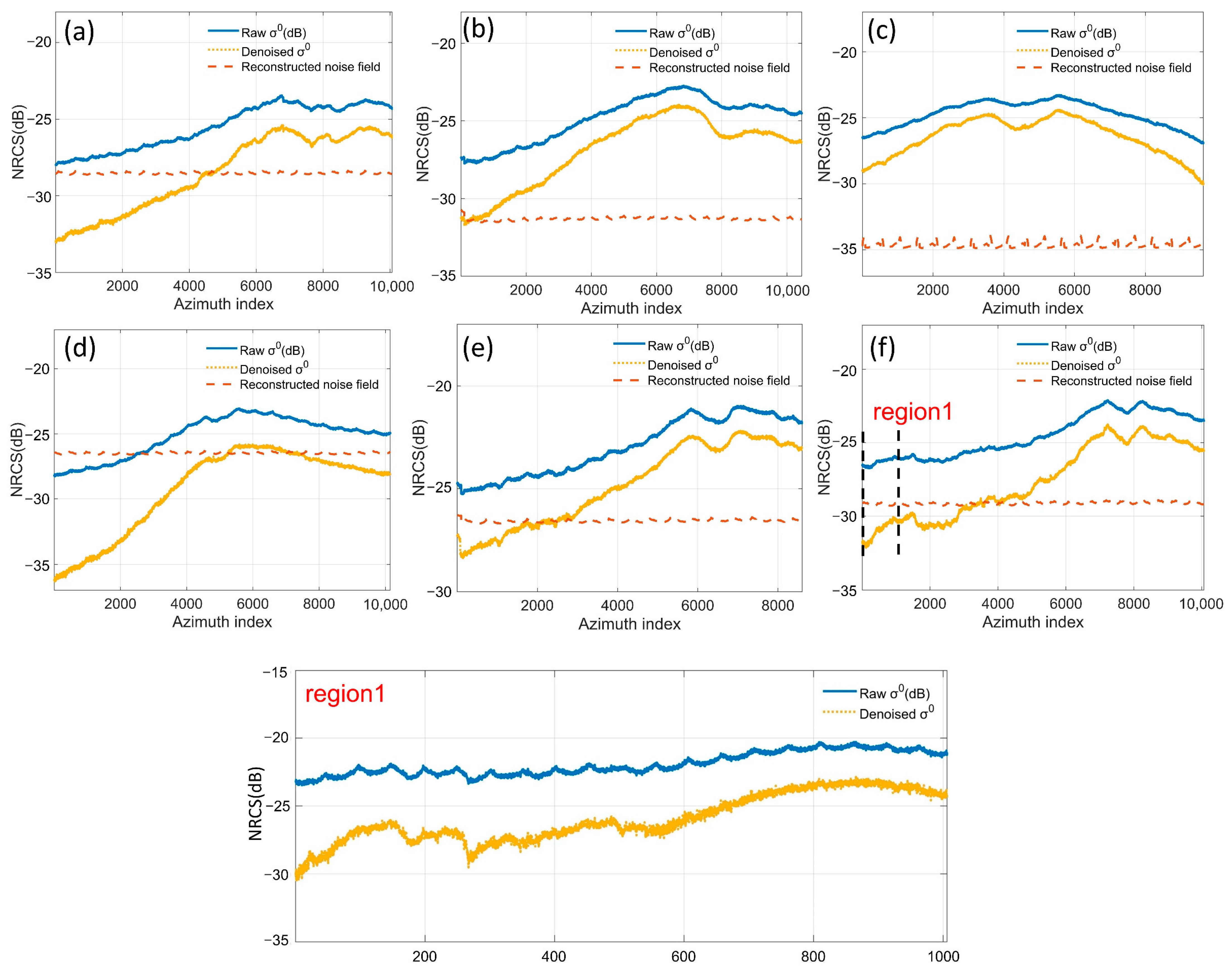
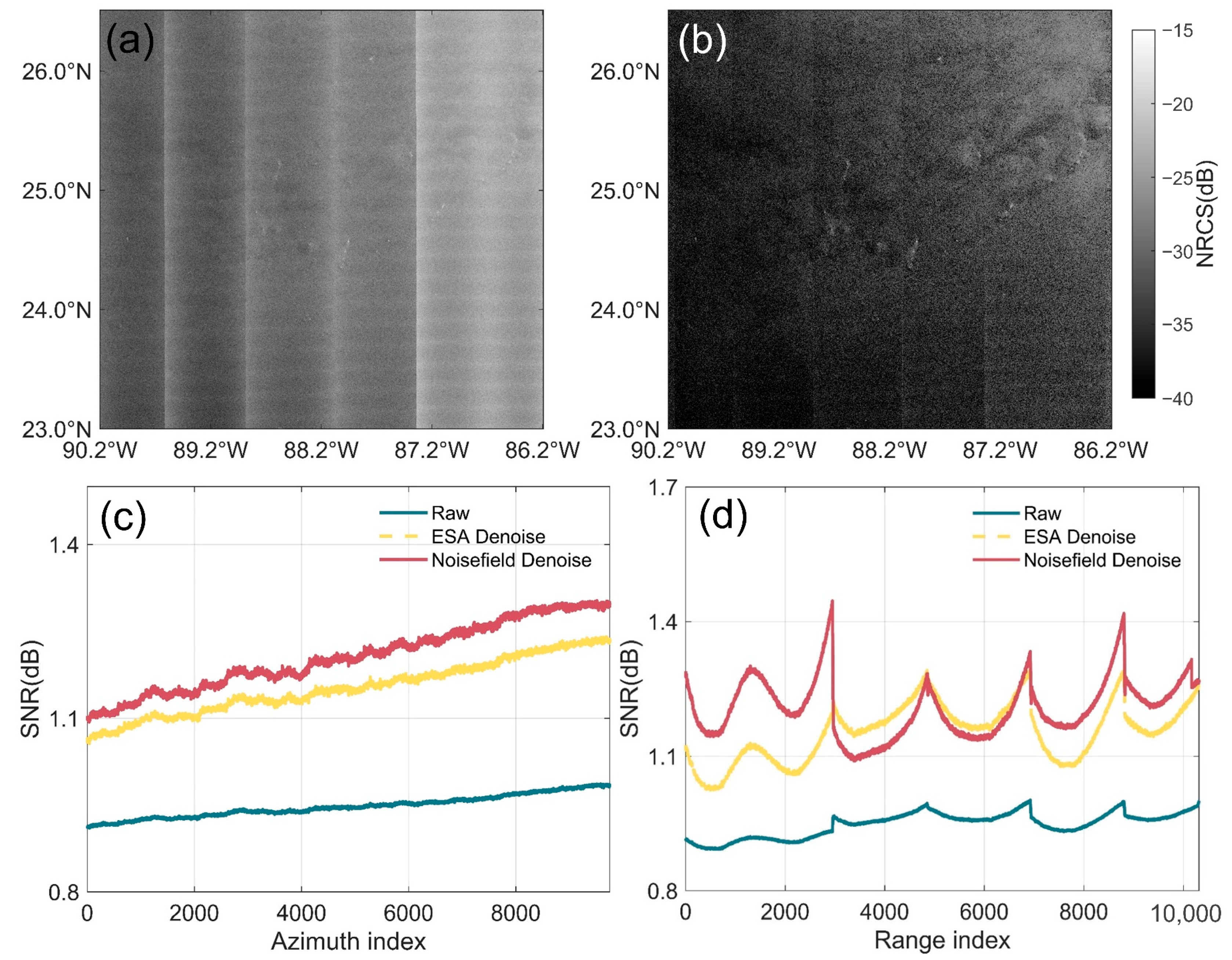
5.1.3. Denoising Results of Non-TC SAR Data
5.2. Discussion of TC Wind Speed Retrieval Results
5.2.1. Effect of SAR Noise on TC Wind Speed Retrieval
5.2.2. Other Factors Affecting the Accuracy of TC Wind Speed Retrieval
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pichel, W.G.; Monaldo, F.M.; Jackson, C.; Li, X.; Sapper, J. NOAA operational SAR winds—Current status and plans for Sentinel-1A. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4916–4919. [Google Scholar]
- Fernandez, D.E.; Carswell, J.R.; Frasier, S.; Chang, P.S.; Black, P.G.; Marks, F.D. Dual-polarized C-and Ku-band ocean backscatter response to hurricane-force winds. J. Geophys. Res. Ocean 2006, 111. [Google Scholar] [CrossRef]
- Mouche, A.; Chapron, B. Global C-Band Envisat, RADARSAT-2 and Sentinel-1 SAR measurements in copolarization and cross-polarization. J. Geophys. Res.-Ocean. 2015, 120, 7195–7207. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W. Cross-polarized synthetic aperture radar: A new potential measurement technique for hurricanes. Bull. Am. Meteorol. Soc. 2012, 93, 531–541. [Google Scholar] [CrossRef]
- Hwang, P.A.; Zhang, B.; Toporkov, J.V.; Perrie, W. Comparison of composite Bragg theory and quad-polarization radar backscatter from RADARSAT-2: With applications to wave breaking and high wind retrieval. J. Geophys. Res. Ocean 2010, 115. [Google Scholar] [CrossRef]
- Zhang, B.; Mouche, A.A.; Perrie, W. First quasi-synchronous hurricane quad-polarization observations by C-band radar constellation mission and RADARSAT-2. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Yang, J.; Zhong, L.; Yuan, X.; Wang, X.; Han, B.; Hu, Y. First assessment of Noise-Equivalent Sigma-Zero in GF3-02 TOPSAR mode with sea surface wind speed retrieval. Acta Oceanol. Sin. 2023, 42, 84–96. [Google Scholar] [CrossRef]
- De Zan, F.; Guarnieri, A.M. TOPSAR: Terrain observation by progressive scans. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Frank, D.C. (Ed.) Microwave Remote Sensing of Sea Ice; American Geophysical Union: Washington, DC, USA, 1992. [Google Scholar]
- Balss, U.; Breit, H.; Niedermeier, A. Computation of signal gain and noise gain of a SAR processor. In Proceedings of the CEOS Strategic Implementation Team (SIT) Technical Workshop, Darmstadt, Germany, 17–18 September 2015. [Google Scholar]
- Piantanida, R.; Hajduch, G.; Poullaouec, J. Sentinel-1 Level 1 Detailed Algorithm Definition; Techreport SEN-TN-52-7445; ESA: Paris, France, 2016. [Google Scholar]
- Iqbal, M.; Chen, J.; Yang, W.; Wang, P.; Sun, B. Kalman filter for removal of scalloping and inter-scan banding in scansar images. Prog. Electromagn. Res. 2012, 132, 443–461. [Google Scholar] [CrossRef]
- Tan, W.; Li, J.; Xu, L.; Chapman, M.A. Semiautomated segmentation of Sentinel-1 SAR imagery for mapping sea ice in Labrador coast. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1419–1432. [Google Scholar] [CrossRef]
- Kasapoğlu, N.G. Sea ice concentration retrieval using composite ScanSAR features in a SAR data assimilation process. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2085–2089. [Google Scholar] [CrossRef]
- Ren, L.; Yang, J.; Mouche, A.; Wang, H.; Wang, J.; Zheng, G.; Zhang, H. Preliminary analysis of Chinese GF-3 SAR quad-polarization measurements to extract winds in each polarization. Remote Sens. 2017, 9, 1215. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, B.; Perrie, W.; Zheng, G.; Yang, J.; Fang, H. Assessment of Thermal Noise Effect on Wind Speed Retrieval Accuracy Using Sentinel-1 Cross-polarized TOPSAR Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–11. [Google Scholar] [CrossRef]
- Yang, W.; Li, Y.; Liu, W.; Chen, J.; Li, C.; Men, Z. Scalloping suppression for ScanSAR images based on modified Kalman filter with preprocessing. IEEE Trans. Geosci. Remote Sens. 2020, 59, 7535–7546. [Google Scholar] [CrossRef]
- Miranda, N.; Piantanida, R.; Recchia, A.; Franceschi, N.; Small, D.; Schubert, A.; Meadows, P.J. S-1 instrument and product performance status: 2018 update. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 1551–1554. [Google Scholar]
- Piantanida, R.; Miranda, N.; Franceschi, N.; Meadows, P.; Hajduch, G. Thermal Denoising of Products Generated by the S-1 IPF; DI-MPC-TN, MPC-0392; Sentinel-1 Mission Perform: Ramonville-Saint-Agne, France, 2017. [Google Scholar]
- Karvonen, J. Baltic sea ice concentration estimation using SENTINEL-1 SAR and AMSR2 microwave radiometer data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2871–2883. [Google Scholar] [CrossRef]
- Park, J.W.; Korosov, A.A.; Babiker, M.; Sandven, S.; Won, J.-S. Efficient thermal noise removal for Sentinel-1 TOPSAR cross-polarization channel. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1555–1565. [Google Scholar] [CrossRef]
- Korosov, A.; Demchev, D.; Miranda, N.; Franceschi, N.; Park, J.-W. Thermal denoising of cross-polarized Sentinel-1 data in interferometric and extra wide swath modes. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–11. [Google Scholar] [CrossRef]
- Park, J.W.; Won, J.S.; Korosov, A.A.; Babiker, M.; Miranda, N. Textural noise correction for Sentinel-1 TOPSAR cross-polarization channel images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4040–4049. [Google Scholar] [CrossRef]
- Lee, P.Q.; Xu, L.; Clausi, D.A. Estimating Noise Floor in Sentinel-1 Images with Linear Programming and Least Squares. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Lee, P.Q.; Xu, L.; Clausi, D.A. Sentinel-1 additive noise removal from cross-polarization extra-wide TOPSAR with dynamic least-squares. Remote Sens. Environ. 2020, 248, 111982. [Google Scholar] [CrossRef]
- Hu, Y.; Shao, W.; Shen, W.; Zhou, Y.; Jiang, X. Machine learning applied to a dual-polarized Sentinel-1 image for wind retrieval of tropical cyclones. Remote Sens. 2023, 15, 3948. [Google Scholar] [CrossRef]
- Zhou, Y.; Shao, W.; Nunziata, F.; Wang, W.; Li, C. An Algorithm to Retrieve Range Ocean Current Speed under Tropical Cyclone Conditions from Sentinel-1 Synthetic Aperture Radar Measurements Based on XGBoost. Remote Sens. 2024, 16, 3271. [Google Scholar] [CrossRef]
- Shao, W.; Wei, M.; Hu, Y.; Marino, A.; Jiang, X. Wind speed retrieval approach for VV-polarized synthetic aperture radar during tropical cyclone based on XGBoost model. Int. J. Remote Sens. 2024, 45, 4367–4384. [Google Scholar] [CrossRef]
- Li, X.M.; Qin, T.; Wu, K. Retrieval of sea surface wind speed from spaceborne SAR over the Arctic marginal ice zone with a neural network. Remote Sens. 2020, 12, 3291. [Google Scholar] [CrossRef]
- Mu, S.; Li, X.; Wang, H. The fusion of physical, textural, and morphological information in SAR imagery for hurricane wind speed retrieval based on deep learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Vachon, P.W.; Wolfe, J. C-band cross-polarization wind speed retrieval. IEEE Geosci. Remote Sens. Lett. 2010, 8, 456–459. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W.; Zhang, J.A.; Uhlhorn, E.W.; He, Y. High-resolution hurricane vector winds from C-band dual-polarization SAR observations. J. Atmos. Ocean. Technol. 2014, 31, 272–286. [Google Scholar] [CrossRef]
- Horstmann, J.; Falchetti, S.; Wackerman, C.; Maresca, S.; Caruso, M.J.; Graber, H.C. Tropical cyclone winds retrieved from C-band cross-polarized synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2887–2898. [Google Scholar] [CrossRef]
- Zhang, K.; Huang, J.; Mansaray, L.R.; Guo, Q.; Wang, X. Developing a subswath-based wind speed retrieval model for Sentinel-1 VH-polarized SAR data over the ocean surface. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1561–1572. [Google Scholar] [CrossRef]
- Zhou, L.; Zheng, G.; Yang, J.; Li, X.; Zhang, B.; Wang, H.; Chen, P.; Wang, Y. Sea surface wind speed retrieval from textures in synthetic aperture radar imagery. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–11. [Google Scholar] [CrossRef]
- Gao, Y.; Guan, C.; Sun, J.; Xie, L. Tropical cyclone wind speed retrieval from dual-polarization Sentinel-1 EW mode products. J. Atmos. Ocean. Technol. 2020, 37, 1713–1724. [Google Scholar] [CrossRef]
- Olsen, A.M.; Øiestad, M.; Berge, E.; Køltzow, M.Ø.; Valkonen, T. Evaluation of Marine Wind Profiles in the North Sea and Norwegian Sea Based on Measurements and Satellite-Derived Wind Products. Tellus A: Dyn. Meteorol. Oceanogr. 2022, 74, 1–16. [Google Scholar] [CrossRef]
- Sun, Y.; Li, X.M. Denoising Sentinel-1 Extra-Wide Mode Cross-Polarization Images Over Sea Ice. IEEE Trans. Geosci. Remote. Sens. 2020, 59, 2116–2131. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; Perrie, W.; Hwang, P.A.; Zhang, B.; Yang, X. A hurricane wind speed retrieval model for C-band RADARSAT-2 cross-polarization ScanSAR images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4766–4774. [Google Scholar] [CrossRef]
- Troitskaya, Y.; Abramov, V.; Baidakov, G.; Ermakova, O.; Zuikova, E.; Sergeev, D.; Ermoshkin, A.; Kazakov, V.; Kandaurov, A.; Rusakov, N.; et al. Cross-Polarization GMF for High Wind Speed and Surface Stress Retrieval. J. Geophys. Res. Ocean 2018, 123, 5842–5855. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Fan, S.; Zhang, B.; Mouche, A.A.; Chapron, B. On quad-polarized SAR measurements of the ocean surface. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8362–8370. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, X.; Perrie, W.; Kudryavtsev, V. On modeling of quad-polarization radar scattering from the ocean surface with breaking waves. J. Geophys. Res. Ocean 2020, 125, e2020JC016319. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W. Remote Sensing of Tropical Cyclones by Spaceborne Synthetic Aperture Radar: Past, present, and future. IEEE Geosci. Remote Sens. Mag. 2024, 12, 79–109. [Google Scholar] [CrossRef]
- Guo, C.; Ai, W.; Hu, S.; Du, X.; Chen, N. Effect of precipitation on synthetic aperture radar hurricane wind field retrieval. Front. Environ. Sci. 2022, 10, 1034045. [Google Scholar] [CrossRef]

| No. | Name | Date and Time | Category | Validation Data | ESA Method | Proposed Method | ||
|---|---|---|---|---|---|---|---|---|
| Mean Noise Level (dB) | Mean SNR (dB) | Mean Noise Level (dB) | Mean SNR (dB) | |||||
| 1 | KARL | 2016.09.23-22:22 | TS | SMAP, SFMR, Dropsondes | −30.3 | 0.07 | −28.3 | 2.33 |
| 2 | LESLIE | 2018.10.05-10:01 | TS | SMAP | −29.3 | 1.04 | −27.0 | 3.43 |
| 3 | MARIE | 2020.10.04-14:29 | C1 | −30.5 | 3.14 | −27.2 | 4.41 | |
| 4 | KHANUN | 2023.08.04-21:34 | C1 | −28.9 | 2.53 | −25.7 | 2.90 | |
| 5 | ROSA | 2018.09.30-01:54 | C2 | −30.5 | 2.60 | −26.4 | 4.62 | |
| 6 | JULIETTE | 2019.09.04-13:39 | C2 | −26.9 | −0.36 | −28.5 | 0.09 | |
| 7 | TEDDY | 2020.09.22-10:17 | C2 | −28.8 | 6.20 | −22.8 | 7.39 | |
| 8 | LARRY | 2021.09.07-21:48 | C2 | SMAP, SFMR, Dropsondes | −30.3 | 5.54 | −24.8 | 5.80 |
| 9 | BONNIE | 2022.07.06-13:07 | C2 | SMAP | −29.7 | −0.15 | −29.3 | 0.21 |
| 10 | DOUGLAS | 2020.07.25-03:50 | C3 | SMAP, SFMR, Dropsondes | −26.4 | −0.57 | −28.7 | 0.16 |
| 11 | MOLAVE | 2020.10.27-10:39 | C3 | SMAP | −28.8 | 4.87 | −23.7 | 5.15 |
| 12 | MINDULLE | 2021.09.29-21:01 | C3 | −30.5 | 6.77 | −23.6 | 6.93 | |
| 13 | KONG-REY | 2018.10.02-21:12 | C4 | −29.1 | 6.97 | −26.4 | 7.01 | |
| 14 | SAM | 2021.09.29-22:03 | C4 | SFMR | −30.4 | 1.11 | −30.4 | 1.12 |
| 15 | HILARY | 2023.08.19-01:37 | C4 | SMAP | −28.7 | 1.40 | −24.7 | 3.93 |
| 16 | FRANKLIN | 2023.08.29-10:44 | C4 | −28.9 | 3.08 | −28.3 | 3.37 | |
| 17 | MANGKHUT | 2018.09.14-09:50 | C5 | −29.2 | 7.51 | −21.5 | 7.70 | |
| 18 | MICHAEL | 2018.10.09-23:44 | C5 | SMAP, SFMR, Buoy, Dropsondes | −29 | −0.69 | −27.3 | 1.69 |
| 19 | GONI | 2020.10.30-09:25 | C5 | SMAP | −28.9 | −3.22 | −29.5 | −2.94 |
| 20 | KHANUN | 2023.08.02-09:45 | C5 | −28.6 | 3.72 | −23.8 | 4.70 | |
| U10 | Case | RMSE | Bias | MAE | Std | |
|---|---|---|---|---|---|---|
| 30 m/s | Raw | 5.34 | −2.43 | 4.26 | 4.76 | 0.72 |
| Denoise | 4.26 | 1.11 | 3.39 | 4.11 | 0.8 | |
| 30 m/s | Raw | 7.41 | −3.58 | 5.86 | 6.49 | 0.37 |
| Denoise | 6.16 | −0.79 | 4.88 | 6.12 | 0.46 | |
| All range | Raw | 5.81 | −2.69 | 4.57 | 5.15 | 0.84 |
| Denoise | 4.67 | 0.65 | 3.66 | 4.63 | 0.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, D.; Wang, L.; Sun, W.; Wang, H.; Jiang, W.; Feng, T. Sentinel-1 Noise Suppression Algorithm for High-Wind-Speed Retrieval in Tropical Cyclones. Remote Sens. 2025, 17, 1827. https://doi.org/10.3390/rs17111827
Ge D, Wang L, Sun W, Wang H, Jiang W, Feng T. Sentinel-1 Noise Suppression Algorithm for High-Wind-Speed Retrieval in Tropical Cyclones. Remote Sensing. 2025; 17(11):1827. https://doi.org/10.3390/rs17111827
Chicago/Turabian StyleGe, Dechen, Lihua Wang, Weiwei Sun, Hongmei Wang, Wenjing Jiang, and Tian Feng. 2025. "Sentinel-1 Noise Suppression Algorithm for High-Wind-Speed Retrieval in Tropical Cyclones" Remote Sensing 17, no. 11: 1827. https://doi.org/10.3390/rs17111827
APA StyleGe, D., Wang, L., Sun, W., Wang, H., Jiang, W., & Feng, T. (2025). Sentinel-1 Noise Suppression Algorithm for High-Wind-Speed Retrieval in Tropical Cyclones. Remote Sensing, 17(11), 1827. https://doi.org/10.3390/rs17111827






