Estimation of Tree Canopy Closure Based on U-Net Image Segmentation and Machine Learning Algorithms
Abstract
1. Introduction
2. Study Area and Data
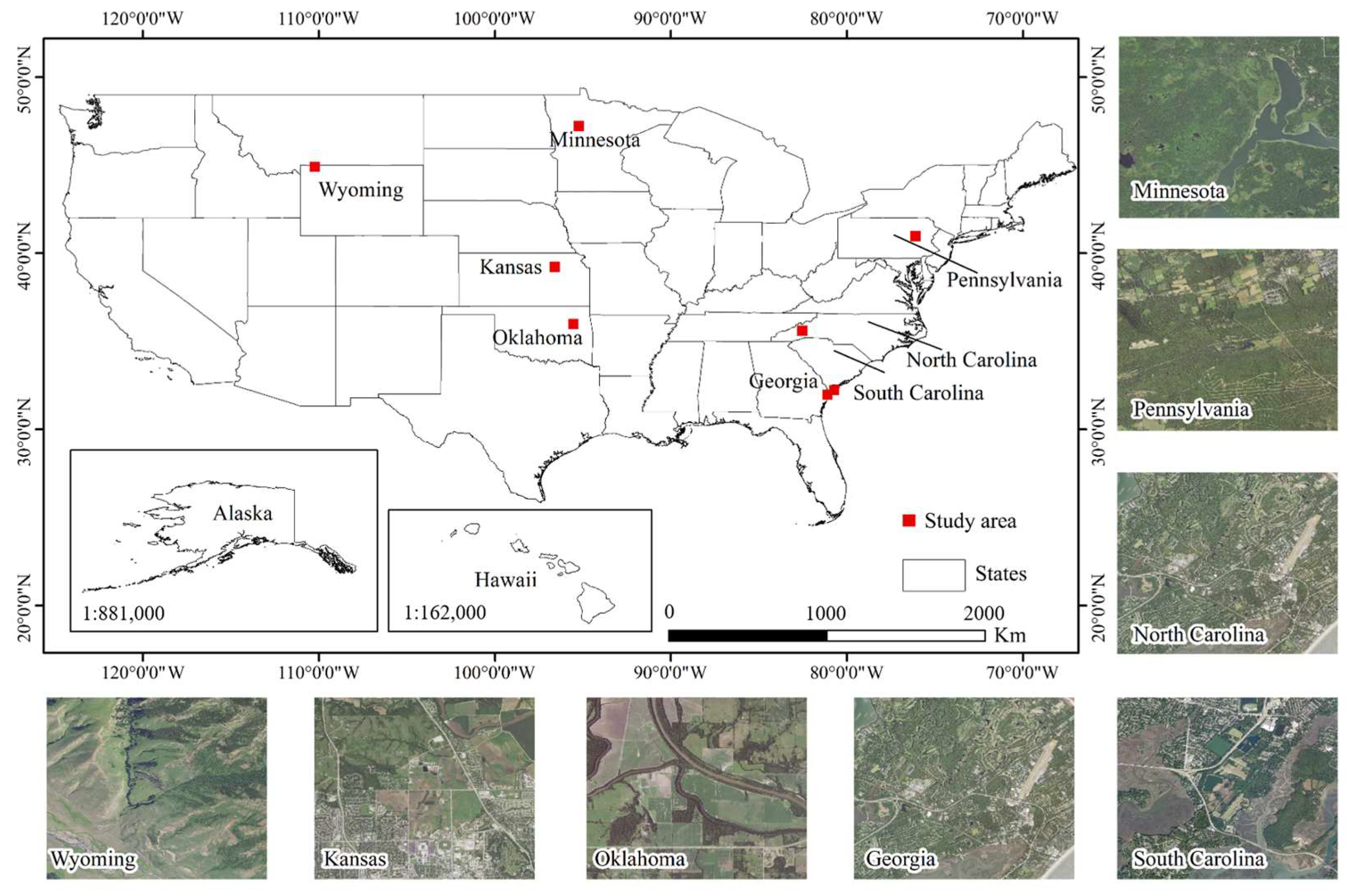
2.1. Study Area
2.2. Acquisition and Preprocessing of Multi-Source Remote Sensing Data
2.2.1. Sentinel-1 Data
2.2.2. Sentinel-2 Data
2.2.3. National Agriculture Imagery Program (NAIP) Aerial Imagery
2.2.4. NLCD TCC Product
2.2.5. Remote Sensing Vegetation Index
2.2.6. Auxiliary Data
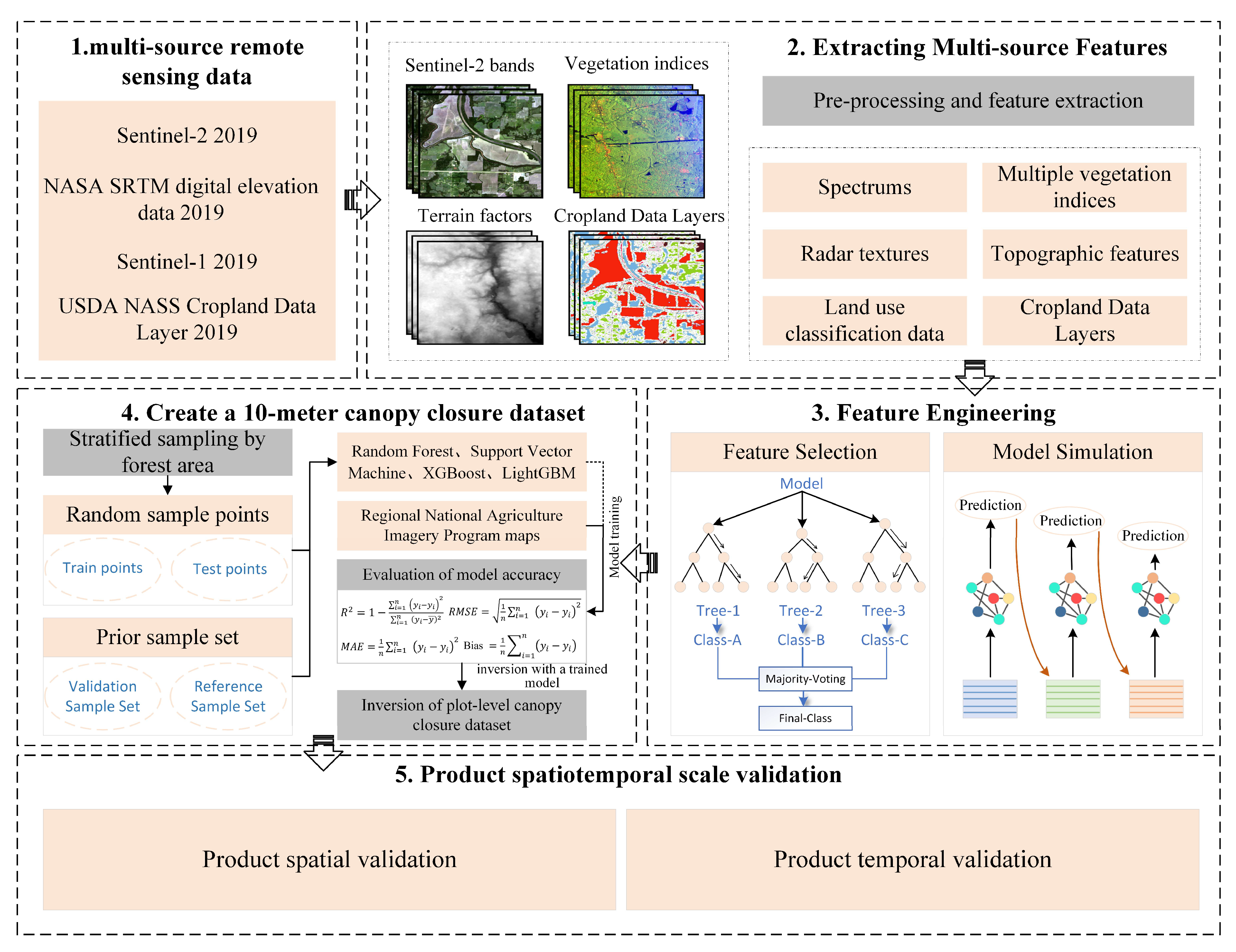
3. Methods
3.1. True Canopy Closure Modeling
3.2. Selection of Study Area Samples
3.3. Tree Canopy Closure Estimation Based on Machine Learning Models
3.3.1. Machine Learning Algorithms
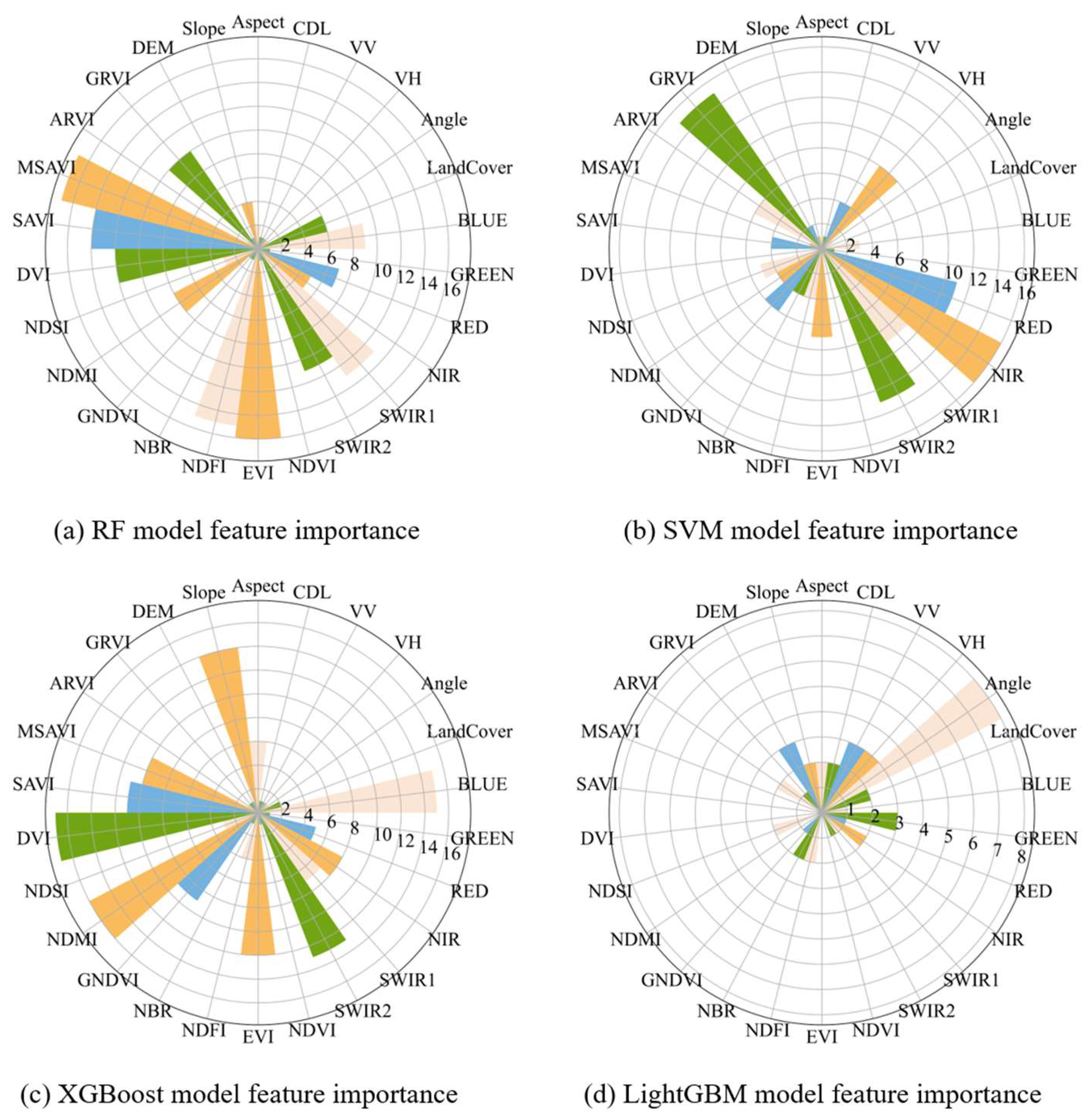
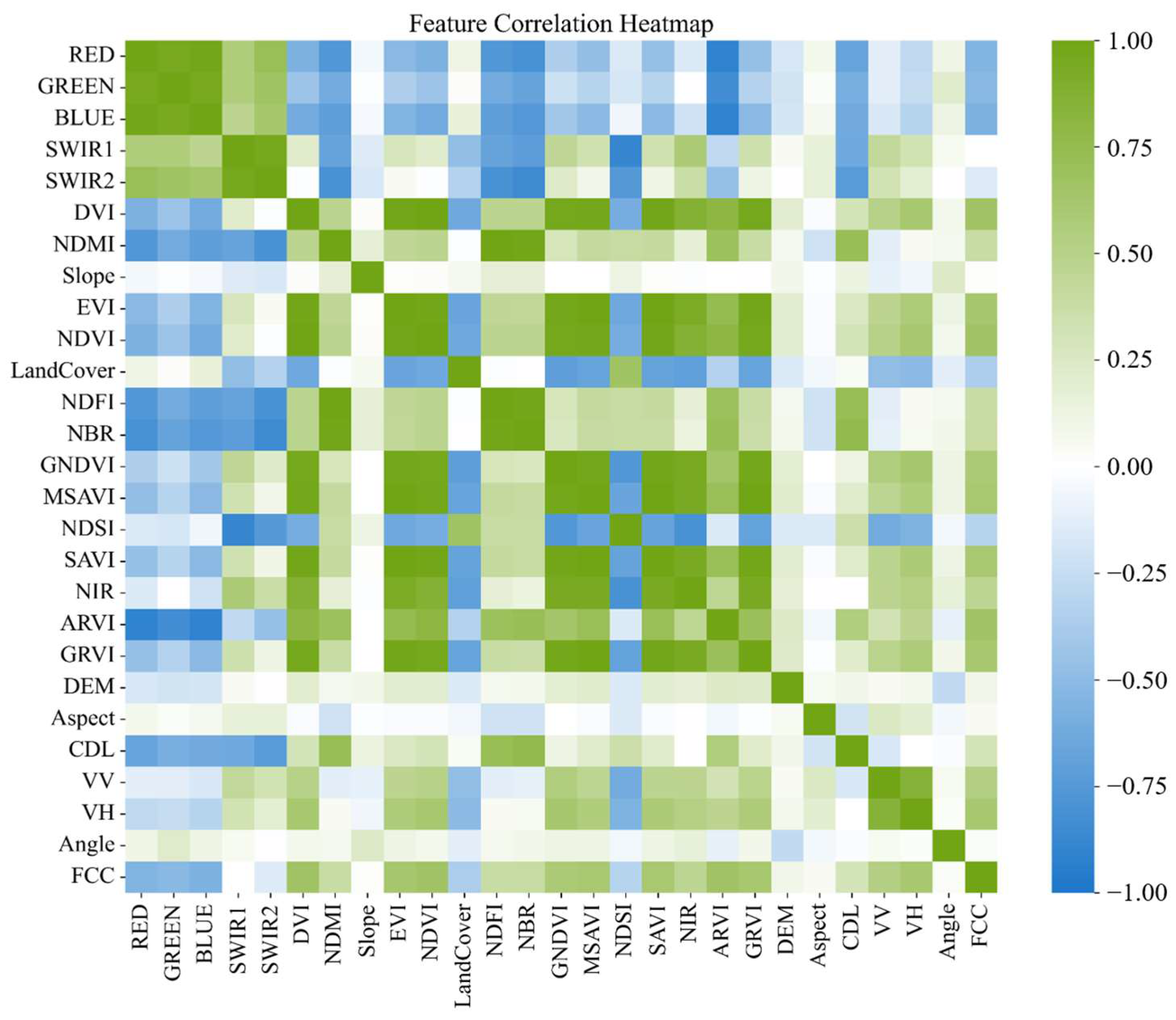
3.3.2. Feature Selection
3.3.3. Parameter Tuning
3.3.4. Evaluation Metrics
3.4. Spatiotemporal Comparison of Canopy Closure Estimation Result
4. Results and Analysis
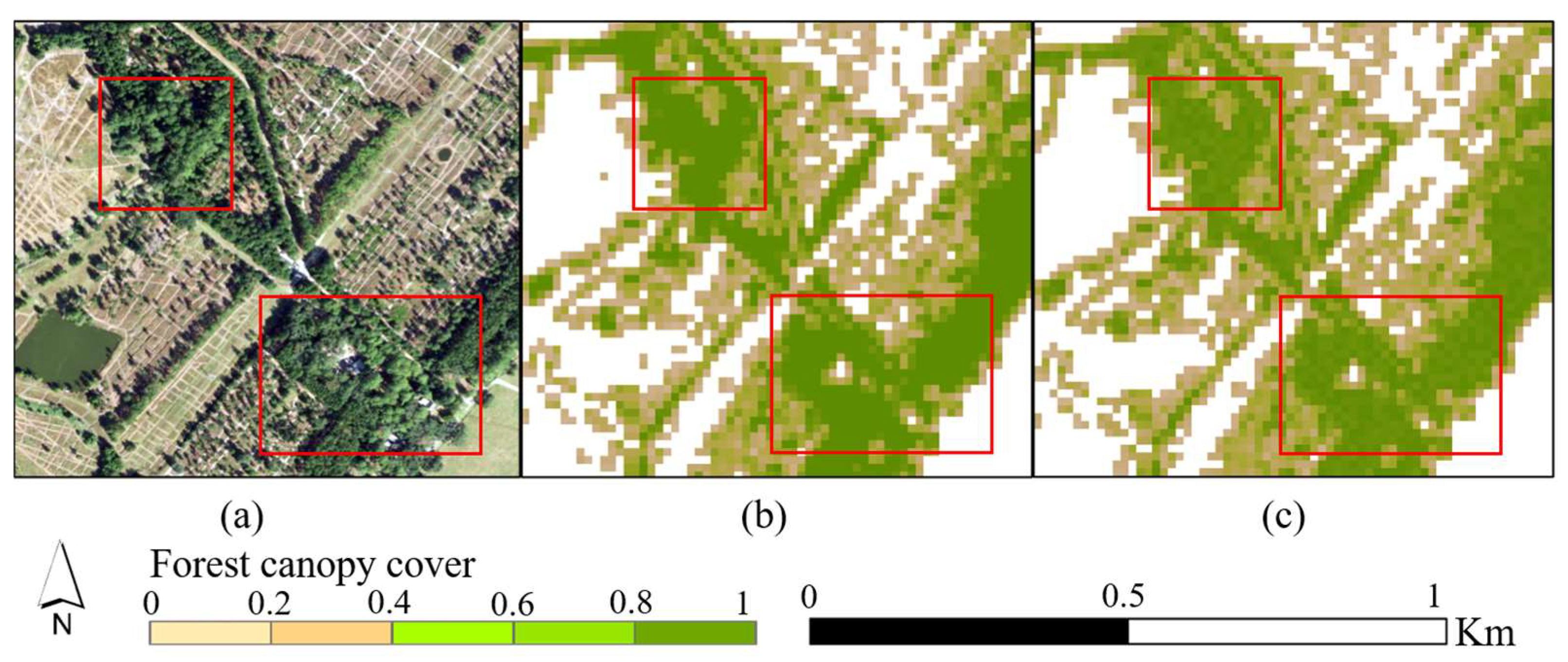
4.1. Crown Identification
4.2. Machine Learning-Based Estimation of Tree Canopy Closure
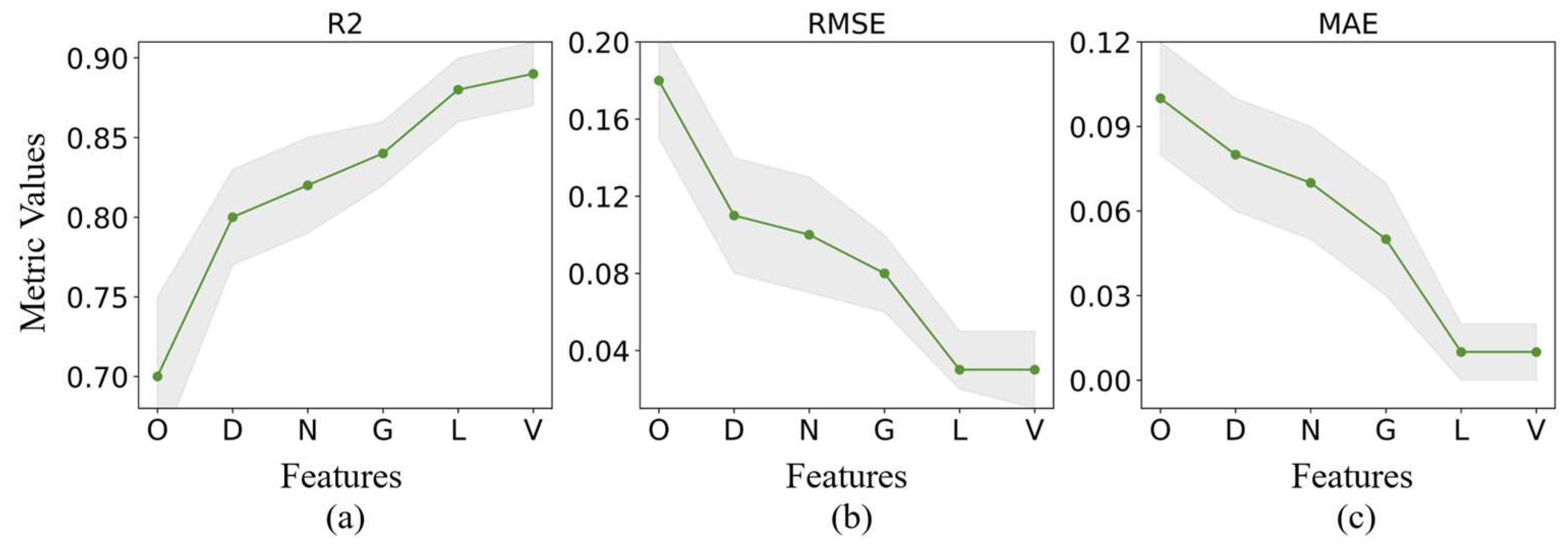
4.2.1. Feature Selection and Parameter Tuning
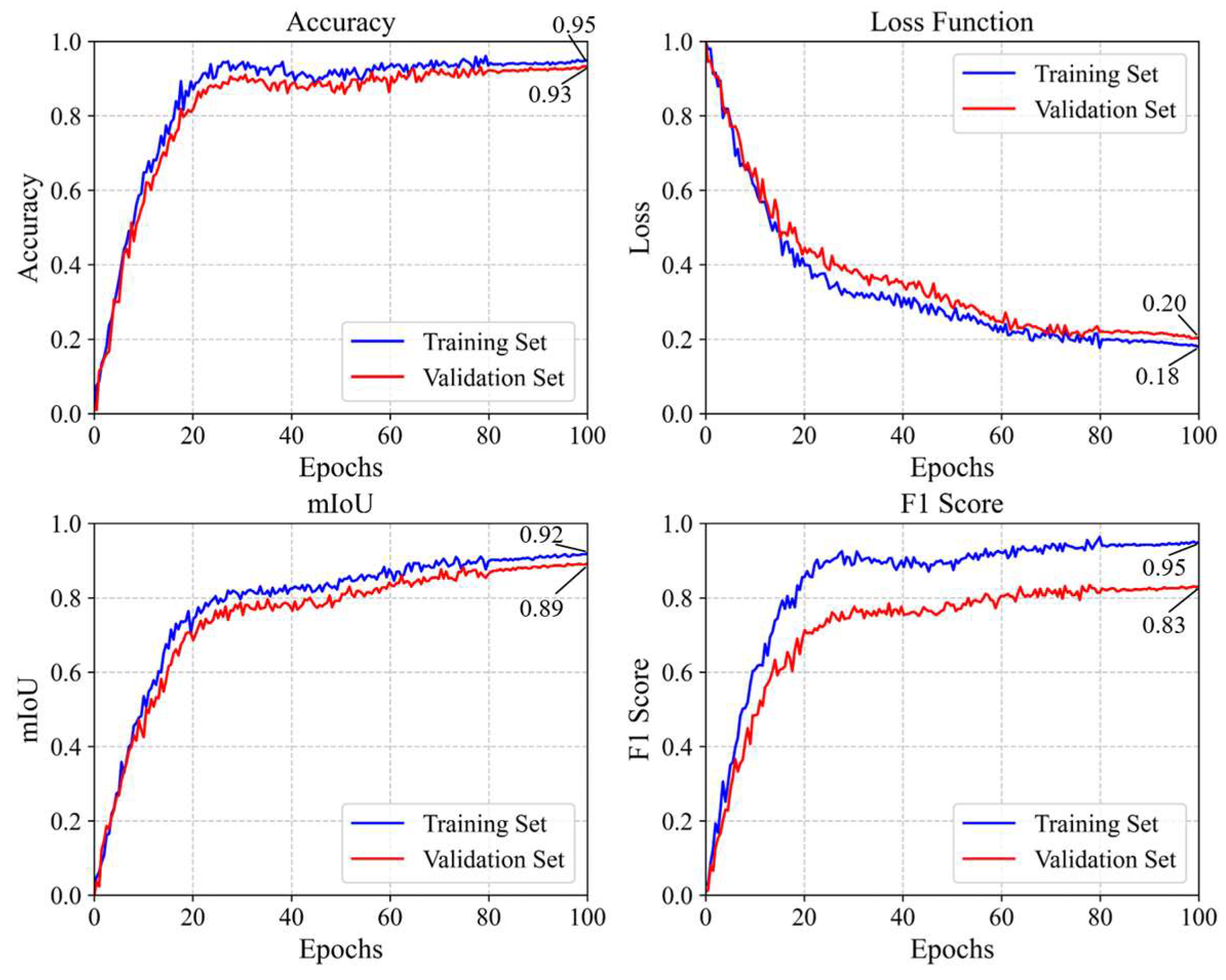
4.2.2. Model Estimation Accuracy
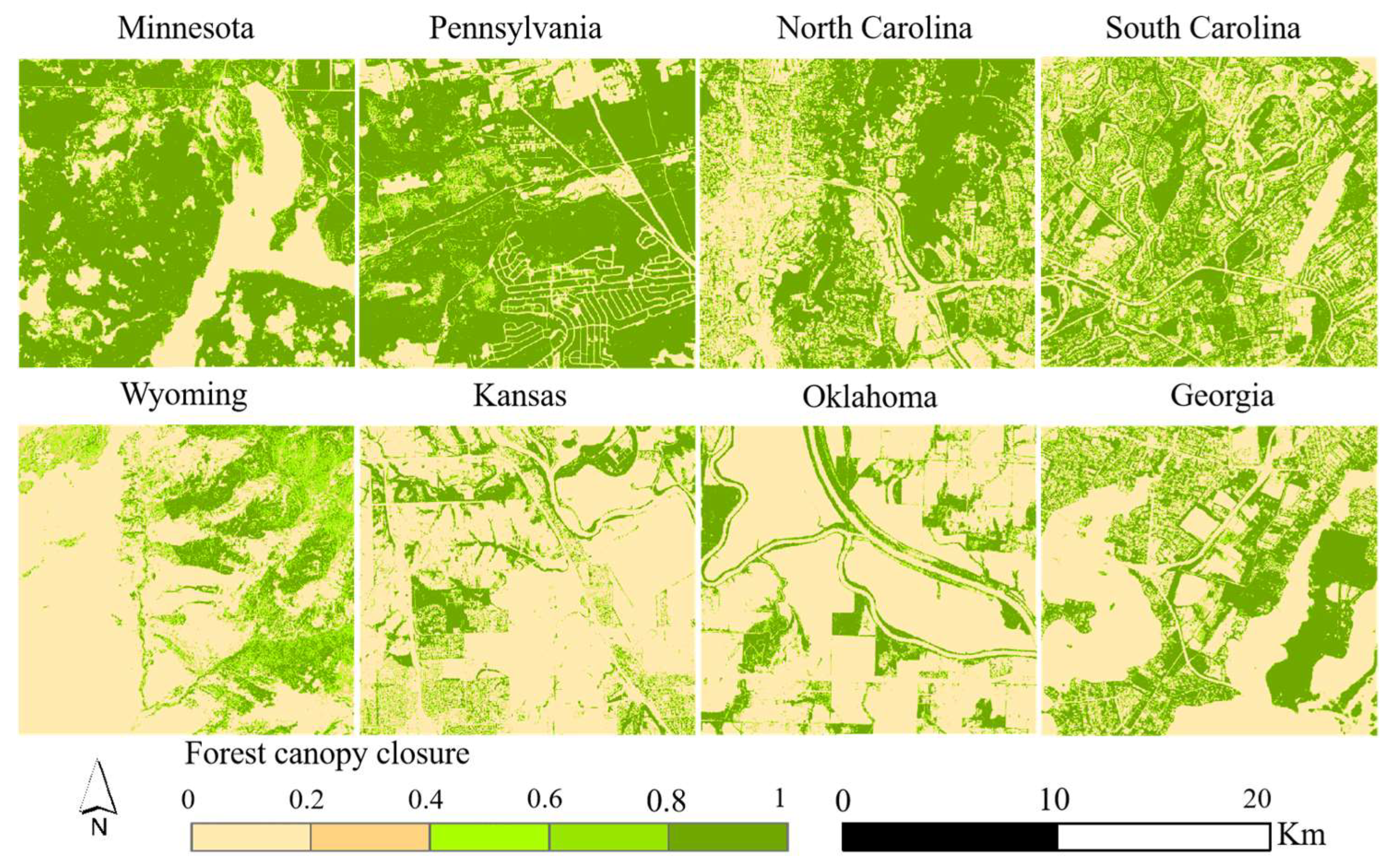
4.3. Canopy Closure Model Estimation Results
4.4. Comparison of Model Estimation Results with NLCD TCC Product on Temporal and Spatial Scales
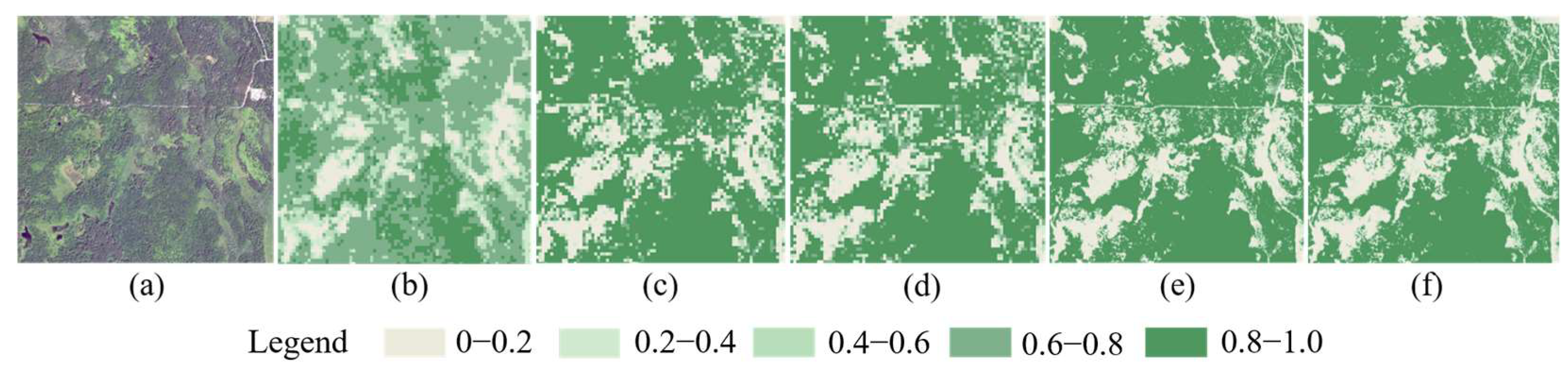
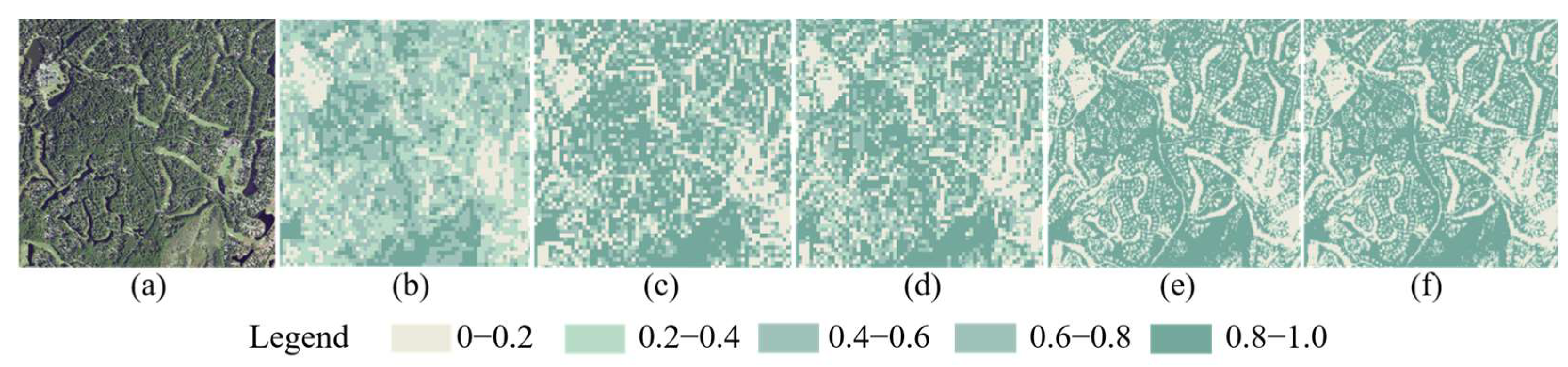
4.4.1. Comparison on Spatial Scale
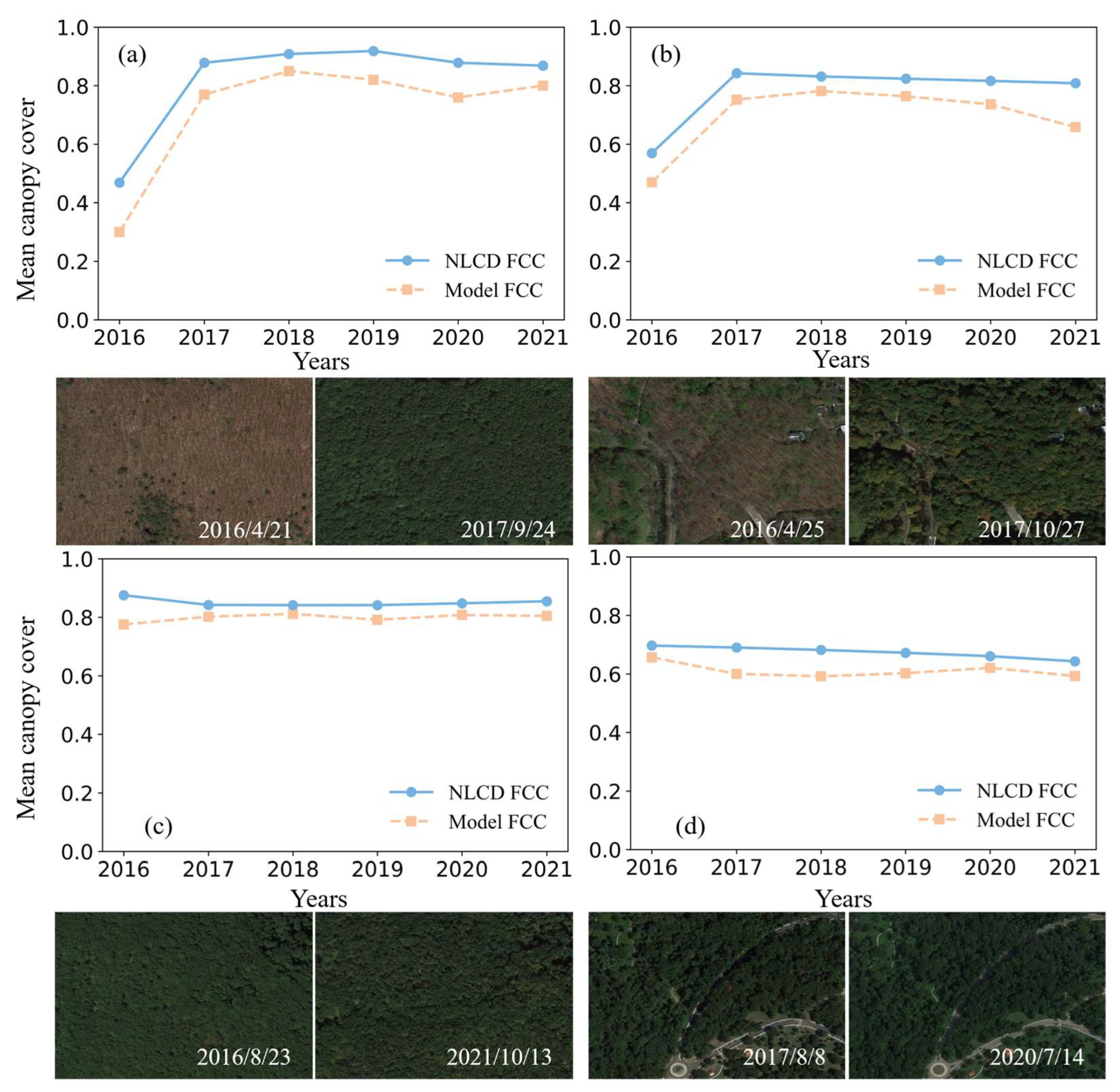
4.4.2. Comparison on Temporal Scale
5. Discussion
5.1. Application of Deep Learning in Canopy Closure Estimation
5.2. Multi-Source Remote Sensing Data Fusion
5.3. Limitations and Uncertainties
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anderegg, W.R.L.; Trugman, A.T.; Badgley, G.; Anderson, C.M.; Bartuska, A.; Ciais, P.; Cullenward, D.; Field, C.B.; Freeman, J.; Goetz, S.J.; et al. Climate-driven risks to the climate mitigation potential of forests. Science 2020, 368, eaaz7005. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, A.; Turner, W.R.; Spawn, S.A.; Anderson-Teixeira, K.J.; Cook-Patton, S.; Fargione, J.; Gibbs, H.K.; Griscom, B.; Hewson, J.H.; Howard, J.F.; et al. Protecting irrecoverable carbon in Earth’s ecosystems. Nat. Clim. Change 2020, 10, 287–295. [Google Scholar] [CrossRef]
- Rustad, L.E. The response of terrestrial ecosystems to global climate change: Towards an integrated approach. Sci. Total Environ. 2008, 404, 222–235. [Google Scholar] [CrossRef] [PubMed]
- Watson, J.E.M.; Evans, T.; Venter, O.; Williams, B.; Tulloch, A.; Stewart, C.; Thompson, I.; Ray, J.C.; Murray, K.; Salazar, A.; et al. The exceptional value of intact forest ecosystems. Nat. Ecol. Evol. 2018, 2, 599–610. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, P.S.; Huettmann, F.; Liu, S.R. Where should China practice forestry in a warming world? Glob. Change Biol. 2022, 28, 2461–2475. [Google Scholar] [CrossRef]
- Cai, W.X.; He, N.P.; Li, M.X.; Xu, L.; Wang, L.Z.; Zhu, J.H.; Zeng, N.; Yan, P.; Si, G.X.; Zhang, X.Q.; et al. Carbon sequestration of Chinese forests from 2010 to 2060 spatiotemporal dynamics and its regulatory strategies. Sci. Bull. 2022, 67, 836–843. [Google Scholar] [CrossRef]
- Cao, S.X.; Lu, C.X.; Yue, H. Optimal Tree Canopy Cover during Ecological Restoration: A Case Study of Possible Ecological Thresholds in Changting, China. Bioscience 2017, 67, 221–232. [Google Scholar] [CrossRef]
- Nakamura, A.; Kitching, R.L.; Cao, M.; Creedy, T.J.; Fayle, T.M.; Freiberg, M.; Hewitt, C.N.; Itioka, T.; Koh, L.P.; Ma, K.; et al. Forests and Their Canopies: Achievements and Horizons in Canopy Science. Trends Ecol. Evol. 2017, 32, 438–451. [Google Scholar] [CrossRef]
- Zomer, R.J.; Bossio, D.A.; Trabucco, A.; van Noordwijk, M.; Xu, J. Global carbon sequestration potential of agroforestry and increased tree cover on agricultural land. Circ. Agric. Syst. 2022, 2, 1–10. [Google Scholar] [CrossRef]
- Taneja, R.; Wallace, L.; Reinke, K.; Hilton, J.; Jones, S. Differences in Canopy Cover Estimations from ALS Data and Their Effect on Fire Prediction. Environ. Model. Assess. 2023, 28, 565–583. [Google Scholar] [CrossRef]
- Büchi, L.; Wendling, M.; Mouly, P.; Charles, R. Comparison of Visual Assessment and Digital Image Analysis for Canopy Cover Estimation. Agron. J. 2018, 110, 1289–1295. [Google Scholar] [CrossRef]
- Martin, D.A.; Wurz, A.; Osen, K.; Grass, I.; Hölscher, D.; Rabemanantsoa, T.; Tscharntke, T.; Kreft, H. Shade-Tree Rehabilitation in Vanilla Agroforests is Yield Neutral and May Translate into Landscape-Scale Canopy Cover Gains. Ecosystems 2021, 24, 1253–1267. [Google Scholar] [CrossRef]
- Tang, H.; Armston, J.; Hancock, S.; Marselis, S.; Goetz, S.; Dubayah, R. Characterizing global forest canopy cover distribution using spaceborne lidar. Remote Sens. Environ. 2019, 231, 11. [Google Scholar] [CrossRef]
- Bonney, M.T.; He, Y.H.; Vogeler, J.; Conway, T.; Kaye, E. Mapping canopy cover for municipal forestry monitoring: Using free Landsat imagery and machine learning. Urban For. Urban Green. 2024, 100, 18. [Google Scholar] [CrossRef]
- Wang, X.J.; Scott, C.E.; Dallimer, M. High summer land surface temperatures in a temperate city are mitigated by tree canopy cover. Urban CLim. 2023, 51, 11. [Google Scholar] [CrossRef]
- Qiu, Z.X.; Feng, Z.K.; Song, Y.N.; Li, M.L.; Zhang, P.P. Carbon sequestration potential of forest vegetation in China from 2003 to 2050: Predicting forest vegetation growth based on climate and the environment. J. Clean. Prod. 2020, 252, 14. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, J.; You, C.M.; Cao, R.; Tan, B.; Li, H.; Yang, W.Q. Contributions of National Key Forestry Ecology Projects to the forest vegetation carbon storage in China. For. Ecol. Manag. 2020, 462, 8. [Google Scholar] [CrossRef]
- Li, Z.; Ota, T.; Mizoue, N. Monitoring tropical forest change using tree canopy cover time series obtained from Sentinel-1 and Sentinel-2 data. Int. J. Digit. Earth 2024, 17, 17. [Google Scholar] [CrossRef]
- Schleeweis, K.; Goward, S.N.; Huang, C.Q.; Masek, J.G.; Moisen, G.; Kennedy, R.E.; Thomas, N.E. Regional dynamics of forest canopy change and underlying causal processes in the contiguous US. J. Geophys. Res.-Biogeosci. 2013, 118, 1035–1053. [Google Scholar] [CrossRef]
- Dash, J.P.; Watt, M.S.; Pearse, G.D.; Heaphy, M.; Dungey, H.S. Assessing very high resolution UAV imagery for monitoring forest health during a simulated disease outbreak. ISPRS-J. Photogramm. Remote Sens. 2017, 131, 1–14. [Google Scholar] [CrossRef]
- Ulmer, J.M.; Wolf, K.L.; Backman, D.R.; Tretheway, R.L.; Blain, C.J.A.; O’Neil-Dunne, J.P.M.; Frank, L.D. Multiple health benefits of urban tree canopy: The mounting evidence for a green prescription. Health Place 2016, 42, 54–62. [Google Scholar] [CrossRef] [PubMed]
- De Lombaerde, E.; Vangansbeke, P.; Lenoir, J.; Van Meerbeek, K.; Lembrechts, J.; Rodríguez-Sánchez, F.; Luoto, M.; Scheffers, B.; Haesen, S.; Aalto, J.; et al. Maintaining forest cover to enhance temperature buffering under future climate change. Sci. Total Environ. 2022, 810, 9. [Google Scholar] [CrossRef]
- Halpern, C.B.; Lutz, J.A. Canopy closure exerts weak controls on understory dynamics: A 30-year study of overstory-understory interactions. Ecol. Monogr. 2013, 83, 221–237. [Google Scholar] [CrossRef]
- Parent, J.R.; Volin, J.C. Assessing the potential for leaf-off LiDAR data to model canopy closure in temperate deciduous forests. ISPRS-J. Photogramm. Remote Sens. 2014, 95, 134–145. [Google Scholar] [CrossRef]
- Paletto, A.; Tosi, V. Forest canopy cover and canopy closure: Comparison of assessment techniques. Eur. J. For. Res. 2009, 128, 265–272. [Google Scholar] [CrossRef]
- Gyawali, A.; Aalto, M.; Peuhkurinen, J.; Villikka, M.; Ranta, T. Comparison of Individual Tree Height Estimated from LiDAR and Digital Aerial Photogrammetry in Young Forests. Sustainability 2022, 14, 3720. [Google Scholar] [CrossRef]
- Gonçalves, F.; Treuhaft, R.; Law, B.; Almeida, A.; Walker, W.; Baccini, A.; dos Santos, J.R.; Graça, P. Estimating Aboveground Biomass in Tropical Forests: Field Methods and Error Analysis for the Calibration of Remote Sensing Observations. Remote Sens. 2017, 9, 47. [Google Scholar] [CrossRef]
- Ganz, S.; Käber, Y.; Adler, P. Measuring Tree Height with Remote Sensing-A Comparison of Photogrammetric and LiDAR Data with Different Field Measurements. Forests 2019, 10, 694. [Google Scholar] [CrossRef]
- Gonzalez, P.; Asner, G.P.; Battles, J.J.; Lefsky, M.A.; Waring, K.M.; Palace, M. Forest carbon densities and uncertainties from Lidar, QuickBird, and field measurements in California. Remote Sens. Environ. 2010, 114, 1561–1575. [Google Scholar] [CrossRef]
- Fleck, S.; Mölder, I.; Jacob, M.; Gebauer, T.; Jungkunst, H.F.; Leuschner, C. Comparison of conventional eight-point crown projections with LIDAR-based virtual crown projections in a temperate old-growth forest. Ann. For. Sci. 2011, 68, 1173–1185. [Google Scholar] [CrossRef]
- Atkins, J.W.; Bhatt, P.; Carrasco, L.; Francis, E.; Garabedian, J.E.; Hakkenberg, C.R.; Hardiman, B.S.; Jung, J.H.; Koirala, A.; Larue, E.A.; et al. Integrating forest structural diversity measurement into ecological research. Ecosphere 2023, 14, 17. [Google Scholar] [CrossRef]
- Jurjevic, L.; Liang, X.L.; Gasparovic, M.; Balenovic, I. Is field-measured tree height as reliable as believed—Part II, A comparison study of tree height estimates from conventional field measurement and low-cost close-range remote sensing in a deciduous forest. ISPRS-J. Photogramm. Remote Sens. 2020, 169, 227–241. [Google Scholar] [CrossRef]
- Unger, D.R.; Hung, I.K.; Brooks, R.; Williams, H. Estimating number of trees, tree height and crown width using Lidar data. GISci. Remote Sens. 2014, 51, 227–238. [Google Scholar] [CrossRef]
- Ma, Q.; Su, Y.J.; Guo, Q.H. Comparison of Canopy Cover Estimations From Airborne LiDAR, Aerial Imagery, and Satellite Imagery. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 4225–4236. [Google Scholar] [CrossRef]
- McIntosh, A.C.S.; Gray, A.N.; Garman, S.L. Estimating Canopy Cover from Standard Forest Inventory Measurements in Western Oregon. For. Sci. 2012, 58, 154–167. [Google Scholar] [CrossRef]
- Ucar, Z.; Bettinger, P.; Merry, K.; Siry, J.; Bowker, J.M.; Akbulut, R. A comparison of two sampling approaches for assessing the urban forest canopy cover from aerial photography. Urban For. Urban Green. 2016, 16, 221–230. [Google Scholar] [CrossRef]
- Joshi, C.; De Leeuw, J.; Skidmore, A.K.; van Duren, I.C.; van Oosten, H. Remotely sensed estimation of forest canopy density: A comparison of the performance of four methods. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 84–95. [Google Scholar] [CrossRef]
- Zhu, Y.Y.; Jeon, S.; Sung, H.; Kim, Y.; Park, C.; Cha, S.; Jo, H.W.; Lee, W.K. Developing UAV-Based Forest Spatial Information and Evaluation Technology for Efficient Forest Management. Sustainability 2020, 12, 10150. [Google Scholar] [CrossRef]
- Michez, A.; Huylenbroeck, L.; Bolyn, C.; Latte, N.; Bauwens, S.; Lejeune, P. Can regional aerial images from orthophoto surveys produce high quality photogrammetric Canopy Height Model? A single tree approach in Western Europe. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 10. [Google Scholar] [CrossRef]
- Corona, P.; Chirici, G.; Franceschi, S.; Maffei, D.; Marcheselli, M.; Pisani, C.; Fattorini, L. Design-based treatment of missing data in forest inventories using canopy heights from aerial laser scanning. Can. J. For. Res. 2014, 44, 892–902. [Google Scholar] [CrossRef]
- Kangas, A.; Astrup, R.; Breidenbach, J.; Fridman, J.; Gobakken, T.; Korhonen, K.T.; Maltamo, M.; Nilsson, M.; Nord-Larsen, T.; Næsset, E.; et al. Remote sensing and forest inventories in Nordic countries—Roadmap for the future. Scand. J. For. Res. 2018, 33, 397–412. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar remote sensing for ecosystem studies: Lidar, an emerging remote sensing technology that directly measures the three-dimensional distribution of plant canopies, can accurately estimate vegetation structural attributes and should be of particular interest to forest, landscape, and global ecologists. Bioscience 2002, 52, 19–30. [Google Scholar]
- Zhao, K.G.; Popescu, S.; Meng, X.L.; Pang, Y.; Agca, M. Characterizing forest canopy structure with lidar composite metrics and machine learning. Remote Sens. Environ. 2011, 115, 1978–1996. [Google Scholar] [CrossRef]
- Brandt, J.; Ertel, J.; Spore, J.; Stolle, F. Wall-to-wall mapping of tree extent in the tropics with Sentinel-1 and Sentinel-2. Remote Sens. Environ. 2023, 292, 19. [Google Scholar] [CrossRef]
- Nasiri, V.; Darvishsefat, A.A.; Arefi, H.; Griess, V.C.; Sadeghi, S.M.M.; Borz, S.A. Modeling Forest Canopy Cover: A Synergistic Use of Sentinel-2, Aerial Photogrammetry Data, and Machine Learning. Remote Sens. 2022, 14, 1453. [Google Scholar] [CrossRef]
- Silveira, E.M.O.; Radeloff, V.C.; Martinuzzi, S.; Pastur, G.J.M.; Bono, J.; Politi, N.; Lizarraga, L.; Rivera, L.O.; Ciuffoli, L.; Rosas, Y.M.; et al. Nationwide native forest structure maps for Argentina based on forest inventory data, SAR Sentinel-1 and vegetation metrics from Sentinel-2 imagery. Remote Sens. Environ. 2023, 285, 17. [Google Scholar] [CrossRef]
- Heckel, K.; Urban, M.; Schratz, P.; Mahecha, M.D.; Schmullius, C. Predicting Forest Cover in Distinct Ecosystems: The Potential of Multi-Source Sentinel-1 and-2 Data Fusion. Remote Sens. 2020, 12, 302. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.C.; Wang, L.; Chen, H.Y. High-resolution mapping of forest canopy height using machine learning by coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 14. [Google Scholar] [CrossRef]
- Tang, X.; Bratley, K.H.; Cho, K.; Bullock, E.L.; Olofsson, P.; Woodcock, C.E. Near real-time monitoring of tropical forest disturbance by fusion of Landsat, Sentinel-2, and Sentinel-1 data. Remote Sens. Environ. 2023, 294, 113626. [Google Scholar] [CrossRef]
- Waldeland, A.U.; Trier, O.D.; Salberg, A.B. Forest mapping and monitoring in Africa using Sentinel-2 data and deep learning. Int. J. Appl. Earth Obs. Geoinf. 2022, 111, 13. [Google Scholar] [CrossRef]
- Fiore, N.M.; Goulden, M.L.; Czimczik, C.I.; Pedron, S.A.; Tayo, M.A. Do recent NDVI trends demonstrate boreal forest decline in Alaska? Environ. Res. Lett. 2020, 15, 095007. [Google Scholar] [CrossRef]
- Abrams, J.F.; Vashishtha, A.; Wong, S.T.; Nguyen, A.; Mohamed, A.; Wieser, S.; Kuijper, A.; Wilting, A.; Mukhopadhyay, A. Habitat-Net: Segmentation of habitat images using deep learning. Ecol. Inform. 2019, 51, 121–128. [Google Scholar] [CrossRef]
- Niedballa, J.; Axtner, J.; Döbert, T.F.; Tilker, A.; Nguyen, A.; Wong, S.T.; Fiderer, C.; Heurich, M.; Wilting, A. imageseg: An R package for deep learning-based image segmentation. Methods Ecol. Evol. 2022, 13, 2363–2371. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Camarero, J.J.; Olano, J.M.; Martín-Hernández, N.; Peña-Gallardo, M.; Tomás-Burguera, M.; Gazol, A.; Azorin-Molina, C.; Bhuyan, U.; El Kenawy, A. Diverse relationships between forest growth and the Normalized Difference Vegetation Index at a global scale. Remote Sens. Environ. 2016, 187, 14–29. [Google Scholar] [CrossRef]
- Yang, Q.L.; Zhang, H.; Peng, W.S.; Lan, Y.Y.; Luo, S.S.; Shao, J.M.; Chen, D.Z.; Wang, G.Q. Assessing climate impact on forest cover in areas undergoing substantial land cover change using Landsat imagery. Sci. Total Environ. 2019, 659, 732–745. [Google Scholar] [CrossRef]
- Krishnan, S.; Pradhan, A.; Indu, J. Estimation of high-resolution precipitation using downscaled satellite soil moisture and SM2RAIN approach. J. Hydrol. 2022, 610, 14. [Google Scholar] [CrossRef]
- Phompila, C.; Lewis, M.; Ostendorf, B.; Clarke, K. MODIS EVI and LST Temporal Response for Discrimination of Tropical Land Covers. Remote Sens. 2015, 7, 6026–6040. [Google Scholar] [CrossRef]
- Huang, C.Y.; Durán, S.M.; Hu, K.T.; Li, H.J.; Swenson, N.G.; Enquist, B.J. Remotely sensed assessment of increasing chronic and episodic drought effects on a Costa Rican tropical dry forest. Ecosphere 2021, 12, 19. [Google Scholar] [CrossRef]
- Wang, L.L.; Hunt, E.R.; Qu, J.J.; Hao, X.J.; Daughtry, C.S.T. Towards estimation of canopy foliar biomass with spectral reflectance measurements. Remote Sens. Environ. 2011, 115, 836–840. [Google Scholar] [CrossRef]
- Danson, F.M.; Hetherington, D.; Morsdorf, F.; Koetz, B.; Allgöwer, B. Forest canopy gap fraction from terrestrial laser scanning. IEEE Geosci. Remote Sens. Lett. 2007, 4, 157–160. [Google Scholar] [CrossRef]
- Gonsamo, A. Leaf area index retrieval using gap fractions obtained from high resolution satellite data: Comparisons of approaches, scales and atmospheric effects. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 233–248. [Google Scholar] [CrossRef]
- Chen, A.; Orlov-Levin, V.; Meron, M. Applying high-resolution visible-channel aerial imaging of crop canopy to precision irrigation management. Agric. Water Manag. 2019, 216, 196–205. [Google Scholar] [CrossRef]
- Su, Y.J.; Guo, Q.H.; Ma, Q.; Li, W.K. SRTM DEM Correction in Vegetated Mountain Areas through the Integration of Spaceborne LiDAR, Airborne LiDAR, and Optical Imagery. Remote Sens. 2015, 7, 11202–11225. [Google Scholar] [CrossRef]
- Li, H.; Di, L.P.; Zhang, C.; Lin, L.; Guo, L.Y.; Yu, E.G.; Yang, Z.W. Automated In-Season Crop-Type Data Layer Mapping Without Ground Truth for the Conterminous United States Based on Multisource Satellite Imagery. IEEE Trans. Geosci. Remote Sensing 2024, 62, 14. [Google Scholar] [CrossRef]
- Chaaban, F.; El Khattabi, J.; Darwishe, H. Accuracy Assessment of ESA WorldCover 2020 and ESRI 2020 Land Cover Maps for a Region in Syria. J. Geovis. Spat. Anal. 2022, 6, 23. [Google Scholar] [CrossRef]
- Freudenberg, M.; Magdon, P.; Nölke, N. Individual tree crown delineation in high-resolution remote sensing images based on U-Net. Neural Comput. Appl. 2022, 34, 22197–22207. [Google Scholar] [CrossRef]
- Ko, D.; Bristow, N.; Greenwood, D.; Weisberg, P. Canopy Cover Estimation in Semiarid Woodlands: Comparison of Field-Based and Remote Sensing Methods. For. Sci. 2009, 55, 132–141. [Google Scholar] [CrossRef]
- Ke, C.Y.; He, S.; Qin, Y.G. Comparison of natural breaks method and frequency ratio dividing attribute intervals for landslide susceptibility mapping. Bull. Eng. Geol. Environ. 2023, 82, 18. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Xu, X. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev.-Data Mining Knowl. Discov. 2019, 9, 15. [Google Scholar]
- Zhou, Z.G.; Zhao, L.; Lin, A.W.; Qin, W.M.; Lu, Y.B.; Li, J.Y.; Zhong, Y.; He, L.J. Exploring the potential of deep factorization machine and various gradient boosting models in modeling daily reference evapotranspiration in China. Arab. J. Geosci. 2020, 13, 20. [Google Scholar] [CrossRef]
- Mushava, J.; Murray, M. Flexible loss functions for binary classification in gradient-boosted decision trees: An application to credit scoring. Expert Syst. Appl. 2024, 238, 16. [Google Scholar] [CrossRef]
- Mo, X.L.; Chen, X.J.; Leong, C.F.; Zhang, S.; Li, H.Y.; Li, J.L.; Lin, G.H.; Sun, G.C.; He, F.; He, Y.L.; et al. Early Prediction of Clinical Response to Etanercept Treatment in Juvenile Idiopathic Arthritis Using Machine Learning. Front. Pharmacol. 2020, 11, 9. [Google Scholar] [CrossRef]
- Peng, R.T.; Xiao, Z.L.; Peng, Y.H.; Zhang, X.X.; Zhao, L.F.; Gao, J.X. Research on multi-source information fusion tool wear monitoring based on MKW-GPR model. Measurement 2025, 242, 14. [Google Scholar] [CrossRef]
- Beeche, C.; Singh, J.P.; Leader, J.K.; Gezer, N.S.; Oruwari, A.P.; Dansingani, K.K.; Chhablani, J.; Pu, J.T. Super U-Net: A modularized generalizable architecture. Pattern Recognit. 2022, 128, 12. [Google Scholar] [CrossRef]
- Li, X.X.; Liu, X.J.; Xiao, Y.; Zhang, Y.; Yang, X.M.; Zhang, W.H. An Improved U-Net Segmentation Model That Integrates a Dual Attention Mechanism and a Residual Network for Transformer Oil Leakage Detection. Energies 2022, 15, 4238. [Google Scholar] [CrossRef]
- Poonguzhali, R.; Ahmad, S.; Sivasankar, P.T.; Babu, S.A.; Joshi, P.; Joshi, G.P.; Kim, S.W. Automated Brain Tumor Diagnosis Using Deep Residual U-Net Segmentation Model. CMC-Comput. Mat. Contin. 2023, 74, 2179–2194. [Google Scholar]
- Shwartz-Ziv, R.; Armon, A. Tabular data: Deep learning is not all you need. Inf. Fusion 2022, 81, 84–90. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, R.R.; Lu, Y.J.; Huang, J.D. Prediction of Compressive Strength of Geopolymer Concrete Landscape Design: Application of the Novel Hybrid RF-GWO-XGBoost Algorithm. Buildings 2024, 14, 591. [Google Scholar] [CrossRef]
- Tang, M.Z.; Liang, Z.X.; Wu, H.W.; Wang, Z.M. Fault Diagnosis Method for Wind Turbine Gearboxes Based on IWOA-RF. Energies 2021, 14, 6283. [Google Scholar] [CrossRef]
- Nanko, K.; Giambelluca, T.W.; Sutherland, R.A.; Mudd, R.G.; Nullet, M.A.; Ziegler, A.D. Erosion Potential under Miconia calvescens Stands on the Island of Hawai’i. Land Degrad. Dev. 2015, 26, 218–226. [Google Scholar] [CrossRef]
- Lin, Y.Y.; Jin, Y.D.; Ge, Y.; Hu, X.S.; Weng, A.F.; Wen, L.S.; Zhou, Y.R.; Li, B.Y. Insights into forest vegetation changes and landscape fragmentation in Southeastern China: From a perspective of spatial coupling and machine learning. Ecol. Indic. 2024, 166, 13. [Google Scholar] [CrossRef]
- Zhu, W.B.; Zhang, X.D.; Zhang, J.J.; Zhu, L.Q. A comprehensive analysis of phenological changes in forest vegetation of the Funiu Mountains, China. J. Geogr. Sci. 2019, 29, 131–145. [Google Scholar] [CrossRef]
- Narine, L.; Malambo, L.; Popescu, S. Characterizing canopy cover with ICESat-2: A case study of southern forests in Texas and Alabama, USA. Remote Sens. Environ. 2022, 281, 14. [Google Scholar] [CrossRef]
- Ashapure, A.; Jung, J.H.; Chang, A.J.; Oh, S.; Maeda, M.; Landivar, J. A Comparative Study of RGB and Multispectral Sensor-Based Cotton Canopy Cover Modelling Using Multi-Temporal UAS Data. Remote Sens. 2019, 11, 2757. [Google Scholar] [CrossRef]
- Zhou, Q.B.; Yu, Q.Y.; Liu, J.; Wu, W.B.; Tang, H.J. Perspective of Chinese GF-1 high-resolution satellite data in agricultural remote sensing monitoring. J. Integr. Agric. 2017, 16, 242–251. [Google Scholar] [CrossRef]
- Wu, X.H.; Zuo, W.M.; Lin, L.; Jia, W.; Zhang, D. F-SVM: Combination of Feature Transformation and SVM Learning via Convex Relaxation. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5185–5199. [Google Scholar] [CrossRef]
- Cai, Y.H.; Feng, J.X.; Wang, Y.Q.; Ding, Y.M.; Hu, Y.; Fang, H. The Optuna-LightGBM-XGBoost Model: A Novel Approach for Estimating Carbon Emissions Based on the Electricity-Carbon Nexus. Appl. Sci. 2024, 14, 4632. [Google Scholar] [CrossRef]
- Shi, M.Y.; Gao, Y.S.; Chen, L.; Liu, X.Z. Multisource Information Fusion Network for Optical Remote Sensing Image Super-Resolution. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2023, 16, 3805–3818. [Google Scholar] [CrossRef]
- Wei, X.L.; Bai, K.X.; Chang, N.B.; Gao, W. Multi-source hierarchical data fusion for high-resolution AOD mapping in a forest fire event. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 11. [Google Scholar] [CrossRef]
- Denny, C.K.; Nielsen, S.E. Spatial Heterogeneity of the Forest Canopy Scales with the Heterogeneity of an Understory Shrub Based on Fractal Analysis. Forests 2017, 8, 146. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Bian, Z.Q.; Ding, S.Y. Consequences of Spatial Heterogeneity of Forest Landscape on Ecosystem Water Conservation Service in the Yi River Watershed in Central China. Sustainability 2020, 12, 1170. [Google Scholar] [CrossRef]
- Armstrong, A.H.; Huth, A.; Osmanoglu, B.; Sun, G.; Ranson, K.J.; Fischer, R. A multi-scaled analysis of forest structure using individual-based modeling in a costa rican rainforest. Ecol. Model. 2020, 433, 10. [Google Scholar] [CrossRef]
- Camarero, J.J.; Colangelo, M.; Gazol, A.; Pizarro, M.; Valeriano, C.; Igual, J.M. Effects of Windthrows on Forest Cover, Tree Growth and Soil Characteristics in Drought-Prone Pine Plantations. Forests 2021, 12, 817. [Google Scholar] [CrossRef]
- Xu, J.L.; Xiao, L.; López, A.M. Self-Supervised Domain Adaptation for Computer Vision Tasks. IEEE Access 2019, 7, 156694–156706. [Google Scholar] [CrossRef]







| Feature | Descriptions | Feature | Descriptions |
|---|---|---|---|
| NDVI | SAVI | ||
| EVI | MSAVI | ||
| NDFI | ARVI | ||
| GNDVI | GRVI | ||
| NDMI | NBR | ||
| NDSI | DVI |
| TCC | 0.20–0.32 | 0.32–0.76 | 0.76–1.00 | |
|---|---|---|---|---|
| Study Area (km2) | ||||
| WY | 2.97/375 1 | 3.70/500 | 6.13/750 | |
| KS | 4.43/432 | 3.46/329 | 7.75/864 | |
| OK | 3.00/348 | 2.28/233 | 8.63/1044 | |
| GA | 4.36/308 | 3.65/239 | 14.13/1078 | |
| MN | 4.12/200 | 3.33/125 | 26.70/1300 | |
| PA | 3.96/184 | 3.38/153 | 27.82/1288 | |
| NC | 6.70/322 | 5.53/291 | 21.67/1012 | |
| SC | 6.40/336 | 5.60/281 | 17.08/1008 | |
| Component | Description | Hardware Requirements | Time Cost |
|---|---|---|---|
| Data preprocessing | Image cropping (256 × 256), normalization, augmentation | CPU (11th Gen Intel Core i7-11700, 8 cores, 16 threads) | ~10 min (5000 images with sliding window method, multi-threaded) |
| U-Net Training | Encoder–decoder structure for segmentation | GPU (RTX 4090, 24 GB VRAM) + CPU (16 threads), RAM (16 GB) | ~1–1.5 h (100 epochs, batch size 16, mixed precision) |
| RF | Post-segmentation classification (100 trees) | CPU (16 threads), RAM (16 GB) | ~10 min (5000 samples, 100 trees) |
| SVM | High-dimensional feature classification | CPU (16 threads), RAM (32 GB recommended for large datasets) | ~20–25 min (if dataset > 10,000 samples) |
| XGBoost | Gradient boosting tree optimization | GPU (RTX 4090) or CPU (16 threads) | ~3–5 min (5000 samples, max depth = 6, GPU acceleration) |
| LightGBM | Histogram-based gradient boosting decision tree | GPU (RTX 4090) or CPU (16 threads) | ~2–4 min (5000 samples, max depth = 6, GPU acceleration) |
| Storage requirements | Large-scale image and model storage | SSD (512 GB+) | - |
| Study Area | Data | 10 m Tree Canopy Closure Data (True TCC) | |||
|---|---|---|---|---|---|
| R2 | RMSE | MAE | Bias | ||
| GA | NLCD TCC | 0.59 | 0.43 | 9.50% | −7.7% |
| Model FCC | 0.87 | 0.16 | 6.47% | 0.47% | |
| KS | NLCD TCC | 0.64 | 0.35 | 13.50% | −6.97% |
| Model FCC | 0.81 | 0.18 | 11.41% | 2.85% | |
| MN | NLCD TCC | 0.37 | 0.47 | 8.58% | −9.67% |
| Model FCC | 0.85 | 0.13 | 5.08% | 2.67% | |
| OK | NLCD TCC | 0.68 | 0.26 | 23.33% | −14.21% |
| Model FCC | 0.89 | 0.10 | 19.72% | 0.07% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Wang, J.; Song, Z.; Zhou, M.; Lv, M.; Han, X. Estimation of Tree Canopy Closure Based on U-Net Image Segmentation and Machine Learning Algorithms. Remote Sens. 2025, 17, 1828. https://doi.org/10.3390/rs17111828
Zhou Y, Wang J, Song Z, Zhou M, Lv M, Han X. Estimation of Tree Canopy Closure Based on U-Net Image Segmentation and Machine Learning Algorithms. Remote Sensing. 2025; 17(11):1828. https://doi.org/10.3390/rs17111828
Chicago/Turabian StyleZhou, Yuefei, Jinghan Wang, Zengjing Song, Miaohang Zhou, Mengnan Lv, and Xujun Han. 2025. "Estimation of Tree Canopy Closure Based on U-Net Image Segmentation and Machine Learning Algorithms" Remote Sensing 17, no. 11: 1828. https://doi.org/10.3390/rs17111828
APA StyleZhou, Y., Wang, J., Song, Z., Zhou, M., Lv, M., & Han, X. (2025). Estimation of Tree Canopy Closure Based on U-Net Image Segmentation and Machine Learning Algorithms. Remote Sensing, 17(11), 1828. https://doi.org/10.3390/rs17111828






