On the Potential of Bayesian Neural Networks for Estimating Chlorophyll-a Concentration from Satellite Data
Abstract
1. Introduction
2. Data and Methods
2.1. Training and Validation Data
2.2. Standard Ocean Color Models
2.2.1. Ocean Chlorophyll 4-Band
2.2.2. Ocean Color Index
2.3. Bayesian Neural Network
2.4. Stochastic Variational Inference
2.4.1. Bayesian Statistics
2.4.2. Variational Inference
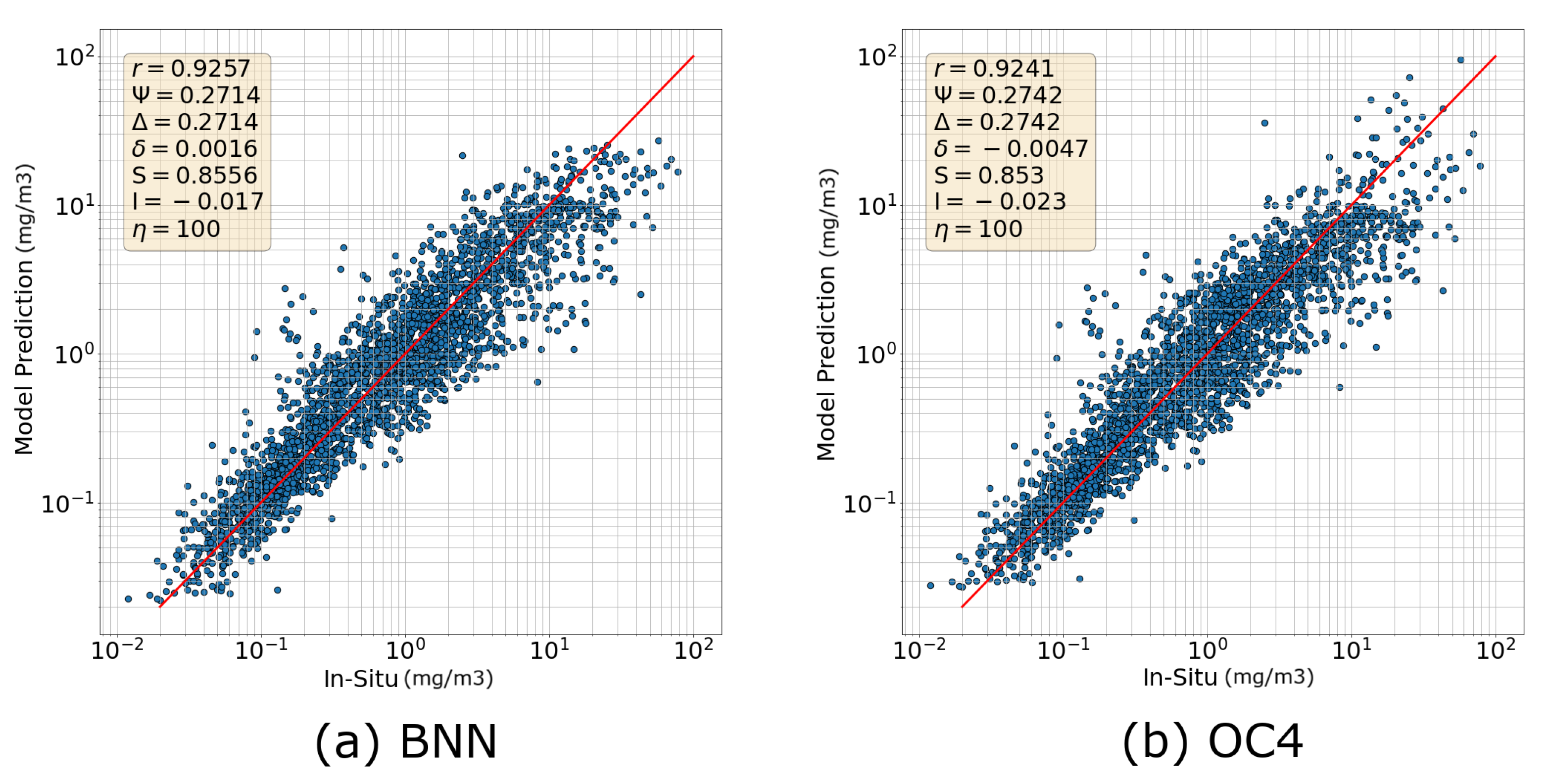
2.5. Evaluation Metrics
3. Results and Discussion
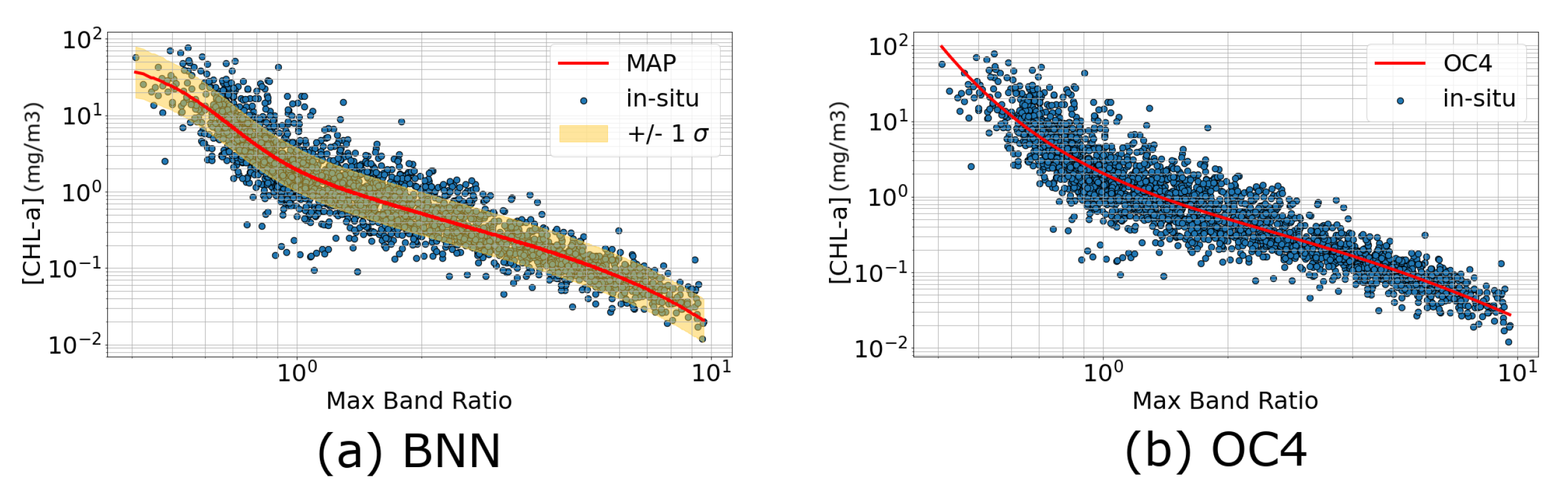
3.1. Numerical Comparison with Standard Algorithms
3.1.1. Comparison with OC4
3.1.2. Comparison with OCI
3.1.3. Maximum Band Ratio from Multiple Sensors
3.2. Advancing Beyond Standard Ocean Color Algorithm Capabilities
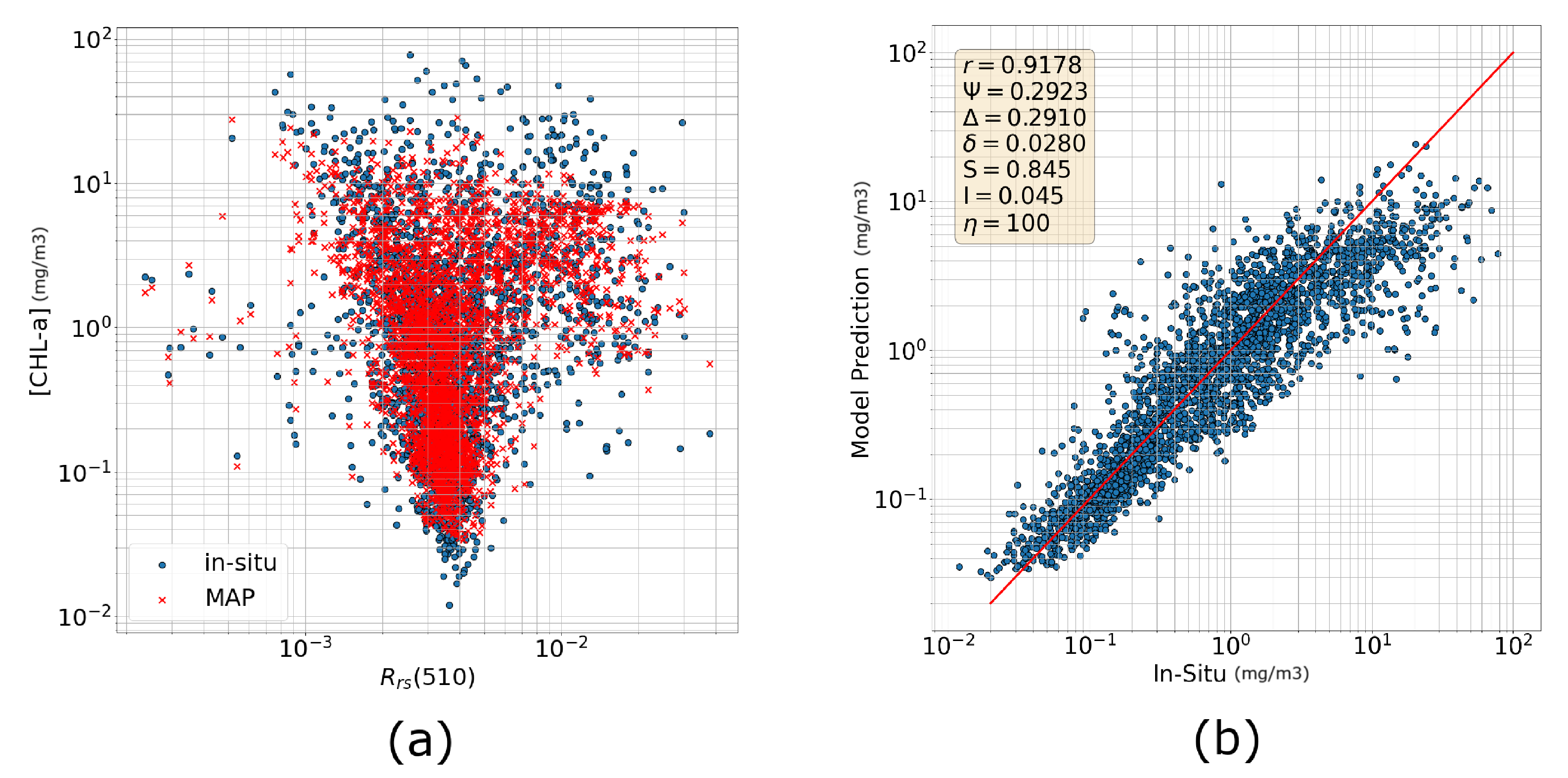
3.2.1. Training Directly with Reflectances
3.2.2. Incorporating IOPs
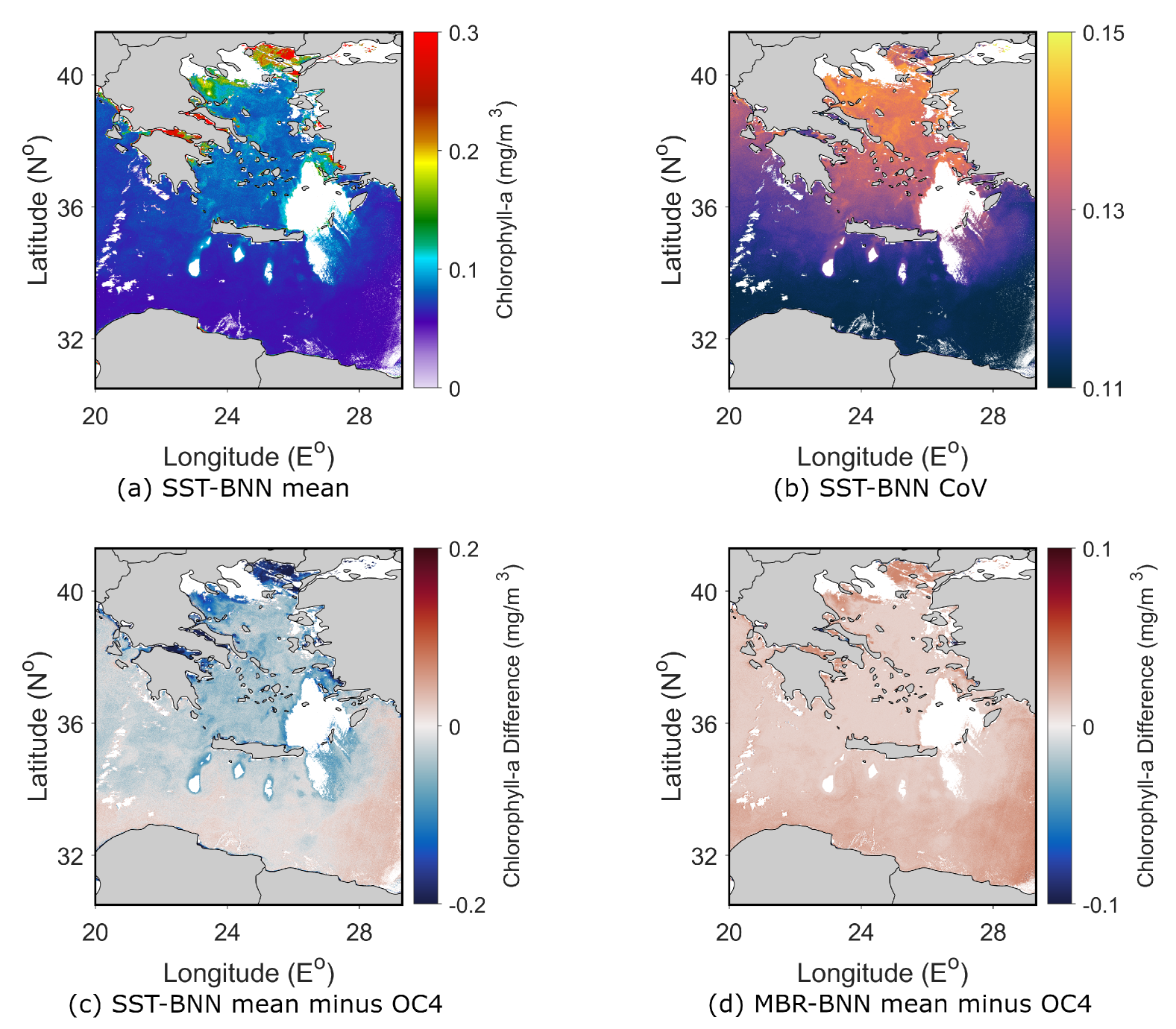
3.2.3. Incorporating Coordinates and Sea Surface Temperature
4. Spatial Evaluation of the BNN Models
4.1. Sentinel-3 Daily Imagery
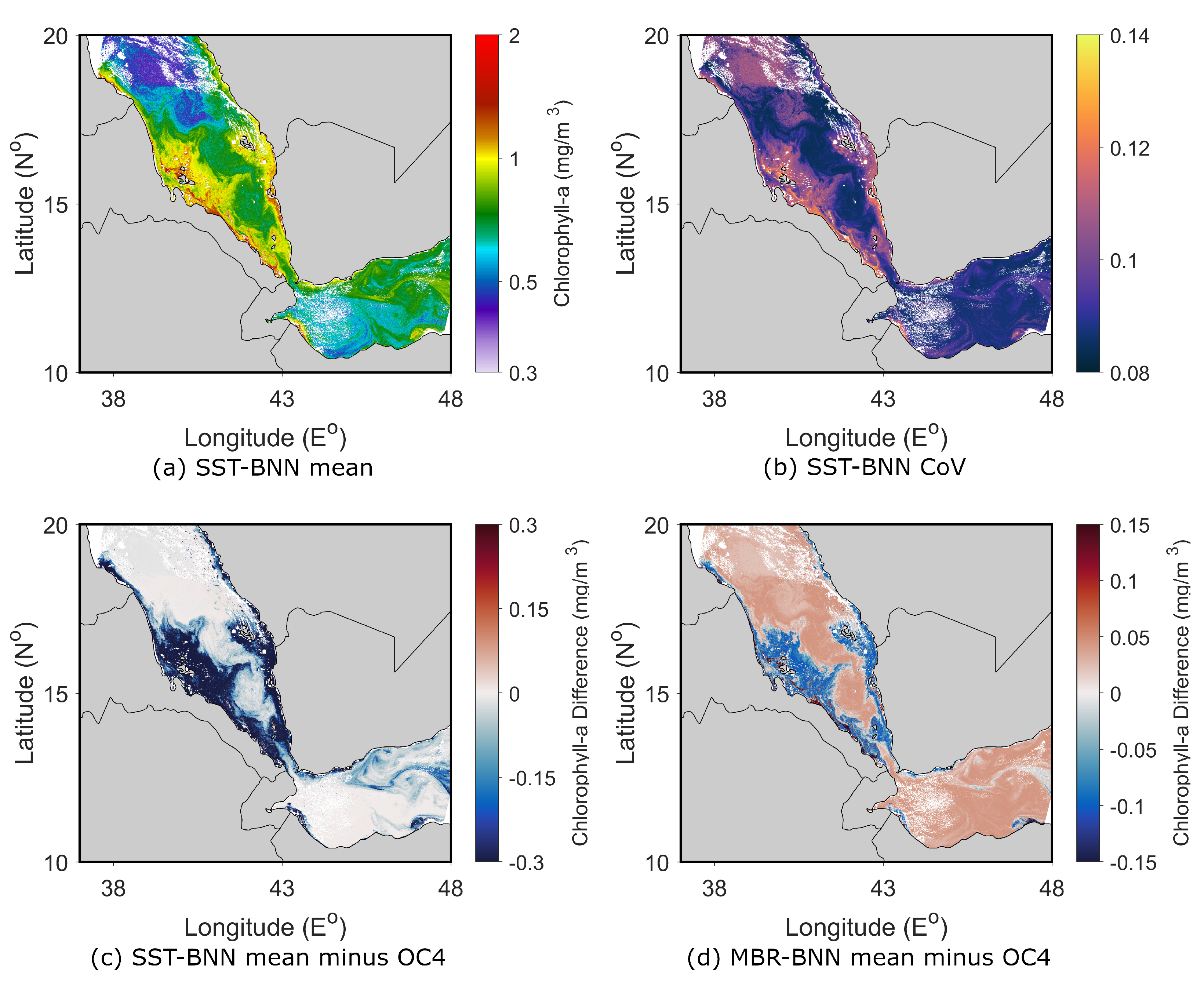
4.1.1. Aegean Sea
4.1.2. Southern Red Sea
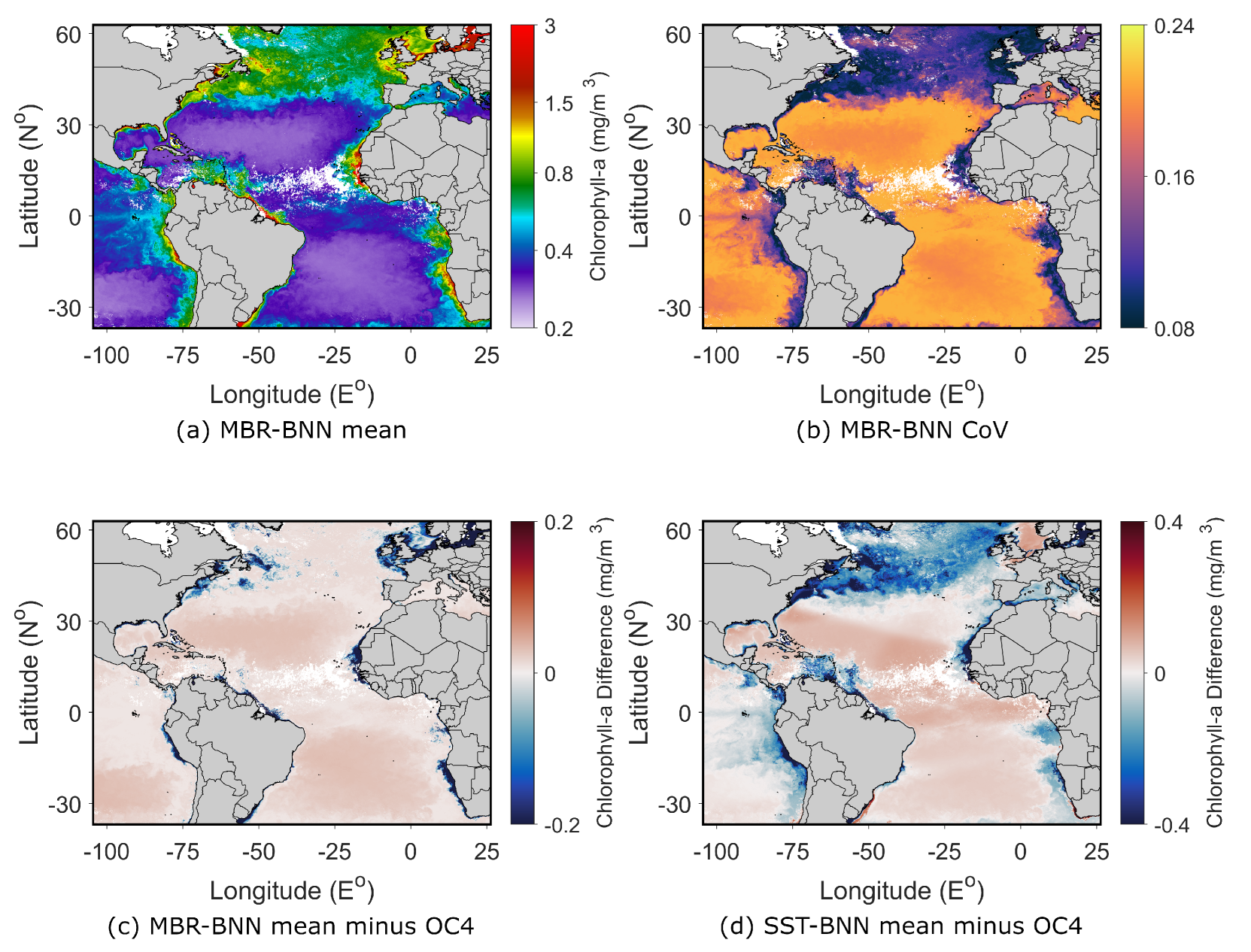
4.2. MODIS Monthly Imagery
5. Limitations and Future Directions
6. Conclusions
| r | Ψ | Δ | δ | |
|---|---|---|---|---|
| OC4 | - | - | - | - |
| BNN-MBR | 0.173 | −1.021 | −1.021 | −134.043 |
| OCI | −1.244 | 10.613 | 10.175 | −659.574 |
| BNN-OCI | −0.931 | 8.680 | 8.643 | −36.170 |
| BNN-MBR (merged dataset) | −0.887 | 8.242 | 8.060 | 261.702 |
| BNN-Rrs | −0.682 | 6.601 | 6.127 | −695.745 |
| BNN-abs | 4.188 | −39.278 | −39.314 | 46.809 |
| BNN-enhanced | 2.316 | −12.874 | −12.874 | −4.255 |
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Harris, G. Phytoplankton Ecology: Structure, Function and Fluctuation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Jones, R.I. Phytoplankton, primary production and nutrient cycling. In Aquatic Humic Substances: Ecology and Biogeochemistry; Springer: Berlin/Heidelberg, Germany, 1998; pp. 145–175. [Google Scholar]
- Falkowski, P.G.; Raven, J.A. Aquatic Photosynthesis; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Hays, G.C.; Richardson, A.J.; Robinson, C. Climate change and marine plankton. Trends Ecol. Evol. 2005, 20, 337–344. [Google Scholar] [CrossRef] [PubMed]
- Haeder, D.P.; Villafane, V.E.; Helbling, E.W. Productivity of aquatic primary producers under global climate change. Photochem. Photobiol. Sci. 2014, 13, 1370–1392. [Google Scholar] [CrossRef] [PubMed]
- Basu, S.; Mackey, K.R. Phytoplankton as key mediators of the biological carbon pump: Their responses to a changing climate. Sustainability 2018, 10, 869. [Google Scholar] [CrossRef]
- Platt, T.; Fuentes-Yaco, C.; Frank, K.T. Spring algal bloom and larval fish survival. Nature 2003, 423, 398–399. [Google Scholar] [CrossRef]
- Anderson, D.M.; Glibert, P.M.; Burkholder, J.M. Harmful algal blooms and eutrophication: Nutrient sources, composition, and consequences. Estuaries 2002, 25, 704–726. [Google Scholar] [CrossRef]
- Gokul, E.A.; Raitsos, D.E.; Gittings, J.A.; Alkawri, A.; Hoteit, I. Remotely sensing harmful algal blooms in the Red Sea. PLoS ONE 2019, 14, e0215463. [Google Scholar] [CrossRef]
- Klemas, V. Remote sensing of algal blooms: An overview with case studies. J. Coast. Res. 2012, 28, 34–43. [Google Scholar] [CrossRef]
- Racault, M.F.; Platt, T.; Sathyendranath, S.; Ağirbaş, E.; Martinez Vicente, V.; Brewin, R. Plankton indicators and ocean observing systems: Support to the marine ecosystem state assessment. J. Plankton Res. 2014, 36, 621–629. [Google Scholar] [CrossRef]
- Platt, T.; White III, G.N.; Zhai, L.; Sathyendranath, S.; Roy, S. The phenology of phytoplankton blooms: Ecosystem indicators from remote sensing. Ecol. Model. 2009, 220, 3057–3069. [Google Scholar] [CrossRef]
- Hazen, E.L.; Suryan, R.M.; Santora, J.A.; Bograd, S.J.; Watanuki, Y.; Wilson, R.P. Scales and mechanisms of marine hotspot formation. Mar. Ecol. Prog. Ser. 2013, 487, 177–183. [Google Scholar] [CrossRef]
- Racault, M.F.; Le Quéré, C.; Buitenhuis, E.; Sathyendranath, S.; Platt, T. Phytoplankton phenology in the global ocean. Ecol. Indic. 2012, 14, 152–163. [Google Scholar] [CrossRef]
- Shu, C.; Xiu, P.; Xing, X.; Qiu, G.; Ma, W.; Brewin, R.J.; Ciavatta, S. Biogeochemical Model Optimization by Using Satellite-Derived Phytoplankton Functional Type Data and BGC-Argo Observations in the Northern South China Sea. Remote Sens. 2022, 14, 1297. [Google Scholar] [CrossRef]
- Joint, I.; Groom, S.B. Estimation of phytoplankton production from space: Current status and future potential of satellite remote sensing. J. Exp. Mar. Biol. Ecol. 2000, 250, 233–255. [Google Scholar] [CrossRef] [PubMed]
- Morel, A.; Prieur, L. Analysis of variations in ocean color1. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Bricaud, A.; Babin, M.; Morel, A.; Claustre, H. Variability in the chlorophyll-specific absorption coefficients of natural phytoplankton: Analysis and parameterization. J. Geophys. Res. Ocean. 1995, 100, 13321–13332. [Google Scholar] [CrossRef]
- Groom, S.; Sathyendranath, S.; Ban, Y.; Bernard, S.; Brewin, R.; Brotas, V.; Brockmann, C.; Chauhan, P.; Choi, J.k.; Chuprin, A.; et al. Satellite ocean colour: Current status and future perspective. Front. Mar. Sci. 2019, 6, 485. [Google Scholar] [CrossRef] [PubMed]
- O’Reilly, J.E.; Werdell, P.J. Chlorophyll algorithms for ocean color sensors—OC4, OC5 & OC6. Remote Sens. Environ. 2019, 229, 32–47. [Google Scholar]
- Mélin, F. Uncertainties in Ocean Colour Remote Sensing; International Ocean Colour Coordinating Group (IOCCG): Dartmouth, NS, Canada, 2019. [Google Scholar] [CrossRef]
- Neil, C.; Spyrakos, E.; Hunter, P.D.; Tyler, A.N. A global approach for chlorophyll-a retrieval across optically complex inland waters based on optical water types. Remote Sens. Environ. 2019, 229, 159–178. [Google Scholar] [CrossRef]
- Doerffer, R.; Schiller, H. The MERIS Case 2 water algorithm. Int. J. Remote Sens. 2007, 28, 517–535. [Google Scholar] [CrossRef]
- Yu, B.; Xu, L.; Peng, J.; Hu, Z.; Wong, A. Global chlorophyll-a concentration estimation from moderate resolution imaging spectroradiometer using convolutional neural networks. J. Appl. Remote Sens. 2020, 14, 034520. [Google Scholar] [CrossRef]
- Ye, H.; Tang, S.; Yang, C. Deep learning for Chlorophyll-a concentration retrieval: A case study for the Pearl River Estuary. Remote Sens. 2021, 13, 3717. [Google Scholar] [CrossRef]
- Fan, D.; He, H.; Wang, R.; Zeng, Y.; Fu, B.; Xiong, Y.; Liu, L.; Xu, Y.; Gao, E. CHLNET: A novel hybrid 1D CNN-SVR algorithm for estimating ocean surface chlorophyll-a. Front. Mar. Sci. 2022, 9, 934536. [Google Scholar] [CrossRef]
- Hadjal, M.; Medina-Lopez, E.; Ren, J.; Gallego, A.; McKee, D. An artificial neural network algorithm to retrieve chlorophyll a for Northwest European shelf seas from top of atmosphere ocean colour reflectance. Remote Sens. 2022, 14, 3353. [Google Scholar] [CrossRef]
- MacKay, D.J. Bayesian neural networks and density networks. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1995, 354, 73–80. [Google Scholar] [CrossRef]
- Jospin, L.V.; Laga, H.; Boussaid, F.; Buntine, W.; Bennamoun, M. Hands-On Bayesian Neural Networks—A Tutorial for Deep Learning Users. IEEE Comput. Intell. Mag. 2022, 17, 29–48. [Google Scholar] [CrossRef]
- Shen, G.; Chen, X.; Deng, Z. Variational Learning of Bayesian Neural Networks via Bayesian Dark Knowledge. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, IJCAI-20; Bessiere, C., Ed.; International Joint Conferences on Artificial Intelligence Organization: Montreal, QC, Canada, 2020; pp. 2037–2043. [Google Scholar] [CrossRef]
- Izmailov, P.; Vikram, S.; Hoffman, M.D.; Wilson, A.G.G. What Are Bayesian Neural Network Posteriors Really Like? In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; Meila, M., Zhang, T., Eds.; Proceedings of Machine Learning Research. Volume 139, pp. 4629–4640. [Google Scholar]
- Magris, M.; Iosifidis, A. Bayesian learning for neural networks: An algorithmic survey. Artif. Intell. Rev. 2023, 56, 11773–11823. [Google Scholar] [CrossRef]
- Kendall, A.; Gal, Y. What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? In Proceedings of the Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Newry, UK, 2017; Volume 30. [Google Scholar]
- Goan, E.; Fookes, C. Bayesian Neural Networks: An Introduction and Survey. In Case Studies in Applied Bayesian Data Science: CIRM Jean-Morlet Chair, Fall 2018; Mengersen, K.L., Pudlo, P., Robert, C.P., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 45–87. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, A.; Cao, L. Autonomous intelligent decision-making system based on Bayesian SOM neural network for robot soccer. Neurocomputing 2014, 128, 447–458. [Google Scholar] [CrossRef]
- Abdullah, A.A.; Hassan, M.M.; Mustafa, Y.T. A Review on Bayesian Deep Learning in Healthcare: Applications and Challenges. IEEE Access 2022, 10, 36538–36562. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Ha, N.; et al. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Saranathan, A.M.; Smith, B.; Pahlevan, N. Per-Pixel Uncertainty Quantification and Reporting for Satellite-Derived Chlorophyll-a Estimates via Mixture Density Networks. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4200718. [Google Scholar] [CrossRef]
- Saranathan, A.M.; Werther, M.; Balasubramanian, S.V.; Odermatt, D.; Pahlevan, N. Assessment of advanced neural networks for the dual estimation of water quality indicators and their uncertainties. Front. Remote Sens. 2024, 5, 1383147. [Google Scholar] [CrossRef]
- Frouin, R.; Pelletier, B. Bayesian methodology for inverting satellite ocean-color data. Remote Sens. Environ. 2015, 159, 332–360. [Google Scholar] [CrossRef]
- Valente, A.; Sathyendranath, S.; Brotas, V.; Groom, S.; Grant, M.; Jackson, T.; Chuprin, A.; Taberner, M.; Airs, R.; Antoine, D.; et al. A compilation of global bio-optical in situ data for ocean colour satellite applications–version three. Earth Syst. Sci. Data 2022, 14, 5737–5770. [Google Scholar] [CrossRef]
- Werdell, P.; Bailey, S. The SeaWiFS Bio-Optical Archive and Storage System (SeaBASS): Current Architecture and Implementation; Technical Memorandum 2002-211617; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2002. [Google Scholar]
- Werdell, P.J.; Bailey, S.W. An improved in-situ bio-optical data set for ocean color algorithm development and satellite data product validation. Remote Sens. Environ. 2005, 98, 122–140. [Google Scholar] [CrossRef]
- Barker, K.; Mazeran, C.; Lerebourg, C.; Bouvet, M.; Antoine, D.; Ondrusek, M.; Zibordi, G.; Lavender, S. Mermaid: The MERIS matchup in-situ database. In Proceedings of the 2nd (A) ATSR and MERIS Workshop, Frascati, Italy, 22–26 September 2008; pp. 22–26. [Google Scholar]
- Matrai, P.; Olson, E.; Suttles, S.; Hill, V.; Codispoti, L.; Light, B.; Steele, M. Synthesis of primary production in the Arctic Ocean: I. Surface waters, 1954–2007. Prog. Oceanogr. 2013, 110, 93–106. [Google Scholar] [CrossRef]
- Devine, L.; Galbraith, P.S.; Joly, P.; Plourde, S.; Saint-Amand; Pierre, J.S.; Starr, M. Chemical and Biological Oceanographic Conditions in the Estuary and Gulf of St. Lawrence During 2015; Fisheries and Oceans Canada, Ecosystems and Oceans Science: Sidney, BC, Canada, 2015. [Google Scholar]
- Nechad, B.; Ruddick, K.; Schroeder, T.; Oubelkheir, K.; Blondeau-Patissier, D.; Cherukuru, N.; Brando, V.; Dekker, A.; Clementson, L.; Banks, A.C.; et al. CoastColour Round Robin data sets: A database to evaluate the performance of algorithms for the retrieval of water quality parameters in coastal waters. Earth Syst. Sci. Data 2015, 7, 319–348. [Google Scholar] [CrossRef]
- Peloquin, J.M.; Swan, C.; Gruber, N.; Vogt, M.; Claustre, H.; Ras, J.; Uitz, J.; Barlow, R.G.; Behrenfeld, M.J.; Bidigare, R.R.; et al. The MAREDAT global database of high performance liquid chromatography marine pigment measurements - Gridded data product (NetCDF) - Contribution to the MAREDAT World Ocean Atlas of Plankton Functional Types. Earth Syst. Sci. Data 2013, 5, 109–123. [Google Scholar] [CrossRef]
- Clark, D.; Murphy, M.; Yarbrough, M.; Feinholz, M.; Flora, S.; Broenkow, W.; Johnson, B.; Brown, S.; Kim, Y.; Mueller, J. MOBY, A Radiometric Buoy for Performance Monitoring and Vicarious Calibration of Satellite Ocean Color Sensors: Measurement and Data Analysis Protocols. 2003. Available online: https://ntrs.nasa.gov/api/citations/20030063145/downloads/20030063145.pdf (accessed on 19 May 2025).
- Stark, J.D.; Donlon, C.J.; Martin, M.J.; McCulloch, M.E. OSTIA: An operational, high resolution, real time, global sea surface temperature analysis system. In Proceedings of the OCEANS 2007-Europe, Aberdeen, UK, 18–21 June 2007; pp. 1–4. [Google Scholar] [CrossRef]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- O’Reilly, J.; Maritorena, S.; Siegel, D.; O’Brien, M.; Toole, D.; Mitchell, B.; Kahru, M.; Chavez, F.; Strutton, P.; Cota, G. Ocean Color Chlorophyll a Algorithms for SeaWiFS, OC2, and OC4: Technical Report; SeaWiFS Postlaunch Technical Report Series; SeaWiFS Postlaunch Calibration and Validation Analyses Part 3; NASA, Goddard Space Flight Center: Greenbelt, MD, USA, 2000; Volume 11. [Google Scholar]
- Hammoud, M.A.E.R.; Mittal, H.V.R.; Le Maître, O.; Hoteit, I.; Knio, O. Variance-based sensitivity analysis of oil spill predictions in the Red Sea region. Front. Mar. Sci. 2023, 10, 1185106. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll aalgorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Brewin, R.J.; Sathyendranath, S.; Müller, D.; Brockmann, C.; Deschamps, P.Y.; Devred, E.; Doerffer, R.; Fomferra, N.; Franz, B.; Grant, M.; et al. The Ocean Colour Climate Change Initiative: III. A round-robin comparison on in-water bio-optical algorithms. Remote Sens. Environ. 2015, 162, 271–294. [Google Scholar] [CrossRef]
- Neal, R.M. Bayesian Learning for Neural Networks; Springer: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Bingham, E.; Chen, J.P.; Jankowiak, M.; Obermeyer, F.; Pradhan, N.; Karaletsos, T.; Singh, R.; Szerlip, P.; Horsfall, P.; Goodman, N.D. Pyro: Deep Universal Probabilistic Programming. J. Mach. Learn. Res. 2019, 20, 973–978. [Google Scholar] [CrossRef]
- Samaniego, F.J. A comparison of the Bayesian and Frequentist Approaches to Estimation; Springer: New York, NY, USA, 2010; Volume 24. [Google Scholar]
- Chen, T.; Chen, H. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems. IEEE Trans. Neural Netw. 1995, 6, 911–917. [Google Scholar] [CrossRef] [PubMed]
- Moore, T.S.; Campbell, J.W.; Dowell, M.D. A class-based approach to characterizing and mapping the uncertainty of the MODIS ocean chlorophyll product. Remote Sens. Environ. 2009, 113, 2424–2430. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational Inference: A Review for Statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Hoffman, M.D.; Blei, D.M.; Wang, C.; Paisley, J. Stochastic variational inference. J. Mach. Learn. Res. 2013, 14, 1303–1347. [Google Scholar]
- Ranganath, R.; Gerrish, S.; Blei, D. Black box variational inference. In Proceedings of the Artificial Intelligence and Statistics, Reykjavik, Iceland, 22–25 April 2014; pp. 814–822. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2022, arXiv:1312.6114. [Google Scholar]
- Olivier, A.; Shields, M.D.; Graham-Brady, L. Bayesian neural networks for uncertainty quantification in data-driven materials modeling. Comput. Methods Appl. Mech. Eng. 2021, 386, 114079. [Google Scholar] [CrossRef]
- Li, D.; Marshall, L.; Liang, Z.; Sharma, A.; Zhou, Y. Bayesian LSTM with Stochastic Variational Inference for Estimating Model Uncertainty in Process-Based Hydrological Models. Water Resour. Res. 2021, 57, e2021WR029772. [Google Scholar] [CrossRef]
- Campagne, J.E.; Lanusse, F.; Zuntz, J.; Boucaud, A.; Casas, S.; Karamanis, M.; Kirkby, D.; Lanzieri, D.; Peel, A.; Li, Y. JAX-COSMO: An End-to-End Differentiable and GPU Accelerated Cosmology Library. Open J. Astrophys. 2023, 6. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Ben Hammouda, C.; Ben Rached, N.; Tempone, R. Importance sampling for a robust and efficient multilevel Monte Carlo estimator for stochastic reaction networks. Stat. Comput. 2020, 30, 1665–1689. [Google Scholar] [CrossRef]
- Bishop, C.M. Mixture Density Networks; Technical Report NCRG/94/004; Aston University: Birmingham, UK, 1994. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 1050–1059. [Google Scholar]
- Woźniak, S.B.; Meler, J.; Stoń-Egiert, J. Inherent optical properties of suspended particulate matter in the southern Baltic Sea in relation to the concentration, composition and characteristics of the particle size distribution; new forms of multicomponent parameterizations of optical properties. J. Mar. Syst. 2022, 229, 103720. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hammoud, M.A.E.R.; Papagiannopoulos, N.; Krokos, G.; Brewin, R.J.W.; Raitsos, D.E.; Knio, O.; Hoteit, I. On the Potential of Bayesian Neural Networks for Estimating Chlorophyll-a Concentration from Satellite Data. Remote Sens. 2025, 17, 1826. https://doi.org/10.3390/rs17111826
Hammoud MAER, Papagiannopoulos N, Krokos G, Brewin RJW, Raitsos DE, Knio O, Hoteit I. On the Potential of Bayesian Neural Networks for Estimating Chlorophyll-a Concentration from Satellite Data. Remote Sensing. 2025; 17(11):1826. https://doi.org/10.3390/rs17111826
Chicago/Turabian StyleHammoud, Mohamad Abed El Rahman, Nikolaos Papagiannopoulos, George Krokos, Robert J. W. Brewin, Dionysios E. Raitsos, Omar Knio, and Ibrahim Hoteit. 2025. "On the Potential of Bayesian Neural Networks for Estimating Chlorophyll-a Concentration from Satellite Data" Remote Sensing 17, no. 11: 1826. https://doi.org/10.3390/rs17111826
APA StyleHammoud, M. A. E. R., Papagiannopoulos, N., Krokos, G., Brewin, R. J. W., Raitsos, D. E., Knio, O., & Hoteit, I. (2025). On the Potential of Bayesian Neural Networks for Estimating Chlorophyll-a Concentration from Satellite Data. Remote Sensing, 17(11), 1826. https://doi.org/10.3390/rs17111826








