A Grid-Based Hierarchical Representation Method for Large-Scale Scenes Based on Three-Dimensional Gaussian Splatting

Abstract

Efficient and realistic large-scale scene modeling is an important application of low-altitude remote sensing. Although the emerging 3DGS technology offers a simple process and realistic results, its high computational resource demands hinder direct application in large-scale 3D scene reconstruction. To address this, this paper proposes a novel grid-based scene-segmentation technique for the process of reconstruction. Sparse point clouds, acting as an indirect input for 3DGS, are first processed by Z-Score and a percentile-based filter to prepare the pure scene for segmentation. Then, through grid creation, grid partitioning, and grid merging, rational and widely applicable sub-grids and sub-scenes are formed for training. This is followed by integrating Hierarchy-GS’s LOD strategy. This method achieves better large-scale reconstruction effects within limited computational resources. Experiments on multiple datasets show that this method matches others in single-block reconstruction and excels in complete scene reconstruction, achieving superior results in PSNR, LPIPS, SSIM, and visualization quality.

1. Introduction

Low-altitude remote sensing images are highly flexible, spatially resolved, and offer strong timeliness. Thus, they are crucial in virtual geographic environments across fields [1]. Before the popularity of artificial intelligence, the most common 3D reconstruction methods included artificial construction, oblique photogrammetry, laser scanning [2], and multi-view stereo matching [3,4], representing objects using explicit geometric models, such as meshes [5], point clouds [6], voxels [7], and depth [8]. Despite the extensive application of these established methods in the industry, they still exhibit certain limitations [9,10,11]. Recently, numerous neural implicit representation methods have emerged with the deep integration of neural networks and rendering [12,13,14,15]. Neural Radiance Fields (NeRF) [16], a leading technique, uses neural networks to compute spatial sampling points’ color and density. These are integrated along viewing rays to generate view pixel colors, achieving impressive photo-realistic view synthesis. However, NeRF has slow training and inference speed and is mostly limited to small-scale scenes. Moreover, its 3D modeling quality still has room for improvement.

Introduced as an advancement on NeRF, 3D Gaussian Splatting (3DGS) [17] starts with Structure from Motion (SFM) to calculate the input image’s camera pose, forming a sparse point cloud. This cloud initializes a 3D Gaussian cloud, which is projected onto the image plane via EWA and then rasterized with alpha-blending. The result is a point-cloud file containing all rendering information, representing the reconstructed scene. Notably, 3DGS outperforms NeRF in rendering speed and quality, and its storage format allows easy integration with existing explicit models like meshes and point clouds [17,18]. But, it is a memory-intensive 3D modeling method. For large-scale 3D scene reconstruction, conventional GPUs fall short in computational resources, failing to complete the task.

To achieve the research objective of efficiently reconstructing large-scale photorealistic geographic scenes, this study comprehensively analyzes the 3D scene modeling effects of NeRF and 3DGS. To mitigate the high memory demands of large-scene 3D reconstruction on GPU and enhance the visualization quality, this method introduces two innovations. Firstly, based on the distribution of the input sparse point cloud, Z-score and a percentile-based filter are employed to cleanse the point cloud, thereby eliminating isolated points and minimizing artifacts. Secondly, considering the 3D spatial distribution characteristic of the point cloud, the entire scene is segmented into uniform grids to mitigate the occurrence of excessively small or large segments, ensuring smooth large-scale reconstruction on normal GPUs.

2. Related Work

2.1. Three-Dimensional Modeling Using NeRF

Neural Radiance Fields (NeRF) was first introduced in 2020 [16]. This technique enables the photo-realistic visualization of 3D scenes through neural implicit stereo representation, significantly surpassing traditional methods in terms of fidelity and detail. Consequently, it has garnered extensive attention and experienced rapid development [19,20,21,22,23,24,25,26,27,28,29]. Current research hotspots can be categorized into four main areas [30]: enhancing the robustness of source data, enabling dynamic controllable scenes, improving rendering efficiency, and optimizing visual effects.

To boost source data robustness using NeRF, Ref. [31] enhances image pose accuracy via camera parameter optimization. Deblur-NeRF [32] uses denoising for high-quality view synthesis from poor images. Mirror-NeRF [33] uses a standardized multi-view system to improve source data quality. In dynamic scenes, D-NeRF and H-NeRF [34,35] enable scene editing via parameterizing the NeRF scene. Clip-NeRF [36] integrates generative models for autonomous scene generation. To render efficiency improvement, three main strategies are employed: incorporating explicit model data to enhance prior knowledge, such as Point-NeRF and E-NeRF [28,37]; optimizing sampling methods to cut down invalid sampling calculations, such as DONERF [38]; and decomposing scenes to improve parallel computing rates, such as KiloNeRF [39]. Among these, Instant-NGP [40] achieves the best results. In effect optimization, geometric reasoning with MVS improves accuracy. MVSNeRF [41] simulates some physical processes, like refraction, transmission, and reflection, while NeRFReN and Ref-NeRF [42,43] enhance the regularization terms to fully optimize reconstructed optical properties.

2.2. Three-Dimensional Modeling Using 3DGS

Three-dimensional Gaussian Splatting (3DGS), introduced in 2023 as an extension of NeRF [17], utilizes an explicit representation and a highly parallelized workflow. It projects millions of 3D Gaussians into the imaging space for alpha-blending to achieve scene representation.

Compared to NeRF, 3DGS significantly enhances computational and rendering efficiency while preserving the realism of the rendering effect. Research focused on 3DGS can be categorized into three primary areas [18,44]: enhancing detail rendering, extending dynamic scene modeling, and compressing Gaussian storage.

To enhance detail rendering, methods such as Multi-Scale 3DGS [45], Deblur-GS [46], and Mip-Splatting [47] tackle issues like low-resolution aliasing, high-frequency artifacts, blurring in training images, and color inaccuracies of 3D objects. For dynamic scene modeling, Gaussian-Flow [48] captures and reproduces temporal changes in a scene’s 3D structure and appearance. GaussianEditor and Gaussian Grouping [49,50,51] integrate semantic segmentation to segment the complete scene and then edit it based on objects’ attributes, such as geometry and surface. Animatable Gaussians [52] use explicit face models to better simulate complex facial expressions and details. To compress Gaussian storage, LightGaussian [53] and HiFi4G [54] focus on optimizing memory utilization during both the training and model storage phases. They have achieved significant compression rates while largely preserving visual quality.

2.3. Large-Scale 3D Scene Reconstruction

To support geographical applications, comprehensive scene reconstruction must be conducted over large areas with high efficiency. To date, there has been some progress in utilizing NeRF and 3DGS for the 3D modeling of geographical scenes.

On the NeRF side, several approaches have been proposed. S-NeRF [55], Sat-NeRF [27], and GC-NeRF [56] leverage multi-view high-resolution satellite images with known poses to achieve view synthesis, thereby obtaining more accurate digital surface models (DSMs). However, these methods still exhibit significant limitations in model generalization and handling illumination effects. Mega-NeRF [57] and Block-NeRF [58] divide scenes into multiple sub-blocks for parallel training, fusing information from adjacent blocks to mitigate boundary effects and ensure continuity across the entire large-scale scene.

Several 3D Gaussian Splatting (3DGS) methodologies, including VastGaussian [59], Octree-GS [60], DoGaussian [61], and Hierarchy-GS [62], have been developed. Due to the significant memory resources required for 3DGS training, large-scale scene modeling often needs extensive computational resources, incurring high costs. To tackle this, VastGaussian, DoGaussian, and Hierarchy-GS put forward their own scene-segmentation strategies to enable large-scene reconstruction using normal-level GPUs. However, these methods mainly focus on the XY-plane, overlooking the Z-axis distribution and causing uneven segmentation. To boost rendering speed and ease rendering pressure, Octree-GS and Hierarchy-GS adopt the Level of Detail (LOD) concept as another basic strategy. But Octree-GS’s transitions between different scene levels are less smooth than Hierarchy-GS due to its limited number of levels.

After analyzing these methods, this paper proposes a grid-based strategy based on point-cloud 3D distribution for more reasonable, universal, and uniform scene segmentation. It also integrates Hierarchy-GS’s LOD hierarchical rendering strategy to ensure a more complete 3D scene representation.

3. Preliminary

3.1. Three-Dimensional Gaussian Splatting

Three-dimensional Gaussian Splatting starts with a set of Sfm points and initializes the point cloud into several 3D Gaussians. Its mathematical representation is as follows:

$$G(x)=e^{-{\displaystyle \frac{1}{2}}(x-\mu {)}^T{\mathsf{\Sigma }}^{-1}(x-\mu )}$$

(1)

where $x$ is an arbitrary position in the 3D space, $\mu$ is the center (average) position of the Gaussian, and $\mathsf{\Sigma }$ represents the covariance matrix of the Gaussian. $\mathsf{\Sigma }$ is the product of the rotation matrix $\mathrm{R}$ and the scale matrix $\mathrm{S}$.

$$\mathsf{\Sigma }=\mathrm{R}\mathrm{S}{\mathrm{S}}^{\mathrm{T}}{\mathrm{R}}^{\mathrm{T}}$$

(2)

After initialization and training, millions of Gaussians are distributed in the 3D space. These Gaussians are projected onto a 2D image plane for rendering by splatting, as follows:

$${\mathsf{\Sigma }}^{\prime }=\mathrm{J}\mathrm{W}\mathsf{\Sigma }{\mathrm{W}}^{\mathrm{T}}{\mathrm{J}}^{\mathrm{T}}$$

(3)

where J and W represent the first-order affine approximation of perspective projection transformation and the viewing angle transformation matrix, respectively.

Each Gaussian has properties such as position, opacity, rotation, scale, and spherical harmonic coefficients (color). When rendering, for each pixel on the imaging plane, its color is accumulated from several ellipses projected above it, and the rendering formula is as follows:

$$C_{blend}=\sum _{i=1}^n o_i{c}_i\prod _{j=1}^{i-1} \left(1-o_j\right)$$

(4)

where $o_i$ is the Gaussians’ opacity and $c_i$ is the color. The expression of the scene is shown in Figure 1.

3.2. Hierarchy-GS

During the 3DGS training process, tens of thousands to millions of Gaussians are generated, and most of these dozens of attributes are fed into the GPU for computation, thereby causing a heavy computational load. Hierarchy-GS introduces a skybox pre-trained with SfM points during training, which turns the unbounded scene into a bounded one and reduces the number of Gaussians generated during training. It also modifies the densification strategy of 3DGS, replacing the average with the maximum of the observed screen-space gradients for densification, thereby better controlling Gaussian growth. In addition, it adopts a scene-segmentation strategy, generating the Gaussians of the entire scene in separate time intervals to reduce their peak memory usage. These work together to achieve computational resource reduction.

Additionally, it proposes an LOD strategy based on the trained Gaussian set. Firstly, an AABB (Axis-Aligned Bounding Box) is created for the Gaussian set. Then, based on the binary median segmentation method, the Gaussian set in the bounding box is recursively split into each leaf node, and each leaf node is guaranteed to contain only one Gaussian. A Gaussian hierarchical tree with a binary tree structure is constructed, but only the leaf nodes have Gaussians. Finally, bottom–up Gaussian merging is performed, starting from the leaf node and merging upwards according to the weight $w_i^{\prime }$ of the node to form a new Gaussian as the internal node. The formula is as follows:

$${\mu }^{\left(l+1\right)}=\sum _i^N w_i{\mu }_i^{\left(l\right)}$$

(5)

$${\mathsf{\Sigma }}^{\left(l+1\right)}=\sum _i^N w_i({\mathsf{\Sigma }}_i^{\left(l\right)}+\left({\mu }_i^{\left(l\right)}-{\mu }^{\left(l+1\right)}\right)\left({\mu }_i^{\left(l\right)}-{\mu }^{\left(l+1\right)}{)}^T\right)$$

(6)

$$w_i^{\prime }={\mathrm{o}}_{\mathrm{i}}\sqrt{\mid {\mathsf{\Sigma }}_i^{\prime }\mid }$$

(7)

When consolidating the structure hierarchy trees of each sub-scene, almost repeated Gaussians and some Gaussians that are out of range will be deleted. When rendering, calculate the size of the AABB and the long side of the node Gaussian projected onto the imaging screen as the hierarchical granularity $ϵ\left(n\right)$. If the $ϵ\left(n\right)$ of node $n$ is smaller than the given granularity ${\tau }_{ϵ}$, but its parent node does not meet the requirement, it will be used as the Gaussian participating in the rendering process.

4. Methodology

4.1. Architecture Overview

The general architecture proposed in this article, illustrated in the accompanying Figure 2, integrates advancements in the original 3DGS approach and the LOD strategy from Hierarchy-GS with our own segmentation strategy.

To acquire low-altitude remote sensing images via UAVs, this method uses Colmap for sparse reconstruction to obtain camera poses and sparse point clouds in the scene. It filters the point clouds with Z-Score and percentile-based approaches to remove redundant and stray points, yielding a cleaner point cloud. Then, the point cloud is mapped to the XY-plane for grid initialization. The scene is segmented into preset grid numbers and undergoes iterative grid partitioning and adjacent grid merging to obtain final scene blocks. Based on Hierarchy-GS’s training and LOD strategy, each block is trained with low computing resources and its hierarchical structure tree is built to obtain the complete scene rendering result.

4.2. Point Cloud Filtering

Three-dimensional Gaussian Splatting (3DGS) and its derivative methods heavily rely on the distribution of sparse point clouds obtained through SfM during the progress of Gaussian cloud initialization. Each point location generates a randomly initialized Gaussian. However, SfM-generated point clouds inevitably contain outlier points that deviate from the main structure, which consequently leads to redundant Gaussians. These will negatively impact optimization efficiency and rendering quality during subsequent training. To address this issue, this paper proposes a straightforward filtering approach for effective point selection and elimination.

From Figure 3, several characteristics of the sparse point cloud reconstructed by SfM can be analyzed: ① The overall distribution is generally uniform, concentrated within a specific space, but there are still some stray points far from the main subject. ② The histogram distribution along the X-axis and Y-axis (red and green histograms) shows a class of normal distribution centered at the origin, gradually decreasing towards both sides, with a few stray points at the extreme edges. ③ From the Z-axis perspective, in addition to those concentrated near the origin, there are also a few stray points far from the main subject, often concentrated in the negative region.

Therefore, this method employs two filtering approaches for the $x$-axis, $y$-axis, and Z-axis directions. The point-cloud data exhibit characteristics of a normal distribution along the X- and Y-axis; hence, the Z-Score method is used for filtering, following the steps shown in Formula (8). The point-cloud data are mapped separately onto the X-axis and Y-axis and filtered directionally. For each data point $x_i$ in the point cloud, calculate the difference between it and the mean value $\mu$ of the dataset, then divide this difference by the standard deviation $\sigma$ of the dataset. This yields the Z-score $Z_i$, representing the position of the data point relative to the center of the data distribution. Z-scores with absolute values exceeding 2 are considered outliers, as they deviate from the mean by more than 2 standard deviations. According to the normal distribution, this approach retains 95.45% of the data points.

$$Z_i={\displaystyle \frac{\left(x_i-\mu \right)}{\sigma }}$$

(8)

The threshold value is set to 2 instead of 3 due to the characteristics of the 3DGS class method in reconstructing scene edges. Points at the scene edges play a relatively minor role during training, and the reconstructed edge areas lack ground truth for comparison, resulting in poorer performance in these regions, as shown in Figure 4 with the Polytech edge reconstruction. Therefore, for the $XY$-plane, the range can be appropriately reduced to concentrate the data more effectively and eliminate stray points more thoroughly.

Regarding the Z-axis, there is no need for extensive consideration. It can be observed that the majority of points in the point cloud are concentrated near the origin, with only a very small number of points being extremely distant from the center of aggregation. Therefore, a simpler percentile filtering method can be employed to remove these outlier points, as shown in Equation (9).

$$\mathrm{X}=\left\{{\mathrm{x}}_{\mathrm{i}}∣{\mathrm{P}}_{2.5}<{\mathrm{x}}_{\mathrm{i}}<{\mathrm{P}}_{99}\right\}$$

(9)

After mapping all point-cloud data to the z-axis, sort them by size, and then select points between the 2.5th percentile and the 99th percentile. The final filtering result is shown in Figure 5.

4.3. Grid-Based Scene Segmentation

4.3.1. Create Initial Grid

The first step is to establish the initial grid by constructing a regular grid area according to the pre-specified number of blocks ($n_x$ and $n_y$, which are set at 2 and 3 by default) using the entire spatial range of the point set, with an optional overlap ratio. The method begins by projecting the 3D point cloud onto the $XY$-plane to form a 2D point set $\mathcal{P}=\left\{\left(x_i,y_i\right)∣i=\mathrm{1,2},\dots ,N\right\}$. The maximum and minimum values of the point set $\mathcal{P}$ in the $X$ and $Y$ directions are determined to define the extent of the grid. Based on the preset number of blocks and the overall range, this method then determines the width $w$ and height $h$ of each subgrid. Given the overlap ratio $\rho$ (here set to 5%) between blocks, the horizontal and vertical overlap distances ${\delta }_x$ and ${\delta }_y$ are computed. Following this, the lower-left corner coordinates ($x_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}^{\left(i\right)}, y_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}^{\left(j\right)}$) and upper-right corner coordinates ($x_{\mathrm{e}\mathrm{n}\mathrm{d}}^{\left(i\right)}, y_{\mathrm{e}\mathrm{n}\mathrm{d}}^{\left(j\right)}$) of each sub-grid $G_{ij}$ are calculated to define the grid boundaries. Finally, the number of 3D points within each block is counted based on the block’s boundaries. Through projection, the point set not only accurately reflects the distribution on the $XY$-plane, but also considers the distribution characteristics along the $z$-axis, thereby completing the initialization of the point cloud grid.

$$w={\displaystyle \frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}-x_{\mathrm{m}\mathrm{i}\mathrm{n}}}{n_x}},h={\displaystyle \frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}-y_{\mathrm{m}\mathrm{i}\mathrm{n}}}{n_y}}$$

(10)

$${\delta }_x=\rho w,{\delta }_y=\rho h$$

(11)

$$x_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}^{\left(i\right)}=x_{\mathrm{m}\mathrm{i}\mathrm{n}}+i\left(w-{\delta }_x\right),y_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}^{\left(j\right)}=y_{\mathrm{m}\mathrm{i}\mathrm{n}}+j\left(h-{\delta }_y\right)$$

(12)

$$x_{\mathrm{e}\mathrm{n}\mathrm{d}}^{\left(i\right)}=x_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}^{\left(i\right)}+w,y_{\mathrm{e}\mathrm{n}\mathrm{d}}^{\left(j\right)}=y_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}^{\left(j\right)}+h$$

(13)

$$G_{ij}=\left\{\left(x,y\right)\in {\mathbb{R}}^2∣x_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}^{\left(i\right)}\le x\le x_{\mathrm{e}\mathrm{n}\mathrm{d}}^{\left(i\right)},y_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}^{\left(j\right)}\le y\le y_{\mathrm{e}\mathrm{n}\mathrm{d}}^{\left(j\right)}\right\}$$

(14)

$${\mathbb{P}}_G=\left\{\left(x,y\right)\in \mathbb{P}∣x_{\mathrm{m}\mathrm{i}\mathrm{n}}\le x\le x_{\mathrm{m}\mathrm{a}\mathrm{x}},y_{\mathrm{m}\mathrm{i}\mathrm{n}}\le y\le y_{\mathrm{m}\mathrm{a}\mathrm{x}}\right\}$$

(15)

Table 1. Points in different original sub-grids.

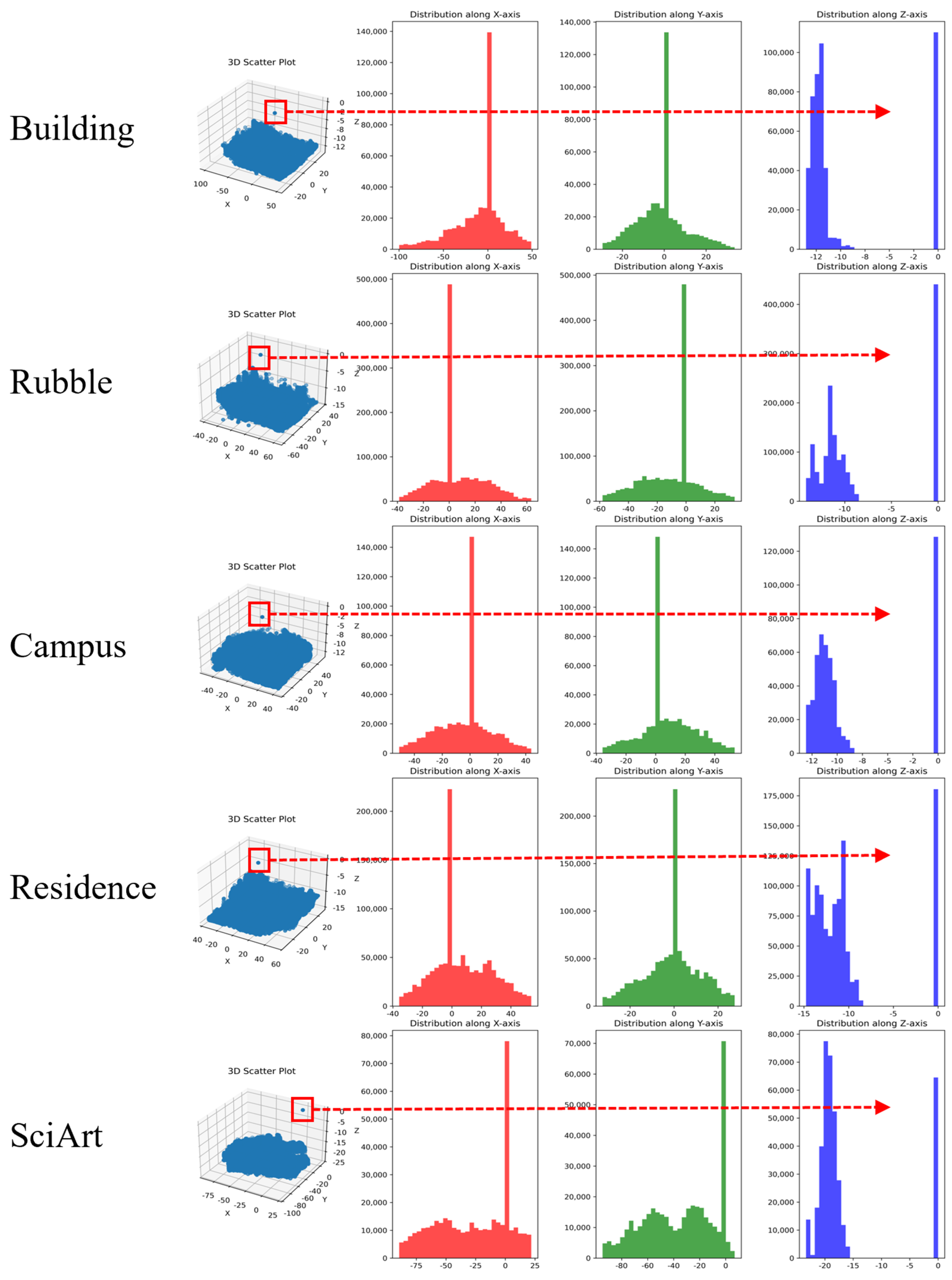
Grid|Points	Building	Rubble	Campus	Residence	SciArt
Grid 0	8738	102,052	44,354	114,020	38,764
Grid 1	59,739	720,013	99,433	410,024	64,313
Grid 2	45,488	164,498	64,408	135,380	52,740
Grid 3	108,314	201,176	40,313	79,331	40,785
Grid 4	252,504	185,314	236,387	234,410	67,292
Grid 5	11,003	73,592	34,348	117,398	119,335
Max/Min	28.9	9.78	6.88	5.17	3.08
Mean	80,964.33	241,107.5	86,540.5	181,760.5	63,871.5
Std	91,645.16	239,718.5	77,137.25	123,491.26	29,581.68

and Figure 6 present the grid initialization results for five datasets, revealing significant uneven distributions. On SciArt, the point count difference is 3.08 times; on Building, it is 28.9 times; on Campus, 6.88 times; on Residence, 5.17 times; and on Rubble, 9.78 times. These large disparities lead to the poor performance of 3DGS-class methods in sparse areas. To address the distribution differences and fully utilize all valid data, iterative partitioning and block merging were performed on the grid, resulting in more uniform scene point-cloud segmentation.

4.3.2. Grid Partitioning

The aforementioned process generated several sub-grids of equal size; however, due to the highly uneven distribution of point clouds, the number of points contained in each sub-grid varies significantly. If the point cloud distribution were uniform, the ideal scenario would be that the number of points in each sub-grid would differ only slightly. Given a total of $N$ points and $n_x\ast n_y$ sub-grid blocks, each grid should contain approximately $N/{(n}_x\ast n_y)$ points. This segmentation method is proposed based on this concept, with specific implementation details as follows:

If the number of points $\mid {\mathcal{P}}_G\mid$ in the current grid $G_{ij}$ exceeds the specified threshold $\mathit{\tau }=N/{(n}_x\ast n_y)$, the approach in this paper will partition the grid into two sub-grids, ensuring that the resulting sub-grids remain rectangular and have approximately equal numbers of points. It is known that a rectangle can be divided into two rectangles along the X-axis (major axis) or along the Y-axis (minor axis). Therefore, the first step is to choose the division direction and then choose the division position. Orthographically project the points in the grid onto the X-axis and Y-axis, and then calculate the variance of the points along the $x$ and $y$ directions. Select the direction with the larger variance for the division. If the X-axis is chosen as the division direction, the division position ($y_s$) should be the median value of the point projected onto the y-axis. Based on the division direction and position, divide the grid into a bottom sub-grid (${\mathcal{P}}_{\mathrm{b}\mathrm{o}\mathrm{t}\mathrm{t}\mathrm{o}\mathrm{m}}$) and a top sub-grid (${\mathcal{P}}_{\mathrm{t}\mathrm{o}\mathrm{p}}$). Iteratively repeat this process for each grid and its sub-grids until the number of points in each grid meets the requirement or the maximum iteration $M$ is reached. Here, M is set to 10, which means each sub-grid will be split at most ten times.

$${\sigma }_X^2={\displaystyle \frac{1}{\left|P_G\right|}}\sum _{\left(x,y\right)\in P_G}{\left(x-\bar{x}\right)}^2,\bar{x}={\displaystyle \frac{1}{\left|P_G\right|}}\sum _{\left(x,y\right)\in P_G}x$$

(16)

$${\sigma }_y^2={\displaystyle \frac{1}{\left|{\mathcal{P}}_G\right|}}\sum _{\left(x,y\right)\in {\mathcal{P}}_G}{\left(y-\bar{y}\right)}^2,\bar{y}={\displaystyle \frac{1}{\left|{\mathcal{P}}_G\right|}}\sum _{\left(x,y\right)\in {\mathcal{P}}_G}y$$

(17)

$${\mathcal{P}}_{\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t}}=\left\{\left(x,y\right)\in {\mathcal{P}}_G∣x\le x_s\right\},{\mathcal{P}}_{\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}=\left\{\left(x,y\right)\in {\mathcal{P}}_G∣x>x_s\right\}$$

(18)

$${\mathcal{P}}_{\mathrm{b}\mathrm{o}\mathrm{t}\mathrm{t}\mathrm{o}\mathrm{m}}=\left\{\left(x,y\right)\in {\mathcal{P}}_G∣y\le y_s\right\},{\mathcal{P}}_{\mathrm{t}\mathrm{o}\mathrm{p}}=\left\{\left(x,y\right)\in {\mathcal{P}}_G∣y>y_s\right\}$$

(19)

It is noteworthy that grid partitioning aims to alleviate the computational resource requirements for subsequent training processes while ensuring the final fused scene effect. To avoid point cloud distribution being too dense in certain areas, which may lead to significant differences in the area of two sub-grids, or even the occurrence of extremely small sub-grids, it is necessary to make judgments during the partitioning process to avoid such issues. This method determines that if the difference in the number of points included in the two sub-grids exceeds $\lambda \ast \tau$, the partitioning process will be halted, and the original grid will remain unchanged (where $\lambda$ is set to 0.7). The results after partitioning are shown in Figure 7, and the number of points within each sub-block is relatively uniform, as shown in

Table 2. Points in different partitioned sub-grids.

Grid|Points	Building	Rubble	Campus	Residence	SciArt
Grid 0	8738	102,052	44,354	114,020	38,764
Grid 1	59,739	141,656	49,717	104,188	32,157
Grid 2	45,488	578,357	49,716	247,996	32,156
Grid 3	54,158	164,498	64,408	57,840	52,740
Grid 4	54,156	201,176	40,313	135,380	40,785
Grid 5	54,410	185,314	152,091	79,331	33,647
Grid 6	24,215	73,592	30,714	117,206	33,645
Grid 7	133,025	-	53,582	117,204	40,675
Grid 8	40,854	-	34,348	117,398	78,660
Grid 9	11,003	-	-	-	-
Max/Min	15.22	7.86	4.95	4.29	2.45
Mean	48,578.6	206,663.57	57,693.67	121,173.67	42,581
Std	34,982.53	170,941.22	39,226.94	62,935.49	19,536.76

.

4.3.3. Grid Merging

Although uniform point distribution grids were obtained through grid partitioning, each grid contains fewer points and has a smaller area, resulting in the selection of only a limited number of cameras in subsequent processes. This leads to an insufficient acquisition of camera-pose data, which significantly affects the modeling performance of 3DGS methods. Additionally, excessive partitioning increases training time substantially, indirectly raising the cost of scene modeling. Therefore, this method incorporates an additional grid merging module to consolidate overly fragmented partition grids, ultimately yielding uniformly distributed sub-grids with an appropriate number of segments.

If the number of points in a grid $\mid {\mathcal{P}}_G\mid$ is less than $\tau$, attempt to merge it with adjacent grids. Let the two grids to be merged be $G_1$ and $G_2$, and the merged grid be $G_{merged}$, with the merged point set being $P_{merged}$. If $\mid {\mathcal{P}}_{\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{d}}\mid \le {\tau }_{\mathrm{m}\mathrm{a}\mathrm{x}}$, then perform the merge operation; otherwise, keep the original grid unchanged. Here, ${\tau }_{\mathrm{m}\mathrm{a}\mathrm{x}}=2\ast \tau$. After merging, each grid undergoes a certain degree of contraction to more tightly enclose its internal points, with a contraction rate of 99%, resulting in the final merged outcome as shown in

Table 3. Points in different merged sub-grids.

Grid|Points	Building	Rubble	Campus	Residence	SciArt
Grid 0	113,965	243,708	143,787	218,208	103,077
Grid 1	108,314	578,357	64,408	305,836	52,740
Grid 2	78,625	164,498	40,313	135,380	108,077
Grid 3	133,025	460,082	152,091	313,741	40,675
Grid 4	51,857	-	118,644	117,398	78,660
Max/Min	2.57	3.52	3.77	2.67	2.66
Mean	97,157.2	361,661.25	103,848.6	218,112.6	76,645.8
Std	31,972.75	190,988.66	49,329.61	91,962.37	29,815.98

.

After undergoing the partitioning and merging steps, the distribution of sub-grid points for the five scenarios significantly improved. Even for the scenario with the largest difference, Campus, the ratio between the maximum and minimum values is only 3.77 times, and the standard deviation is within a reasonable range relative to the mean. The final result is shown in Figure 8.

4.3.4. Choose the Camera

After obtaining each segmented sub-grid and the number of points it contains, it is also necessary to match the corresponding camera pose for each sub-grid. The camera pose and 3D points already obtained a complete matching relationship in the previous Colmap process, so here we only need to divide them accordingly.

Traverse all cameras, filter out valid cameras based on the position of the 3D point and the position of the camera center, and then make a judgment. If the camera is within the double range of the sub-grid and has a matching relationship with the points in the grid, then the camera is chosen. Combined with the overlap ratio $\rho$, the wider range of camera selection here can ensure that there is certain coverage between the sub-scene modeling to avoid a sense of separation between adjacent sub-scenes.

4.4. Evaluation Metrics

This paper uses PSNR (peak signal-to-noise ratio), LPIPS, (Learned Perceptual Image Patch Similarity) and SSIM (structural similarity index) to evaluate the reconstruction results and compare methods. PSNR is a measure of image generation quality. A higher PSNR value means the generated image is closer to the reference image. SSIM assesses the similarity between two images by comparing brightness, contrast, and structural information. A higher SSIM value indicates greater structural similarity. LPIPS is a deep learning-based method. It uses pre-trained deep neural networks to extract high-level features from images and evaluates similarity by comparing these features. A larger LPIPS value means greater perceptual differences between images, which implies poorer quality of the generated image. The calculation of PSNR, SSIM, and LPIPS indicators is as follows:

$$MSE={\displaystyle \frac{1}{mn}}\sum _{i=0}^{m-1} \sum _{j=0}^{n-1} [I(i,j)-K(i,j){]}^2$$

(20)

$$PSNR=10\ast lo{g}_{10}({\displaystyle \frac{MA{X}_I^2}{MSE}})$$

(21)

$$SSIM(x,y)={\displaystyle \frac{(2{\mu }_x{\mu }_y+C_1)(2{\sigma }_{xy}+C_2)}{({\mu }_x^2+{\mu }_y^2+C_1)({\sigma }_x^2+{\sigma }_y^2+C_2)}}$$

(22)

where $MSE$ is the mean square error and $MA{X}_I$ is the maximum possible pixel value of the image. $\mu$ is the mean value of the image; $\sigma$ is the covariance of the image; and $C_1$ and C₂ are constants to avoid calculation errors caused by division by zero.

5. Experiments and Results

5.1. Data

5.1.1. Mill19

The Mill 19 dataset, created by Carnegie Mellon University, is a large-scale scene dataset designed to boost NeRF and 3DGS development in computer vision. The Rubble and Building data from this dataset are chosen for the experiments. The Building scene consists of 1920 images, and the Rubble scene has 1657 images, both with a resolution of 4608 × 3456.

5.1.2. Urban Scene 3D

The UrbanScene3D dataset, developed by Shenzhen University’s Visual Computing Research Centre, promotes urban-scene awareness and reconstruction research. It contains over 128,000 images with a resolution of 5472 × 3648, covering 16 scenes, including real urban areas and 136 km² of synthetic urban zones. The Campus (2129 images), Residence (2582 images), and SciArt (3620 images) scenes are used in the experiments.

5.1.3. Self-Collected

The NJU and CMCC-NanjingIDC datasets are acquired via DJI Mavic 2 Pro with a resolution of 5280 × 3956. The NJU dataset contains images of Nanjing University’s Xianlin Campus, and the CMCC-NanjingIDC dataset includes images of China Mobile Yangtze River Delta (Nanjing) data center. In this experiment, 304 and 2520 images are used for the scene reconstruction of these two datasets, respectively, to conduct ablation studies. The comparison between the datasets can be seen in

Table 4. Basic attributes of datasets.

	Original Resolution	Sampling Resolution	Original Images	Colmap Images
Rubble	4608 × 3456	1152 × 864	1657	1657
Building	4608 × 3456	1152 × 864	1920	685
Campus	5472 × 3648	1368 × 912	2129	1290
Residence	5472 × 3648	1368 × 912	2582	2346
SciArt	5472 × 3648	1368 × 912	3620	668
NJU	5280 × 3956	1320 × 989	304	286
CMCC-NanjingIDC	5280 × 3956	1320 × 989	2520	2098

. Original Images represents the original number of images, and Colmap Images represents the number of images actually involved in the acquisition of sparse point clouds by Colmap.

5.2. Preprocessing

To make fair comparisons between the methods, data are preprocessed in the same way in this paper. The images are downsampled to a quarter of their original resolution. During resampling, this paper uses a DOG method with a 3 × 3 convolution kernel and Lanczos interpolation to preserve image details.

5.3. Training Details

To demonstrate the effectiveness of the proposed method, comparative experiments are conducted against NeRF-like and 3DGS-like approaches. For NeRF-like methods, Nerfacto-big and Instant-NGP are reproduced using nerfstudio, which is an open-source modular NeRF development framework. The two models maintain their original model parameters and the training iterations are each set to 100,000. For 3DGS-like methods, the original 3DGS, Octree-GS, and Hierarchy-GS datasets are implemented based on their official open code. The training iterations of 3DGS and Hierarchy-GS are set to 30,000 and Octree-GS to 40,000. The more training iterations, the better the effect of the final result in theory. Additionally, Hierarchy-GS uses a fixed chunk size to segment the full scene into fixed-size sub-scenes. In this paper, it is uniformly set to 50.

For dataset preparation, training and test sets are selected by sampling one out of every ten images from those used in Colmap. Specifically, 90% of the images are used for training, and 10% are reserved for testing. All models are trained on the same dataset processed by Colmap to ensure a fair comparison.

The computational setup consists of a single standard 4090 GPU with 2G memory.

5.4. Comparison with SOTA Implicit Methods

To demonstrate the method’s feasibility, two types of comparisons are made. One compares the reconstruction of individual blocks with 3DGS, Octree-GS, and Hierarchy-GS, demonstrating the method’s competitiveness in individual block reconstruction. The other compares the modeling of complete scenes with Nerfacto-big, Instant-NGP, and Hierarchy-GS, highlighting the advantage of better visualization in full-scene reconstruction. Note that VastGaussian and DoGaussian are not compared due to the lack of official code, and Mega-NeRF is excluded for its excessive camera-pose requirements.

5.4.1. Single Block

Table 5. Metric results of single block.

Data		Building			Rubble			Campus			Residence			SciArt
Method	Metric	PSNR	LPIPS	SSIM	PSNR	LPIPS	SSIM	PSNR	LPIPS	SSIM	PSNR	LPIPS	SSIM	PSNR	LPIPS	SSIM
3DGS		27.83	0.180	0.872	28.84	0.173	0.877	24.30	0.256	0.783	24.56	0.197	0.831	19.88	0.576	0.484
Octree-GS		27.63	0.171	0.857	28.35	0.209	0.857	24.19	0.277	0.769	24.29	0.207	0.825	21.83	0.399	0.608
Hierarchy-GS		27.36	0.184	0.870	27.28	0.238	0.837	24.78	0.346	0.766	23.72	0.247	0.799	22.14	0.387	0.611
Ours		28.15	0.179	0.875	28.42	0.204	0.855	24.91	0.233	0.799	24.36	0.221	0.821	21.49	0.461	0.562

presents the single-block results on the Mill 19 and Urban Scene datasets. Notably, 3DGS and Octree-GS use blocks from this paper’s partitioning method, whereas Hierarchy-GS uses its own, with the most similar selected for comparison. Our method performs well across all five datasets. It achieves the best PSNR, LPIPS, and SSIM results on Building and SciArt, with minimal gaps in some cases. On Rubble, Campus, and Residence, though slightly underperforming compared to the original 3DGS method, it surpasses other large-scene modeling methods. Due to VRAM overflow, 3DGS reconstruction of the SciArt block scene stops at 8900 iterations, so the table shows results at 7000 iterations.

As shown in

Table 6. Max memory usage of single block.

	Building	Rubble	Campus	Residence	SciArt
3DGS	18.8 GB	19.7 GB	22.6 GB	22.8 GB	OOM
Octree-GS	19.7 GB	20.0 GB	20.2 GB	20.1 GB	22.4 GB
Hierarchy-GS	10.8 GB	12.6 GB	11.8 GB	12.2 GB	13.3 GB
Ours	9.4 GB	12.4 GB	11.5 GB	11.3 GB	12.9 GB

, this method achieves good single-block modeling and requires less in terms of machine performance. Moreover, 3DGS and Octree-GS can consume up to nearly 24 GB of VRAM for individual scenes, the limit for a standard 4090 GPU. In contrast, both Hierarchy-GS and our method significantly reduce VRAM usage, with ours being slightly lower than Hierarchy-GS.

Figure 9 visually compares the results. In Building, 3DGS and our method better restore texture details. In Rubble, Hierarchy-GS fails to model shaded vehicles. In Campus, Octree-GS darkens shaded trees and loses details. In Residence, the results are mostly consistent, with minor differences on the road. In SciArt, Hierarchy-GS produces a more refined result.

5.4.2. Full Scene

Table 7. Metric results of full scene.

Dataset		Building			Rubble			Camps			Residence			SciArt
Method	Metric	PSNR	LPIPS	SSIM	PSNR	LPIPS	SSIM	PSNR	LPIPS	SSIM	PSNR	LPIPS	SSIM	PSNR	LPIPS	SSIM
Nerfacto-big		15.70	0.465	0.325	18.38	0.452	0.440	18.05	0.537	0.463	16.46	0.405	0.464	17.31	0.758	0.363
Instant-NGP		20.47	0.460	0.574	18.67	0.537	0.525	19.53	0.625	0.529	16.16	0.533	0.495	20.28	0.713	0.453
Hierarchy-GS		26.28	0.210	0.836	26.73	0.246	0.830	23.62	0.364	0.731	21.47	0.282	0.702	20.05	0.426	0.558
Ours		26.67	0.185	0.844	27.36	0.221	0.846	23.74	0.344	0.745	22.89	0.239	0.799	20.38	0.441	0.561

compares the full-scene performance of our method, Nerfacto-big, Instant-NGP, and Hierarchy-GS. Our method generally achieves higher PSNR and SSIM scores and lower LPIPS scores, except possibly in the SciArt scene. The method achieves an average 2.45%, 6.41%, and 3.77% improvement in PSNR, SSIM, and LPIPS. During the experiments, Nerfacto-big uses 15–23 GB of VRAM, Instant-NGP uses 14–18 GB, and both Hierarchy-GS and our method use 10–14 GB.

As shown in Figure 10, Nerfacto and Instant-NGP have less ideal reconstruction effects. Hierarchy-GS also underperforms in some details. In the Campus scene, it produces artifacts in the vehicles and trees marked by the red box. In the Residence scene, it lacks details in the roller. In the SciArt scene, it loses the stripes on the blue roof and the surrounding green vegetation.

6. Discussion

6.1. Importance of Filtering

The initial distribution of the input point cloud impacts the modeling results and our proposed region-segmentation method. As our approach is point-distribution-based, noise points can greatly affect the segmentation. Figure 11 shows the segmentation results without filtering. Stray points cause grid-range misjudgment in grid initialization, leading to extremely uneven segmentation. This affects the iterative partitioning and final grid merging, easily creating large-area blocks with few points and small-area blocks with many points. Such unreasonable partitioning is detrimental to subsequent scene modeling. The impact on Building, Rubble, Campus, and Residence is significant, while SciArt is less affected. This is because SciArt has fewer stray points, which are also close to the main body.

6.2. Ablation Analysis

To demonstrate the effectiveness of the proposed point cloud filter and scene segmentation, ablation experiments were conducted on the self-collected NJU and CMCC-NanjingIDC datasets, as well as the public Rubble dataset. As shown in

Table 8. Ablation analysis results.

Model	Dataset	PSNR ↑	LPIPS ↓	SSIM ↑
Complete	NJU	27.58	0.161	0.904
	CMCC-NanjingIDC	24.66	0.283	0.787
	Rubble	27.36	0.221	0.846
Remove Grid-based Scene Segmentation	NJU	27.23	0.162	0.895
	CMCC-NanjingIDC	24.59	0.291	0.779
	Rubble	26.81	0.247	0.831
Remove Point Cloud Filter	NJU	27.12	0.166	0.897
	CMCC-NanjingIDC	24.10	0.303	0.772
	Rubble	26.32	0.254	0.825

, on the NJU dataset, the complete scene achieves slightly higher PSNR and SSIM values than removing only the segmentation or filtering module, with a similar LPIPS. On the CMCC-NanjingIDC and Rubble datasets, all three indicators show more significant improvements, especially on the Rubble dataset. Here, PSNR increases by 0.55 (2.05%) and 1.04 (3.95%) compared to removing partitioning or filtering; LPIPS decreases by 0.026 (10.5%) and 0.033 (12.9%); and SSIM rises by 0.015 (1.81%) and 0.021 (2.55%). Notably, removing only the filtering module generally has a larger impact across all datasets. Without filtering, redundant points affect both scene reconstruction and segmentation, causing double the negative effects on the final results.

6.3. Shortcomings

Although this method has realized large-scale scene reconstruction and has certain advantages over other methods in both individual blocks and complete scenes, it still has its own drawbacks. Both Instant-NGP and Nerfacto take about 40 min to complete full-scene training; 3DGS and Octree-GS take about half an hour to complete single-scene training. To cut down GPU usage, this method trades time for space. Each scene block takes nearly an hour to train, which is the same as Hierarchy-GS. Thus, the reconstruction time for a complete scene is directly proportional to the number of blocks, negatively affecting overall efficiency.

7. Conclusions

Low-altitude remote sensing images are one crucial data source for large-scale urban 3D reconstruction. This study introduces a novel approach to large-scale 3D scene reconstruction leveraging 3DGS. Initially, the sparse point cloud derived from indirect input data undergoes filtering to enhance data robustness, thereby improving the final reconstruction quality. The filtered point cloud also provides a more reliable foundation for scene segmentation, minimizing erroneous segmentations. During scene segmentation, the 3D distribution characteristics of the point cloud are fully exploited to develop a grid-based three-step strategy, ensuring high generalizability and rationality. To validate the effectiveness of the proposed method, experiments are conducted on five public datasets and two self-collected datasets. The results demonstrate that the method yields satisfactory outcomes. This method successfully achieves large-scale scene reconstruction with good visualization effects on low computing resources. However, due to the creation of the hierarchical tree, many intermediate node Gaussians are formed, resulting in the final result occupying about 1.5–1.8 times the disk space of the original 3DGS approach. In addition, the training time for each sub-scene is also relatively long—about 1 h—while the original 3DGS approach only takes half an hour. Improving these features could be undertaken in future works.