A Review of Machine Learning Applications in Ocean Color Remote Sensing

Abstract

Ocean color remote sensing technology has proven to be an indispensable tool for monitoring ocean conditions, as it has consistently provided critical data on global ocean optical properties, color, and biogeochemical parameters over several decades. With the rapid advancement of artificial intelligence, the integration of machine learning (ML) models into ocean color remote sensing has become a significant focus within the scientific community. This article provides a comprehensive review of the current status and challenges associated with ML models in ocean color remote sensing, assessing their applications in atmospheric correction, color inversion, carbon cycle analysis, and data reconstruction. This review highlights the advancements made in applying ML techniques, such as neural networks and deep learning, to improve data accuracy, enhance resolution, and enable more precise predictions of oceanic phenomena. Despite challenges such as model generalization and computational complexity, ML has significant potential for enhancing our understanding of marine ecosystems, facilitating real-time monitoring, and supporting global climate models.

1. Introduction

The vastness and complexity of the world’s oceans present formidable challenges to scientists seeking to understand and monitor their critical roles in global climate regulation, ecosystem dynamics, and biogeochemical cycles. Ocean color remote sensing (OCRS), a noninvasive observational technique, has emerged as an indispensable tool for monitoring the marine environment. This technology has been instrumental in advancing our understanding of various oceanographic processes, including the detection and analysis of phytoplankton blooms [1,2], assessments of ocean primary production [3,4], evaluations of particulate carbon standing stock [5,6,7], and investigations into the impacts of climate change [8,9].

While traditional remote sensing methods have provided valuable insights, they encounter limitations, particularly with the vast and intricate datasets yielded by contemporary satellite sensors. The integration of machine learning (ML) has led to a significant paradigm shift, introducing sophisticated algorithms capable of discerning patterns, extracting features, and generating predictions with remarkable accuracy and efficiency [10]. The ability of ML to evolve from data has significantly facilitated the advancement of ocean color remote sensing. Techniques such as neural networks for classifying oceanic phenomena and algorithms that foresee shifts in marine ecosystems are expanding our understanding of the ocean’s role within the Earth’s systems [11,12].

The integration of ML is not just a technological advancement but also an essential evolution, necessitated by the immense data volumes produced by contemporary satellite sensors and the increasing demand for precise, actionable insights [13]. ML algorithms have exhibited considerable efficacy in the processing and interpretation of complex datasets, thereby facilitating more accurate retrievals of oceanographic parameters, including chlorophyll-a concentrations (Chl-a) [14] and the partial pressure of CO₂ (pCO₂) at the air–sea interface [15,16]. The advancement of novel ML methodologies in ocean color remote sensing, such as neural networks for atmospheric correction [17,18,19] and self-organizing maps for pCO₂ estimation [20], has been pivotal in overcoming the limitations inherent in traditional data analysis techniques. These innovations have not only enhanced the accuracy of ocean color data interpretation but also significantly extended the spatial and temporal coverage of marine observations [21,22].

While the previous study discussed machine learning techniques for ocean color remote sensing, it focused primarily on the general trends and challenges associated with the application of ML in this field, neglecting the systematic conceptual description and outlook on future development [23]. This study aims to explore recent advances in machine learning applications within the field of ocean color remote sensing. We investigate the development and training of ML models and algorithms designed to analyze ocean color data, the innovative applications that are enhancing our understanding of marine processes, and the challenges and opportunities that lie ahead in this rapidly evolving field. This work introduces several key innovations that were not covered in the earlier work including the integration of deep learning models for atmospheric correction and the use of multisource data fusion for more accurate and reliable ocean color retrievals. Furthermore, the current work introduces the novel application of physics-informed neural networks and explainable artificial intelligence, which were not discussed in the earlier study, offering a more advanced and comprehensive framework for interpreting ocean color data.

2. Fundamentals of Ocean Color Remote Sensing

2.1. Principles of Ocean Color Remote Sensing

Ocean color remote sensing is fundamentally based on the interaction between light and the surface and column of the ocean, which is influenced by the biological, chemical, and physical properties of the water. When light reaches the ocean, it is absorbed, scattered, and reflected by marine constituents such as phytoplankton, suspended sediments, and dissolved organic matter. This interaction produces a distinct spectral signature that varies across different wavelengths, enabling inference of the concentration of these constituents through analysis of the reflected light. Satellite sensors, equipped with specialized spectral bands, facilitate the detection of subtle variations in ocean color, which can be systematically translated into quantitative data regarding the optical properties of water.

The process of ocean color remote sensing relies on the precise measurement of water-leaving radiance—the fraction of light that emerges from the water after interacting with its constituents—and its subsequent conversion into meaningful environmental data. This process requires correction for atmospheric effects that can alter the light detected by sensors and involves the application of bio-optical models to link optical measurements to the biological and chemical properties of the water. The remote sensing reflectance, defined as the ratio of water-leaving radiance to incident light, serves as a standardized metric for these measurements, enabling comparisons across different temporal scales and sensor platforms [24]. The accuracy of these measurements is crucial for obtaining reliable information about marine ecosystems and environmental conditions.

2.2. Traditional Challenges in Data Interpretation and Analysis

Ocean color remote sensing provides a unique capability for monitoring the marine environment; however, the interpretation and analysis of the resulting data have historically presented significant challenges. One of the primary concerns is the atmospheric influence on light measured by remote sensors. The atmosphere can scatter and absorb light, complicating the distinction between the atmospheric signal and that originating from the ocean surface. Accurate interpretation of the data necessitates the use of sophisticated atmospheric correction models designed to estimate and mitigate these atmospheric effects. This process can be intricate and is particularly susceptible to errors in regions characterized by high aerosol concentrations or variable weather conditions [19,24,25].

In addition to atmospheric correction, the optical complexity of coastal waters presents another significant challenge. Coastal and inland waters frequently contain high concentrations of suspended sediments, colored dissolved organic matter (CDOM), and diverse types of phytoplankton, all of which contribute to complex spectral signals that are difficult to disentangle. Traditional approaches have employed bio-optical models to link optical measurements with the biogeochemical properties of water [26,27,28,29]. These models are typically based on empirical relationships derived from in situ measurements and vary in their complexity and accuracy. This variability presents a challenge for the accurate retrieval of key parameters, such as chlorophyll-a concentration [30], which is a crucial indicator of phytoplankton biomass.

The spatial and temporal resolutions of satellite sensors pose significant challenges for traditional data interpretation in ocean color remote sensing. The relatively coarse spatial resolution of certain sensors can limit their ability to capture small-scale features and transient events, such as algal blooms or upwelling phenomena. Moreover, the temporal resolution, often dictated by the orbital characteristics of the satellite, may lead to data gaps caused by cloud cover, particularly in regions prone to high cloudiness or frequent storm activity. These data gaps can hinder the capacity to conduct time-series analyses, which are essential for detecting trends and seasonal variations in marine ecosystems [31,32].

Moreover, the traditional approach to ocean color data interpretation has largely depended on handcrafted algorithms that are based on specific assumptions regarding the relationships between optical properties and biogeochemical parameters. These algorithms often require a priori knowledge of the water type and can be highly sensitive to changes in environmental conditions. For example, the presence of optically active constituents other than phytoplankton, such as CDOM or suspended sediments, can introduce biases in the retrieved chlorophyll concentrations if not properly accounted for [33,34].

Overall, traditional methods face several limitations, such as atmospheric interference requiring complex correction models. Optical complexity in coastal waters arises from high concentrations of suspended sediments, CDOM, and diverse phytoplankton, which generate complex spectral signals that traditional models struggle to separate. The low spatial and temporal resolutions of satellite sensors limit their ability to capture small-scale features, such as algal blooms or upwelling, and results in data gaps due to cloud cover. Algorithm limitations often rely on predefined assumptions about water types, which can introduce biases when conditions change. The advent of artificial intelligence (AI), particularly through ML, has opened new avenues for addressing the traditional challenges associated with ocean color remote sensing. ML algorithms are uniquely equipped to detect complex patterns and relationships in data that conventional empirical methods may not capture effectively [35,36,37]. By harnessing the power of ML, researchers can significantly enhance atmospheric correction, overcoming the challenges posed by atmospheric interference, and more accurately interpret optically complex waters [38,39,40,41,42]. Additionally, ML has been demonstrated as an effective tool for improving spatial and temporal resolution, helping to detect small-scale phenomena such as algal blooms while filling data gaps caused by cloud covers [43]. ML can also ensure sensor consistency across different platforms and adapt to dynamic environmental conditions [44], offering a more flexible, accurate, and scalable approach to ocean color remote sensing that addresses the limitations of traditional methods.

3. Machine Learning Models and Algorithms

Machine learning is a subset of artificial intelligence that focuses on the development of algorithms capable of learning from and making decisions on the basis of data. It involves the creation and application of statistical models that enable computers to improve their performance on a specific task through experience learned from data [45]. The essence of ML lies in constructing models that can be generalized from the provided data to make predictions or decisions without being explicitly programmed for specific outcomes [46]. The ML process typically begins with data preprocessing—a critical phase involving the cleaning, normalization, and transformation of raw data into a format suitable for analysis [47]. This is followed by feature selection, wherein the most informative variables are identified to encapsulate the essence of the data [48]. The subsequent step is model selection, where an appropriate algorithm is chosen based on the nature of the problem, whether it involves classification, regression, or clustering. Selecting the right algorithm is vital to ensure that the model efficiently addresses the problem at hand [49]. The chosen model is then trained on a dataset, enabling it to recognize complex relationships and patterns. After training, it is imperative to evaluate the model’s performance via validation techniques, such as cross-validation, to ensure that it generalizes well to new data [50]. Ultimately, the trained model is deployed to make predictions or decisions on new data.

There are several types of ML, including supervised learning, unsupervised learning and reinforcement learning [51], each of which is suitable for different scenarios. Supervised learning is applied when the training data include labeled examples, enabling the model to learn how to predict outputs based on input features. The primary objective of supervised learning is to develop a model that can accurately map relationships between input data and corresponding output labels, thereby enabling it to make reliable predictions on new, unseen data. Typically, in supervised learning, the dataset is divided into a training set and a test set, where the model learns from the training set and subsequently has its performance evaluated on the test set. In contrast, unsupervised learning is utilized when the data lack labels, prompting the model to identify inherent structures or patterns within the data itself. The goal of unsupervised learning is for the model to uncover hidden structures or clusters in the data without any predefined output labels. This approach is frequently used in exploratory data analysis to reveal underlying patterns or groupings within a dataset. Reinforcement learning, on the other hand, centers on making a series of decisions aimed at maximizing a cumulative reward signal. The goal of reinforcement learning is for an agent to learn optimal decision-making strategies through interactions with its environment, where it continuously adjusts its actions based on the rewards or penalties received as feedback. This trial-and-error learning process enables the agent to develop strategies that maximize long-term rewards.

ML encompasses a diverse array of algorithms, each suited to different types of data and tasks. Linear models, known for their simplicity, are effective when dealing with linearly separable data. Decision trees and support vector machines (SVMs) are particularly powerful for both classification and regression tasks [30,52,53,54], with SVMs being renowned for their ability to handle high-dimensional spaces. Artificial neural networks (ANNs), inspired by the architecture of the human brain, excel in learning from vast amounts of data and form the foundation of deep learning. Deep learning involves multiple layers within neural networks, enabling the capture of intricate and complex patterns [21,22,55]. Ensemble methods, such as random forests [56,57] and gradient boosting machines [18,19,58,59,60], improve prediction accuracy and robustness by combining the strengths of multiple models. In the realm of unsupervised learning, clustering algorithms are employed to group similar data points without the need for prior labels. Dimensionality reduction techniques, such as principal component analysis (PCA), are utilized to simplify and visualize complex datasets [61,62], making them more manageable for analysis. The choice of an ML model is often dictated by the specific requirements of the task, the nature of the data, and the desired outcome. Each model has its unique strengths, making it well suited to particular types of problems. The field of ML is highly dynamic, with ongoing research continually introducing new algorithms and techniques to address an ever-expanding array of challenges.

As ML models have advanced in sophistication, they are increasingly being applied to complex domains such as ocean color remote sensing. Indeed, ML is particularly useful in ocean color remote sensing when the relationships between variables are nonlinear or too complex for traditional analytical models. Historically, radiative transfer models have been used to relate the observed remote sensing reflectance (Rrs) to the underlying oceanic properties. While these models are effective in simple cases, they struggle with more complex scenarios involving factors such as CDOM and suspended particles, which independently influence the water-leaving radiance. ML models, such as multi-layer perceptrons (MLPs), can better handle these complexities by capturing nonlinear relationships and processing multidimensional inputs from the data [16,63,64,65]. The process of machine learning for ocean color remote sensing begins with the collection of a large dataset from observations or simulations, which is subsequently divided into training and test sets. These datasets are used to train ML algorithms, allowing them to develop high-accuracy models through iterative parameter optimization. In the prediction phase, these models are employed to infer results from new data.

The integration of ML with OCRS significantly improves prediction accuracy, enhances data processing capabilities, and provides better insights into environmental factors, facilitating a more comprehensive understanding of marine ecosystems (Figure 1a). Furthermore, this combination enables seamless coverage of large ocean areas, while also improving long-term and short-term predictions by analyzing complex patterns and factors such as atmospheric effects and phytoplankton blooms. The key advantage of ML in this field is its ability to improve prediction accuracy by incorporating complex environmental factors, which are difficult to model using traditional methods. Moreover, deep learning models eliminate the need for manual feature extraction by learning directly from the data, offering a more flexible and robust approach to solving inverse problems in ocean color remote sensing. The application of ML in this field highlights its transformative potential in enhancing our ability to analyze and understand complex environmental systems.

4. Machine Learning-Enhanced Ocean Color Remote Sensing

Since Heinemann first applied machine learning in ocean color remote sensing in 1997 [66], the exponential growth of data in the domain of ocean color remote sensing has facilitated the increasing integration of ML techniques. This bibliometric analysis was conducted by performing a search in the Web of Science Core Collection via the following query:

“(TS = (artificial intelligence) OR TS = (machine learning) OR TS = (machine-learning) OR TS = (deep learning) OR TS = (deep-learning) OR TS = (data mining) OR TS = (data-mining) OR TS = (neural network *) OR TS = (transfer learning)) AND (TS = (ocean color remote sensing))”. The results of this search were then exported and analyzed via Bibliometrix ver4.3.3 [67].

The analysis highlights the dramatic rise in scientific production, as shown in Figure 1b, where the number of publications sharply increased after 2015, indicating a period of significant expansion in ML applications within this field. The co-occurrence network in Figure 1c further offers a deeper understanding of the key themes driving research in this area. The network reveals the interconnections between crucial terms such as “machine learning” “remote sensing” “ocean color” and “chlorophyll” among others, emphasizing how these terms collectively define the focal points of current research. These interconnected themes highlight the central role that machine learning techniques are playing in ocean color retrieval, showing how advancements in computational methods are allowing for more accurate and comprehensive analysis of oceanic data. The evolution of key research topics over time shown in Figure 1d highlights the development and growing prominence of various themes within the intersection of machine learning and ocean color remote sensing. Deep learning and machine learning have seen a rapid increase in relevance starting from the early 2010s, signaling the growing integration of these computational techniques into oceanographic studies. This rise coincides with the broader adoption of remote sensing reflectance algorithms and advancements in atmospheric correction, both of which are critical for improving the accuracy of satellite-based ocean color measurements, particularly in the context of complex coastal waters and varying atmospheric conditions. The continuous increase in research surrounding chlorophyll reflects their importance as key parameters in ocean color remote sensing for monitoring phytoplankton growth and marine ecosystem health. The neural network term, representing a critical aspect of ML applied to remote sensing, has also demonstrated a significant uptick, emphasizing the growing use of neural network-based approaches for processing ocean color data. Harmful algal blooms and phytoplankton are additional prominent topics that have emerged as critical areas of focus, highlighting the role of ML models in detecting and predicting these phenomena through the analysis of ocean color data.

Table 1. List of high-frequency keywords in ML-OCRS.

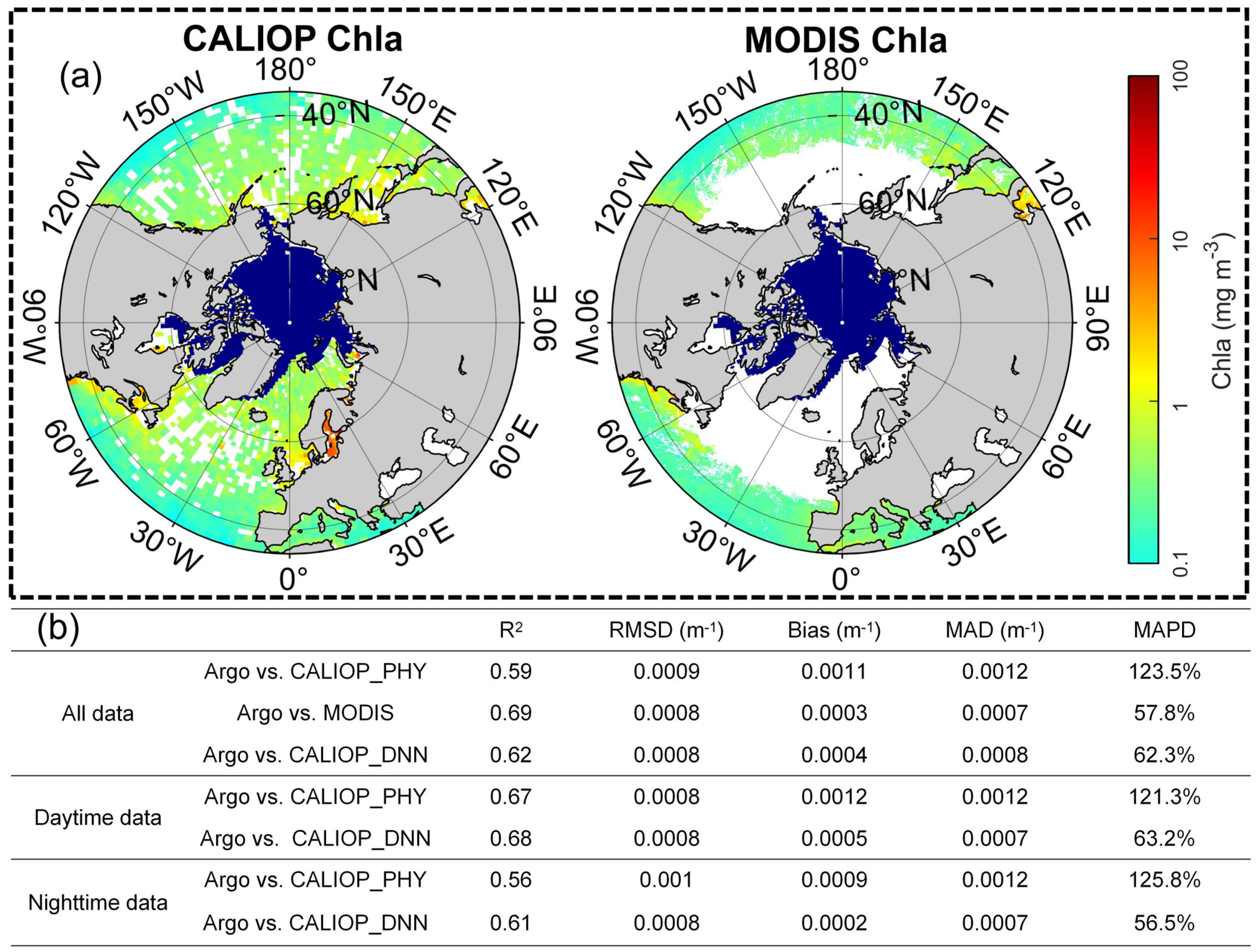
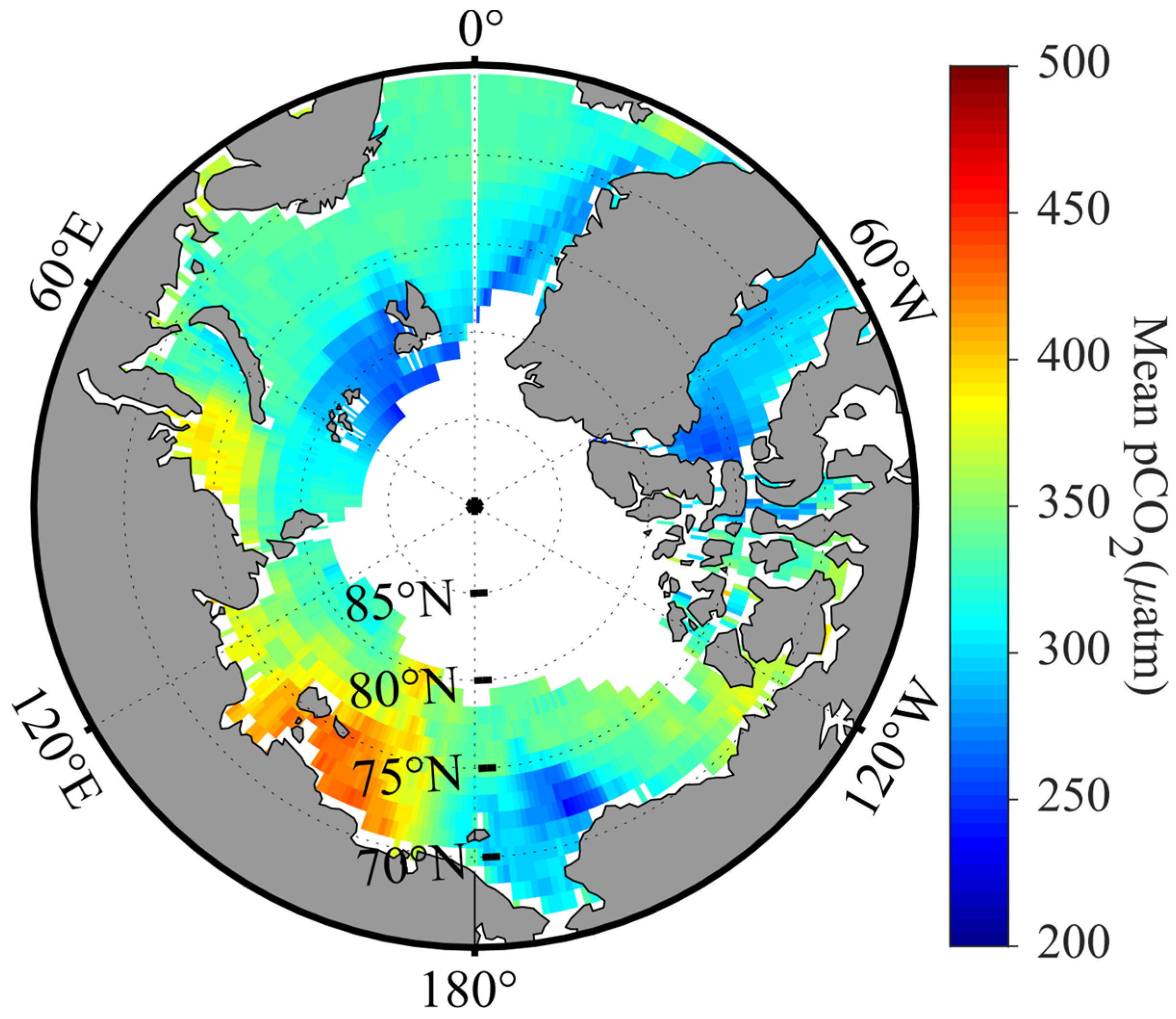
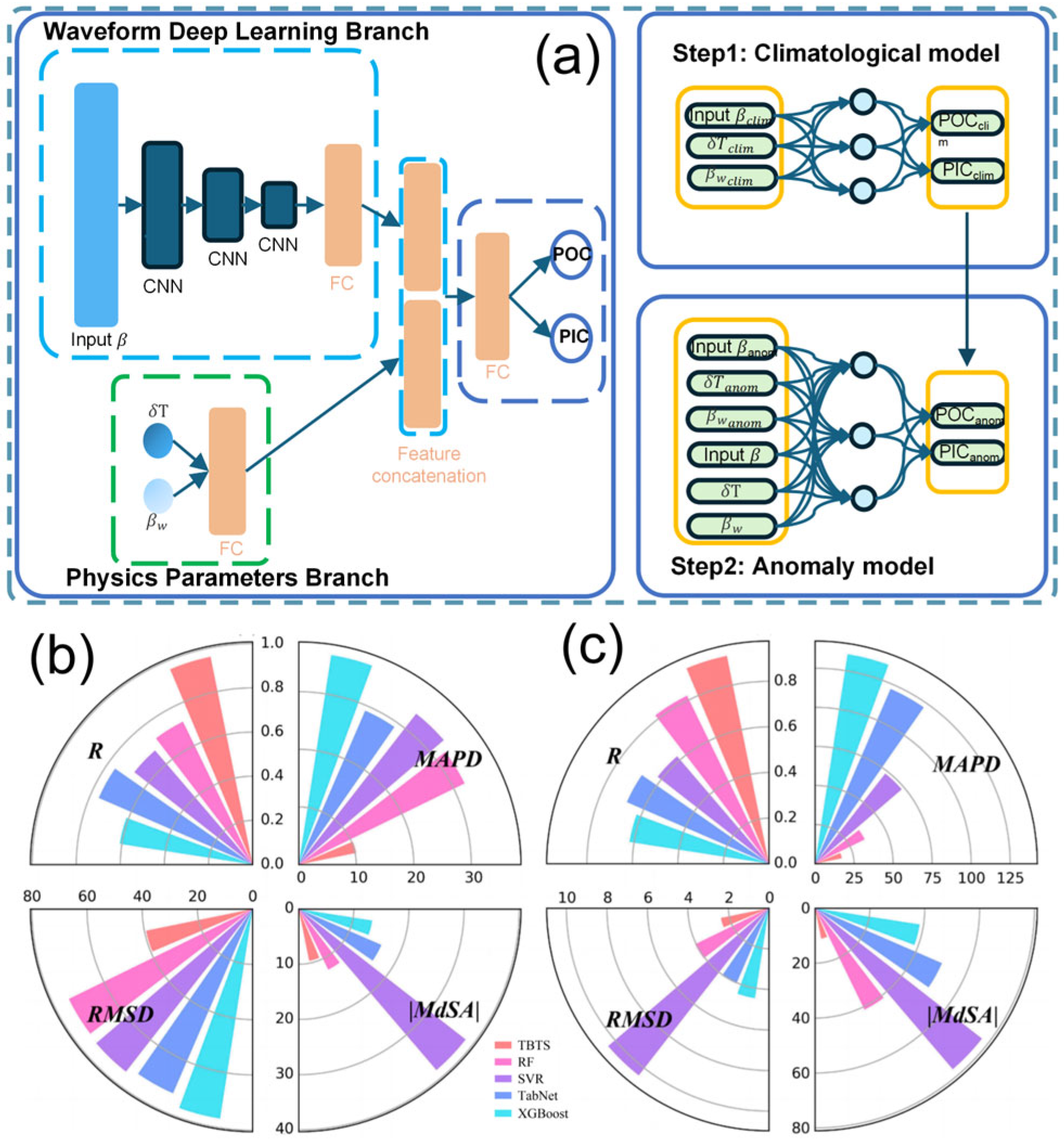
Keywords	Occurrences	Keywords	Occurrences	Keywords	Occurrences
remote sensing	104	meris	8	chlorophyll-a (chl-a)	5
ocean color	69	algorithm development	7	classification	5
machine learning	60	artificial neural network	7	feature extraction	5
neural network	36	cdom	7	inland and coastal waters	5
atmospheric correction	25	chlorophyll-a concentration	7	normalized fluorescence height	5
chlorophyll-a	24	ocean color	7	radiative transfer	5
neural networks	23	random forest	7	arctic ocean	4
water quality	22	satellite	7	artificial intelligence	4
deep learning	21	satellites	7	Barents sea	4
modis	21	seawifs	7	coastal water	4
ocean color remote sensing	20	aerosols	6	geostationary ocean color imager (goci)	4
phytoplankton	17	Baltic sea	6	hyperspectral	4
chlorophyll	14	inherent optical properties	6	image color analysis	4
remote sensing reflectance	11	karenia brevis	6	inland waters	4
coastal waters	10	oceans	6	inversion	4
harmful algal blooms	10	satellite remote sensing	6	machine learning algorithm	4
olci	9	sea measurements	6	new Caledonia	4
sentinel-3	9	viirs	6	ocean color remote sensing reflectance	4
chlorophyll a	8	west Florida shelf	6	ocean color remote sensing	4
goci	8	algorithm	5	ocean optics	4

lists the high-frequency keywords in machine learning in ocean color remote sensing, with terms like “remote sensing”, “ocean color”, and “machine learning” appearing most frequently, reflecting the central themes in the field. Other notable keywords include “chlorophyll-a”, “atmospheric correction”, and “satellite remote sensing”, indicating key areas of focus in ML applications for ocean color remote sensing. The specific improvement of ML over canonical methods can be seen in

Table 2. Performance metrics of machine learning models in ocean color remote sensing.

	Research Focus	Model Performance
(Gross et al., 1999) [68]	NN inversion for chlorophyll-a retrieval from satellite reflectances.	ANN achieved ±3% accuracy compared to 15–30% error in polynomial fits.	Used SeaWiFS simulated data.
(Gross et al., 2004) [69]	NN to retrieve chlorophyll-a from marine reflectance in the Western Equatorial Pacific Ocean.	Improved performance by 75% compared to classical algorithms using reflectance ratios.	Model calibrated with synthetic and in situ data.
(Jamet et al., 2012) [70]	NN to estimate Kd from SeaWiFS data.	ANN method has RMSE of 0.27 m−1 for Kd(490), significantly better than traditional methods: Kd(Werdell) RMSE = 1.41 m−1, Kd(Zhang) RMSE = 0.71 m−1, Kd(Morel) RMSE = 1.56 m−1.	Model trained with synthetic data and in situ data and evaluated with field measurement data.
(Ioannou et al., 2013) [71]	NN for retrieving IOP and Chl from MODIS Rrs.	NN algorithms improve chlorophyll retrieval with R2 of ~0.90, compared to OC3 (~0.84).	Used both simulated and field data.
(Fan et al., 2017) [24]	Atmospheric correction using NN for coastal waters.	NN algorithm reduced the Average Percentage Difference (APD) in AOD retrievals by up to 25% in the blue bands (412 nm and 443 nm) compared to SeaDAS NIR and NIR/SWIR algorithms.	Model trained with synthetic data and in situ data and evaluated with field measurement data.
(Cao et al., 2020) [60]	XGBoost to estimate Chl-a in turbid inland lakes using Landsat-8 data.	BST performed well with MAPD = 24% compared to RF (MAPD = 30%) and band-ratio algorithms (MAPD = 64%).	Field data from 8 lakes in eastern China (N = 225) and SeaWiFS Bio-optical Archive (N = 97).
(Li et al., 2020) [72]	NN for atmospheric correction of GOCI data at high solar zenith angles.	The NN AC algorithm yielded stable Rrs even at solar zenith angles ≥70° (APD = 30%), outperforming traditional NIR algorithms (APD = 87%).	Model trained with GOCI Rayleigh-corrected radiance and noontime Rrs matchups and evaluated with in situ data from AERONET-.
(Pahlevan et al., 2020) [73]	MDN for estimating Chl-a from Sentinel-2 MSI and Sentinel-3 OLCI data in inland and coastal waters.	MDN outperformed OC algorithms (MAPE was improved by 2–3 times).	Model trained with 1000 co-located in situ Rrs–Chla pairs and evaluated with independent in situ data (n > 1900) from multiple regions, including lakes, rivers, and estuaries.
(Zhao et al., 2023) [74]	ANN for HY-1C CZI atmospheric correction.	APD was reduced to 9.78% on average compared to ACAOD’s 105.48%.	Model trained with HY-1C CZI and Landsat 8 OLI spatio-temporally synchronized datasets and evaluated with in situ data and quasi-synchronous Landsat 8 Rrs data.
(He et al., 2024) [18]	XGBoost for polarization atmospheric correction.	MAPE of Rrs(490) was reduced to 34.43 compared to GlobColour products (MAPE > 60%).	Model trained with simulated data and evaluated with field measurement data.

.

4.1. Atmospheric and Optical Correction Innovations

Atmospheric correction represents a fundamental and critical step in numerous ocean color remote sensing algorithms. The primary objective of atmospheric correction is to eliminate the radiative contributions of the atmosphere—including those from air molecules, aerosols, and surface reflection—from the satellite-measured top-of-atmosphere (TOA) radiance. This refined radiance, known as water-leaving radiance, is essential for deriving ocean color products such as chlorophyll-a concentration. Notably, atmospheric contributions can constitute up to 90% of the TOA radiance observed by satellite sensors, with this influence being even more pronounced in coastal areas, particularly within the blue spectral band, or in highly turbid waters dominated by sediment. In these scenarios, the atmospheric influence diminishes in the red and near-infrared bands [75]. Consequently, the development of accurate atmospheric correction algorithms is crucial for the precise processing of ocean color data [24]. Early research often relied on various data interpolation methods, including statistical interpolation, linear regression, nonlinear regression, and multiple regression, to reconstruct marine atmospheric parameters. These methods typically utilize commonly available satellite data, encompassing variables such as air temperature, atmospheric pressure, humidity, wind speed, and aerosol optical depth.

However, due to the diverse and complex factors influencing atmospheric parameters across different marine environments, traditional models often lack universality when applied to varying sea areas worldwide. Historically, research has predominantly concentrated on developing atmospheric correction algorithms tailored to open ocean environments, with relatively few studies addressing the unique challenges posed by inland waters and coastal regions characterized by high turbidity. In recent years, ML-based algorithms have been increasingly adopted for predicting specific marine weather phenomena [38,39,40,41,42]. The rapid advancement of ML has similarly opened new avenues for modeling the nonlinear relationships inherent in global marine atmospheric environmental parameters involving inputs such as the solar zenith angle, viewing zenith angle, relative azimuth angle, and TOA radiance, and retrieving Rrs, which is essential for accurate ocean color analysis. These ML algorithms, which account for the complex interplay of regional factors and various environmental influences, have been extensively applied in the field of atmospheric correction [17,74,76,77,78,79,80]. A development in this domain is the intelligent polarization atmospheric correction (IPAC) algorithm proposed by He et al. (2024). This algorithm leverages the vector radiative transfer simulation model to simulate polarized TOA vector apparent reflectance over open ocean areas. The extreme gradient boosting (XGBoost) algorithm is employed for atmospheric correction. Compared to conventional atmospheric correction algorithms, the IPAC algorithm demonstrates a significant improvement in the accuracy of retrieved ocean color products [18]. In a related advancement, Song et al. (2023) introduced the OC-XGBRT algorithm, which integrates XGBoost with radiative transfer simulation. This approach addresses and mitigates the limitations of traditional atmospheric correction algorithms, particularly in scenarios involving absorbing aerosols [19]. Bayesian methodology proposed by Frouin et al. (2015) for inverting satellite ocean-color data uses a probability distribution framework to estimate marine reflectance from TOA reflectance, which can effectively model uncertainties and improve the reliability of ocean color retrievals [42].

Additionally, ANNs have emerged as critical tools in the atmospheric correction process. The FastMAPOL algorithm developed by Gao et al. (2021) employed an NN model to efficiently retrieve aerosol properties and water-leaving signals from polarimetric data [81]. Wang et al. (2022) introduced an atmospheric correction algorithm based on NASA’s SeaDAS, known as ACANIR-NN. This algorithm effectively performs atmospheric correction across both clear and turbid waters, even for sensors that lack shortwave infrared capabilities [82]. In another study, Sun et al. (2021) proposed a time-dependent neural network designed for automatic atmospheric correction and target detection using multi-scan hyperspectral data collected at various elevation angles. This neural network is capable of estimating atmospheric bulk properties under conditions of seasonal and diurnal variations and can address the challenges posed by missing data [83]. Similarly, Li et al. (2020) developed a novel ANN algorithm by training it on extensive matches between Rayleigh-corrected radiance from the morning and evening of GOCI (Geostationary Ocean Color Imager) observations and high-quality noontime Rrs. This approach yielded diurnally stable Rrs values in open ocean waters from morning to evening, effectively resolving data anomalies in GOCI inversions under high solar zenith angles [72].

Concurrent advancements are also being made in ML-based atmospheric correction inversion algorithms. Brockmann et al. (2016) further refined the Case 2 algorithm for Sentinel-2 satellites and developed the Case 2 Regional CoastColour (C2RCC) algorithm. This algorithm is versatile and applicable to all heritage, current, and potential future multispectral and hyperspectral ocean color sensors [84]. Additionally, Rusia et al. (2021) optimized an existing algorithm using ML by framing interpolation as a regression problem, significantly reducing data processing time and enhancing overall effectiveness [85]. Moreover, some researchers have proposed ML algorithms driven by coupled atmosphere-ocean radiative transfer simulations [86]. Compared with NASA’s standard products, these ML models, particularly those based on neural networks, exhibit superior performance under nearshore turbid water conditions. Unlike the traditional physical method-based lookup table and linear interpolation approaches, which are often complex and less adaptable, the nonlinear fitting capabilities of ML are better suited to handling intricate environments, especially in processing data from nearshore turbid areas and regions with absorbing aerosols.

4.2. Applications in Bio-Optical Property Retrieval

Significant progress has been made in monitoring Chl-a via satellite remote sensing technologies. A variety of algorithms have been developed to estimate Chl-a across different water types and seasonal conditions, employing multiple sensors. These include two-band ratio algorithms (BR), three-band algorithms (TBA), four-band algorithms (FBA), baseline subtraction algorithms (BS), nested band ratio algorithms (NBR), quasi-analytical algorithms (QAA), and QAA-based algorithms [26,29,87,88,89,90,91,92,93]. Furthermore, the optical water type (OWT) classification strategy has proven to be an effective tool for assessing optically complex waters. This approach facilitates the retrieval of Chl-a from widely dispersed in situ data [94,95,96].

Accurate prediction of coastal ocean Chl-a is essential for dynamic water quality monitoring, particularly given the critical role of eutrophication. The neural network method was introduced for chlorophyll pigment retrieval in ocean color remote sensing in 1999 [68,97]. Since then, the development of chlorophyll-a concentration retrieval methods based on the ANN method has been rapid [69,98,99,100]. The subsequent mixture density network (MDN) provides not only a single output but also a probability distribution, capturing uncertainty and multimodal predictions [73,101,102,103,104]. Gross-Colzy and Frouin (2003) proposed a methodology that uses PCA to retrieve marine reflectance and chlorophyll-a concentrations from satellite data [105]. The support vector machine algorithm has demonstrated strong performance in the inversion of Chl-a [52,53] and the mapping of phytoplankton function types [54]. The study by Niu et al. (2023) underscores the effectiveness of the Gaussian process regression (GPR) model in estimating Chl-a, highlighting the significance of including particulate organic carbon (POC) when modeling Chl-a [14]. Similarly, Cui et al. (2022) developed a Chl-a prediction model based on the XGBoost algorithm, employing an intelligent parameter optimization strategy. This model effectively uncovers the potential relationships between environmental factors and Chl-a in oceanic contexts [58]. In addition, XGBoost was used to derive Chl-a in turbid lakes from Landsat-8 Operational Land Imager [60]. Blix and Eltoft (2018) introduced an automatic model selection algorithm (AMSA) designed for global estimation of marine Chl-a in optically complex waters. This algorithm utilizes four ML feature ranking methods and three ML regression models, including Gaussian process regression (GPR), support vector regression (SVR), and partial least squares regression (PLSR) [30]. Additionally, Kolluru and Tiwari (2022) proposed a novel approach to derive Chl-a using an MLP neural network with resilient backpropagation, leveraging four ocean color bands available in most ocean color sensors [63]. Combined with self-organizing maps (SOMs), the accuracy of chlorophyll concentration retrieval can be significantly improved [106,107,108,109,110,111,112]. Moreover, Zhang et al. (2023) developed a spatial–temporal–ecological ensemble (STEE) model, which integrates gradient-boosted decision trees (GBDTs), ANN, and attentive interpretable tabular learning (TabNet) to construct a robust prediction framework for estimating Chl-a across eight distinct phytoplankton groups [59]. In another advancement, Zhang et al. (2023) employed deep learning techniques for spaceborne LiDAR, enabling the inversion of chlorophyll concentration in polar waters (as depicted in Figure 2a) [55]. This deep learning-based spaceborne LiDAR water parameter inversion model demonstrates a promising capability to extend the detection range of marine remote sensing.

Inherent optical properties (IOPs) are intrinsic characteristics of water bodies that depend solely on the constituents within the water, independent of external lighting conditions [113]. These properties are fundamental to oceanographic research and play crucial roles in understanding marine ecosystems, biogeochemical cycles, and ocean remote sensing. Many algorithms related to IOPs have employed the generalized stacked constraints model (GSCM) [114]. Compared to traditional regression models, ANNs offer advantages such as flexibility, fast computation, high reliability, and consistent output, particularly in handling nonlinear problems. In the field of ocean color, ANNs have been effectively utilized to derive various water quality parameters, including total IOPs [22,115,116], sub-component IOPs [71], and diffuse attenuation coefficients [70]. Zhang et al. (2023) reconstructed a spaceborne LiDAR water particulate backscattering inversion model using deep learning techniques [22]. Compared with traditional methods (as illustrated in Figure 2b), the deep learning approach provided results that were closer to the measured values, significantly enhancing the inversion accuracy. Additionally, random forest (RF) has been employed to retrieve the diffuse attenuation coefficient (Kd) from ICEsat-2 ATLAS Spaceborne Lidar, achieving high accuracy and efficacy [56].

The concentrations of optically significant marine components, such as phytoplankton, nonalgal particles, and CDOM, are critical in controlling light propagation in aquatic environments [117]. Liu et al. (2021) evaluated three ML algorithms—XGBoost, SVM, and ANN—for retrieving POC concentrations. Their study found that XGBoost was the most robust, whereas ANN was more effective in optically complex waters with extremely high POC concentrations [118]. Liu et al. (2022) developed an ML method to reconstruct monthly concentrations of dissolved inorganic nitrogen (DIN), dissolved inorganic phosphorus (DIP), and dissolved silicate (DSi) in the surface layer of the Yellow Sea and Bohai Sea from 2003 to 2019. This method is significant for monitoring spatiotemporal changes in nutrient concentrations in shelf seas, contributing to the understanding of marine primary productivity and ecological dynamics [119].

4.3. Enhanced Analysis of the Ocean Carbon Cycle

The role of the ocean in the carbon cycle can be estimated through the pCO₂ in seawater. The high spatiotemporal heterogeneity of seawater pCO₂ is a critical parameter for quantifying air–sea CO₂ exchange. Consequently, reconstructing seawater pCO₂ datasets through observational methods, including ship surveys, buoys, and satellite remote sensing, is essential for accurately understanding the dynamics of the ocean carbon reservoirs [120]. Among these methods, satellite remote sensing of seawater pCO₂ holds significant potential for reducing observation time and costs, making it a promising approach. However, practical challenges remain in the remote sensing of seawater pCO₂ due to the complex and diverse environmental factors influencing its variability. In early studies, various data interpolation techniques, such as statistical interpolation, linear regression, nonlinear regression, and multiple regression, were commonly employed to reconstruct seawater pCO₂. These techniques utilize satellite-derived data, including sea surface temperature (SST), sea surface salinity (SSS), Chl-a, Kd, wind speed, and mixed layer depth (MLD) [121,122,123,124,125,126,127].

However, because the diverse and complex factors influence seawater pCO₂ across different oceanic regions, traditional models often lack universal applicability at the global scale. The rapid development of ML has provided a new tool to capture the nonlinear relationships between global marine ecological environmental parameters and seawater pCO₂. ML algorithms, which account for the complex interplay of various factors across different regions, have been widely applied in the construction of global seawater pCO₂ datasets [12,20,64,128,129,130,131,132,133]. Landschützer et al. (2013) pioneered the use of a two-step neural network based on self-organizing maps to classify Atlantic seawater pCO₂, successfully reconstructing the monthly average seawater pCO₂ in the Atlantic with a spatial resolution of 1° for each region and season [130]. This remote sensing inversion algorithm has since been widely applied, enabling the inversion of seawater pCO₂ in various regions, including the global open ocean [134], global marginal seas [12], Arctic [131], and Northeast Pacific [135]. Another significant algorithm in the reconstruction of seawater pCO₂ is the MLPs. Jo et al. (2012) utilized MLPs to create a comprehensive dataset of marine parameters, facilitating the estimation of the global carbon budget [65]. Zeng et al. reconstructed the monthly average distribution datasets of the tropical Atlantic [136] and the global [137] using MLPs. Denvil-Sommer et al. (2019) proposed the use of an MLP model to achieve the inversion of seawater pCO₂ in the open ocean [64] and marginal seas [133]. Zhang et al. (2022, 2023) further expanded the application of MLPs in the Arctic [16] and the global day/night carbon cycle [138] utilizing spaceborne LiDAR data. Their work addressed the gaps in traditional datasets during the polar winter, marking the first time the nighttime distribution of global seawater pCO₂ has been depicted (as shown in Figure 3).

4.4. Development of Data Reconstruction Methods Based on Machine Learning

By integrating multiple remote sensing data sources with in situ observational data and utilizing multisource data fusion techniques alongside the processing power of large models, a comprehensive marine environmental monitoring framework can be developed. These models are capable of accurately reflecting trends and changes in the marine environment. However, the complexity of marine environments poses significant challenges in obtaining comprehensive and precise data, often necessitating substantial costs and advanced technical expertise. In many fields, including vertical temperature and salinity, the accumulated marine data remain insufficient for practical use [139]. Additionally, traditional global ocean models frequently exhibit low resolution, which limits their ability to capture regional details effectively [140]. The sparsity and discontinuity of observational data—constrained by financial and technical limitations—seriously hinder the study of marine processes and mechanisms, resulting in an incomplete understanding of local marine phenomena. To address these challenges, data reconstruction techniques serve as widely utilized and effective solutions, offering a means to provide continuous and comprehensive marine datasets.

In traditional data reconstruction tasks, commonly used methods include data assimilation based on dynamic frameworks, numerical-driven statistical approaches such as empirical orthogonal functions (EOFs) to infer missing data, and spatial autocorrelation-based data interpolation techniques like Kriging/optimal interpolation (OI) [141,142,143]. An advanced extension of EOF, the data interpolating empirical orthogonal functions (DINEOF), has demonstrated significant effectiveness in reconstructing marine remote sensing data. DINEOF utilizes the dominant modes of variability within the dataset to iteratively infer missing values without requiring external datasets or prior assumptions [144,145]. It has been widely applied in the reconstruction of variables such as SST [146], Chl-a [147], and other oceanographic parameters [148] by filling data gaps caused by cloud cover, sensor limitations, or noise.

However, these methods often face challenges, including difficulties in model construction, limited applicability to specific regions, challenges in handling nonlinear relationships, and high sensitivity to outliers. In recent years, ML methods have gained significant traction in the field of marine data reconstruction due to their ability to efficiently manage complex, multi-source, and multi-scale data [43]. ML models exhibit strong adaptability and scalability, making them applicable to diverse datasets and tasks [120]. Additionally, their automated and intelligent nature reduces human intervention and the potential for errors, thereby enhancing the efficiency and quality of data processing. By constructing complex mathematical models, ML can fill data gaps and reduce uncertainty. [149]. ML has been employed to optimize interpolation methods for data reconstruction [150,151,152,153,154]. Moreover, ML can complete existing datasets [155,156,157], and generate new high-quality datasets [57,158,159].

In various studies, researchers have employed different ML techniques to optimize interpolation methods for predicting missing continuous data. For instance, Martinez et al. (2020) use a nonlinear statistical approach based on SVR to reconstruct global chlorophyll-a variations, demonstrating its ability to accurately reproduce interannual and decadal variability in Chl-a from satellite observations and physical model predictors [160]. Mohebzadeh et al. (2021) utilized SVR to perform spatiotemporal interpolation of chlorophyll concentration based on MODIS satellite data and other environmental parameters [153]. Similarly, Ouala et al. (2018) implemented a neural network-based Kalman filter, integrating satellite-derived sea surface temperature and sea surface height data, to carry out spatiotemporal interpolation of sea surface temperature data [154]. Roussillon et al. (2023) propose a multi-mode convolutional neural network to reconstruct global satellite-derived Chl-a time series, accounting for regional biogeochemical variations and improving reconstruction performance while offering insights into physical–biogeochemical processes controlling phytoplankton variability [161]. Zhang et al. (2024) applied the optimal interpolation model to fuse data from multiple sources, including MERSI-II and MWR SST data, reconstructed data, and background field data, resulting in high-quality SST fusion products with a temporal resolution of 12 h and a spatial resolution of 5 km [151]. Cutolo et al. (2024) proposed the CLOINet model, which was trained to optimize the interpolation network by combining remote sensing data, in situ sparse observations, and deep learning techniques. This approach aims to reconstruct a comprehensive marine state image encompassing multiple ocean parameters, such as sea surface temperature, salinity, and chlorophyll concentration [150].

Researchers have also employed ML techniques to reconstruct low-quality marine datasets impacted by noise and cloud cover, thereby enhancing dataset integrity. For example, Hirahara et al. (2019) utilized a generative adversarial network (GAN) to learn the distribution of sea surface temperature images. By integrating physical model constraints into the GAN’s loss function, they improved the model’s accuracy and physical plausibility, resulting in the denoising and restoration of sea surface temperature images [156]. Similarly, Jouini et al. (2013) used neural networks to identify and reconstruct areas obscured by clouds, generating complete chlorophyll images [157]. Barth et al. (2021) applied a multivariate convolutional neural network, DINCAE 2.0, to reconstruct sea surface temperature and altimeter observation data, effectively filling data gaps caused by cloud cover and orbital gaps [155].

In addition to these methods, other researchers have integrated multiple data sources to create new, more comprehensive, and accurate marine datasets. For instance, Park et al. (2020) employed a random forest method based on ensemble learning to integrate remote sensing chlorophyll concentration data from the Ross Sea with various environmental parameters (such as sea ice, water depth, air temperature, etc.), resulting in more complete and accurate chlorophyll data [57]. Similarly, Ćatipović et al. (2023) used a GAN to reconstruct more complete and accurate chlorophyll concentration data by integrating satellite-derived chlorophyll data with other related datasets [158].

5. Challenges and Opportunities

5.1. Challenges

5.1.1. Limitations in Generalization and Model Adaptability

While ML has been widely used in ocean color remote sensing and excels at regression fitting, it does not generate any “new” information beyond the distribution of its training data [162]. This limitation is particularly evident in the context of the ocean’s inherent complexity and dynamic nature, where ML models can struggle with inadequate generalization, particularly when trained on limited or biased datasets [163]. As a result, models trained on region-specific datasets often fail when applied to other areas, due to variations in water properties, optical characteristics, and biological activity [163]. This limitation is further exacerbated by shifts in data distribution, which is a common issue in marine environments. For example, seasonal changes in phytoplankton dynamics or atmospheric conditions can significantly alter the spectral reflectance captured by remote sensors, leading to performance degradation in pre-trained models. Ensuring robust performance across varying spatial and temporal scales remains a significant challenge, highlighting the need for well-designed data segmentation and evaluation strategies to simulate intended use cases effectively.

In ocean remote sensing, changes in data distribution are common, and ML models are highly sensitive to these variations. Many ML models are also highly sensitive to local biases in training data, limiting their application to global-scale monitoring. Transferring models across sensors or geographic regions often requires significant pretraining or adaptation [70], which can be overlooked. Moreover, spatial and temporal autocorrelations, which occur when nearby data points or those taken at similar times exhibit dependencies, can further impact model performance. These dependencies can introduce information leakage between training and test datasets, leading to overestimated model performance [164]. To address this, it is critical to adopt appropriate sampling strategies. Although widely used, random sampling methods can introduce biases and negatively affect model accuracy [165]. Spatial and temporal fold cross-validation is a more robust approach, offering a more accurate representation of model errors [59]. Additionally, when simulation datasets are used, it is essential to validate model performance with additional measured datasets [18,19]. In addition, domain adaptation techniques, such as transfer learning, can further improve model robustness across regions and sensors, enabling their application to diverse datasets and environments [166].

5.1.2. Data Availability and Quality

A significant challenge in applying ML to marine environments is the quality and availability of training data. As encapsulated by the principle of “garbage in, garbage out” [167], ML models depend on large, high-quality datasets for effective training. However, collecting such datasets in marine environments is both costly and logistically challenging. The high cost and technical limitations of data collection result in insufficient spatial and temporal coverage, leaving critical gaps in the datasets. Additionally, data noise and biases are often underestimated, significantly impacting model performance. For example, noise in certain satellite datasets can directly increase the uncertainty of inversion results. Furthermore, the dynamic nature of the ocean necessitates continuous updates and retraining of models to maintain accuracy over time. A case in point is the combined use of Argo float and satellite monitoring data, where sparse temporal coverage makes it difficult for models to accurately capture small-scale phenomena. To address these challenges, several solutions have been proposed. Self-supervised learning techniques can reduce dependence on labeled data by leveraging latent information in unlabeled datasets to improve model performance [168]. Additionally, the integration of process-guided deep learning, which combines physical constraints with statistical models [169,170], has shown promise in enhancing adaptability to sparse datasets. Initiatives such as the global Ocean Color Climate Change Initiative (OC-CCI) aim to build open data platforms that promote the sharing and standardization of high-quality data, further enabling robust and scalable ML applications in ocean research [171,172].

5.1.3. Computational Complexity and Resource Limitations

Another challenge is the computational complexity associated with many ML algorithms. The processing power and time required to train sophisticated models can be substantial, which may hinder the feasibility of real-time applications or the analysis of extensive datasets [173]. For example, training deep learning models on global-scale satellite datasets, such as multiyear ocean color data from MODIS or Sentinel-3, often involves processing petabytes of data, requiring extensive GPU resources and days or weeks of computation. This poses significant barriers for resource-limited research institutions. The complexity of deep learning models not only limits their scalability but also makes real-time applications nearly impossible. Traditional optimization algorithms, while computationally more efficient, often fail to provide the level of accuracy needed, further restricting the practical application of these models [174]. To address these issues, potential solutions include leveraging cloud computing and distributed computing technologies [175] to reduce hardware costs and improve computational efficiency. Additionally, the development of low-complexity models, such as lightweight neural networks [176] optimized for sparse data, can significantly reduce training time and energy consumption while maintaining acceptable performance levels. These approaches not only make ML models more accessible to institutions with limited resources but also increase their scalability and adaptability for broader applications in ocean science.

Furthermore, as oceanographic monitoring increasingly involves remote or field-based applications, developing efficient AI models suitable for edge devices [177] (e.g., drones, autonomous vehicles, or mobile platforms) can help reduce latency, improve real-time decision-making, and increase operational feasibility. By deploying AI models directly on edge devices, the need to transmit vast amounts of data to centralized servers is minimized, enabling faster response times and more efficient use of available resources. Key strategies to achieve this include model pruning [178], where unnecessary parts of the model are removed to reduce its size, knowledge distillation, which transfers knowledge from a larger model to a smaller one, and algorithm optimization, which ensures that AI models run effectively in low-power, resource-constrained environments. These methods are essential for ensuring that AI-powered oceanographic monitoring systems can function effectively in remote locations, where traditional computational resources are limited. Such models are crucial for autonomous marine vehicles or drones used for continuous monitoring in challenging environments, providing real-time feedback for more timely and informed decision-making.

5.1.4. Model Interpretability and Transparency

Model interpretability presents another critical limitation, particularly for deep learning techniques. While these models are based on well-defined algorithms and cost functions, their complexity arises from the high-dimensional data they process, which can make it challenging to visualize the relationships they model. For instance, in ocean color remote sensing tasks such as atmospheric correction, deep learning models may capture statistical correlations within the data rather than true causal relationships. This can lead to failures under changing environmental conditions or unseen scenarios, raising concerns about the reliability of predictions. Unlike polynomial fitting, which can be represented in a two-dimensional input-output space (e.g., Chl-a versus Rrs slope), ML models often deal with multidimensional data that cannot be easily visualized. However, the advantage of ML models is their flexibility, which allows them to require less preprocessing and efficiently minimize cost functions, making them valuable tools for complex ocean color remote sensing problems.

5.1.5. Explainable AI for Ocean Color Remote Sensing

As discussed in Section 5.1.4, model interpretability is a key challenge in ocean color remote sensing, particularly for deep learning models that handle high-dimensional and complex data. While model transparency is essential for scientific and practical applications, explainable AI (XAI) techniques [179] offer specialized solutions to address the lack of interpretability, which can undermine trust in model predictions. XAI focuses on making the “black-box” nature of machine learning models more transparent, allowing users to understand how predictions are made and ensuring that these predictions align with physical principles governing the ocean environment.

XAI methods such as Shapley additive explanations (SHAP) [180] and local interpretable model-agnostic explanations (LIME) [181] are critical tools in this context. They provide insights into the contributions of individual input features to the output, enabling researchers to trace and validate the model’s decision-making process. These tools can help clarify how environmental variables, such as chlorophyll concentration or water turbidity, influence the model’s predictions, providing confidence in its results, especially when applied to unseen data or novel environmental conditions. Furthermore, the integration of physics-informed neural networks (PINNs) offers a powerful way to enhance both model interpretability and scientific validity [182]. By embedding physical constraints, such as radiative transfer models, within AI architectures, PINNs ensure that the model’s predictions remain consistent with established oceanographic principles. This hybrid approach addresses the challenge of physical interpretability, ensuring that AI predictions are not only understandable but also scientifically grounded. Overall, XAI serves a dual purpose: improving the transparency of AI models while ensuring that they remain aligned with the physical processes inherent in ocean color remote sensing. The combination of XAI techniques and hybrid models will be essential for advancing oceanographic research, enabling AI models to be more reliable, scientifically valid, and easier to interpret, fostering trust and facilitating their application in real-world scenarios.

5.2. Opportunities and the Way Forward

5.2.1. Harnessing Technological Innovation and Computational Advances

Despite these challenges, ML is rapidly evolving and presents significant opportunities for advancing ocean color remote sensing. The combination of emerging algorithms and powerful computational infrastructures has opened new frontiers for analyzing large, complex datasets. For example, advanced architectures such as transformers and self-supervised learning techniques [183] could help researchers process and extract insights from satellite imagery and in situ observations, uncovering patterns that would otherwise remain hidden. A notable example is the CyanoTracker project, which employs advanced DL and ML methods to monitor and predict cyanobacterial harmful algal blooms in near real-time [184]. Using satellite-based remote sensing data and in situ observations, models such as CNN and long short-term memory networks detect and forecast bloom dynamics, providing timely alerts for water resource management and environmental protection. This ability to combine multiple data sources and generate actionable insights exemplifies the power of ML in addressing pressing environmental challenges. Beyond algorithmic innovation, advances in computational infrastructure have dramatically enhanced the feasibility of ML applications. Cloud-based platforms, such as Google Earth Engine, and distributed computing systems have significantly reduced the computational costs associated with processing large-scale satellite data, enabling a broader range of research institutions to adopt these technologies. Additionally, hardware innovations such as tensor processing units (TPUs) and neural network accelerators have improved the speed and efficiency of training ML models. These developments pave the way for more responsive monitoring systems, allowing researchers to address challenges such as detecting transient oceanographic phenomena or generating high-resolution spatial predictions.

5.2.2. Leveraging Open Data and Interdisciplinary Collaboration

The availability of high-quality, accessible data is fundamental to the success of ML in ocean color remote sensing. Open data initiatives such as the Ocean Color Climate Change Initiative [171,172], Tara Oceans [185,186], and Argo Program [187,188] play pivotal roles in providing high-quality, freely accessible datasets for the research community. In addition to these global efforts, platforms such as the Open Science Framework and Dryad [189] further ensure that these datasets adhere to FAIR (findable, accessible, interoperable, and reusable) principles, facilitating their integration into ML workflows. Moreover, initiatives such as EcoDataScience and Openscapes [190] promote inclusive and transparent data science practices, building capacity for collaborative research in marine environments. By investing further in the collection, curation, and sharing of both satellite imagery and in situ observations, these efforts not only enhance the quality of available data but also foster innovation in ML applications, enabling models to generate more robust and reliable predictions.

Interdisciplinary collaboration is equally critical in ensuring that ML models are scientifically rigorous and operationally effective. Oceanographers provide essential domain knowledge, guiding the selection of meaningful features and ensuring that predictions align with physical and biological processes. Remote sensing specialists ensure that input data are accurately calibrated, whereas data scientists optimize ML algorithms to handle high-dimensional datasets efficiently. By integrating these disciplines, collaborative teams can address key challenges such as data heterogeneity, overfitting, and generalization. Moreover, these collaborations facilitate the development of hybrid models (discussed further in Section 5.2.3) and the adoption of interpretability tools such as SHAP, which enhance model transparency by quantifying the contributions of individual input variables. To maximize the potential of these partnerships, initiatives such as joint training programs, interdisciplinary workshops, and shared research platforms should be promoted. These efforts will help bridge knowledge gaps and foster innovation across disciplines.

5.2.3. The Use of Hybrid Models for Scientific and Practical Applications

Data-driven scientific exploration should not overlook the importance of understanding the underlying systems. While ML excels at making predictions, it is important to complement these predictions with inferences about the underlying mechanisms. Hybrid modeling represents a powerful tool to achieve this balance by combining the strengths of data-driven ML techniques with the mechanistic understanding provided by physical models. By embedding physical constraints into ML architectures, hybrid models ensure that predictions are not only accurate but also consistent with established scientific principles. For example, radiative transfer models can be incorporated into neural networks to constrain outputs, reducing the likelihood of spurious correlations and improving generalizability. Several studies have demonstrated the benefits of hybrid modeling in ocean color remote sensing. For instance, incorporating physical feature information into models can increase their accuracy and generalizability, as illustrated in Figure 4 [21,191]. This integration is particularly valuable in scenarios where observational data are sparse or when models must extrapolate beyond the range of the training dataset. By incorporating physical feature information, such as light attenuation or nutrient transport, hybrid models enhance not only predictive power but also model robustness under varying environmental conditions. By revealing which variables drive predictions, SHAP can identify potential biases or limitations in the data and ensure that models are interpretable and aligned with real-world processes. The combination of physical consistency, interpretability, and improved generalizability makes hybrid modeling a transformative approach for advancing Earth system science and operational oceanographic monitoring. By bridging the gap between data-driven exploration and mechanistic understanding, hybrid models can provide actionable insights while retaining the transparency needed for scientific rigor and practical decision-making.

Another way to enhance the embedding of physical processes with AI models is through the use of PINNs [182]. PINNs combine the power of machine learning with the constraints imposed by physical laws, ensuring that the models’ predictions remain consistent with known physical processes such as light absorption, scattering, and the behavior of ocean constituents. This integration not only enhances the interpretability of AI models but also improves their generalization capability across different environments, reducing the risk of overfitting and making the models more robust [192]. Moving forward, effective integration of AI with physical principles will involve developing hybrid models where physical laws are incorporated into the loss function of AI algorithms, guiding them toward physically plausible solutions. This approach facilitates the training of AI models that are interpretable and better aligned with real-world oceanographic phenomena. The advancement of PINNs in this context will drive the future of ocean color remote sensing by enhancing both the transparency of AI models and their ability to generalize when exposed to new, unseen data. This development will be crucial for the reliable interpretation and application of remote sensing data in diverse ocean environments.

5.2.4. Building Capacity for Uncertainty-Aware Models

Uncertainty quantification is a critical component of deploying ML in complex and dynamic marine environments. Reliable uncertainty estimates help researchers assess the confidence of model predictions and guide decision-making in applications such as resource management or environmental risk assessment. To improve the performance of models in complex and uncertain environments, several key technologies can be considered: (1) MC-Dropout is a method that introduces randomness during the model training process. By activating dropout layers during the training phase, the model can consider multiple different network structures during inference, thereby providing uncertainty estimates [193,194]. This method has been proven to effectively improve the model’s generalization ability on small sample data and has the potential to estimate uncertainty in ocean remote sensing data. (2) Deep ensemble improves the overall model performance and uncertainty estimation by training multiple deep learning models and integrating their predictions [195,196]. Each model is exposed to slightly different data during training, offering a more comprehensive perspective on prediction uncertainty. This approach is especially beneficial given the variability and complexity inherent in ocean remote sensing data. (3) Pixelwise uncertainty estimation is crucial for generating robust and reliable inversion products. Advanced statistical methods, such as bootstrap methods and Bayesian approaches, have been adopted to assess the uncertainty of each predicted pixel. These methods can provide confidence intervals for each prediction [197], helping users understand the credibility of model predictions. By introducing these technologies, we have not only improved the model’s ability to assess uncertainty when dealing with ocean remote sensing data but also enhanced the model’s generalization ability and the reliability of inversion products. The application of these methods enables the model to provide more accurate and reliable prediction results when facing complex and uncertain marine environments.

5.2.5. Data Fusion and Integration from Multiple Platforms

In ocean color remote sensing, integrating data from multiple platforms, such as satellites, in situ sensors, and aerial imagery, enhances the accuracy and robustness of models. Combining these diverse data types provides a more comprehensive understanding of environmental conditions, improving monitoring of ocean health and water quality [44]. However, the integration of data from different sources presents challenges, such as differences in spatial resolution, temporal coverage, and sensor characteristics. For instance, satellite imagery offers global coverage with limited temporal resolution, whereas in situ sensors provide high-frequency, localized measurements but lack broad spatial reach. Aerial imagery offers high spatial resolution but limited coverage. To overcome these challenges, advanced data fusion techniques—such as multisource remote sensing fusion, spatiotemporal interpolation, and sensor calibration—are applied to harmonize datasets. These methods ensure consistent and reliable combined datasets, enhance model robustness and support more effective monitoring. By combining satellite data with in situ measurements, models can improve estimates of parameters such as chlorophyll-a concentration or turbidity. Aerial imagery can further increase model accuracy, particularly for localized phenomena such as algal blooms or coastal changes.

6. Conclusions

The integration of ML into ocean color remote sensing represents a significant advancement in our ability to monitor, analyze, and understand the marine environment. ML has substantially contributed to this field by enhancing the accuracy of atmospheric correction and bio-optical property retrieval, providing actionable insights into marine ecosystem dynamics, and assessing the impacts of climate change. The transformative potential of ML is evident in its ability to process vast datasets, improve spatial and temporal resolution, and fill data gaps, thereby enabling a more comprehensive and nuanced understanding of the role of the ocean in global climate and biogeochemical cycles. Despite challenges such as data quality issues, model generalizability, and computational complexity, the opportunities presented by ML are considerable. The ongoing development of new algorithms, increased accessibility to computational resources, and the potential for interdisciplinary collaboration promise to further enhance the capabilities of ocean color remote sensing. The fusion of ML with ocean color remote sensing is poised to play a pivotal role in advancing oceanographic research and environmental monitoring. Continued innovation and the application of ML techniques will enable us to fully exploit the potential of satellite observations, leading to more accurate, efficient, and insightful analyses of our planet’s vast and vital marine ecosystems.