Mapping Windthrow Risk in Pinus radiata Plantations Using Multi-Temporal LiDAR and Machine Learning: A Case Study of Cyclone Gabrielle, New Zealand
Abstract
1. Introduction
2. Materials and Methods
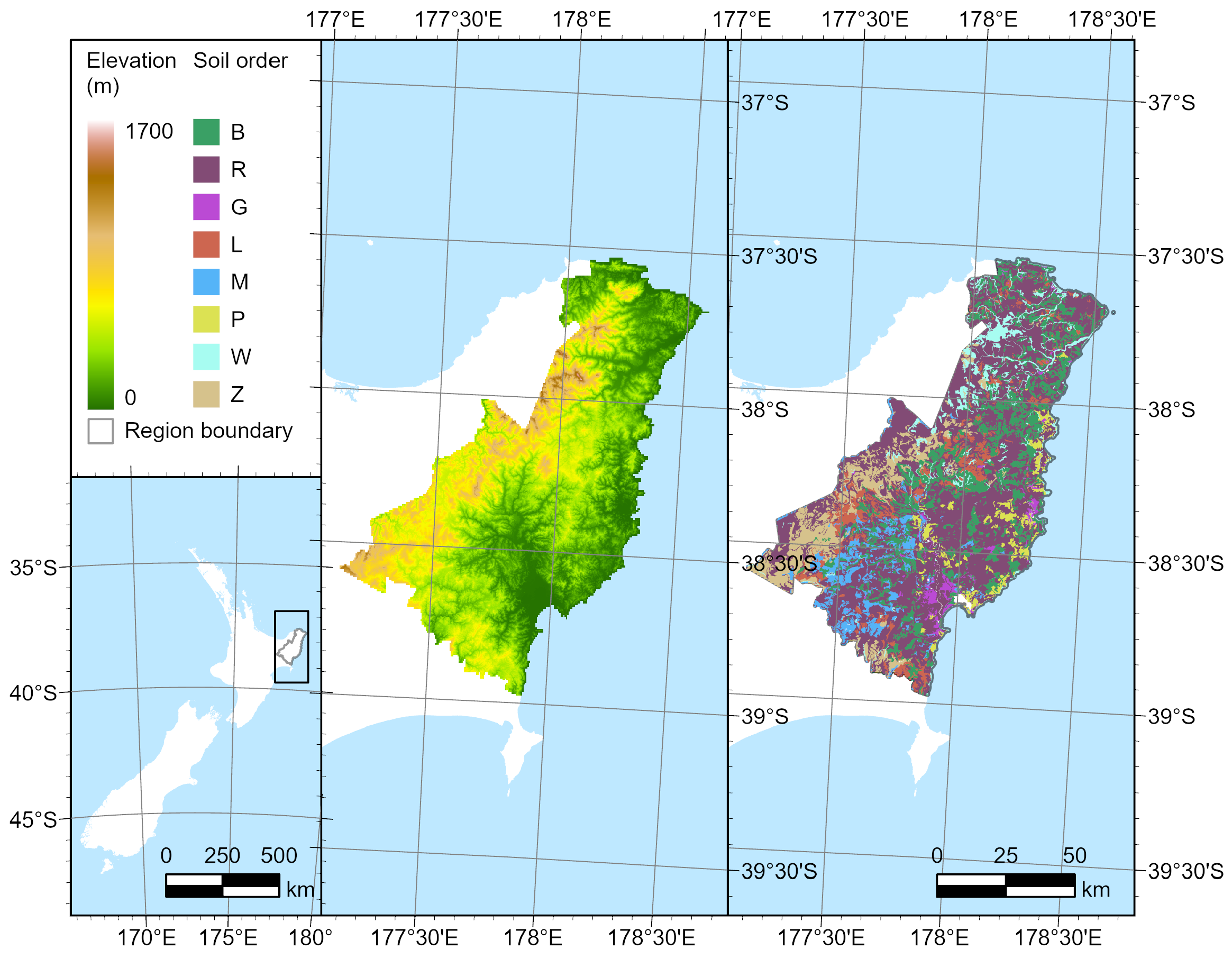
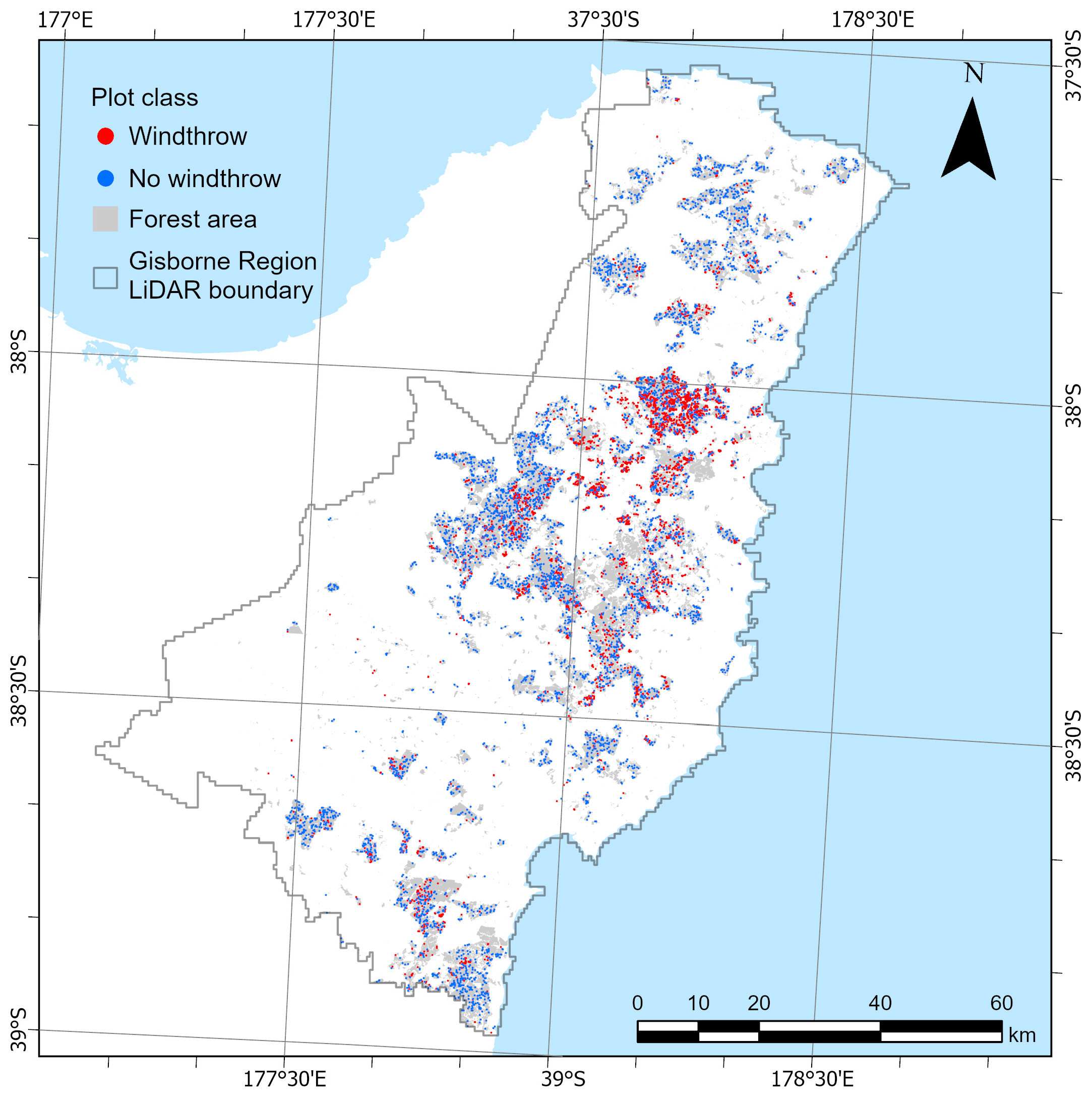
2.1. Study Region
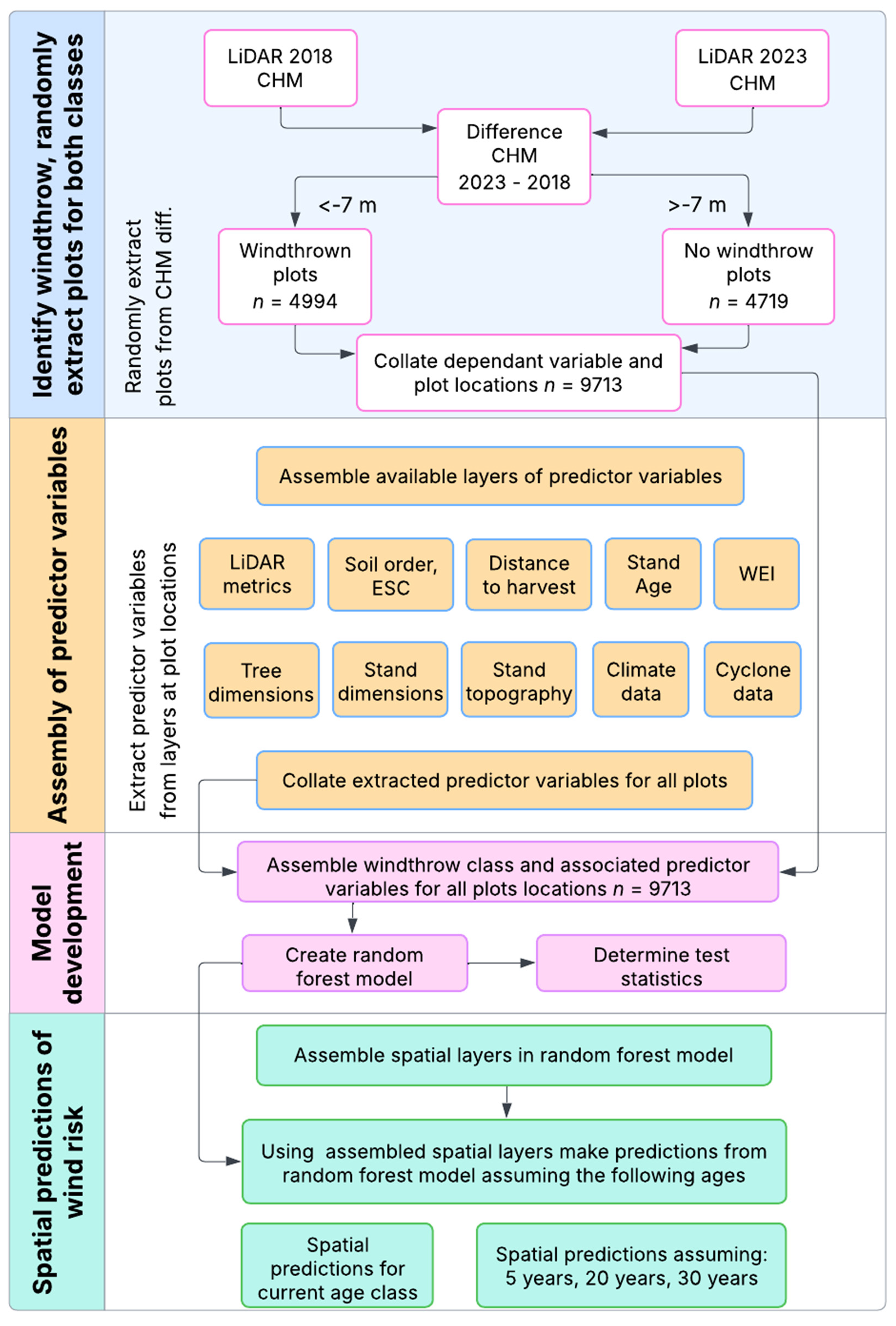
2.2. Overview of Method
2.3. LiDAR Data
2.4. Plantation Identification and Windthrow Characterization
2.5. Assembly of Predictor Variables
2.5.1. Site Characterization
2.5.2. Stand Age
2.5.3. Stand Dimensions
2.5.4. Tree Dimensions
2.5.5. Cyclone Characterization
2.6. Data Analysis
2.6.1. Influence of Individual Variables on Windthrow Classes
2.6.2. Classification Model
2.6.3. Spatial Prediction of Windthrow
3. Results
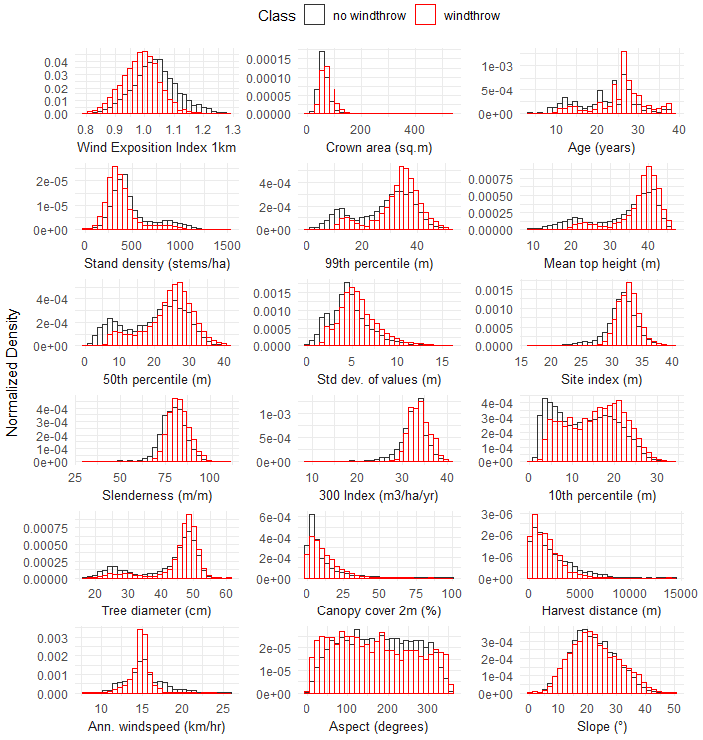
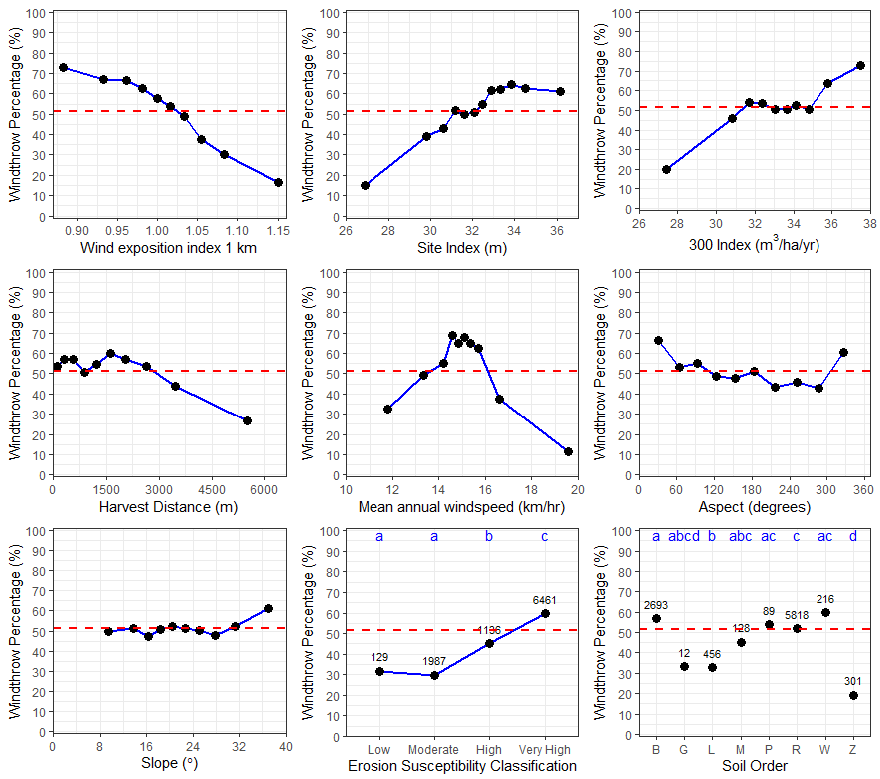
3.1. Variation in Site Characteristics Between Windthrow Classes
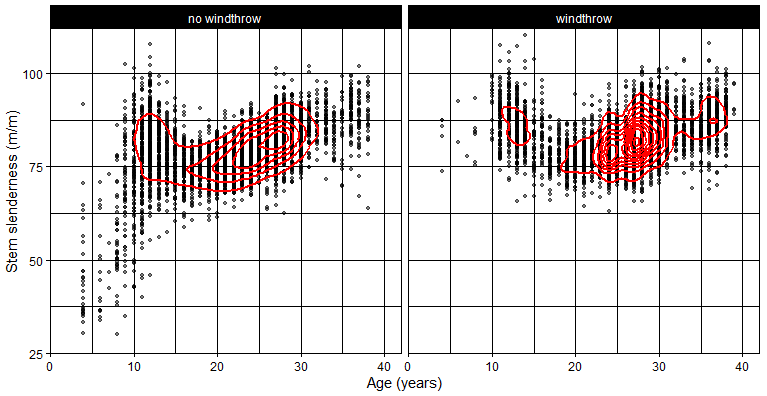
3.2. Variation in Stand Characteristics Between Windthrow Classes
3.3. Classification Models
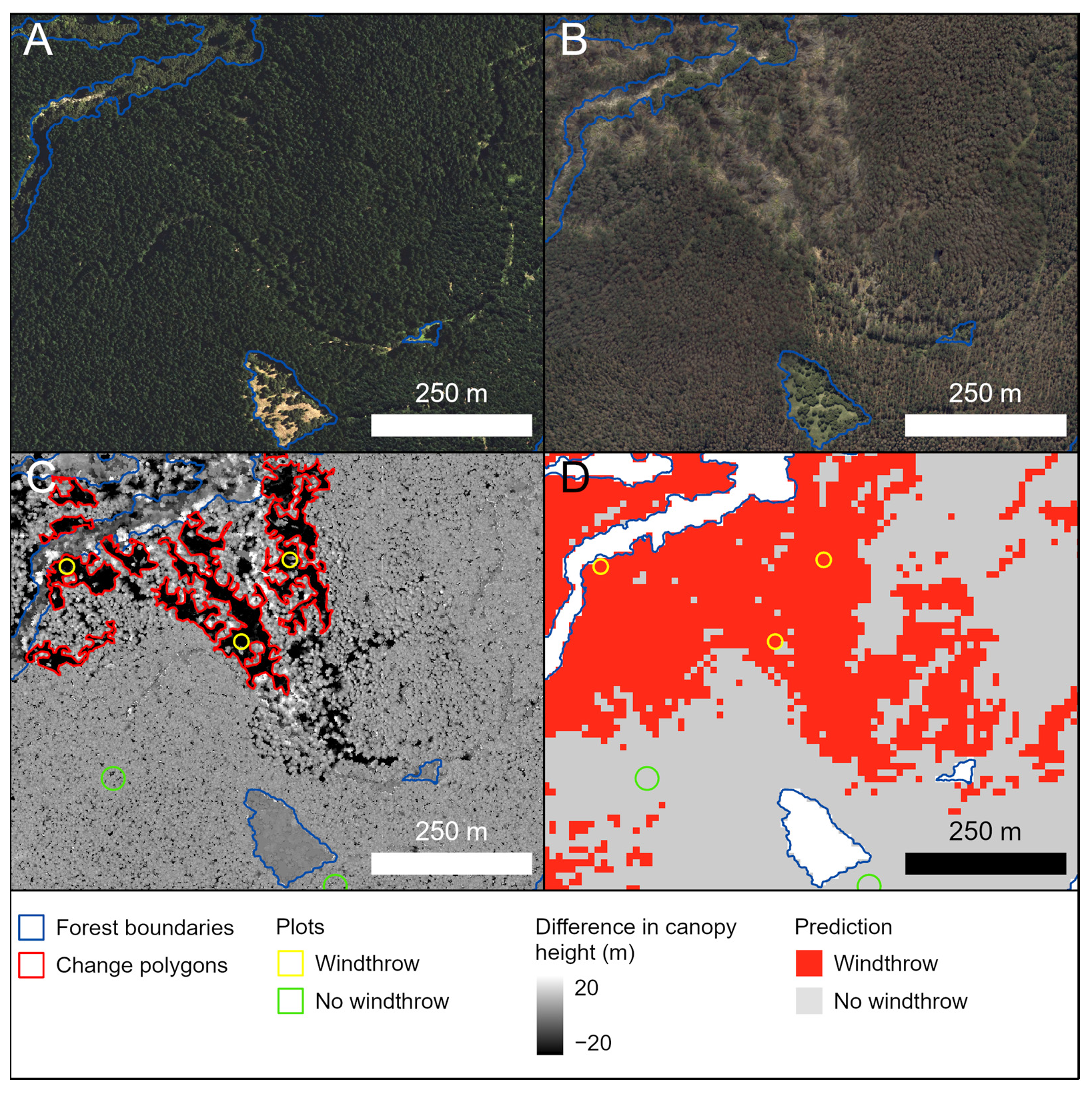
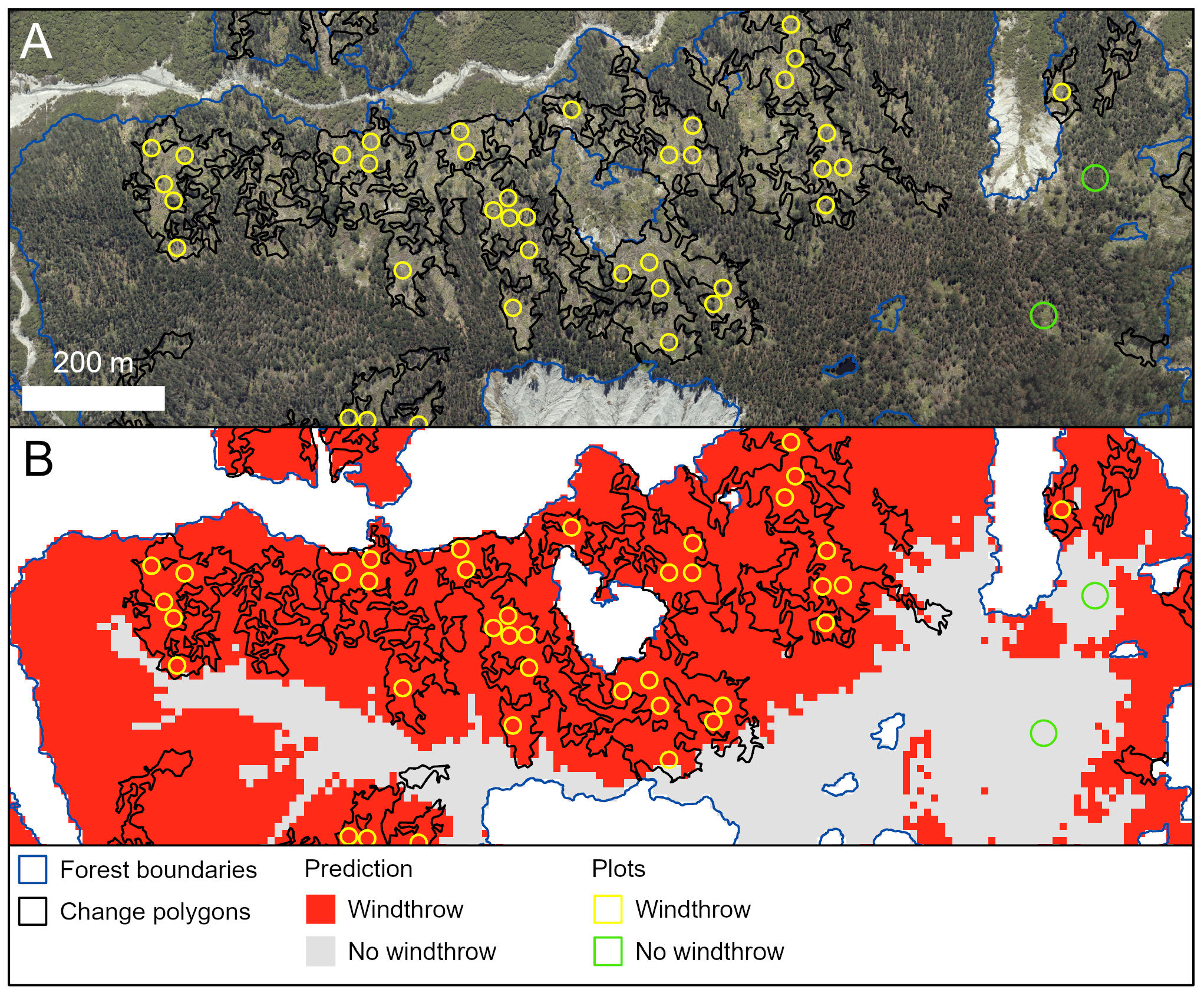
3.4. Predictions of Windthrow
4. Discussion
4.1. Use of Repeat LiDAR Captures to Identify Windthrow
4.2. Wind Risk Model
4.3. Important Factors Influencing Wind Risk
4.4. Planning and Management Implications
4.5. Study Limitations and Further Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALS | Airborne laser scanning |
| CHM | Canopy height model |
| DBH | Diameter at breast height |
| DAP | Digital aerial photogrammetry |
| DSM | Digital surface model |
| ESC | Erosion susceptibility class |
| LiDAR | Light detection and ranging |
| MTH | Mean top height |
Appendix A
| Label | Variable | No Windthrow | Windthrow | ANOVA | |||
|---|---|---|---|---|---|---|---|
| Mean (SD) | Range | Mean (SD) | Range | H Val. | η2 | ||
| LiDAR variables | |||||||
| abv | Number of pixels > 2 m | 1145 (669) | 3.5–6387 | 1144 (636) | 236–5136 | 0.080 ns | −9.5 × 10−5 |
| all | Total number of points | 1409 (742) | 355–7192 | 1433 (754) | 387–6312 | 1.4 ns | 4.2 × 10−5 |
| cov.gap | Gap in canopy cover > 2 m (%) | 10.9 (14.4) | 0–99.1 | 11.4 (9.77) | 0–86.8 | 176 *** | 0.0181 |
| dns.gap | Gap in canopy density > 2 m (%) | 20.7 (14.0) | 0.078–99.2 | 21.2 (9.59) | 0.35–82.0 | 113 *** | 0.0115 |
| min | Minimum height value (m) | 5.65 (4.78) | 0.448–25.2 | 5.95 (4.74) | 2.0–25.4 | 24.8 *** | 0.00245 |
| max | Maximum height value (m) | 28.9 (11.0) | 0.909–53.8 | 34.4 (8.24) | 9.86–54.3 | 669 *** | 0.0688 |
| avg | Average height value (m) | 19.4 (8.43) | 0.695–39.9 | 23.4 (6.7) | 5.52–40.4 | 541 *** | 0.0556 |
| p10 | 10th percentile of height (m) | 12.9 (7.14) | 0.485–33.3 | 15.6 (6.7) | 2.34–34.5 | 366 *** | 0.0375 |
| p25 | 25th percentile of height (m) | 16.5 (7.92) | 0.531–36.6 | 20.0 (6.75) | 3.14–38.6 | 455 *** | 0.0468 |
| p50 | 50th percentile of height (m) | 20.0 (8.8) | 0.596–40.4 | 24.1 (7) | 5.45–41.9 | 541 *** | 0.0556 |
| p75 | 75th percentile of height (m) | 22.8 (9.54) | 0.680–44.6 | 27.5 (7.38) | 6.91–45.8 | 604 *** | 0.0621 |
| p90 | 90th percentile of height (m) | 24.9 (10.1) | 0.815–48.2 | 30.0 (7.72) | 7.97–49.3 | 643 *** | 0.0661 |
| p95 | 95th percentile of height (m) | 26 (10.3) | 0.851–49.9 | 31.3 (7.9) | 8.52–50.9 | 656 *** | 0.0675 |
| p99 | 99th percentile of height (m) | 27.7 (10.7) | 0.896–52.3 | 33.2 (8.15) | 9.28–52.9 | 673 *** | 0.0692 |
| skew | Skewness of height values | −0.50 (0.54) | −2.56–1.22 | −0.68 (0.512) | −2.9–1.31 | 279 *** | 0.0286 |
| kur | Kurtosis of height values | 3.67 (1.54) | 0.421–14.7 | 4.07 (1.86) | 1.26–19.7 | 131 *** | 0.0134 |
| std.dev | Standard deviation, height (m) | 4.76 (2.36) | 0.083–15.9 | 5.72 (2.2) | 1.52–16 | 532 *** | 0.0547 |
| LiDAR-derived variables | |||||||
| Aspect | Aspect (degrees) | 179 (88.4) | 4.7–352 | 168 (98.2) | 2.09–358 | 39.1 *** | 0.00392 |
| Slope | Slope (degrees) | 21.8 (7.73) | 0.637–49.5 | 22.6 (8.28) | 0.85–50.4 | 15.6 *** | 0.00151 |
| TPI | Topographic position index | 0.035 (0.59) | −2.52–2.75 | −0.082 (0.678) | −3.97–3.33 | 64.4 *** | 0.00653 |
| TRI | Terrain ruggedness index | 11 (4.12) | 0.386–30.1 | 11.2 (4.4) | 0.528–30 | 0.35 ns | −6.6 × 10−5 |



| Variables | Model 1 | Model 2 |
|---|---|---|
| WindFeb | 0.154 | 0.103 |
| WEI1km | 0.143 | 0.135 |
| DrainSum | 0.106 | 0.078 |
| Age | 0.098 | 0.084 |
| 300 Index | 0.097 | 0.076 |
| Site index | 0.090 | 0.068 |
| Harvest distance | 0.087 | 0.070 |
| Aspect | 0.079 | 0.070 |
| Slope | 0.072 | 0.065 |
| Erosion susceptibility classification | 0.034 | 0.028 |
| Potential rooting depth | 0.020 | 0.015 |
| Recent soil order | 0.0082 | 0.0060 |
| Brown soil order | 0.0078 | 0.0052 |
| Allophanic soil order | 0.0031 | 0.0025 |
| 14 February relative humidity | 0.078 | |
| 14 February windspeed | 0.060 | |
| 13 February rainfall | 0.056 |
References
- Schütz, J.-P.; Götz, M.; Schmid, W.; Mandallaz, D. Vulnerability of spruce (Picea abies) and beech (Fagus sylvatica) forest stands to storms and consequences for silviculture. Eur. J. For. Res. 2006, 125, 291–302. [Google Scholar] [CrossRef]
- Duan, F.; Wan, Y.; Deng, L. A novel approach for coarse-to-fine windthrown tree extraction based on unmanned aerial vehicle images. Remote Sens. 2017, 9, 306. [Google Scholar] [CrossRef]
- Joyce, M.J.; Erb, J.D.; Sampson, B.A.; Moen, R.A. Detection of coarse woody debris using airborne light detection and ranging (LiDAR). For. Ecol. Manag. 2019, 433, 678–689. [Google Scholar] [CrossRef]
- Senf, C.; Seidl, R. Storm and fire disturbances in Europe: Distribution and trends. Glob. Change Biol. 2021, 27, 3605–3619. [Google Scholar] [CrossRef]
- Tamura, Y.; Cao, S. International group for wind-related disaster risk reduction (IG-WRDRR). J. Wind Eng. Ind. Aerodyn. 2012, 104, 3–11. [Google Scholar] [CrossRef]
- Seidl, R.; Thom, D.; Kautz, M.; Martin-Benito, D.; Peltoniemi, M.; Vacchiano, G.; Wild, J.; Ascoli, D.; Petr, M.; Honkaniemi, J. Forest disturbances under climate change. Nat. Clim. Chang. 2017, 7, 395–402. [Google Scholar] [CrossRef]
- Patacca, M.; Lindner, M.; Lucas-Borja, M.E.; Cordonnier, T.; Fidej, G.; Gardiner, B.; Hauf, Y.; Jasinevičius, G.; Labonne, S.; Linkevičius, E.; et al. Significant increase in natural disturbance impacts on European forests since 1950. Glob. Change Biol. 2023, 29, 1359–1376. [Google Scholar] [CrossRef]
- Gardiner, B.; Schuck, A.R.T.; Schelhaas, M.-J.; Orazio, C.; Blennow, K.; Nicoll, B. Living with Storm Damage to Forests; European Forest Institute Joensuu: Joensuu, Finland, 2013; Volume 3. [Google Scholar]
- Xi, W.; Peet, R.K.; Urban, D.L. Changes in forest structure, species diversity and spatial pattern following hurricane disturbance in a Piedmont North Carolina forest, USA. J. Plant Ecol. 2008, 1, 43–57. [Google Scholar] [CrossRef]
- Mitchell, J.C.; Kashian, D.M.; Chen, X.; Cousins, S.; Flaspohler, D.; Gruner, D.S.; Johnson, J.S.; Surasinghe, T.D.; Zambrano, J.; Buma, B. Forest ecosystem properties emerge from interactions of structure and disturbance. Front. Ecol. Environ. 2023, 21, 14–23. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Ehbrecht, M.; Camarretta, N. Application of point cloud data to assess edge effects on rainforest structural characteristics in tropical Sumatra, Indonesia. Landsc. Ecol. 2023, 38, 1191–1208. [Google Scholar] [CrossRef]
- Hlásny, T.; König, L.; Krokene, P.; Lindner, M.; Montagné-Huck, C.; Müller, J.; Qin, H.; Raffa, K.F.; Schelhaas, M.-J.; Svoboda, M. Bark beetle outbreaks in Europe: State of knowledge and ways forward for management. Curr. For. Rep. 2021, 7, 138–165. [Google Scholar] [CrossRef]
- Dun, H.F.; MacKay, J.J.; Green, S. Expansion of natural infection of Japanese larch by Phytophthora ramorum shows trends associated with seasonality and climate. Plant Pathol. 2024, 73, 419–430. [Google Scholar] [CrossRef]
- Watt, M.S.; Holdaway, A.; Watt, P.; Pearse, G.D.; Palmer, M.E.; Steer, B.S.C.; Camarretta, N.; McLay, E.; Fraser, S. Early Prediction of Regional Red Needle Cast Outbreaks Using Climatic Data Trends and Satellite-Derived Observations. Remote Sens. 2024, 16, 1401. [Google Scholar] [CrossRef]
- Abram, N.J.; Henley, B.J.; Gupta, A.S.; Lippmann, T.J.R.; Clarke, H.; Dowdy, A.J.; Sharples, J.J.; Nolan, R.H.; Zhang, T.; Wooster, M.J.; et al. Connections of climate change and variability to large and extreme forest fires in southeast Australia. Commun. Earth Environ. 2021, 2, 1–17. [Google Scholar] [CrossRef]
- Hashim, J.H.; Hashim, Z. Climate change, extreme weather events, and human health implications in the Asia Pacific region. Asia Pac. J. Public Health 2016, 28 (Suppl. S2), 8S–14S. [Google Scholar] [CrossRef]
- Korznikov, K.; Kislov, D.; Doležal, J.; Petrenko, T.; Altman, J. Tropical cyclones moving into boreal forests: Relationships between disturbance areas and environmental drivers. Sci. Total Environ. 2022, 844, 156931. [Google Scholar] [CrossRef]
- Kossin, J.P.; Knapp, K.R.; Olander, T.L.; Velden, C.S. Global increase in major tropical cyclone exceedance probability over the past four decades. Proc. Natl. Acad. Sci. USA 2020, 117, 11975–11980. [Google Scholar] [CrossRef]
- Janda, P.; Ukhvatkina, O.N.; Vozmishcheva, A.S.; Omelko, A.M.; Doležal, J.; Krestov, P.V.; Zhmerenetsky, A.A.; Song, J.S.; Altman, J. Tree canopy accession strategy changes along the latitudinal gradient of temperate Northeast Asia. Glob. Ecol. Biogeogr. 2021, 30, 738–748. [Google Scholar] [CrossRef]
- Aldridge, J.; Bell, R.G. Climate change impacts to extreme weather events associated with insured losses in New Zealand: A review. Environ. Res. Clim. 2024, 4, 012001. [Google Scholar] [CrossRef]
- Potterf, M.; Eyvindson, K.; Blattert, C.; Burgas, D.; Burner, R.; Stephan, J.G.; Mönkkönen, M. Interpreting wind damage risk–how multifunctional forest management impacts standing timber at risk of wind felling. Eur. J. For. Res. 2022, 141, 347–361. [Google Scholar] [CrossRef]
- Cremer, K.W.; Borough, C.J.; McKinnell, F.H.; Carter, P.R. Effects of stocking and thinning on wind damage in plantations. N. Z. J. For. Sci. 1982, 12, 245–268. [Google Scholar]
- Zubizarreta-Gerendiain, A.; Pukkala, T.; Peltola, H. Effects of wind damage on the optimal management of boreal forests under current and changing climatic conditions. Can. J. For. Res. 2017, 47, 246–256. [Google Scholar] [CrossRef]
- Heinonen, T.; Pukkala, T.; Ikonen, V.P.; Peltola, H.; Venäläinen, A.; Dupont, S. Integrating the risk of wind damage into forest planning. For. Ecol. Manag. 2009, 258, 1567–1577. [Google Scholar] [CrossRef]
- Einzmann, K.; Immitzer, M.; Böck, S.; Bauer, O.; Schmitt, A.; Atzberger, C. Windthrow detection in European forests with very high-resolution optical data. Forests 2017, 8, 21. [Google Scholar] [CrossRef]
- Jarron, L.R.; Coops, N.C.; MacKenzie, W.H.; Dykstra, P. Detection and quantification of coarse woody debris in natural forest stands using airborne LiDAR. For. Sci. 2021, 67, 550–563. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Puletti, N.; Tattoni, C.; Ferrara, C.; Pirotti, F. Estimated biomass loss caused by the Vaia windthrow in Northern Italy: Evaluation of active and passive remote sensing options. Remote Sens. 2021, 13, 4924. [Google Scholar] [CrossRef]
- Giannetti, F.; Pecchi, M.; Travaglini, D.; Francini, S.; D’Amico, G.; Vangi, E.; Cocozza, C.; Chirici, G. Estimating VAIA windstorm damaged forest area in Italy using time series Sentinel-2 imagery and continuous change detection algorithms. Forests 2021, 12, 680. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Surový, P.; Kuželka, K. Detection of fallen logs from high-resolution UAV images. N. Z. J. For. Sci. 2019, 49, 2. [Google Scholar] [CrossRef]
- Francini, S.; McRoberts, R.E.; D’Amico, G.; Coops, N.C.; Hermosilla, T.; White, J.C.; Wulder, M.A.; Marchetti, M.; Mugnozza, G.S.; Chirici, G. An open science and open data approach for the statistically robust estimation of forest disturbance areas. Int. J. Appl. Earth Obs. Geoinf. 2022, 106, 102663. [Google Scholar] [CrossRef]
- Chirici, G.; Bottalico, F.; Giannetti, F.; Del Perugia, B.; Travaglini, D.; Nocentini, S.; Kutchartt, E.; Marchi, E.; Foderi, C.; Fioravanti, M. Assessing forest windthrow damage using single-date, post-event airborne laser scanning data. For. Int. J. For. Res. 2018, 91, 27–37. [Google Scholar] [CrossRef]
- Bohlin, I.; Olsson, H.; Bohlin, J.; Granström, A. Quantifying post-fire fallen trees using multi-temporal lidar. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 186–195. [Google Scholar] [CrossRef]
- Nyström, M.; Holmgren, J.; Fransson, J.E.S.; Olsson, H. Detection of windthrown trees using airborne laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 21–29. [Google Scholar] [CrossRef]
- Leitold, V.; Morton, D.C.; Martinuzzi, S.; Paynter, I.; Uriarte, M.; Keller, M.; Ferraz, A.; Cook, B.D.; Corp, L.A.; González, G. Tracking the rates and mechanisms of canopy damage and recovery following Hurricane Maria using multitemporal lidar data. Ecosystems 2022, 25, 892–910. [Google Scholar] [CrossRef]
- Gardiner, B.; Peltola, H.; Kellomaki, S. Comparison of two models for predicting the critical wind speeds required to damage coniferous trees. Ecol. Model. 2000, 129, 1–23. [Google Scholar] [CrossRef]
- Hale, S.E.; Gardiner, B.; Peace, A.; Nicoll, B.; Taylor, P.; Pizzirani, S. Comparison and validation of three versions of a forest wind risk model. Environ. Model. Softw. 2015, 68, 27–41. [Google Scholar] [CrossRef]
- Nicoll, B.C.; Achim, A.; Mochan, S.; Gardiner, B.A. Does steep terrain influence tree stability? A field investigation. Can. J. For. Res. 2005, 35, 2360–2367. [Google Scholar]
- Costa, M.; Gardiner, B.; Locatelli, T.; Marchi, L.; Marchi, N.; Lingua, E. Evaluating wind damage vulnerability in the Alps: A new wind risk model parametrisation. Agric. For. Meteorol. 2023, 341, 109660. [Google Scholar] [CrossRef]
- Suárez, J.C.; Gardiner, B.A.; Quine, C.P. A comparison of three methods for predicting wind speeds in complex forested terrain. Meteorol. Appl. 1999, 6, 329–342. [Google Scholar] [CrossRef]
- Blennow, K.; Olofsson, E. The probability of wind damage in forestry under a changed climate. Clim. Chang. 2008, 87, 347–360. [Google Scholar] [CrossRef]
- Gardiner, B.A.; Quine, C.P. Management of forests to reduce the risk of abiotic damage—A review with particular reference to the effects of strong winds. For. Ecol. Manag. 2000, 135, 261–277. [Google Scholar] [CrossRef]
- Locatelli, T.; Gardiner, B.; Hale, S.; Nicoll, B. fgr: The R Version of the ForestGALES Wind Risk Model. R Package Version 1.0. 2021. Available online: https://www.forestresearch.gov.uk/tools-and-resources/fthr/forestgales/fgr-the-forestgales-r-package/ (accessed on 10 February 2025).
- Hale, S.E.; Gardiner, B.A.; Wellpott, A.; Nicoll, B.C.; Achim, A. Wind loading of trees: Influence of tree size and competition. Eur. J. For. Res. 2012, 131, 203–217. [Google Scholar] [CrossRef]
- Hart, E.; Sim, K.; Kamimura, K.; Meredieu, C.; Guyon, D.; Gardiner, B. Use of machine learning techniques to model wind damage to forests. Agric. For. Meteorol. 2019, 265, 16–29. [Google Scholar] [CrossRef]
- Albrecht, A.T.; Jung, C.; Schindler, D. Improving empirical storm damage models by coupling with high-resolution gust speed data. Agric. For. Meteorol. 2019, 268, 23–31. [Google Scholar] [CrossRef]
- Kabir, E.; Guikema, S.; Kane, B. Statistical modeling of tree failures during storms. Reliab. Eng. Syst. Saf. 2018, 177, 68–79. [Google Scholar] [CrossRef]
- Albrecht, A.; Hanewinkel, M.; Bauhus, J.; Kohnle, U. How does silviculture affect storm damage in forests of south-western Germany? Results from empirical modeling based on long-term observations. Eur. J. For. Res. 2012, 131, 229–247. [Google Scholar]
- Hanewinkel, M.; Peltola, H.; Soares, P.; González-Olabarria, J.R. Recent approaches to model the risk of storm and fire. For. Syst. 2011, 3, 30–47. [Google Scholar] [CrossRef]
- Krejci, L.; Kolejka, J.; Vozenilek, V.; Machar, I. Application of GIS to empirical windthrow risk model in mountain forested landscapes. Forests 2018, 9, 96. [Google Scholar] [CrossRef]
- Hanewinkel, M.; Hummel, S.; Albrecht, A. Assessing natural hazards in forestry for risk management: A review. Eur. J. For. Res. 2011, 130, 329–351. [Google Scholar] [CrossRef]
- Saarinen, N.; Vastaranta, M.; Honkavaara, E.; Wulder, M.A.; White, J.C.; Litkey, P.; Holopainen, M.; Hyyppä, J. Using multi-source data to map and model the predisposition of forests to wind disturbance. Scand. J. For. Res. 2016, 31, 66–79. [Google Scholar] [CrossRef]
- Suvanto, S.; Peltoniemi, M.; Tuominen, S.; Strandström, M.; Lehtonen, A. High-resolution mapping of forest vulnerability to wind for disturbance-aware forestry. For. Ecol. Manag. 2019, 453, 117619. [Google Scholar] [CrossRef]
- Watson, A.; O’loughlin, C. Structural root morphology and biomass of three age-classes of Pinus radiata. N. Z. J. For. Sci. 1990, 20, 97–110. [Google Scholar]
- Moore, J.R. Differences in maximum resistive bending moments of Pinus radiata trees grown on a range of soil types. For. Ecol. Manag. 2000, 135, 63–71. [Google Scholar] [CrossRef]
- Stone, D.A.; Noble, C.J.; Bodeker, G.E.; Dean, S.M.; Harrington, L.J.; Rosier, S.M.; Rye, G.D.; Tradowsky, J.S. Cyclone Gabrielle as a design storm for northeastern Aotearoa New Zealand under anthropogenic warming. Earth Future 2024, 12, e2024EF004772. [Google Scholar] [CrossRef]
- Harrington, L.J.; Dean, S.M.; Awatere, S.; Rosier, S.; Queen, L.; Gibson, P.B.; Barnes, C.; Zachariah, M.; Philip, S.; Kew, S. The Role of Climate Change in Extreme Rainfall Associated with Cyclone Gabrielle Over Aotearoa New Zealand’s East Coast; Imperial College London: London, UK, 2023. [Google Scholar]
- Chappell, P.R. The Climate and Weather of Gisborne, 2nd ed.; NIWA Science and Technology Series Number 70; NIWA Science and Technology: Auckland, New Zealand, 2016. [Google Scholar]
- Pearse, G.D.; Jayathunga, S.; Camarretta, N.; Palmer, M.E.; Steer, B.S.C.; Watt, M.S.; Watt, P.; Holdaway, A. Developing a forest description from remote sensing: Insights from New Zealand. Sci. Remote Sens. 2025, 11, 100183. [Google Scholar] [CrossRef]
- Ministry for Primary Industries. National Exotic Forest Description, as at 1 April 2023; Ministry of Primary Industries: Wellington, New Zealand, 2024. [Google Scholar]
- Watt, M.S.; Palmer, D.J.; Leonardo, E.M.C.; Bombrun, M. Use of advanced modelling methods to estimate radiata pine productivity indices. For. Ecol. Manag. 2021, 479, 118557. [Google Scholar] [CrossRef]
- Wratt, D.S.; Tait, A.; Griffiths, G.; Espie, P.; Jessen, M.; Keys, J.; Ladd, M.; Lew, D.; Lowther, W.; Mitchell, N.; et al. Climate for crops: Integrating climate data with information about soils and crop requirements to reduce risks in agricultural decision-making. Meteorol. Appl. 2006, 13, 305–315. [Google Scholar] [CrossRef]
- Leathwick, J.; Morgan, F.; Wilson, G.; Rutledge, D.; McLeod, M.; Johnston, K. Land Environments of New Zealand: A Technical Guide; Ministry for the Environment and Manaaki Whenua Landcare Research: Auckland, New Zealand, 2002; p. 184. [Google Scholar]
- Ministry for Primary Industries. Erosion Susceptibility Classification (March 2018); Ministry for Primary Industries: Wellington, New Zealand, 2018; Available online: https://data-mpi.opendata.arcgis.com/datasets/MPI::erosion-susceptibility-classification-march-2018-1/explore (accessed on 13 February 2015).
- Landcare Research. FSL Potential Rooting Depth. 2025. Available online: https://doi.org/10.26060/TRMT-VT34 (accessed on 13 February 2025).
- Webb, T.H.; Wilson, A.D. A Manual of Land Characteristics for Evaluation of Rural Land; Landcare Research Science Series 10; Manaaki Whenua Press: Lincoln, New Zealand, 1995; 32p. [Google Scholar]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for automated geoscientific analyses (SAGA) v. 2.1. 4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Kimberley, M.O.; West, G.; Dean, M.; Knowles, L. Site Productivity: The 300 Index—A volume productivity index for radiata pine. N. Z. J. For. 2005, 50, 13–18. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 10 December 2024).
- Akinwande, M.O.; Dikko, H.G.; Samson, A. Variance inflation factor: As a condition for the inclusion of suppressor variable (s) in regression analysis. Open J. Stat. 2015, 5, 754. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.-F.; De Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Plowright, A.; Roussel, J. Tools for Analyzing Remote Sensing Forest Data. 2021. Available online: https://cran.r-project.org/package=ForestTools (accessed on 27 November 2024).
- Hijmans, R. terra: Spatial Data Analysis. R Package Version 8–9. 2025. Available online: https://github.com/rspatial/terra (accessed on 27 November 2024).
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Levene, H. Robust Tests for Equality of Variances. In Contributions to Probability and Statistics; Olkin, I., Ed.; Stanford University Press: Redwood City, CA, USA, 1960; pp. 278–292. [Google Scholar]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398. [Google Scholar]
- McCarthy, J.K.; Hood, I.A.; Brockerhoff, E.G.; Carlson, C.A.; Pawson, S.M.; Forward, M.; Walbert, K.; Gardner, J.F. Predicting sapstain and degrade in fallen trees following storm damage in a Pinus radiata forest. For. Ecol. Manag. 2010, 260, 1456–1466. [Google Scholar] [CrossRef]
- Tolan, J.; Yang, H.-I.; Nosarzewski, B.; Couairon, G.; Vo, H.V.; Brandt, J.; Spore, J.; Majumdar, S.; Haziza, D.; Vamaraju, J. Very high resolution canopy height maps from RGB imagery using self-supervised vision transformer and convolutional decoder trained on aerial lidar. Remote Sens. Environ. 2024, 300, 113888. [Google Scholar] [CrossRef]
- Pearse, G.D.; Dash, J.P.; Persson, H.J.; Watt, M.S. Comparison of high-density LiDAR and satellite photogrammetry for forest inventory. ISPRS J. Photogramm. Remote Sens. 2018, 142, 257–267. [Google Scholar] [CrossRef]
- Gardiner, B.; Lorenz, R.; Hanewinkel, M.; Schmitz, B.; Bott, F.; Szymczak, S.; Frick, A.; Ulbrich, U. Predicting the risk of tree fall onto railway lines. For. Ecol. Manag. 2024, 553, 121614. [Google Scholar] [CrossRef]
- Seidl, R.; Rammer, W.; Blennow, K. Simulating wind disturbance impacts on forest landscapes: Tree-level heterogeneity matters. Environ. Model. Softw. 2014, 51, 1–11. [Google Scholar] [CrossRef]
- Kamimura, K.; Gardiner, B.; Dupont, S.; Guyon, D.; Meredieu, C. Mechanistic and statistical approaches to predicting wind damage to individual maritime pine (Pinus pinaster) trees in forests. Can. J. For. Res. 2016, 46, 88–100. [Google Scholar] [CrossRef]
- Telewski, F.W.; Jaffe, M.J. Thigmomorphogenesis: Anatomical, morphological and mechanical analysis of genetically different sibs of Pinus taeda in response to mechanical perturbation. Physiol. Plant. 1986, 66, 219–226. [Google Scholar] [CrossRef] [PubMed]
- Telewski, F.W.; Jaffe, M.J. Thigmomorphogenesis: Field and laboratory studies of Abies fraseri in response to wind or mechanical perturbation. Physiol. Plant. 1986, 66, 211–218. [Google Scholar] [CrossRef] [PubMed]
- Telewski, F.W. Structure and function of flexure wood in Abies fraseri. Tree Physiol. 1989, 5, 113–121. [Google Scholar] [CrossRef]
- Jacobs, M.R. The effect of wind sway on the form and development of Pinus radiata D. Don. Aust. J. Bot. 1954, 2, 35–51. [Google Scholar] [CrossRef]
- Nicoll, B.C.; Dunn, A.J. The Effects of Wind Speed and Direction on Radial Growth of Structural Roots. In The Supporting Roots of Trees and Woody Plants: Form, Function and Physiology; Springer: Berlin/Heidelberg, Germany, 2000; pp. 219–225. [Google Scholar]
- Watt, M.S.; Kirschbaum, M.U.F. Moving beyond simple linear allometric relationships between tree height and diameter. Ecol. Model. 2011, 222, 3910–3916. [Google Scholar] [CrossRef]
- Gardiner, B. Wind damage to forests and trees: A review with an emphasis on planted and managed forests. J. For. Res. 2021, 26, 248–266. [Google Scholar] [CrossRef]
- Quine, C.; Coutts, M.; Gardiner, B.; Pyatt, G. Forests and Wind: Management to Minimise Damage; Forestry Commission Bulletin 114, HMSO: London, UK, 1995; 27p. [Google Scholar]
- Slodicak, M.; Novak, J. Silvicultural measures to increase the mechanical stability of pure secondary Norway spruce stands before conversion. For. Ecol. Manag. 2006, 224, 252–257. [Google Scholar] [CrossRef]
- Zubizarreta-Gerendiain, A.; Pellikka, P.; Garcia-Gonzalo, J.; Ikonen, V.-P.; Peltola, H. Factors affecting wind and snow damage of individual trees in a small management unit in Finland: Assessment based on inventoried damage and mechanistic modelling. Silva Fenn. 2012, 46, 181–196. [Google Scholar] [CrossRef]
- Gardiner, B.A.; Stacey, G.R.; Belcher, R.E.; Wood, C.J. Field and wind tunnel assessments of the implications of respacing and thinning for tree stability. For. Res. 1997, 70, 233–252. [Google Scholar] [CrossRef]
- Skovsgaard, J.P.; Johansson, U.; Holmström, E.; Tune, R.M.; Ols, C.; Attocchi, G. Effects of thinning practice, high pruning and slash management on crop tree and stand growth in young even-aged stands of planted silver birch (Betula pendula Roth). Forests 2021, 12, 225. [Google Scholar] [CrossRef]
- Somerville, A. Wind stability: Forest layout and silviculture. N. Z. J. For. Sci. 1980, 10, 476–501. [Google Scholar]
- Tabbush, P.M.; White, I.M. Canopy closure in Sitka spruce-the relationship between crown width and stem diameter for open grown trees. For. Int. J. For. Res. 1988, 61, 23–27. [Google Scholar] [CrossRef]
- Urban, S.T.; Lieffers, V.J.; MacDonald, S.E. Release in radial growth in the trunk and structural roots of white spruce as measured by dendrochronology. Can. J. For. Res. 1994, 24, 1550–1556. [Google Scholar] [CrossRef]
- Coutts, M.P. Components of tree stability in Sitka spruce on peaty gley soil. For. Int. J. For. Res. 1986, 59, 173–197. [Google Scholar] [CrossRef]
- Fraser, A.I. The soil and roots as factors in tree stability. For. Int. J. For. Res. 1962, 35, 117–127. [Google Scholar] [CrossRef]
- Anderson, C.J.; Campbell, D.J.; Ritchie, R.M.; Smith, D.L.O. Soil shear strength measurements and their relevance to windthrow in Sitka spruce. Soil Use Manag. 1989, 5, 62–66. [Google Scholar] [CrossRef]
- Dupont, S.; Ikonen, V.-P.; Väisänen, H.; Peltola, H. Predicting tree damage in fragmented landscapes using a wind risk model coupled with an airflow model. Can. J. For. Res. 2015, 45, 1065–1076. [Google Scholar] [CrossRef]
- Gardiner, B.; Berry, P.; Moulia, B. Wind impacts on plant growth, mechanics and damage. Plant Sci. 2016, 245, 94–118. [Google Scholar] [CrossRef]
- Watt, M.S.; Kimberley, M.O. Financial Comparison of Afforestation Using Redwood and Radiata Pine within New Zealand for Regimes That Derive Value from Timber and Carbon. Forests 2023, 14, 2262. [Google Scholar] [CrossRef]
- Bown, H.E.; Watt, M.S. Financial Comparison of Continuous-Cover Forestry, Rotational Forest Management and Permanent Carbon Forest Regimes for Redwood within New Zealand. Forests 2024, 15, 344. [Google Scholar] [CrossRef]
- Dubayah, R.; Armston, J.; Healey, S.P.; Bruening, J.M.; Patterson, P.L.; Kellner, J.R.; Duncanson, L.; Saarela, S.; Ståhl, G.; Yang, Z. GEDI launches a new era of biomass inference from space. Environ. Res. Lett. 2022, 17, 095001. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E. Mapping global forest canopy height through integration of GEDI and Landsat data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Lang, N.; Jetz, W.; Schindler, K.; Wegner, J.D. A high-resolution canopy height model of the Earth. Nat. Ecol. Evol. 2023, 7, 1778–1789. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Rodríguez, F.A.; Aguilar, M.A.; Nemmaoui, A.; Álvarez-Taboada, F. Forestry applications of space-borne LiDAR sensors: A worldwide bibliometric analysis. Sensors 2024, 24, 1106. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; White, J.C.; Wulder, M.A.; Næsset, E. Remote sensing in forestry: Current challenges, considerations and directions. For. Int. J. For. Res. 2024, 97, 11–37. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Strunk, J.; Packalen, P.; Gould, P.; Gatziolis, D.; Maki, C.; Andersen, H.-E.; McGaughey, R.J. Large area forest yield estimation with pushbroom digital aerial photogrammetry. Forests 2019, 10, 397. [Google Scholar] [CrossRef]
- Strunk, J.L.; Gould, P.J.; Packalen, P.; Gatziolis, D.; Greblowska, D.; Maki, C.; McGaughey, R.J. Evaluation of pushbroom DAP relative to frame camera DAP and lidar for forest modeling. Remote Sens. Environ. 2020, 237, 111535. [Google Scholar] [CrossRef]
- Yang, L.; Kang, B.; Huang, Z.; Xu, X.; Feng, J.; Zhao, H. Depth anything: Unleashing the power of large-scale unlabeled data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2024, Seattle WA, USA, 17–21 June 2024. [Google Scholar]
- Mitchell, S.J.; Hailemariam, T.; Kulis, Y. Empirical modeling of cutblock edge windthrow risk on Vancouver Island, Canada, using stand level information. For. Ecol. Manag. 2001, 154, 117–130. [Google Scholar] [CrossRef]
- Scott, R.E.; Mitchell, S.J. Empirical modelling of windthrow risk in partially harvested stands using tree, neighbourhood, and stand attributes. For. Ecol. Manag. 2005, 218, 193–209. [Google Scholar] [CrossRef]
- Watt, P.; Watt, M.S. Development of a national model of Pinus radiata stand volume from LiDAR metrics for New Zealand. Int. J. Remote. Sens. 2013, 34, 5892–5904. [Google Scholar] [CrossRef]
- Beets, P.; Kimberley, M.; McKinley, R. Predicting wood density of Pinus radiata annual growth increments. N. Z. J. For. Sci. 2007, 37, 241–266. [Google Scholar]
- Kimberley, M.O.; Cown, D.J.; McKinley, R.B.; Moore, J.R.; Dowling, L.J. Modelling variation in wood density within and among trees in stands of New Zealand-grown radiata pine. N. Z. J. For. Sci. 2015, 45, 22. [Google Scholar] [CrossRef]
- Beets, P.N.; Roberston, K.A.; Ford-Robertson, J.B.; Gordon, J.; Maclaren, J.P. Description and validation of C_Change: A model for simulating carbon content in managed Pinus radiata stands. N. Z. J. For. Sci. 1999, 29, 409–427. [Google Scholar]
- Watt, M.S.; Kimberley, M.O. Spatial comparisons of carbon sequestration for redwood and radiata pine within New Zealand. For. Ecol. Manag. 2022, 513, 120190. [Google Scholar] [CrossRef]


| Target | Model Statistics | Model Variables | |||
|---|---|---|---|---|---|
| Variable | R2 | RMSE | RMSE% | MBE | |
| MTH (m) | 0.918 | 2.65 | 8.02 | 0.414 | p90 |
| DBH (cm) | 0.867 | 4.21 | 10.1 | −0.506 | p95, cov.gap, WEI1km, TRI, skew, TPI |
| SD (stems/ha) | 0.640 | 179 | 37.3 | −4.09 | std.dev, dns.gap, DSMSD, min |
| Label | Variable | No Windthrow | Windthrow | ANOVA | |||
|---|---|---|---|---|---|---|---|
| Mean (SD) | Range | Mean (SD) | Range | H Value | η2 | ||
| Site variables | |||||||
| WEI1km | Wind exposition index 1 km | 1.04 (0.077) | 0.807–1.29 | 0.99 (0.064) | 0.797–1.28 | 1081 *** | 0.1110 |
| SI | Site index (m) | 31.5 (2.75) | 16.3–39.5 | 32.7 (1.87) | 17.6–40.1 | 520 *** | 0.0535 |
| 300 Index | 300 Index (m3/ha/yr) | 32.4 (3.17) | 8.84–40.8 | 33.8 (2.34) | 12.2–40.9 | 408 *** | 0.0419 |
| HD | Harvest distance (m) | 2124 (1919) | 18.0–14330 | 1561 (1295) | 13.2–13,991 | 135 *** | 0.0138 |
| WindAnn | Mean annual wind (km/h) | 15.4 (2.57) | 7.80–25.6 | 14.8 (1.37) | 7.79–24.0 | 67.3 *** | 0.0068 |
| Aspect | Aspect (degrees) | 179 (88.4) | 4.7–352 | 168 (98.2) | 2.09–358 | 39.1 *** | 0.0039 |
| Slope | Slope (degrees) | 21.8 (7.73) | 0.637–49.5 | 22.6 (8.28) | 0.85–50.4 | 15.6 *** | 0.0015 |
| PRD | Potential rooting depth (m) | 1.22 (0.157) | 0.23–1.35 | 1.22 (0.171) | 0.35–1.35 | 8.69 ** | 0.0008 |
| Stand dimensions | |||||||
| CA | Crown area (m2) | 61.4 (19) | 2.5–191 | 74.8 (25.1) | 29.3–536 | 880 *** | 0.0905 |
| Age | Age (years) | 22.1 (7.01) | 13,971 | 25.8 (6.11) | 14,336 | 780 *** | 0.0802 |
| SD | Stand density (stems/ha) | 490 (234) | 20–1456 | 384 (189) | 20–1534 | 760 *** | 0.0782 |
| MTH | Mean top height (m) | 33.7 (8.56) | 8.54–45.9 | 37.9 (5.73) | 18–46.1 | 643 *** | 0.0661 |
| Slend. | Stem slenderness (m/m) | 79.1 (8.19) | 30–108 | 82.7 (5.98) | 63.2–110 | 517 *** | 0.0532 |
| DBH | Tree diameter (cm) | 42.4 (9.5) | 17–56.2 | 45.9 (6.86) | 17.9–61 | 315 *** | 0.0324 |
| Key LiDAR metrics | |||||||
| p99 | 99th percentile of height (m) | 27.7 (10.7) | 0.896–52.3 | 33.2 (8.15) | 9.28–52.9 | 673 *** | 0.0692 |
| p50 | 50th percentile of height (m) | 20 (8.8) | 0.596–40.4 | 24.1 (7) | 5.45–41.9 | 541 *** | 0.0556 |
| std.dev | Standard deviation of height (m) | 4.76 (2.36) | 0.083–15.9 | 5.72 (2.2) | 1.52–16 | 532 *** | 0.0547 |
| p10 | 10th percentile of height (m) | 12.9 (7.14) | 0.485–33.3 | 15.6 (6.7) | 2.34–34.5 | 366 *** | 0.0375 |
| cov.gap | Gap in canopy cover > 2 m (%) | 10.9 (14.4) | 0–99.1 | 11.4 (9.77) | 0–86.8 | 176 *** | 0.0181 |
| Model | Confusion Matrix (%) | Classification Statistics | |||||||
|---|---|---|---|---|---|---|---|---|---|
| TN | FP | FN | TP | Accuracy | Precision | Recall | F1 Score | AUC | |
| 1 | 39.8 | 8.8 | 7.7 | 43.7 | 0.835 | 0.832 | 0.851 | 0.841 | 0.913 |
| 2 | 40.1 | 8.5 | 7.3 | 44.1 | 0.841 | 0.838 | 0.857 | 0.847 | 0.917 |
| Category | Current Estate | Unplanted Area | Entire Region |
|---|---|---|---|
| Age within current estate | 23.9% | ||
| Simulated age | |||
| Age 5 | 1.5% | 0.4% | 0.6% |
| Age 20 | 20.2% | 9.5% | 11.2% |
| Age 30 | 34.3% | 20.9% | 23.1% |
| ESC very high category | 55.4% | 35.1% | 38.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watt, M.S.; Holdaway, A.; Camarretta, N.; Locatelli, T.; Jayathunga, S.; Watt, P.; Tao, K.; Suárez, J.C. Mapping Windthrow Risk in Pinus radiata Plantations Using Multi-Temporal LiDAR and Machine Learning: A Case Study of Cyclone Gabrielle, New Zealand. Remote Sens. 2025, 17, 1777. https://doi.org/10.3390/rs17101777
Watt MS, Holdaway A, Camarretta N, Locatelli T, Jayathunga S, Watt P, Tao K, Suárez JC. Mapping Windthrow Risk in Pinus radiata Plantations Using Multi-Temporal LiDAR and Machine Learning: A Case Study of Cyclone Gabrielle, New Zealand. Remote Sensing. 2025; 17(10):1777. https://doi.org/10.3390/rs17101777
Chicago/Turabian StyleWatt, Michael S., Andrew Holdaway, Nicolò Camarretta, Tommaso Locatelli, Sadeepa Jayathunga, Pete Watt, Kevin Tao, and Juan C. Suárez. 2025. "Mapping Windthrow Risk in Pinus radiata Plantations Using Multi-Temporal LiDAR and Machine Learning: A Case Study of Cyclone Gabrielle, New Zealand" Remote Sensing 17, no. 10: 1777. https://doi.org/10.3390/rs17101777
APA StyleWatt, M. S., Holdaway, A., Camarretta, N., Locatelli, T., Jayathunga, S., Watt, P., Tao, K., & Suárez, J. C. (2025). Mapping Windthrow Risk in Pinus radiata Plantations Using Multi-Temporal LiDAR and Machine Learning: A Case Study of Cyclone Gabrielle, New Zealand. Remote Sensing, 17(10), 1777. https://doi.org/10.3390/rs17101777








