An Explainable Machine Learning Model for Predicting Macroseismic Intensity for Emergency Management
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Methods
2.2.1. Predictive Machine Learning Framework and XGBoost Model
2.2.2. SHAP Method: Explaining ML Model Predictions
3. Results
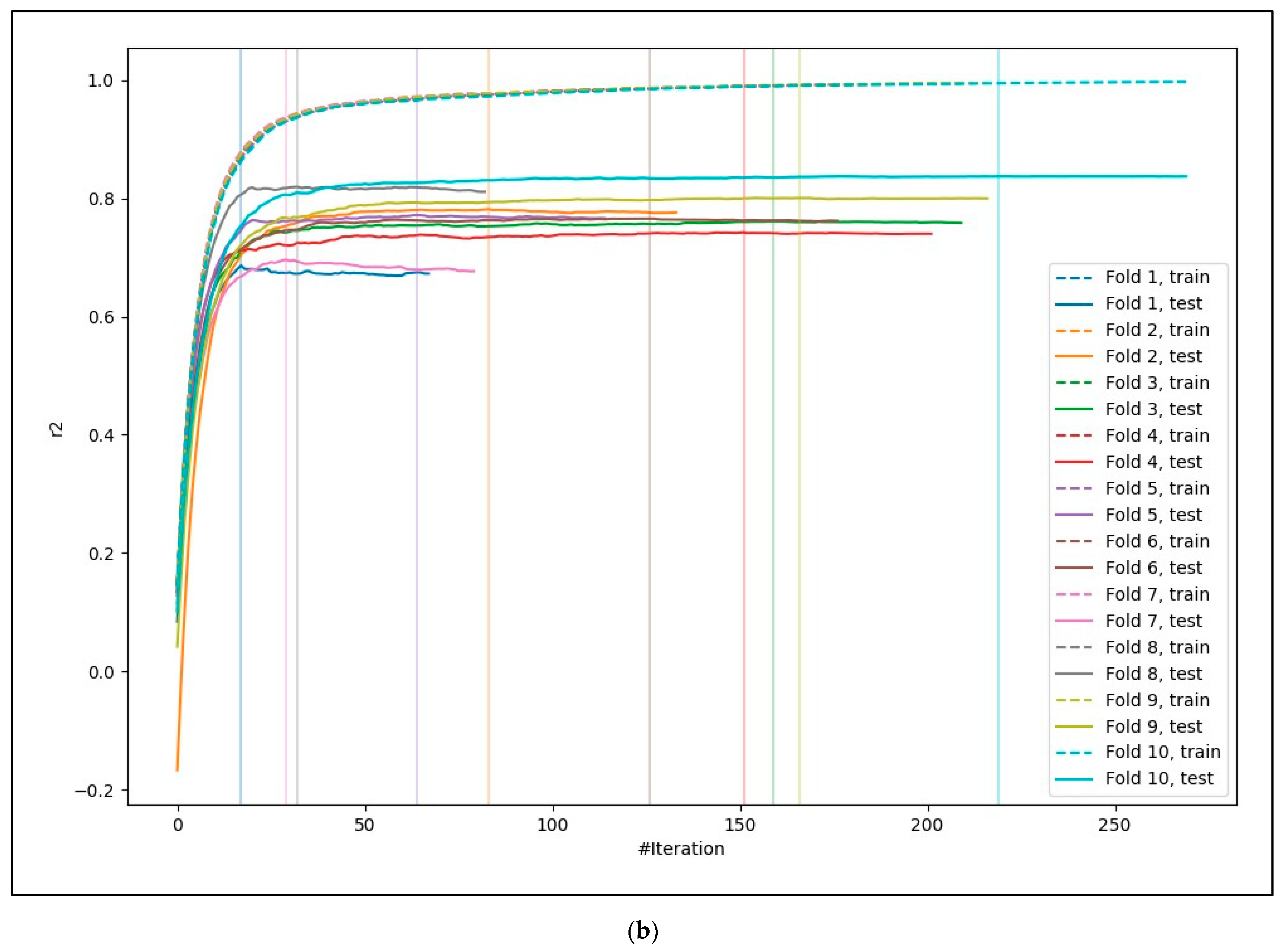
3.1. Model Performance
3.2. SHAP Analysis: Model Explanation
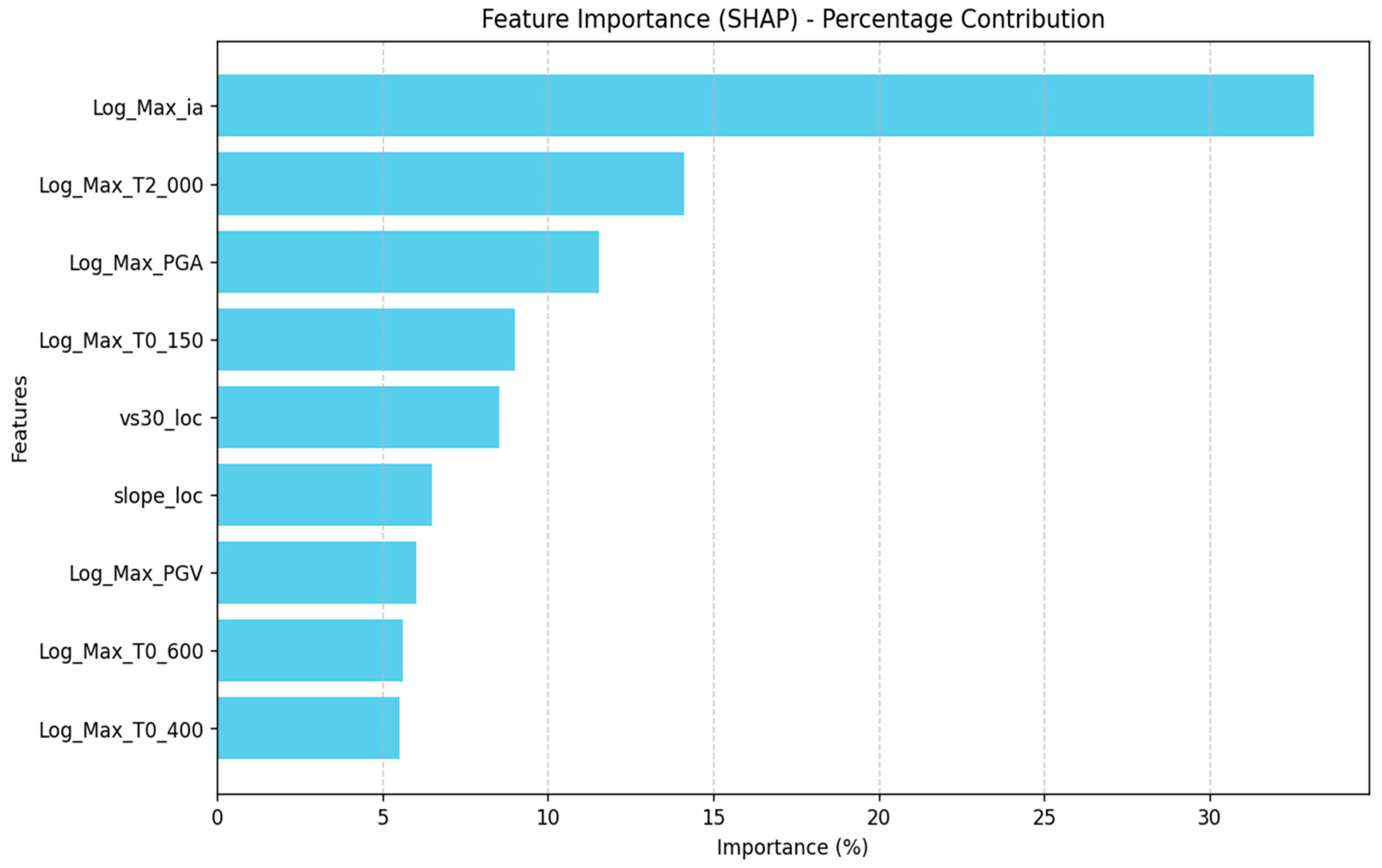
3.2.1. Global Analysis: Feature Ranking Across the Entire Dataset (Figure 4)
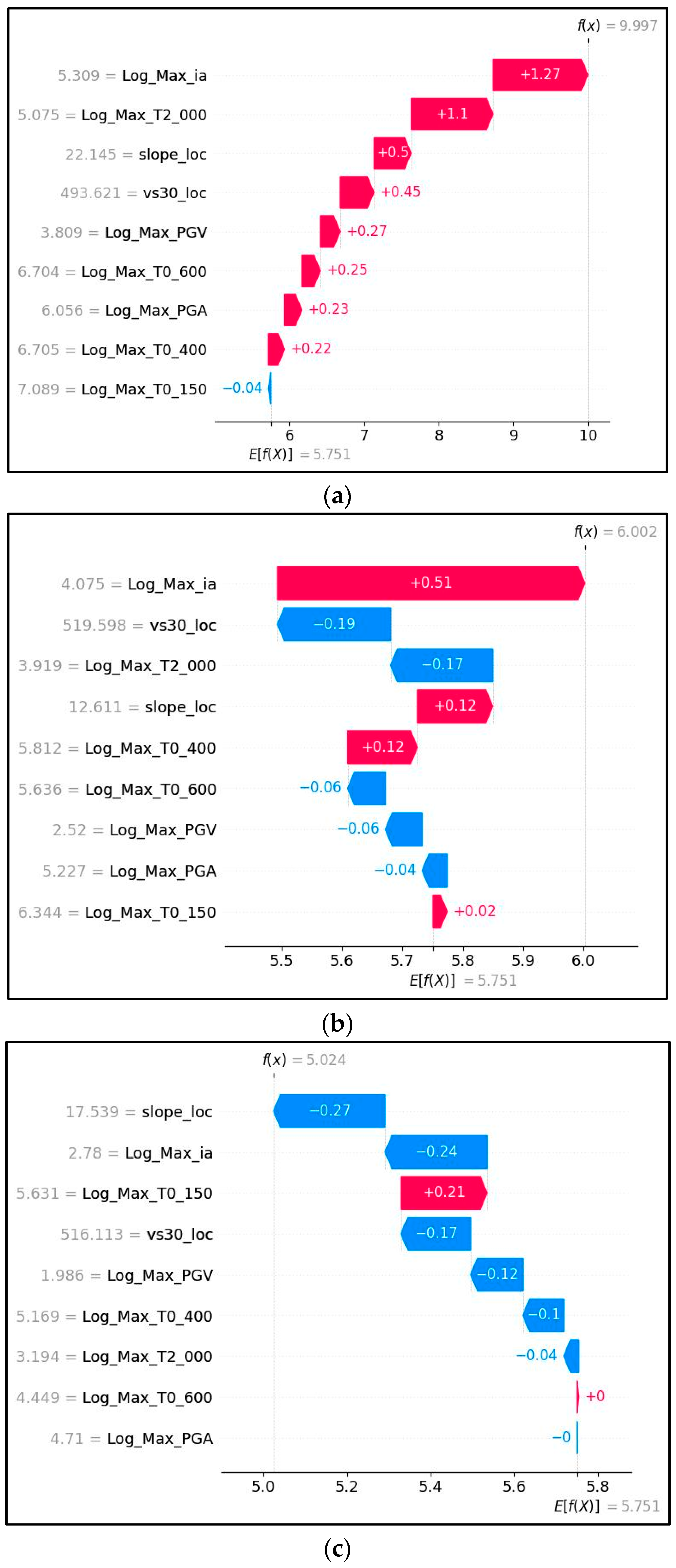
3.2.2. Local Analysis: Insights from the 30 October 2016 Earthquake (Figure 5)
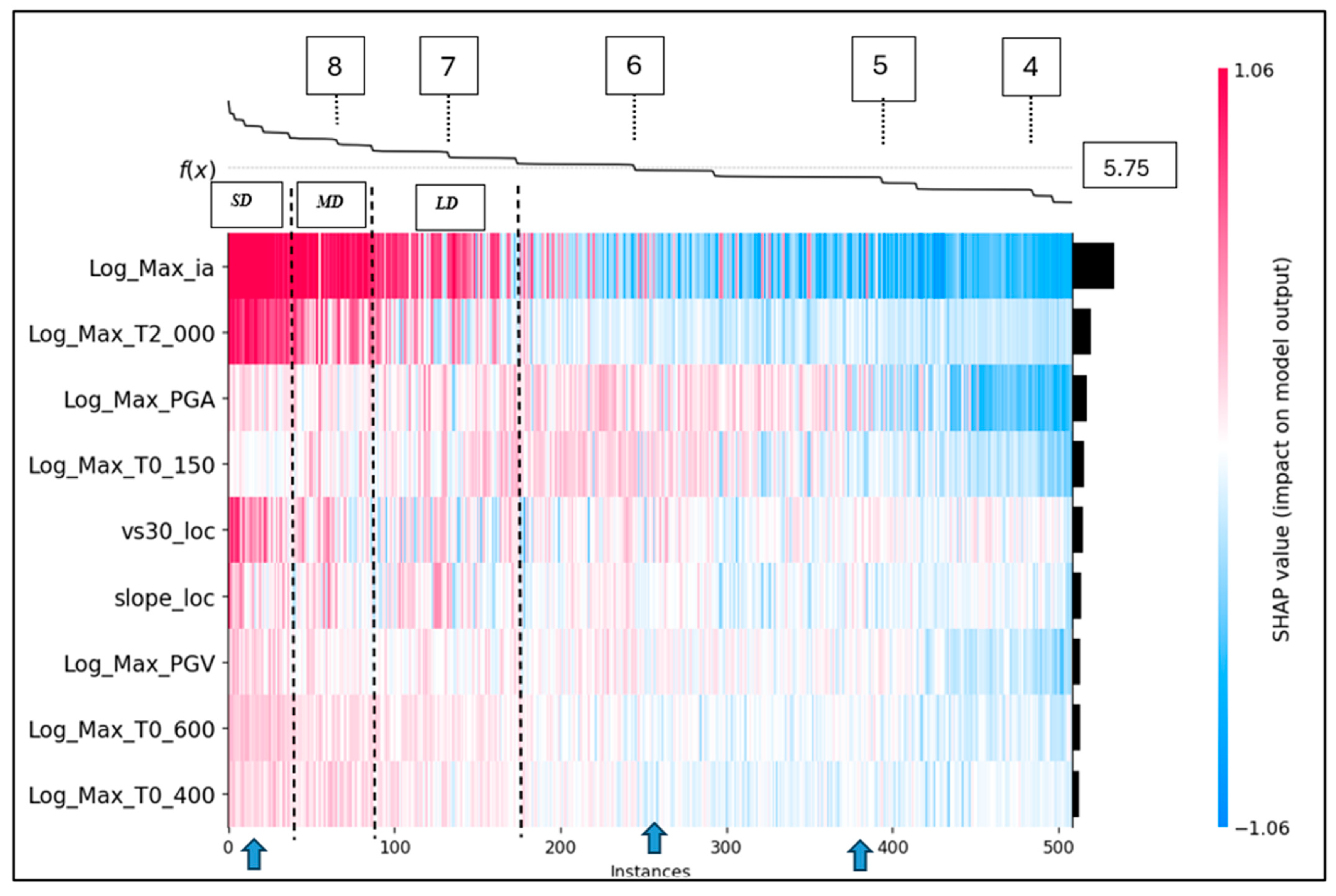
3.2.3. Synthesizing Global and Local Perspectives: The SHAP Heatmap (Figure 6 and Table 5)
| Importance Ranking | Light Damage I_MCS 6.5–7.0 | Moderate Damage I_MCS 7.5–8.0 | Severe Damage I_MCS 8.5–11 |
|---|---|---|---|
| 1 | Log_Max_ia | Log_Max_ia | Log_Max_ia |
| 2 | Log_Max_T2_000 | Log_Max_T2_000 | Log_Max_T2_000 |
| 3 | Log_Max_T0_600 | Log_Max_T0_400 | vs30_loc |
| 4 | Log_Max_PGA | Log_Max_T0_600 | Log_Max_T0_600 |
| 5 | Log_Max_T0_150 | vs30_loc | Log_Max_T0_400 |
| 6 | Log_Max_T0_400 | Log_Max_PGA | slope_loc |
| 7 | slope_loc | Log_Max_T0_150 | Log_Max_PGV |
| 8 | Log_Max_PGV | slope_loc | Log_Max_PGA |
| 9 | vs30_loc | Log_Max_PGV | Log_Max_T0_150 |
4. Discussion
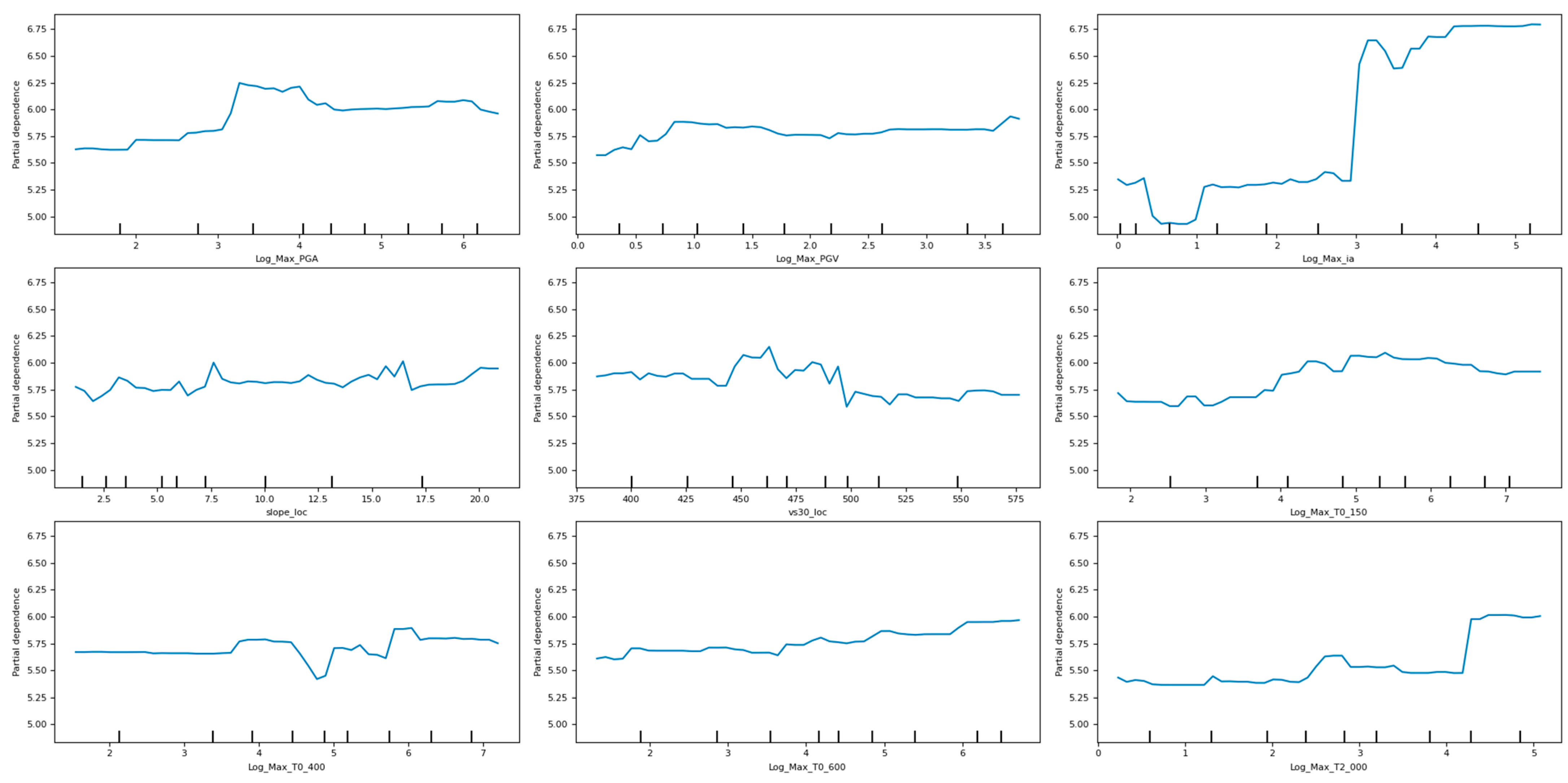
- 2.0 s spectral period remains a stable driver across all damage levels, reflecting deep-seated impedance contrasts that regulate seismic motion amplification at regional scales.
- intermediate periods (0.4 s–0.6 s) capture the transition to velocity-based damage mechanics, marking the shift between acceleration-sensitive and deformation-driven effects.
- Short-period (0.15 s) spectral accelerations and PGA govern light to moderate structural damage, where acceleration-driven forces dominate the response.
5. Conclusions
- Expanding the macroseismic dataset to enhance the model’s ability to generalize across a wider range of seismic contexts.
- Incorporating building vulnerability metrics, such as construction type, age, and material, to better account for structural differences in damage response.
- Integrating physical seismological metrics, including magnitude, fault distance, and other relevant factors, to improve the accuracy and robustness of damage prediction.
- Macroseismic intensity prediction model for assessing direct earthquake damage to buildings and infrastructure.
- Landslide and liquefaction predictive models, calibrated with ground motion parameters and geospatial predictors.
- Network-based impact assessments, considering disruptions to transportation and emergency response logistics.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| I_MCS | Macroseismic Intensity |
| EMS-98 | European Macroseismic Scale 1998 |
| GMP | Ground Motion Parameter |
| PGA | Peak Ground Acceleration |
| PGV | Peak Ground Velocity |
| IA | Arias Intensity |
| Vs30 | Time-averaged shear wave velocity over the top 30 m of soil |
| GMICE | Ground Motion to Intensity Conversion Equations |
| DBMI15 | Database Macrosismico Italiano 2015 |
| CPTI15 | Catalogo Parametrico dei Terremoti Italiani 2015 |
| ITACA | Italian Accelerometric Archive |
| SHAP | Shapley Additive Explanations |
| XGBoost | eXtreme Gradient Boosting |
| LightGBM | Light Gradient Boosting Machine |
| CatBoost | Categorical Boosting |
| ML | Machine Learning |
| RMSE | Root Mean Square Error |
| R2 | Coefficient of Determination |
| AutoML | Automated Machine Learning |
| INGe | Intensity-ground Motion Dataset for Italy |
| MLJAR | Machine Learning Jar (AutoML Platform) |
| σr | Standard Deviation |
| T0_150, T0_400, T0_600, T2_000 | Spectral acceleration periods (0.15 s, 0.4 s, 0.6 s, 2 s) |
| DEM | Digital Elevation Model |
| MERIT | Multi-Error-Removed Improved-Terrain DEM |
References
- Cito, P.; Chioccarelli, E.; Iervolino, I. Macroseismic intensity hazard maps for Italy based on a recent grid source model. Bull. Earthq. Eng. 2022, 20, 2245–2258. [Google Scholar] [CrossRef]
- Galli, P.; Bosi, V.; Piscitelli, S.; Giocoli, A.; Scionti, V. Late Holocene earthquakes in southern Apennine: Paleoseismology of the Caggiano fault. Int. J. Earth Sci. 2006, 95, 855–870. [Google Scholar] [CrossRef]
- Galli, P.; Molin, D. Il Terremoto del 1905 Della Calabria Meridionale. Studio Analitico Degli Effetti ed Ipotesi Sismogenetiche; IlMioLibro: Perugia, Italy, 2007; 124p, Available online: https://emidius.mi.ingv.it/ASMI/study/GALMO007 (accessed on 18 February 2025).
- Faenza, L.; Michelini, A. Regression analysis of MCS intensity and ground motion parameters in Italy and its application in ShakeMap. Geophys. J. Int. 2010, 180, 1138–1152. [Google Scholar] [CrossRef]
- Rotondi, R.; Varini, E.; Brambilla, C. Probabilistic modelling of macroseismic attenuation and forecast of damage scenarios. Bull. Earthq. Eng. 2016, 14, 1777–1796. [Google Scholar] [CrossRef]
- Rossi, A.; Tertulliani, A.; Azzaro, R.; Graziani, L.; Rovida, A.; Maramai, A.; Pessina, V.; Hailemikael, S.; Buffarini, G.; Bernardini, F.; et al. The 2016–2017 earthquake sequence in Central Italy: Macroseismic survey and damage scenario through the EMS-98 intensity assessment. Bull. Earthq. Eng. 2019, 17, 2407–2431. [Google Scholar] [CrossRef]
- Del Mese, S.; Graziani, L.; Meroni, F.; Pessina, V.; Tertulliani, A. Considerations on using MCS and EMS-98 macroseismic scales for the intensity assessment of contemporary Italian earthquakes. Bull. Earthq. Eng. 2023, 21, 4167–4189. [Google Scholar] [CrossRef]
- Locati, M.; Camassi, R.; Rovida, A.; Ercolani, E.; Bernardini, F.; Castelli, V.; Caracciolo, C.H.; Tertulliani, A.; Rossi, A.; Azzaro, R.; et al. Database Macrosismico Italiano (DBMI15); Versione 4.0; Istituto Nazionale di Geofisica e Vulcanologia (INGV): Rome, Italy, 2022. [Google Scholar] [CrossRef]
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P.; Antonucci, A. Italian Parametric Earthquake Catalogue (CPTI15); Vers. 4.0; Istituto Nazionale di Geofisica e Vulcanologia (INGV): Rome, Italy, 2022. [Google Scholar] [CrossRef]
- Wald, D.J.; Quitoriano, V.; Heaton, T.H.; Kanamori, H. Relationships between peak ground acceleration, peak ground velocity, and modified Mercalli intensity in California. Earthq. Spectra 1999, 15, 557–564. [Google Scholar] [CrossRef]
- Masi, A.; Chiauzzi, L.; Nicodemo, G.; Manfredi, V. Correlations between macroseismic intensity estimations and ground motion measures of seismic events. Bull. Earthq. Eng. 2020, 18, 1899–1932. [Google Scholar] [CrossRef]
- Vannucci, G.; Lolli, B.; Gasperini, P. A theoretical comparison among macroseismic scales used in Italy. Bull. Earthq. Eng. 2024, 22, 4245–4263. [Google Scholar] [CrossRef]
- Cataldi, L.; Tiberi, L.; Costa, G. Estimation of MCS intensity for Italy from high quality accelerometric data, using GMICEs and Gaussian Naïve Bayes Classifiers. Bull. Earthq. Eng. 2021, 19, 2325–2342. [Google Scholar] [CrossRef]
- Oliveti, I.; Faenza, L.; Michelini, A. New reversible relationships between ground motion parameters and macroseismic intensity for Italy and their application in ShakeMap. Geophys. J. Int. 2022, 231, 1117–1137. [Google Scholar] [CrossRef]
- Arias, A. A measure of earthquake intensity. In Seismic Design for Nuclear Power Plants; Hansen, R.J., Ed.; MIT Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Trifunac, M.D.; Brady, A.G. A study on the duration of strong earthquake ground motion. Bull. Seismol. Soc. Am. 1975, 65, 581–626. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Bertero, V.V.; Mahin, S.A.; Herrera, R.A. Aseismic design implications of strong-motion records. Earthq. Eng. Struct. Dyn. 1978, 6, 31–42. [Google Scholar] [CrossRef]
- Papageorgiou, A.S.; Aki, K. A specific barrier model for the quantitative description of inhomogeneous faulting and the prediction of strong ground motion. Bull. Seismol. Soc. Am. 1983, 73, 693–722. [Google Scholar] [CrossRef]
- Bard, P.Y.; Bouchon, M. The two-dimensional resonance of sediment-filled valleys. Bull. Seismol. Soc. Am. 1985, 75, 519–541. [Google Scholar] [CrossRef]
- Boore, D.M.; Joyner, W.B. Site amplifications for generic rock sites. Bull. Seismol. Soc. Am. 1997, 87, 327–341. [Google Scholar] [CrossRef]
- Spudich, P.; Hellweg, M.; Lee, W.H.K. Directional topographic site response at Tarzana observed in aftershocks of the 1994 Northridge, California, earthquake: Implications for mainshock motions. Bull. Seismol. Soc. Am. 1996, 86, S193–S208. [Google Scholar] [CrossRef]
- Ashford, S.A.; Sitar, N. Analysis of topographic amplification of inclined shear waves in a steep coastal bluff. Bull. Seismol. Soc. Am. 1997, 87, 692–700. [Google Scholar] [CrossRef]
- Borcherdt, R.D. Estimates of site-dependent response spectra for design (methodology and justification). Earthq. Spectra. 1994, 10, 617–653. [Google Scholar] [CrossRef]
- Boore, D.M.; Thompson, E.M.; Cadet, H. Regional correlations of VS30 and velocities averaged over depths less than and greater than 30 m. Bull. Seismol. Soc. Am. 2011, 101, 3046–3059. [Google Scholar] [CrossRef]
- Grünthal, G. (Ed.) European Macroseismic Scale 1998 (EMS-98); Cahiers du Centre Européen de Géodynamique et de Séismologie: Luxembourg, 1998; Volume 15. [Google Scholar]
- Worden, C.B.; Gerstenberger, M.C.; Rhoades, D.A.; Wald, D.J. Probabilistic relationships between ground-motion parameters and modified Mercalli intensity in California. Bull. Seismol. Soc. Am. 2012, 102, 204–221. [Google Scholar] [CrossRef]
- Oliveti, I.; Faenza, L.; Michelini, A. INGe: Intensity-Ground Motion Dataset for Italy [Dataset] Version 2. Zenodo. 2021. Available online: https://zenodo.org/records/4623732 (accessed on 13 May 2025).
- Felicetta, C.; Russo, E.; D’Amico, M.; Sgobba, S.; Lanzano, G.; Mascandola, C.; Pacor, F.; Luzi, L. ITACA: The Italian Accelerometric Archive. 2023. Available online: https://itaca.mi.ingv.it (accessed on 13 May 2025).
- Yamazaki, D. MERIT DEM: A global DEM derived from multiple datasets. Water Resour. Res. 2017, 53, 5549–5573, Dataset Availability 1987-01-01T00:00:00Z–2017-01-01T00:00:00Z. [Google Scholar]
- Mori, F.; Mendicelli, A.; Moscatelli, M.; Romagnoli, G.; Peronace, E.; Naso, G. A new Vs30 map for Italy based on the seismic microzonation dataset. Eng. Geol. 2020, 275, 105745. [Google Scholar] [CrossRef]
- Mori, F.; Mendicelli, A.; Moscatelli, M.; Varone, C. Shear Wave Velocity Profiles Dataset. Zenodo. 2024. Available online: https://zenodo.org/records/11263471 (accessed on 13 May 2025).
- Gomez-Capera, A.A.; D’Amico, M.; Lanzano, G.; Locati, M.; Santulin, M. Relationships between ground motion parameters and macroseismic intensity for Italy. Bull. Earthq. Eng. 2020, 18, 5143–5164. [Google Scholar] [CrossRef]
- Cornou, C.; Bard, P.-Y.; Dietrich, M. Contribution of dense array analysis to the identification and quantification of basin-edge-induced waves. Part I: Methodology. Bull. Seismol. Soc. Am. 2003, 93, 2604–2623. [Google Scholar] [CrossRef]
- Bard, P.Y.; Brian, E.; Tucker, E. Underground and ridge site effects: A comparison of observation and theory. Bull. Seismol. Soc. Am. 1985, 75, 905–922. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3149–3157. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 6638–6648. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Shapley, L. A theoretical framework for n-person cooperative games. In Contributions to the Theory of Games II; Kuhn, H., Tucker, A., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; pp. 307–317. [Google Scholar] [CrossRef]
- Bruno, P.P.G.; Villani, F.; Improta, L. High-resolution seismic imaging of fault-controlled basins: A case study from the 2009 Mw 6.1 central Italy earthquake. Tectonics 2022, 41, e2022TC007207. [Google Scholar] [CrossRef]
- Buttinelli, M.; Petracchini, L.; Maesano, F.E.; D’Ambrogi, S.; Scrocca, D.; Marino, M.; Capotorti, F.; Bigi, S.; Cavinato, G.P.; Mariucci, M.T.; et al. The impact of structural complexity, fault segmentation, and reactivation on seismotectonics: Constraints from the upper crust of the 2016–2017 Central Italy seismic sequence area. Tectonophysics 2021, 810, 228861. [Google Scholar] [CrossRef]
- Mori, F.; Gena, A.; Mendicelli, A.; Naso, G.; Spina, D. Seismic emergency system evaluation: The role of seismic hazard and local effects. Eng. Geol. 2020, 270, 105587. [Google Scholar] [CrossRef]
- Lawal, A.; Yang, Y.; He, H.; Baisa, N.L. Machine Learning in Oil and Gas Exploration: A Review. IEEE Access 2024, 12, 19035–19058. [Google Scholar] [CrossRef]
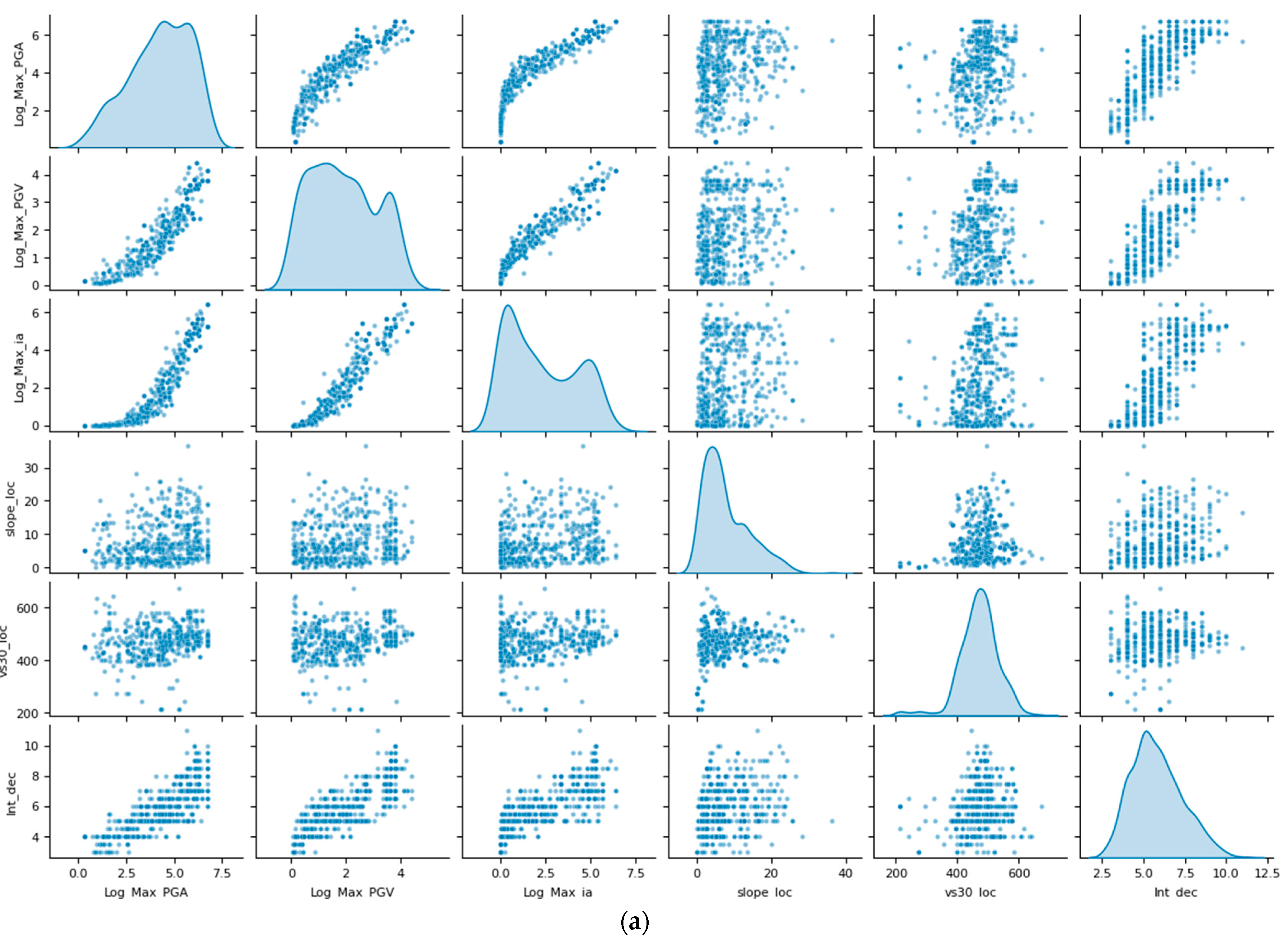
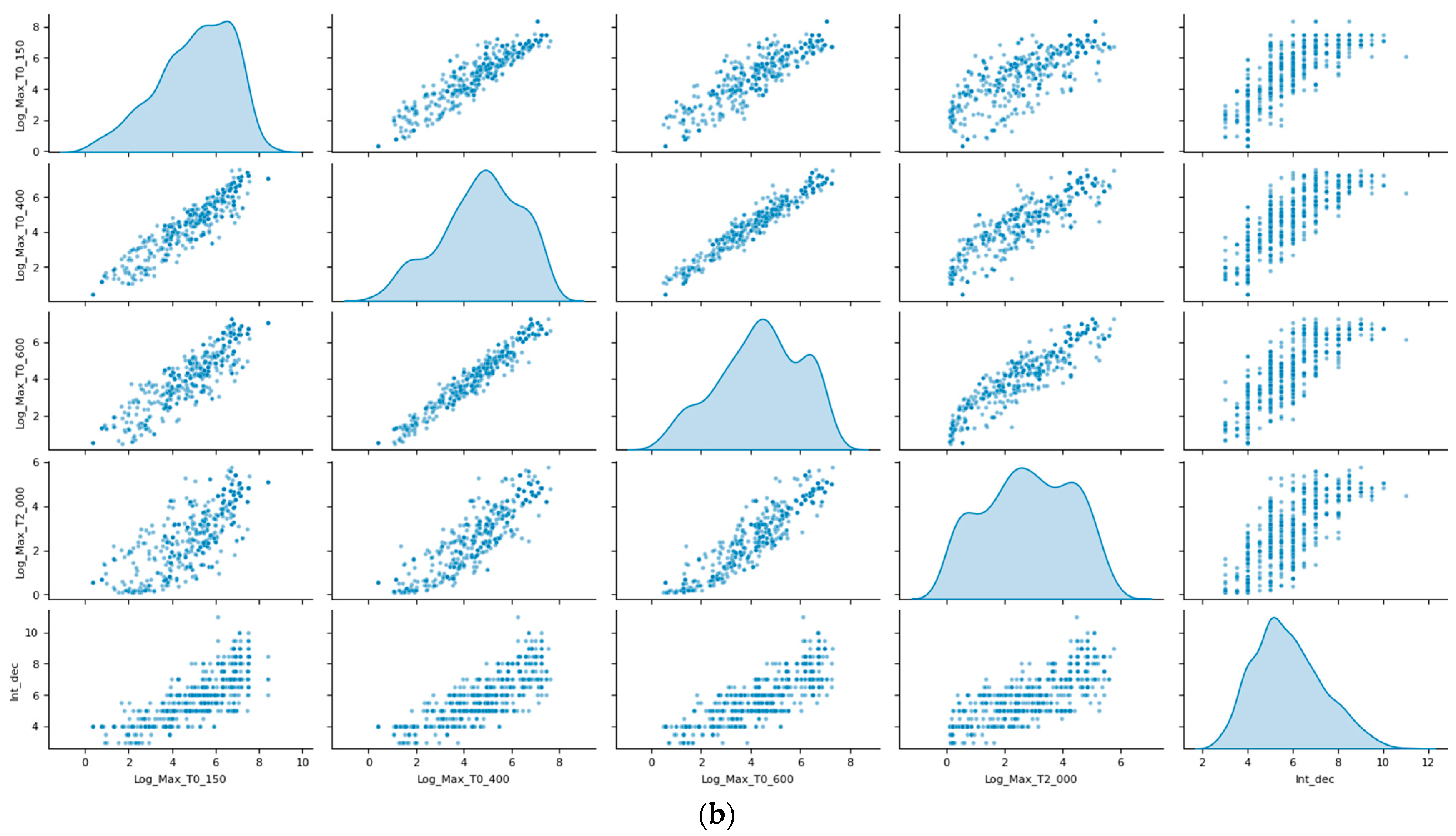


| Datasets Feature Label (Type) | Description (in Bold as Cited in the Text) | Role on Earthquake Damage Potential |
|---|---|---|
| Max_ia (Physical) | Maximum among the two horizontal components of the Arias Intensity (IA) measured at the station | Governs damage intensity at all scales; represents the total energy released by seismic shaking [15,16] |
| Max_PGA (Physical) | Maximum among the two horizontal components of the Peak Ground Acceleration (PGA) measured at the station | More relevant for light damage; peak accelerations dominate the elastic response of structures and are associated with short-period spectral components [17] |
| Max_PGV (Physical) | Maximum among the two horizontal components of the Peak Ground Velocity (PGV) measured at the station | More important for severe damage and collapses; accumulated deformation plays important role, especially in longer-duration shaking [18,19] |
| Max_Tx_xx (Physical) | Maximum among the two horizontal components of the spectral acceleration at specific periods (e.g., 0.15 s, 0.40 s, 0.60 s, 2.00 s spectral periods) measured at the station | Indicator of impedance contrasts at different depths, corresponding to various seismic horizons that regulate wave propagation [20,21] |
| slope_loc (accelerometric station-locality correction) | Slope correction at the locality, sampled from the MERIT Digital Elevation Model at 3 arcsecond resolution (~90 m at the equator) | Correction factor accounting for topographic effects in local intensity estimations. Topographic amplification is more pronounced on steep slopes and rigid substrates [22,23] |
| vs30_loc (accelerometric station-locality correction) | Vs30 correction at the locality, representing the time-averaged shear wave velocity over the top 30 m of soil (m/s), predicted with kriging from Vs dataset (https://zenodo.org/records/11263471, accessed on 18 February 2025) | Correction factor adjusting the ground motion recorded at the station to reflect site-specific shear wave velocity conditions. Soil stiffness modulates the local seismic response and influences ground motion amplification [24,25] |
| int_dec (OUTPUT) | Decimal value of macroseismic intensity (I_MCS) at the locality, based on the DBMI15 manual | Macroseismic intensity (I_MCS) estimated at the locality, integrating ground shaking, site effects, and structural vulnerability [26,27] |
| Parameter | Optuna Range | Best Value |
|---|---|---|
| learning_rate | 0.02–0.5 | 0.05 |
| max_depth | 3–10 | 5 |
| min_child_weight | 0.5–6 | 1 |
| subsample | 0.6–1.0 | 0.8 |
| colsample_bytree | 0.6–1.0 | 0.8 |
| gamma | 0–2 | 0 |
| lambda | 0.1–5.0 | 1 |
| Dataset: Features | Model | RMSE | R2 |
|---|---|---|---|
| Dataset 1: Max_PGA, Max_PGV, Max_T0_300, Max_T1_000, Max T3_000 | Linear regression | 0.965 | 0.581 |
| LightGBM | 0.830 | 0.680 | |
| Xgboost | 0.810 | 0.710 | |
| CatBoost | 0.823 | 0.685 | |
| Neural Network | 0.956 | 0.588 | |
| Random Forest | 0.888 | 0.640 | |
| Dataset 2: Max_ia, Max_PGA, Max_PGV, Max_T0_300, Max T1_000, Max T3_000 slope_loc, vs30_loc | Linear regression | 0.900 | 0.648 |
| LightGBM | 0.792 | 0.714 | |
| Xgboost | 0.770 | 0.740 | |
| CatBoost | 0.793 | 0.713 | |
| Neural Network | 0.877 | 0.666 | |
| Random Forest | 0.794 | 0.726 | |
| Dataset 3: Max_ia, Max_PGA, Max_PGV, Max_T0_150, Max_T0_400, Max_T0_600 Max_T2_000, slope_loc, vs30_loc | Linear regression | 0.895 | 0.652 |
| LightGBM | 0.743 | 0.760 | |
| Xgboost | 0.732 | 0.767 | |
| CatBoost | 0.747 | 0.758 | |
| Neural Network | 0.905 | 0.644 | |
| Random Forest | 0.812 | 0.729 |
| Feature | RMSE (XGBoost) | R2 (XGBoost) |
|---|---|---|
| Max_T0_600 | 0.86 | 0.67 |
| Max_ia | 0.88 | 0.66 |
| Max_T0_150 | 0.89 | 0.64 |
| Max_PGV | 0.9 | 0.64 |
| Max_PGA | 0.91 | 0.63 |
| Max_T0_400 | 0.91 | 0.63 |
| Max_T2_000 | 0.92 | 0.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mori, F.; Naso, G. An Explainable Machine Learning Model for Predicting Macroseismic Intensity for Emergency Management. Remote Sens. 2025, 17, 1754. https://doi.org/10.3390/rs17101754
Mori F, Naso G. An Explainable Machine Learning Model for Predicting Macroseismic Intensity for Emergency Management. Remote Sensing. 2025; 17(10):1754. https://doi.org/10.3390/rs17101754
Chicago/Turabian StyleMori, Federico, and Giuseppe Naso. 2025. "An Explainable Machine Learning Model for Predicting Macroseismic Intensity for Emergency Management" Remote Sensing 17, no. 10: 1754. https://doi.org/10.3390/rs17101754
APA StyleMori, F., & Naso, G. (2025). An Explainable Machine Learning Model for Predicting Macroseismic Intensity for Emergency Management. Remote Sensing, 17(10), 1754. https://doi.org/10.3390/rs17101754







