Assessing the Robustness of Multispectral Satellite Imagery with LiDAR Topographic Attributes and Ancillary Data to Predict Vertical Structure in a Wet Eucalypt Forest
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Remote Sensing Data
2.3. Data Pre-Processing
2.4. Response and Predictor Variables
- Spectral bands (B);
- Topographic attributes and geology (A + G);
- Spectral indices (I);
- Spectral bands, topographic attributes, and geology (B + A + G);
- Spectral bands and spectral indices (B + I);
- Topographic attributes, geology, and spectral indices (A + G + I);
- Spectral bands, topographic attributes, geology, and spectral indices (B + A + G + I);
- Texture features (T);
- Spectral bands and texture features (B + T);
- Topographic attributes, geology, and texture features (A + G + T);
- Spectral indices and texture features (I + T);
- Topographic attributes, geology, spectral indices, and texture features (A + G + I + T);
- Spectral bands, topographic attributes, geology, spectral indices, and texture features (B + A + G + I + T).
2.5. Random Forest Modelling
3. Results
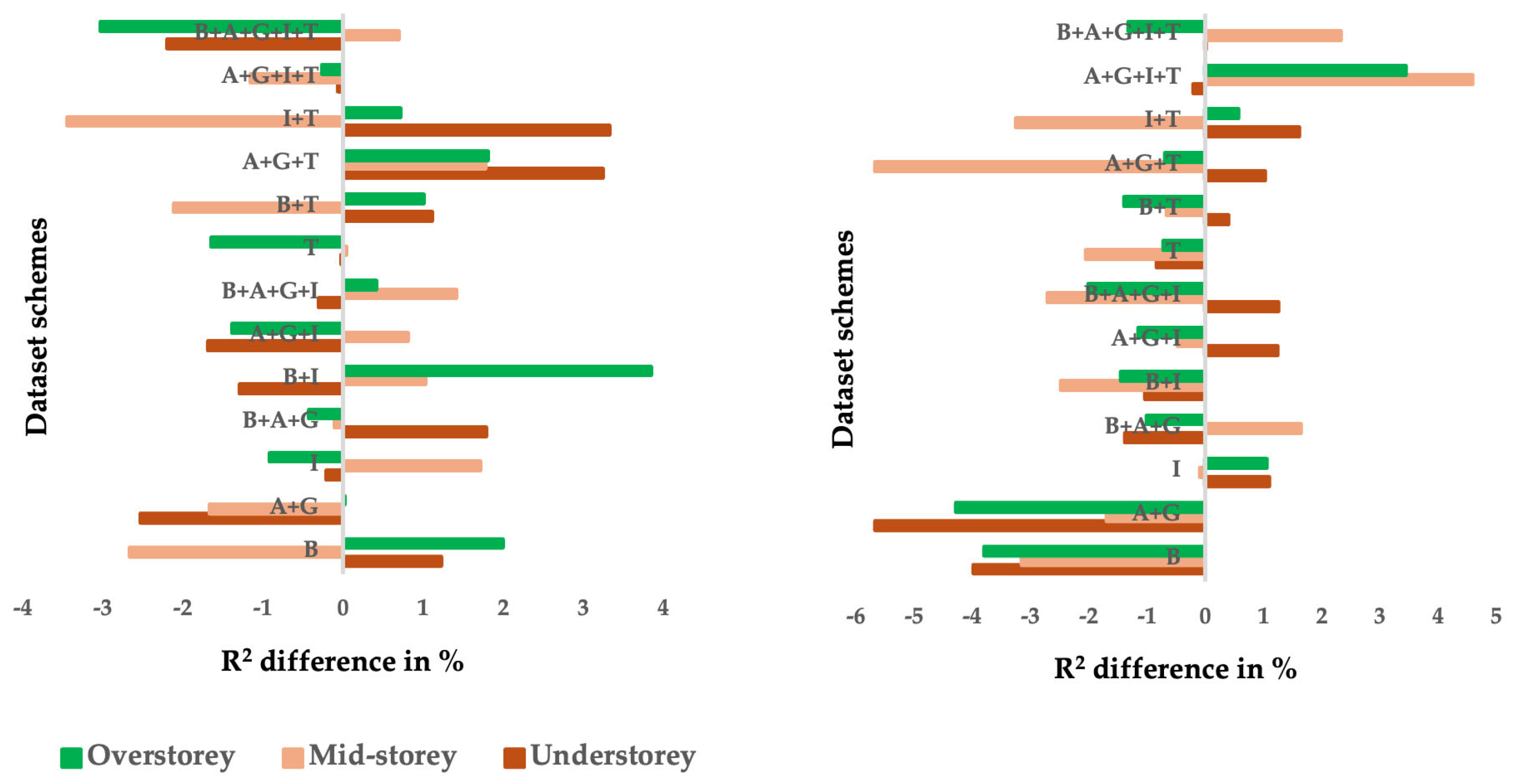
3.1. Model Accuracy Assessment
3.2. Model Validation
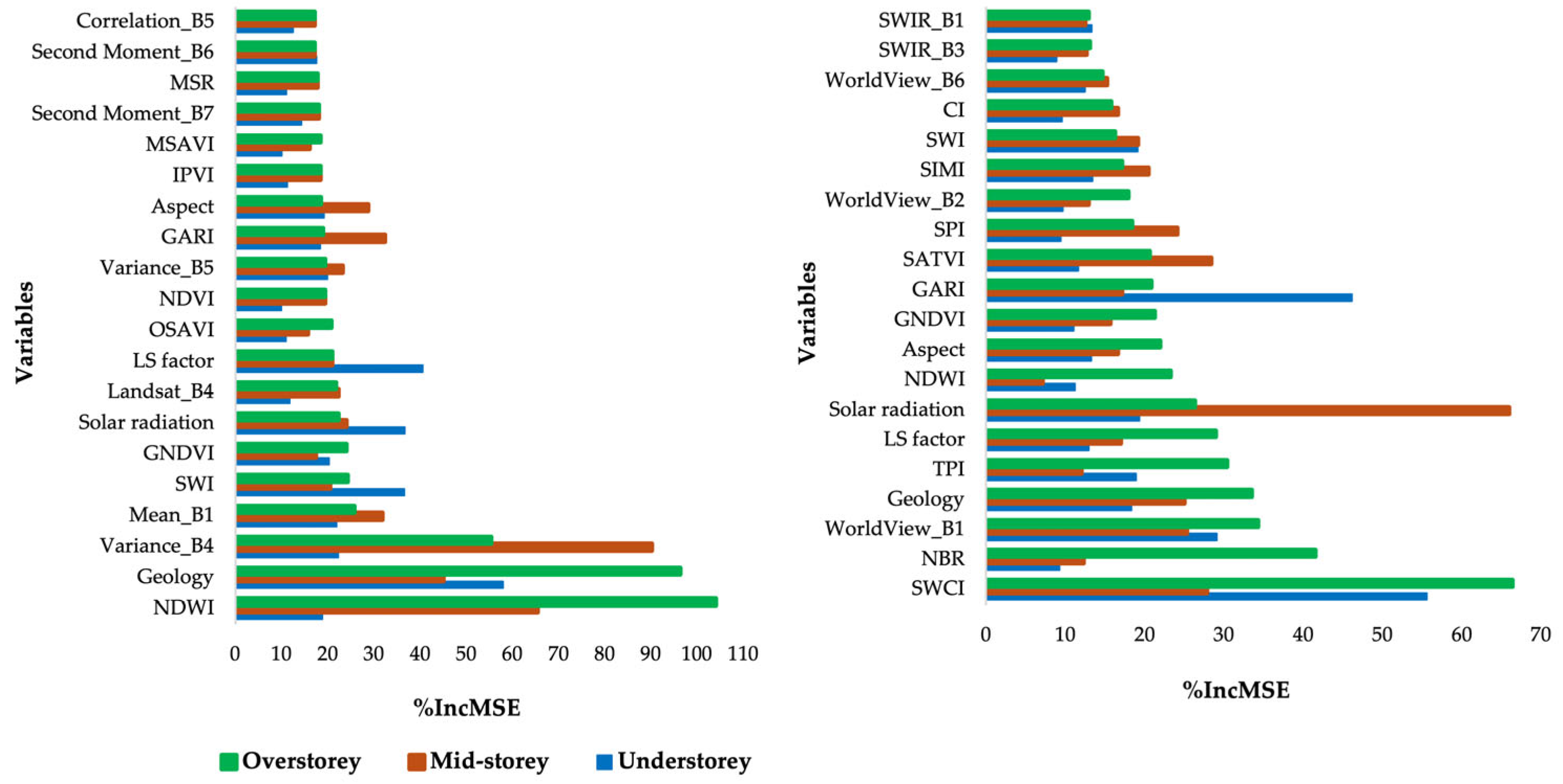
3.3. Importance of Individual Predictor Variables
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LiDAR | Light Detection and Ranging |
| VFS | Vertical forest structure |
| DEM | Digital elevation model |
| VNIR | Visible near-infrared |
| SWIR | Shortwave infrared |
| OLI | Operational Land Imager |
| RF | Random forest |
| VIF | Variance inflation factor |
Appendix A
| Texture Feature | Description | Equations | References |
|---|---|---|---|
| Contrast | The grey level of the two pixels of the same image varies | [22] | |
| Correlation | Captures how the pairs of pixels are correlated to other pixel pairs | [22] | |
| Dissimilarity | Two samples vary with the number of grey levels | [138] | |
| Entropy | Captures the amount of variation in the co-occurrence of the grey level distribution | [86] | |
| Homogeneity | measures how close the distribution of elements in the GLCM | [138] | |
| Mean | Mean value of intensities over the image | [86] | |
| Angular second moment | a measure of homogeneity of an image/measures the local uniformity of the grey levels | [86] | |
| Variance | a measure of “roughness” | [22] |
| Spectral Indices | Acronyms | Equations | Reference |
|---|---|---|---|
| Green Atmospherically Resistant Index | GARI | [139] | |
| Green Normalised Difference Vegetation Index | GNDVI | [91] | |
| Infrared Percentage Vegetation Index | IPVI | [92] | |
| Modified Non-Linear Index | MNLI | [96] | |
| Modified Soil-Adjusted Vegetation Index | MSAVI | [140] | |
| Modified Simple Ratio | MSR | [97] | |
| Non-Linear Index | NLI | [95] | |
| Normalised Difference Vegetation Index | NDVI | [89] | |
| Renormalised Difference Vegetation Index | RDVI | [94] | |
| Optimised Soil-Adjusted Vegetation Index | OSAVI | [93] | |
| Soil-Adjusted Total Vegetation Index | SATVI | [141,142,143] | |
| Normalised Burn Ratio (not for Landsat (OLI)) data | NBR | [144,145] | |
| Normalised Difference Water Index | NDWI | [145,146] | |
| Surface Water Capacity Index | SWCI | [147] | |
| Shortwave Infrared Soil Moisture Index | SIMI | [147] |

References
- Zhou, X.; Li, C. Mapping the vertical forest structure in a large subtropical region using airborne LiDAR data. Ecol. Indic. 2023, 154, 110731. [Google Scholar] [CrossRef]
- Blondeel, H.; Landuyt, D.; Vangansbeke, P.; De Frenne, P.; Verheyen, K.; Perring, M.P. The need for an understory decision support system for temperate deciduous forest management. For. Ecol. Manag. 2021, 480, 118634. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Jarron, L.R.; Coops, N.C.; MacKenzie, W.H.; Tompalski, P.; Dykstra, P. Detection of sub-canopy forest structure using airborne LiDAR. Remote Sens. Environ. 2020, 244, 111770. [Google Scholar] [CrossRef]
- Peng, X.; Zhao, A.; Chen, Y.; Chen, Q.; Liu, H.; Wang, J.; Li, H. Comparison of Modeling Algorithms for Forest Canopy Structures Based on UAV-LiDAR: A Case Study in Tropical China. Forests 2020, 11, 1324. [Google Scholar] [CrossRef]
- Wei, L.; Gosselin, F.; Rao, X.; Lin, Y.; Wang, J.; Jian, S.; Ren, H. Overstory and niche attributes drive understory biomass production in three types of subtropical plantations. For. Ecol. Manag. 2021, 482, 118894. [Google Scholar] [CrossRef]
- Rutten, G.; Ensslin, A.; Hemp, A.; Fischer, M. Vertical and horizontal vegetation structure across natural and modified habitat types at Mount Kilimanjaro. PLoS ONE 2015, 10, e0138822. [Google Scholar] [CrossRef]
- Dash, J.P.; Watt, M.S.; Bhandari, S.; Watt, P. Characterising forest structure using combinations of airborne laser scanning data, RapidEye satellite imagery and environmental variables. Forestry 2016, 89, 159–169. [Google Scholar] [CrossRef]
- Wilkes, P.; Jones, S.D.; Suarez, L.; Haywood, A.; Mellor, A.; Woodgate, W.; Soto-Berelov, M.; Skidmore, A.K.; McMahon, S. Using discrete-return airborne laser scanning to quantify number of canopy strata across diverse forest types. Methods Ecol. Evol. 2016, 7, 700–712. [Google Scholar] [CrossRef]
- Furlaud, J.M.; Prior, L.D.; Williamson, G.J.; Bowman, D.M.J.S. Fire risk and severity decline with stand development in Tasmanian giant Eucalyptus forest. For. Ecol. Manag. 2021, 502, 119724. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Lee, S.; Jung, H.-S. Mapping Forest Vertical Structure in Gong-ju, Korea Using Sentinel-2 Satellite Images and Artificial Neural Networks. Appl. Sci. 2020, 10, 1666. [Google Scholar] [CrossRef]
- Taneja, R.; Wallace, L.; Hillman, S.; Reinke, K.; Hilton, J.; Jones, S.; Hally, B. Up-Scaling Fuel Hazard Metrics Derived from Terrestrial Laser Scanning Using a Machine Learning Model. Remote Sens. 2023, 15, 1273. [Google Scholar] [CrossRef]
- Viedma, O.; Moreno, J.M. Impact of LiDAR pulse density on forest fuels metrics derived using LadderFuelsR. Ecol. Inform. 2025, 88, 103135. [Google Scholar] [CrossRef]
- Silva, I.; Rocha, R.; López-Baucells, A.; Farneda, F.Z.; Meyer, C.F.J. Effects of Forest Fragmentation on the Vertical Stratification of Neotropical Bats. Diversity 2020, 12, 67. [Google Scholar] [CrossRef]
- Wilkes, P.; Jones, S.; Suarez, L.; Mellor, A.; Woodgate, W.; Soto-Berelov, M.; Haywood, A.; Skidmore, A. Mapping forest canopy height across large areas by upscaling ALS estimates with freely available satellite data. Remote Sens. 2015, 7, 12563. [Google Scholar] [CrossRef]
- Terryn, L.; Calders, K.; Bartholomeus, H.; Bartolo, R.E.; Brede, B.; D’Hont, B.; Disney, M.; Herold, M.; Lau, A.; Shenkin, A.; et al. Quantifying tropical forest structure through terrestrial and UAV laser scanning fusion in Australian rainforests. Remote Sens. Environ. 2022, 271, 112912. [Google Scholar] [CrossRef]
- Cardenas-Martinez, A.; Pascual, A.; Guisado-Pintado, E.; Rodriguez-Galiano, V. Using airborne LiDAR and enhanced-geolocated GEDI metrics to map structural traits over a Mediterranean forest. Sci. Remote Sens. 2025, 11, 100195. [Google Scholar] [CrossRef]
- Linderman, M.; Liu, J.; Qi, J.; An, L.; Ouyang, Z.; Yang, J.; Tan, Y. Using artificial neural networks to map the spatial distribution of understorey bamboo from remote sensing data. Int. J. Remote Sens. 2004, 25, 1685–1700. [Google Scholar] [CrossRef]
- Culbert, P.; Radeloff, V.; Flather, C.; Kellndorfer, J.; Rittenhouse, C.; Pidgeon, A. The influence of vertical and horizontal habitat structure on nationwide patterns of avian biodiversity. Ornithology 2013, 130, 656–665. [Google Scholar] [CrossRef]
- Masek, J.G.; Hayes, D.J.; Joseph Hughes, M.; Healey, S.P.; Turner, D.P. The role of remote sensing in process-scaling studies of managed forest ecosystems. For. Ecol. Manag. 2015, 355, 109–123. [Google Scholar] [CrossRef]
- Ozdemir, I.; Karnieli, A. Predicting forest structural parameters using the image texture derived from WorldView-2 multispectral imagery in a dryland forest, Israel. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 701–710. [Google Scholar] [CrossRef]
- Kayitakire, F.; Hamel, C.; Defourny, P. Retrieving forest structure variables based on image texture analysis and IKONOS-2 imagery. Remote Sens. Environ. 2006, 102, 390–401. [Google Scholar] [CrossRef]
- Bolton, D.K.; White, J.C.; Wulder, M.A.; Coops, N.C.; Hermosilla, T.; Yuan, X. Updating stand-level forest inventories using airborne laser scanning and Landsat time series data. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 174–183. [Google Scholar] [CrossRef]
- Zald, H.S.J.; Wulder, M.A.; White, J.C.; Hilker, T.; Hermosilla, T.; Hobart, G.W.; Coops, N.C. Integrating Landsat pixel composites and change metrics with LiDAR plots to predictively map forest structure and aboveground biomass in Saskatchewan, Canada. Remote Sens. Environ. 2016, 176, 188–201. [Google Scholar] [CrossRef]
- Zald, H.S.J.; Ohmann, J.L.; Roberts, H.M.; Gregory, M.J.; Henderson, E.B.; McGaughey, R.J.; Braaten, J. Influence of LiDAR, Landsat imagery, disturbance history, plot location accuracy, and plot size on accuracy of imputation maps of forest composition and structure. Remote Sens. Environ. 2014, 143, 26–38. [Google Scholar] [CrossRef]
- Gebreslasie, M.T.; Ahmed, F.B.; van Aardt, J.A.N. Predicting forest structural attributes using ancillary data and ASTER satellite data. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S23–S26. [Google Scholar] [CrossRef]
- Venier, L.A.; Swystun, T.; Mazerolle, M.J.; Kreutzweiser, D.P.; Wainio-Keizer, K.L.; McIlwrick, K.A.; Woods, M.E.; Wang, X. Modelling vegetation understory cover using LiDAR metrics. PLoS ONE 2019, 14, e0220096. [Google Scholar] [CrossRef]
- Kamal, M.; Phinn, S.; Johansen, K. Characterizing the spatial structure of mangrove features for optimizing image-based mangrove mapping. Remote Sens. 2014, 6, 984. [Google Scholar] [CrossRef]
- Kunin, W.E.; Harte, J.; He, F.; Hui, C.; Jobe, R.T.; Ostling, A.; Polce, C.; Šizling, A.; Smith, A.B.; Smith, K.; et al. Upscaling biodiversity: Estimating the species–area relationship from small samples. Ecol. Monogr. 2018, 88, 170–187. [Google Scholar] [CrossRef]
- Zhang, N. Scale issues in ecology: Upscaling. Acta Ecol. Sin. 2007, 27, 4252–4266. [Google Scholar]
- Yang, X.; Qiu, S.; Zhu, Z.; Rittenhouse, C.; Riordan, D.; Cullerton, M. Mapping understory plant communities in deciduous forests from Sentinel-2 time series. Remote Sens. Environ. 2023, 293, 113601. [Google Scholar] [CrossRef]
- Luo, Y.; Qi, S.; Liao, K.; Zhang, S.; Hu, B.; Tian, Y. Mapping the Forest Height by Fusion of ICESat-2 and Multi-Source Remote Sensing Imagery and Topographic Information: A Case Study in Jiangxi Province, China. Forests 2023, 14, 454. [Google Scholar] [CrossRef]
- Ni, M.; Wu, Q.; Li, G.; Li, D. Remote Sensing Technology for Observing Tree Mortality and Its Influences on Carbon–Water Dynamics. Forests 2025, 16, 194. [Google Scholar] [CrossRef]
- Miura, N.; Jones, S.D. Characterizing forest ecological structure using pulse types and heights of airborne laser scanning. Remote Sens. Environ. 2010, 114, 1069–1076. [Google Scholar] [CrossRef]
- Moudrý, V.; Cord, A.F.; Gábor, L.; Laurin, G.V.; Barták, V.; Gdulová, K.; Malavasi, M.; Rocchini, D.; Stereńczak, K.; Prošek, J.; et al. Vegetation structure derived from airborne laser scanning to assess species distribution and habitat suitability: The way forward. Divers. Distrib. 2022, 29, 39–50. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T.; Guan, H.; Jin, S.; Zhang, J.; Zhao, X.; Xu, K.; Wei, D.; Kelly, M.; et al. Lidar Boosts 3D Ecological Observations and Modelings: A Review and Perspective. IEEE Geosci. Remote Sens. Mag. 2021, 9, 232–257. [Google Scholar] [CrossRef]
- Atkins, J.W.; Costanza, J.; Dahlin, K.M.; Dannenberg, M.P.; Elmore, A.J.; Fitzpatrick, M.C.; Hakkenberg, C.R.; Hardiman, B.S.; Kamoske, A.; LaRue, E.A.; et al. Scale dependency of lidar-derived forest structural diversity. Methods Ecol. Evol. 2023, 14, 708–723. [Google Scholar] [CrossRef]
- Kim, J.; Popescu, S.C.; Lopez, R.R.; Wu, X.B.; Silvy, N.J. Vegetation mapping of No Name Key, Florida using lidar and multispectral remote sensing. Int. J. Remote Sens. 2020, 41, 9469–9506. [Google Scholar] [CrossRef]
- Bigdeli, B.; Amini Amirkolaee, H.; Pahlavani, P. DTM extraction under forest canopy using LiDAR data and a modified invasive weed optimization algorithm. Remote Sens. Environ. 2018, 216, 289–300. [Google Scholar] [CrossRef]
- Bolton, D.K.; Coops, N.C.; Wulder, M.A. Characterizing residual structure and forest recovery following high-severity fire in the western boreal of Canada using Landsat time-series and airborne lidar data. Remote Sens. Environ. 2015, 163, 48–60. [Google Scholar] [CrossRef]
- Hagar, J.C.; Yost, A.; Haggerty, P.K. Incorporating LiDAR metrics into a structure-based habitat model for a canopy-dwelling species. Remote Sens. Environ. 2020, 236, 111499. [Google Scholar] [CrossRef]
- Lesak, A.A.; Radeloff, V.C.; Hawbaker, T.J.; Pidgeon, A.M.; Gobakken, T.; Contrucci, K. Modeling forest songbird species richness using LiDAR-derived measures of forest structure. Remote Sens. Environ. 2011, 115, 2823–2835. [Google Scholar] [CrossRef]
- Carrasco, L.; Giam, X.; Papeş, M.; Sheldon, K.S. Metrics of Lidar-Derived 3D Vegetation Structure Reveal Contrasting Effects of Horizontal and Vertical Forest Heterogeneity on Bird Species Richness. Remote Sens. 2019, 11, 743. [Google Scholar] [CrossRef]
- Wang, D.; Wan, B.; Liu, J.; Su, Y.; Guo, Q.; Qiu, P.; Wu, X. Estimating aboveground biomass of the mangrove forests on northeast Hainan Island in China using an upscaling method from field plots, UAV-LiDAR data and Sentinel-2 imagery. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101986. [Google Scholar] [CrossRef]
- Dupuis, C.; Lejeune, P.; Michez, A.; Fayolle, A. How Can Remote Sensing Help Monitor Tropical Moist Forest Degradation?—A Systematic Review. Remote Sens. 2020, 12, 1087. [Google Scholar] [CrossRef]
- LaRue, E.A.; Wagner, F.W.; Fei, S.; Atkins, J.W.; Fahey, R.T.; Gough, C.M.; Hardiman, B.S. Compatibility of Aerial and Terrestrial LiDAR for Quantifying Forest Structural Diversity. Remote Sens. 2020, 12, 1407. [Google Scholar] [CrossRef]
- Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Falkowski, M.J.; Smith, A.M.S.; Gessler, P.E.; Morgan, P. Regression modeling and mapping of coniferous forest basal area and tree density from discrete-return lidar and multispectral satellite data. Can. J. Remote Sens. 2006, 32, 126–138. [Google Scholar] [CrossRef]
- Sun, X.; Li, G.; Wu, Q.; Ruan, J.; Li, D.; Lu, D. Mapping Forest Carbon Stock Distribution in a Subtropical Region with the Integration of Airborne Lidar and Sentinel-2 Data. Remote Sens. 2024, 16, 3847. [Google Scholar] [CrossRef]
- Arroyo, L.A.; Johansen, K.; Armston, J.; Phinn, S. Integration of LiDAR and QuickBird imagery for mapping riparian biophysical parameters and land cover types in Australian tropical savannas. For. Ecol. Manag. 2010, 259, 598–606. [Google Scholar] [CrossRef]
- Cohen, W.B.; Spies, T.A. Estimating structural attributes of Douglas-fir/western hemlock forest stands from landsat and SPOT imagery. Remote Sens. Environ. 1992, 41, 1–17. [Google Scholar] [CrossRef]
- Muscarella, R.; Kolyaie, S.; Morton, D.C.; Zimmerman, J.K.; Uriarte, M. Effects of topography on tropical forest structure depend on climate context. J. Ecol. 2020, 108, 145–159. [Google Scholar] [CrossRef]
- Gracia, M.; Montané, F.; Piqué, J.; Retana, J. Overstory structure and topographic gradients determining diversity and abundance of understory shrub species in temperate forests in central Pyrenees (NE Spain). For. Ecol. Manag. 2007, 242, 391–397. [Google Scholar] [CrossRef]
- Odom, R.; Henry McNab, W. Using Digital Terrain Modeling to Predict Ecological Types in the Balsam Mountains of Western North Carolina; RN-SRS008; Department of Agriculture, Forest Service, Southern Research Station: Asheville, NC, USA, 2000; p. 13. [Google Scholar]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Mikita, T.; Klimánek, M.; Miloš, C. Evaluation of airborne laser scanning data for tree parameters and terrain modelling in forest environment. Acta Univ. Agric. Silvic. Mendel. Brun. 2013, LXI, 1339–1347. [Google Scholar] [CrossRef]
- Yun, Z.; Zheng, G.; Geng, Q.; Monika Moskal, L.; Wu, B.; Gong, P. Dynamic stratification for vertical forest structure using aerial laser scanning over multiple spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103040. [Google Scholar] [CrossRef]
- TERN. Warra Tall Eucalypt SuperSite. Available online: https://www.tern.org.au/tern-ecosystem-processes/warra-tall-eucalypt-supersite/ (accessed on 15 July 2017).
- Bureau of Meteorology. Climate Statistics for Australian Locations (2004–2017); Bureau of Meteorology: Canberra, Australia, 2017. [Google Scholar]
- Hickey, J.E.; Su, W.; Rowe, P.; Brown, M.J.; Edwards, L. Fire history of the tall wet eucalypt forests of the Warra ecological research site, Tamania. Aust. For. 1999, 62, 66–71. [Google Scholar] [CrossRef]
- Baker, S.C.; Garandel, M.; Deltombe, M.; Neyland, M.G. Factors influencing initial vascular plant seedling composition following either aggregated retention harvesting and regeneration burning or burning of unharvested forest. For. Ecol. Manag. 2013, 306, 192–201. [Google Scholar] [CrossRef]
- Neyland, M.G. Vegetation of the Warra silvicultural systems trial. Tasforests 2001, 13, 183–192. [Google Scholar]
- Mineral Resources Tasmania. Digital Geological Atlas 1:25,000 Scale Series. Available online: http://www.mrt.tas.gov.au/products/geoscience_maps/digital_geological_atlas_125_000_scale_series (accessed on 30 January 2019).
- Assmann, J.J.; Moeslund, J.; Treier, U.; Normand, S. EcoDes-DK15: High-resolution ecological descriptors of vegetation and terrain derived from Denmark’s national airborne laser scanning data set. Earth Syst. Sci. Data 2022, 14, 823–844. [Google Scholar] [CrossRef]
- Meijer, C.; Grootes, M.; Koma, Z.; Dzigan, Y.; Gonçalves, R.; Andela, B.; Oord, G.; Ranguelova, E.; Renaud, N.; Kissling, W.D. Laserchicken—A tool for distributed feature calculation from massive LiDAR point cloud datasets. SoftwareX 2020, 12, 100626. [Google Scholar] [CrossRef]
- Ferro, J.C.; Warner, T. Scale and texture in digital image classification. Photogramm. Eng. Remote Sens. 2002, 68, 51–63. [Google Scholar]
- Neyland, M.G.; Jarman, S.J. Early impacts of harvesting and burning disturbances on vegetation communities in the Warra silvicultural systems trial, Tasmania, Australia. Aust. J. Bot. 2011, 59, 701–712. [Google Scholar] [CrossRef]
- Wardlaw, T.J.; Grove, S.J.; Hingston, A.B.; Balmer, J.M.; Forster, L.G.; Musk, R.A.; Read, S.M. Responses of flora and fauna in wet eucalypt production forest to the intensity of disturbance in the surrounding landscape. For. Ecol. Manag. 2018, 409, 694–706. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.-F.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, T.; Skidmore, A.K.; Holzwarth, S.; Heiden, U.; Heurich, M. Mapping individual silver fir trees using hyperspectral and LiDAR data in a Central European mixed forest. Int. J. Appl. Earth Obs. Geoinf. 2021, 98, 102311. [Google Scholar] [CrossRef]
- Ehlers, S.; Saarela, S.; Lindgren, N.; Lindberg, E.; Nyström, M.; Persson, H.; Olsson, H.; Ståhl, G. Assessing Error Correlations in Remote Sensing-Based Estimates of Forest Attributes for Improved Composite Estimation. Remote Sens. 2018, 10, 667. [Google Scholar] [CrossRef]
- Kuester, M. Radiometric Use of WorldView-3 Imagery-Technical Note; DigitalGlobe: Longmont, CO, USA, 2016; pp. 1–12. [Google Scholar]
- Flood, N. Continuity of reflectance data between Landsat-7 ETM+ and Landsat-8 OLI, for both top-of-atmosphere and surface reflectance: A study in the Australian landscape. Remote Sens. 2014, 6, 7952. [Google Scholar] [CrossRef]
- Thuillier, G.; Hersé, M.; Labs, D.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.C.; Mandel, H. The solar spectral irradiance from 200 to 2400 nm as measured by the SOLSPEC Spectrometer from the Atlas and Eureca Missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar] [CrossRef]
- Travis, M.R.; Elsner, G.H.; Iverson, W.D.; Jonnson, C.G. VIEWIT: Computation of Seen Areas, Slope, and Aspect for Landuse Planning; USDA Forest Service, General Technical Report, PSW-1111975, 70; Pacific Southwest Forest and Range Exp. Stn.: Berkeley, CA, USA; Forest Service, U.S. Department of Agriculture: Berkeley, CA, USA, 1975; p. 67. [Google Scholar]
- Kiss, R. Determination of drainage network in digital elevation models, utilities and limitations. J. Hung. Geomath. 2004, 2, 16–29. [Google Scholar]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Zhou, F.; Ma, G.; Xie, C.; Zhang, Y.; Xiao, Z. Application of Compound Terrain Factor LSW in Vegetation Cover Evaluation. Appl. Sci. 2023, 13, 11806. [Google Scholar] [CrossRef]
- Wilson, M.F.J.; O’Connell, B.; Brown, C.; Guinan, J.C.; Grehan, A.J. Multiscale terrain analysis of multibeam bathymetry data for habitat mapping on the continental slope. Mar. Geod. 2007, 30, 3–35. [Google Scholar] [CrossRef]
- Shary, P. Land surface in gravity points classification by a complete system of curvatures. Math. Geol. 1995, 27, 373–390. [Google Scholar] [CrossRef]
- Riley, S.; Degloria, S.; Elliot, S.D. A terrain ruggedness index that quantifies topographic heterogeneity. Int. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Jacoby, B.; Peterson, E.; Dogwiler, T. Identifying the Stream Erosion Potential of Cave Levels in Carter Cave State Resort Park, Kentucky, USA. J. Geogr. Inf. Syst. 2011, 3, 323–333. [Google Scholar] [CrossRef]
- Gessler, P.E.; Moore, I.D.; McKenzie, N.J.; Ryan, P.J. Soil-landscape modelling and spatial prediction of soil attributes. Int. J. Geogr. Inf. Syst. 1995, 9, 421–432. [Google Scholar] [CrossRef]
- Lukovic, J.; Bajat, B.; Kilibarda, M.; Filipovic, D. High resolution grid of potential incoming solar radiation for Serbia. Therm. Sci. 2015, 19, 427–435. [Google Scholar] [CrossRef]
- Dobrowski, S.Z.; Safford, H.D.; Cheng, Y.B.; Ustin, S.L. Mapping mountain vegetation using species distribution modeling, image-based texture analysis, and object-based classification. Appl. Veg. Sci. 2008, 11, 499–508. [Google Scholar] [CrossRef]
- Ge, S.; Carruthers, R.; Gong, P.; Herrera, A. Texture analysis for mapping Tamarix parviflora using aerial photographs along the Cache Creek, California. Environ. Monit. Assess. 2006, 114, 65–83. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Darra, N.; Espejo-Garcia, B.; Psiroukis, V.; Psomiadis, E.; Fountas, S. Spectral bands vs. vegetation indices: An AutoML approach for processing tomato yield predictions based on Sentinel-2 imagery. Smart Agric. Technol. 2025, 10, 100805. [Google Scholar] [CrossRef]
- Anand, S.; Kumar, H.; Kumar, P.; Kumar, M. Analyzing landscape changes and their relationship with land surface temperature and vegetation indices using remote sensing and AI techniques. Geosci. Lett. 2025, 12, 7. [Google Scholar] [CrossRef]
- Rouse, J.; Haas, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the great plains with ERTS (Earth Resources Technology Satellite). In Proceedings of the Third ERTS Symposium, Goddard Space Flight Center, Greenbelt, MD, USA, 10–14 December 1973; pp. 309–317. [Google Scholar]
- Taddeo, S.; Dronova, I.; Depsky, N. Spectral vegetation indices of wetland greenness: Responses to vegetation structure, composition, and spatial distribution. Remote Sens. Environ. 2019, 234, 111467. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote sensing of chlorophyll concentration in higher plant leaves. Adv. Space Res. 1998, 22, 689–692. [Google Scholar] [CrossRef]
- Crippen, R.E. Calculating the vegetation index faster. Remote Sens. Environ. 1990, 34, 71–73. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Breon, F.-M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Goel, N.S.; Qin, W. Influences of canopy architecture on relationships between various vegetation indices and LAI and Fpar: A computer simulation. Remote Sens. Rev. 1994, 10, 309–347. [Google Scholar] [CrossRef]
- Yang, Z.; Willis, P.; Mueller, R. Impact of band-ratio enhanced AWIFS image on crop classification accuracy. In Proceedings of the Pecora 17—The Future of Land Imaging…Going Operational, Denver, CO, USA, 18–20 November 2008; p. 11. [Google Scholar]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Ghazali, N.N.; Saraf, N.M.; Rasam, A.R.A.; Othman, A.N.; Salleh, S.A.; Saad, N.M. Forest Fire Severity Level Using dNBR Spectral Index. Rev. Int. Geomat. 2025, 34, 89–101. [Google Scholar] [CrossRef]
- Iqbal, I.A.; Musk, R.A.; Osborn, J.; Stone, C.; Lucieer, A. A comparison of area-based forest attributes derived from airborne laser scanner, small-format and medium-format digital aerial photography. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 231–241. [Google Scholar] [CrossRef]
- Lukman, A.F.; Mohammed, S.; Olaluwoye, O.; Farghali, R.A. Handling Multicollinearity and Outliers in Logistic Regression Using the Robust Kibria–Lukman Estimator. Axioms 2024, 14, 19. [Google Scholar] [CrossRef]
- Shrestha, N. Detecting Multicollinearity in Regression Analysis. Am. J. Appl. Math. Stat. 2020, 8, 39–42. [Google Scholar] [CrossRef]
- Imdadullah, M.; Aslam, M.; Altaf, S. mctest: An R package for detection of collinearity among regressors. R J. 2016, 8, 495–505. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Li, C.; Liu, Z. Forest aboveground biomass estimation using Landsat 8 and Sentinel-1A data with machine learning algorithms. Sci. Rep. 2020, 10, 9952. [Google Scholar] [CrossRef]
- Abonazel, M.R. A New Biased Estimation Class to Combat the Multicollinearity in Regression Models: Modified Two--Parameter Liu Estimator. Comput. J. Math. Stat. Sci. 2025, 4, 316–347. [Google Scholar] [CrossRef]
- Jaskierniak, D.; Lane, P.N.J.; Robinson, A.; Lucieer, A. Extracting LiDAR indices to characterise multilayered forest structure using mixture distribution functions. Remote Sens. Environ. 2011, 115, 573–585. [Google Scholar] [CrossRef]
- Martinuzzi, S.; Vierling, L.A.; Gould, W.A.; Falkowski, M.J.; Evans, J.S.; Hudak, A.T.; Vierling, K.T. Mapping snags and understory shrubs for a LiDAR-based assessment of wildlife habitat suitability. Remote Sens. Environ. 2009, 113, 2533–2546. [Google Scholar] [CrossRef]
- Campbell, M.J.; Dennison, P.E.; Hudak, A.T.; Parham, L.M.; Butler, B.W. Quantifying understory vegetation density using small-footprint airborne LiDAR. Remote Sens. Environ. 2018, 215, 330–342. [Google Scholar] [CrossRef]
- Criminisi, A.; Shotton, J.; Konukoglu, E. Decision Forests for Classification, Regression, Density Estimation, Manifold Learning and Semi-Supervised Learning; Microsoft Research Technical Report TR-2011-114; Microsoft: Cambridge, UK, 2011; p. 151. [Google Scholar]
- Kemppinen, J.; Niittynen, P.; Riihimäki, H.; Luoto, M. Modelling soil moisture in a high-latitude landscape using LiDAR and soil data. Earth Surf. Process. Landf. 2018, 43, 1019–1031. [Google Scholar] [CrossRef]
- Wang, M.; Zheng, Y.; Huang, C.; Meng, R.; Pang, Y.; Jia, W.; Zhou, J.; Huang, Z.; Fang, L.; Zhao, F. Assessing Landsat-8 and Sentinel-2 spectral-temporal features for mapping tree species of northern plantation forests in Heilongjiang Province, China. For. Ecosyst. 2022, 9, 100032. [Google Scholar] [CrossRef]
- van Galen, L.G.; Jordan, G.J.; Musk, R.A.; Beeton, N.J.; Wardlaw, T.J.; Baker, S.C. Quantifying floristic and structural forest maturity: An attribute-based method for wet eucalypt forests. J. Appl. Ecol. 2018, 55, 1668–1681. [Google Scholar] [CrossRef]
- Astola, H.; Häme, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 imagery for forest variable prediction in boreal region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Freeman, E.A.; Moisen, G.G.; Coulston, J.W.; Wilson, B.T. Random forests and stochastic gradient boosting for predicting tree canopy cover: Comparing tuning processes and model performance. Can. J. For. Res. 2015, 46, 323–339. [Google Scholar] [CrossRef]
- Valbuena, R.; Hernando, A.; Manzanera, J.A.; Görgens, E.B.; Almeida, D.R.A.; Silva, C.A.; García-Abril, A. Evaluating observed versus predicted forest biomass: R-squared, index of agreement or maximal information coefficient? Eur. J. Remote Sens. 2019, 52, 345–358. [Google Scholar] [CrossRef]
- Mohammed, K.; Kpienbaareh, D.; Wang, J.; Goldblum, D.; Luginaah, I.; Lupafya, E.; Dakishoni, L. Synthesizing Local Capacities, Multi-Source Remote Sensing and Meta-Learning to Optimize Forest Carbon Assessment in Data-Poor Regions. Remote Sens. 2025, 17, 289. [Google Scholar] [CrossRef]
- Ling, Q.; Chen, Y.; Feng, Z.; Pei, H.; Wang, C.; Yin, Z.; Qiu, Z. Monitoring Canopy Height in the Hainan Tropical Rainforest Using Machine Learning and Multi-Modal Data Fusion. Remote Sens. 2025, 17, 966. [Google Scholar] [CrossRef]
- Nagelkerke, N.J.D. A Note on a General Definition of the Coefficient of Determination. Biometrika 1991, 78, 691–692. [Google Scholar] [CrossRef]
- Sapra, R.L. Using R2 with caution. Curr. Med. Res. Pract. 2014, 4, 130–134. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing, Version 3.4.1; R Foundation for Statistical Computing: Vienna, Austria, 2017. Available online: https://www.r-project.org/ (accessed on 20 July 2018).
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Tuszynski, J. Tools: Moving Window Statistics, GIF, Base64, ROC AUC, etc. R Package Version 1.18.0. Available online: https://cran.r-project.org/package=caTools (accessed on 15 March 2020).
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. VSURF: An R package for variable selection using random forests. R J. 2015, 7, 19–33. [Google Scholar] [CrossRef]
- Yadav, B.K.V.; Lucieer, A.; Jordan, G.J.; Baker, S.C. Using topographic attributes to predict the density of vegetation layers in a wet eucalypt forest. Aust. For. 2022, 85, 25–37. [Google Scholar] [CrossRef]
- White, R.J. Searching for Rainforest Understorey in Wet Eucalyptus Forest. Bachelor’s Thesis, School of Biological Sciences, University of Tasmania, Hobart, Australia, 2017. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Investigating the robustness of the new Landsat-8 Operational Land Imager derived texture metrics in estimating plantation forest aboveground biomass in resource constrained areas. ISPRS J. Photogramm. Remote Sens. 2015, 108, 12–32. [Google Scholar] [CrossRef]
- Latifi, H.; Nothdurft, A.; Straub, C.; Koch, B. Modelling stratified forest attributes using optical/LiDAR features in a central European landscape. Int. J. Digit. Earth 2012, 5, 106–132. [Google Scholar] [CrossRef]
- Azaele, S.; Cornell, S.J.; Kunin, W.E. Downscaling species occupancy from coarse spatial scales. Ecol. Appl. 2012, 22, 1004–1014. [Google Scholar] [CrossRef] [PubMed]
- Munsamy, R.; Gebreslasie, M.; Peerbhay, K.; Ismail, R. Modelling the effect of terrain variability in even-aged Eucalyptus species using LiDAR-derived DTM variables. S. Afr. J. Geomat. 2020, 9, 118–135. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping global forest canopy height through integration of GEDI and Landsat data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Mäyrä, J.; Keski-Saari, S.; Kivinen, S.; Tanhuanpää, T.; Hurskainen, P.; Kullberg, P.; Poikolainen, L.; Viinikka, A.; Tuominen, S.; Kumpula, T.; et al. Tree species classification from airborne hyperspectral and LiDAR data using 3D convolutional neural networks. Remote Sens. Environ. 2021, 256, 112322. [Google Scholar] [CrossRef]
- Wallner, A.; Elatawneh, A.; Knoke, T.; Schneider, T. Estimation of forest structural information using RapidEye satellite data. For. Int. J. For. Res. 2014, 88, 96–107. [Google Scholar] [CrossRef]
- Halperin, J.; LeMay, V.; Coops, N.; Verchot, L.; Marshall, P.; Lochhead, K. Canopy cover estimation in miombo woodlands of Zambia: Comparison of Landsat 8 OLI versus RapidEye imagery using parametric, nonparametric, and semiparametric methods. Remote Sens. Environ. 2016, 179, 170–182. [Google Scholar] [CrossRef]
- Nasiri, V.; Darvishsefat, A.A.; Arefi, H.; Griess, V.C.; Sadeghi, S.M.M.; Borz, S.A. Modeling Forest Canopy Cover: A Synergistic Use of Sentinel-2, Aerial Photogrammetry Data, and Machine Learning. Remote Sens. 2022, 14, 1453. [Google Scholar] [CrossRef]
- Chen, L.; Ren, C.; Zhang, B.; Wang, Z.; Liu, M.; Man, W.; Liu, J. Improved estimation of forest stand volume by the integration of GEDI LiDAR data and multi-sensor imagery in the Changbai Mountains Mixed forests Ecoregion (CMMFE), northeast China. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102326. [Google Scholar] [CrossRef]
- Yadav, B.K.V.; Lucieer, A.; Baker, S.C.; Jordan, G.J. Tree crown segmentation and species classification in a wet eucalypt forest from airborne hyperspectral and LiDAR data. Int. J. Remote Sens. 2021, 42, 7952–7977. [Google Scholar] [CrossRef]
- Soh, L.-K.; Tsatsoulis, C. Texture analysis of SAR sea ice imagery using gray level co-occurrence matrices. IEEE Trans. Geosci. Remote Sens. 1999, 37, 780–795. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Marsett, R.C.; Qi, J.; Heilman, P.; Biedenbender, S.H.; Carolyn Watson, M.; Amer, S.; Weltz, M.; Goodrich, D.; Marsett, R. Remote sensing for grassland management in the arid southwest. Rangel. Ecol. Manag. 2006, 59, 530–540. [Google Scholar] [CrossRef]
- Hagen, S.C.; Heilman, P.; Marsett, R.; Torbick, N.; Salas, W.; van Ravensway, J.; Qi, J. Mapping total vegetation cover across western rangelands with moderate-resolution imaging spectroradiometer data. Rangel. Ecol. Manag. 2012, 65, 456–467. [Google Scholar] [CrossRef]
- Torbick, N.; Ledoux, L.; Salas, W.; Zhao, M. Regional mapping of plantation extent using multisensor imagery. Remote Sens. 2016, 8, 236. [Google Scholar] [CrossRef]
- Key, C.H.; Benson, N.C. Landscape assessment: Ground measure of severity, the composite burn index; and remote sensing of severity, the normalized burn ratio. In FIREMON: Fire Effects Monitoring and Inventory System, RMRS-GTR-164 ed.; Lutes, D.C., Keane, R.E., Caratti, J.F., Key, C.H., Benson, N.C., Sutherland, S., Gangi, L.J., Eds.; USDA Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 2006; p. 56. [Google Scholar]
- Ji, L.; Zhang, L.; Wylie, B.; Rover, J. On the terminology of the spectral vegetation index (NIR − SWIR)/(NIR + SWIR). Int. J. Remote Sens. 2011, 32, 6901–6909. [Google Scholar] [CrossRef]
- Chen, D.; Huang, J.; Jackson, T.J. Vegetation water content estimation for corn and soybeans using spectral indices derived from MODIS near- and short-wave infrared bands. Remote Sens. Environ. 2005, 98, 225–236. [Google Scholar] [CrossRef]
- Zhang, N.; Hong, Y.; Qin, Q.; Zhu, L. Evaluation of the visible and shortwave infrared drought index in China. Int. J. Disaster Risk Sci. 2013, 4, 68–76. [Google Scholar] [CrossRef]
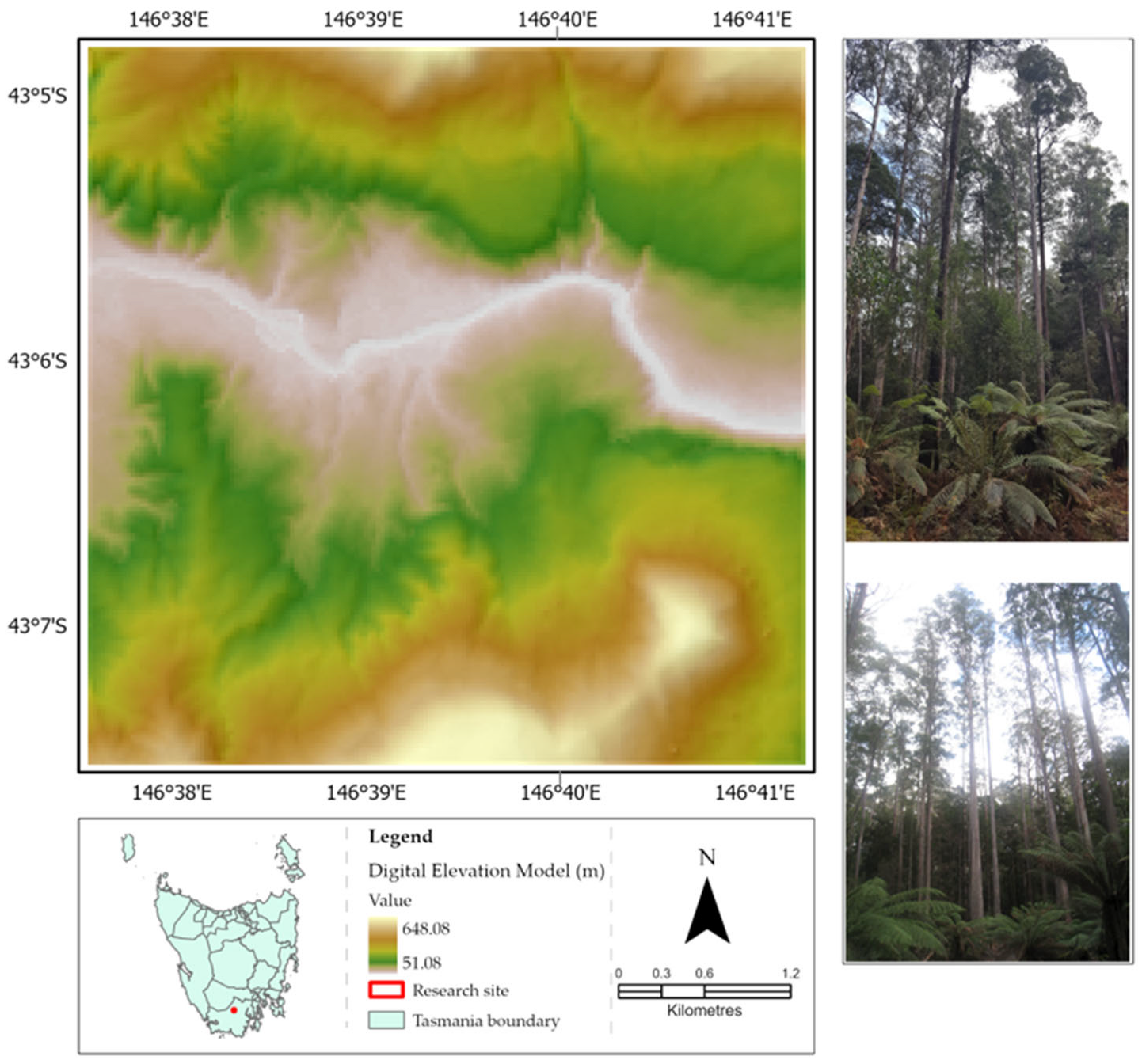
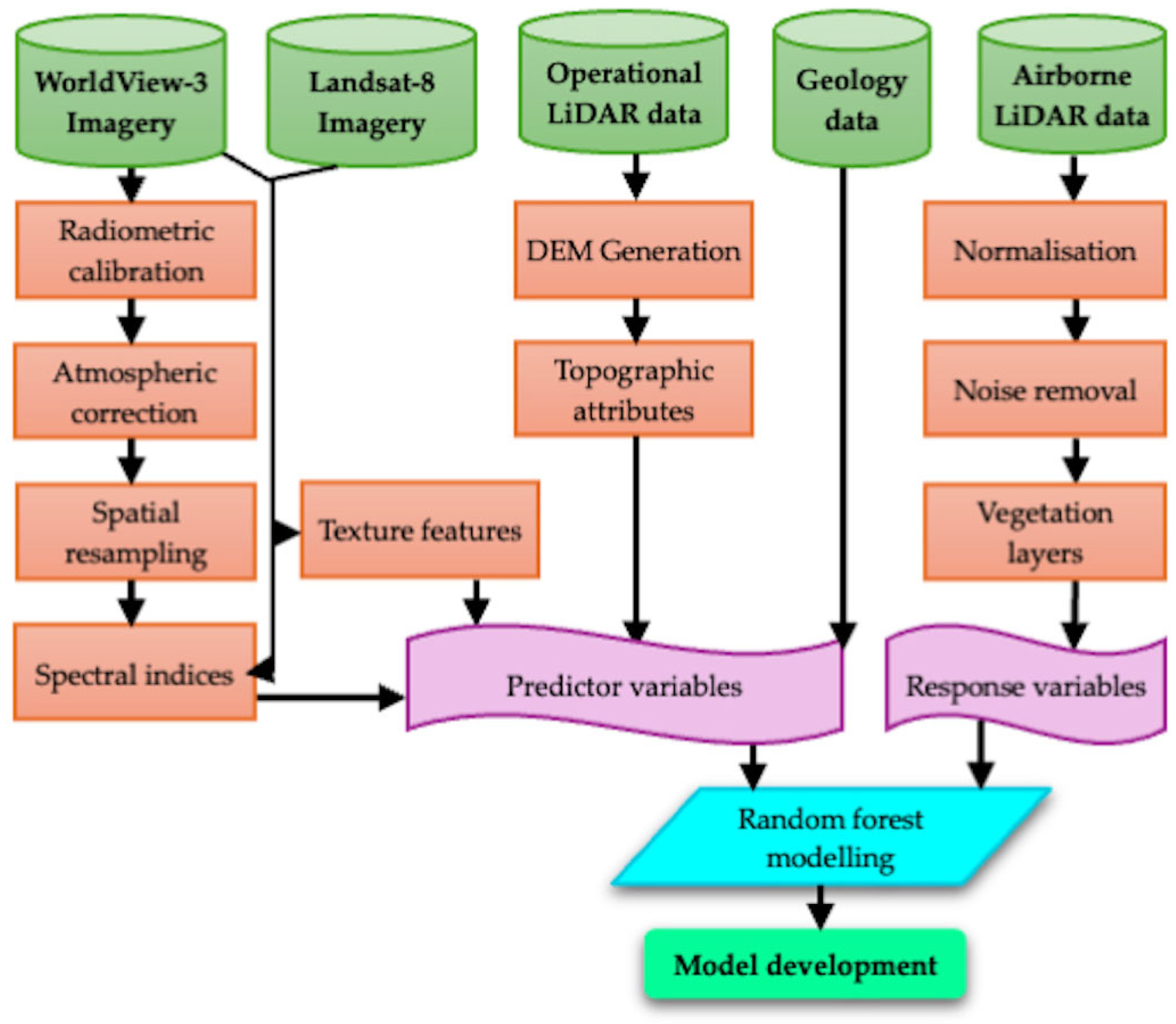

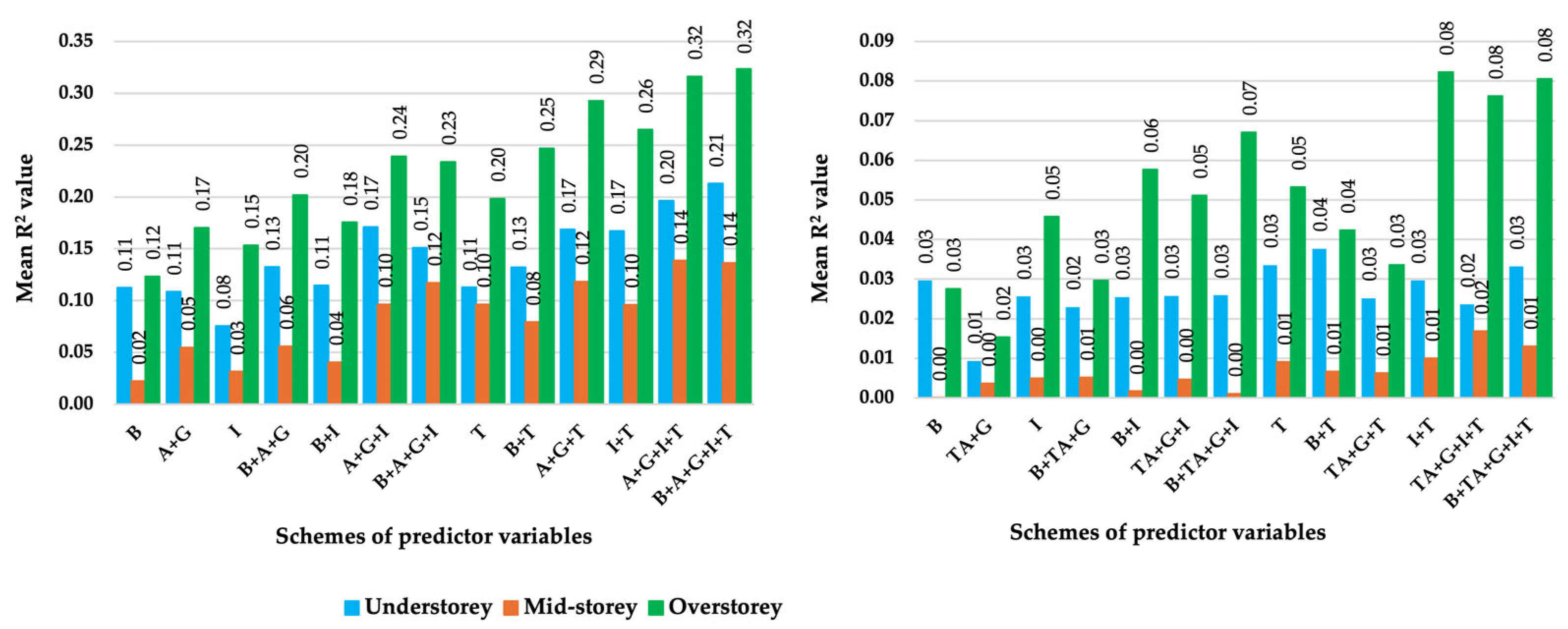
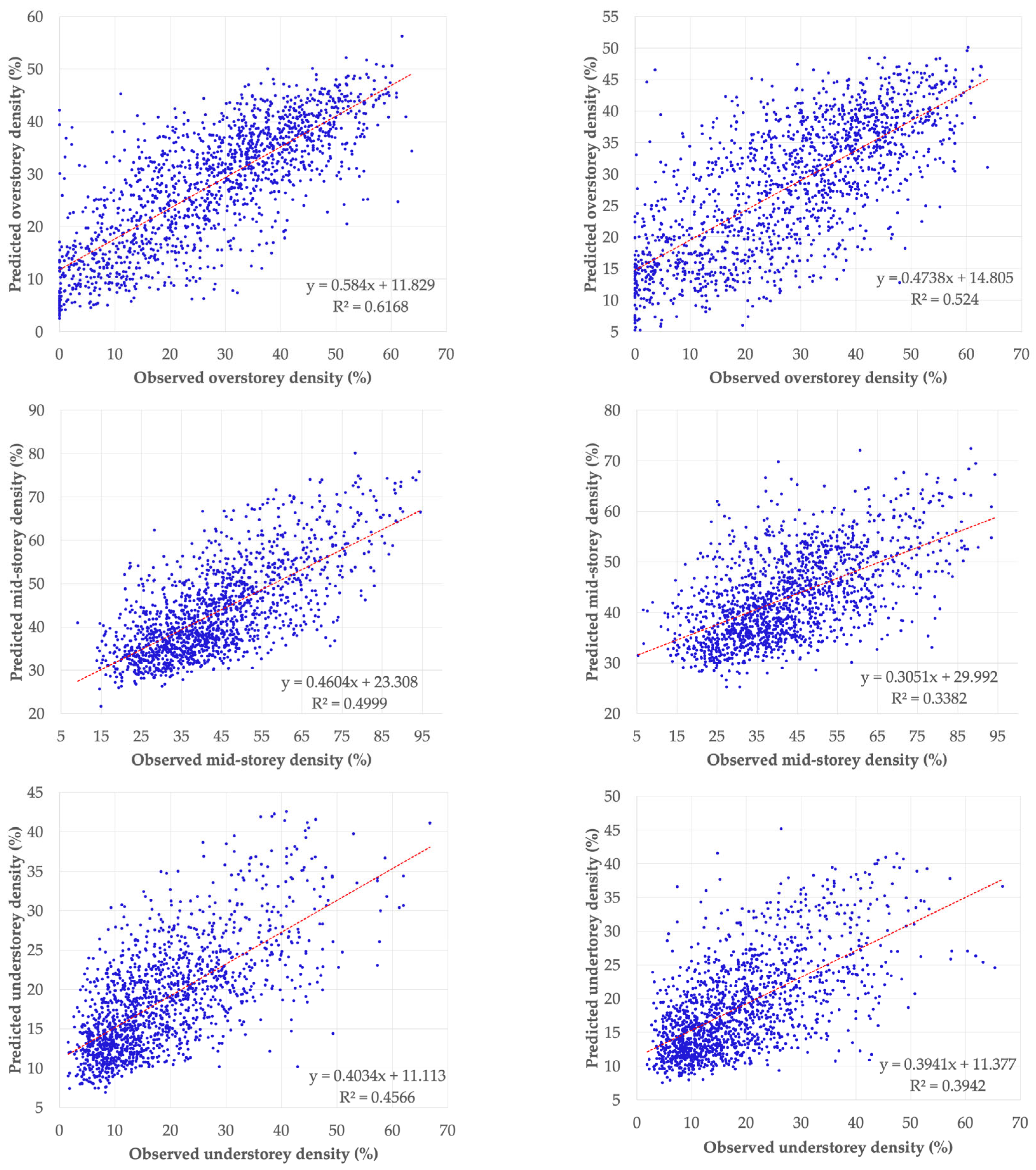
| Specification Item | WorldView-3 Imagery | Landsat-8 Imagery |
|---|---|---|
| Date of acquisition | 5 October 2015 | 21 October 2014 |
| Spatial resolution | 1.60 m (VNIR bands) 7.50 m (SWIR bands) | 30 m (VNIR and SWIR bands) |
| Sun azimuth | 42.400 | 48.800454560 |
| Sun Elevation | 43.700 | 48.182282610 |
| Product Type Level | “Standard” LV2A | OLI_TIRS_L1TP |
| Bands (In Nanometres) | Coastal = 427.40 Blue = 481.90 Green = 547.10 Yellow = 604.30 Red = 660.10 Red Edge = 722.70 NIR1 = 824.00 NIR2 = 913.60 SWIR1 = 1209.10 SWIR2 = 1571.60 SWIR3 = 1661.10 SWIR4 = 1729.50 SWIR5 = 2163.70 SWIR6 = 2202.20 SWIR7 = 2259.30 SWIR8 = 2329.20 | Coastal = 442.96 Blue = 482.04 Green = 561.41 Red = 654.59 NIR = 864.67 SWIR 1 = 1608.86 SWIR 2 = 2200.73 |
| Band | Gain Value | Offset Value | Solar Irradiance Value (W − M−2 − μm−1) [73] |
|---|---|---|---|
| Coastal | 0.863 | −7.154 | 1757.89 |
| Blue | 0.905 | −4.189 | 2004.61 |
| Green | 0.907 | −3.287 | 1830.18 |
| Yellow | 0.938 | −1.816 | 1712.07 |
| Red | 0.945 | −1.350 | 1535.33 |
| Red-Edge | 0.980 | −2.617 | 1348.08 |
| NIR 1 | 0.982 | −3.752 | 1055.94 |
| NIR 2 | 0.954 | −1.507 | 858.77 |
| SWIR 1 | 1.160 | −4.479 | 479.019 |
| SWIR 2 | 1.184 | −2.248 | 263.797 |
| SWIR 3 | 1.173 | −1.806 | 225.283 |
| SWIR 4 | 1.187 | −1.507 | 197.552 |
| SWIR 5 | 1.286 | −0.622 | 90.4178 |
| SWIR 6 | 1.336 | −0.605 | 85.0642 |
| SWIR 7 | 1.340 | −0.423 | 76.9507 |
| SWIR 8 | 1.392 | −0.302 | 68.0988 |
| Landsat 30 m | Resampled WorldView 30 m | Resampled WorldView 7.5 m | WorldView 1.6 m | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset Scheme | Understorey | Mid-Storey | Overstorey | Understorey | Mid-Storey | Overstorey | Understorey | Mid-Storey | Overstorey | Understorey | Mid-Storey | Overstorey |
| Bands only | 0.151 | 0.243 | 0.439 | 0.319 | 0.217 | 0.396 | 0.112 | 0.022 | 0.123 | 0.030 | 0.000 | 0.028 |
| Topographic attributes only | 0.322 | 0.226 | 0.390 | 0.350 | 0.230 | 0.438 | 0.108 | 0.055 | 0.170 | 0.009 | 0.004 | 0.015 |
| Indices only | 0.165 | 0.232 | 0.478 | 0.294 | 0.191 | 0.437 | 0.075 | 0.031 | 0.153 | 0.026 | 0.005 | 0.046 |
| Bands, topographic attributes and geology | 0.334 | 0.359 | 0.573 | 0.382 | 0.279 | 0.482 | 0.132 | 0.056 | 0.202 | 0.023 | 0.005 | 0.030 |
| Bands and indices | 0.203 | 0.237 | 0.455 | 0.354 | 0.253 | 0.481 | 0.114 | 0.041 | 0.175 | 0.026 | 0.002 | 0.058 |
| Topographic attributes, geology and indices | 0.399 | 0.367 | 0.588 | 0.340 | 0.329 | 0.524 | 0.171 | 0.096 | 0.239 | 0.026 | 0.005 | 0.051 |
| Bands, topographic attributes, geology and indices | 0.366 | 0.366 | 0.580 | 0.374 | 0.357 | 0.547 | 0.151 | 0.117 | 0.234 | 0.026 | 0.001 | 0.067 |
| Textures only | 0.254 | 0.348 | 0.471 | 0.370 | 0.335 | 0.474 | 0.113 | 0.096 | 0.198 | 0.034 | 0.009 | 0.053 |
| Bands and textures | 0.282 | 0.412 | 0.560 | 0.361 | 0.347 | 0.482 | 0.132 | 0.079 | 0.247 | 0.038 | 0.007 | 0.042 |
| Topographic attributes, geology and textures | 0.389 | 0.419 | 0.561 | 0.279 | 0.263 | 0.400 | 0.169 | 0.118 | 0.293 | 0.025 | 0.006 | 0.034 |
| Indices and textures | 0.270 | 0.416 | 0.560 | 0.362 | 0.380 | 0.505 | 0.167 | 0.096 | 0.265 | 0.030 | 0.010 | 0.082 |
| Topographic attributes, geology, indices and textures | 0.436 | 0.457 | 0.630 | 0.352 | 0.255 | 0.461 | 0.196 | 0.138 | 0.316 | 0.024 | 0.017 | 0.076 |
| Bands, topographic attributes, geology, indices and textures | 0.445 | 0.449 | 0.654 | 0.394 | 0.296 | 0.535 | 0.213 | 0.136 | 0.324 | 0.033 | 0.013 | 0.081 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yadav, B.K.V.; Lucieer, A.; Jordan, G.J.; Baker, S.C. Assessing the Robustness of Multispectral Satellite Imagery with LiDAR Topographic Attributes and Ancillary Data to Predict Vertical Structure in a Wet Eucalypt Forest. Remote Sens. 2025, 17, 1733. https://doi.org/10.3390/rs17101733
Yadav BKV, Lucieer A, Jordan GJ, Baker SC. Assessing the Robustness of Multispectral Satellite Imagery with LiDAR Topographic Attributes and Ancillary Data to Predict Vertical Structure in a Wet Eucalypt Forest. Remote Sensing. 2025; 17(10):1733. https://doi.org/10.3390/rs17101733
Chicago/Turabian StyleYadav, Bechu K. V., Arko Lucieer, Gregory J. Jordan, and Susan C. Baker. 2025. "Assessing the Robustness of Multispectral Satellite Imagery with LiDAR Topographic Attributes and Ancillary Data to Predict Vertical Structure in a Wet Eucalypt Forest" Remote Sensing 17, no. 10: 1733. https://doi.org/10.3390/rs17101733
APA StyleYadav, B. K. V., Lucieer, A., Jordan, G. J., & Baker, S. C. (2025). Assessing the Robustness of Multispectral Satellite Imagery with LiDAR Topographic Attributes and Ancillary Data to Predict Vertical Structure in a Wet Eucalypt Forest. Remote Sensing, 17(10), 1733. https://doi.org/10.3390/rs17101733







