An Ultra-Wide Swath Synthetic Aperture Radar Imaging System via Chaotic Frequency Modulation Signals and a Random Pulse Repetition Interval Variation Strategy
Abstract
1. Introduction
- (1)
- Replacing the chirp signal, chaotic FM signals are transmitted to avoid mutual interferences from the raw data of near-range and far-range scatters to achieve ultra-wide swath observation. Chaotic FM signals are time-variant transmitting signals and have different matched filters so that the raw data of near-range and far-range scatters after signal processing avoid mutual interferences in ultra-wide imaging. The alternative, transmitting signals, brings superior imaging performance with an improved mean peak sidelobe ratio (PSLR) and preserved resolution, assuming that the chaotic map obeys the uniform distribution.
- (2)
- An optimized random PRI variation strategy is proposed to keep the PRI variation nonlinear so that the blind ranges are discontinuously and nonuniformly distributed on the whole swath. To achieve azimuth focusing under nonuniform sampling, a reconstruction algorithm based on the sparsity Bayesian learning (SBL) is proposed in the optimized random PRI variation strategy. After range compression based on the matched filtering (MF) method, range cell migration correction (RCMC) is accomplished by interpolating and summing up. During the RCMC, an innovative back-projection technique is adopted to achieve signal enhancement. Instead of resampling the nonuniform sampling signal into a uniform grid, an observation model is established and reconstructed using SBL to achieve azimuthal compression. Our proposed sampling strategy and reconstruction algorithm take full advantage of nonuniform sampling to suppress the high sidelobes due to the periodicity of the lost pulses and improve reconstruction performance under low oversampling or even sub-Nyquist sampling.
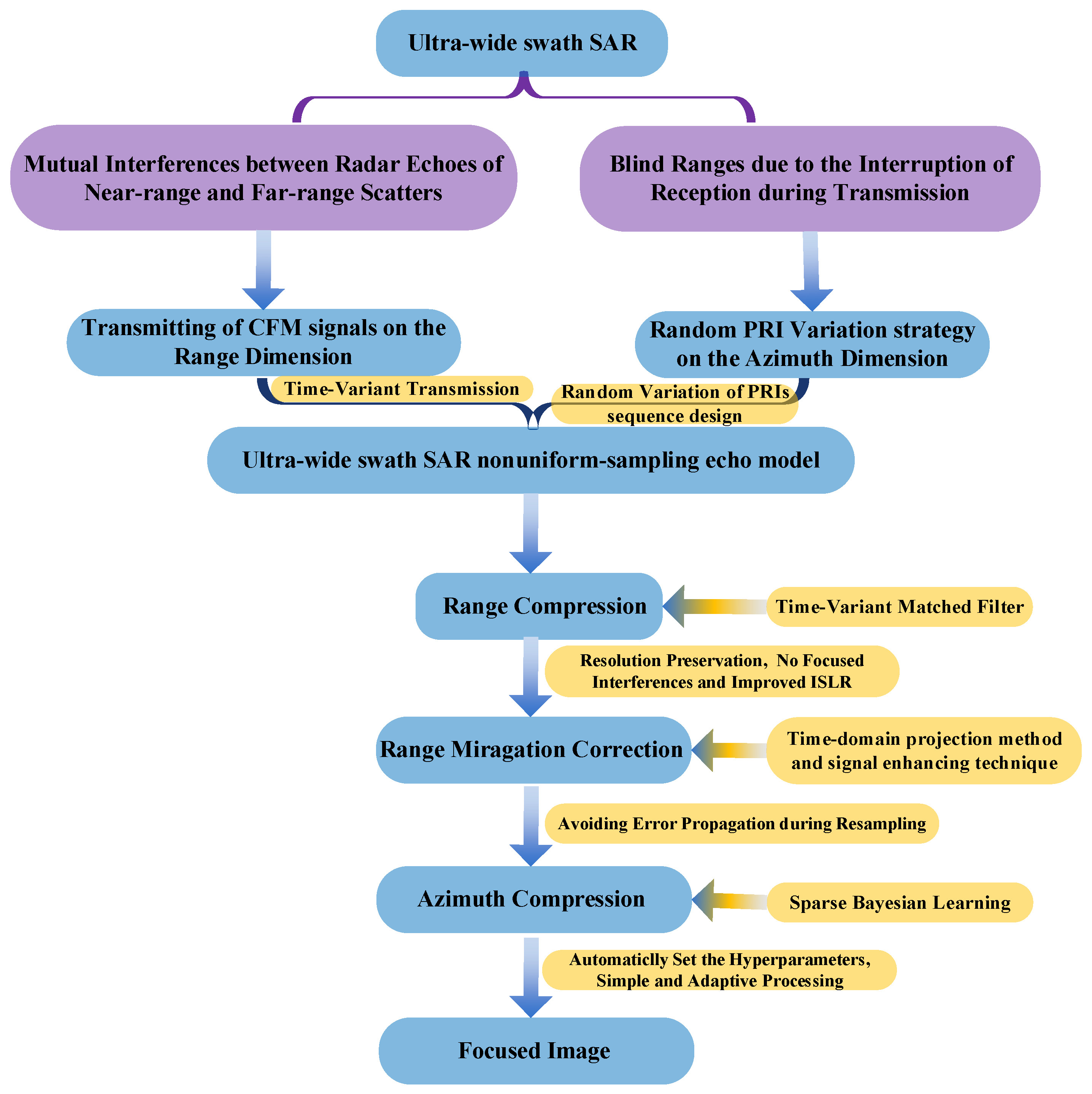
2. Materials and Methods
2.1. Limitation of Conventional SAR Systems
2.2. Ultra-Wide Swath SAR System Via Chaotic FM Signals and a Random PRI Variation Strategy
2.2.1. Chaotic FM Signals
2.2.2. Random PRI Variation Strategy
2.2.3. System Analysis
- (1)
- System Performance after Range Compression
- (2)
- Integral Sidelobe Ratio (ISLR) Performance Along Range After Azimuth Compression
2.3. Imaging Algorithm for the Proposed Ultra-Wide Swath SAR System
2.3.1. Range Compression Based on Matched Filtering
2.3.2. Time Domain RCMC for Random Sampling
2.3.3. Azimuth Reconstruction Based on SBL
| Algorithm 1 SBL Algorithm for Azimuth Compression |
| Input: raw data , serial of system parameters, e.g., wavelength; Initialization: , , , ; Iterations:
Terminal the iteration
|
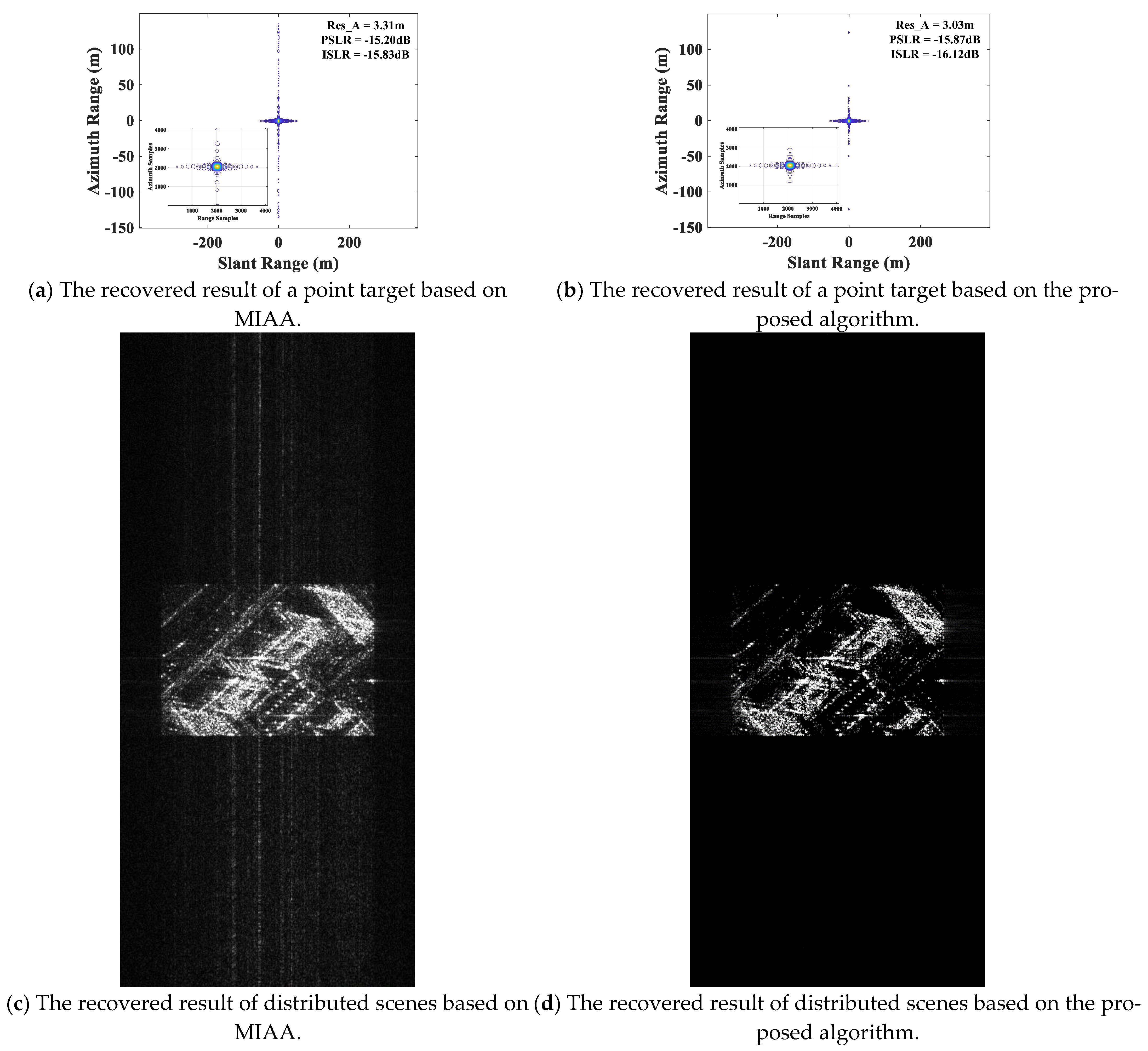
3. Results
3.1. Imaging Simulations with Transmission of Chaotic FM Signals
- (1)
- Resolution Preservation
- (2)
- Range Ambiguity Suppression
3.2. Imaging Simulations with Random PRI Variation Strategy
3.3. Ultra-Wide Swath Imaging System Based on Chaotic FM Signals in the Presence of a PRI Variation Strategy
4. Discussion
- (1)
- Regarding the technologies such as DBF and SCORE
- (2)
- Regarding the PRI sequence optimization
- (3)
- Regarding the optimal processing for low oversampling ratios
- (4)
- Regarding the computational cost
- (a)
- One real multiplication and addition operation both take 1 floating point operations per second (FLOPS), and one complex multiplication and addition operation take 6 and 2 FLOPS, respectively.
- (b)
- The numbers of range cells and azimuth pulses are denoted by and , respectively. The scene is divided into and grids along range and azimuth, respectively.
- (c)
- One -point fast Fourier transform (FFT) requires times complex multiplication and times complex addition, so the total computational cost is FLOPS.
- (d)
- -point complex interpolation requires times complex multiplications and times complex additions, so the total computational cost of one single pixel point is FLOPS.For the traditional range Doppler (RD) imaging algorithm, consider the following:
- a.
- Parameter extraction
- b.
- Clutter suppression
- c.
- BCS Reconstruction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B

Appendix C
References
- Cumming, I.; Wong, F. Digital Signal Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2004. [Google Scholar]
- Dong, B.; Li, G.; Zhang, Q. High-resolution and wide-swath imaging of spaceborne SAR via random PRF variation constrained by the coverage diagram. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5241016. [Google Scholar] [CrossRef]
- Yang, X.; Li, G.; Sun, J.; Liu, Y.; Xia, X. High-resolution and wide-swath imaging via Poisson disk sampling and iterative shrinkage thresholding. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4692–4704. [Google Scholar] [CrossRef]
- Guo, H.; Wang, Z.; Li, Z.; Zhang, Q.; Liu, L.; Tang, F. Wide-swath ocean current measurement based on MIMO along-track interferometry SAR. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5221216. [Google Scholar] [CrossRef]
- Trumpf, S.; Prats-Iraola, P.; Moreira, A. Along-track deformation retrieval performance with the ROSE-L multi-channel SAR system using two-look ScanSAR. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5208815. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, B.; Perrie, W.; Zheng, G.; Yang, J.; Fang, H. Assessment of thermal noise effect on wind speed retrieval accuracy using Sentinel-1 cross-polarized TOPSAR images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4208011. [Google Scholar] [CrossRef]
- Castillo, J.P.N.; Scheiber, R.; Jäger, M.; Moreira, A. Subaperture motion-adaptive reconstruction techniques for digital beamforming airborne SAR. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5229518. [Google Scholar]
- Li, B.; Zhao, Q.; Zhang, Y.; Liang, Y.; Wang, W.; Cai, Y. An advanced sparse multichannel system for spaceborne DBF-SAR. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5211513. [Google Scholar] [CrossRef]
- Wang, R.; Deng, Y.; Wang, W.; Zhao, Q.; Zhang, Y.; Chen, Z. A novel adaptive digital beamforming method based on beam-space phase-center cross correlation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5212213. [Google Scholar] [CrossRef]
- Gerhard, K. MIMO-SAR: Opportunities and pitfalls. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2628–2645. [Google Scholar]
- Zhang, M.; Liao, G.; Xu, J.; Lan, L.; Zhu, S.; Xing, M. High-resolution and wide-swath imaging based on multifrequency pulse diversity and DPCA technique. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4502505. [Google Scholar] [CrossRef]
- Zhang, M.; Liao, G.; Xu, J.; He, X.; Liu, Q.; Lan, L.; Li, S. High-resolution and wide-swath SAR imaging with sub-band frequency diverse array. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 172–183. [Google Scholar] [CrossRef]
- Wang, J.; Chen, L.; Liang, X.; Li, K. Implementation of the OFDM chirp waveform on MIMO SAR systems. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5218–5228. [Google Scholar] [CrossRef]
- Blunt, S.D.; Mokole, E.L. Overview of radar waveform diversity. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 2–42. [Google Scholar] [CrossRef]
- Vespe, M.; Jones, G.; Baker, C. Lessons for radar: Waveform diversity in echolocating mammals. IEEE Signal Process. Mag. 2009, 26, 65–75. [Google Scholar] [CrossRef]
- Xu, W.; Huang, P.; Tan, W. Azimuth phase coding by up and down chirp modulation for range ambiguity suppression. IEEE Access. 2019, 7, 143780–143791. [Google Scholar] [CrossRef]
- Mittermayer, J.; Martinez, J.M. Analysis of range ambiguity suppression in SAR by up and down chirp modulation for point and distributed targets. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Toulouse, France, 21–25 July 2003. [Google Scholar]
- Wang, W. MIMO SAR Chirp Modulation Diversity Waveform Design. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1644–1648. [Google Scholar] [CrossRef]
- Gao, C.; The, K.C.; Liu, A. Piecewise nonlinear frequency modulation waveform for MIMO radar. IEEE J. Sel. Topics Signal Process. 2017, 11, 379–390. [Google Scholar] [CrossRef]
- Jin, G.; Aubry, A.; De Maio, A.; Wang, R.; Wang, W. Quasi-orthogonal waveforms for ambiguity suppression in spaceborne quadpol SAR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5204617. [Google Scholar] [CrossRef]
- Hague, D.A. Adaptive transmit waveform design using multitone sinusoidal frequency modulation. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1274–1287. [Google Scholar] [CrossRef]
- Xie, Q.; Yang, J.; Liu, C.; Li, W. Low sidelobe quasi-orthogonal NLFM waveforms with reciprocating frequency modulation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4027805. [Google Scholar] [CrossRef]
- Pappu, C.S.; Flores, B.C.; Debroux, P.; Boehm, J. An electronic implementation of Lorenz chaotic oscillator for bistatic radar applications. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2001–2013. [Google Scholar] [CrossRef]
- Willsey, M.S.; Cuomo, K.V.; Oppenheim, A.V. Quasi-orthogonal wideband radar waveforms based on chaotic systems. IEEE Trans. Aerosp. Electron. Syst. 2010, 47, 1974–1984. [Google Scholar] [CrossRef]
- Pappu, C.S.; Flores, B.C.; Debroux, P.S.; Verdin, B.; Boehm, J. Synchronization of bistatic radar using chaotic AM and chaos-based FM waveforms. IET Radar Sonar Navigat. 2016, 11, 90–97. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Moreira, G. Staggered SAR: High-resolution wide-swath imaging by continuous PRI variation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4462–4479. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Moreira, A. Staggered SAR: Performance Analysis and Experiments With Real Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6617–6638. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Moreira, A. A novel processing strategy for staggered SAR. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1891–1895. [Google Scholar] [CrossRef]
- Wang, X.; Wang, R.; Deng, Y.; Wang, W.; Li, N. SAR signal recovery and reconstruction in staggered mode with low oversampling factors. IEEE Geosci. Remote Sens. Lett. 2018, 15, 704–708. [Google Scholar] [CrossRef]
- Liu, Z.; Liao, X.; Wu, J. Image reconstruction for low-oversampled staggered SAR via HDM-FISTA. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5204514. [Google Scholar] [CrossRef]
- Zhang, Y.; Qi, X.; Jiang, Y.; Li, H.; Liu, Z. Image reconstruction for low-oversampled staggered SAR based on sparsity Bayesian learning in the presence of a nonlinear PRI variation strategy. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5229824. [Google Scholar] [CrossRef]
- Zhou, Z.; Deng, Y.; Wang, W.; Jia, X.; Wang, R. Linear Bayesian approaches for low-oversampled stepwise staggered SAR data. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5206123. [Google Scholar] [CrossRef]
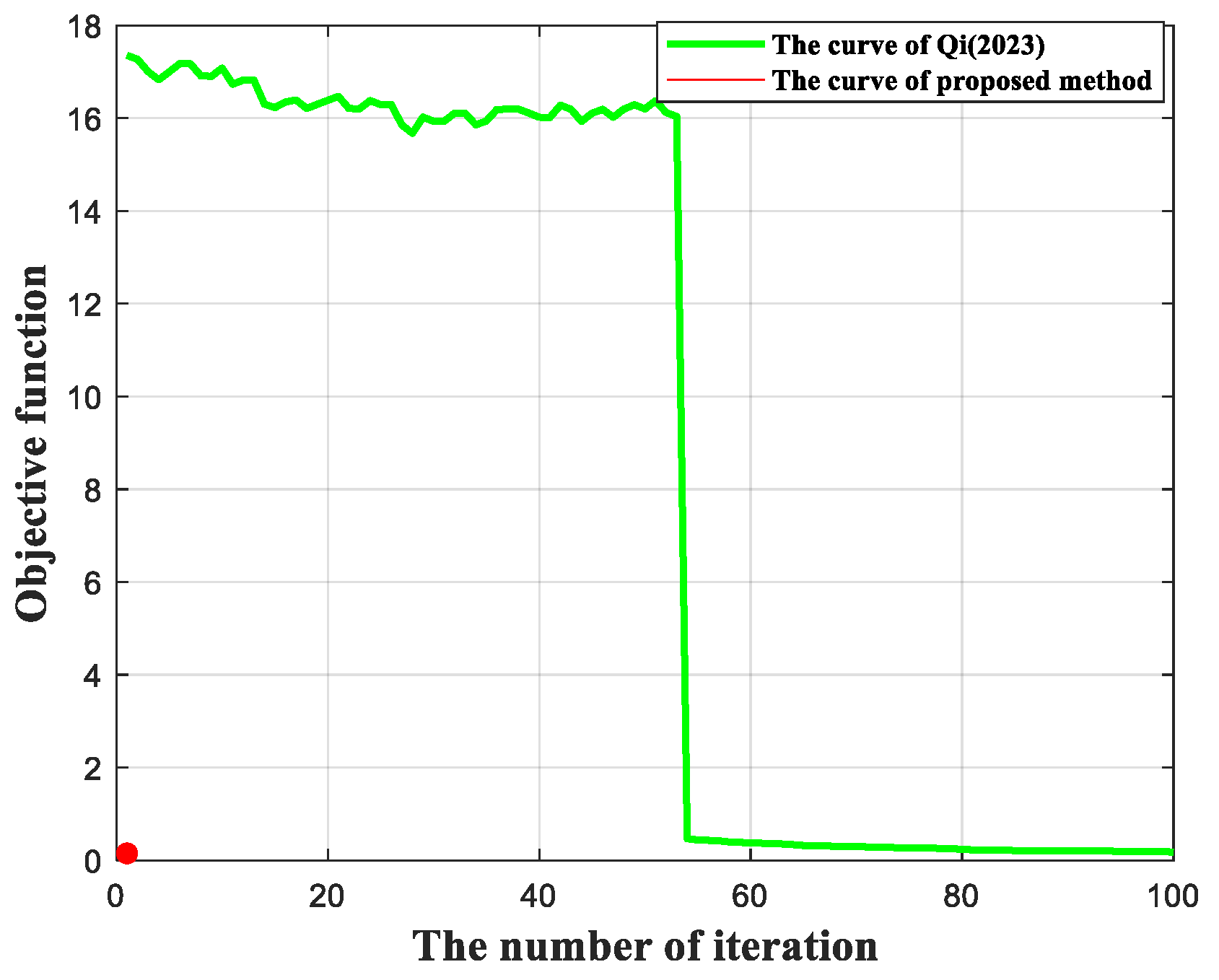
- Qi, X.; Zhang, Y.; Jiang, Y.; Giusti, E.; Martorella, M. Optimized nonlinear PRI variation strategy using knowledge-guided genetic algorithm for staggered SAR imaging. IEEE J. Sel. Topics Signal Process. 2023, 16, 2624–2643. [Google Scholar] [CrossRef]
- Wu, Y.; Fu, K.; Diao, W.; Yan, Z.; Wang, P.; Sun, X. Range sidelobe suppression approach for SAR images using chaotic FM signals. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5219915. [Google Scholar] [CrossRef]
- Callegari, S.; Rovatti, R.; Setti, G. Spectral properties of chaos-based FM signals: Theory and simulation results. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 3–15. [Google Scholar] [CrossRef]
- Soussen, C.; Gribonval, R.; Ldier, J.; Herzet, C. Joint K-Step Analysis of Orthogonal Matching Pursuit and Orthogonal Least Squares. IEEE Trans. Inf. Theory 2013, 59, 3158–3174. [Google Scholar] [CrossRef]
- Cerrone, C.; Cerull, R.; Golden, B. Carousel greedy: A generalized greedy algorithm with applications in optimization. Comput. Oper. Res. 2017, 85, 97–112. [Google Scholar] [CrossRef]
- Candes, E.; Tao, T. The Dantzig selector: Statistical estimation when p is much larger than n. Ann. Stat. 2007, 35, 2313–2351. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Tipping, M.E.; Faul, A.C. Fast marginal likelihood maximization for sparse Bayesian models. In Proceedings of the Ninth International Workshop on Artificial Intelligence and Statistics, Key West, FL, USA, 3–6 January 2003. [Google Scholar]
- Babacan, S.D.; Molina, R.; Katsaggelos, A.K. Bayesian compressive sensing using Laplace priors. IEEE Trans. Image Process. 2010, 19, 53–63. [Google Scholar] [CrossRef]
- George, E.I.; McCulloch, R.E. Approaches for Bayesian variable selection. Stat. Sin. 1997, 7, 339–373. [Google Scholar]
- George, E.I.; Foster, D.P. Calibration and empirical Bayes variable selection. Biometrika 2000, 87, 731–747. [Google Scholar] [CrossRef]
- Robert, C.P. The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation, 2nd ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Wipf, D.P. Sparse estimation with structured dictionaries. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Granada, Spain, 12–15 December 2011. [Google Scholar]
- Pearson, K. The Problem of the Random Walk. Nature 1905, 72, 294. [Google Scholar] [CrossRef]
- Davenport, W.B. Probability and Random Processes: An Introduction for Applied Scientists and Engineers; McGraw-Hill Book Company: New York, NY, USA, 1970. [Google Scholar]
- Starck, J.L.; Murtagh, F.; Fadili, J. Sparse Image and Signal Processing: Wavelets and Related Geometric Multiscale Analysis; Cambridge Univ. Press: Cambridge, UK, 2015. [Google Scholar]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn Res. 2001, 1, 211–244. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Pinheiro, M.; Prats-Iraola, P.; Rodriguez-Cassola, M.; Villano, M. Analysis of low-oversampled staggered SAR data. IEEE J. Sel. Topics Signal Process. 2019, 13, 241–255. [Google Scholar] [CrossRef]
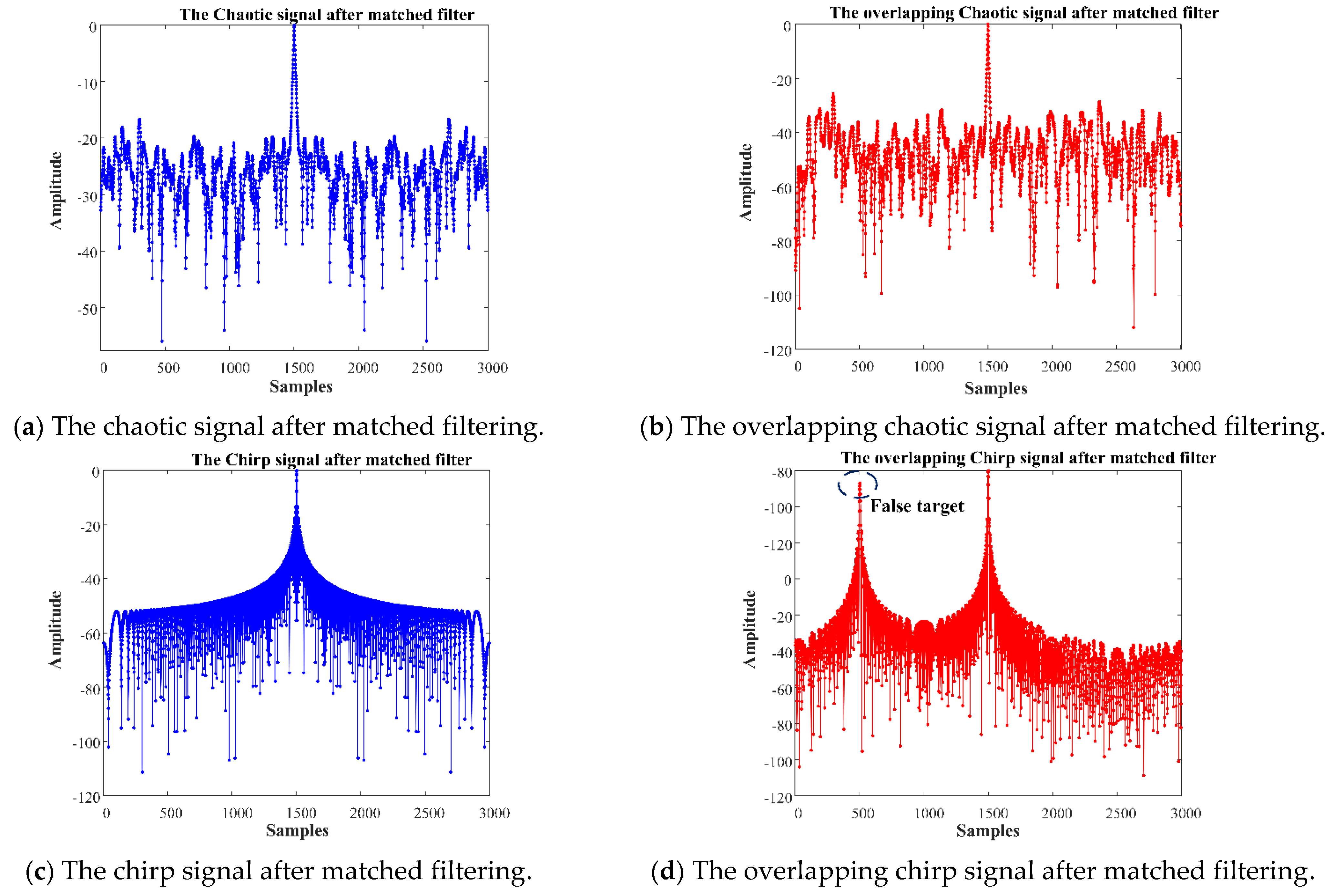


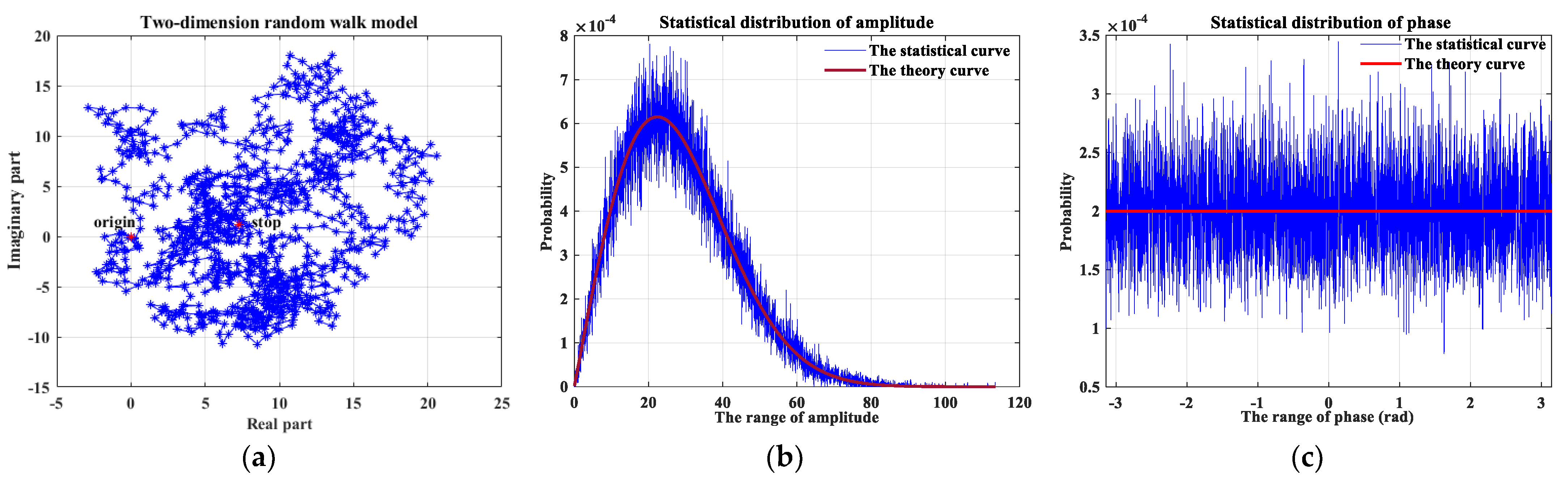
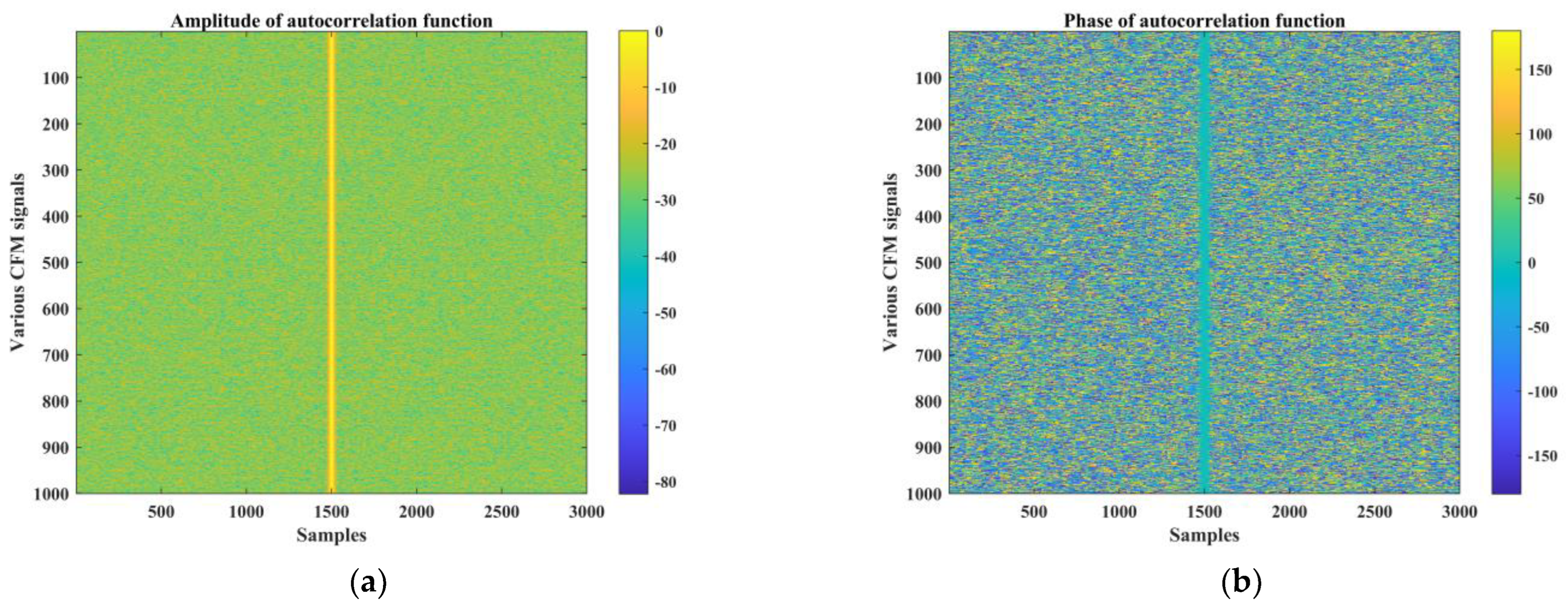
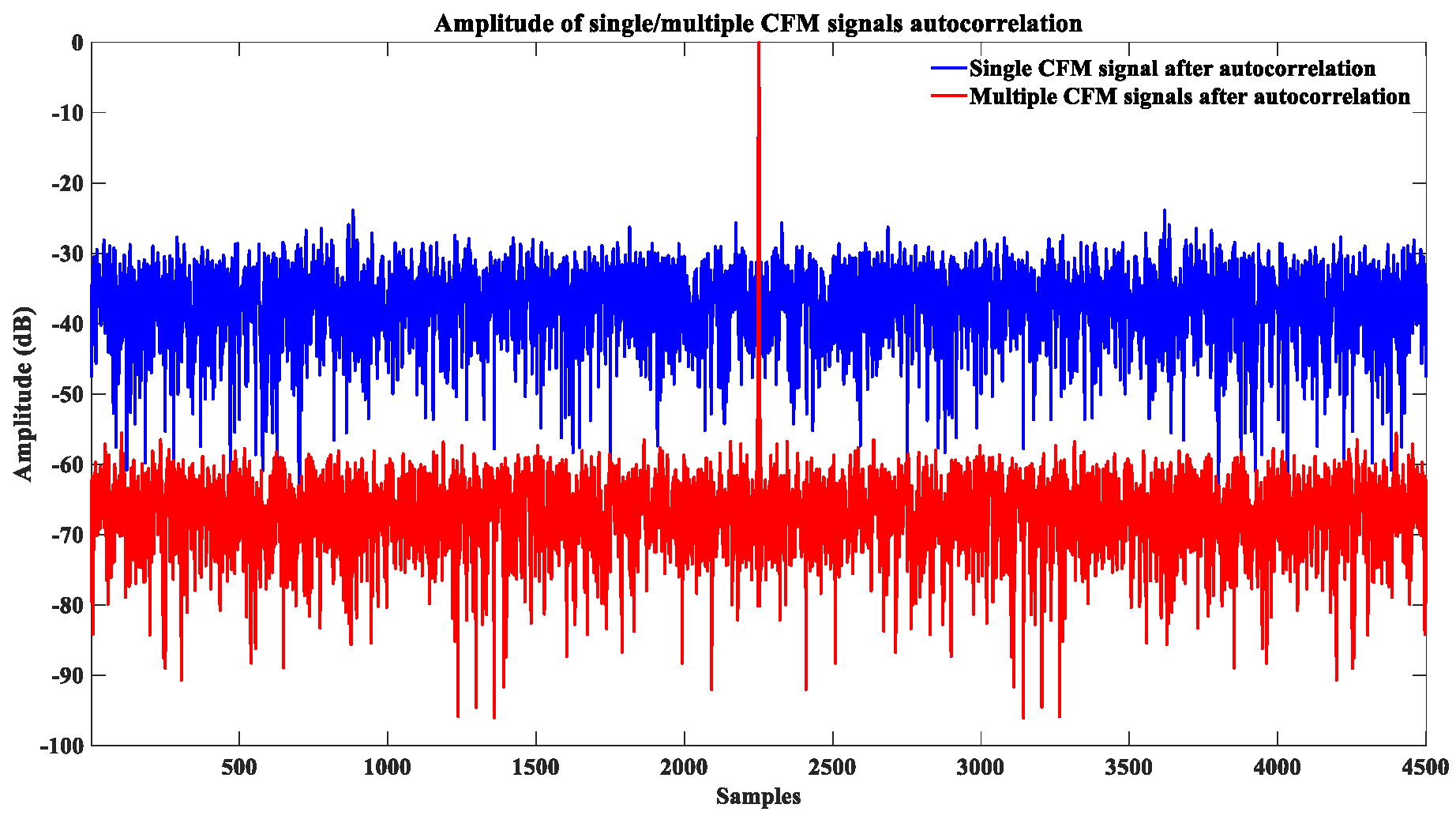
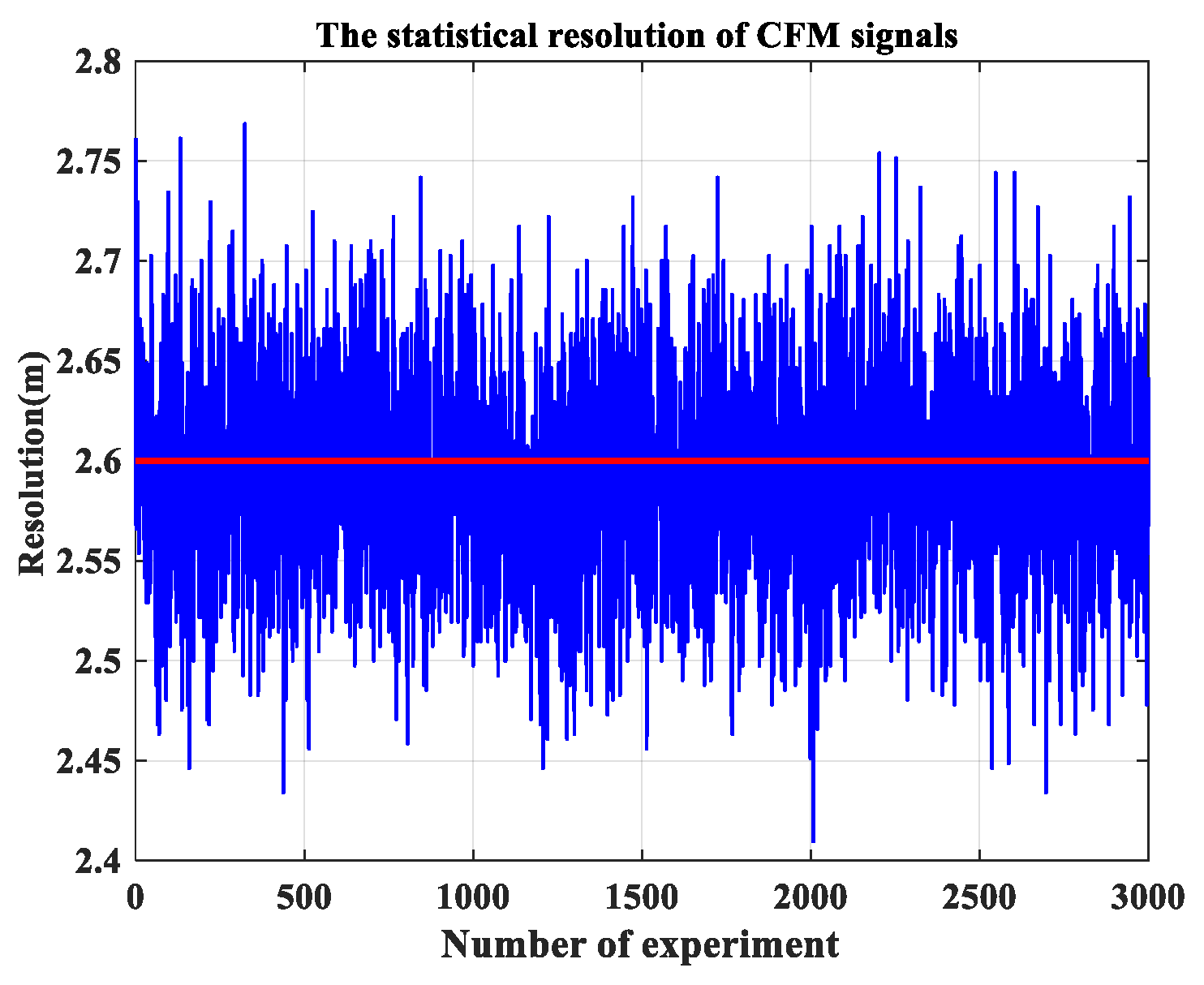
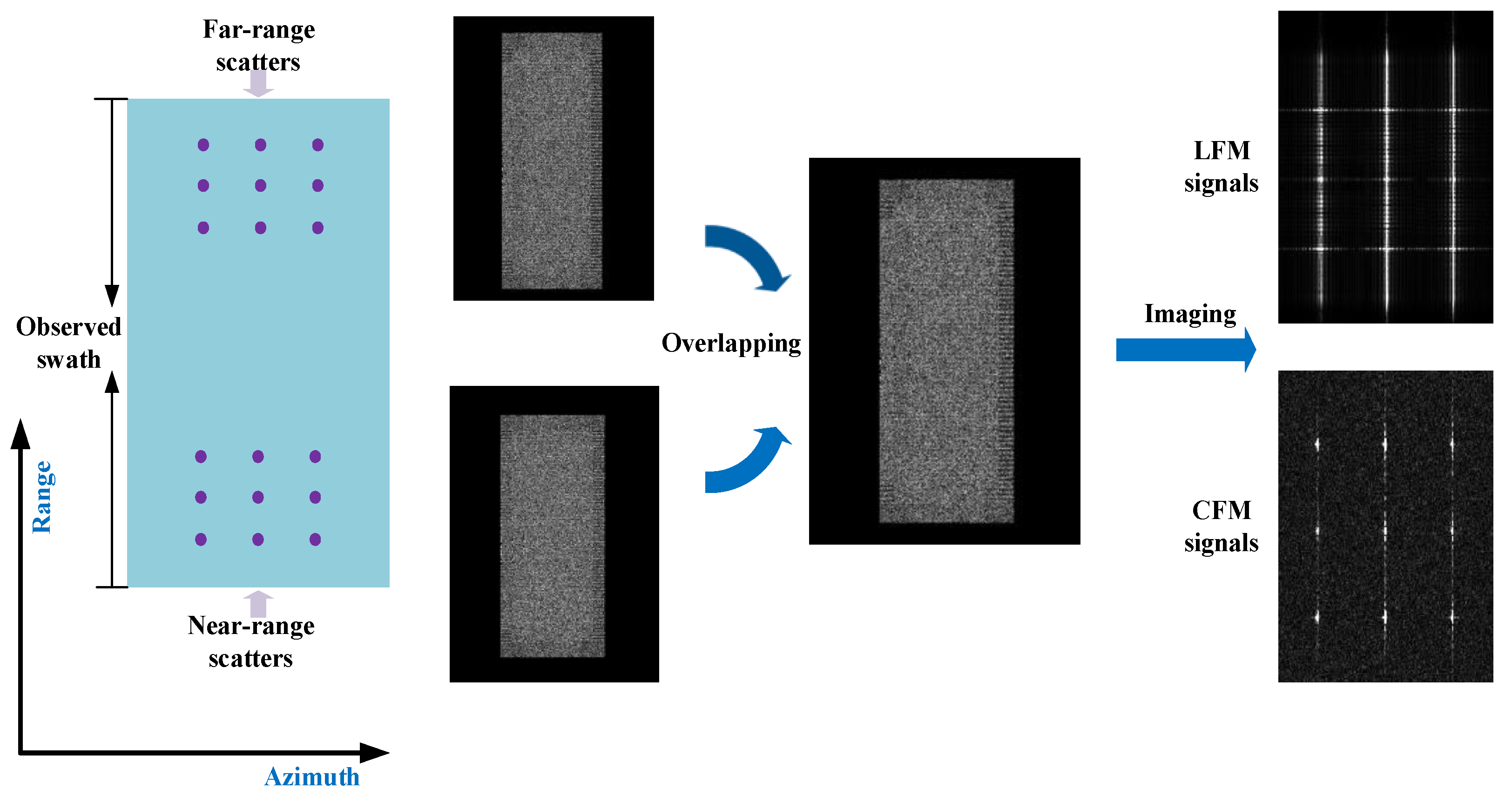
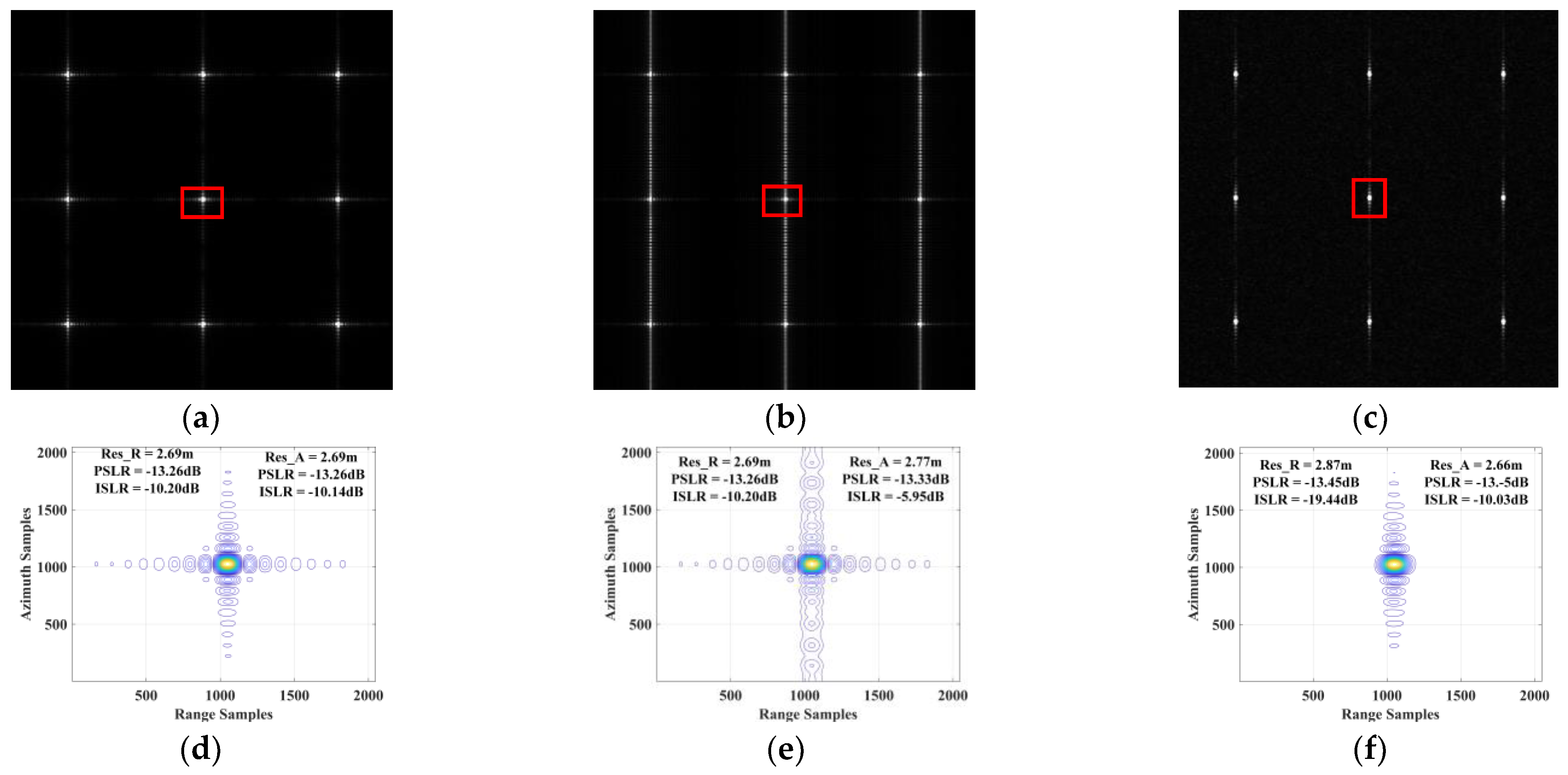
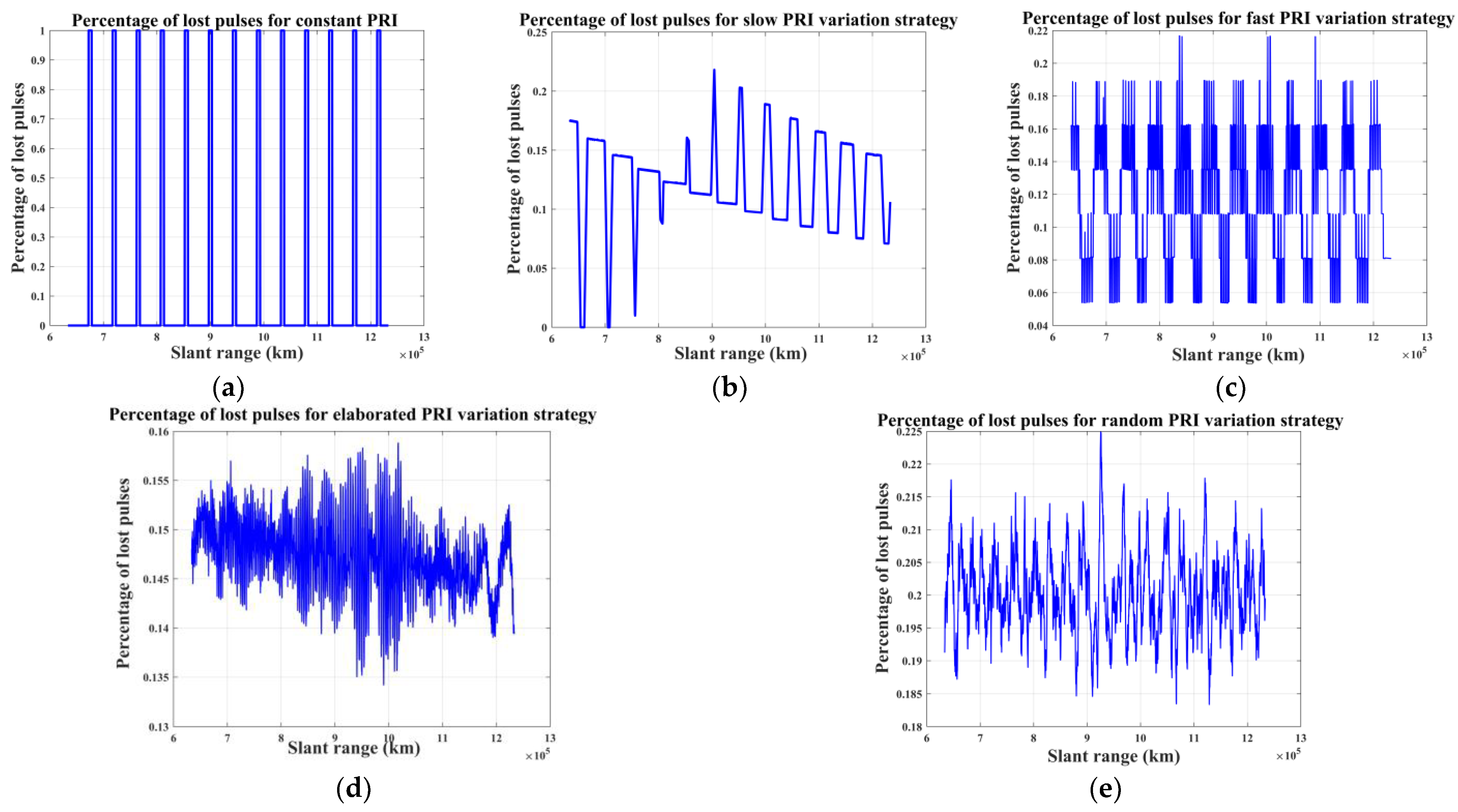





| Parameter | Chaotic FM Signals | LFM Signals |
|---|---|---|
| Signal Bandwidth (MHz) | 50 | 50 |
| Sampling Frequency (MHz) | 60 | 60 |
| Subpulse Width (us) | 1.67 × 10−2 | |
| Subpulse Number | 600 | |
| Modulated Rate (MHz/s) | 50 | |
| Pulse Width (us) | 10 | 10 |
| Wavelength (m) | 0.03 | 0.03 |
| Chaotic Mapping Name | Bernoulli | |
| Height (Km) | 600 | 600 |
| Velocity (m/s) | 7100 | 7100 |
| Antenna Length (m) | 5.32 | 5.32 |
| (Mean) Pulse Repetition Frequency (Hz) | 2775 | 3593 |
| Doppler Bandwidth (Hz) | 2671 | 2671 |
| Looking Angle in the near-range (rad) | 0.4 | 0.4 |
| Looking Angle in the far-range (rad) | 0.8 | 0.8 |
| Parameter | Chaotic FM Signals | LFM Signals |
|---|---|---|
| Signal Bandwidth (MHz) | 26.58 | 26.58 |
| Sampling Frequency (MHz) | 39.5 | 39.5 |
| Modulated Rate (MHz/s) | 26.58 | |
| Pulse Width (us) | 10 | 10 |
| Wavelength (m) | 0.03 | 0.03 |
| Chaotic Mapping Name | Bernoulli | |
| Height (Km) | 600 | 600 |
| Velocity (m/s) | 7100 | 7100 |
| Antenna Length (m) | 10 | 10 |
| (Mean) Pulse Repetition Frequency (Hz) | 1491 | 1860 |
| Doppler Bandwidth (Hz) | 1420 | 1420 |
| RE | SSIM | ||
|---|---|---|---|
| Figure 12 | (b) | 6.0629 | 0.6887 |
| (c) | 0.7770 | 0.9809 | |
| Figure 13 | (b) | 1.1258 | 0.6693 |
| (c) | 0.6869 | 0.9759 |
| Parameter | Value |
|---|---|
| The Doppler Bandwidth (Hz) | 2367 |
| The oversampling ratio | 1.06 |
| The percentage of lost pulses | 10% |
| Antenna Length (m) | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Geng, J.; Guo, Y.; Zhang, L. An Ultra-Wide Swath Synthetic Aperture Radar Imaging System via Chaotic Frequency Modulation Signals and a Random Pulse Repetition Interval Variation Strategy. Remote Sens. 2025, 17, 1719. https://doi.org/10.3390/rs17101719
Chen W, Geng J, Guo Y, Zhang L. An Ultra-Wide Swath Synthetic Aperture Radar Imaging System via Chaotic Frequency Modulation Signals and a Random Pulse Repetition Interval Variation Strategy. Remote Sensing. 2025; 17(10):1719. https://doi.org/10.3390/rs17101719
Chicago/Turabian StyleChen, Wenjiao, Jiwen Geng, Yufeng Guo, and Li Zhang. 2025. "An Ultra-Wide Swath Synthetic Aperture Radar Imaging System via Chaotic Frequency Modulation Signals and a Random Pulse Repetition Interval Variation Strategy" Remote Sensing 17, no. 10: 1719. https://doi.org/10.3390/rs17101719
APA StyleChen, W., Geng, J., Guo, Y., & Zhang, L. (2025). An Ultra-Wide Swath Synthetic Aperture Radar Imaging System via Chaotic Frequency Modulation Signals and a Random Pulse Repetition Interval Variation Strategy. Remote Sensing, 17(10), 1719. https://doi.org/10.3390/rs17101719






