Advancing Corn Yield Mapping in Kenya Through Transfer Learning
Abstract
1. Introduction
2. Materials and Methods
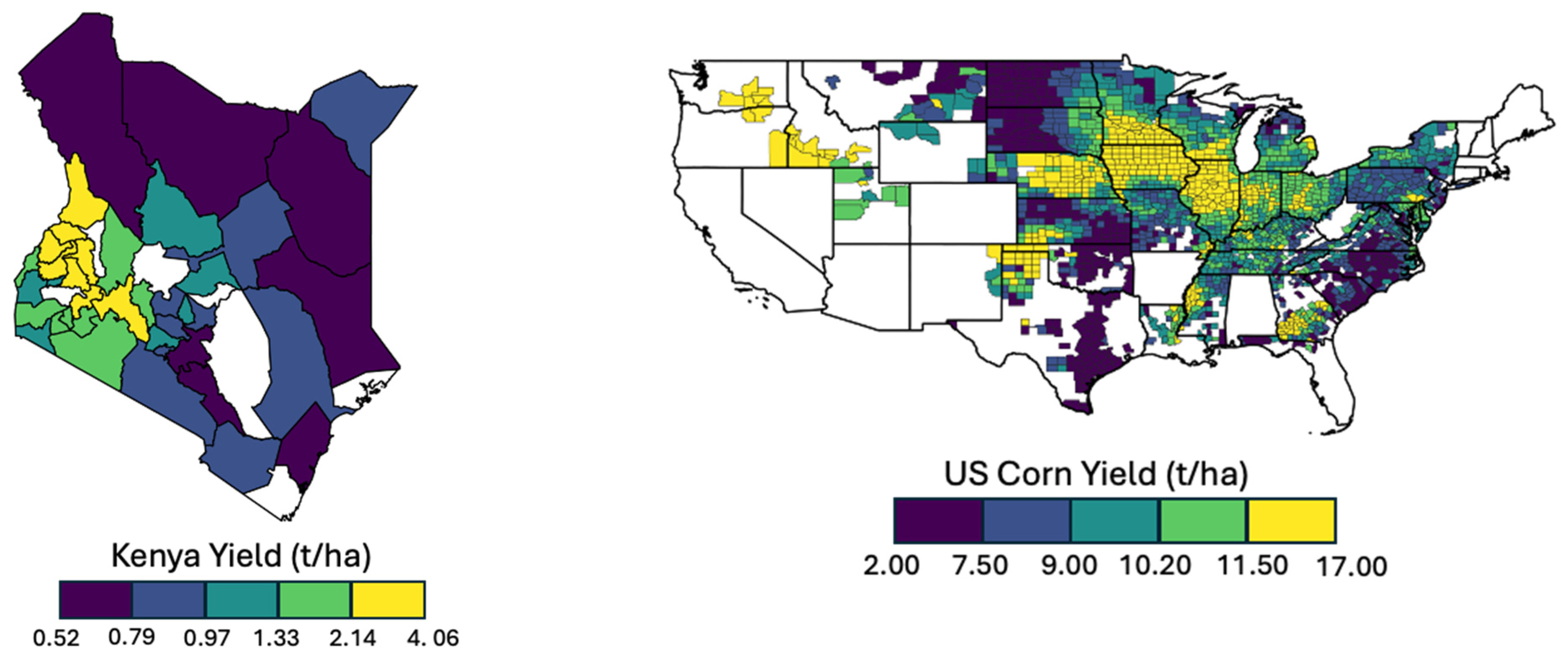
2.1. Study Areas and Yield Data
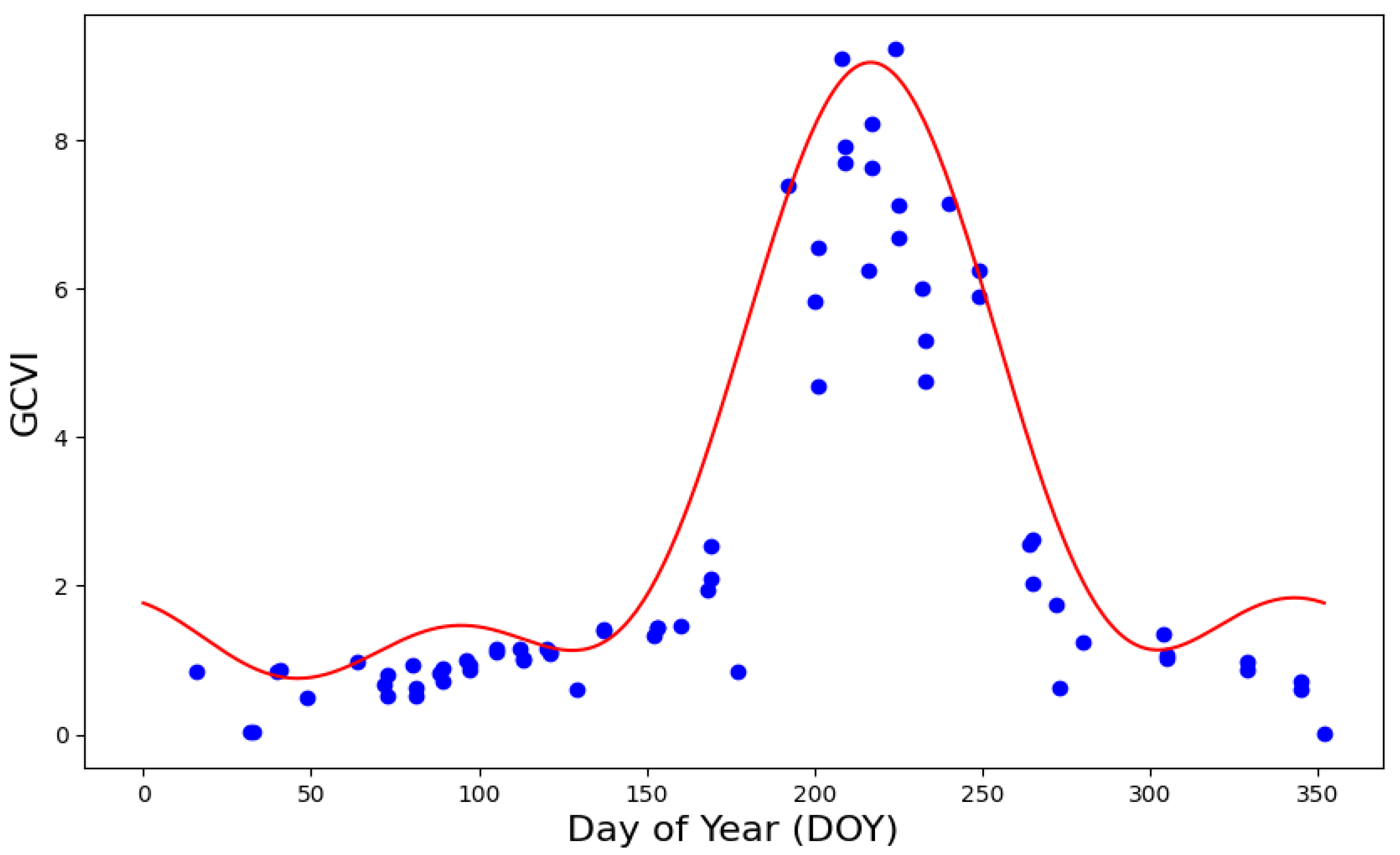
2.2. Satellite Data and Meteorologic Variables
3. Methodology
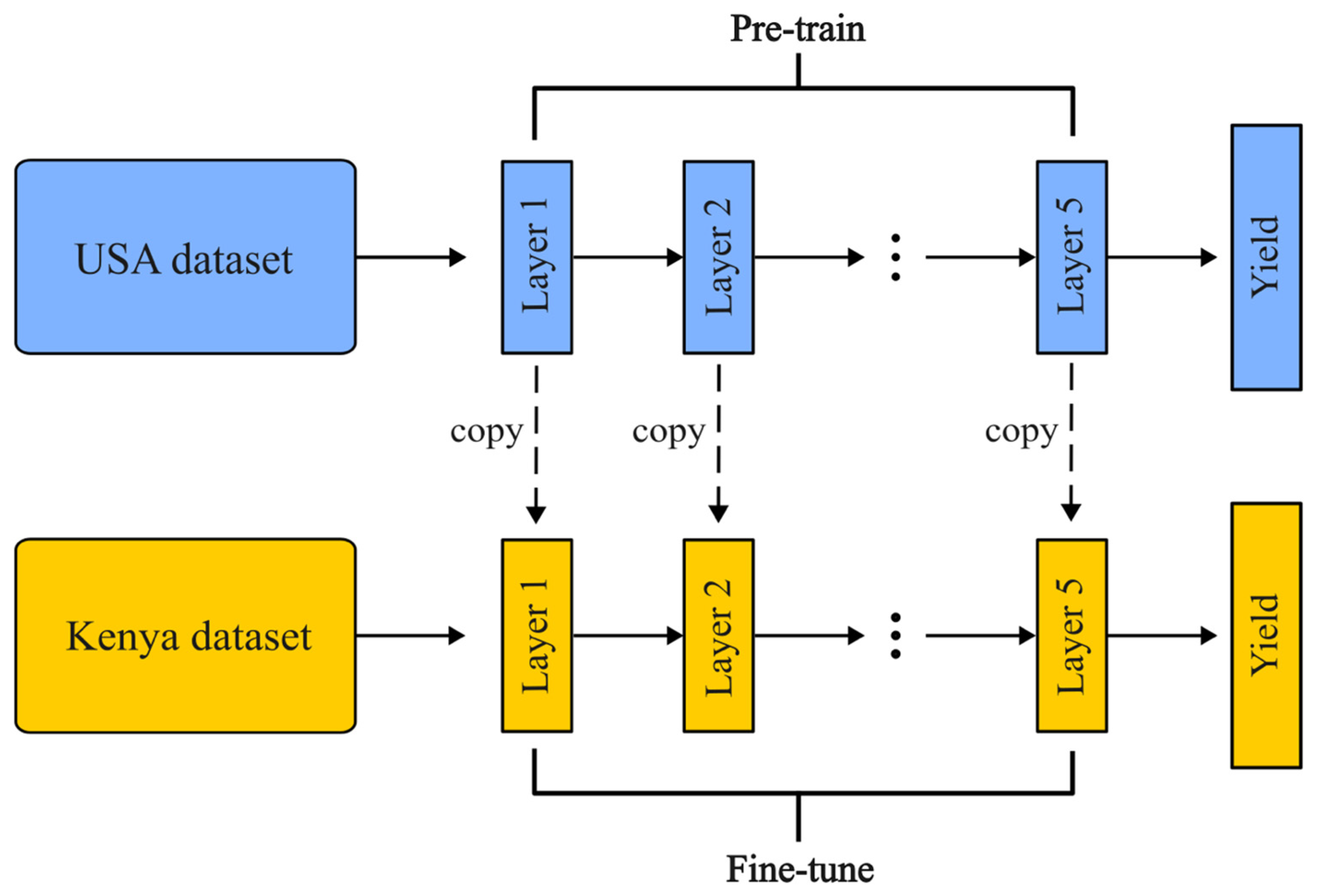
3.1. Fundamentals of Fine-Tuning-Based Transfer Learning
3.2. Designed Fine-Tuning Architecture
3.3. Model Evaluation
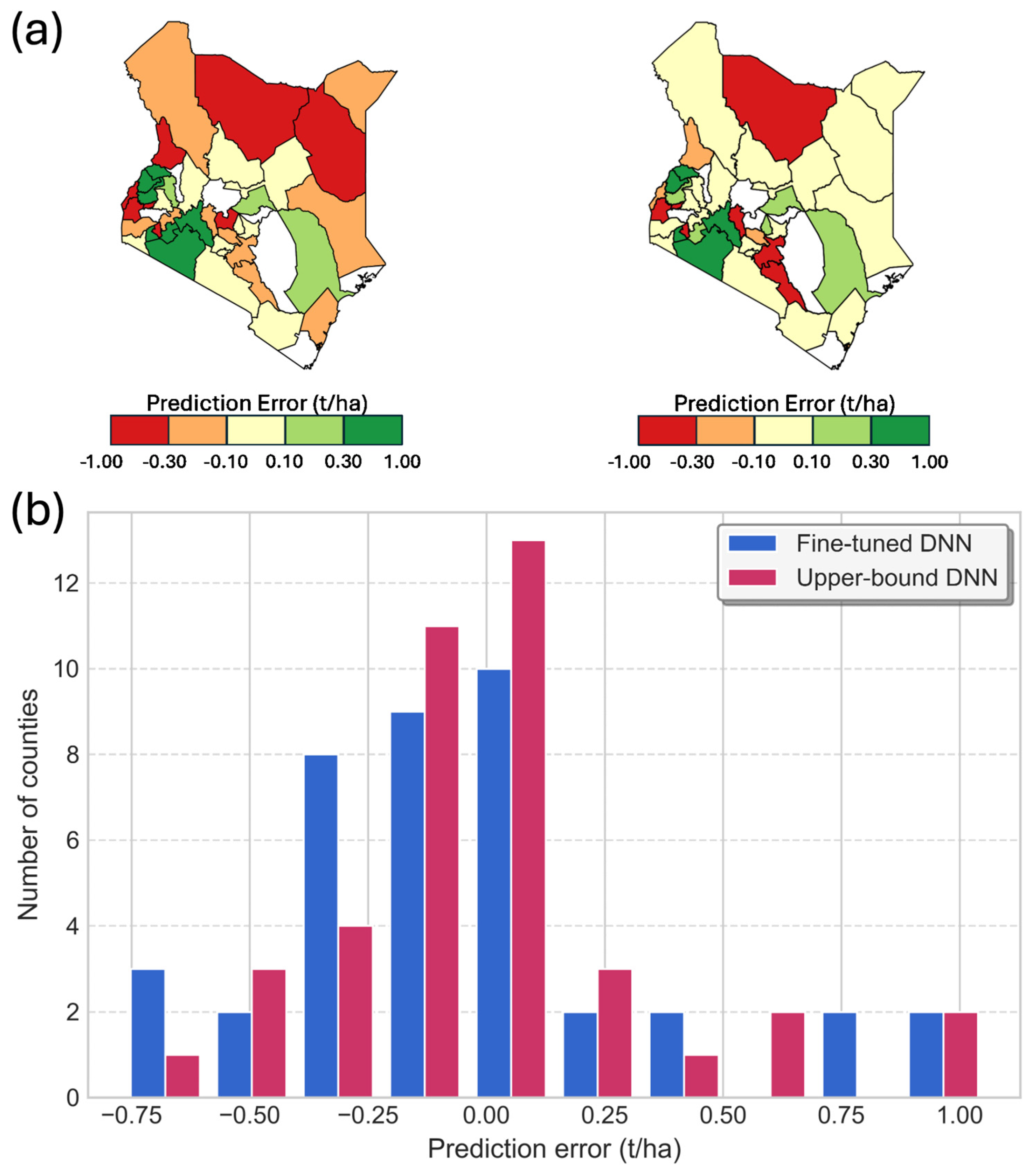
4. Results
5. Discussion
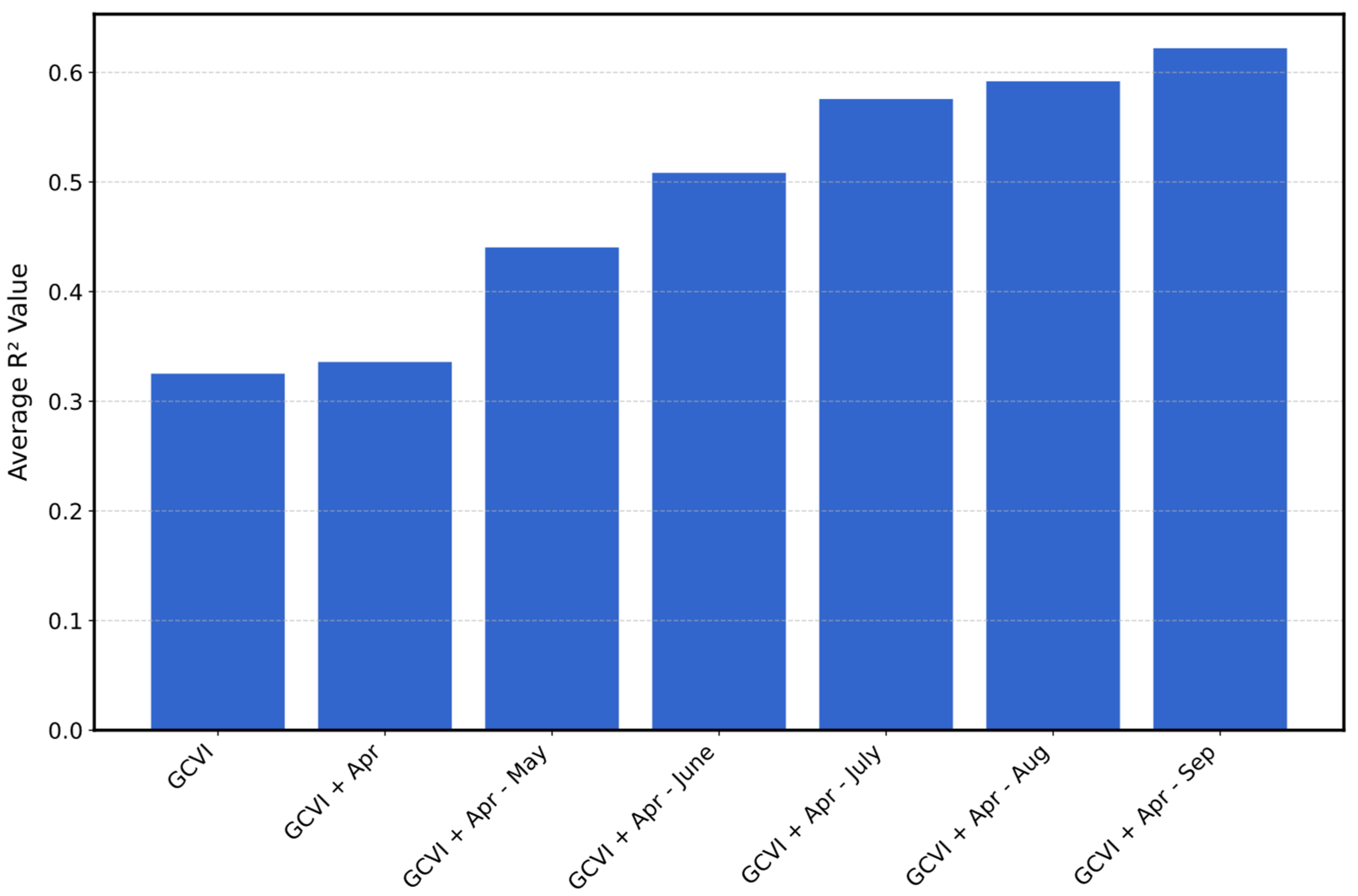
5.1. Feature Importance
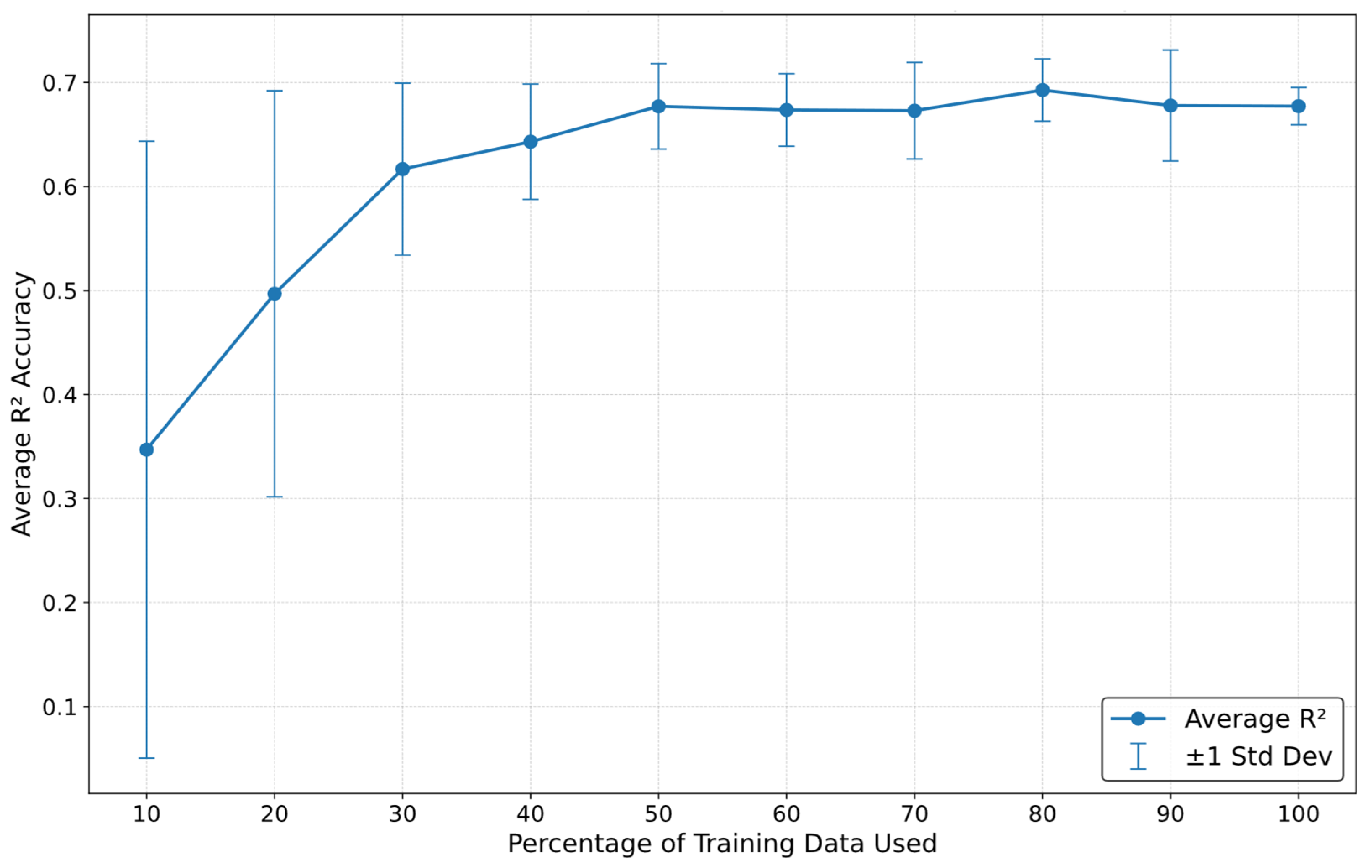
5.2. Sensitivity Analysis
5.3. Limitations and Future Work
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tigchelaar, M.; Battisti, D.S.; Naylor, R.L.; Ray, D.K. Future warming increases probability of globally synchronized maize production shocks. Proc. Natl. Acad. Sci. USA 2018, 115, 6644–6649. [Google Scholar] [CrossRef] [PubMed]
- Shafi, U.; Mumtaz, R.; Anwar, Z.; Ajmal, M.M.; Khan, M.A.; Mahmood, Z.; Qamar, M.; Jhanzab, H.M. Tackling Food Insecurity Using Remote Sensing and Machine Learning-Based Crop Yield Prediction. IEEE Access 2023, 11, 108640–108657. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Feng, L.; Ma, Y.; Du, Q. A new attention-based CNN approach for crop mapping using time series Sentinel-2 images. Comput. Electron. Agric. 2021, 184, 106090. [Google Scholar] [CrossRef]
- Lv, Z.; Huang, H.; Li, X.; Zhao, M.; Benediktsson, J.A.; Sun, W.; Falco, N. Land Cover Change Detection with Heterogeneous Remote Sensing Images: Review, Progress, and Perspective. Proc. IEEE 2022, 110, 1976–1991. [Google Scholar] [CrossRef]
- Kang, Y.; Ozdogan, M.; Zhu, X.; Ye, Z.; Hain, C.R.; Anderson, M.C. Comparative assessment of environmental variables and machine learning algorithms for maize yield prediction in the US Midwest. Environ. Res. Lett. 2020, 15, 064005. [Google Scholar] [CrossRef]
- Johnson, D.M. An assessment of pre- and within-season remotely sensed variables for forecasting corn and soybean yields in the United States. Remote Sens. Environ. 2014, 141, 116–128. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Robinson, S.; Galpern, P. Medium-resolution multispectral satellite imagery in precision agriculture: Mapping precision canola (Brassica napus L.) yield using Sentinel-2 time series. Precis. Agric. 2022, 23, 1051–1071. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Deep Neural Networks. In Efficient Learning Machines; Apress: Berkeley, CA, USA, 2015; pp. 127–147. [Google Scholar] [CrossRef]
- Cerulli, G. Fundamentals of Supervised Machine Learning: With Applications in Python, R, and Stata; Statistics and Computing; Springer International Publishing: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Juang, B.H. Deep neural networks–A developmental perspective. APSIPA Trans. Signal Inf. Process. 2016, 5, 127–147. [Google Scholar] [CrossRef]
- Balestriero, R.; Baraniuk, R. Deep Neural Networks. arXiv 2017, arXiv:1710.09302. [Google Scholar] [CrossRef]
- Sun, J.; Di, L.; Sun, Z.; Shen, Y.; Lai, Z. County-Level Soybean Yield Prediction Using Deep CNN-LSTM Model. Sensors 2019, 19, 4363. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Luo, Y.; Cao, J.; Xie, R.; Li, S. Integrating satellite-derived climatic and vegetation indices to predict smallholder maize yield using deep learning. Agric. For. Meteorol. 2021, 311, 108666. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Z.; Kang, Y.; Özdoğan, M. Corn yield prediction and uncertainty analysis based on remotely sensed variables using a Bayesian neural network approach. Remote Sens. Environ. 2021, 259, 112408. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Feng, L.; Du, Q.; Runge, T. Combining Multi-Source Data and Machine Learning Approaches to Predict Winter Wheat Yield in the Conterminous United States. Remote Sens. 2020, 12, 1232. [Google Scholar] [CrossRef]
- Lv, Z.; Zhang, P.; Sun, W.; Benediktsson, J.A.; Li, J.; Wang, W. Novel Adaptive Region Spectral–Spatial Features for Land Cover Classification with High Spatial Resolution Remotely Sensed Imagery. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5609412. [Google Scholar] [CrossRef]
- Sarron, J.; Beillouin, D.; Huat, J.; Koffi, J.; Diatta, J.; Malézieux, É.; Faye, E. Digital agriculture to fulfil the shortage of horticultural data and achieve food security in sub-Saharan Africa. Acta Hortic. 2022, 1348, 239–246. [Google Scholar] [CrossRef]
- Jones, J.W.; Antle, J.M.; Basso, B.; Boote, K.J.; Conant, R.T.; Foster, I.; Godfray, H.C.J.; Herrero, M.; Howitt, R.E.; Janssen, S.; et al. Toward a new generation of agricultural system data, models, and knowledge products: State of agricultural systems science. Agric. Syst. 2017, 155, 269–288. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, S.; Ermon, S.; Lobell, D.B. Transfer learning in environmental remote sensing. Remote Sens. Environ. 2023, 301, 113924. [Google Scholar] [CrossRef]
- Hilbert, M. Big Data for Development: From Information-to Knowledge Societies. SSRN Electron. J. 2013, 2205145. [Google Scholar] [CrossRef]
- Kuria, A.W.; Bolo, P.; Adoyo, B.; Korir, H.; Sakha, M.; Gumo, P.; Mbelwa, M.; Orero, L.; Ntinyari, W.; Syano, N.; et al. Understanding farmer options, context and preferences leads to the co-design of locally relevant agroecological practices for soil, water and integrated pest management: A case from Kiambu and Makueni agroecology living landscapes, Kenya. Front. Sustain. Food Syst. 2024, 8, 1456620. [Google Scholar] [CrossRef]
- Alvarado-Cárdenas, L.O.; Martínez-Meyer, E.; Feria, T.P.; Eguiarte, L.E.; Hernández, H.M.; Midgley, G.; Olson, M.E. To converge or not to converge in environmental space: Testing for similar environments between analogous succulent plants of North America and Africa. Ann. Bot. 2013, 111, 1125–1138. [Google Scholar] [CrossRef]
- Hosna, A.; Merry, E.; Gyalmo, J.; Alom, Z.; Aung, Z.; Azim, M.A. Transfer learning: A friendly introduction. J. Big Data 2022, 9, 102. [Google Scholar] [CrossRef]
- Tajbakhsh, N.; Shin, J.Y.; Gurudu, S.R.; Hurst, R.T.; Kendall, C.B.; Gotway, M.B.; Liang, J. Convolutional Neural Networks for Medical Image Analysis: Full Training or Fine Tuning? IEEE Trans. Med. Imaging 2016, 35, 1299–1312. [Google Scholar] [CrossRef] [PubMed]
- Chew, R.; Rineer, J.; Beach, R.; O’neil, M.; Ujeneza, N.; Lapidus, D.; Miano, T.; Hegarty-Craver, M.; Polly, J.; Temple, D.S. Deep Neural Networks and Transfer Learning for Food Crop Identification in UAV Images. Drones 2020, 4, 7. [Google Scholar] [CrossRef]
- Zhao, Y.; Han, S.; Meng, Y.; Feng, H.; Li, Z.; Chen, J.; Song, X.; Zhu, Y.; Yang, G. Transfer-Learning-Based Approach for Yield Prediction of Winter Wheat from Planet Data and SAFY Model. Remote Sens. 2022, 14, 5474. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Stewart, A.J.; Bastani, F.; Wolters, P.; Kannan, S.; Huber, G.R.; Wang, J.; Banerjee, A. On the Generalizability of Foundation Models for Crop Type Mapping. arXiv 2024, arXiv:2409.09451. [Google Scholar] [CrossRef]
- United States Department of Agriculture, National Agricultural Statistics Service. Quick Stats Database. United States Department of Agriculture (USDA-NASS). 2025. Available online: https://quickstats.nass.usda.gov/ (accessed on 18 April 2025).
- United States Department of Agriculture, National Agricultural Statistics Service. 2017 Census of Agriculture. USDA NASS. 2019. Available online: https://www.nass.usda.gov/Publications/AgCensus/2017/ (accessed on 21 April 2025).
- Corn: United States Area, Yield, and Production. USDA Foreign Agricultural Service, PS&D Online. Available online: https://ipad.fas.usda.gov/countrysummary/Default.aspx?crop=Corn&id=US (accessed on 21 April 2025).
- KilimoSTAT. Ministry of Agriculture and Livestock Development. Available online: https://statistics.kilimo.go.ke/en/ (accessed on 4 March 2025).
- Food and Agriculture Organization of the United Nations. Family Farming Data Portrait–Kenya. Food and Agriculture Organization of the United Nations (FAO). Available online: https://www.fao.org/family-farming/data-sources/dataportrait/country-details/en/?cnt=KEN (accessed on 21 April 2025).
- FAOSTAT (FAO). Kenya Maize Yield–FAOSTAT. FAOSTAT (Food and Agriculture Organization of the United Nations). Available online: https://www.fao.org/faostat/en/#data/QCL (accessed on 21 April 2025).
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Boryan, C.; Yang, Z.; Mueller, R.; Craig, M. Monitoring US agriculture: The US Department of Agriculture, National Agricultural Statistics Service, Cropland Data Layer Program. Geocarto Int. 2011, 26, 341–358. [Google Scholar] [CrossRef]
- Van Tricht, K.; Degerickx, J.; Gilliams, S.; Zanaga, D.; Battude, M.; Grosu, A.; Brombacher, J.; Lesiv, M.; Bayas, J.C.L.; Karanam, S.; et al. WorldCereal: A dynamic open-source system for global-scale, seasonal, and reproducible crop and irrigation mapping. Earth Syst. Sci. Data 2023, 15, 5491–5515. [Google Scholar] [CrossRef]
- Ma, Y.; Liang, S.-Z.; Myers, D.B.; Swatantran, A.; Lobell, D.B. Subfield-level crop yield mapping without ground truth data: A scale transfer framework. Remote Sens. Environ. 2024, 315, 114427. [Google Scholar] [CrossRef]
- Deines, J.M.; Patel, R.; Liang, S.-Z.; Dado, W.; Lobell, D.B. A million kernels of truth: Insights into scalable satellite maize yield mapping and yield gap analysis from an extensive ground dataset in the US Corn Belt. Remote Sens. Environ. 2021, 253, 112174. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service. ERA5-Land Monthly Averaged Data from 1950 to Present; Copernicus Climate Change Service (C3S) Climate Data Store (CDS): Brussels, Belgium, 2019. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Bai, J.; Al-Sabaawi, A.; Santamaría, J.; Albahri, A.S.; Al-Dabbagh, B.S.N.; Fadhel, M.A.; Manoufali, M.; Zhang, J.; Al-Timemy, A.H.; et al. A survey on deep learning tools dealing with data scarcity: Definitions, challenges, solutions, tips, and applications. J. Big Data 2023, 10, 46. [Google Scholar] [CrossRef]
- Li, Y. Deep Learning with Very Few and No Labels. Ph.D. Thesis, University of Missouri--Columbia, Columbia, MO, USA, 2021. [Google Scholar] [CrossRef]
- Wang, M.; Deng, W. Deep visual domain adaptation: A survey. Neurocomputing 2018, 312, 135–153. [Google Scholar] [CrossRef]
- Cook, D.; Feuz, K.D.; Krishnan, N.C. Transfer learning for activity recognition: A survey. Knowl. Inf. Syst. 2013, 36, 537–556. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Tan, C.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A Survey on Deep Transfer Learning. arXiv 2018, arXiv:1808.01974. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D.D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-learn: Machine Learning in Python. arXiv 2012, arXiv:1201.0490. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. arXiv 2019, arXiv:1912.01703. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Z.; Yang, H.L.; Yang, Z. An adaptive adversarial domain adaptation approach for corn yield prediction. Comput. Electron. Agric. 2021, 187, 106314. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, Z.; Huang, Q.; Zhang, Z. Improving the Transferability of Deep Learning Models for Crop Yield Prediction: A Partial Domain Adaptation Approach. Remote Sens. 2023, 15, 4562. [Google Scholar] [CrossRef]
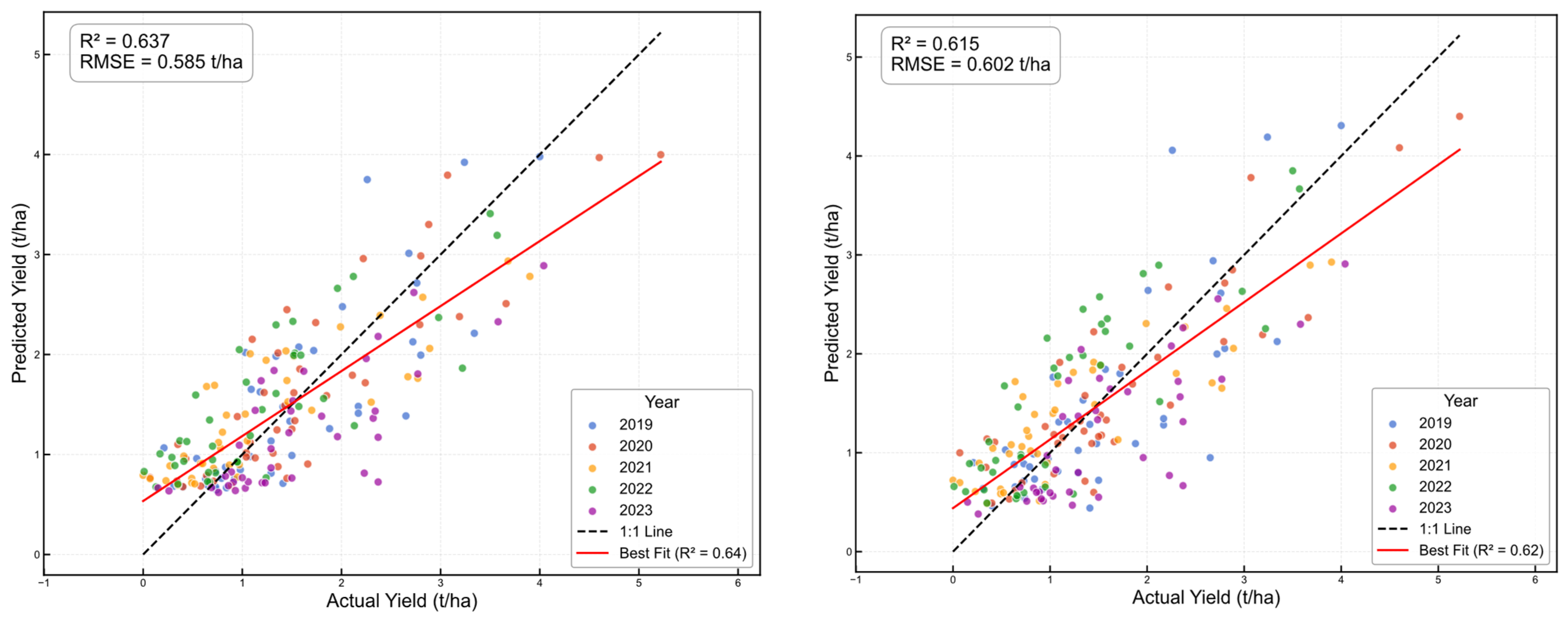
| Years | Number of Testing Samples | Fine-Tuned DNN | DNN | RF | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Upper-Bound | Lower-Bound | Upper-Bound | Lower-Bound | ||||||||
| RMSE | RMSE | RMSE | RMSE | RMSE | |||||||
| 2019 | 40 | 0.607 | 0.572 | 0.566 | 0.601 | −29.900 | 5.070 | 0.625 | 0.559 | −5.140 | 2.260 |
| 2020 | 40 | 0.769 | 0.536 | 0.768 | 0.536 | −22.100 | 5.370 | 0.685 | 0.626 | −3.160 | 2.270 |
| 2021 | 40 | 0.637 | 0.581 | 0.682 | 0.543 | −25.000 | 4.910 | 0.734 | 0.497 | −5.070 | 2.370 |
| 2022 | 39 | 0.553 | 0.604 | 0.527 | 0.621 | −30.000 | 5.000 | 0.389 | 0.706 | −7.070 | 2.570 |
| 2023 | 38 | 0.404 | 0.647 | 0.328 | 0.687 | −29.100 | 4.600 | 0.487 | 0.601 | −5.900 | 2.200 |
| Overall | 197 | 0.632 | 0.589 | 0.618 | 0.598 | −25.600 | 4.990 | 0.616 | 0.598 | −4.800 | 2.330 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bohra, A.; Nottmeyer, S.; Ren, C.; Chen, S.; Ma, Y. Advancing Corn Yield Mapping in Kenya Through Transfer Learning. Remote Sens. 2025, 17, 1717. https://doi.org/10.3390/rs17101717
Bohra A, Nottmeyer S, Ren C, Chen S, Ma Y. Advancing Corn Yield Mapping in Kenya Through Transfer Learning. Remote Sensing. 2025; 17(10):1717. https://doi.org/10.3390/rs17101717
Chicago/Turabian StyleBohra, Ahaan, Sophie Nottmeyer, Chenchen Ren, Shuo Chen, and Yuchi Ma. 2025. "Advancing Corn Yield Mapping in Kenya Through Transfer Learning" Remote Sensing 17, no. 10: 1717. https://doi.org/10.3390/rs17101717
APA StyleBohra, A., Nottmeyer, S., Ren, C., Chen, S., & Ma, Y. (2025). Advancing Corn Yield Mapping in Kenya Through Transfer Learning. Remote Sensing, 17(10), 1717. https://doi.org/10.3390/rs17101717







