Evolution of Rockfall Based on Structure from Motion Reconstruction of Street View Imagery and Unmanned Aerial Vehicle Data: Case Study from Koto Panjang, Indonesia
Abstract
1. Introduction
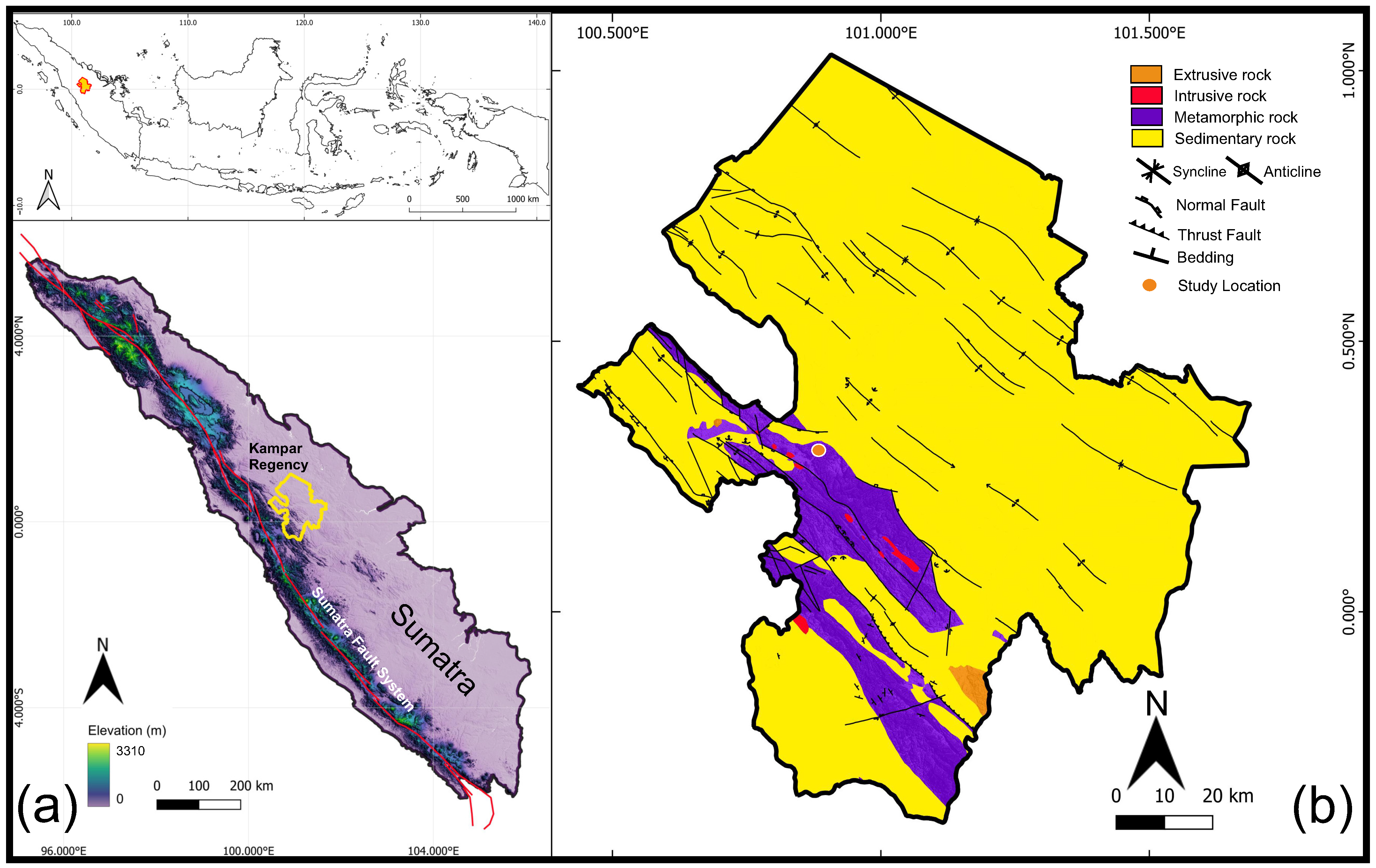
2. Geological and Geographical Setting

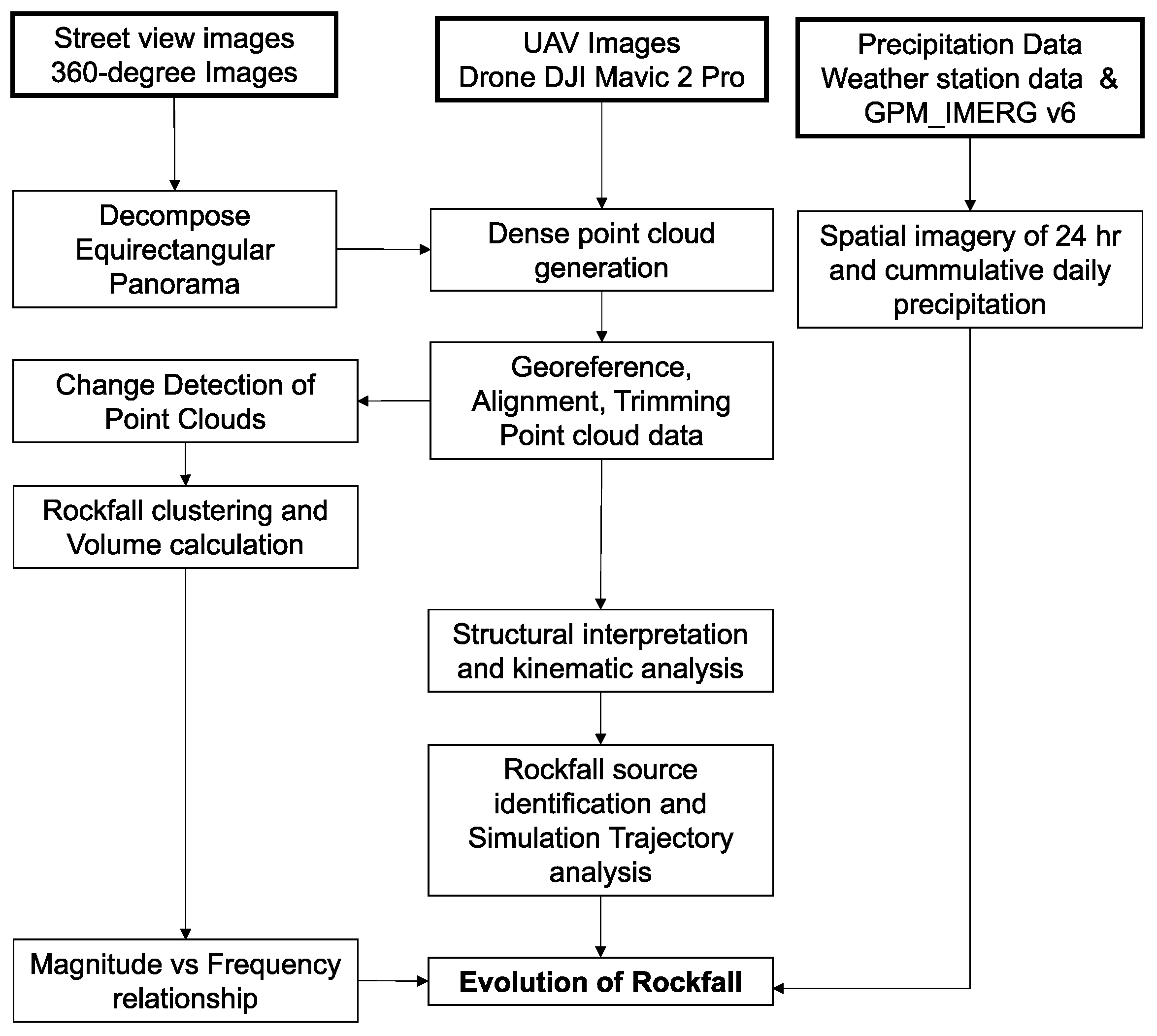
3. Methodology
3.1. Image Acquisition
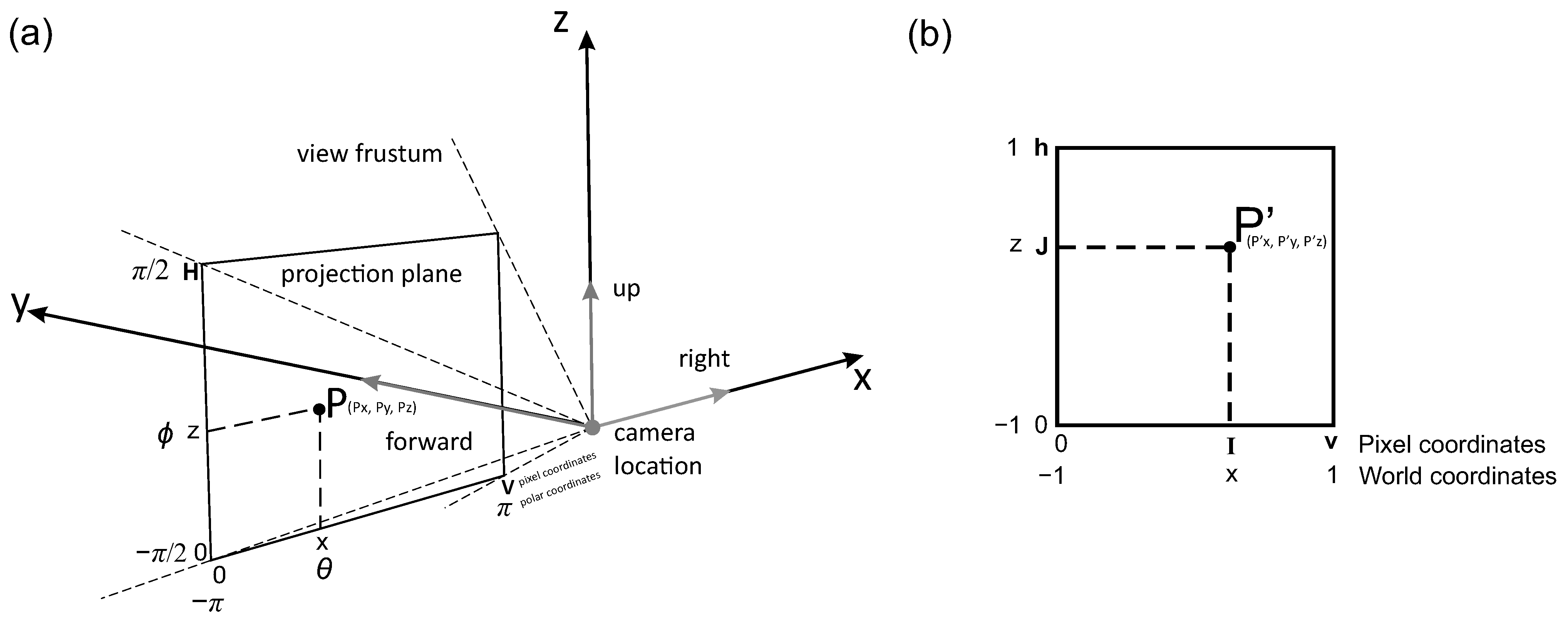
3.2. Decomposing 360-Degree SVI Images
3.3. Data Processing
3.3.1. Dense Points Cloud Model Generation
3.3.2. Georeferencing and Registration of 3D Model
3.3.3. Change Detection of Point Clouds
3.3.4. Rockfall Clustering and Volume Calculation
3.3.5. Structural Measurement and Kinematic Analysis
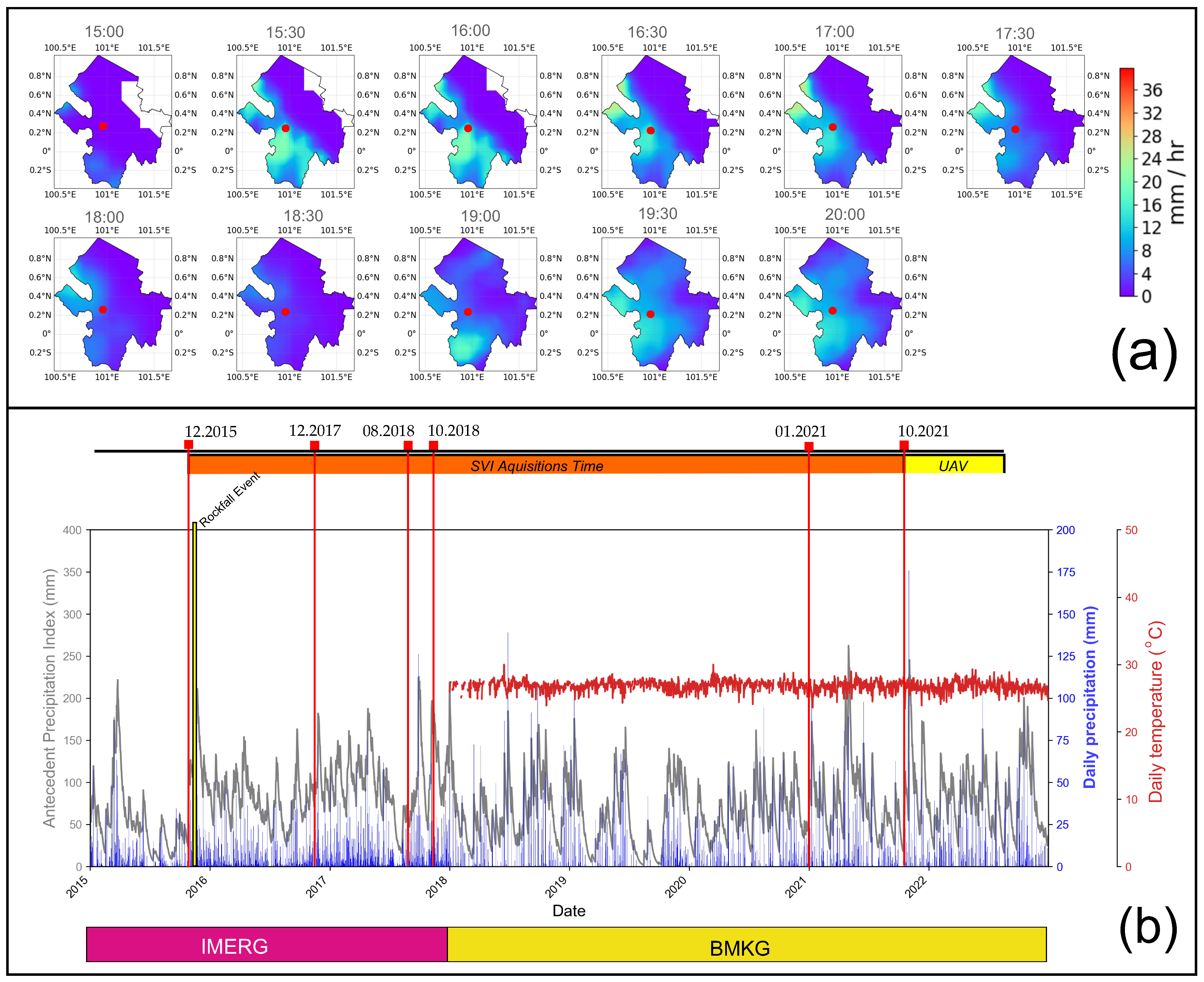
3.3.6. Precipitation Analysis
3.3.7. Trajectography Analysis
4. Results
4.1. Structural Interpretation
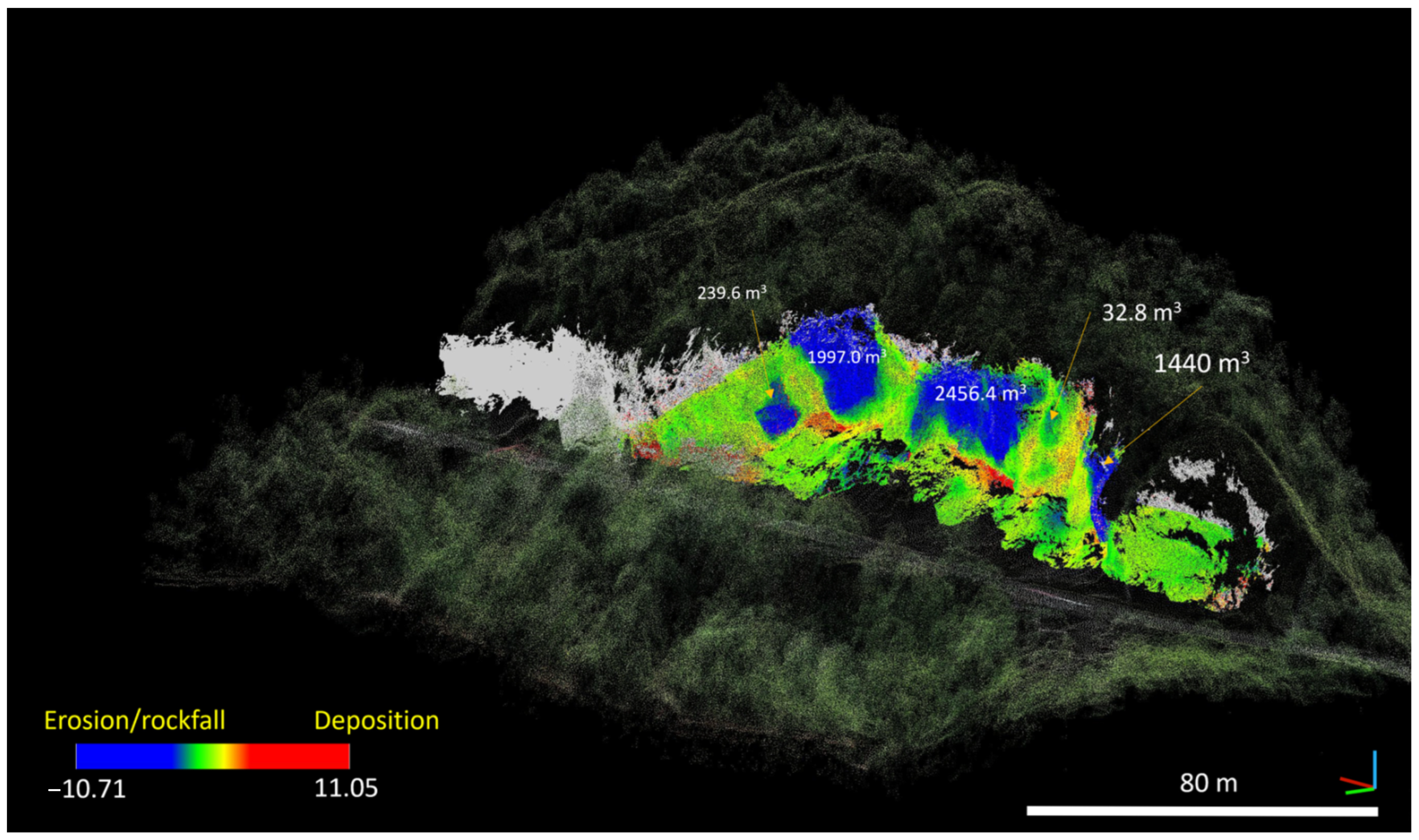
4.2. Comparison of Point Cloud Data
4.3. Precipitation Analysis
4.4. Trajectography Results
5. Discussion
5.1. Volume Calculation
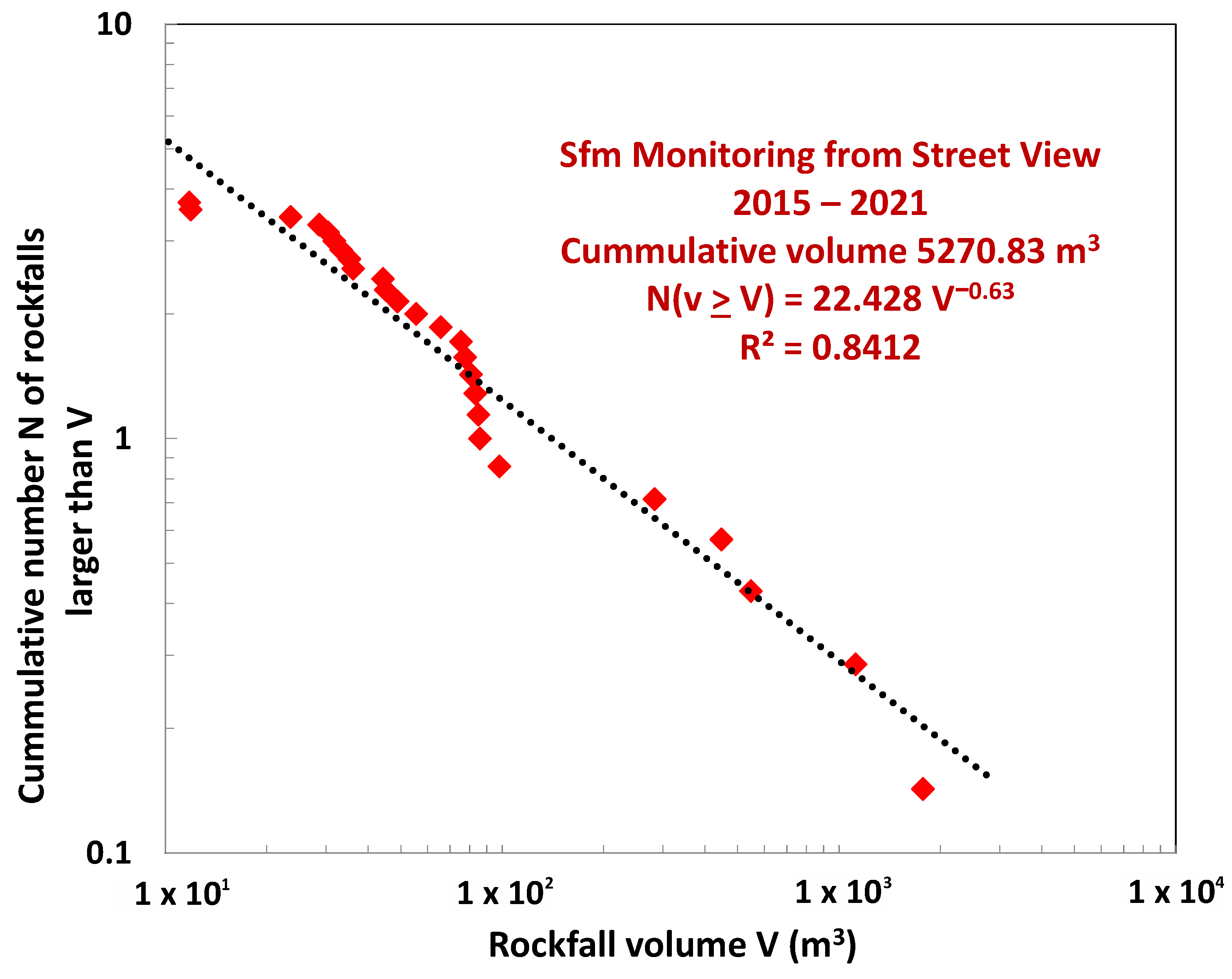
5.2. Rockfall Magnitude vs. Frequencies
5.3. Simulation Accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Voumard, J.; Abellán, A.; Nicolet, P.; Penna, I.; Chanut, M.A.; Derron, M.H.; Jaboyedoff, M. Using street view imagery for 3-D survey of rock slope failures. Nat. Hazards Earth Syst. Sci. 2017, 17, 2093–2107. [Google Scholar] [CrossRef]
- Kromer, R.A.; Hutchinson, D.J.; Lato, M.J.; Gauthier, D.; Edwards, T. Identifying rock slope failure precursors using LiDAR for transportation corridor hazard management. Eng. Geol. 2015, 195, 93–103. [Google Scholar] [CrossRef]
- Oppikofer, T.; Jaboyedoff, M.; Blikra, L.; Derron, M.H.; Metzger, R. Characterization and monitoring of the Åknes rockslide using terrestrial laser scanning. Nat. Hazards Earth Syst. Sci. 2009, 9, 1003–1019. [Google Scholar] [CrossRef]
- Rosser, N.J.; Petley, D.; Lim, M.; Dunning, S.; Allison, R. Terrestrial laser scanning for monitoring the process of hard rock coastal cliff erosion. Q. J. Eng. Geol. Hydrogeol. 2005, 38, 363–375. [Google Scholar] [CrossRef]
- Fernandez-Hernández, M.; Paredes, C.; Castedo, R.; Llorente, M.; de la Vega-Panizo, R. Rockfall detachment susceptibility map in El Hierro Island, Canary Islands, Spain. Nat. Hazards 2012, 64, 1247–1271. [Google Scholar] [CrossRef]
- Graber, A.; Santi, P. UAV-photogrammetry rockfall monitoring of natural slopes in Glenwood Canyon, CO, USA: Background activity and post-wildfire impacts. Landslides 2023, 20, 229–248. [Google Scholar] [CrossRef]
- Guerin, A.; Abellán, A.; Matasci, B.; Jaboyedoff, M.; Derron, M.H.; Ravanel, L. Brief communication: 3-D reconstruction of a collapsed rock pillar from Web-retrieved images and terrestrial lidar data–the 2005 event of the west face of the Drus (Mont Blanc massif). Nat. Hazards Earth Syst. Sci. 2017, 17, 1207–1220. [Google Scholar] [CrossRef]
- Lucieer, A.; Jong, S.M.d.; Turner, D. Mapping landslide displacements using Structure from Motion (SfM) and image correlation of multi-temporal UAV photography. Prog. Phys. Geogr. 2014, 38, 97–116. [Google Scholar] [CrossRef]
- Walstra, J.; Chandler, J.; Dixon, N.; Dijkstra, T. Aerial photography and digital photogrammetry for landslide monitoring. Geol. Soc. Lond. Spec. Publ. 2007, 283, 53–63. [Google Scholar] [CrossRef]
- Vassilakis, E.; Konsolaki, A.; Soukis, K.; Laskari, S.; Kotsi, E.; Lialiaris, J.; Lekkas, E. Rockfall Mapping and Monitoring Across the Kalymnos Sport Rock Climbing Sites, Based on Ultra-High-Resolution Remote Sensing Data and Integrated Simulations. Land 2024, 13, 1873. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Oppikofer, T.; Abellán, A.; Derron, M.H.; Loye, A.; Metzger, R.; Pedrazzini, A. Use of LIDAR in landslide investigations: A review. Nat. Hazards 2012, 61, 5–28. [Google Scholar] [CrossRef]
- Lan, H.; Martin, C.D.; Zhou, C.; Lim, C.H. Rockfall hazard analysis using LiDAR and spatial modeling. Geomorphology 2010, 118, 213–223. [Google Scholar] [CrossRef]
- Tonini, M.; Abellan, A. Rockfall detection from terrestrial LiDAR point clouds: A clustering approach using R. J. Spat. Inf. Sci. 2014, 8, 95–105. [Google Scholar] [CrossRef]
- Vanneschi, C.; Camillo, M.D.; Aiello, E.; Bonciani, F.; Salvini, R. SFM-MVS photogrammetry for rockfall analysis and hazard assessment along the ancient roman via Flaminia road at the Furlo gorge (Italy). ISPRS Int. J. Geo-Inf. 2019, 8, 325. [Google Scholar] [CrossRef]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J.; Afana, A.A. Optimising 4-D surface change detection: An approach for capturing rockfall magnitude–frequency. Earth Surf. Dyn. 2018, 6, 113–116. [Google Scholar] [CrossRef]
- Li, Y.; Peng, L.; Wu, C.; Zhang, J. Street View Imagery (SVI) in the Built Environment: A Theoretical and Systematic Review. Buildings 2022, 12, 1167. [Google Scholar] [CrossRef]
- Google. Explore Street View and Add Your Own 360 Images to Google Maps. Available online: https://www.google.com/streetview/ (accessed on 16 June 2023).
- Biljecki, F.; Ito, K. Street view imagery in urban analytics and GIS: A review. Landsc. Urban Plan. 2021, 215, 104217. [Google Scholar] [CrossRef]
- Anguelov, D.; Dulong, C.; Filip, D.; Frueh, C.; Lafon, S.; Lyon, R.; Ogale, A.; Vincent, L.; Weaver, J. Google Street View: Capturing the World at Street Level. Computer 2010, 43, 32–38. [Google Scholar] [CrossRef]
- William, S.; Yonathan, A. Using google earth and google street view to rate rock slope hazards. Environ. Eng. Geosci. 2018, 24, 237–250. [Google Scholar] [CrossRef]
- Guerin, A.; Stock, G.M.; Radue, M.J.; Jaboyedoff, M.; Collins, B.D.; Matasci, B.; Avdievitch, N.; Derron, M.H. Quantifying 40 years of rockfall activity in Yosemite Valley with historical Structure-from-Motion photogrammetry and terrestrial laser scanning. Geomorphology 2020, 356, 1–17. [Google Scholar] [CrossRef]
- Cameron, N.R. The geological evolution of Northern Sumatra. In Proceedings of the Indonesia Petroleum Association 9th Annual Convention, Jakarta, Indonesia, 27–28 May 1980; pp. 149–187. [Google Scholar]
- Crowell, J.C. Origin of Pebbly Mudstones. GSA Bull. 1957, 68, 993–1010. [Google Scholar] [CrossRef]
- Koesoemadinata, R.P. An Inroduction Into the Geology of Indonesia (General Inroduction and Part I Western Indonesia); Ikatan Alumni Teknik Geologi ITB: Jakarta, Indonesia, 2016; Volume 1, pp. 41–133. ISBN 978-602-7861-38-1. [Google Scholar]
- Cameron, N.R. The stratigraphy of the Sihapas Formation in the Northwest of the Central Sumatra Basin. In Proceedings of the 12th Annual Convention, Jakarta, Indonesia, 11–16 August 1983; Indonesian Petroleum Association: Jakarta, Indonesia, 1983; Volume 1, pp. 43–66. [Google Scholar]
- Curray, J.R. The Sunda Arc: A model for oblique plate convergence. Neth. J. Sea Res. 1989, 24, 131–134. [Google Scholar] [CrossRef]
- Huchon, P.; Le Pichon, X. Sunda strait and central sumatra fault. Geology 1984, 12, 668–672. [Google Scholar] [CrossRef]
- Hamilton, W.B. Tectonics of the Indonesian Region; Report 1078; USGS: Denver, CO, USA, 1979; pp. 32–38. [CrossRef]
- Katili, J.A. A review of the geotectonic theories and tectonic maps of Indonesia. Earth-Sci. Rev. 1971, 7, 143–163. [Google Scholar] [CrossRef]
- McCaffrey, R. The tectonic framework of the Sumatran subduction zone. Annu. Rev. Earth Planet. Sci. 2009, 37, 345–366. [Google Scholar] [CrossRef]
- Barber, A.J. The origin of the Woyla Terranes in Sumatra and the late Mesozoic evolution of the Sundaland margin. J. Asian Earth Sci. 2000, 18, 713–738. [Google Scholar] [CrossRef]
- Barber, A.J.; Crow, M.J.; Milsom, J. Sumatra: Geology, resources and tectonic evolution. Tectonics 2005, 21, 1040. [Google Scholar] [CrossRef]
- Bruno, N.; Roncella, R. Accuracy assessment of 3d models generated from Google Street View imagery. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W9, 181–188. [Google Scholar] [CrossRef]
- Yin, L.; Cheng, Q.; Wang, Z.; Shao, Z. ‘Big data’ for pedestrian volume: Exploring the use of Google Street View images for pedestrian counts. Appl. Geogr. 2015, 63, 337–345. [Google Scholar] [CrossRef]
- Phan, R. equi2cubic: MATLAB Script That Converts Equirectangular Images into Six Cube Faces. 2015. Available online: https://github.com/rayryeng/equi2cubic (accessed on 12 April 2023).
- Bourke, P. Converting to/from Cubemaps. 2020. Available online: https://paulbourke.net/panorama/cubemaps/ (accessed on 12 April 2023).
- Harvey, P. ExifTool 10.11. Available online: https://exiftool.org/ (accessed on 20 June 2022).
- Agisoft. Agisoft Metashape User Manual-Professional Edition; Agisoft: St. Petersburg, Russia, 2022; p. 212. [Google Scholar]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 243–245. [Google Scholar] [CrossRef]
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. 2013, 32, 2–4. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- CloudCompare. CloudCompare 2.12 [GPL Software] 2022. Available online: https://www.cloudcompare.org/release/notes/20220330/ (accessed on 1 June 2020).
- van Veen, M.J. Building a Rockfall Database Using Remote Sensing: Techniques for Hazard Management in Canadian Rail Corridors. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2016. [Google Scholar]
- Jaboyedoff, M.; Metzger, R.; Oppikofer, T.; Couture, R.; Derron, M.H.; Locat, J.; Turmel, D. New insight techniques to analyze rock-slope relief using DEM and 3D-imaging cloud points: COLTOP-3D software. In Proceedings of the 1st Canada-US Rock Mechanics Symposium–Rock Mechanics Meeting Society’s Challenges and Demands, Vancouver, BC, Canada, 27–31 May 2007; Taylor & Francis: Boca Raton, FL, USA, 2007; Volume 1, pp. 61–68. [Google Scholar] [CrossRef]
- Matasci, B.; Stock, G.M.; Jaboyedoff, M.; Carrea, D.; Collins, B.D.; Guérin, A.; Matasci, G.; Ravanel, L. Assessing rockfall susceptibility in steep and overhanging slopes using three-dimensional analysis of failure mechanisms. Landslides 2018, 15, 859–860. [Google Scholar] [CrossRef]
- Hufmann, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. GPM IMERG Final Precipitation L3 Half Hourly 0.1 Degree × 0.1 Degree V06; NASA Goddard Earth Sciences Data and Information Services Center: Greenbelt, MD, USA, 2019.
- Fedora, M.; Beschta, R. Storm runoff simulation using an antecedent precipitation index (API) model. J. Hydrol. 1989, 112, 121–133. [Google Scholar] [CrossRef]
- Noël, F.; Cloutier, C.; Jaboyedoff, M.; Locat, J. Impact-Detection Algorithm That Uses Point Clouds as Topographic Inputs for 3D Rockfall Simulations. Geosciences 2021, 11, 188. [Google Scholar] [CrossRef]
- Noel, F. stnParabel Documentation. 2021. Available online: https://stnparabel.org/ (accessed on 20 October 2021).
- Graber, A. Power law models for rockfall frequency-magnitude distributions: Review and identification of factors that influence the scaling exponent. Geomorphology 2022, 418, 14–18. [Google Scholar] [CrossRef]
- Hantz, D.; Corominas, J.; Crosta, G.B.; Jaboyedoff, M. Definitions and Concepts for Quantitative Rockfall Hazard and Risk Analysis. Geosciences 2021, 11, 158. [Google Scholar] [CrossRef]
- Corominas, J.; Mavrouli, O.; Ruiz-Carulla, R. Rockfall Occurrence and Fragmentation. In Proceedings of the Advancing Culture of Living with Landslides; Sassa, K., Mikoš, M., Yin, Y., Eds.; Springer: Cham, Switzerland, 2017; pp. 75–97. [Google Scholar] [CrossRef]
- Moos, C.; Bontognali, Z.; Dorren, L.; Jaboyedoff, M.; Hantz, D. Estimating rockfall and block volume scenarios based on a straightforward rockfall frequency model. Eng. Geol. 2022, 309, 106828. [Google Scholar] [CrossRef]
- Hantz, D.; Colas, B.; Dewez, T.; Lévy, C.; Rossetti, J.P.; Guerin, A.; Jaboyedoff, M. Caractérisation quantitative des aléas rocheux de départ diffus. Rev. Fr. Geotech. 2020, 163, 2. [Google Scholar] [CrossRef]
- Mavrouli, O.; Corominas, J.; Jaboyedoff, M. Size distribution for potentially unstable rock masses and in situ rock blocks using LIDAR-generated digital elevation models. Rock Mech. Rock Eng. 2015, 48, 1589–1604. [Google Scholar] [CrossRef]
- Hantz, D.; Lévy, C. Quantification de l’aléa diffus. In Rapport C2ROP, 2019; C2ROP: Paris, France, 2019; pp. 1–29. [Google Scholar]
- Noël, F.; Nordang, S.F. Quantitative Rockfall Hazard Assessment of the Norwegian Road Network and Residences at an Indicative Level from Simulated Trajectories. Remote Sens. 2025, 17, 819. [Google Scholar] [CrossRef]


| Time of Acquisition (MM.YYYY) | No. of Images | Acquisition Method |
|---|---|---|
| 12.2015 | 26 | SVI |
| 12.2017 | 19 | SVI |
| 08.2018 | 26 | SVI |
| 10.2018 | 28 | SVI |
| 01.2021 | 36 | SVI |
| 10.2021 | 280 | UAV |
| Cube Face | Rotation |
|---|---|
| front | - |
| left | Pan by 90 degrees |
| right | Pan by −90 degrees |
| back | Pan by 180 degrees |
| top | Tilt by −90 degrees |
| bottom | Tilt by 90 degrees |
| Discontinuity Set | Dip Direction/Dip from Field Measurements (°) | Discontinuity/m | Dip Direction/Dip from Point Cloud Measurements (°) | Tolerance Angle |
|---|---|---|---|---|
| J1 | 5 | ±15.0 | ||
| J2 | 5 | ±15.0 | ||
| J3 | 5 | ±15.0 | ||
| J4 | 5 | ±15.0 | ||
| J5 | 5 | ±15.0 | ||
| J6 | 5 | ±15.0 |
| Parameter | Value |
|---|---|
| 3D terrain model | 22,625,890 points |
| Friction Angle | |
| Cohesion | 30 kPa |
| Volume | 1 m3 |
| Density | 2700 kg/m3 |
| No. of Simulations | 100 each sources |
| Parameter | UAV Imagery | Street View Imagery |
|---|---|---|
| Perspective | Aerial (top-down), variable altitudes. | Ground-level (human-eye height), 360° panoramas. |
| Resolution and Detail | Sub-centimeter resolution; excels in overhead details (e.g., outcrops). | 5–10 cm/pixel at ground level; captures horizontal features (e.g., hillsides, signs). |
| Coverage | Flexible: remote areas, off-road, hazardous zones. | Road-focused: urban/rural streets with vehicle access. |
| Data | Real-time updates possible; customizable frequency, Sufficiently generated visuals. | Historical archives available, often outdated (1–2+ years old), limited image availability. |
| Cost | Higher cost (USD 1k–USD 50 k with equipment, permits, skilled operators). | Free/low-cost (Google Maps, APIs); instant access to existing data. |
| Limitations | Regulatory hurdles, weather-dependent, short battery life (20–60 min). | Limited coverage (e.g., narrow alleys, private property), privacy blurring obscures details. |
| Strengths | High spatial accuracy, 3D modeling, dynamic monitoring. | Human-scale context, street visual analysis. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choanji, T.; Jaboyedoff, M.; Yuskar, Y.; Samsu, A.; Fei, L.; Derron, M.-H. Evolution of Rockfall Based on Structure from Motion Reconstruction of Street View Imagery and Unmanned Aerial Vehicle Data: Case Study from Koto Panjang, Indonesia. Remote Sens. 2025, 17, 1888. https://doi.org/10.3390/rs17111888
Choanji T, Jaboyedoff M, Yuskar Y, Samsu A, Fei L, Derron M-H. Evolution of Rockfall Based on Structure from Motion Reconstruction of Street View Imagery and Unmanned Aerial Vehicle Data: Case Study from Koto Panjang, Indonesia. Remote Sensing. 2025; 17(11):1888. https://doi.org/10.3390/rs17111888
Chicago/Turabian StyleChoanji, Tiggi, Michel Jaboyedoff, Yuniarti Yuskar, Anindita Samsu, Li Fei, and Marc-Henri Derron. 2025. "Evolution of Rockfall Based on Structure from Motion Reconstruction of Street View Imagery and Unmanned Aerial Vehicle Data: Case Study from Koto Panjang, Indonesia" Remote Sensing 17, no. 11: 1888. https://doi.org/10.3390/rs17111888
APA StyleChoanji, T., Jaboyedoff, M., Yuskar, Y., Samsu, A., Fei, L., & Derron, M.-H. (2025). Evolution of Rockfall Based on Structure from Motion Reconstruction of Street View Imagery and Unmanned Aerial Vehicle Data: Case Study from Koto Panjang, Indonesia. Remote Sensing, 17(11), 1888. https://doi.org/10.3390/rs17111888






