Improving the Regional Precipitation Simulation Corrected by Satellite Observation Using Quantile Mapping

Abstract

This study investigates how to use the gridded satellite datasets of observational precipitation to improve the performance of the climatological simulation by using the method of non-parametric quantile mapping (QM). The precipitation in Southeast Asia is simulated in 2001–2005 using the climate model of Weather Research and Forecasting (WRF). Two satellite datasets of observational precipitation, GSMaP and CHIRPS, are used for model training, simulation evaluation, and cross-validation. The evaluations of simulation and bias correction suggest that QM is able to perfectly correct the overall quantile distributions of the simulated precipitation, which is characterized by overestimation at most quantiles, especially for light and extreme precipitation. After the QM correction based on GSMaP (CHIRPS), the relative bias of the monthly average for all months is reduced from 39.3% to 4.1% (from 57.2% to 4.2%). The biases of spatial patterns are largely narrowed from 43.5% (59.4%) to 4.0% (2.5%) for annual-mean precipitation and from 43.5% (59.4%) to 4.0% (2.5%) for extreme precipitation. The results indicate that the QM correction based on the gridded satellite datasets outperforms the raw model output and greatly improves the estimates of the simulated precipitation.

1. Introduction

Regional climate models have been widely used in the downscaling modeling of global data products in some regions like the western United States [1], West Africa [2], and Eastern China [3]. Convection-permitting simulation with high resolution [4] can improve the simulation and prediction of precipitation by better capturing the spatiotemporal distribution in terms of the intensity and frequency of precipitation [5], the extreme precipitation [6], the orographic precipitation [7], and the precipitation diurnal cycle [8].

Regional climate models are important tools to study climate and its change over a desired region at high spatial resolutions. However, there exists some uncertainty, especially for precipitation estimates, owing to its highly variable nature in space and time. Ehret et al. [9] reviewed the bias-correction methods and discussed whether and when to apply the bias correction to the global and regional climate model data. Because of the chaos effect, point-to-point bias correction with the observation for the modeled output is not meaningful in the long-term climatological simulations, which prevents the application of regression predictions using machine learning methods. The probability distribution is a critical metric for evaluating climatological simulations, especially for extremes. Due to the imperfections of the climate model, the biases in the probability distribution reflect the model uncertainty. For daily precipitation and surface mean temperature over Southeast Asia, the study by Ngai et al. [10] indicated that additional improvement is not evident when the regional climate model downscales from the global climate models before bias correction, and correcting the bias distribution stemming out of downscaling is a challenge.

The quantile mapping (QM) technique has been widely employed in bias corrections for regional climate modeling. Pastén-Zapata et al. [11] applied different parametric quantile-mapping methods to the output of the Euro-CORDEX regional climate models and evaluated the performance skills of precipitation and temperature. Rajczak et al. [12] found that the regional climate model output has systematic biases of precipitation in transition probabilities and spell lengths, but deterministic QM shows an improvement in bias correction. Instead of assuming parametric distributions, non-parametric distribution mapping has been widely applied in the dynamical and statistical downscaling of daily precipitation and other hydrologic processes from climate model outputs [13,14,15], satellite soil moisture [16], as well as the bias correction of precipitation in the regional climate models for historical simulation [17].

What is more, QM has also been applied to climate change and future projections [18]. Because QM can artificially corrupt future model-projected trends, QM, detrended QM, and quantile delta mapping are presented to evaluate how much reserve changes in the bias correction of precipitation of the global climate model [19]. To preserve the raw projected change in climate models, Switanek et al. [20] proposed a method of scaled distribution mapping and Grillakis et al. [21] also documented an advanced method. Soriano et al. [22] confirmed that the QM technique can reduce the errors of climate projection of flood frequency.

As mentioned above, there have been relatively few studies previously on bias correction for the high-resolution simulation by using the QM. This study aims to develop the algorithm for non-parametric QM and improve the skills in correcting the climatological simulations of precipitation based on the gridded dataset of satellite observations. In this study, we designed an approach to solving the bias correction of quantile distribution for regional modeling through gridded observations, which can effectively eliminate both seasonal dependency and regional dependency. Under the constraint of the observed and modeled training datasets in history, the correction model can be effectively applied in the regimes without available observations, like the long-term climatological simulation or the future projection for the regional climate. Therefore, for the sake of robustness, cross-validation is used to evaluate the corrected performance.

In the following paper, Section 2 introduces the observed and modeled datasets and the QM method. Section 3 analyzes the evaluation results of bias correction in terms of quantile distribution, annual cycle, and spatial pattern. Section 4 provides a discussion. Finally, Section 5 summarizes the main conclusions of this study.

2. Datasets and Methods

2.1. Study Area

The study area is Southeast Asia (90–140°E, 15°S–26°N), which is shown in the red box in Figure 1. The Southeast Asia region features complex and diverse terrains, such as the mountains in the Indochinese Peninsula, the Mekong Delta plain, and numerous islands. This region is located in the tropical warm pool, and the numerous islands complicate the distribution of land and sea. These factors disrupt atmospheric circulation and water-vapor transport, which increases the difficulty of regional precipitation simulation [10,23].

2.2. Observational Datasets of Precipitation

The observations include two gridded datasets of satellite remote sensing, which are calibrated by gauge observations during the production process: (a) Global Satellite Mapping of Precipitation (GSMaP), Gauge-calibrated Rainfall Product (Version 5), with a 0.1° × 0.1° horizontal resolution on both sea and land [24], which is available on the JAXA website [25]. (b) Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS), Rainfall Estimates from Rain Gauge and Satellite Observations (Version 2.0), with a 0.05° × 0.05° horizontal resolution on only land [26]. The temporal frequency is at hourly intervals and the period considered in this study is 2001–2005. CHIRPS data can be downloaded from the CHIRPS website of the Climate Hazards Center (CHC) [27]. The daily mean of precipitation rate (units: mm day⁻¹) is used as the observed reference for this study.

2.3. WRF Simulations

This study uses the Weather Research and Forecasting (WRF) model (3.9.1 version). The description of WRF is available on the website of WRF Users Page [28]. The climatological simulation in Southeast Asia (90–140°E, 15°S–26°N) is at a 0.075° × 0.075° horizontal resolution. As a state-of-the-art atmospheric numerical model, WRF uses the fully compressible Eulerian non-hydrostatic equations [29]. The vertical coordinate adopts the hybrid terrain-following pressure levels. This study used 50 levels with the top pressure at 50 hPa. As to the configurations of physics parameterization schemes, the WRF Single-Moment 6-class scheme (microphysics) [30], Rapid Radiative Transfer Model (Longwave) [31], Goddard shortwave (Shortwave) [32], MM5 surface layer scheme [33], Noah Land-Surface Model [34] and Yonsei University scheme (Planetary Boundary Layer) [35], along with the convection-permitting simulation (closed cumulus convection scheme) [4], were applied. The model spins up from 1 October 2000 and ends on 31 December 2005. The 5 full years (2001–2005) were selected for the evaluation period. The daily precipitation (units: mm day⁻¹) was derived from the average of the hourly WRF model output and remapped into 0.1° and 0.05° horizontal grids as that of GSMaP and CHIRPS. Later, the QM was applied over remapped WRF outputs with reference to GSMaP and CHIRPS datasets.

2.4. Non-Parametric Quantile Mapping

In a distribution of random variables, the quantiles related to the values can be expressed by the cumulative distribution function (CDF) [36] as

$$quantile=\mathrm{CDF}\left(value\right).$$

(1)

The CDF is invertible and the values can be obtained from the inverse CDF as

$$value={\mathrm{CDF}}^{-1}\left(quantile\right).$$

(2)

The CDFs of simulation and observation are denoted by the ${\mathrm{CDF}}_{sim}$ and ${\mathrm{CDF}}_{obs}$, respectively. Because simulation and observation should be under a similar scenario, it is reasonable to make the assumption that simulation and observation have the same quantile distribution. In principle, QM aims to correct the simulation biases so that the corrected simulations and the observation are equal at the same quantiles [11,12,15,19]. Equation (1) is applied on the simulation dataset to obtain the quantile of the simulated values. Then, this quantile is input to Equation (2) trained from the observed dataset to obtain the corrected values. Therefore, the function of corrected values is expressed as

$$correct={\mathrm{CDF}}_{obs}^{-1}\left(quantile\right)={\mathrm{CDF}}_{obs}^{-1}\left({\mathrm{CDF}}_{sim}\left(valu{e}_{sim}\right)\right).$$

(3)

For the non-parametric QM, the CDFs for both observation and simulation have no parameterized analytical function, which are empirically estimated from the sorted discrete data [15,37,38,39]. The number of observation and the number of simulation are allowed to be different, and point-to-point correspondence of samples is not required. The empirical estimation of CDF is conducted by the following the method.

The samples are sorted from small to large and labeled by the permutation numbers from 1 to N with the increment of 1. The quantile is equal to the permutation numbers divided by N. If the samples have duplicated values, only the one with the larger quantile remains, to keep the values unique. Hence, the discrete series of the pairs of quantile and value constructs the mapping relationship to describe the empirical CDF. Because both the quantile and value are unique and strictly increase monotonically, the CDF is therefore invertible and its inverse function CDF⁻¹ can also be empirically estimated. Since CDF is described by a discrete series of the quantile–value pair, if the values of the quantile or value do not exist in the discrete series, the estimation is obtained by the linear interpolation from the adjacent values on both sides.

2.5. Training and Prediction

The samples are separated into training set and validation set for both observation and simulation. The hypothesis is that the simulations in the validation and training sets have the same quantile distribution [12]. Thereby, for each value of simulation in the validation set, we can find the same value in the training set and locate its quantile in the training set. The corresponding value in the observation with the same quantile will be then regarded as the corrected value of the simulations in the validation. The calculation follows the two steps:

Step 1: The ${\mathrm{CDF}}_{sim}$ (Equation (1)) of simulation and ${\mathrm{CDF}}_{obs}^{-1}$ (Equation (2)) of observation are empirically estimated from the training set.

Step 2: For each value of simulation in the validation set, the correction is estimated according to Equation (3). Considering that the minimum of precipitation is 0, the simulation values with a quantile smaller than the quantile of the minimum in the training set are corrected to the minimum. If the simulation values in the validation set are greater than the maximum of the training set, the data are not enough for linear interpolation. The corrected bias takes the corrected bias at the quantile of 0.995.

Due to the distinction of the dominant circulation systems related to the various surface properties and annual climatological cycle, the probability distributions vary in different regions and seasons [40]. Given the regional dependency, the correction is based on the training at the same location and processed grid by grid. If QM corrects bias based on the complete distribution, the errors still exists in the annual cycle, so the sub-annual sampling can further improve the reliability [41]. Considering the seasonal dependency, when correcting a specified month, the data of the closest three months are used for training first. Then, if the values are greater than the 99% quantile in the seasonal training set, the full-year data are used for training.

To better reflect the robustness of this method, a cross-validation procedure is employed, which can separate between training and validation [42]. To make the most of the limited 5 years of data, when correcting a specified year for validation, the data in the other years are used as the training set. For example, when correcting the simulated data in 2002, the observed and simulated data in 2001, 2003, 2004, and 2005 are used for training. Through this method, the corrected year is not used in training the parameters. After 5 years are corrected, the observed data are used for validation and evaluation.

3. Results

3.1. Correction of Quantile Distribution

Firstly, we validated the bias correction of the overall distribution through QM. The purpose of using two different datasets of observed precipitation is to test whether QM can adapt well to the observed dependence, where GSMaP comprises 0.1° × 0.1° grids on both sea and land while CHIRPS comprises 0.05° × 0.05° grids on only land. The empirical CDFs of daily precipitation in Figure 2 are estimated from all the daily time steps and spatial grids in the observations and WRF simulations. The WRF simulations and the QM correction are compared using observed precipitation, GSMaP and CHIRPS, respectively. At most quantiles, the WRF simulates noticeably overestimated precipitation in comparison to the observations. Relative to the smaller bias at the median, the simulation of light precipitation (0–3 mm day⁻¹), and extreme precipitation have much greater biases. The results agree with the previous study, which identified that all six regional models they considered produced more rainfall than the observations over Southeast Asia [10].

WRF tends to produce a smaller proportion of no precipitation relative to observations. As shown in Figure 2a, the percentages of no precipitation in GSMaP observation and WRF simulation are 47.1% and 15.5%, respectively. The QM correction shows the proportion of no precipitation is 44.4%. Based on CHIRPS in Figure 2b, the percentages of observations and WRF simulations are 63.6% and 26.1%, respectively. After the QM correction, the proportion of no precipitation is 63.3%. Therefore, the QM corrections are both much closer to observations in comparison to the raw WRF simulation.

Figure 2 shows that, after QM, the curves of the empirical CDF almost overlay the observations. Furthermore, at the key quantiles of 50%, 75%, and 95%, the precipitation corrected by the QM is also much better than the WRF simulation based on both GSMaP and CHIRPS, which is shown in

Table 1. A comparison of precipitation at the key quantiles (units: mm day⁻¹).

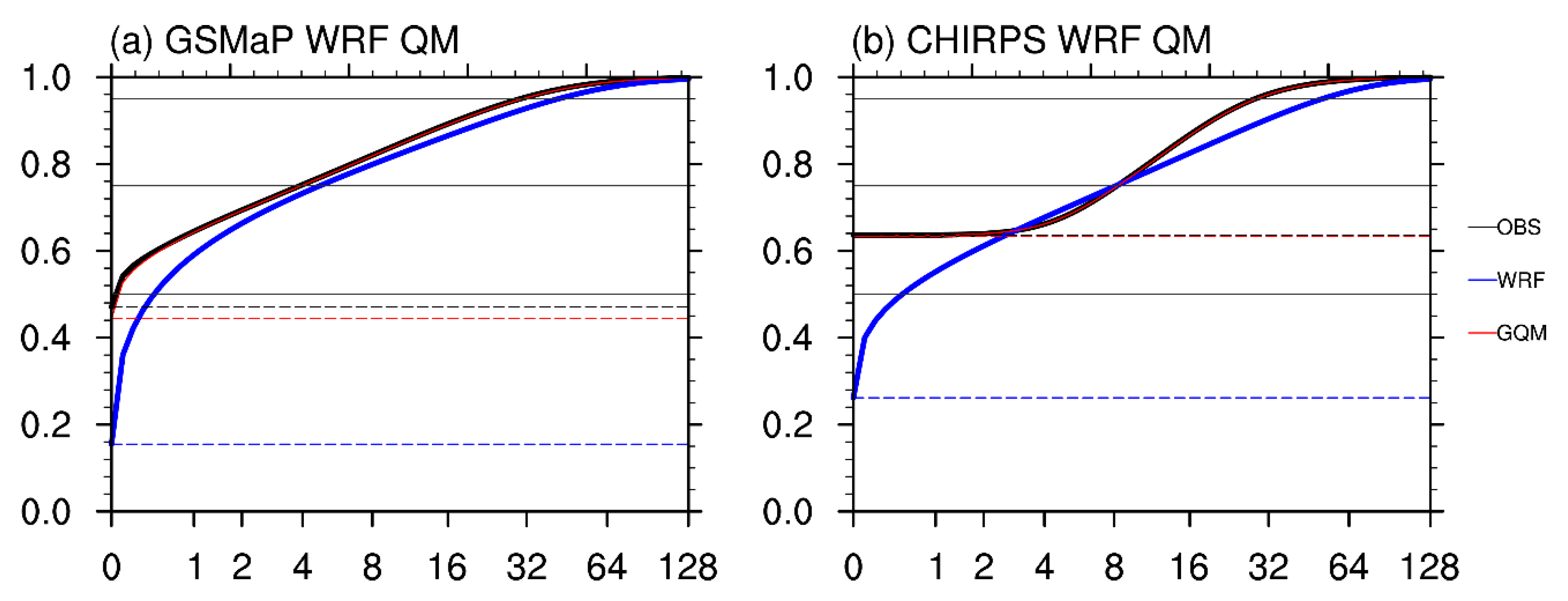
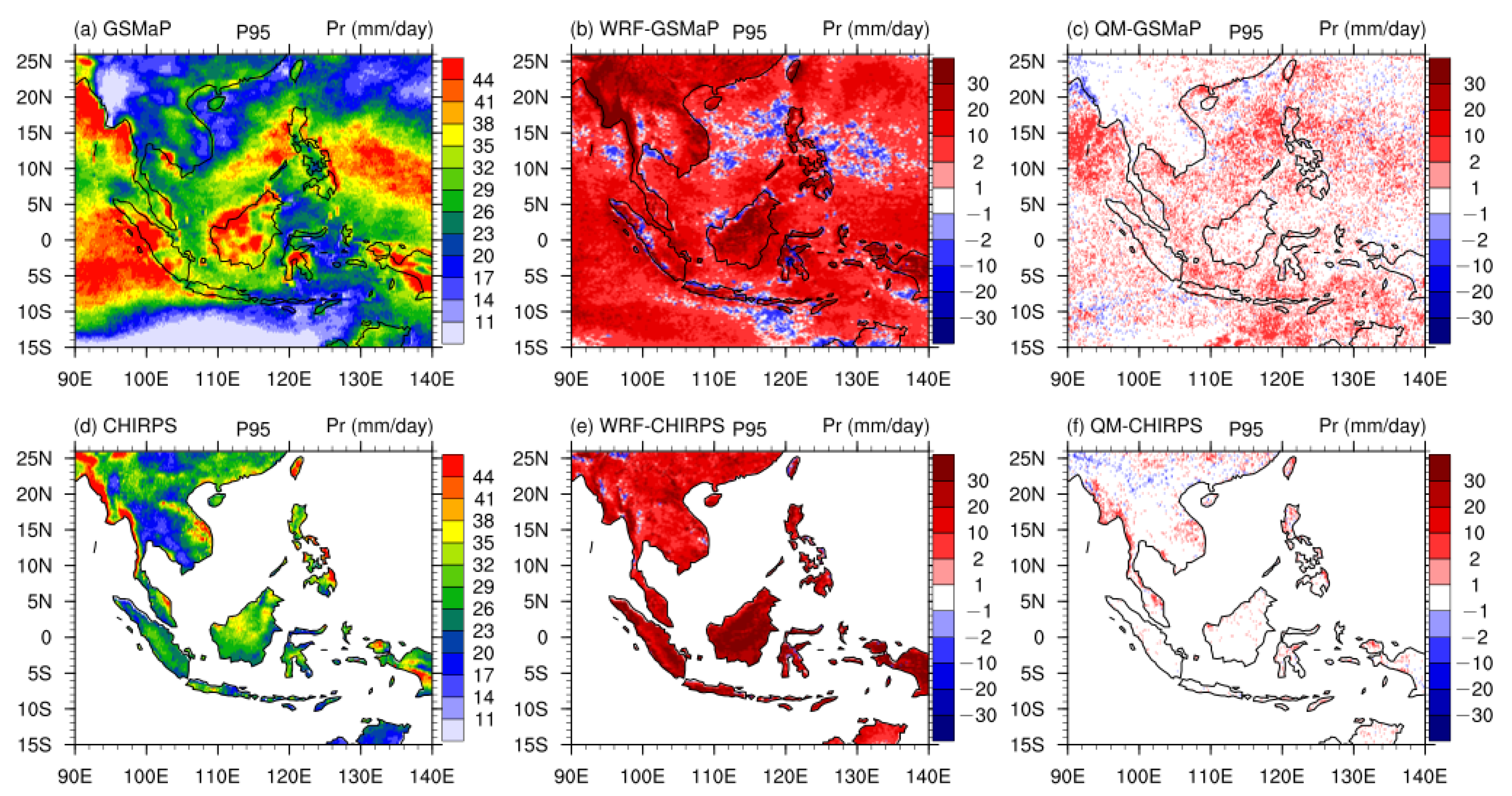
Reference	Quantiles	Observation	WRF Simulation	QM Correction	Bias of WRF	Bias After QM
GSMaP	50%	0.02	0.43	0.05	0.41	0.03
	75%	3.89	4.79	3.95	0.90	0.06
	95%	30.19	42.03	30.83	11.84	0.64
CHIRPS	50%	0	0.51	0	0.51	0
	75%	8.23	8.14	8.28	–0.09	0.05
	95%	28.45	50.87	28.76	22.42	0.31

. The results indicate that, besides the training dataset, QM can also perfectly correct the systematic biases between the WRF simulations and observations in terms of overall quantile distribution.

3.2. Validation of Annual Correction

Due to the monsoonal contrast, the precipitation over Southeast Asia is relatively greater from May to September than in the other months [43]. To validate whether the bias correction of QM performs well in the annual cycle without seasonal dependency, Figure 3 compares the observations, the WRF simulations, and the QM corrections for all months, whose quantile distribution is collected from all the spatial grids in the 5-year validation sets. Based on GSMaP and CHIRPS, the results show that WRF simulated higher averages and extremes of precipitation in all months, while the QM correction is close to observation.

We evaluated metrics on an average of 12 months. Relative to the WRF simulation, the QM correction reduces the absolute bias of the precipitation average from 2.16 mm day⁻¹ to 0.23 mm day⁻¹ (from 3.44 mm day⁻¹ to 0.25 mm day⁻¹) and the relative bias from 39.3% to 4.1% (from 57.2% to 4.2%) based on GSMaP (CHIRPS). In addition, the QM correction reduces the absolute bias of the precipitation extremes at the 95% quantile from 11.65 mm day⁻¹ to 0.74 mm day⁻¹ (from 21.64 mm day⁻¹ to 0.80 mm day⁻¹) and the relative bias from 38.7% to 2.5% (from 76.6% to 2.8%) based on GSMaP (CHIRPS). Regarding the quantiles of 25%, 50%, and 75%, the QM correction reduces the absolute bias from 0.02 mm day⁻¹ to 0 mm day⁻¹ (from 0.02 mm day⁻¹ to 0 mm day⁻¹), from 0.42 mm day⁻¹ to 0.02 mm day⁻¹ (from 0.79 mm day⁻¹ to 0 mm day⁻¹), and from 1.10 mm day⁻¹ to 0.22 mm day⁻¹ (2.12 mm day⁻¹ to 0.40 mm day⁻¹), respectively. Therefore, the results conclude that QM in this study was able to effectively correct the biases in the annual cycle without seasonal dependency.

3.3. Validation of Spatial Correction

Due to the diversity of the surface terrain property and land–sea distribution, the local distribution of precipitation varies in different regions. Considering the regional dependency, this study adopted grid-by-grid correction by using QM. Figure 4 and Figure 5 show the spatial patterns of the annual mean and extremes of precipitation in 2001–2005, respectively. The precipitation displays a strong heterogeneity over Southeast Asia and the heavy precipitation is distributed between 10°S and 15°N (Figure 4a,d and Figure 5a,d). The overestimated precipitation of the WRF simulation is pronounced in most regions in terms of annual mean (Figure 4b,e) and 95% quantile (Figure 5b,e). In most regions, the QM correction is skillful, especially for land precipitation, and can reduce the biases within 0.2 mm day⁻¹ for annual mean precipitation (Figure 4c,f) and within 1 mm day⁻¹ for precipitation extremes (Figure 5c,f). Concerning annual-mean precipitation based on GSMaP (CHIRPS), the QM correction reduces the grid-averaged absolute bias from 2.39 mm day⁻¹ (3.58 mm day⁻¹) to 0.22 mm day⁻¹ (0.15 mm day⁻¹) and reduces the relative bias from 43.5% (59.4%) to 4.0% (2.5%). Meanwhile, regarding precipitation extremes based on GSMaP (CHIRPS), the QM correction reduces the grid-averaged absolute bias from 11.38 mm day⁻¹ (19.54 mm day⁻¹) to 0.93 mm day⁻¹ (0.66 mm day⁻¹) and reduces the relative bias from 40.3% (68.8%) to 3.3% (2.3%).

4. Discussion

Generally, more samples are better for training the model when using QM. However, the practical applications are often limited by the number of samples. The question is how many such data samples are suitable for training the QM for bias correction. In the cross-validation of this study, we used 4-year daily data to correct the other year, while the application of the correction was grid by grid, sampling from three months. Therefore, the training samples are around 360, which is sufficient to build the empirical CDFs and obtain accurate bias corrections.

In this study, we used the high-resolution gridded observed precipitation datasets to correct the bias of the regional model output. The resolution of observation (0.1° × 0.1° and 0.05° × 0.05°) is close to the simulation (0.075° × 0.075°). Making use of the available observation, this study provides an efficient solution to correct the bias of the grided output of the regional climate model, which may be applied to a wide variety of scenarios and increase the confidence of simulation. However, for most variables, it is difficult to find the observation at a resolution scale of model simulations. As to how to apply the low-resolution observations to correct the high-resolution simulations, or only apply the QM on the large scale of coarse resolution but maintaining the small-scale perturbation, will be useful to consider in future studies.

In previous studies, QM has achieved certain developments, but there are also some problems in its application [30,31,32,33,34,35,36]. The QM was used as a statistical downscaling method from the regional model output to the station scale [44]. Regarding the bias correction of precipitation and temperature, Gudmundsson et al. [37] and Enayati et al. [38] introduced and compared multiple methods of QM, including distribution-derived transformations, parametric transformations, and non-parametric transformations (empirical quantiles, robust empirical quantiles, smoothing splines). Their results concluded that non-parametric transformations have the best-corrected skills to reduce the systematic bias for simulated precipitation. In addition, multivariate QM also was developed for bias-correcting climate model output [45,46]. However, Maraun [47] pointed out that the variance inflation issue existed in downscaling with the local gauged observation. QM could not introduce the variability to the smaller scale to resolve the scale mismatch. QM could not resolve the problems of bias, reliability, and coherence which pre-exist in the forecasting data [48].

Nonetheless, QM has promising value in other applications, especially correcting climate projections and conserving the climate-change signal, and further exploration is possible, such as bias correction for satellite-based precipitation products [49,50], data fusion for generating long-term continuous datasets [51], post-processing for the probabilistic forecast of precipitation [52], and the impacts of the future temperature on the health risk [53]. We will continue to apply the methods of this study to bias correction for the simulation of other variables, such as temperature, wind, cloud, ocean, and so on. The QM will be further developed and applied to the bias correlation in extreme climate events and climate future projection.

5. Conclusions

Based on the satellite observations, the present study applied the QM bias corrections to improve the regional climate simulations of precipitation in Southeast Asia from 2001 to 2005. A novel method was designed to correct the systematic bias of daily precipitation by using QM for the gridded output of the regional climate model WRF. Two observed gridded datasets of precipitation (GSMaP and CHIRPS) were used to train the transformation. The biases of the WRF simulation and the QM correction were compared with respect to these two observed datasets. In terms of the overall distribution, annual cycle, and spatial patterns, the performance of the QM correction is evaluated via cross-validation. The results indicate that the QM correction clearly outperforms the raw model output. The main findings are as follows.

(1) The WRF simulates noticeably overestimated precipitation at most quantiles, especially for light and extreme precipitation. The QM can successfully correct the quantile distribution of simulation onto the observation, which can be seen by the well overlaid CDF curves.

(2) The QM was able to effectively correct the distribution biases for all months in the annual cycle without seasonal dependency. Regarding the average, the relative bias is reduced from 39.3% to 4.1% (from 57.2% to 4.2%) based on GSMaP (CHIRPS).

(3) Based on GSMaP (CHIRPS), the validation of spatial patterns verifies that the QM correction can largely narrow the biases from 43.5% (59.4%) to 4.0% (2.5%) for annual-mean precipitation and from 43.5% (59.4%) to 4.0% (2.5%) for precipitation extremes.