A Distributed Low-Degree-of-Freedom Aerial Target Localization Method Based on Hybrid Measurements
Abstract
1. Introduction
2. Materials and Methods
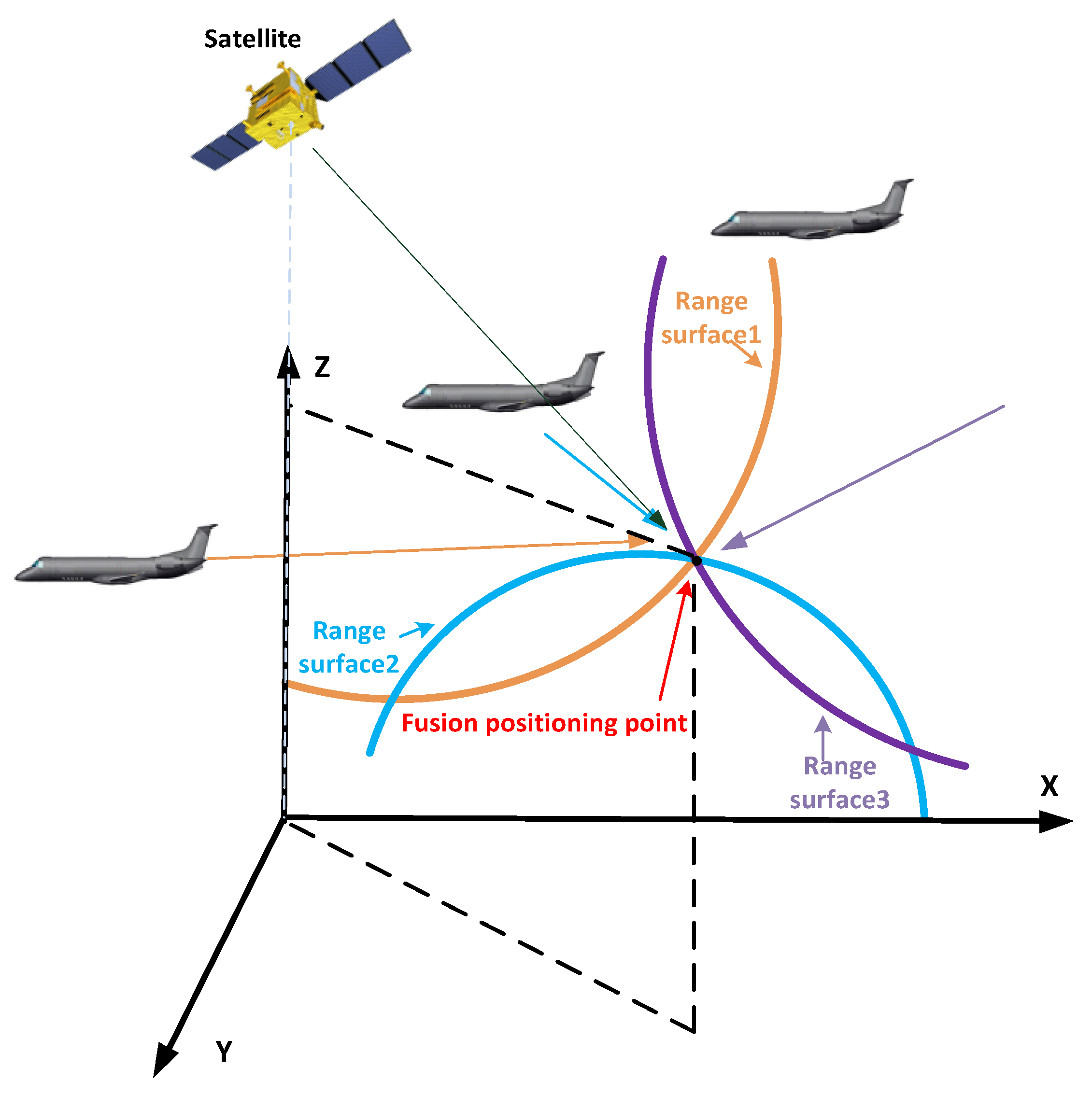
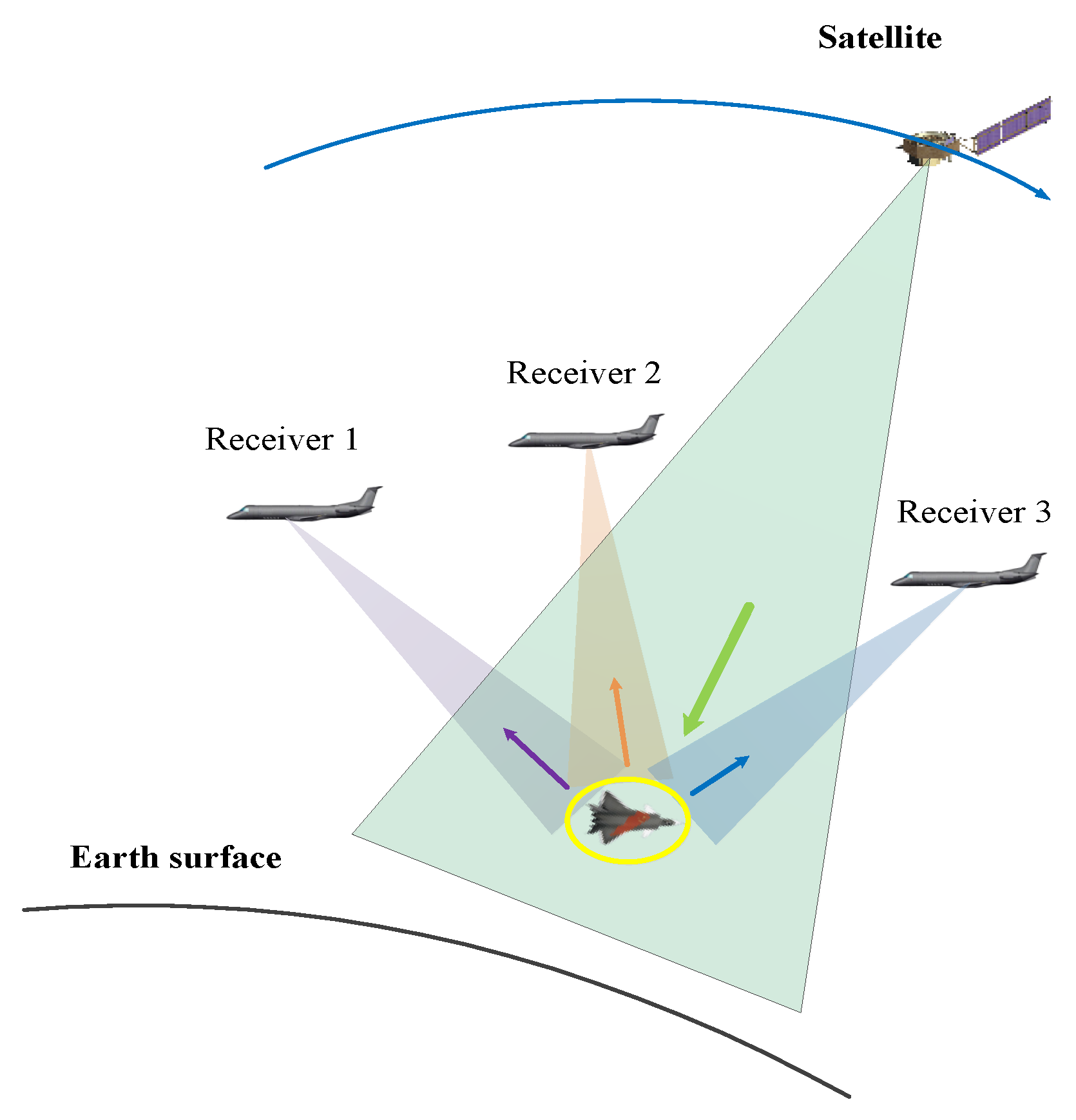
2.1. Measurement Model
2.1.1. Intra-Station Measurements
2.1.2. Inter-Station Measurements
2.2. Proposed Method
2.2.1. Intra-Station and Inter-Station Hybrid Measurements for Estimating the X-Coordinate and Reference Distance
2.2.2. Enhancing Parameter Estimation Accuracy with FDOA Measurements
2.2.3. Utilizing Inter-Station Measurements to Achieve Three-Station Target Localization
2.2.4. Cramér–Rao Lower Bound
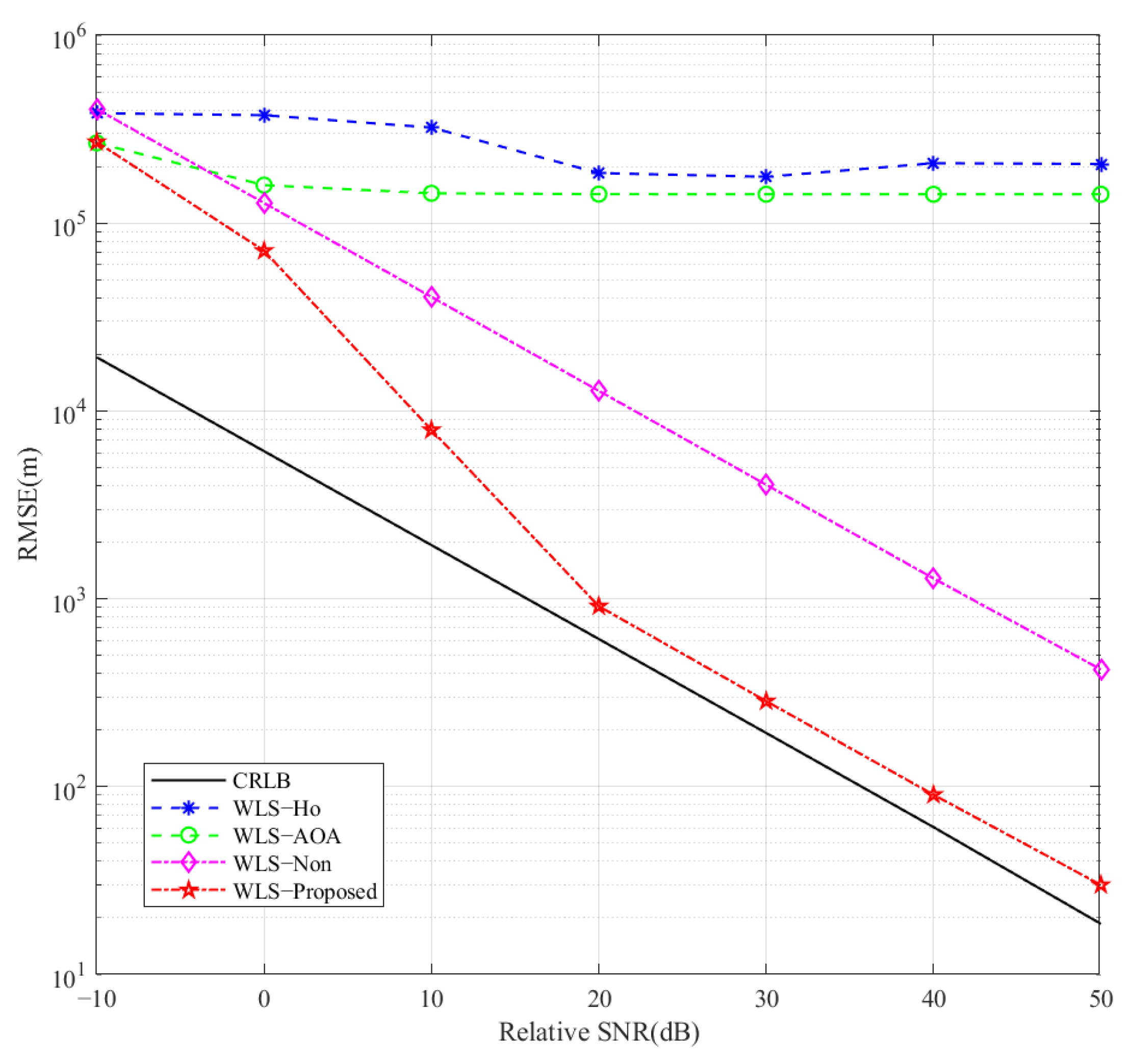
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poisel, R.A. Information Warfare and Electronic Warfare Systems, 1st ed.; Artech House: Norwood, MA, USA, 2013. [Google Scholar]
- Reza, A.; Buehrer, R.M. Handbook of Position Location: Theory, Practice and Advances, 1st ed.; IEEE: Hoboken, NJ, USA, 2019. [Google Scholar]
- Chen, L.; Luo, J. Localization in Radar Networks: Techniques, Challenges, and Applications. IEEE Access 2020, 8, 115653–115668. [Google Scholar]
- Yang, J.; Wen, C.K.; Jin, S. Hybrid Active and Passive Sensing for SLAM in Wireless Communication Systems. IEEE J. Sel. Areas Commun. 2022, 40, 2146–2163. [Google Scholar] [CrossRef]
- Zuo, L.; Wang, J.; Li, N. Detection of weak target based on stretch processing and chirp-z transform in passive bistatic radar. In Proceedings of the CIE International Conference on Radar, Haikou, China, 15–19 December 2021. [Google Scholar]
- Feng, S.; Wang, G.L.; Ma, W. Eliminating False Localization from Passive TDOA Measurements. In Proceedings of the CIE International Conference on Radar, Guangzhou, China, 10–13 October 2016. [Google Scholar]
- Motie, S.; Zayyani, H. Self UAV Localization Using Multiple Base Stations Based on TDOA Measurements. IEEE Wirel. Commun. Lett. 2024, 13, 2432–2436. [Google Scholar] [CrossRef]
- Ren, W.; Wei, Y. Optimal Algorithm of Dual-satellite Navigation Information Based on Inertial Assistance. In Proceedings of the International Conference on Information Science and Technology, Chengdu, China, 21–23 May 2021. [Google Scholar]
- Wei, F.; Yan, S. Target location in distributed MIMO radar based on Coherent Processing. In Proceedings of the 2024 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Zhuhai, China, 22–24 November 2024. [Google Scholar]
- Jabbari, M.R.; Taban, M.R. Asymptotically Efficient Moving Target Localization in Distributed Radar Networks. IEEE Trans. Signal Inf. Process. Over Networks 2023, 9, 569–580. [Google Scholar] [CrossRef]
- Xiong, K.; Cui, G.L. Distributed Localization of Target for MIMO Radar with Widely Separated Directional Transmitters and Omnidirectional Receivers. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3171–3187. [Google Scholar] [CrossRef]
- Marino, A.; Soldi, G. 3D Localization and Tracking Methods for Multiplatform Radar Networks. IEEE Aerosp. Electron. Syst. Mag. 2024, 39, 18–37. [Google Scholar] [CrossRef]
- Bosse, J.; Krasnov, O. A simple direct target localization and deghosting algorithm in active radar network. In Proceedings of the International Radar Conference, Lille, France, 13–17 October 2014. [Google Scholar]
- Decarli, N.; Guidi, F. A Novel Joint RFID and Radar Sensor Network for Passive Localization: Design and Performance Bounds. IEEE J. Sel. Top. Signal Process. 2014, 8, 80–95. [Google Scholar] [CrossRef]
- Dang, L.F.; Yang, H.C. Application of Time-Difference-of-Arrival Localization Method in Impulse System Radar and the Prospect of Application of Impulse System Radar in the Internet of Things. IEEE Access 2018, 6, 44846–44857. [Google Scholar] [CrossRef]
- Li, J.Z.; Lv, S. Performance Analysis for Space-Air-Ground Integrated Passive Localization using TDOA Measurements. In Proceedings of the IEEE International Conference on Unmanned Systems (ICUS), Guangzhou, China, 28–30 October 2022. [Google Scholar]
- Matharia, A.S.; Kaity, S. Improvement of Position Measurement by TDOA Technique using K-Means Clustering. In Proceedings of the International Conference on Range Technology (ICORT), Balasore, India, 23–25 February 2023. [Google Scholar]
- Zhou, Z.; Liang, C. Comprehensive Node Selection Strategy for Multi-Target TDOA Localization in UAV Swarm. In Proceedings of the IEEE 7th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 15–17 September 2023. [Google Scholar]
- Wang, D.; Zhang, P.C. A Novel Estimator for TDOA and FDOA Positioning of Multiple Disjoint Sources in the Presence of Calibration Emitters. IEEE Access 2019, 8, 2169–3536. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Nguyen, V.L. Tracking Risks from Muti-path TDOA-based Localization in Wireless Communications. In Proceedings of the International Conference on Advanced Communication Technology (ICACT), Pyeongchang, Republic of Korea, 19–22 February 2023. [Google Scholar]
- Sahu, C.; Banavar, M. Data-Driven Nonlinear TDOA for Accurate Source Localization in Complex Signal Dynamics. IEEE Sens. J. 2024, 24, 31018–31025. [Google Scholar] [CrossRef]
- Yang, L.J.; Gao, H.T. 3D Joint Estimation of Position and Velocity for a Moving Target in Multistatic Radar System by VHC-2WLS Algorithm. IEEE Commun. Lett. 2020, 24, 1939–1943. [Google Scholar] [CrossRef]
- Cui, C.; Dong, X.C. Performance Analysis and Configuration Design of Geosynchronous Spaceborne-Airborne Bistatic Moving Target Indication System. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020. [Google Scholar]
- Godrich, H.; Petropulu, A.P. Power Allocation Strategies for Target localization in Distributed Multiple-Radar Architectures. IEEE Trans. Signal Process. 2011, 59, 3226–3240. [Google Scholar] [CrossRef]
- Wang, W.Q.; So, H.C. Transmit Subaperturing for Range and Angle Estimation in Frequency Diverse Array Radar. IEEE Trans. Signal Process. 2014, 62, 2000–2011. [Google Scholar] [CrossRef]
- Hui, J.; Chai, H.Z. Enhancement of Target Localization based on angle-of-arrival measurement via quantum sensor networks. IEEE Sens. J. 2024, 25, 9298–9306. [Google Scholar] [CrossRef]
- Tsinos, C.G.; Arora, A. Joint Radar-Communication Systems by Optimizing Radar Performance and Quality of Service for Communication Users. IEEE Trans. Radar Syst. 2024, 7, 778–790. [Google Scholar] [CrossRef]
- Hull, B.; Kuza, L. A model-based systems approach to radar design utilizing muti-attribute decision analysis techniques. In Proceedings of the 2018 Systems and Information Engineering Design Symposium (SIEDS), Charlottesville, VA, USA, 27 April 2018. [Google Scholar]
- Wang, X.; Zhou, S.H. Waveform Design of Conformal MIMO Radar for Polarization Parameters Estimation. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021. [Google Scholar]
- Shajaiah, H.; Abdelhadi, A. Spectrum Sharing Approach between Radar and communication System and Its Impact on Radar’s Detectable Target Parameters. In Proceedings of the 2015 IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, UK, 11–14 May 2015. [Google Scholar]
- Xu, Z.Y.; Petropulu, A. A Bandwidth Efficient Dual-Function Radar Communication System based on a MIMO Radar Using OFDM Waveforms. IEEE Trans. Signal Process. 2023, 71, 401–416. [Google Scholar] [CrossRef]
- Chan, Y.T.; Ho, K.C. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef]
- Zou, Y.B.; Fan, J.N. Improved Weighted Least Squares Algorithm for Hybrid AOA and TDOA Localization. In Proceedings of the 2023 IEEE Statistical Signal Processing Workshop (SSP), Hanoi, Vietnam, 2–5 July 2023. [Google Scholar]
- Ho, K.C.; Kovavisaruch, L.; Parikh, H. Source localization using TDOA with erroneous receiver positions. In Proceedings of the 2004 IEEE International Symposium on Circuits and Systems (ISCAS), Vancouver, BC, Canada, 23–26 May 2004; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar]
- Chen, J.M.; Li, Y.; Yang, X.; Li, Q.; Liu, F.; Wang, W.; Li, C.; Duan, C. A Two-Stage Aerial Target Localization Method Using Time Difference of Arrival Measurements with the Minimum Number of Radars. Remote Sens. 2023, 15, 2829. [Google Scholar] [CrossRef]
- Jiao, X.; Zhang, J. An Aerial Target Localization Method Using TOA and AOA Measurements with GEO-UAV Bistatic Configuration. Adv. Electr. Comput. Eng. 2024, 24, 19–26. [Google Scholar] [CrossRef]
- Roland, O.; Peter, W.; Uwe, A. Cognitive Radar Performance Analysis with different Types of Targets. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019. [Google Scholar]
- Zhang, Z.; Nian, Y.J.; Chen, J.; He, M. An Experimental Study to Optimize the Stepped-Frequency Continuous-Wave Radar Parameters for Noncontact Multi-target Vital Sign Monitoring. In Proceedings of the 2019 IEEE International Conference on Computational Electromagnetics (ICCEM), Shanghai, China, 20–22 March 2019. [Google Scholar]
- Gong, J.K.; Yan, J.; Kong, D.; Li, D. Introduction to cognitive micro-Doppler radar: Optimization and Experiment. In Proceedings of the 2023 IEEE International Radar Conference(RADAR), Sydney, Australia, 6–10 November 2023. [Google Scholar]
- Wang, Y.Q.; Wu, N.; Zhang, X. Research on multi-satellite distributed passive coherent location method. Chin. Space Sci. Technol. 2023, 43, 63–68. [Google Scholar]
- Zhu, Z.R.; Zhu, L.d. A single satellite location algorithm based on weighted least square carrier frequency estimation. Space Electron. Technol. 2021, 18, 9–15. [Google Scholar]
- Li, J.; Ding, J.S.; Wen, L.; Yu, Z.; Huang, D. An improved planar approximation localization method in distributed airborne radars. In Proceedings of the 2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Hyderabad, India, 6–11 April 2025. [Google Scholar]
- Xu, Z.; Song, Y.P.; Chen, L.; Zhu, J.; Zhang, P.; An, D.; Jin, T. SAR simultaneous localization and imaging method based on closed-loop structure along arc-line motion. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–14. [Google Scholar] [CrossRef]
- Niu, W.; Guo, Y.; Han, X.; Ma, R.; Zheng, W.; Peng, X.; Yang, Z. A high-frame-rate-imaging-based framework for moving point target detection in very low SNR. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 943–958. [Google Scholar] [CrossRef]
- Caffery, J.; Stuber, G.L. Overview of radiolocation in CDMA cellular systems. IEEE Commun. Mag. 1998, 36, 38–45. [Google Scholar] [CrossRef]
- Smith, J.O.; Abel, J.S. Closed-form least-squares source location estimation from range-difference measurements. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1661–1669. [Google Scholar] [CrossRef]
- Torrieri, D. Statistical theory of passive location systems. IEEE Trans. Aerosp. Electron. Syst. 1984, AES-20, 2183–2198. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory, 1st ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]



| Symbol | Meaning |
|---|---|
| Bold lowercase letters | Vectors |
| Bold uppercase letters | Matrices |
| Superscript T | Transpose operation |
| Inverse operator | Inverse of a matrix or vector |
| Arccos | Inverse cosine function |
| Tilde (~) on a vector | Estimated or approximate value of the vector |
| Hat (^) on a vector | Best estimate obtained through least squares method |
| The Euclidean norm |
| Types | WLS-Ho | WLS-AOA | WLS-Non | WLS-Update |
|---|---|---|---|---|
| X direction bias (m) | 84,920 | 327 | 13 | 13 |
| Y direction bias (m) | 7414 | 328 | 95 | 95 |
| Z direction bias (m) | 145,218 | 62,844 | 8144 | 847 |
| Localization accuracy (m) | 168,389 | 62,846 | 8145 | 853 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, X.; Chen, J.; Jiang, L.; Li, W.; Yang, X.; Wang, W.; Zhang, J. A Distributed Low-Degree-of-Freedom Aerial Target Localization Method Based on Hybrid Measurements. Remote Sens. 2025, 17, 1705. https://doi.org/10.3390/rs17101705
Jiao X, Chen J, Jiang L, Li W, Yang X, Wang W, Zhang J. A Distributed Low-Degree-of-Freedom Aerial Target Localization Method Based on Hybrid Measurements. Remote Sensing. 2025; 17(10):1705. https://doi.org/10.3390/rs17101705
Chicago/Turabian StyleJiao, Xiaoshuang, Jinming Chen, Lifeng Jiang, Weiping Li, Xiaochao Yang, Weiwei Wang, and Jun Zhang. 2025. "A Distributed Low-Degree-of-Freedom Aerial Target Localization Method Based on Hybrid Measurements" Remote Sensing 17, no. 10: 1705. https://doi.org/10.3390/rs17101705
APA StyleJiao, X., Chen, J., Jiang, L., Li, W., Yang, X., Wang, W., & Zhang, J. (2025). A Distributed Low-Degree-of-Freedom Aerial Target Localization Method Based on Hybrid Measurements. Remote Sensing, 17(10), 1705. https://doi.org/10.3390/rs17101705








