Using Geodetic Data to Monitor Hydrological Drought at Different Spatial Scales: A Case Study of Brazil and the Amazon Basin
Abstract
1. Introduction
2. Study Area and Datasets
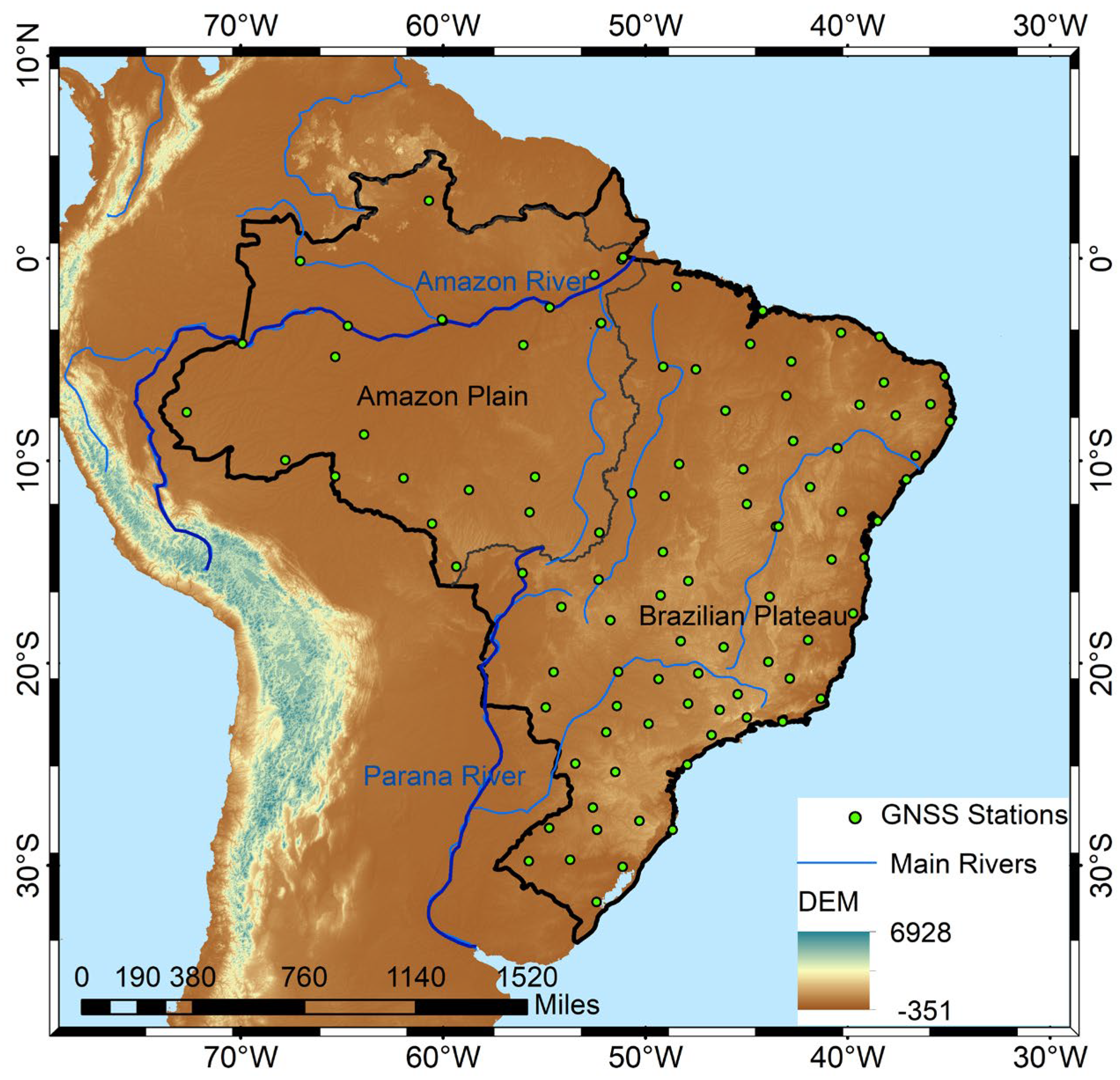
2.1. Study Area
2.2. GNSS Data
2.3. GRACE/GFO Data
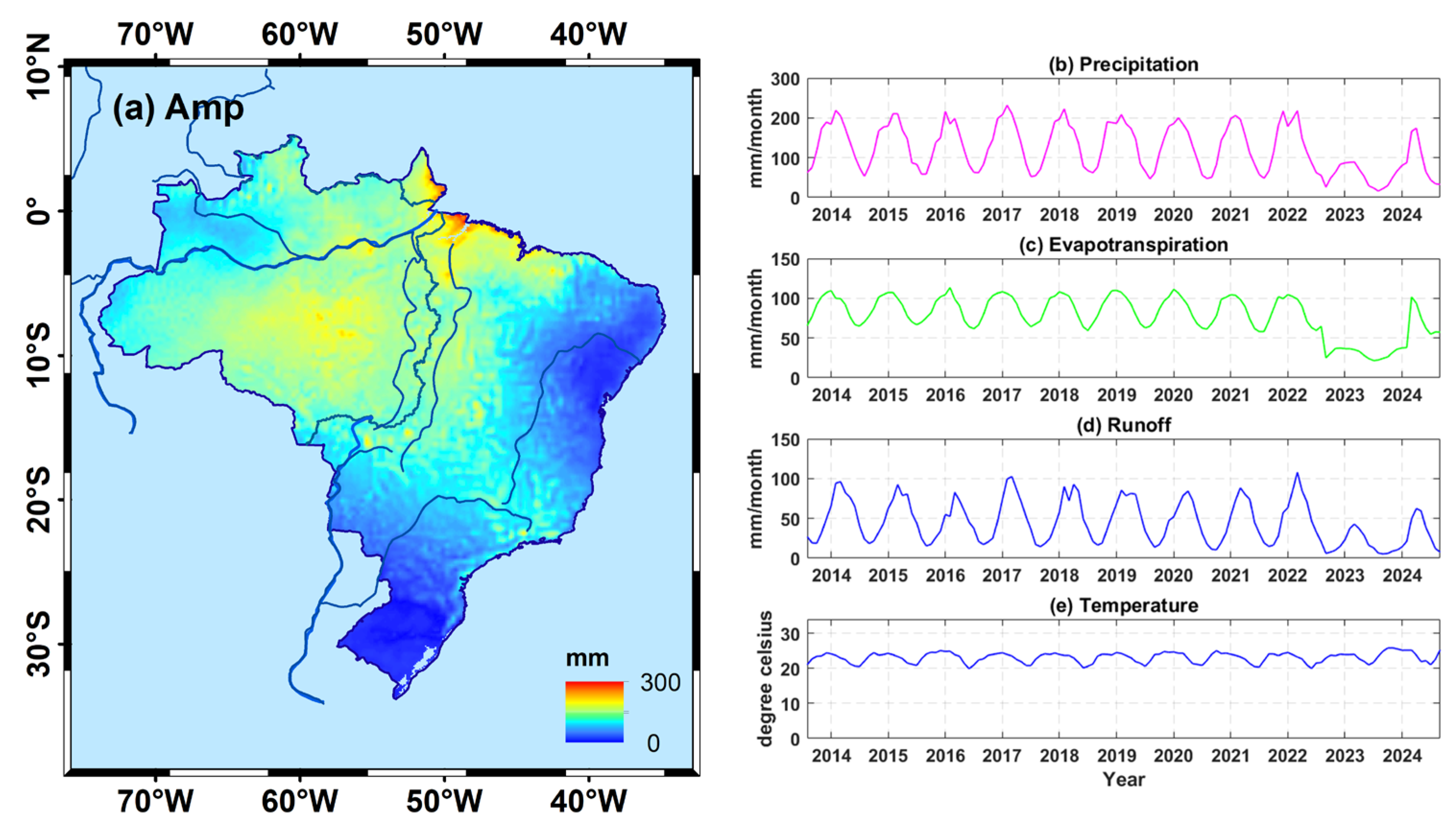
2.4. Hydrometeorological Data
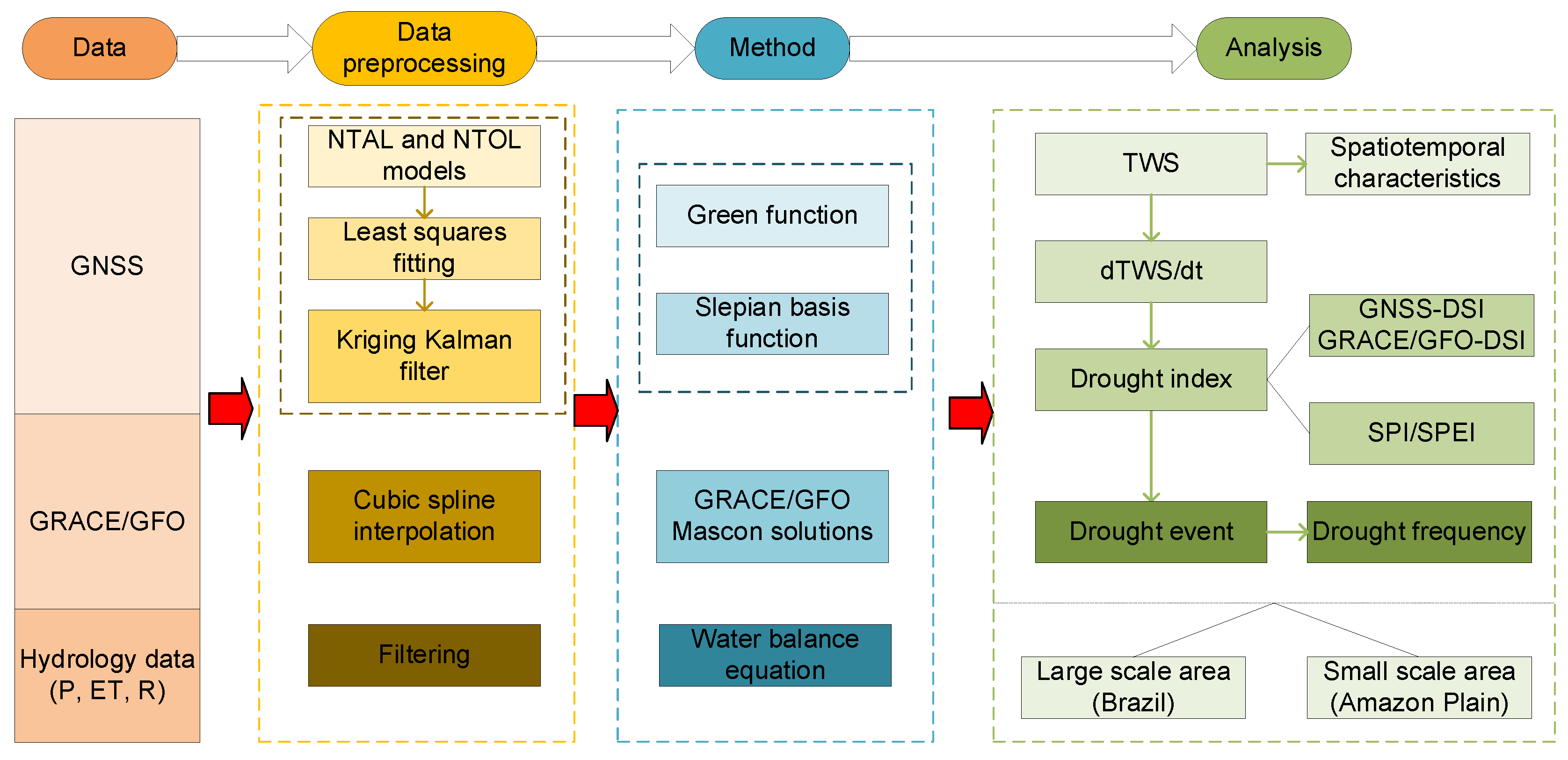
3. Methodology
3.1. Green’s Function Method
3.2. Slepian Basis Function Method
3.3. Drought Index
4. Results
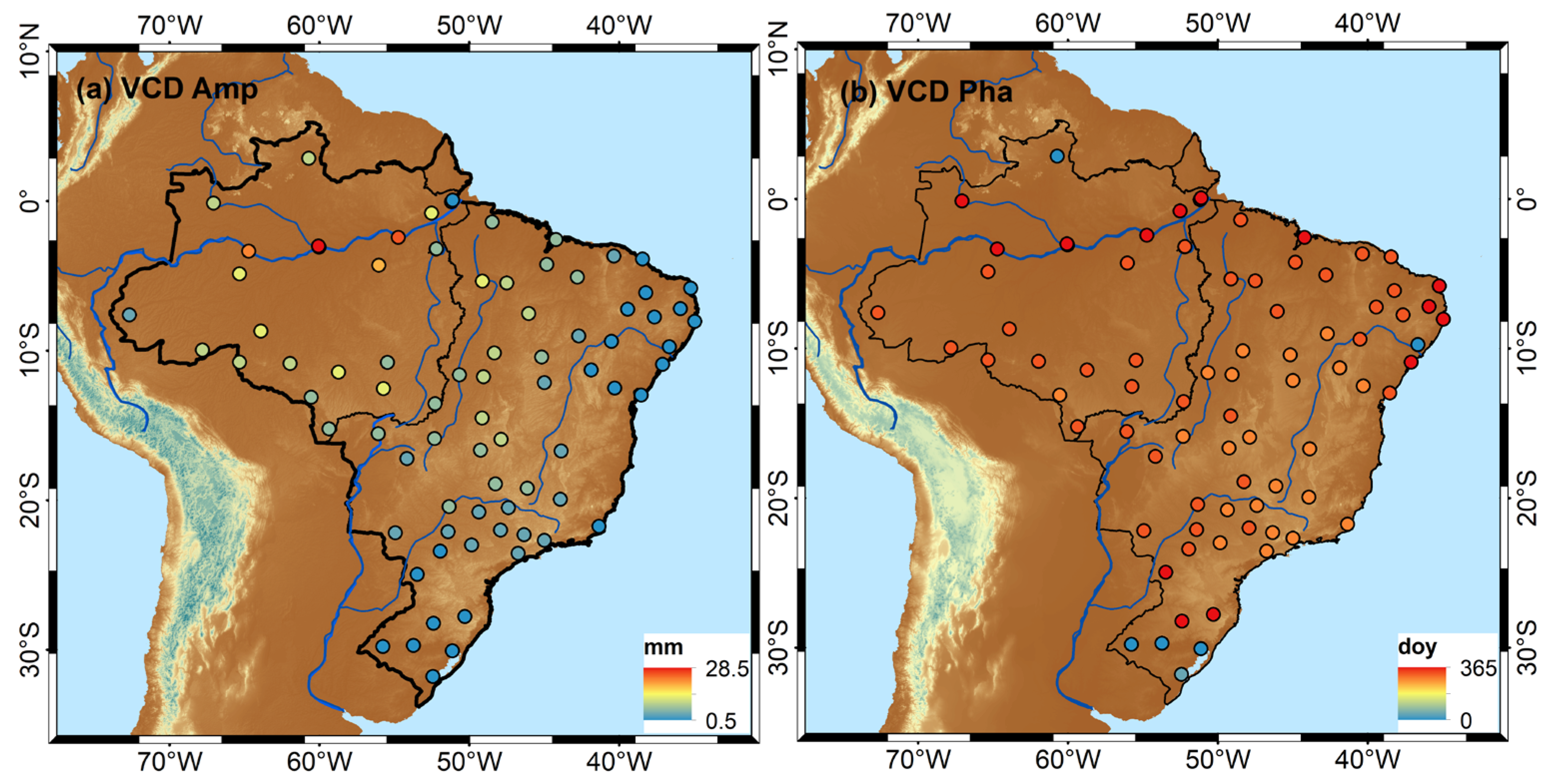
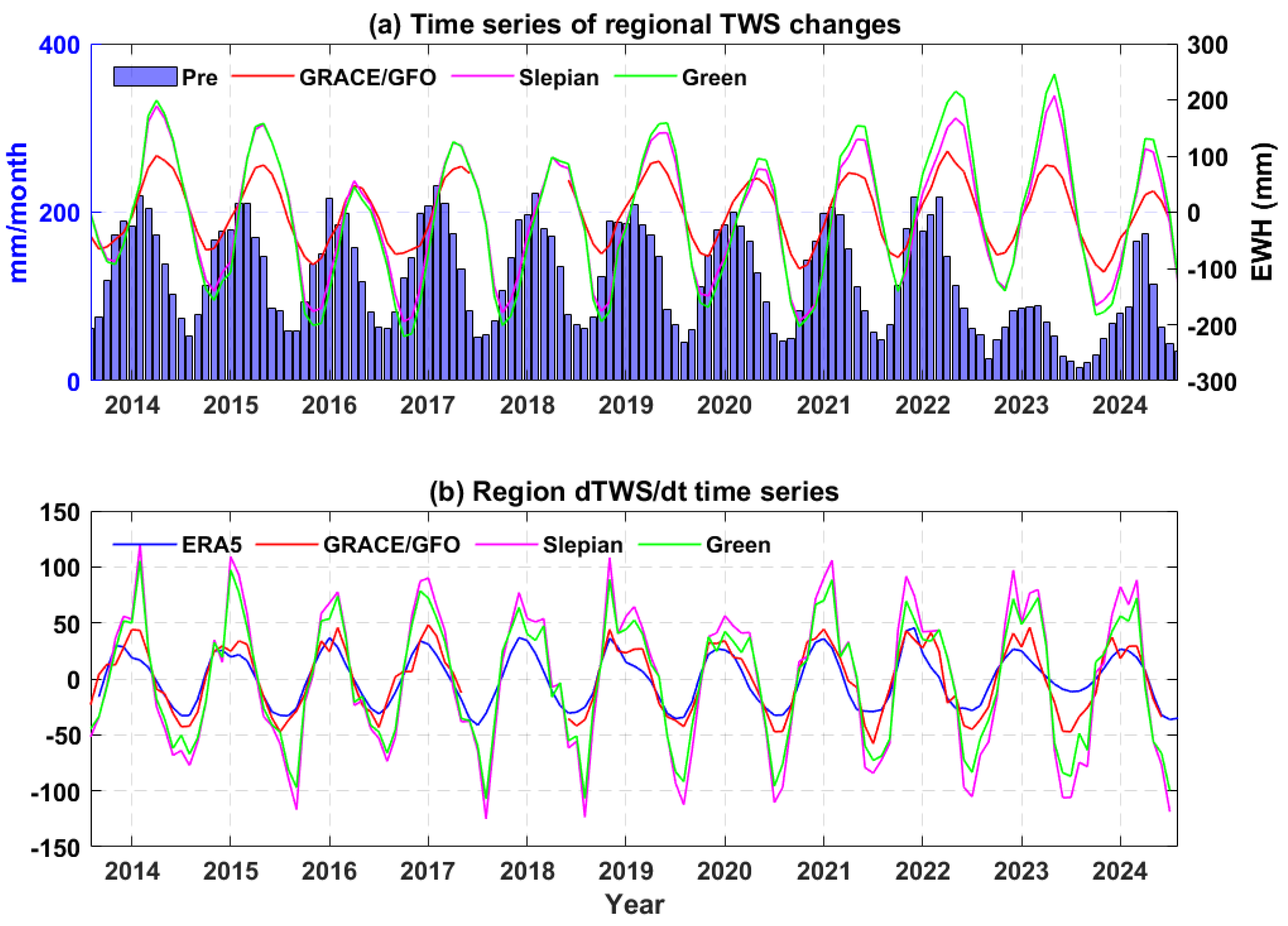
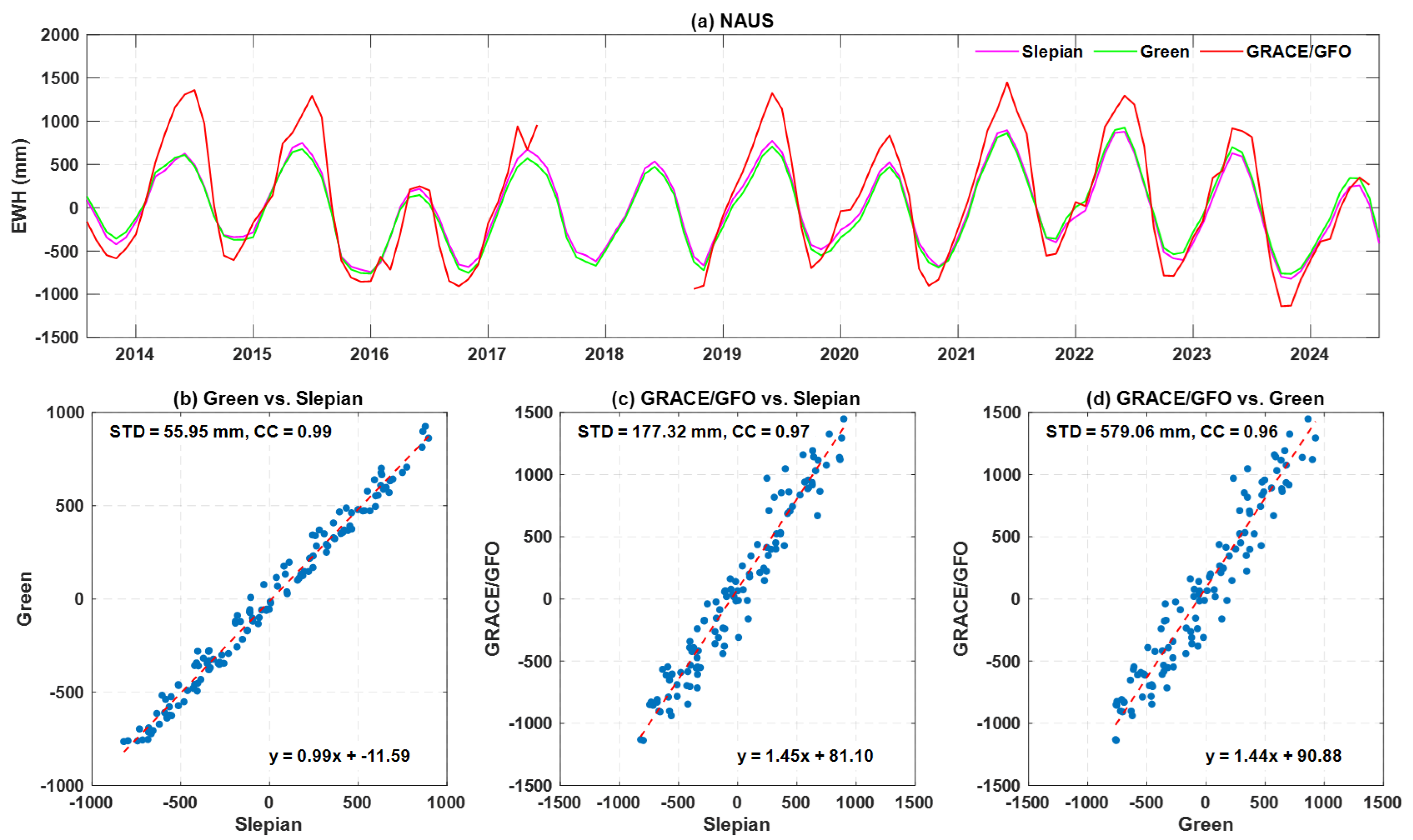
4.1. Spatiotemporal Characteristics of GNSS-Derived Hydrological Mass Loading
4.2. Spatiotemporal Characteristics of TWS Inversion Using Geodetic Data
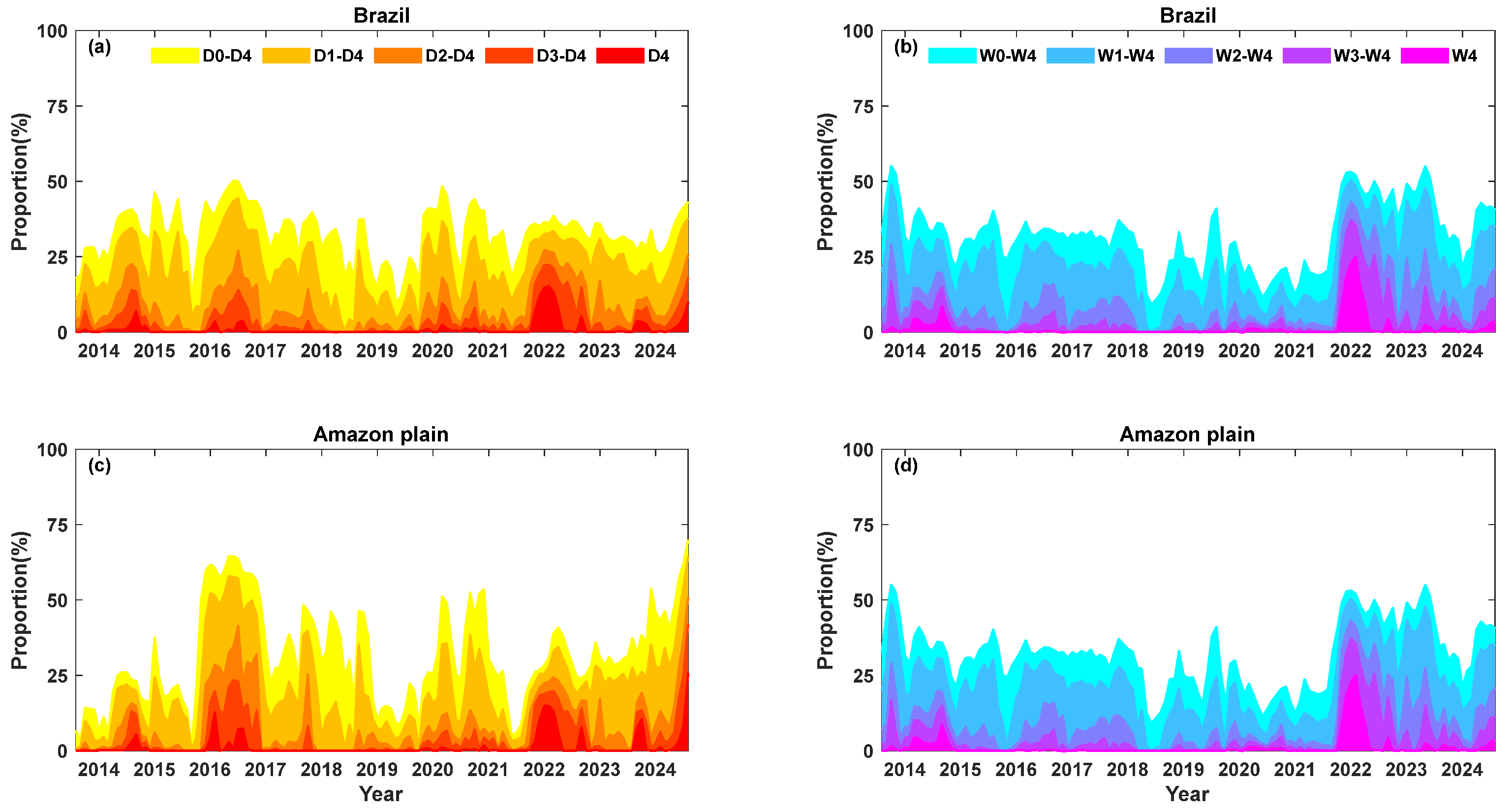
4.3. Hydrological Drought Characteristics Monitoring Using Geodetic Techniques
5. Discussion
5.1. TWS Variation Characteristics on a Small-Scale Range
5.2. Quantification of Regional Hydrological Drought Characteristics for 2023–2024
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, X.G.; Pan, M.; Wei, Z.W.; Wood, E.F.; Sheffield, J. A Global Drought and Flood Catalogue from 1950 to 2016. B. Am. Meteorol. Soc. 2020, 101, E508–E535. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, K.; Hu, S.; Liu, J.; Shi, H.; Wei, G.; Chai, H.; Li, J.; Wang, T. Using the global navigation satellite system and precipitation data to establish the propagation characteristics of meteorological and hydrological drought in Yunnan, China. Water Resour. Res. 2023, 59, e2022WR033126. [Google Scholar] [CrossRef]
- Zhang, W.; Lu, X. Inversion Method for Monitoring Daily Variations in Terrestrial Water Storage Changes in the Yellow River Basin Based on GNSS. Water 2024, 16, 1919. [Google Scholar] [CrossRef]
- Han, Z.; Huang, S.; Huang, Q.; Leng, G.; Wang, H.; Bai, Q.; Zhao, J.; Ma, L.; Wang, L.; Du, M. Propagation dynamics from meteorological to groundwater drought and their possible influence factors. J. Hydro. 2019, 578, 124102. [Google Scholar] [CrossRef]
- Cunha, A.P.M.A.; Zeri, M.; Leal, K.D.; Costa, L.; Cuartas, L.A.; Marengo, J.A.; Tomasella, J.; Vieira, R.M.; Barbosa, A.A.; Cunningham, C.; et al. Extreme Drought Events over Brazil from 2011 to 2019. Atmosphere 2019, 10, 642. [Google Scholar] [CrossRef]
- Chen, C.; Zou, R.; Fang, Z.; Cao, J.; Wang, Q. Using geodetic measurements derived terrestrial water storage to investigate the characteristics of drought in Yunnan, China. GPS Solut. 2023, 28, 51. [Google Scholar] [CrossRef]
- Pintori, F.; Serpelloni, E. Drought-Induced Vertical Displacements and Water Loss in the Po River Basin (Northern Italy) From GNSS Measurements. Earth Spa. Sci. 2024, 11, e2023EA003326. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S. Detectability of variations in continental water storage from satellite observations of the time dependent gravity field. Water Resour. Res. 1999, 35, 2705–2723. [Google Scholar] [CrossRef]
- White, A.M.; Gardner, W.P.; Borsa, A.A.; Argus, D.F.; Martens, H.R. A review of GNSS/GPS in hydrogeodesy: Hydrologic loading applications and their implications for water resource research. Water Resour. Res. 2022, 58, e2022WR032078. [Google Scholar] [CrossRef]
- Feng, W. GRAMAT: A comprehensive Matlab toolbox for estimating global mass variations from GRACE satellite data. Earth Sci. Inform. 2018, 12, 389–404. [Google Scholar] [CrossRef]
- Luan, K.; Hu, J.; Feng, G.; Qiu, Z.; Zhang, K.; Zhu, W.; Wang, J.; Wang, Z. Terrestrial Water Storage Changes over the Last 20 Years in the Amazon Basin. Sens. Mater. 2022, 34, 4053–4069. [Google Scholar] [CrossRef]
- Zhong, B.; Li, X.; Li, Q.; Tan, J.; Dai, X. Evaluating the weekly changes in terrestrial water storage estimated by two different inversion strategies in the Amazon River Basin. Geod. Geodyn. 2023, 14, 614–626. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Sci. 2004, 305, 503–505. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE- based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef]
- Argus, D.F.; Fu, Y.N.; Landerer, F.W. Seasonal variation in total water storage in California inferred from GPS observations of vertical land motion. Geophys. Res. Lett. 2014, 41, 1971–1980. [Google Scholar] [CrossRef]
- Carlson, G.; Werth, S.; Shirzaei, M. Joint Inversion of GNSS and GRACE for Terrestrial Water Storage Change in California. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023135. [Google Scholar] [CrossRef]
- Carlson, G.; Werth, S.; Shirzaei, M. A novel hybrid GNSS, GRACE, and InSAR joint inversion approach to constrain water loss during a record-setting drought in California. Remote Sens. Environ. 2024, 311, 114303. [Google Scholar] [CrossRef]
- Fu, Y.N.; Argus, D.F.; Landerer, F.W. GPS as an independent measurement to estimate terrestrial water storage variations in Washington and Oregon. J. Geophys. Res. Solid Earth 2015, 120, 552–566. [Google Scholar] [CrossRef]
- Han, S.-C.; Razeghi, S.M. GPS Recovery of Daily Hydrologic and Atmospheric Mass Variation: A Methodology and Results from the Australian Continent. J. Geophys. Res. Solid Earth 2017, 122, 9328–9343. [Google Scholar] [CrossRef]
- Jiang, Z.S.; Tang, M.; Yang, X.H.; Wen, H.P.; Yuan, L.G.; Shen, Y.C.; Feng, W.; Zhong, M. Characterizing multifarious hydroclimatic patterns using geodetic measurements in the Australian mainland. J. Hydrol. 2024, 642, 131792. [Google Scholar] [CrossRef]
- Fok, H.S.; Liu, Y. An improved GPS-inferred seasonal terrestrial water storage using terrain-corrected vertical crustal displacements constrained by GRACE. Remote Sens. 2019, 11, 1433. [Google Scholar] [CrossRef]
- Li, X.P.; Zhong, B.; Li, J.C.; Liu, R.L. Inversion of GNSS Vertical Displacements for Terrestrial Water Storage Changes Using Slepian Basis Functions. Earth Space Sci. 2023, 10, e2022EA002608. [Google Scholar] [CrossRef]
- Yang, X.; Yuan, L.; Jiang, Z.; Tang, M.; Feng, X.; Li, C. Investigating terrestrial water storage changes in Southwest China by integrating GNSS and GRACE/GRACE-FO observations. J. Hydrol. Reg. Stud. 2023, 48, 101457. [Google Scholar] [CrossRef]
- Li, X.P.; Zhong, B.; Li, J.C.; Liu, R.L. Joint inversion of GNSS and GRACE/GFO data for terrestrial water storage changes in the Yangtze River Basin. Geophys. J. Int. 2023, 233, 1596–1616. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D.; Clarke, P.; Nurutdinov, K. A new global mode of Earth deformation: Seasonal cycle detected. Science 2001, 294, 2342–2345. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.S.; Hsu, Y.-J.; Yuan, L.G.; Huang, D.F. Monitoring time-varying terrestrial water storage changes using daily GNSS measurements in Yunnan, southwest China. Remote Sen. Environ. 2021, 254, 112249. [Google Scholar] [CrossRef]
- Tang, M.; Yuan, L.; Jiang, Z.; Yang, X.; Li, C.; Li, W. Characterization of hydrological droughts in Brazil usinga novel multiscale index from GNSS. J. Hydrol. 2023, 617, 128934. [Google Scholar] [CrossRef]
- Qiu, K.; You, W.; Jiang, Z.; Tang, M. Tracking the water storage and runoff variations in the Parana ’ basin via GNSS measurements. Sci. Total Environ. 2023, 912, 168831. [Google Scholar] [CrossRef]
- Peng, Y.J.; Chen, G.; Chao, N.F.; Wang, Z.T.; Wu, T.T.; Luo, X.Y. Detection of extreme hydrological droughts in the poyang lake basin during 2021–2022 using GNSS-derived daily terrestrial water storage anomalies. Sci. Total Environ. 2024, 919, 170875. [Google Scholar] [CrossRef]
- Li, X.P.; Zhong, B.; Chen, J.L.; Cheng Li, J.; Wang, H.H. Investigation of 2020–2022 extreme floods and droughts in Sichuan Province of China based on joint inversion of GNSS and GRACE/GFO data. J. Hydrol. 2024, 2024, 130868. [Google Scholar] [CrossRef]
- Jiang, Z.; Hsu, Y.-J.; Yuan, L.; Cheng, S.; Feng, W.; Tang, M.; Yang, X. Insights into hydrological drought characteristics using GNSS-inferred large-scale terrestrial water storage deficits. Earth Planet. Sci. Lett. 2022, 578, 117294. [Google Scholar] [CrossRef]
- Blewitt, G.; Hammond, W.; Kreemer, C. Harnessing the GPS Data Explosion for Interdisciplinary Science. Eos 2018, 99, e2020943118. [Google Scholar] [CrossRef]
- Dill, R.; Dobslaw, H. Numerical simulations of global-scale high-resolution hydrological crustal deformations. J. Geophys. Res. Solid Earth 2013, 118, 5008–5017. [Google Scholar] [CrossRef]
- Liu, N.; Dai, W.J.; Santerre, R.; Kuang, C.L. A MATLAB-based Kriged Kalman Filter software for interpolating missing data in GNSS coordinate time series. GPS Solut. 2018, 22, 25. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Muñoz Sabater, J. ERA5-Land Hourly Data from 1950 to Present; Copernicus Climate Change Service (C3S) Climate Data Store (CDS): Berkshire, UK, 2019. [Google Scholar] [CrossRef]
- Chen, J.; Tapley, B.; Rodell, M.; Seo, K.W.; Wilson, C.; Scanlon, B.R.; Pokhrel, Y. Basin-Scale River Runoff Estimation From GRACE Gravity Satellites, Climate Models, and In Situ Observations: A Case Study in the Amazon Basin. Water Resour. Res. 2020, 56, e2020WR028032. [Google Scholar] [CrossRef]
- Landerer, F.W.; Dickey, J.O.; Güntner, A. Terrestrial water budget of the Eurasian pan-Arctic from GRACE satellite measurements during 2003–2009. J. Geophys. Res. Atmos. 2010, 115, D23. [Google Scholar] [CrossRef]
- Zhao, M.; Aa, G.; Velicogna, I.; Kimball, J.S. Satellite Observations of Regional Drought Severity in the Continental United States Using GRACE-Based Terrestrial Water Storage Changes. J. Clim. 2017, 30, 6297–6308. [Google Scholar] [CrossRef]

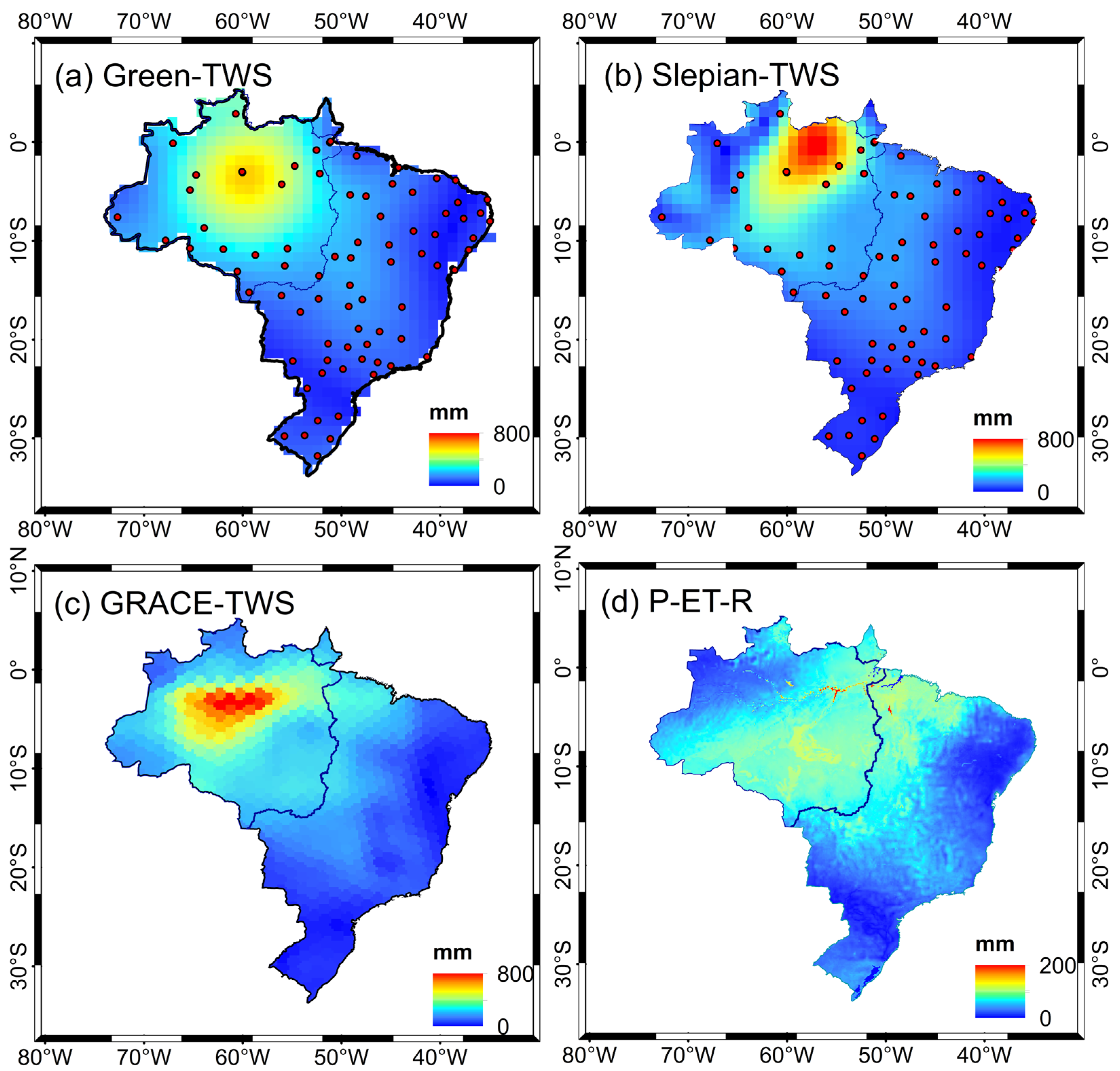



| Green-TWS | Slepian-TWS | GRACE-TWS | P-ET-R | |
|---|---|---|---|---|
| Green-TWS | - | - | - | - |
| Slepian-TWS | 0.99 | - | - | - |
| GRACE-TWS | 0.90 | 0.90 | - | - |
| P-ET-R | 0.87 | 0.87 | 0.93 | - |
| Occurrence Time | Duration (Month) | DSI Peak | Average DSI | Main Drought Types | |
|---|---|---|---|---|---|
| Slepian-DSI | November 2015–December 2016 | 14 | −1.95 (June 2016) | −1.38 | D2 |
| January 2020–June 2020 | 6 | −1.73 (April 2020) | −1.06 | D1 | |
| August 2020–February 2021 | 7 | −1.40 (September 2020) | −1.06 | D1 | |
| December 2023–August 2024 | 9 | −2.23 (August 2024) | −1.00 | D1 | |
| Green-DSI | November 2015–December 2016 | 14 | −2.06 (July 2016) | −1.48 | D2 |
| March 2018–July 2018 | 5 | −0.83 (May 2018) | −0.67 | D0 | |
| January 2020–May 2020 | 5 | −1.44 (April 2020) | −1.00 | D1 | |
| August 2020–January 2021 | 6 | −1.26 (September 2020) | −0.85 | D1 | |
| December 2023–August 2024 | 9 | −2.09 (August 2024) | −0.82 | D1 | |
| GRACE/GFO-DSI | November 2015–September 2016 | 11 | −1.79 (June 2016) | −1.42 | D2 |
| September 2023–July 2024 | 11 | −1.97 (March 2024) | −1.59 | D2 | |
| SPI | May 2021–August 2021 | 4 | −0.74 (all time) | −0.74 | D0 |
| September 2022–August 2024 | 24 | −1.64 (February 2024) | −1.33 | D2 | |
| SPEI | June 2015–September 2015 | 4 | −1.09 (August 2015) | −0.87 | D1 |
| June 2016–September 2016 | 4 | −1.03 (August 2016) | −0.86 | D1 | |
| June 2017–September 2017 | 4 | −1.18 (June 2017) | −0.97 | D1 | |
| June 2018–September 2018 | 4 | −1.03 (August 2018) | −0.89 | D1 | |
| June 2019–September 2019 | 4 | −1.27 (August 2019) | −0.98 | D1 | |
| July 2020–October 2020 | 4 | −1.25 (August 2020) | −1.07 | D1 | |
| May 2021–September 2021 | 4 | −1.24 (August 2021) | −1.00 | D1 | |
| June 2022–February 2024 | 21 | −1.67 (August 2023) | −1.07 | D1 |
| Occurrence Time | Duration (Month) | DSI Peak | Average DSI | Main Drought Types | |
|---|---|---|---|---|---|
| Slepian-DSI | November 2015–December 2016 | 14 | −2.03 (January 2016) | −1.31 | D2 |
| August 2020–January 2021 | 6 | −1.23 (September 2020) | −0.87 | D1 | |
| August 2023–August 2024 | 13 | −2.31 (August 2024) | −1.39 | D2 | |
| Green-DSI | November 2015–December 2016 | 14 | −2.19 (February 2016) | −1.51 | D2 |
| December 2017–May 2018 | 6 | −0.84 (March 2018) | −0.69 | D0 | |
| August 2023–August 2024 | 13 | −2.26 (August 2024) | −1.32 | D2 | |
| GRACE/GFO-DSI | November 2015–June 2016 | 8 | −1.79 (June 2016) | −1.41 | D2 |
| September 2023–July 2024 | 11 | −1.97 (March 2024) | −1.60 | D3 | |
| SPI | October 2015–February 2016 | 5 | −0.74 (February 2016) | −0.74 | D0 |
| September 2022–August 2024 | 24 | −1.64 (August 2023) | −1.36 | D2 | |
| SPEI | July 2015–October 2015 | 4 | −1.41 (September 2015) | −1.04 | D1 |
| July 2020–October 2020 | 4 | −1.26 (August 2020) | −1.07 | D1 | |
| June 2021–October 2021 | 5 | −1.12 (August 2021) | −0.75 | D0 | |
| July 2022–February 2024 | 20 | −1.71 (September 2023) | −1.18 | D1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Wu, T.; Lu, L.; Chao, N.; Liu, Z.; Peng, Y. Using Geodetic Data to Monitor Hydrological Drought at Different Spatial Scales: A Case Study of Brazil and the Amazon Basin. Remote Sens. 2025, 17, 1670. https://doi.org/10.3390/rs17101670
Luo X, Wu T, Lu L, Chao N, Liu Z, Peng Y. Using Geodetic Data to Monitor Hydrological Drought at Different Spatial Scales: A Case Study of Brazil and the Amazon Basin. Remote Sensing. 2025; 17(10):1670. https://doi.org/10.3390/rs17101670
Chicago/Turabian StyleLuo, Xinyu, Tangting Wu, Liguo Lu, Nengfang Chao, Zhanke Liu, and Yujie Peng. 2025. "Using Geodetic Data to Monitor Hydrological Drought at Different Spatial Scales: A Case Study of Brazil and the Amazon Basin" Remote Sensing 17, no. 10: 1670. https://doi.org/10.3390/rs17101670
APA StyleLuo, X., Wu, T., Lu, L., Chao, N., Liu, Z., & Peng, Y. (2025). Using Geodetic Data to Monitor Hydrological Drought at Different Spatial Scales: A Case Study of Brazil and the Amazon Basin. Remote Sensing, 17(10), 1670. https://doi.org/10.3390/rs17101670






