Multi-Hazard Susceptibility Mapping Using Machine Learning Approaches: A Case Study of South Korea
Abstract
1. Introduction
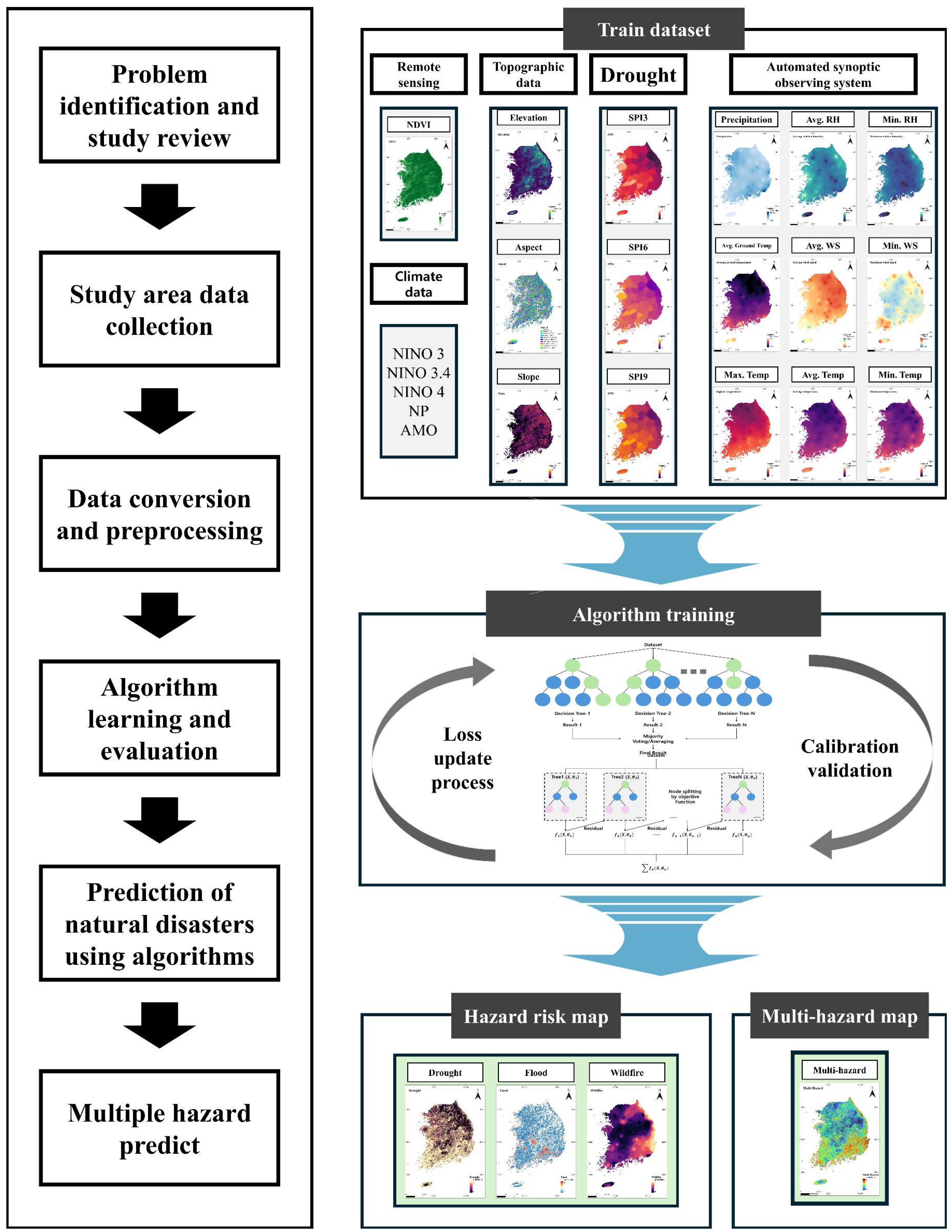
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.2.1. Meteorological and Drought Data
2.2.2. Water-Level Data
2.2.3. Wildfire Data
2.2.4. Topographic Data
2.2.5. Climate Indices Data
2.2.6. Remote Sensing Data
2.3. Model Developments
2.4. Machine Learning Algorithms
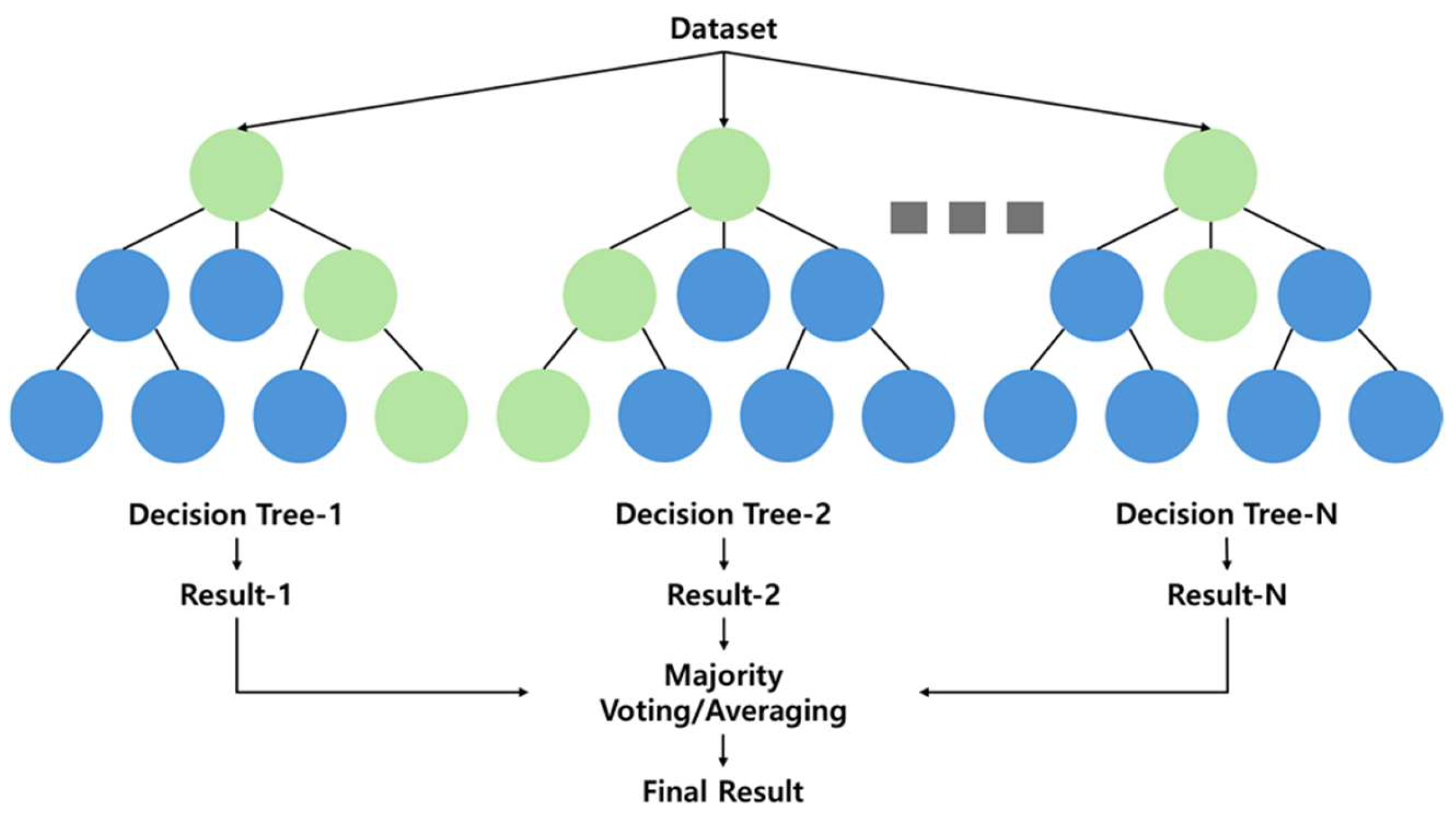
2.4.1. Random Forest
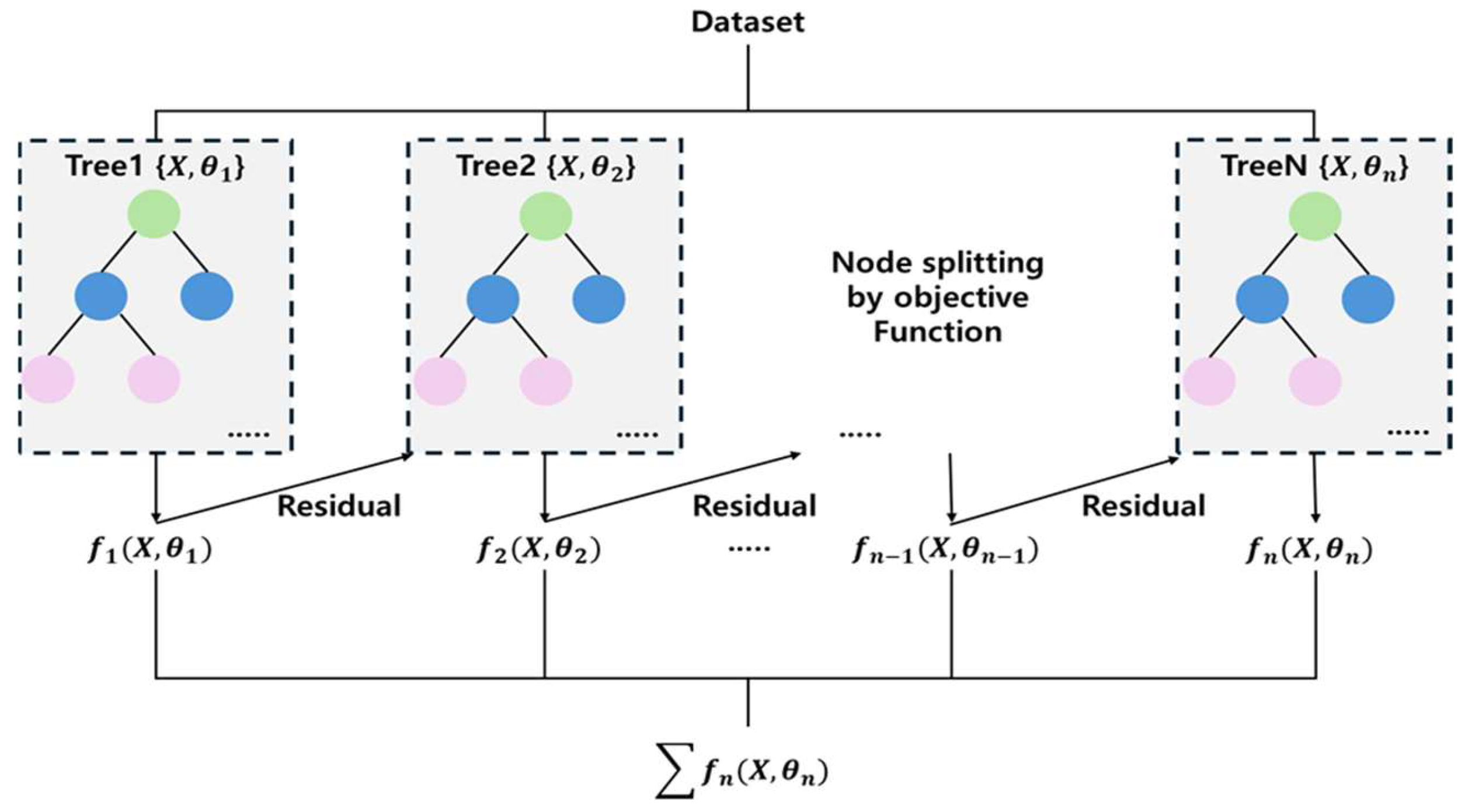
2.4.2. Extreme Gradient Boosting Architecture
2.5. Evaluation Metrics
2.5.1. Accuracy
2.5.2. Precision
2.5.3. Recall
2.5.4. F1-Score
3. Results
3.1. Optimization Results
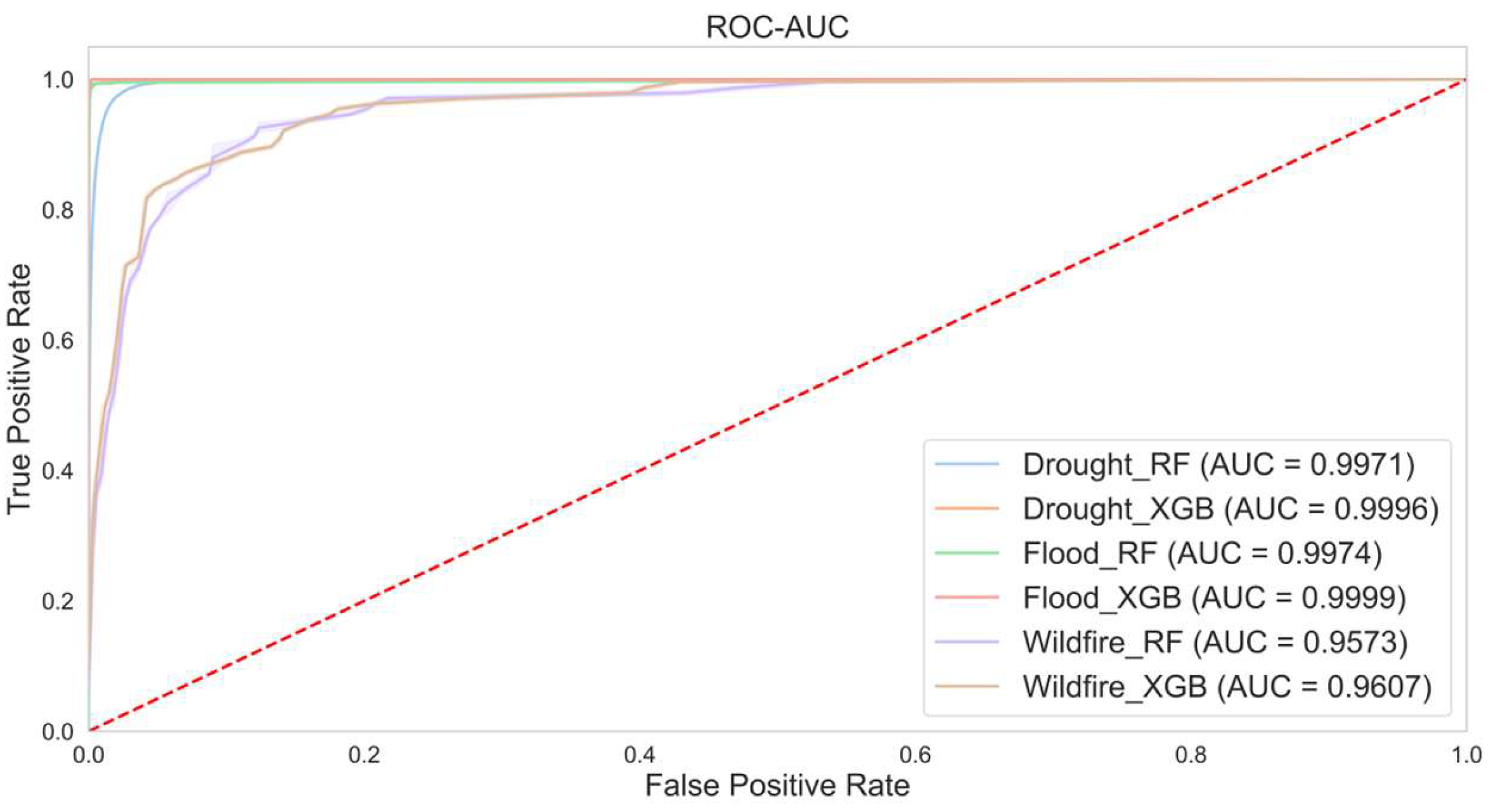
3.2. Modeling Performance
3.3. Feature Importance Analysis
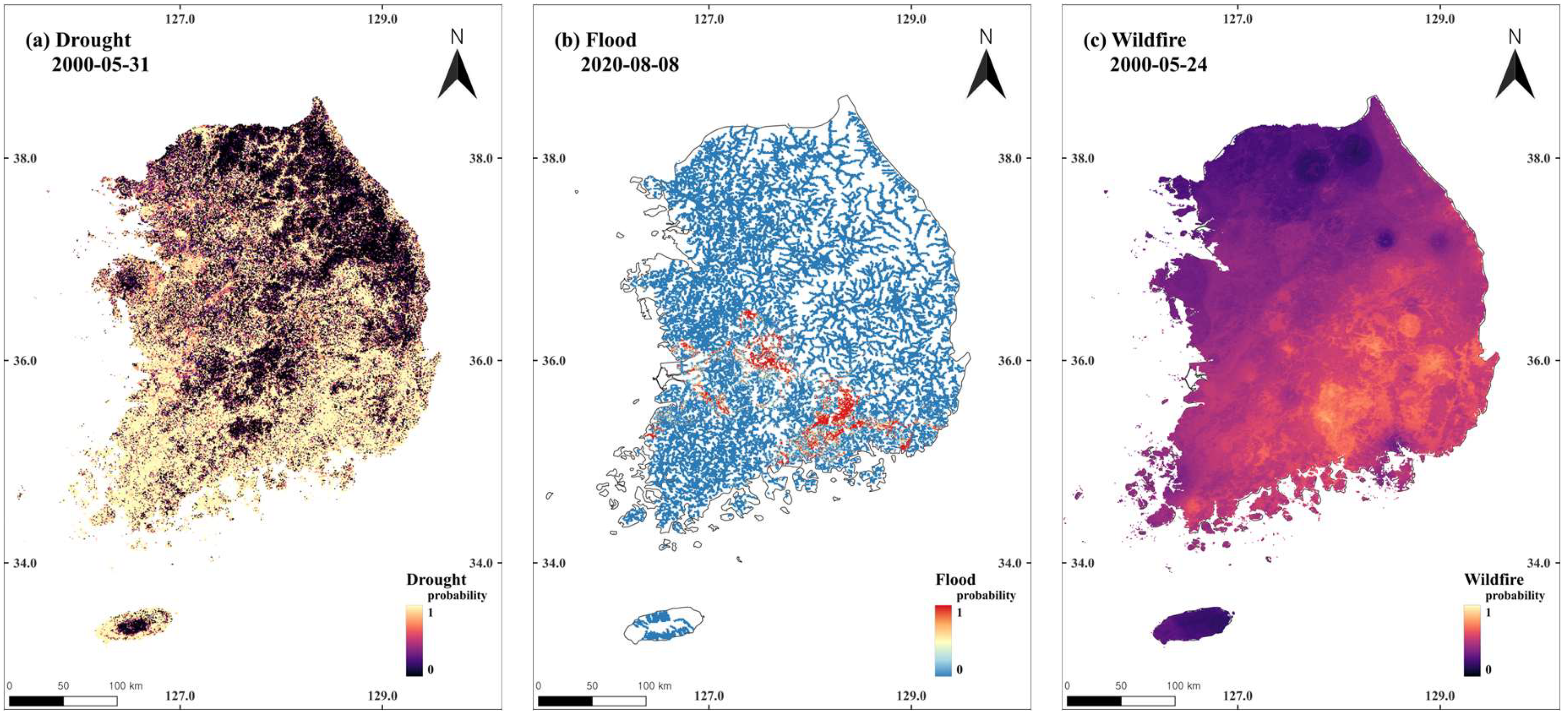
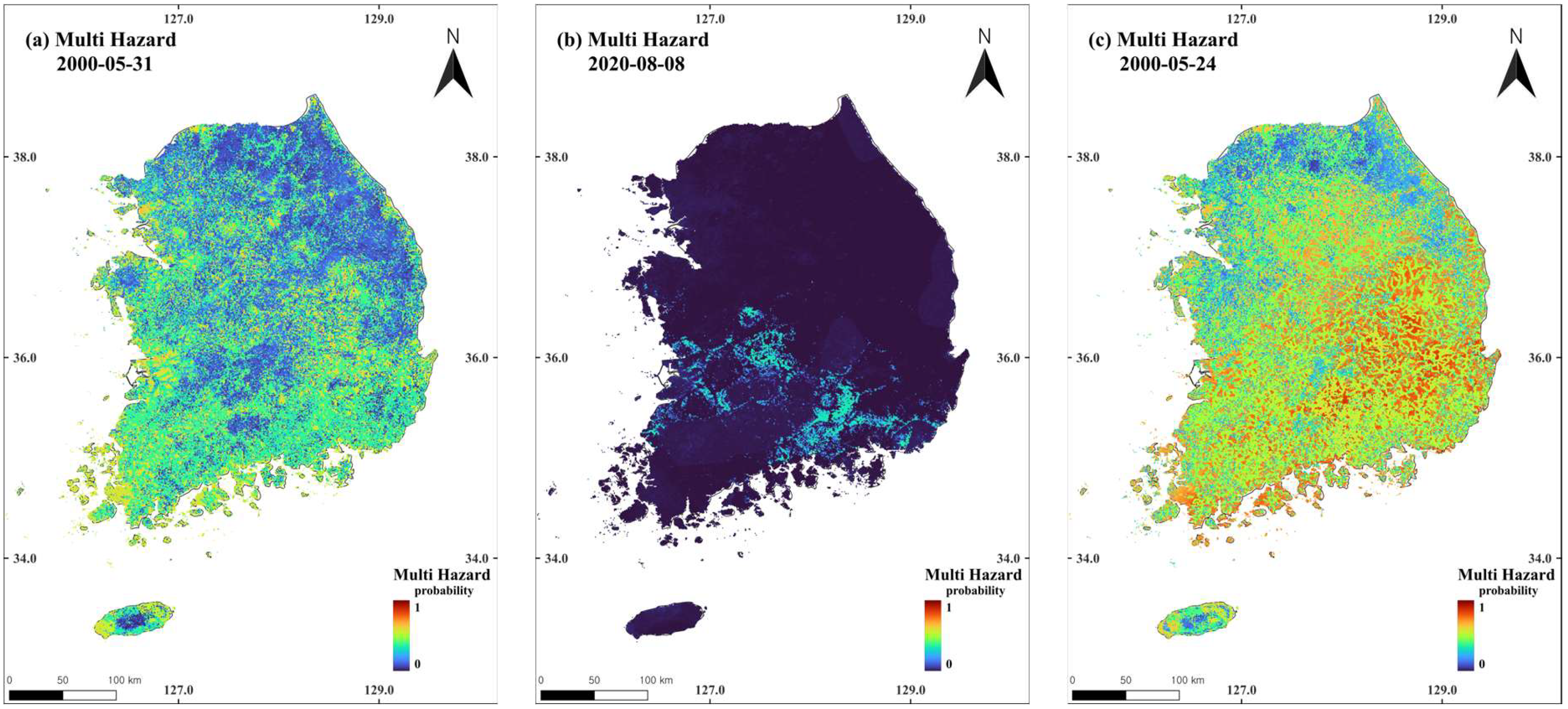
3.4. Multi-Hazard Prediction and Mapping of Susceptibility in South Korea
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wilhite, D.A.; Sivakumar, M.V.; Pulwarty, R. Managing drought risk in a changing climate: The role of national drought policy. Weather Clim. Extrem. 2014, 3, 4–13. [Google Scholar] [CrossRef]
- Merz, B.; Kreibich, H.; Schwarze, R.; Thieken, A. Review article “Assessment of economic flood damage”. Nat. Hazards Earth Syst. Sci. 2010, 10, 1697–1724. [Google Scholar] [CrossRef]
- Kappes, M.S.; Keiler, M.; von Elverfeldt, K.; Glade, T. Challenges of analyzing multi-hazard risk: A review. Nat. Hazards 2012, 64, 1925–1958. [Google Scholar] [CrossRef]
- Wang, J.; He, Z.; Weng, W. A review of the research into the relations between hazards in multi-hazard risk analysis. Nat. Hazards 2020, 104, 2003–2026. [Google Scholar] [CrossRef]
- Flannigan, M.D.; Stocks, B.J.; Wotton, B.M. Climate change and forest fires. Sci. Total Environ. 2000, 262, 221–229. [Google Scholar] [CrossRef]
- Kelman, I.; Spence, R. An overview of flood actions on buildings. Eng. Geol. 2004, 73, 297–309. [Google Scholar] [CrossRef]
- Plate, E.J. Flood risk and flood management. J. Hydrol. 2002, 267, 2–11. [Google Scholar] [CrossRef]
- Wotton, B.M.; Nock, C.A.; Flannigan, M.D. Forest fire occurrence and climate change in Canada. Int. J. Wildland Fire 2010, 19, 253–271. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Svoboda, M.; LeComte, D.; Hayes, M.; Heim, R.; Gleason, K.; Angel, J.; Stephens, S. The drought monitor. Bull. Am. Meteorol. Soc. 2002, 83, 1181–1190. [Google Scholar] [CrossRef]
- Luo, L.; Wood, E.F. Monitoring and predicting the 2007 US drought. Geophys. Res. Lett. 2007, 34, L22702. [Google Scholar] [CrossRef]
- Moreira, E.E.; Coelho, C.A.; Paulo, A.A.; Pereira, L.S.; Mexia, J.T. SPI-based drought category prediction using loglinear models. J. Hydrol. 2008, 354, 116–130. [Google Scholar] [CrossRef]
- Schumann, G.J.-P.; Neal, J.C.; Voisin, N.; Andreadis, K.M.; Pappenberger, F.; Phanthuwongpakdee, N.; Hall, A.C.; Bates, P.D. A first large-scale flood inundation forecasting model: Large-Scale Flood Inundation Forecasting. Water Resour. Res. 2013, 49, 6248–6257. [Google Scholar] [CrossRef]
- Rocchi, A.; Chiozzi, A.; Nale, M.; Nikolic, Z.; Riguzzi, F.; Mantovan, L.; Benvenuti, E. A machine learning framework for multi-hazard risk assessment at the regional scale in earthquake and flood-prone areas. Appl. Sci. 2022, 12, 583. [Google Scholar] [CrossRef]
- Khan, N.; Sachindra, D.A.; Shahid, S.; Ahmed, K.; Shiru, M.S.; Nawaz, N. Prediction of droughts over Pakistan using machine learning algorithms. Adv. Water Resour. 2020, 139, 103562. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Avand, M.; Al-Ansari, N.; Dinh Du, T.; Yen, H.P.H.; Tuyen, T.T. Performance evaluation of machine learning methods for forest fire modeling and prediction. Symmetry 2020, 12, 1022. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. Predicting flood susceptibility using LSTM neural networks. J. Hydrol. 2021, 594, 125734. [Google Scholar] [CrossRef]
- Mohajane, M.; Costache, R.; Karimi, F.; Pham, Q.B.; Essahlaoui, A.; Nguyen, H.; Oudija, F. Application of remote sensing and machine learning algorithms for forest fire mapping in a Mediterranean area. Ecol. Indic. 2021, 129, 107869. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Sankaranarayanan, S.; Prabhakar, M.; Satish, S.; Jain, P.; Ramprasad, A.; Krishnan, A. Flood prediction based on weather parameters using deep learning. J. Water Clim. Change 2020, 11, 1766–1783. [Google Scholar] [CrossRef]
- Antzoulatos, G.; Kouloglou, I.O.; Bakratsas, M.; Moumtzidou, A.; Gialampoukidis, I.; Karakostas, A.; Kompatsiaris, I. Flood hazard and risk mapping by applying an explainable machine learning framework using satellite imagery and GIS data. Sustainability 2022, 14, 3251. [Google Scholar] [CrossRef]
- Iban, M.C.; Aksu, O. SHAP-driven explainable artificial intelligence framework for wildfire susceptibility mapping using MODIS active fire pixels: An in-depth interpretation of contributing factors in Izmir, Türkiye. Remote Sens. 2024, 16, 2842. [Google Scholar] [CrossRef]
- Tilloy, A.; Malamud, B.D.; Winter, H.; Joly-Laugel, A. A review of quantification methodologies for multi-hazard inter-relationships. Earth Sci. Rev. 2019, 196, 102881. [Google Scholar] [CrossRef]
- Korea Forest Service. 2022 Wildfire Statistics Yearbook; Korea Forest Service: Daejeon, Republic of Korea, 2023. [Google Scholar]
- Syeed, M.M.A.; Farzana, M.; Namir, I.; Ishrar, I.; Nushra, M.H.; Rahman, T. Flood prediction using machine learning models. In Proceedings of the 2022 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 9–11 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Scornet, E.; Biau, G.; Vert, J.-P. Consistency of random forests. Ann. Statist. 2015, 43, 1716–1741. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-Based Method for Flash Flood Risk Assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
- Hossin, M.; Sulaiman, M.N. A review on evaluation metrics for data classification evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1. [Google Scholar] [CrossRef]
- En-Nagre, K.; Aqnouy, M.; Ouarka, A.; Naqvi, S.A.A.; Bouizrou, I.; El Messari, J.E.S.; El-Askary, H. Assessment and prediction of meteorological drought using machine learning algorithms and climate data. Clim. Risk Manage. 2024, 45, 100630. [Google Scholar] [CrossRef]
- Ha, K.J.; Moon, S.; Timmermann, A.; Kim, D. Future changes of summer monsoon characteristics and evaporative demand over Asia in CMIP6 simulations. Geophys. Res. Lett. 2020, 47, e2020GL087492. [Google Scholar] [CrossRef]
- Korea Forest Service. 2010 Wildfire Statistics Yearbook; Korea Forest Service: Daejeon, Republic of Korea, 2011. [Google Scholar]
- Ministry of the Interior and Safety. 2018 National Drought Information Statistics Report; Ministry of the Interior and Safety: Sejong, Republic of Korea, 2020. [Google Scholar]
- Korea Forest Service. 2020 Disaster Yearbook; Ministry of the Interior and Safety: Sejong, Republic of Korea, 2021. [Google Scholar]
- Forzieri, G.; Feyen, L.; Russo, S.; Vousdoukas, M.; Alfieri, L.; Outten, S.; Cid, A. Multi-hazard assessment in Europe under climate change. Clim. Change 2016, 137, 105–119. [Google Scholar] [CrossRef]
- Gill, J.C.; Malamud, B.D. Anthropogenic processes, natural hazards, and interactions in a multi-hazard framework. Earth Sci. Rev. 2017, 166, 246–269. [Google Scholar] [CrossRef]
- Brogan, D.J.; Nelson, P.A.; MacDonald, L.H. Reconstructing extreme post-wildfire floods: A comparison of convective and mesoscale events. Earth Surf. Process. Landf. 2017, 42, 2505–2522. [Google Scholar] [CrossRef]
- Richardson, D.; Black, A.S.; Irving, D.; Matear, R.J.; Monselesan, D.P.; Risbey, J.S.; Tozer, C.R. Global increase in wildfire potential from compound fire weather and drought. NPJ Clim. Atmos. Sci. 2022, 5, 23. [Google Scholar] [CrossRef]
- Demissie, Z.; Rimal, P.; Seyoum, W.M.; Dutta, A.; Rimmington, G. Flood susceptibility mapping: Integrating machine learning and GIS for enhanced risk assessment. Appl. Comput. Geosci. 2024, 23, 100183. [Google Scholar] [CrossRef]
- Hang, H.T.; Mallick, J.; Alqadhi, S.; Bindajam, A.A.; Abdo, H.G. Exploring forest fire susceptibility and management strategies in Western Himalaya: Integrating ensemble machine learning and explainable AI for accurate prediction and comprehensive analysis. Environ. Technol. Innov. 2024, 35, 103655. [Google Scholar] [CrossRef]
- Zhang, B.; Salem, F.K.A.; Hayes, M.J.; Tadesse, T. Quantitative assessment of drought impacts using XGBoost based on the drought impact reporter. arXiv 2022, arXiv:2211.02768. [Google Scholar] [CrossRef]
- Sanders, W.; Li, D.; Li, W.; Fang, Z.N. Data-driven flood alert system (FAS) using extreme gradient boosting (XGBoost) to forecast flood stages. Water 2022, 14, 747. [Google Scholar] [CrossRef]
- Zhang, B.; Salem, F.K.A.; Hayes, M.J.; Smith, K.H.; Tadesse, T.; Wardlow, B.D. Explainable machine learning for the prediction and assessment of complex drought impacts. Sci. Total Environ. 2023, 898, 165509. [Google Scholar] [CrossRef]
- Mehmood, K.; Anees, S.A.; Luo, M.; Akram, M.; Zubair, M.; Khan, K.A.; Khan, W.R. Assessing Chilgoza Pine (Pinus gerardiana) forest fire severity: Remote sensing analysis, correlations, and predictive modeling for enhanced management strategies. Trees For. People 2024, 16, 100521. [Google Scholar] [CrossRef]
- Singha, C.; Swain, K.C.; Moghimi, A.; Foroughnia, F.; Swain, S.K. Integrating geospatial, remote sensing, and machine learning for climate-induced forest fire susceptibility mapping in Similipal Tiger Reserve, India. For. Ecol. Manage. 2024, 555, 121729. [Google Scholar] [CrossRef]
- Abdelkader, M.; Yerdelen, C. Hydrological drought variability and its teleconnections with climate indices. J. Hydrol. 2022, 605, 127290. [Google Scholar] [CrossRef]
- Abdourahamane, Z.S.; Acar, R. Analysis of meteorological drought variability in Niger and its connection with climate indices. Hydrol. Sci. J. 2018, 63, 1203–1218. [Google Scholar] [CrossRef]
- Yue, Y.; Liu, H.; Mu, X.; Qin, M.; Wang, T.; Wang, Q.; Yan, Y. Spatial and temporal characteristics of drought and its correlation with climate indices in Northeast China. PLoS ONE 2021, 16, e0259774. [Google Scholar] [CrossRef]
- Hakim, D.K.; Gernowo, R.; Nirwansyah, A.W. Flood prediction with time series data mining: Systematic review. Nat. Hazard. Res. 2024, 4, 194–220. [Google Scholar] [CrossRef]
- Toth, E.; Brath, A.; Montanari, A. Comparison of short-term rainfall prediction models for real-time flood forecasting. J. Hydrol. 2000, 239, 132–147. [Google Scholar] [CrossRef]
- Dong, H.; Wu, H.; Sun, P.; Ding, Y. Wildfire prediction model based on spatial and temporal characteristics: A case study of a wildfire in Portugal’s Montesinho Natural Park. Sustainability 2022, 14, 10107. [Google Scholar] [CrossRef]
- Malik, A.; Rao, M.R.; Puppala, N.; Koouri, P.; Thota, V.A.K.; Liu, Q.; Gao, J. Data-driven wildfire risk prediction in northern California. Atmosphere 2021, 12, 109. [Google Scholar] [CrossRef]
- Piao, Y.; Lee, D.; Park, S.; Kim, H.G.; Jin, Y.H. Multi-hazard mapping of droughts and forest fires using a multi-layer hazards approach with machine learning algorithms. Geomat. Nat. Hazards Risk 2022, 13, 2649–2673. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kariminejad, N.; Amiri, M.; Edalat, M.; Zarafshar, M.; Blaschke, T.; Cerda, A. Assessing and mapping multi-hazard risk susceptibility using a machine learning technique. Sci. Rep. 2020, 10, 3203. [Google Scholar] [CrossRef]
- Vitolo, C.; Di Napoli, C.; Di Giuseppe, F.; Cloke, H.L.; Pappenberger, F. Mapping combined wildfire and heat stress hazards to improve evidence-based decision making. Environ. Int. 2019, 127, 21–34. [Google Scholar] [CrossRef]



| Category | Variable | Drought | Flood | Wildfire |
|---|---|---|---|---|
| Meteorological data | Precipitation (mm/day) | √ | √ | √ |
| Maximum temperature (°C) | √ | √ | √ | |
| Minimum temperature (°C) | √ | √ | X | |
| Average temperature (°C) | √ | √ | X | |
| Average ground temperature (°C) | √ | √ | X | |
| Minimum relative humidity (%) | √ | √ | √ | |
| Average relative humidity (%) | √ | √ | X | |
| Maximum wind speed (m/s) | √ | √ | √ | |
| Average wind speed (m/s) | √ | √ | X | |
| Drought data | SPI 3 | X | √ | √ |
| SPI 6 | X | √ | √ | |
| SPI 9 | X | √ | √ | |
| Remote sensing data | NDVI | √ | √ | √ |
| Date | Month | X | X | √ |
| Topographic data | Digital elevation model | √ | √ | √ |
| Aspect | √ | √ | √ | |
| Slope | √ | √ | √ | |
| Climate data | NINO 3 | √ | √ | X |
| NINO 3.4 | X | |||
| NINO 4 | √ | |||
| North Pacific Index (NP) | √ | √ | √ | |
| Atlantic Multidecadal Oscillation (AMO) | √ | √ | √ |
| Observed | |||
|---|---|---|---|
| Positive | Negative | ||
| Predictions | Positive | TP | FN |
| Negative | FP | TN | |
| Parameters | Drought | Flood | Wildfire |
|---|---|---|---|
| Total Cases | 2,489,260 | 6,891,358 | 3,646,240 |
| Occurrence Cases | 168,173 | 2189 | 416 |
| Occurrence Rate | 6.75% | 0.03% | 0.01% |
| Model | Parameters | Drought | Flood | Wildfire |
|---|---|---|---|---|
| RF | class_weight | Balanced | Balanced | Balanced |
| Criterion | Gini | Gini | Gini | |
| max_depth | 100 | 150 | 8 | |
| max_features | - | - | 2 | |
| min_samples_leaf | 8 | 8 | 1 | |
| min_samples_split | 8 | 2 | 4 | |
| n_estimators | 100 | 300 | 150 | |
| XGB | scale_pos_weight | Class Imbalance Ratio | Class Imbalance Ratio | 2.583 |
| max_depth | 9 | 9 | 4 | |
| learning_rate | 0.3 | 0.3 | 0.01 | |
| subsample | 0.9 | 0.9 | 0.6 | |
| colsample_bytree | 0.7 | 0.7 | 0.7 |
| Accuracy | Precision | Recall | F1-Score | |
|---|---|---|---|---|
| Drought_RF | 0.9817 | 0.8014 | 0.9669 | 0.8764 |
| Drought_XGB | 0.9974 | 0.9744 | 0.9873 | 0.9808 |
| Flood_RF | 0.9998 | 0.7437 | 0.6319 | 0.6833 |
| Flood_XGB | 0.9999 | 0.9198 | 0.9141 | 0.9169 |
| Wildfire_RF | 0.9073 | 0.7842 | 0.9008 | 0.8385 |
| Wildfire_XGB | 0.8940 | 0.7626 | 0.8760 | 0.8154 |
| Drought (%) | Flood (%) | Wildfire (%) | |
|---|---|---|---|
| Very Low (0–0.2) | 32.01 (40,030) | 90.76 (59,802) | 49.18 (61,488) |
| Low (0.2–0.4) | 6.46 (8075) | 2.23 (1469) | 23.41 (29,264) |
| Moderate (0.4–0.6) | 5.66 (7073) | 1.80 (1189) | 8.89 (11,118) |
| High (0.6–0.8) | 7.31 (9141) | 5.20 (3429) | 9.15 (11,441) |
| Very High (0.8–1) | 48.56 (60,709) | 0 (0) | 9.31 (11,717) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.; Park, S.; Han, H. Multi-Hazard Susceptibility Mapping Using Machine Learning Approaches: A Case Study of South Korea. Remote Sens. 2025, 17, 1660. https://doi.org/10.3390/rs17101660
Kim C, Park S, Han H. Multi-Hazard Susceptibility Mapping Using Machine Learning Approaches: A Case Study of South Korea. Remote Sensing. 2025; 17(10):1660. https://doi.org/10.3390/rs17101660
Chicago/Turabian StyleKim, Changju, Soonchan Park, and Heechan Han. 2025. "Multi-Hazard Susceptibility Mapping Using Machine Learning Approaches: A Case Study of South Korea" Remote Sensing 17, no. 10: 1660. https://doi.org/10.3390/rs17101660
APA StyleKim, C., Park, S., & Han, H. (2025). Multi-Hazard Susceptibility Mapping Using Machine Learning Approaches: A Case Study of South Korea. Remote Sensing, 17(10), 1660. https://doi.org/10.3390/rs17101660









