MAL-Net: Model-Adaptive Learned Network for Slow-Time Ambiguity Function Shaping
Abstract
1. Introduction
- The proposed MAL-Net method solves the problem without objective function relaxation: The proposed MAL-Net is designed by unrolling the CCM gradient descent model into networkayers, enabling relaxation-free optimization of the objective function over the CCM space. This approach effectively addresses the performance degradation commonly caused by objective function relaxation in most existing model optimization methods.
- The proposed MAL-Net method adaptively updates the step sizes of each networkayer: In a MAL-Net, the step sizes for eachayer are adaptively updated through Deep Learning, overcoming the challenge of step size selection in conventional gradient-based methods. Furthermore, a MAL-Net only requires training a single parameter in eachayer, significantly reducing computational cost compared to DNN methods, which requireearning aarge number of network parameters.
- Compared with existing methods, the proposed MAL-Net method offers the following key improvements: (1) the nulls of the ambiguity function are decreased by 157 dB; (2) the Signal-to-Interference Ratio (SIR) gain is increased by 144 dB.
2. System Model
3. Problem Formulation and Analysis
4. The MAL-Net Method
4.1. Gradient Descent Model over the CCM
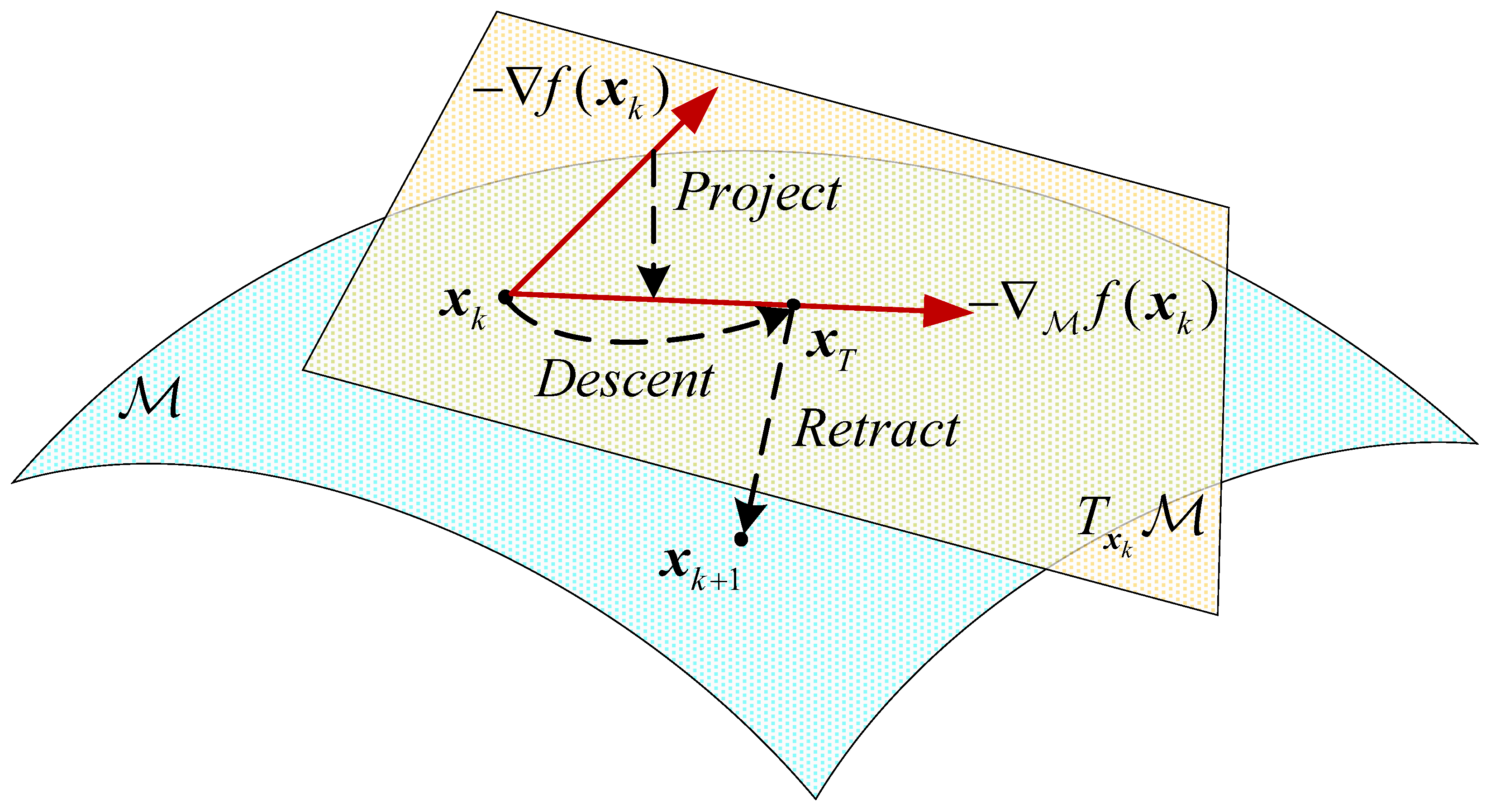
4.1.1. Obtaining the Riemannian Gradient by Projection
- , which is made up of all the tangent vectors at point , is a tangent space. It is defined as
- denotes projection, from the Riemannian space to the tangent space at , which is defined as .
- is the Euclidean gradient at the point . It is given bywhere
- and are, respectively, defined as
4.1.2. Descent over Tangent Space
4.1.3. Retraction Back to the CCM
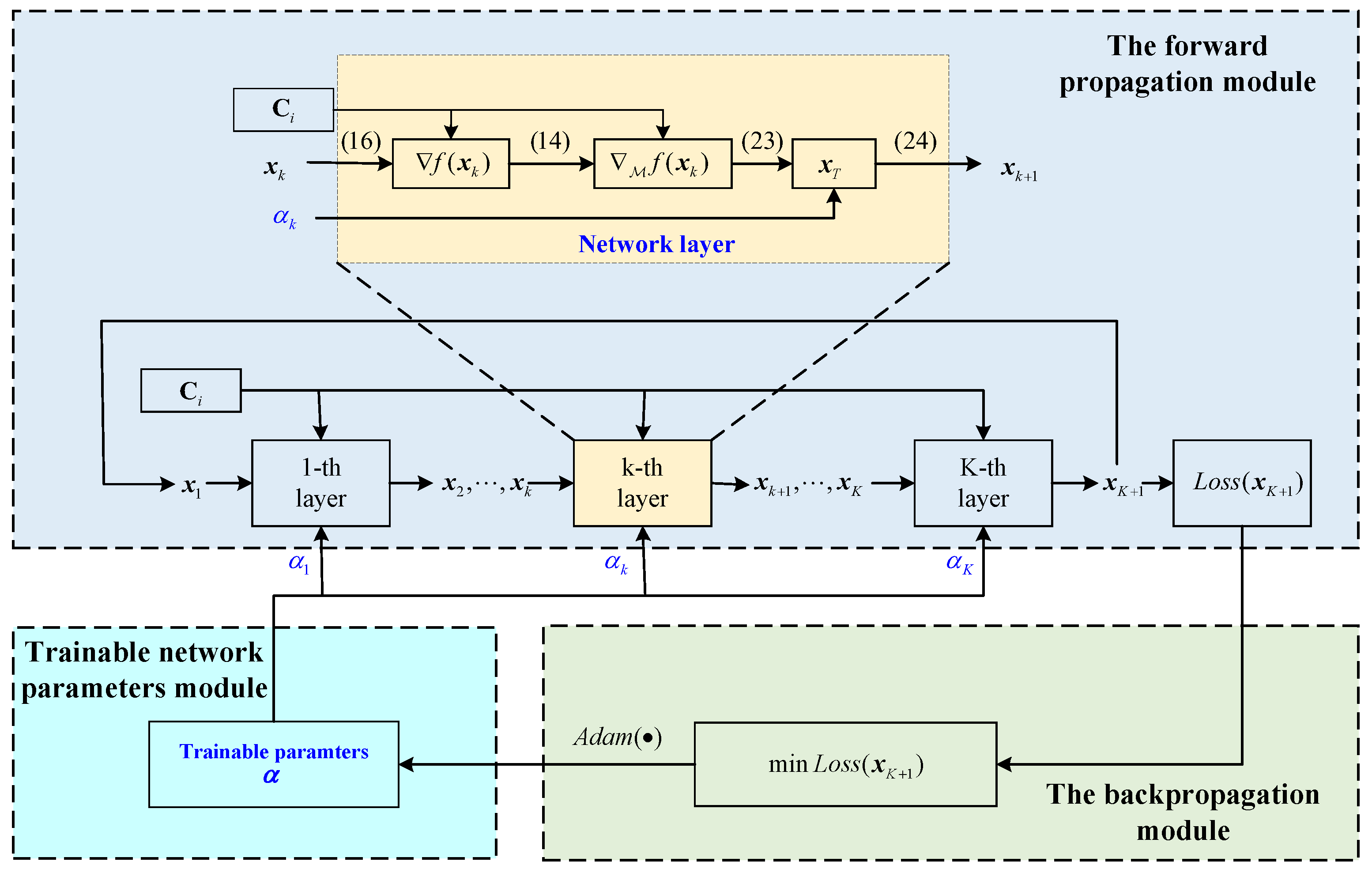
4.2. The Proposed MAL-Net
4.2.1. Forward-Propagation Module
4.2.2. Backward-Propagation Module
4.2.3. Parameters-Training Module
| Algorithm 1 Model-Adaptive Learned Network (MAL-Net) |
|
4.3. Analysis of Complexity and Convergence
4.3.1. Analysis of Complexity
4.3.2. Convergence Analysis
5. Numerical Results
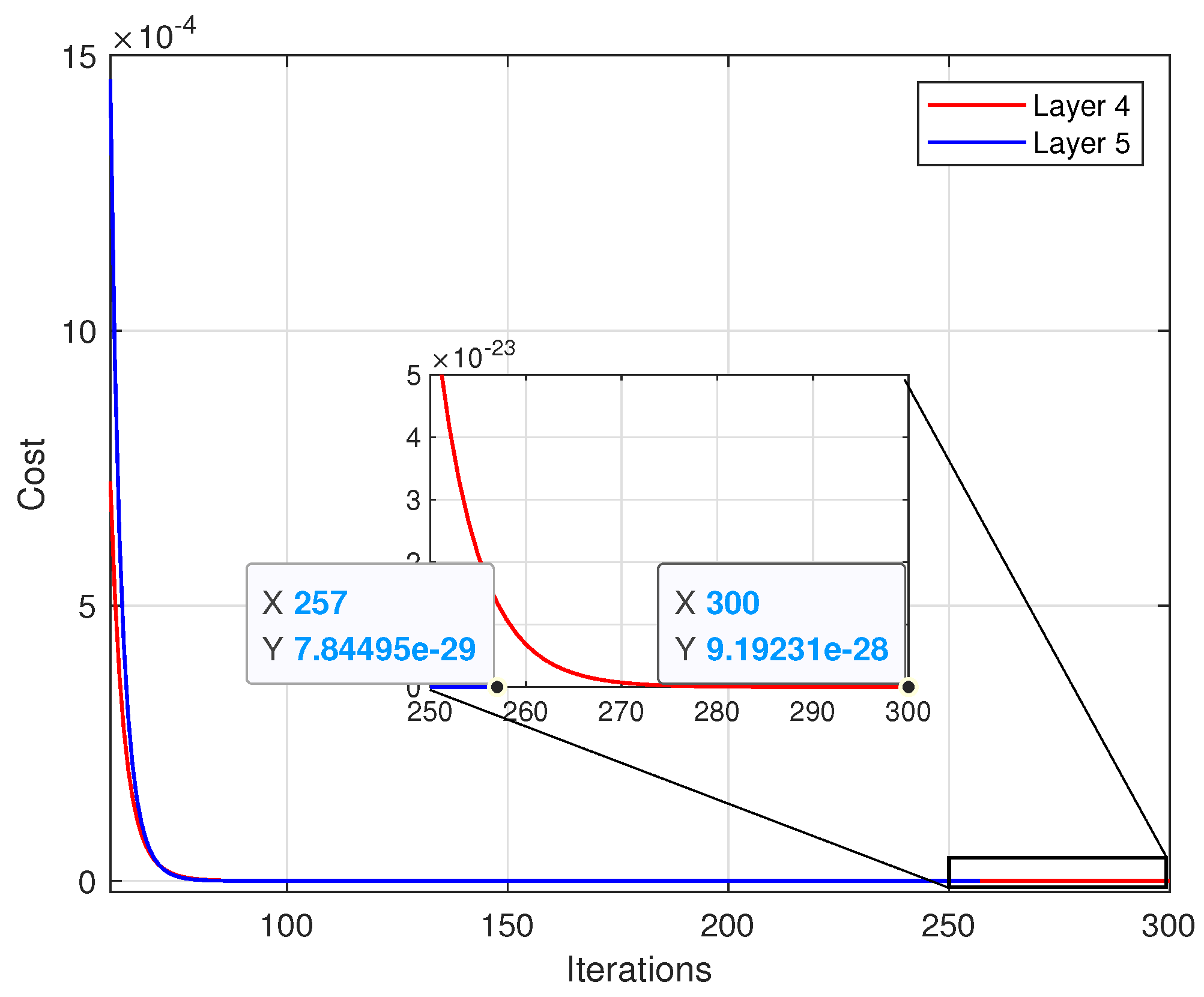
5.1. The Convergence Behavior
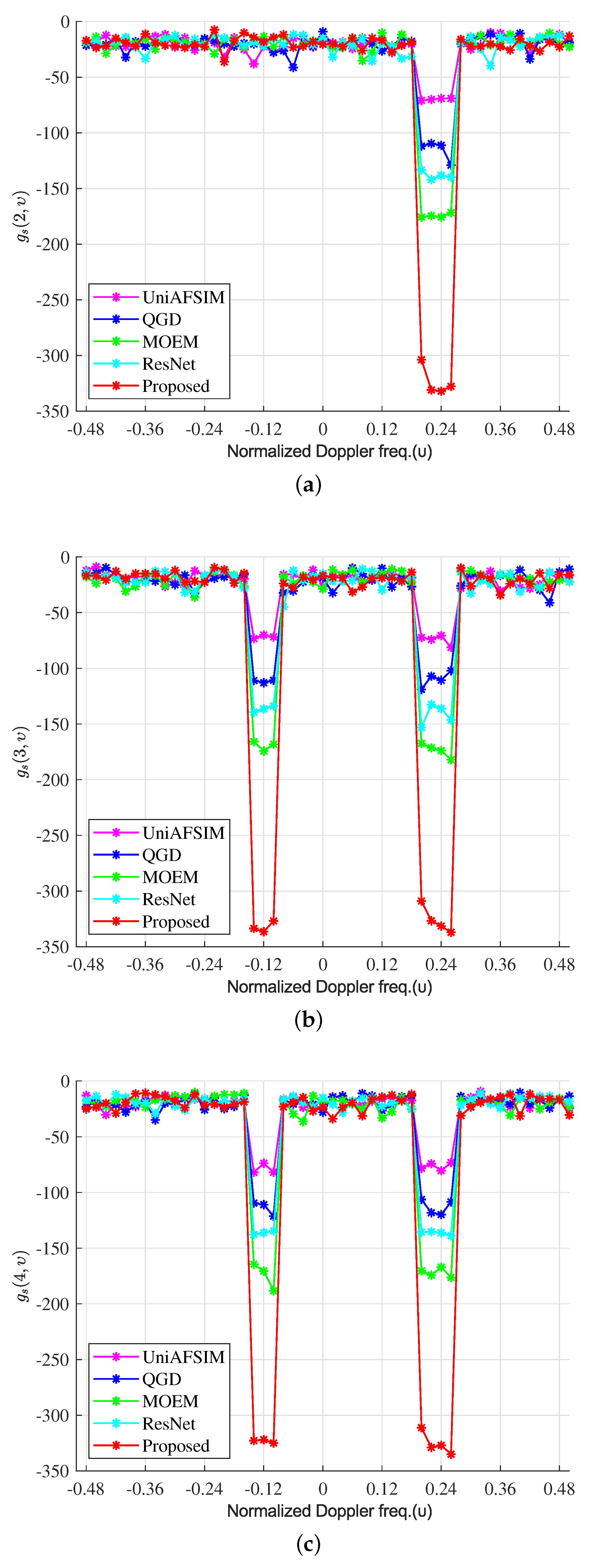
5.2. The Performance Comparison of Nulling STAF
5.3. The Comparison of Time and SIR
5.4. The Performance of Target Detection
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MIMO | Multiple-Input Multiple-Output |
| STAF | Slow-Time Ambiguity Function Shaping |
| CMC | Constant Modulus Constraint |
| DNNs | Deep Neural Networks |
| DL | Deep Learning |
| UQP | Unconstrained Quartic Problem |
| MBI | Maximum Block Improvement |
| MM | Majorization–Minimization |
| GP | Gradient Projection |
| QGD | Quartic Gradient Descent |
| MOEM | Manifold Optimization Embedding with Momentum |
| ISL | Integrated Sidelobe Levels |
| MAL-Net | Model-Adaptive Learned Network |
| SIR | Signal-to-Interference Ratio |
References
- Wang, X.; Li, B.; Chen, H.; Liu, W.; Zhu, Y.; Luo, J.; Ni, L. Interrupted-Sampling Repeater Jamming Countermeasure Based on Intrapulse Frequency–Coded Joint Frequency Modulation Slope Agile Waveform. Remote Sens. 2024, 16, 2810. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Xie, J.; Yang, Y.; Tian, B.; Xu, S. Ultra-Low Sidelobe Waveforms Design for LPI Radar Based on Joint Complementary Phase-Coding and Optimized Discrete Frequency-Coding. Remote Sens. 2022, 14, 2592. [Google Scholar] [CrossRef]
- Wang, F.; Xia, X.G.; Pang, C.; Cheng, X.; Li, Y.; Wang, X. Joint Design Methods of Unimodular Sequences and Receiving Filters With Good Correlation Properties and Doppler Tolerance. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Chen, Z.; Liang, J.; Wang, T.; Tang, B.; So, H.C. Generalized MBI Algorithm for Designing Sequence Set and Mismatched Filter Bank With Ambiguity Function Constraints. IEEE Trans. Signal Process. 2022, 70, 2918–2933. [Google Scholar] [CrossRef]
- Zhu, J.; Xie, Z.; Jiang, N.; Song, Y.; Han, S.; Liu, W.; Huang, X. Delay-Doppler Map Shaping through Oversampled Complementary Sets for High-Speed Target Detection. Remote Sens. 2024, 16, 2898. [Google Scholar] [CrossRef]
- Lei, W.; Zhang, Y.; Chen, Z.; Chen, X.; Song, Q. Spatial–Temporal Joint Design and Optimization of Phase-Coded Waveform for MIMO Radar. Remote Sens. 2024, 16, 2647. [Google Scholar] [CrossRef]
- Cheng, X.; Wu, L.; Ciuonzo, D.; Wang, W. Joint Design of Horizontal and Vertical Polarization Waveforms for Polarimetric Radar via SINR Maximization. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3313–3328. [Google Scholar] [CrossRef]
- Yu, L.; He, F.; Zhang, Y.; Su, Y. Low-PSL Mismatched Filter Design for Coherent FDA Radar Using Phase-Coded Waveform. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Li, D.; Yang, J. Joint Design of Complementary Sequence and Receiving Filter with High Doppler Tolerance for Simultaneously Polarimetric Radar. Remote Sens. 2023, 15, 3877. [Google Scholar] [CrossRef]
- Chang, S.; Yang, F.; Liang, Z.; Ren, W.; Zhang, H.; Liu, Q. Slow-Time MIMO Waveform Design Using Pulse-Agile-Phase-Coding for Range Ambiguity Mitigation. Remote Sens. 2023, 15, 3395. [Google Scholar] [CrossRef]
- Li, M.; Li, W.; Cheng, X.; Wu, M.; Rao, B.; Wang, W. The Transmit and Receive Optimization for Polarimetric Radars Against Interrupted Sampling Repeater Jamming. IEEE Sens. J. 2024, 24, 3927–3943. [Google Scholar] [CrossRef]
- Gui, R.; Huang, B.; Wang, W.Q.; Sun, Y. Generalized Ambiguity Function for FDA Radar Joint Range, Angle and Doppler Resolution Evaluation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Yang, R.; Jiang, H.; Qu, L. Joint Constant-Modulus Waveform and RIS Phase Shift Design for Terahertz Dual-Function MIMO Radar and Communication System. Remote Sens. 2024, 16, 3083. [Google Scholar] [CrossRef]
- Zhong, K.; Hu, J.; Pan, C.; Deng, M.; Fang, J. Joint Waveform and Beamforming Design for RIS-Aided ISAC Systems. IEEE Signal Process. Lett. 2023, 30, 165–169. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Govoni, M.A.; Martino, L. On the Design of Multi-Spectrally Constrained Constant Modulus Radar Signals. IEEE Trans. Signal Process. 2020, 68, 2231–2243. [Google Scholar] [CrossRef]
- Zhong, K.; Hu, J.; Liu, J.; An, D.; Pan, C.; Teh, K.C.; Yu, X.; Li, H. P2C2M: Parallel Product Complex Circle Manifold for RIS-Aided ISAC Waveform Design. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 1441–1451. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Jiang, B.; Zhang, S. Ambiguity Function Shaping for Cognitive Radar Via Complex Quartic Optimization. IEEE Trans. Signal Process. 2013, 61, 5603–5619. [Google Scholar] [CrossRef]
- Wu, L.; Babu, P.; Palomar, D.P. Cognitive Radar-Based Sequence Design via SINR Maximization. IEEE Trans. Signal Process. 2017, 65, 779–793. [Google Scholar] [CrossRef]
- Wang, F.; Feng, S.; Yin, J.; Pang, C.; Li, Y.; Wang, X. Unimodular Sequence and Receiving Filter Design for Local Ambiguity Function Shaping. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Esmaeili-Najafabadi, H.; Leung, H.; Moo, P.W. Unimodular Waveform Design With Desired Ambiguity Function for Cognitive Radar. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 2489–2496. [Google Scholar] [CrossRef]
- Alhujaili, K.; Monga, V.; Rangaswamy, M. Quartic Gradient Descent for Tractable Radar Slow-Time Ambiguity Function Shaping. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1474–1489. [Google Scholar] [CrossRef]
- Hu, H.; Zhong, K.; Pan, C.; Xiao, X. Ambiguity Function Shaping via Manifold Optimization Embedding With Momentum. IEEE Commun. Lett. 2023, 27, 2727–2731. [Google Scholar] [CrossRef]
- Šipoš, D.; Gleich, D. Model-Based Information Extraction From SAR Images Using Deep Learning. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Stanković, Z.Ž.; Olćan, D.I.; Dončov, N.S.; Kolundžija, B.M. Consensus Deep Neural Networks for Antenna Design and Optimization. IEEE Trans. Antennas Propag. 2022, 70, 5015–5023. [Google Scholar] [CrossRef]
- Hu, J.; Wei, Z.; Li, Y.; Li, H.; Wu, J. Designing Unimodular Waveform(s) for MIMO Radar by Deep Learning Method. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1184–1196. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Monga, V.; Li, Y.; Eldar, Y.C. Algorithm Unrolling: Interpretable, Efficient Deep Learning for Signal and Image Processing. IEEE Signal Process. Mag. 2021, 38, 18–44. [Google Scholar] [CrossRef]
- Xiong, W.; Hu, J.; Zhong, K.; Sun, Y.; Xiao, X.; Zhu, G. MIMO Radar Transmit Waveform Design for Beampattern Matching via Complex Circle Optimization. Remote Sens. 2023, 15, 633. [Google Scholar] [CrossRef]
- Cheng, Z.; Shi, S.; Tang, L.; He, Z.; Liao, B. Waveform Design for Collocated MIMO Radar With High-Mix-Low-Resolution ADCs. IEEE Trans. Signal Process. 2021, 69, 28–41. [Google Scholar] [CrossRef]
- Zheng, H.; Jiu, B.; Li, K.; Liu, H. Joint Design of the Transmit Beampattern and Angular Waveform for Colocated MIMO Radar under a Constant Modulus Constraint. Remote Sens. 2021, 13, 3392. [Google Scholar] [CrossRef]
- Qiu, X.; Jiang, W.; Liu, Y.; Chatzinotas, S.; Gini, F.; Greco, M.S. Constrained Riemannian Manifold Optimization for the Simultaneous Shaping of Ambiguity Function and Transmit Beampattern. IEEE Trans. Aerosp. Electron. Syst. 2024, 1–18. [Google Scholar] [CrossRef]
- An, D.; Liu, J.; Zhong, K.; Hu, J.; Yao, H.; Li, H.; Gini, F. Per-User Dynamic Controllable Waveform Design for Dual Function Radar-Communication System. IEEE Trans. Aerosp. Electron. Syst. 2024, 1–15. [Google Scholar] [CrossRef]
- Zhong, K.; Hu, J.; Li, H.; Wang, Y.; Cheng, X.; Cheng, X.; Pan, C.; Teh, K.C.; Cui, G. Joint Design of Power Allocation and Unimodular Waveform for Polarimetric Radar. IEEE Trans. Geosci. Remote. Sens. 2024, 1. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, Q.; Huang, Z.; Li, Z.; Xu, Y.; Zhang, J. Unimodular Waveform Design for the DFRC System with Constrained Communication QoS. Remote Sens. 2023, 15, 5350. [Google Scholar] [CrossRef]
- Zhong, K.; Hu, J.; Zhao, Z.; Yu, X.; Cui, G.; Liao, B.; Hu, H. MIMO Radar Unimodular Waveform Design With Learned Complex Circle Manifold Network. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1798–1807. [Google Scholar] [CrossRef]
- Yu, R.; Fu, Y.; Yang, W.; Bai, M.; Zhou, J.; Chen, M. Waveform Design for Target Information Maximization over a Complex Circle Manifold. Remote Sens. 2024, 16, 645. [Google Scholar] [CrossRef]
- Alhujaili, K.; Monga, V.; Rangaswamy, M. Transmit MIMO Radar Beampattern Design via Optimization on the Complex Circle Manifold. IEEE Trans. Signal Process. 2019, 67, 3561–3575. [Google Scholar] [CrossRef]
- Fan, T.; Yu, X.; Gan, N.; Bu, Y.; Cui, G.; Iommelli, S. Transmit–Receive Design for Airborne Radar With Nonuniform Pulse Repetition Intervals. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4067–4084. [Google Scholar] [CrossRef]
- Khan, A.H.; Cao, X.; Li, S.; Katsikis, V.N.; Liao, L. BAS-ADAM: An ADAM based approach to improve the performance of beetle antennae search optimizer. IEEE/CAA J. Autom. Sin. 2020, 7, 461–471. [Google Scholar] [CrossRef]
- Wan, Q.; Fang, J.; Huang, Y.; Duan, H.; Li, H. A Variational Bayesian Inference-Inspired Unrolled Deep Network for MIMO Detection. IEEE Trans. Signal Process. 2022, 70, 423–437. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]


| Method | SIR (dB) | Time (s) |
|---|---|---|
| UniAFSIM [20] | 60 | 843.8 |
| QGD [21] | 97 | 3.27 |
| MOEM [22] | 157 | 5.04 |
| ResNet [25] | 124 | 3.69 |
| Proposed method | 301 | 3.51 |
| Target | Strong | Weak |
|---|---|---|
| velocity v (m/s) | 320 | 1280 |
| normalized frequency | 0.08 | 0.32 |
| ocation R (km) | 100 | 100.45 |
| range cell | 666 | 669 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Xiao, X.; Hu, J.; Zhao, Z.; Zhong, K.; Li, C. MAL-Net: Model-Adaptive Learned Network for Slow-Time Ambiguity Function Shaping. Remote Sens. 2025, 17, 173. https://doi.org/10.3390/rs17010173
Wang J, Xiao X, Hu J, Zhao Z, Zhong K, Li C. MAL-Net: Model-Adaptive Learned Network for Slow-Time Ambiguity Function Shaping. Remote Sensing. 2025; 17(1):173. https://doi.org/10.3390/rs17010173
Chicago/Turabian StyleWang, Jun, Xiangqing Xiao, Jinfeng Hu, Ziwei Zhao, Kai Zhong, and Chaohai Li. 2025. "MAL-Net: Model-Adaptive Learned Network for Slow-Time Ambiguity Function Shaping" Remote Sensing 17, no. 1: 173. https://doi.org/10.3390/rs17010173
APA StyleWang, J., Xiao, X., Hu, J., Zhao, Z., Zhong, K., & Li, C. (2025). MAL-Net: Model-Adaptive Learned Network for Slow-Time Ambiguity Function Shaping. Remote Sensing, 17(1), 173. https://doi.org/10.3390/rs17010173








