Urban Land Surface Temperature Downscaling in Chicago: Addressing Ethnic Inequality and Gentrification
Abstract
1. Introduction
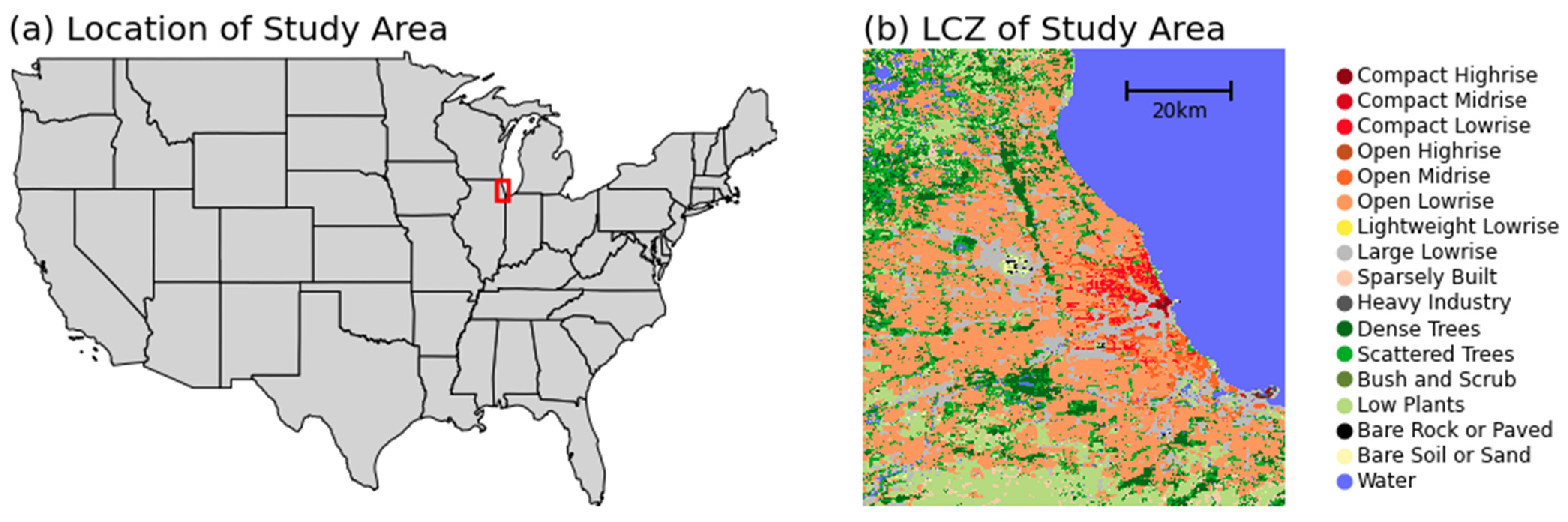
2. Data
2.1. LST Data
2.2. Ancillary Variables
2.3. Collocation and Aggregation of Data
2.4. Socioeconomic Data
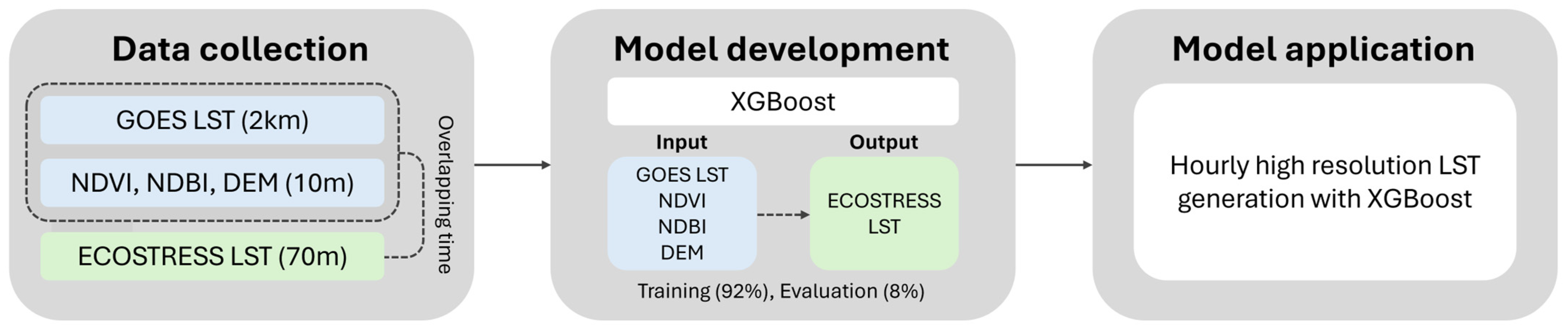
3. Downscaling Methods
3.1. TsHARP-Based Method
3.2. Extreme Gradient Boosting (XGB)
3.3. Accuracy Verification with Evaluation Set
4. Downscaling Results
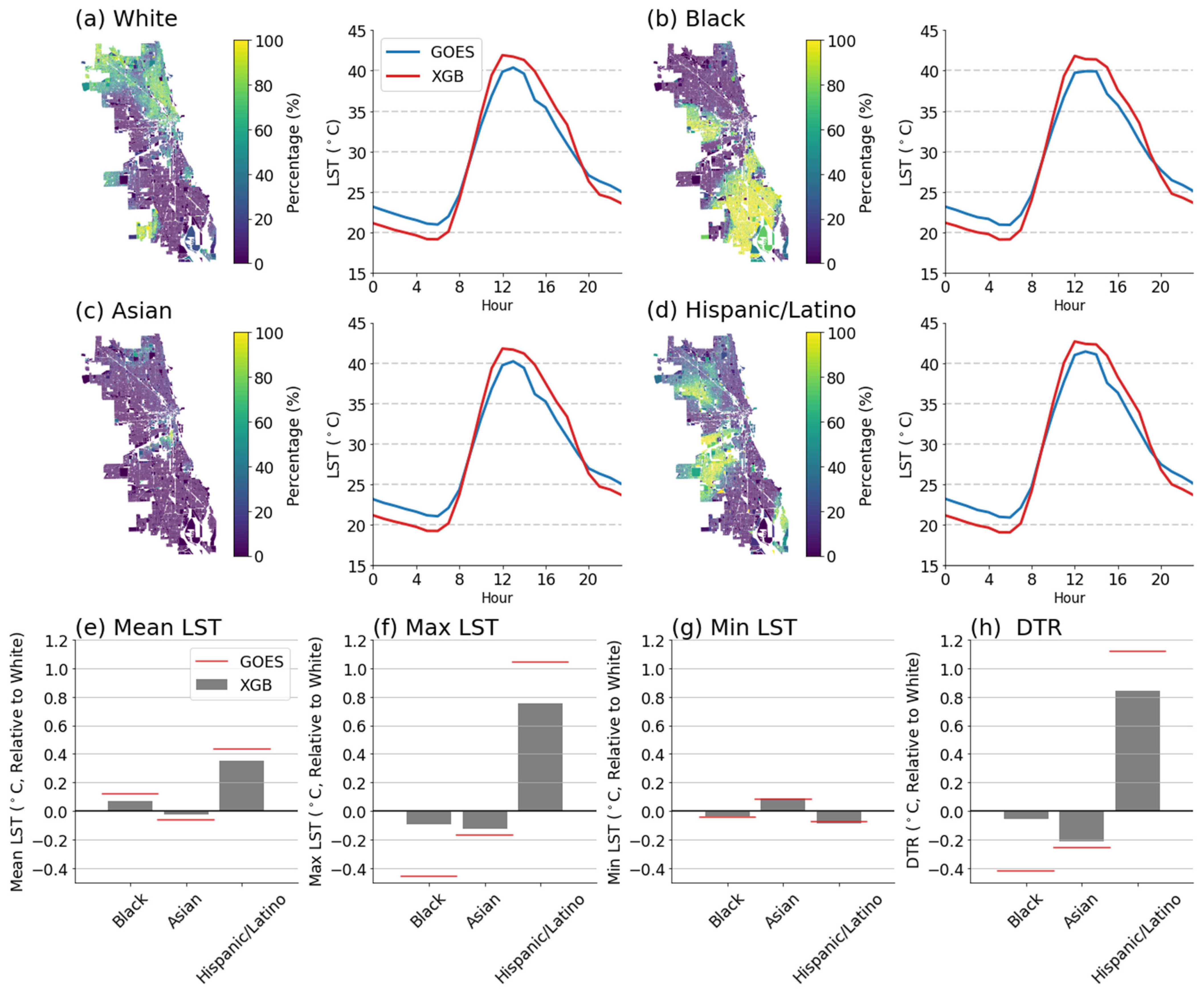
5. Ethnic Inequality of LST Exposure in Chicago
5.1. City-Scale Ethnic Inequality
5.2. Regional Ethnicity Analysis on Humboldt Park
6. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, J.; Yang, Y.; Sun, D.; Jin, C.; Xiao, X. Influence of urban morphological characteristics on thermal environment. Sustain. Cities Soc. 2021, 72, 103045. [Google Scholar] [CrossRef]
- Chen, F.; Yang, S.; Yin, K.; Chan, P. Challenges to quantitative applications of Landsat observations for the urban thermal environment. J. Environ. Sci. 2017, 59, 80–88. [Google Scholar] [CrossRef] [PubMed]
- Sharifi, A.; Pathak, M.; Joshi, C.; He, B.-J. A systematic review of the health co-benefits of urban climate change adaptation. Sustain. Cities Soc. 2021, 74, 103190. [Google Scholar] [CrossRef]
- Moonen, P.; Defraeye, T.; Dorer, V.; Blocken, B.; Carmeliet, J. Urban Physics: Effect of the micro-climate on comfort, health and energy demand. Front. Archit. Res. 2012, 1, 197–228. [Google Scholar] [CrossRef]
- Mashhoodi, B. Environmental justice and surface temperature: Income, ethnic, gender, and age inequalities. Sustain. Cities Soc. 2021, 68, 102810. [Google Scholar] [CrossRef]
- Renteria, R.; Grineski, S.; Collins, T.; Flores, A.; Trego, S. Social disparities in neighborhood heat in the Northeast United States. Environ. Res. 2022, 203, 111805. [Google Scholar] [CrossRef]
- Mitchell, B.C.; Chakraborty, J. Exploring the relationship between residential segregation and thermal inequity in 20 US cities. Local Environ. 2018, 23, 796–813. [Google Scholar] [CrossRef]
- Dialesandro, J.; Brazil, N.; Wheeler, S.; Abunnasr, Y. Dimensions of thermal inequity: Neighborhood social demographics and urban heat in the Southwestern US. Int. J. Environ. Res. Public Health 2021, 18, 941. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Myint, S.W. Exploring the effect of neighboring land cover pattern on land surface temperature of central building objects. Build. Environ. 2016, 95, 346–354. [Google Scholar] [CrossRef]
- Alexander, C. Normalised difference spectral indices and urban land cover as indicators of land surface temperature (LST). Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 102013. [Google Scholar] [CrossRef]
- Tetali, S.; Baird, N.; Klima, K. A multicity analysis of daytime Surface Urban Heat Islands in India and the US. Sustain. Cities Soc. 2022, 77, 103568. [Google Scholar] [CrossRef]
- Guha, S.; Govil, H.; Dey, A.; Gill, N. Analytical study of land surface temperature with NDVI and NDBI using Landsat 8 OLI and TIRS data in Florence and Naples city, Italy. Eur. J. Remote Sens. 2018, 51, 667–678. [Google Scholar] [CrossRef]
- Gage, E.A.; Cooper, D.J. Urban forest structure and land cover composition effects on land surface temperature in a semi-arid suburban area. Urban For. Urban Green. 2017, 28, 28–35. [Google Scholar] [CrossRef]
- Fu, P.; Weng, Q. Variability in annual temperature cycle in the urban areas of the United States as revealed by MODIS imagery. ISPRS J. Photogramm. Remote Sens. 2018, 146, 65–73. [Google Scholar] [CrossRef]
- Al-Hamdan, M.Z.; Quattrochi, D.A.; Bounoua, L.; Lachir, A.; Zhang, P. Using Landsat, MODIS, and a biophysical model to evaluate LST in urban centers. Remote Sens. 2016, 8, 952. [Google Scholar] [CrossRef]
- Mukherjee, S.; Joshi, P.; Garg, R.D. Analysis of urban built-up areas and surface urban heat island using downscaled MODIS derived land surface temperature data. Geocarto Int. 2017, 32, 900–918. [Google Scholar] [CrossRef]
- Keramitsoglou, I.; Kiranoudis, C.T.; Ceriola, G.; Weng, Q.; Rajasekar, U. Identification and analysis of urban surface temperature patterns in Greater Athens, Greece, using MODIS imagery. Remote Sens. Environ. 2011, 115, 3080–3090. [Google Scholar] [CrossRef]
- Elmes, A.; Healy, M.; Geron, N.; Andrews, M.; Rogan, J.; Martin, D.; Sangermano, F.; Williams, C.; Weil, B. Mapping spatiotemporal variability of the urban heat island across an urban gradient in Worcester, Massachusetts using in-situ Thermochrons and Landsat-8 Thermal Infrared Sensor (TIRS) data. GISci. Remote Sens. 2020, 57, 845–864. [Google Scholar] [CrossRef]
- Hulley, G.; Shivers, S.; Wetherley, E.; Cudd, R. New ECOSTRESS and MODIS land surface temperature data reveal fine-scale heat vulnerability in cities: A case study for Los Angeles County, California. Remote Sens. 2019, 11, 2136. [Google Scholar] [CrossRef]
- Chang, Y.; Xiao, J.; Li, X.; Middel, A.; Zhang, Y.; Gu, Z.; Wu, Y.; He, S. Exploring diurnal thermal variations in urban local climate zones with ECOSTRESS land surface temperature data. Remote Sens. Environ. 2021, 263, 112544. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, X.; Wang, F.; Qiao, Z.; An, H.; Han, D.; Luo, J. Exploring the cooling effect of urban parks based on the ECOSTRESS land surface temperature. Front. Ecol. Evol. 2022, 10, 1031517. [Google Scholar] [CrossRef]
- Yao, X.; Zeng, X.; Zhu, Z.; Lan, Y.; Shen, Y.; Liu, Q.; Yang, F. Exploring the diurnal variations of the driving factors affecting block-based LST in a “Furnace city” using ECOSTRESS thermal imaging. Sustain. Cities Soc. 2023, 98, 104841. [Google Scholar] [CrossRef]
- Chang, Y.; Xiao, J.; Li, X.; Zhou, D.; Wu, Y. Combining GOES-R and ECOSTRESS land surface temperature data to investigate diurnal variations of surface urban heat island. Sci. Total Environ. 2022, 823, 153652. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Xiao, J.; Li, X.; Weng, Q. Monitoring diurnal dynamics of surface urban heat island for urban agglomerations using ECOSTRESS land surface temperature observations. Sustain. Cities Soc. 2023, 98, 104833. [Google Scholar] [CrossRef]
- Han, D.; An, H.; Cai, H.; Wang, F.; Xu, X.; Qiao, Z.; Jia, K.; Sun, Z.; An, Y. How do 2D/3D urban landscapes impact diurnal land surface temperature: Insights from block scale and machine learning algorithms. Sustain. Cities Soc. 2023, 99, 104933. [Google Scholar] [CrossRef]
- Lin, Z.; Xu, H.; Yao, X.; Yang, C.; Ye, D. How does urban thermal environmental factors impact diurnal cycle of land surface temperature? A multi-dimensional and multi-granularity perspective. Sustain. Cities Soc. 2024, 101, 105190. [Google Scholar] [CrossRef]
- Chang, Y.; Xiao, J.; Li, X.; Frolking, S.; Zhou, D.; Schneider, A.; Weng, Q.; Yu, P.; Wang, X.; Li, X. Exploring diurnal cycles of surface urban heat island intensity in Boston with land surface temperature data derived from GOES-R geostationary satellites. Sci. Total Environ. 2021, 763, 144224. [Google Scholar] [CrossRef] [PubMed]
- Hrisko, J.; Ramamurthy, P.; Yu, Y.; Yu, P.; Melecio-Vázquez, D. Urban air temperature model using GOES-16 LST and a diurnal regressive neural network algorithm. Remote Sens. Environ. 2020, 237, 111495. [Google Scholar] [CrossRef]
- Hrisko, J.; Ramamurthy, P.; Melecio-Vázquez, D.; Gonzalez, J.E. Spatiotemporal Variability of Heat Storage in Major US Cities—A Satellite-Based Analysis. Remote Sens. 2020, 13, 59. [Google Scholar] [CrossRef]
- Beale, C.; Norouzi, H.; Sharifnezhadazizi, Z.; Bah, A.R.; Yu, P.; Yu, Y.; Blake, R.; Vaculik, A.; Gonzalez-Cruz, J. Comparison of diurnal variation of land surface temperature from GOES-16 ABI and MODIS instruments. IEEE Geosci. Remote Sens. Lett. 2019, 17, 572–576. [Google Scholar] [CrossRef]
- Ha, W.; Gowda, P.H.; Howell, T.A. Downscaling of land surface temperature maps in the Texas high plains with the TsHARP method. GISci. Remote Sens. 2011, 48, 583–599. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Colaizzi, P.D. Utility of thermal sharpening over Texas high plains irrigated agricultural fields. J. Geophys. Res. Atmos. 2007, 112, D19110. [Google Scholar] [CrossRef]
- Chen, X.; Li, W.; Chen, J.; Rao, Y.; Yamaguchi, Y. A combination of TsHARP and thin plate spline interpolation for spatial sharpening of thermal imagery. Remote Sens. 2014, 6, 2845–2863. [Google Scholar] [CrossRef]
- Inamdar, A.K.; French, A. Disaggregation of GOES land surface temperatures using surface emissivity. Geophys. Res. Lett. 2009, 36, L02408. [Google Scholar] [CrossRef]
- Hais, M.; Kučera, T. The influence of topography on the forest surface temperature retrieved from Landsat TM, ETM+ and ASTER thermal channels. ISPRS J. Photogramm. Remote Sens. 2009, 64, 585–591. [Google Scholar] [CrossRef]
- Maeda, E.E. Downscaling MODIS LST in the East African mountains using elevation gradient and land-cover information. Int. J. Remote Sens. 2014, 35, 3094–3108. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, H.; Yang, J. Spatial downscaling of land surface temperature in combination with TVDI and elevation. Int. J. Remote Sens. 2019, 40, 1875–1886. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Pu, R. Assessing scaling effect in downscaling land surface temperature in a heterogenous urban environment. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102256. [Google Scholar] [CrossRef]
- Li, W.; Ni, L.; Li, Z.-l.; Duan, S.-B.; Wu, H. Evaluation of machine learning algorithms in spatial downscaling of MODIS land surface temperature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2299–2307. [Google Scholar] [CrossRef]
- Tu, H.; Cai, H.; Yin, J.; Zhang, X.; Zhang, X. Land surface temperature downscaling in the karst mountain urban area considering the topographic characteristics. J. Appl. Remote Sens. 2022, 16, 034515. [Google Scholar] [CrossRef]
- Anderson, B.G.; Bell, M.L. Weather-related mortality: How heat, cold, and heat waves affect mortality in the United States. Epidemiology 2009, 20, 205. [Google Scholar] [CrossRef] [PubMed]
- Mashhoodi, B. Feminization of surface temperature: Environmental justice and gender inequality among socioeconomic groups. Urban Clim. 2021, 40, 101004. [Google Scholar] [CrossRef]
- Zhu, Y.; Myint, S.W.; Schaffer-Smith, D.; Muenich, R.L.; Tong, D.; Li, Y. Formulating operational mitigation options and examining intra-urban social inequality using evidence-based urban warming effects. Front. Environ. Sci. 2022, 9, 795474. [Google Scholar] [CrossRef]
- Mitchell, B.C.; Chakraborty, J. Landscapes of thermal inequity: Disproportionate exposure to urban heat in the three largest US cities. Environ. Res. Lett. 2015, 10, 115005. [Google Scholar] [CrossRef]
- Benz, S.A.; Burney, J.A. Widespread race and class disparities in surface urban heat extremes across the United States. Earth's Future 2021, 9, e2021EF002016. [Google Scholar] [CrossRef]
- Hsu, A.; Sheriff, G.; Chakraborty, T.; Manya, D. Disproportionate exposure to urban heat island intensity across major US cities. Nat. Commun. 2021, 12, 2721. [Google Scholar] [CrossRef]
- Liu, D.; Kwan, M.-P.; Kan, Z. Analysis of urban green space accessibility and distribution inequity in the City of Chicago. Urban For. Urban Green. 2021, 59, 127029. [Google Scholar] [CrossRef]
- Williams, T.G.; Logan, T.M.; Zuo, C.T.; Liberman, K.D.; Guikema, S.D. Parks and safety: A comparative study of green space access and inequity in five US cities. Landsc. Urban Plan. 2020, 201, 103841. [Google Scholar] [CrossRef]
- Schmit, T.J.; Gunshor, M.M.; Menzel, W.P.; Gurka, J.J.; Li, J.; Bachmeier, A.S. Introducing the next-generation Advanced Baseline Imager on GOES-R. Bull. Am. Meteorol. Soc. 2005, 86, 1079–1096. [Google Scholar] [CrossRef]
- Ching, J.; Mills, G.; Bechtel, B.; See, L.; Feddema, J.; Wang, X.; Ren, C.; Brousse, O.; Martilli, A.; Neophytou, M. WUDAPT: An urban weather, climate, and environmental modeling infrastructure for the anthropocene. Bull. Am. Meteorol. Soc. 2018, 99, 1907–1924. [Google Scholar] [CrossRef]
- Yu, Y.; Tarpley, D.; Privette, J.L.; Flynn, L.E.; Xu, H.; Chen, M.; Vinnikov, K.Y.; Sun, D.; Tian, Y. Validation of GOES-R satellite land surface temperature algorithm using SURFRAD ground measurements and statistical estimates of error properties. IEEE Trans. Geosci. Remote Sens. 2011, 50, 704–713. [Google Scholar] [CrossRef]
- Yu, Y.; Yu, P. Land surface temperature product from the GOES-R series. In The GOES-R Series; Elsevier: Amsterdam, The Netherlands, 2020; pp. 133–144. [Google Scholar]
- Hulley, G.C.; Göttsche, F.M.; Rivera, G.; Hook, S.J.; Freepartner, R.J.; Martin, M.A.; Cawse-Nicholson, K.; Johnson, W.R. Validation and quality assessment of the ECOSTRESS level-2 land surface temperature and emissivity product. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5000523. [Google Scholar] [CrossRef]
- Guha, S.; Govil, H.; Gill, N.; Dey, A. A long-term seasonal analysis on the relationship between LST and NDBI using Landsat data. Quat. Int. 2021, 575, 249–258. [Google Scholar] [CrossRef]
- Guo, A.; Yang, J.; Sun, W.; Xiao, X.; Cecilia, J.X.; Jin, C.; Li, X. Impact of urban morphology and landscape characteristics on spatiotemporal heterogeneity of land surface temperature. Sustain. Cities Soc. 2020, 63, 102443. [Google Scholar] [CrossRef]
- Guha, S.; Govil, H. Seasonal variability of LST-NDVI correlation on different land use/land cover using Landsat satellite sensor: A case study of Raipur City, India. Environ. Dev. Sustain. 2022, 24, 8823–8839. [Google Scholar] [CrossRef]
- Gascon, F.; Bouzinac, C.; Thépaut, O.; Jung, M.; Francesconi, B.; Louis, J.; Lonjou, V.; Lafrance, B.; Massera, S.; Gaudel-Vacaresse, A. Copernicus Sentinel-2A calibration and products validation status. Remote Sens. 2017, 9, 584. [Google Scholar] [CrossRef]
- Maune, D.F.; Kopp, S.; Zerdas, C. Digital elevation model technologies and applications. In The DEM Users Manual; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2007. [Google Scholar]
- Gesch, D.B.; Oimoen, M.J.; Evans, G.A. Accuracy Assessment of the US Geological Survey National Elevation Dataset, and Comparison with other Large-Area Elevation Datasets: SRTM and ASTER; US Department of the Interior, US Geological Survey: Sioux Falls, SD, USA, 2014; Volume 1008.
- Sattari, F.; Hashim, M.; Sookhak, M.; Banihashemi, S.; Pour, A.B. Assessment of the TsHARP method for spatial downscaling of land surface temperature over urban regions. Urban Clim. 2022, 45, 101265. [Google Scholar] [CrossRef]
- Mukherjee, S.; Joshi, P.; Garg, R.D. A comparison of different regression models for downscaling Landsat and MODIS land surface temperature images over heterogeneous landscape. Adv. Space Res. 2014, 54, 655–669. [Google Scholar] [CrossRef]
- Sattari, F.; Hashim, M.; Pour, A.B. Thermal sharpening of land surface temperature maps based on the impervious surface index with the TsHARP method to ASTER satellite data: A case study from the metropolitan Kuala Lumpur, Malaysia. Measurement 2018, 125, 262–278. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 2951. [Google Scholar]
- Mumm, J. Gentrification in color and time: White and Puerto Rican racial histories at work in Humboldt Park. Cent. J. 2016, 28, 88–125. [Google Scholar]
- Wilson, D.; Grammenos, D. Gentrification, discourse, and the body: Chicago’s Humboldt Park. Environ. Plan. D Soc. Space 2005, 23, 295–312. [Google Scholar] [CrossRef]
- Rinaldo, R. Space of resistance: The Puerto Rican cultural center and Humboldt Park. Cult. Crit. 2002, 50, 135–174. [Google Scholar] [CrossRef]
- Chakraborty, T.; Hsu, A.; Manya, D.; Sheriff, G. Disproportionately higher exposure to urban heat in lower-income neighborhoods: A multi-city perspective. Environ. Res. Lett. 2019, 14, 105003. [Google Scholar] [CrossRef]
- Goldblatt, R.; Addas, A.; Crull, D.; Maghrabi, A.; Levin, G.G.; Rubinyi, S. Remotely sensed derived land surface temperature (LST) as a proxy for air temperature and thermal comfort at a small geographical scale. Land 2021, 10, 410. [Google Scholar] [CrossRef]
- Patel, S.; Indraganti, M.; Jawarneh, R.N. A comprehensive systematic review: Impact of Land Use/Land Cover (LULC) on Land Surface Temperatures (LST) and outdoor thermal comfort. Build. Environ. 2023, 249, 111130. [Google Scholar] [CrossRef]
- Imran, H.; Hossain, A.; Islam, A.S.; Rahman, A.; Bhuiyan, M.A.E.; Paul, S.; Alam, A. Impact of land cover changes on land surface temperature and human thermal comfort in Dhaka city of Bangladesh. Earth Syst. Environ. 2021, 5, 667–693. [Google Scholar] [CrossRef]
- Lee, H.; Caldwell, J.T.; Maene, C.; Cagney, K.A.; Saunders, M.R. Racial/ethnic inequities in access to high-quality dialysis treatment in Chicago: Does neighborhood racial/ethnic composition matter? J. Racial Ethn. Health Disparities 2020, 7, 854–864. [Google Scholar] [CrossRef]
- Lee, J.; Dessler, A.E. Future Temperature-Related Deaths in the US: The Impact of Climate Change, Demographics, and Adaptation. GeoHealth 2023, 7, e2023GH000799. [Google Scholar] [CrossRef]
- Davis, R.E.; Hondula, D.M.; Sharif, H. Examining the diurnal temperature range enigma: Why is human health related to the daily change in temperature? Int. J. Biometeorol. 2020, 64, 397–407. [Google Scholar] [CrossRef] [PubMed]
- Betancur, J.J. The politics of gentrification: The case of West Town in Chicago. Urban Aff. Rev. 2002, 37, 780–814. [Google Scholar] [CrossRef]
- Mumm, J. The racial fix: White currency in the gentrification of black and Latino Chicago. Focaal 2017, 2017, 102–118. [Google Scholar] [CrossRef]
- Orta, D. “Mexicans Built This Neighborhood!” Gentrification, Organizations, and the Role of Place-Based Identity in Latinx Chicago. Soc. Sci. 2021, 10, 304. [Google Scholar] [CrossRef]
- Francis, J.; Disney, M.; Law, S. Monitoring canopy quality and improving equitable outcomes of urban tree planting using LiDAR and machine learning. Urban For. Urban Green. 2023, 89, 128115. [Google Scholar] [CrossRef]
- Schwaab, J.; Meier, R.; Mussetti, G.; Seneviratne, S.; Bürgi, C.; Davin, E.L. The role of urban trees in reducing land surface temperatures in European cities. Nat. Commun. 2021, 12, 6763. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhou, W.; Jiao, M. Location matters: Planting urban trees in the right places improves cooling. Front. Ecol. Environ. 2022, 20, 147–151. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, J.; Cadenasso, M.L. Effects of the spatial configuration of trees on urban heat mitigation: A comparative study. Remote Sens. Environ. 2017, 195, 1–12. [Google Scholar] [CrossRef]
- Cole, H.V.; Triguero-Mas, M.; Connolly, J.J.; Anguelovski, I. Determining the health benefits of green space: Does gentrification matter? Health Place 2019, 57, 1–11. [Google Scholar] [CrossRef]
- Li, K.; Guan, K.; Jiang, C.; Wang, S.; Peng, B.; Cai, Y. Evaluation of four new land surface temperature (LST) products in the US corn belt: ECOSTRESS, GOES-R, landsat, and sentinel-3. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9931–9945. [Google Scholar] [CrossRef]
- Sun, D.; Yu, Y.; Fang, L.; Liu, Y. Toward an operational land surface temperature algorithm for GOES. J. Appl. Meteorol. Climatol. 2013, 52, 1974–1986. [Google Scholar] [CrossRef]
- Xu, H.; Yu, Y.; Tarpley, D.; Göttsche, F.-M.; Olesen, F.-S. Evaluation of GOES-R land surface temperature algorithm using SEVIRI satellite retrievals with in situ measurements. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3812–3822. [Google Scholar] [CrossRef]
- Meng, X.; Cheng, J.; Yao, B.; Guo, Y. Validation of the ECOSTRESS land surface temperature product using ground measurements. IEEE Geosci. Remote Sens. Lett. 2021, 19, 3005305. [Google Scholar] [CrossRef]
- Bian, Z.; Roujean, J.-L.; Lagouarde, J.-P.; Cao, B.; Li, H.; Du, Y.; Liu, Q.; Xiao, Q.; Liu, Q. A semi-empirical approach for modeling the vegetation thermal infrared directional anisotropy of canopies based on using vegetation indices. ISPRS J. Photogramm. Remote Sens. 2020, 160, 136–148. [Google Scholar] [CrossRef]
- Kraemer, R.; Remmler, P.; Bumberger, J.; Kabisch, N. Running a dense air temperature measurement field campaign at the urban neighbourhood level: Protocol and lessons learned. MethodsX 2022, 9, 101719. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, J.; Liang, S.; Wang, D. A practical reanalysis data and thermal infrared remote sensing data merging (RTM) method for reconstruction of a 1-km all-weather land surface temperature. Remote Sens. Environ. 2021, 260, 112437. [Google Scholar] [CrossRef]
- Long, D.; Yan, L.; Bai, L.; Zhang, C.; Li, X.; Lei, H.; Yang, H.; Tian, F.; Zeng, C.; Meng, X. Generation of MODIS-like land surface temperatures under all-weather conditions based on a data fusion approach. Remote Sens. Environ. 2020, 246, 111863. [Google Scholar] [CrossRef]
- Duan, S.-B.; Lian, Y.; Zhao, E.; Chen, H.; Han, W.; Wu, Z. A Novel Approach to All-Weather LST Estimation using XGBoost Model and Multi-Source Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5004614. [Google Scholar] [CrossRef]


| Hyperparameter | Description | Search Range | Selected Value |
|---|---|---|---|
| max_depth | Maximum depth of a tree | [3, 10] | 4 |
| learning_rate | Boosting learning rate | [0.01, 0.3] | 0.05 |
| n_estimators | Number of gradient-boosted trees. Equivalent to number of boosting rounds | [50, 1200] | 700 |
| gamma | Minimum loss reduction required to make a further partition on a leaf node of the tree | [0, 5] | 1 |
| subsample | Subsample ratio of the training instance | [0.5, 1] | 0.7 |
| colsample_bytree | Subsample ratio of columns when constructing each tree | [0.5, 1] | 0.75 |
| Variable | Abbreviation | Feature Importance |
|---|---|---|
| Hour of the day | HOD | 0.1016 |
| Day of year | DOY | 0.0345 |
| Normalized Difference Built-up Index | NDBI | 0.0532 |
| Normalized Difference Vegetation Index | NDVI | 0.0142 |
| Elevation | ELEV | 0.0029 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Berkelhammer, M.; Wilson, M.D.; Love, N.; Cintron, R. Urban Land Surface Temperature Downscaling in Chicago: Addressing Ethnic Inequality and Gentrification. Remote Sens. 2024, 16, 1639. https://doi.org/10.3390/rs16091639
Lee J, Berkelhammer M, Wilson MD, Love N, Cintron R. Urban Land Surface Temperature Downscaling in Chicago: Addressing Ethnic Inequality and Gentrification. Remote Sensing. 2024; 16(9):1639. https://doi.org/10.3390/rs16091639
Chicago/Turabian StyleLee, Jangho, Max Berkelhammer, Matthew D. Wilson, Natalie Love, and Ralph Cintron. 2024. "Urban Land Surface Temperature Downscaling in Chicago: Addressing Ethnic Inequality and Gentrification" Remote Sensing 16, no. 9: 1639. https://doi.org/10.3390/rs16091639
APA StyleLee, J., Berkelhammer, M., Wilson, M. D., Love, N., & Cintron, R. (2024). Urban Land Surface Temperature Downscaling in Chicago: Addressing Ethnic Inequality and Gentrification. Remote Sensing, 16(9), 1639. https://doi.org/10.3390/rs16091639






