Abstract
In recent decades, the hydrological processes on the Loess Plateau have undergone significant changes due to the combined effects of climate change and human activities. This study investigates the Qin River basin, the core area of the Loess Plateau. Between 1971 and 2000, the hydrometeorology of the flood season in the Qin basin on the Loess Plateau in China changed abruptly in 1982 and 1992. This study uses distributed hydrologic modeling and statistical analysis to distinguish the spatial and temporal impacts of climate change and human activities. The fastest dynamic changes in land use occurred in grassland and construction land, accounting for 0.36% and −0.1%, respectively, from 1982 to 1991. From 1992 to 2000, it was 0.29% and 0.3%, respectively. The increase in basin area where the Normalized Difference Vegetation Index increased was 95%. However, except for significant changes in runoff from 1981 to 1992, there were no significant changes in precipitation, runoff, and temperature during other flood seasons. During the two studied variation periods, from 1982 to 1991 and from 1992 to 2000, the contribution rate of climate change to flood season runoff () decreased from 83.26% to 74.47%, while the contribution rate of human activity disturbance to flood season runoff () increased from 16.74% to 25.53%. In terms of spatial distribution, from 1982 to 1991, areas with a > 50% were primarily concentrated in the upper reaches of the basin, while from 1992–2000, these areas shifted to the lower reaches. This study offers valuable insights for water resource planning and soil conservation measures in the Loess Plateau and similar arid regions worldwide, aiming to ensure water resource safety and sustainability in response to climate change and human interference.
1. Introduction
With issues such as population growth, pollution, and the development of industrial and agricultural sectors, the scarcity of water resources has increasingly become a problem that hinders social development [1,2,3]. Climate change and human disturbance seriously affect the evolutionary path and direction of hydrology, resulting in changes in runoff, runoff processes, and runoff composition [4,5]. Accordingly, spatial and temporal distributions of hydrological processes in basins have also changed [6]. These changes profoundly affect water security, social security, and ecological and environmental security [7].
The Loess Plateau, a semi-arid area in northwest China, with an altitude of 1000–3000 m and a vast area of 620,000 km2, is the cradle of ancient Chinese civilization and has a long agricultural history [8]. Furthermore, the Loess Plateau experiences the most severe drought and soil erosion in China [9]. As an important agricultural area, the natural scarcity of water resources is a challenge. In addition, the basin ecology is easily disrupted, and the regional hydrological processes are highly complex [10,11]. Therefore, the Loess Plateau is an ecologically sensitive area in which development must be carefully planned. Since the 1970s, large-scale water and soil conservation, groundwater development and utilization, water conservancy, urban expansion, and other projects have substantially reduced runoff on the Loess Plateau, and even some rivers have experienced seasonal flow interruptions [12,13]. Under the combined impact of various driving forces, accurately quantifying the spatial and temporal evolution of water resources is challenging. Not only does this complexity hinder effective water resources planning and management, but it also has a significant impact on the survival and development of human society in the Loess Plateau [14].
Recently, several methods have been proposed to quantitatively analyze runoff changes on the Loess Plateau [1,15,16]. Xu and Jiang [17] summarized the recent research on runoff evolution and impact under changing environments and found that nonlinear statistical methods, regression analysis, and the wavelet theory have been widely employed in quantitative research on hydrological responses because of their low data requirements and strong practicability. Many scholars have studied the quantitative impacts of different driving factors on hydrological processes by improving traditional statistical methods or introducing new theories and methods [18,19,20]. Li et al. [21] conducted a quantitative assessment of runoff changes in the Wuding River basin based on the rainfall–runoff model and reported that the contribution rate of water and soil conservation management (WSCM) to runoff reduction in the basin was 87%. Zhang et al. used the Budyko water–heat balance method to quantitatively detect the hydrological response of different factors to the runoff of eight basins in the Loess Plateau and found that from 1950 to 2000, land use/land cover (LULC) change contributed more than 50% to runoff reduction [22]. A hydrological model is an effective tool for the quantitative analysis of the water cycle and hydrological processes in a basin. Guo et al. [13] used the geomorphology-based hydrological model (GBHM) to analyze runoff changes in the Chabagou River basin of the Loess Plateau. The results showed that the construction of check dams made a greater contribution to runoff reduction. Most studies on quantitative hydrological responses have used a single assessment method [23,24]. Because of differing principles, a variety of methods is typically used to quantitatively explore runoff changes in the same basin, and the results often differ from each other [25,26,27,28]. To better quantitatively detect the hydrological response of each driving factor to basin runoff change, scholars have used statistical analysis (correlation analysis, elastic coefficient, double cumulative curve, etc.) and hydrological simulations (SWAT, VIC, HBV, etc.) to conduct attribution analysis. Then, they discussed the applicability and advantages and disadvantages of the different methods. [13,29,30]. Xu et al. [31] commented on the main analysis methods for runoff attribution, arguing that statistical analysis methods lack physical mechanisms, cannot reflect runoff processes, and can only be used to study annual-scale runoff changes. Hydrological simulation methods are computationally complex and have high uncertainty. Wu et al. [32] used 10 methods to quantitatively detect the contribution of farming and urbanization to flood season runoff () in the Yanhe River basin of the Loess Plateau, which ranged between 39.2% and 87.4%. The results showed that the interaction between regional climate, human activities, and hydrological processes is complex and uncertain. However, considering the complex topography and geomorphology of the Loess Plateau region, the analysis of the driving factors of watershed runoff changes from the perspective of time-series changes has certain limitations, ignoring the particularity of hydrological changes in different regions of the watershed [33]. Therefore, using multiple methods to comprehensively explore the response of runoff changes to temporal and spatial changes can accurately elucidate the evolution law of watershed water resources [30,32].
The Qin River basin is the core area of the Loess Plateau. The upper and middle reaches of the basin are typical valley landforms of the Loess Plateau, with overlapping peaks, high mountains, and deep valleys. Flood disasters of varying degrees often occur during flood seasons [34]. In the latter 30 years of the 20th century, many soil and water conservation measures were implemented in the basin while agricultural land and urban expansion developed. These 30 years represent a period of rapid changes within the environment of this basin [11,35]. The Qin River basin represents the overall characteristics of the Loess Plateau to a certain extent in that it has a complex terrain and is subject to strong human interference [11]. Therefore, accurately understanding the evolution law of water resources in the region and revealing the influence of hydrological driving factors has become a critical issue requiring solutions.
This study comprehensively explored the spatiotemporal hydrological response process of flood season runoff in the Qin River basin, representing a typical basin on the Loess Plateau. Our specific objectives are as follows: (1) Identify abrupt changes in hydrological and meteorological factors during the study period and determine the year of abrupt change. (2) Analyze the changes in LULC and Normalized Difference Vegetation Index (NDVI) during the study period and explore the impact of these changes on basin runoff. (3) Quantitatively detect the impact of different driving factors on surface runoff and analyze the variation patterns of runoff under the influence of these driving factors. (4) Explore the applicability and scope of the application of different methods. Our research is of great significance for scientifically depicting the dynamic evolutionary characteristics of hydrological and water resources in the Qin River basin.
2. Geographical Setting, Data Sources and Research Framework
2.1. Study Area
The Qin River, located at 111°55′–113°30′E and 35°11′–37°08′N, is a primary tributary of the Yellow River. The Qin River basin, covering an area of 7339.98 m2, is a typical landform of the Loess Plateau, which has broken topography and intersecting gullies. The basin is a crucial agricultural area in the Yellow River basin, with cultivated land accounting for 26% [36]. The average annual precipitation is 613 mm, and the flood season (June–October) accounts for 71% of the total precipitation. The multi-year potential evaporation during the flood season is 592.5 mm [37]. In this study, the Qin River basin above the Runcheng Hydrological Station in Shanxi Province was taken as the research area (Figure 1). The severe soil erosion on the Loess Plateau has also caused hidden dangers, such as the erosion of the soil cultivation layer and the siltation of river channels. People have realized that it is necessary to immediately stop the destructive development of the Loess Plateau. [38]. Since the 1950s, because of the expansion of industrial and agricultural land, vegetation in the Qin River basin has been greatly damaged, resulting in a decrease in vegetation coverage and quality. This directly led to the intensification of soil erosion and flood disasters in the region. Therefore, since the 1970s, large-scale soil and water conservation construction projects have been carried out in the basin [11,35].
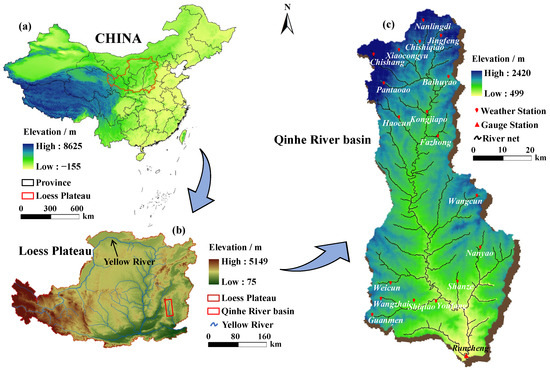
Figure 1.
Location of the study area and hydrological stations: (a) location of the Loess Plateau in China; (b) location of the Qin River basin in the Loess Plateau; (c) spatial distribution of elevation and locations of meteorological stations.
2.2. Data
In this study, daily runoff data of the Qin River basin during the flood season from 1971 to 2000 were collected from the Yellow River Hydrological Yearbook, including the daily meteorological data of 18 meteorological stations (precipitation, temperature, wind speed, and relative humidity) and daily runoff data of Runcheng Hydrological Station. The locations of meteorological and hydrological stations are shown in Figure 1.
In addition, LULC data with a spatial resolution of 0.01° × 0.01° were collected from the remote sensing dataset published by Liu et al. [39], downloaded from the Resource and Environmental Science Data Center (https://www.resdc.com (accessed on 15 January 2023)).
NDVI data with a spatial resolution of 0.01° × 0.01° were collected from the Global GIMMS NDVI3g v1 dataset published by Tucker et al. [40], downloaded from the National Tibetan Plateau Data Center (https://data.tpdc.ac.cn/home (accessed on 28 January 2023)).
Lastly, digital elevation model (DEM) data with a spatial resolution of 30 m were collected from the National Aeronautics and Space Administration (https://lpdaacsvc.cr.usgs.gov/appeears/ (accessed on 28 January 2023)). By analyzing DEM data using the hydrological analysis module in ArcGIS, data such as slope, aspect, and catchment characteristics of the Qin River basin were obtained. These topographic data served as the input data for building the hydrological model.
3. Research Methods
3.1. Trend Analysis of Hydrometeorological Factors
3.1.1. Time Series Analysis
Against the backdrop of changing climate, the intensification of human interference noticeably affects hydrological and meteorological changes. Therefore, studying the changing trends of hydrological and meteorological time series in river basins is of great significance for water resource management and decision-making in changing environments [41]. Due to the different principles underlying different trend methods, there are often differences in their calculation results. The characteristics of sequences, such as autocorrelation and periodic fluctuations, can also lead to deviations in analysis results in specific applications [42]. In order to overcome the uncertainty caused by a single method, scholars often apply multiple methods for comparative analysis when studying the trends of hydrological and meteorological changes. [13,29,43,44]. The Mann–Kendall test (M–K) and non-parametric Spearman’s rho correlation test (Sp) are widely utilized in trend research on hydrological and meteorological factors in the Loess Plateau [36,43]. The advantage of the M–K is that it is not affected by outliers and is suitable for non-normal distribution time series. On the other hand, the Sp can visually present the significance of increasing or decreasing trends in time series [31]. This study uses two methods, the M–K and Sp, to explore the trend changes in hydrological and meteorological elements in the Qin River basin.
Changes in vegetation cover usually have a certain long-term dependence. The Hurst index is an effective method for describing this dependency [45]. NDVI can be used to evaluate the coverage of surface vegetation [46]. This study uses the Hurst index to describe the sustainability of vegetation coverage in the study area. The calculation method is based on the literature of Hurst [47] and Zhou et al. [48].
3.1.2. Spatial Change Trend Analysis
A combination of the Theil–Sen slope estimator (Sen) and the M–K test is a common method for analyzing the spatial trend change of a single factor [49]. Zhang et al. [50] analyzed the spatial change of NDVI in the Qinba Mountains using Sen and M–K coupling and determined that the combination of these two methods could effectively reduce the impact of outliers. The formula for the Sen trend analysis is
Based on the principles of Sen’s trend classification, we categorize the NDVI trends as follows: when , the NDVI exhibits degradation; when , the NDVI remains stable; and when , the NDVI shows improvement.
We used Sen and M–K separately to calculate the changing trends and significance test of each grid during the study period, and these steps were completed in MATLAB. Subsequently, we performed an intersection operation between the spatial distribution maps of Sen and M–K in the Qinhe River Basin using ArcGIS. The coupling rules were as follows: If and , the NDVI is considered to be significantly improving; if and , the NDVI is considered to be slightly improving; if and , the NDVI is considered to be stable; if and , the NDVI is considered to be slightly degrading; and if and , the NDVI is considered to be significantly degrading. represents the statistical value for the M-K test. With a significance level set at , a positive value of signifies that the M-K trend has successfully met the criteria for a 95% significance test.
3.2. Identification of Abrupt Changes Years and Division of Different Periods
Due to the impact of climate change and human activities, maintaining the original consistency of hydrological series has become increasingly difficult, with the potential for abrupt changes [4]. For long-term hydrological and meteorological data, it is usually necessary to compare and study the stages before and after the abrupt changepoint [32]. The runoff attribution methods we use all require the definition of a natural period. It is assumed that the runoff of the natural period is not affected by human activities, while the runoff during the variation period is affected by climate change and human activities. The contributions of climate change and human activities to the runoff changes in the basin during the variation period are not absolute but are calculated relative to this natural period. Therefore, accurately identifying the abrupt change point and determining the natural period and variation period are the prerequisites for studying the changes in hydrological series. Identifying abrupt change points via statistical methods is widely used in the study of hydrology and meteorology [51]. In the study of hydrological processes, M–K can clearly identify the start time and duration of abrupt changes, and a Sliding T-test (T-test) can effectively monitor changes in time series data. To reduce the uncertainty of a single method, this study uses the M–K test and T-test to comprehensively identify abrupt changes in hydrological and meteorological series and then segment the series to determine the natural period and variation period. These two methods are widely used in identifying years of abrupt changes in hydrological and meteorological time series, and their applicability has been verified in other regions of the Loess Plateau [21,52,53]. The principles of the two methods mentioned above and the rules for analyzing their results are based on the studies conducted by Khaliq et al. [54] and Zhao et al. [55].
3.3. Contribution of Climate Change and Human Activities to Runoff Dynamics
In this study, two statistical methods and a distributed hydrological model were used to quantitatively discuss and in the Qin River basin. Because of the uncertainty of the principle of a single method, this study compared the calculation results of conventional statistical methods and hydrological model simulation methods to explore their applicability in the complex environment of the Loess Plateau. The spatial-temporal law of the hydrological response to runoff in the flood season was comprehensively analyzed. The application of these methods presupposes the assumption that the impacts of various driving factors on watershed runoff variations are relatively autonomous, discounting any potential interference among them.
3.3.1. Empirical Statistical Methods
The empirical statistical method was used to establish the relationship between runoff and relevant meteorological variables, and then the time series change in runoff was studied. The advantages of this method include the use of simple and straightforward formulas and relatively few calculations. In this study, two empirical statistical methods (the Runoff Reduction method [Runoff-R], which considers meteorological factors and the Budyko water–heat balance method, which considers meteorological factors and underlying surface changes) were used to quantitatively analyze the impact of different driving factors on watershed runoff [56,57,58].
- (1)
- Runoff-R method
The principle of the Runoff-R is that the difference between the measured runoff, , in the variation period and the measured runoff, , in the natural period is caused by climate change and human activities. The difference between the measured runoff, , and simulated runoff, , during the variation period was caused by human activities. The difference between the measured runoff, , in the natural period and the simulated runoff, , during the variation period was caused by climate change. The calculation formulas of and are as follows:
- (2)
- Budyko-based methods
The various characteristics of runoff can be evaluated via long-term water and heat balance [56,57,58]. Based on the equation proposed by Budyko, many scholars have proposed different forms of expressions through extensive research [59,60,61]. Wang and Tang [62] pointed out through research on various expressions that although these equations have different forms of expression, when appropriate, underlying surface parameters are taken, and different curves will coincide because the principles of these expressions are only different in form, but the relationship between precipitation, potential evaporation, and actual evaporation is consistent. A previous study used the improved Budyko method proposed by Wang and Tang to conduct a quantitative study on the driving factors of runoff changes in the Xiaoli River Basin on the Loess Plateau and concluded that this method is applicable to this basin [63]. The Budyko method is different from other statistical methods in that it has a certain physical mechanism, simple calculation process, and easy parameter calculation [31]. Therefore, this study uses the equation derived by Wang and Tang for calculation. The formula is as follows:
where denotes the actual evaporation; denotes the potential evapotranspiration, calculated using the Penman–Monteith equation [64]; denotes precipitation; and is a parameter that characterizes the changes in the underlying surface, which is used to determine the degree of variation in the watershed’s underlying surface. We have incorporated the measured runoff, precipitation, and potential evaporation from the natural period into Formula (4) and used trial and error to calculate the optimal value of . The calculation formulas of and are as follows:
where denotes the precipitation in the variation period; and denote the natural period and variation period evaporation, respectively; and denotes the amount of runoff change.
3.3.2. Distributed Hydrological Model
The empirical statistical method was used to establish the relationship between runoff and relevant meteorological variables, and then the time series change in runoff was studied. The advantages of this method include simple and straightforward formulas and relatively few calculations.
Distributed hydrological models have been used by many scholars to quantify the impact of different driving factors on runoff. The GBHM, proposed by Yang et al. [65], is a distributed hydrological model based on hillside hydrology, with a hillside valley as a geomorphic unit. It considers the impact of watershed meteorological changes and underlying surface changes on runoff evolution [65]. The key parameters and construction process of GBHM were subsequently adjusted to better explore the hydrological evolution of the study area [29]. The model can be described according to the following components: input, spatial database, calculation of hydrological processes, and output [66]. Model input data include basic geographic information data (e.g., DEM, river network), daily dynamic meteorological data (e.g., precipitation, temperature), annual dynamic LULC data, and annual NDVI data. The parameter values implemented in the hydrological model have already been validated and are based on the previous research of Guo et al. [11,29], as reported in Table 1. In this study, the period from 1971 to 1976 was selected as the calibration period, and the period from 1976 to 1981 was selected as the validation period. The Nash efficiency coefficient (), the ratio of absolute error to daily runoff (S), and the correlation coefficient (P) were used to evaluate the simulation performance of the model. The specific calculation formulas for the three evaluation methods mentioned above refer to our previous research [11,29]. The following four equations are used to quantitatively separate the impact of different driving factors on runoff [36]:
where is the simulated runoff in the natural period, is the measured runoff in the natural period, is the simulated runoff caused by human activities during the variation period, is the measured runoff during the variation period, is the effect of climate change on runoff, and is the effect of human activity on runoff.

Table 1.
Main parameters used for simulations using the GBHM model.
Furthermore, the relative influence proportions of and were defined using the following formulas:
4. Results
4.1. Trend and Abrupt Changes Analysis of Hydrometeorological Elements
4.1.1. Time Series Trend Analysis of Meteorological Elements
The non-parametric Spearman’s rho correlation test and M–K test were used to analyze the trend changes in runoff, temperature, and precipitation series during the flood season. The results are presented in Table 2. Precipitation in the Qin River basin showed an insignificant downward trend under the significance test at a 95% confidence level. Temperature showed a significant upward trend. Runoff showed a significant downward trend. The outcomes of the present study are consistent with the research findings of various scholars who have investigated diverse regions of the Loess Plateau [13,32]. Notable, during the latter three decades of the 20th century, the Loess Plateau experienced a persistent decline in precipitation [67]. The runoff on the Loess Plateau shows a decreasing trend, which can be attributed to the combined effects of global temperature rise, regional precipitation reduction, and anthropogenic interference [68].

Table 2.
Trend analysis of runoff, precipitation and temperature using the Spearman rho (Sp) and Mann–Kendall (M–K) tests.
4.1.2. Division of Different Periods of Hydrometeorological Elements
To reduce the uncertainty of the single abrupt changes in the point identification method, the hydrological and meteorological series of the Qin River basin during the flood season were tested and analyzed using the M–K, Sliding T-test (Figure 2). The calculation results passed the significance test at a 95% confidence level. The M–K test and T-test results relating to the Qin River basin were used as the basis for the division of hydrometeorological elements (Table 3). Our research results suggest that there were two breakpoints in the Qin River Basin in the early 1980s and early 1990s. The two years of abrupt change in the study area were identified as 1982 and 1992. According to our survey, the Qin River Basin entered a period of intensive reservoir construction in the 1970s, and in the early 1980s, the basin dam system dispatching system was basically formed, which had a strong impact on the generation of basin runoff. Therefore, it is reasonable to consider 1982 as the first year where abrupt change occurred. In the late 1980s, the Qin River Basin underwent the large-scale construction of soil and water conservation infrastructure, especially forest and grass measures. Considering the lagging effect of forest and grass measures, 1992 is a reasonable second choice for a year of abrupt change. Further, the overall study period was divided into the natural period, 1971–1981; variation period A, 1982–1991; and variation period B, 1992–2000.
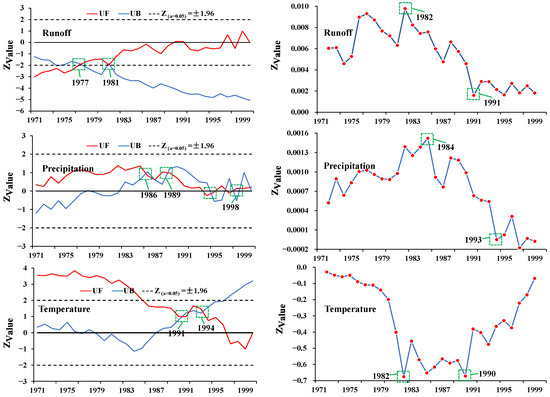
Figure 2.
M–K and T-test results of hydrological and meteorological elements in the Qin River Basin.

Table 3.
Abrupt change analysis of runoff, precipitation and temperature using the Mann–Kendall (MK) tests and Sliding T-test (T-test).
4.2. Spatiotemporal Evolution of Underlying Surface
Changes in the characteristics of the underlying surface can affect the hydrological cycle process of the basin to varying degrees [69]. Variations in land use and NDVI can visually reflect the changing characteristics of the underlying surface of the basin. This study analyzes land use and NDVI during the period of change to investigate the impact of underlying surface changes on runoff in the basin.
4.2.1. Analysis of Spatiotemporal Changes in LULC
During the natural period, except for a 0.26% change in construction land, the rest of the land types showed little change, with dynamic variations remaining below 0.035%. Transitioning to variation period A, grassland emerged as a rapidly expanding land type, experiencing a dynamic shift of 0.357%. Conversely, the remaining land types exhibited varying degrees of decline. In variation period B, both grassland and construction land demonstrated significant dynamic changes, registering 0.292% and 0.303%, respectively (Table 4). Following a brief decline in the natural period, grassland subsequently witnessed a sustained increase. This trend was attributed to the rise in urban employment, which led to the conversion of abandoned arable land into grassland. Furthermore, several regions implemented comprehensive WSCM to foster the development of high-quality grassland. The rapid increase in construction land was due to urban expansion.

Table 4.
Results of dynamic changes in single land use in the Qin River Basin.
Figure 3 illustrates the spatial transfer of land use during the two variation periods. From 1982 to 1992, the land use type space of the basin showed scattered changes, and the LULC change downstream was more significant than that upstream. The upper reaches mostly showed mutual changes among forest, grassland, and farmland. Grassland and farmland have been transformed into construction land in many downstream urban areas. From 1992 to 2000, there were many changes in the LULC space of the basin, and the upper and middle reaches of the basin witnessed a large transformation from forest to grassland. In the downstream area, LULC change primarily reflected the transformation of farmland to grassland and the transformation of various land use types to construction land.
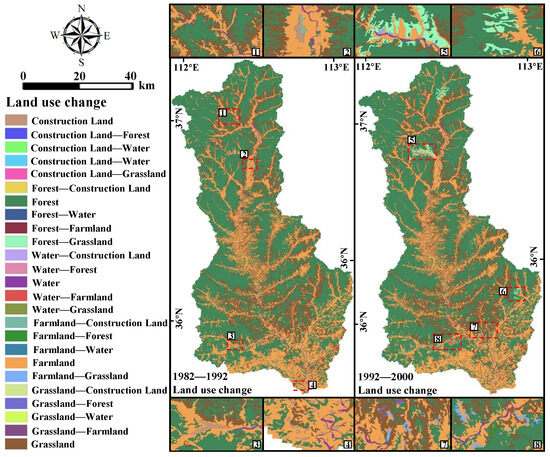
Figure 3.
Spatial transfer map of Qin River basin in variation periods A and B. (The red dashed boxes with numerical labels represent areas with numerous and concentrated types of LULC changes. For ease of viewing, we have enlarged and displayed these eight patches).
4.2.2. Analysis of Spatiotemporal Changes in NDVI
The average NDVI of the Qin River basin increased from 0.57 in variation period A to 0.59 in variation period B. The lowest NDVI occurred in 1990, with a value of 0.51, and the highest NDVI occurred in 2000, with a value of 0.92. It can be observed from Table 5 that the M–K trend test of the NDVI in the two variation periods of the Qin River basin had of 1.76 and 5.34, respectively. The significance test at the 95% confidence level showed that the NDVI in variation period A followed a non-significant increasing trend and that in variation period B shows a significant increase trend. The Hurst index was used to calculate the long series annual average NDVI data, and the Hurst index of NDVI in the two variation periods of the Qin River basin was close to 1. These results indicate that the NDVI in the Qin River basin will steadily increase in the future. The NDVI changes depicted strong and continuous increases (Table 5).

Table 5.
NDVI trends in the Qin River basin.
As can be seen from Figure 4, the NDVI in the Qin River basin has been positively developed, with an NDVI improvement area in the basin of 94.96%. The NDVI stable area was 2.65% and was primarily distributed in the upstream river source area of the basin. NDVI slightly degraded by 2.23%, primarily in the upstream river source area and the urban areas downstream of the basin. The urban agglomeration in the lower reaches of the basin showed severe NDVI degradation of 0.16% and was relatively concentrated (Figure 4). According to the field survey, the NDVI degradation in the upstream headwaters of the Qin River basin was caused by the conversion of some grassland with large slopes into terraces to prevent soil erosion, and the vegetation damage caused by mining and road construction. The expansion of urban agglomerations in the lower reaches of the basin, road hardening and the occupation of industrial land have led to severe vegetation degradation [13,70].
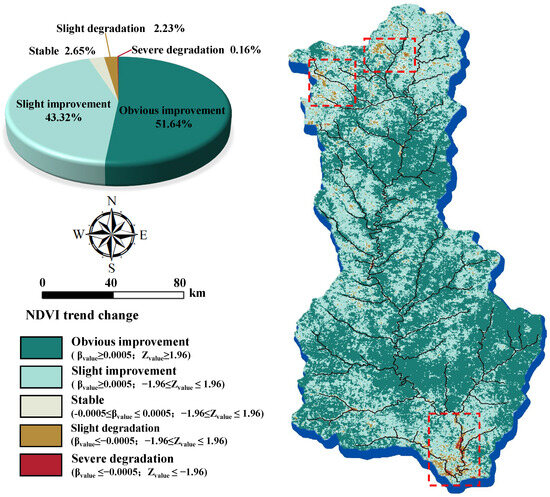
Figure 4.
Spatial variation trend of NDVI in Qin River basin for 1982–2000 years. (The red dotted boxes represent the areas where degradation is concentrated in the basin).
4.3. Temporal and Spatial Evolution of Runoff in Flood Season
The simulation effect of runoff was evaluated from 1971 to 1976 and 1977 to 1982 at the Runcheng Hydrological Station in the Qin River basin using the , , . The , , and for the model from 1971 to 1976 were 0.71, 0.05, and 0.86, respectively, and from 1977 to 1982, they were 0.55, 0.05, and 0.67, respectively. In hydrological forecasting, the allowable error for runoff is 20% of the measured value. According to the simulation results of this study, the values for the calibration and validation periods are only 5%, with high values and En values greater than 0.5. The results indicate that the simulation results of GBHM are in good agreement with the measured values and can be used for subsequent research.
The results of runoff depth, actual evaporation, and soil moisture simulated by the model in different periods (Table 6) were compiled, and the transformation degree of precipitation was explored via their ratio to precipitation. The ratios of runoff depth to precipitation continuously decreased, and its decreasing range continuously increased. The ratio of actual evaporation and soil water to precipitation continuously increased. The increase in actual evaporation was higher than that in soil water. The spatial distribution of runoff depth showed that it decreased in the entire basin, especially in the upstream river source area and downstream urban area. The main areas of increase in soil water were the upper reaches of the basin. This indicates that the vegetation coverage in the basin has significantly improved under the influence of WSCM. An increase in the proportion of forest and grass improved the water storage and evaporation capacity of the basin. This is consistent with the changes in NDVI and LULC during the same period. However, this is only one aspect of runoff reduction, and the other is the interference of human activities, which was more evident in the downstream urban areas. The soil depth and actual evaporation in that area did not increase significantly; however, runoff decreased significantly. Figure 5 shows the spatial results of meteorological and hydrological elements in different periods.

Table 6.
Assessment of runoff depth, actual evaporation, and soil water changes based on GBHM simulation results. (P denotes precipitation; R denotes runoff depth; E denotes actual evaporation; S denotes soil water).
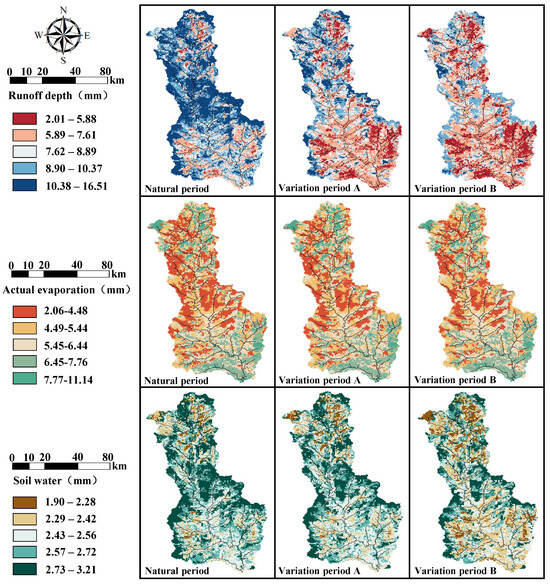
Figure 5.
Simulation results of meteorological and hydrological elements. (natural period denotes 1971–1981; variation period A denotes 1982–1991; variation period B denotes 1992–2000).
4.4. Quantitative Analysis of Different Impact Factors on Runoff Change
4.4.1. Runoff-R
Using the hydrometeorology breakpoint test conducted during the flood season, several breakpoints in the Qin River basin were obtained. The linear equation of precipitation and runoff was Y = 0.27X − 85.77, obtained by fitting the time series of precipitation and runoff in the natural period. The simulated runoff of the Qin River basin during the flood season during the variation periods can be calculated using a linear equation. and in variation period A calculated using Runoff-R were 95.53% and 4.47%, respectively; and in variation period B were 81.95% and 18.05%, respectively. Owing to the common interference of climate change and human activities, runoff of the Qin River basin in the flood season continuously decreased. Under human interference such as WSCM and urban expansion, increased by 13.58%; however, its impact was limited. Climate change was the main reason for the runoff reduction during the two variation periods. Table 7 lists the results of calculating and in the basin based on Runoff-R.

Table 7.
and calculated using Runoff-R.
4.4.2. Budyko Method
In the Budyko method, the changes in the underlying surface of the watershed are described using ; it represents the severity of changes in the underlying surface. We substitute the average flood season runoff, precipitation, and potential evapotranspiration of the Qin River basin into the Budyko method. By using the trial and error method to optimize the parameter of the underlying surface, the optimal value of is 1.61. It can be seen from the calculation results of the Budyko method (Table 8) that and of the Qin River basin were 67.28% and 32.72% in variation period A, respectively. and were 65.80% and 34.20%, respectively, in variation period B. in variation period B increased by 1.49%, and was greater than in both variation periods.

Table 8.
and calculated using Runoff-R.
4.4.3. GBHM
In variation period A, and were 86.96% and 12.04%, respectively, and the runoff change was primarily affected by climate change. In variation period B, and were 76.77% and 23.23%, respectively. The control weight of human activity disturbance on runoff changes increased by 10.19%; however, this increase was limited. Table 9 presents the simulation results for the meteorological and hydrological elements during the flood season.

Table 9.
and calculated using the GBHM.
4.4.4. Spatial Distribution Characteristics of the Contribution Rate of Runoff Change in Flood Season
This study was based on the spatial simulation results of flood season runoff using GBHM and explored the spatial distribution characteristics of and using the grid calculation of Runoff-R. The results are indicated in Figure 6.
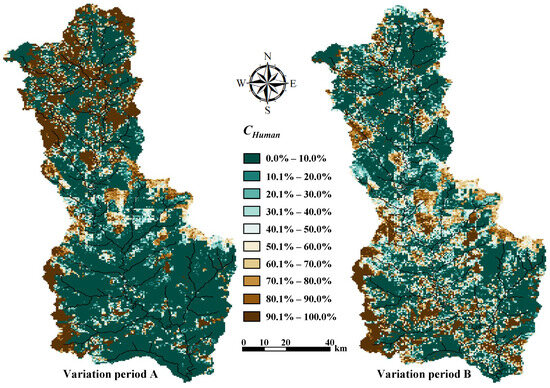
Figure 6.
Spatial distribution characteristic map of (variation period A denotes 1982–1991; variation period B denotes 1992–2000).
During variation period A, areas with > 50% were concentrated in the upper reaches of the basin, owing to the many small reservoirs built in that region and the impact of mine development and WSCM during that period. The downstream urban area had a considerable impact on the runoff process of the basin owing to human aggregation, and scattered, small, dark-blue patches appeared. However, the area of < 50% in the lower reaches of the basin accounted for the vast majority.
Compared with variation period A, the area of > 50% in the upstream river source area of variation period B was significantly reduced. This is owing to the decrease in engineering measures and the increase in ecological measures when conducting WSCM. The drainage basin primarily focused on natural restoration, including mountain closure for afforestation, the conversion of farmland to forests, and environmental mine rehabilitation. Thus, the impact of human disturbance on this area has been reduced. In the downstream urban area, the area of > 50% was significantly expanded because regional urbanization causes city agglomeration and industrial development. The degree of disturbance of human activities on regional runoff changes was enhanced.
5. Discussion
5.1. The Impact of Underlying Surface Changes on Basin Hydrological Systems
The response of basin runoff to changes in the underlying surface is very sensitive. Changes in the underlying surface are mainly manifested in changes in land use and vegetation coverage. Through our research on land use in the basin, during variation period A and variation period B, the land use change in the basin was relatively small. The reason for this is that the Qin River Basin is located in the eastern region of the Loess Plateau, where rocky hilly areas account for 85% of the total area of the basin [71]. Such landforms are not suitable for large-scale agricultural activities. However, the expansion of villages along the riverbank and urban areas downstream has caused changes in the hydrological system to some extent. The research results of NDVI show a significant growth trend. The improved area exceeds 94%. This is due to the impact of climate change and large-scale water and soil conservation measures. According to Yan et al., from 1982 to 1998, the improved area of NDVI on the Loess Plateau was 54.68%, while our study basin is much larger than this value [72]. This, to some extent, illustrates the effect of water and soil conservation measures implemented in the Qin River Basin. However, some studies have also shown that large-scale vegetation restoration will trap precipitation in the canopy and then evaporate. Some areas with high forest density also show a drying trend in soil [73,74,75]. According to our simulation results, during the study period, the soil water in the basin showed a slight increase. This indicates that the vegetation cover in the Qin River Basin is within the local ecological carrying capacity. However, vegetation cover changes the ability of land to conserve water, which can cause changes in runoff in the basin. Since the 1950s, more than 20 reservoirs have been built in the Qin River Basin. The construction period was mainly concentrated in the 1950s and 1970s (Figure 7). These reservoirs have increased evaporation on the one hand, and on the other hand, a large amount of water has been stored for irrigation and industrial water use. Irrigation and industry require the mobilization of large amounts of runoff [71]. The water diversion in the study area transitions from 2.4 km3 in the natural period to 2.9 km3 in variation period A, and then increases to 3.8 km3 in variation period A. These reasons together have caused changes in runoff in the Qin River Basin.
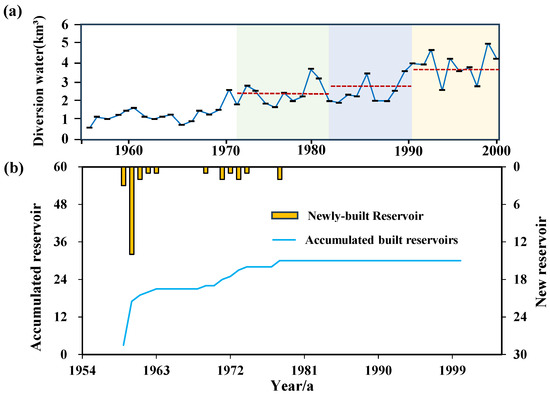
Figure 7.
(a) denotes water diversion situation in the study area (The different colors denotes different periods: green denotes the natural period; blue denotes variation period A; yellow denotes vVariation period B, and the red dotted line represents the average value for the corresponding period.); (b) denotes construction of reservoirs in the study area.
5.2. The Impact of Climate Change on Basin Hydrological Systems
A study conducted by scholars has revealed that the Loess Plateau has generally exhibited a trend of warming and drying over the past half-century, which is consistent with our own findings [76]. Specifically, within the Qin River Basin, precipitation displayed a downward trend from 1971 to 2000; however, temperatures rose. The response of runoff to precipitation changes is mainly reflected in two aspects. On the one hand, changes in precipitation directly affect the amount of recharge received by the basin. On the other hand, the precipitation conversion rate of surface runoff indirectly affects the runoff of the basin. The decrease in precipitation has led to a corresponding decline in recharge within the Qin River Basin. Our simulation results reveal that during the study period, the conversion ratio between precipitation and runoff continuously decreased: from 0.58 in the natural period to 0.47 in variation period B. The diminution in the conversion ratio is multifaceted. Rising temperatures and improved vegetation conditions enhance the evaporation capacity of the basin, while the increased soil water conservation capacity results in more precipitation being absorbed into the soil. Therefore, in the last three decades of the 20th century, the decrease in precipitation and the rise in temperature in the Qin River Basin were one of the reasons for the decrease in runoff in the basin.
5.3. Quantitative Results Comparison of Hydrological Response
Runoff-R, the Budyko method, and GBHM simulation were used to calculate and in the two variation periods, as well as analyze the difference in calculation results of the three methods and conduct qualitative and quantitative analysis of the main driving factors of basin runoff change (Figure 8).
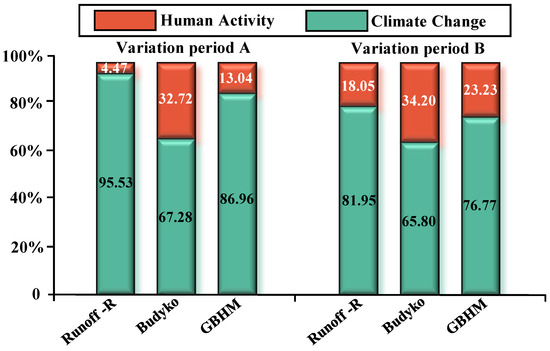
Figure 8.
Comparison of and calculated by three methods.
In variation period A, the results of the three methods showed that climate change was the main driving factor of runoff change during the flood season. The calculation results of was between 67.28% and 95.53%. The calculated using GBHM was between those of the Runoff-R and Budyko methods.
In variation period B, the control weight of climate change on runoff change was still greater than that of human activities. Compared with variation period A, was reduced in variation period B. The calculated using Runoff-R decreased by 13.58%, which was the largest reduction among the three methods. The values calculated using Runoff-R, the Budyko method, and GBHM simulation was 81.95%, 65.80%, and 76.77%, respectively.
In the calculation results of all three methods, showed an upward trend, which is related to the increase in NDVI, rapid urbanization in the lower reaches and reservoir regulation and irrigation. Field investigations have shown that the Qin River basin underwent a phase of rapid construction of small reservoirs and terraces in the 1970s, which persisted until the 1990s. Human intervention resulted in significant modifications to the hydrologic system of the basin. During these three decades, the focus of water and soil conservation measures gradually shifted from engineering measures to natural restoration measures, with afforestation and hillside closure becoming the main means. However, water and soil conservation measures remain one of the important factors affecting runoff changes in the basin [77]. In variation period A, the average of all three methods was 83.26%. In variation period B, decreased, and the average calculated of three methods was 74.84%. Human activities played an important role in the changes in runoff; however, human activity disturbances had a limited impact on the changes in runoff. It is believed that during both variation periods, the runoff change in the Qin River basin during the flood season was primarily affected by climate change.
5.4. Applicability of Quantitative Detection Methods
Because its calculation method is simple, Runoff-R considers only the impact of meteorological changes on runoff changes and ignores changes in the underlying surface. Therefore, when there is a large amount of precipitation, the results obtained using Runoff-R are relatively inaccurate, and the calculated is larger. To prevent the impact of flood disasters on agricultural production, the Qin River basin has built many reservoirs and dams to regulate and store precipitation. However, statistical methods cannot accurately express this interference of human activity. The Budyko method has gained significant traction in assessing changes in runoff across the Loess Plateau, primarily because of its distinctive feature of considering variations in the underlying surface, setting it apart from other simplistic statistical methods [78]. This attribute endows the Budyko method with the capability of generating more dependable calculation results by avoiding unstable outcomes caused by anomalous fluctuations in precipitation or temperature during a particular year. Although the Budyko method considers both meteorological and underlying surface changes, its principle is to simplify the complex underlying surface changes into a parameter that cannot fully express the characteristics of the underlying surface. Therefore, the accuracy of this method remains questionable. In contrast, the GBHM simulation method comprehensively considers the meteorological factors, underlying surface factors, and hydraulic engineering measures. This method is complex, time-consuming, and difficult to perform. However, it is more accurate in reflecting the runoff process of the basin via physical equations.
In general, the distributed hydrological model simulation can more accurately express the rule of basin runoff change; however, the statistical model still has its application value, which can be used to verify the simulation results of the distributed hydrological model. For example, Lyu et al. [29] used GBHM to study the Chabagou River basin on the Loess Plateau and used statistical methods to verify the results. The results of the statistical model were relatively accurate in regions with less human disturbance or small basin areas. Since the 1970s, large-scale WSCM and water conservancy projects have been conducted on the Loess Plateau; however, their distribution in the basin has been uneven; thus, it is likely that the results of the statistical model cannot completely realize the study of basin runoff. Therefore, it is necessary to explore their spatial dynamics further. For example, in this study of the Qin River basin, in variation period A, the upper and middle reaches were the main regions with > 50%, and in variation period B, the lower reaches of the basin were the main regions with > 50%. This result cannot be obtained by studying only time-series changes. Statistical methods and hydrological model simulations can be used in the study of small basins because the change in the underlying surface of small basins is relatively small, and the spatial research value is limited. Accordingly, the spatial simulation of hydrological models is necessary for the study of large basins. A comprehensive study of the complex and changeable regional runoff changes in the Loess Plateau from the perspective of time-series change, and spatial dynamics can provide a valuable reference value for water resource management and ecological protection of the basin.
6. Limitations and Future Challenges
In fact, climate change and human activities do not independently affect changes in watershed runoff, and they also have mutual impacts [79]. For example, building large reservoirs or large-scale afforestation can affect regional climate change. In this case, it is difficult to determine which driving factor has caused the change in runoff in the basin. We can only explore the relationship between these driving factors and the runoff changes during natural periods. This makes determining the natural period one of the key issues. How to more accurately determine the natural period will be the focus of our future research.
With increasing human activity and rapid urbanization in the Loess Plateau, the evolutionary mechanism of the runoff process in the basin will become more complicated; moreover, the uncertainty of runoff simulations to increase. Therefore, it is necessary to study the basin runoff evolutionary mechanism that is affected by typical human activities and optimize the structure of the model accordingly to improve the simulation accuracy of the model in follow-up research.
7. Conclusions
We explored the spatiotemporal variation characteristics of hydrometeorological elements, LULC, and NDVI. We quantitatively detected the contribution rate of each driving factor to runoff changes and further discussed the advantages of each method. Finally, we explored the spatial changes of different driving factors in the basin in the latter 30 years of the 20th century. The conclusions of this study are as follows:
- (1)
- The runoff and precipitation during the flood season from 1971 to 2000 displayed an insignificant decreasing trend, and the temperature showed an insignificant increasing trend.
- (2)
- Under the disturbance of intense human activities, the LULC and NDVI of the basin have undergone changes. Grassland and construction land have become the fastest-growing land types. The NDVI showed a solid increasing trend, and the improved area accounted for 94.96% of the basin.
- (3)
- A comprehensive evaluation of and in the Qin River basin was conducted via various models. Climate change was determined to be the main driving factor of runoff change in the two variation periods A and B, and the average was 83.26% and 74.84, respectively. The quantitative simulation results of the distributed hydrological model and the calculation results of the two hydrological statistical model were compared and analyzed; the quantitative simulation results of the hydrological model had the best accuracy.
- (4)
- In variation period A, the area of > 50% was primarily distributed in the upper reaches of the basin, showing a centralized distribution. Compared with variation period A, the area of > 50% in the upstream river source area of variation period B was significantly reduced. In the downstream urban area, > 50% expanded significantly.
The findings of this study can be expected to assist with the implementation of sustainable basin management and will be of value for basin managers and planners.
Author Contributions
P.G.: Conceptualization, Data curation, Methodology, Software, Writing—original draft, Investigation, Writing—review and editing. Y.W.: Data curation, Writing, Translation, Investigation, review and editing. Y.Y. and J.L.: Writing—original draft, Writing—review and editing, Supervision. F.W., H.C., W.G. and J.J.: offered technical guidance, proofread, Review and edited the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by International Partnership Program of the Chinese Academy of Sciences, (16146KYSB20200001), National Natural Science Foundation of China (No. 42177344), National Natural Science Foundation of China Yellow River Water Science Research Joint Fund Project (U2243213), the Shaanxi Postdoctoral Science Foundation 2018(2018BSHEDZZ21), the General Financial Grant from the China Post-doctoral Science Foundation (2017M623088), and Fundamental Research Funds for the Central Universities, CHD (300102292903). The authors are grateful to the Editor and anonymous reviewers for their constructive comments and suggestions.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding authors upon request. The data are not publicly available because of privacy concerns.
Acknowledgments
We express our sincere gratitude to the State Key Laboratory of Soil Erosion and Dryland Agriculture on the Loess Plateau for their invaluable support and contributions to our research endeavor. We are grateful to the Resource and Environmental Science Data Center (https://www.resdc.com (accessed on 15 January 2023)), the National Tibetan Plateau Data Center (https://data.tpdc.ac.cn/home (accessed on 28 January 2023)) and the National Aeronautics and Space Administration (https://lpdaacsvc.cr.usgs.gov/appeears/ (accessed on 28 January 2023)) for providing the dataset.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water Availability in snow–dominated regions. Nature 2005, 138, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.W.; Yuan, X.; Ji, P.; Sun, S.A.; Leng, G.Y. Shifts in trends and correlation of water scarcity and productivity over China. J. Hydrol. 2024, 37, 131187. [Google Scholar] [CrossRef]
- Zhang, W.B.; Liang, W.; Gao, X.R.; Li, J.R.; Zhao, X.N. Trajectory in water scarcity and potential water savings benefits in the Yellow River basin. J. Hydrol. 2024, 633, 130998. [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Tran, T.N.D.; Do, S.K.; Nguyen, B.Q.; Tran, V.N.; Maria, G.L.; Sinicyn, G.; Lakshmi, V. Investigating the Future Flood and Drought Shifts in the Transboundary Srepok River Basin Using CMIP6 Projections. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 7516–7529. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.Y.; Yang, T. Variability of water resource in the Yellow River basin of past 50 years, China. Water Resour. Manag. 2009, 2, 1157–1170. [Google Scholar] [CrossRef]
- Xia, J.; Shi, W. Perspective on water security issue of changing environment in China. J. Hydraul. Eng. 2016, 47, 292–301. [Google Scholar] [CrossRef]
- Yao, Y.B.; Wang, R.Y.; Yang, J.H.; Yue, P.; Lu, D.R.; Xiao, G.J.; Wang, Y.; Liu, L.C. Changes in terrestrial surface dry and wet conditions on the Loess Plateau (China) during the last half century. J. Arid Land 2013, 5, 15–24. [Google Scholar] [CrossRef]
- Yang, B.; Jiao, J.Y.; Ma, X.W.; Zhao, W.T.; Ling, Q.; Zhang, X.H.; Han, J.Q.; Du, P.F.; Chen, Y.; Chen, H. Distribution and formation of soil balls under heavy rainstorm conditions in the northern Loess Plateau. J. Hydrol. 2023, 625, 130103. [Google Scholar] [CrossRef]
- Liu, Y.H.; Xu, Y.; Liu, Y. Population growth and temporal–spatial differentiation in Loess Plateau region in the last 2000 years. Prog. Geogr. 2012, 31, 156–166. [Google Scholar] [CrossRef]
- Guo, P.; Wang, F.; Zhou, X.W.; Lyu, J.Q. Variation characteristics of hydrological response to water conservancy construction in the Qinhe River Basin of the Loess Plateau, China. Hydrol. Process. 2023, 9, 37. [Google Scholar] [CrossRef]
- Miao, C.Y.; Kong, D.X.; Wu, J.W.; Duan, Q.Y. Functional degradation of the water–sediment regulation scheme in the lower Yellow River: Spatial and temporal analyses. Sci. Total Environ. 2016, 551–552, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.; Lyu, J.Q.; Yuan, W.N.; Zhou, X.W.; Mo, S.H.; Mu, D.R.; Luo, P.P. Detecting the Quantitative Hydrological Response to Changes in Climate and Human Activities at Temporal and Spatial Scales in a Typical Gully Region of the Loess Plateau, China. Water 2022, 14, 257. [Google Scholar] [CrossRef]
- Yang, T.; Xu, C.Y.; Shao, Q.X.; Chen, X.; Lu, G.H.; Hao, Z.C. Temporal and spatial patterns of low–flow changes in the Yellow River in the last half century. Stoch. Environ. Res. Risk Assess. 2010, 24, 297–309. [Google Scholar] [CrossRef]
- Labat, D.; Goddéris, Y.; Probst, J.L.; Guyot, J.L. Evidence for global runoff increase related to climate warming. Adv. Water Resour. 2004, 27, 631–642. [Google Scholar] [CrossRef]
- Novotny, E.V.; Stefan, H.G. Stream flow in Minnesota: Indicator of climate change. J. Hydrol. 2007, 334, 319–333. [Google Scholar] [CrossRef]
- Xu, Z.X.; Jiang, Y. Studies on runoff evolution mechanism under changing environment: A state–of–the–art review. Hydro-Sci. Eng. 2022, 1, 9–18. [Google Scholar] [CrossRef]
- Paul, D.; Wagner, S.; Murty, B.; Balaji, N.; Shamita, K.; Nicola, F.P.F. Comparing the effects of dynamic versus static representations of land use change in hydrologic impact assessments. Environ. Model Softw. 2019, 122, 103987. [Google Scholar] [CrossRef]
- Paul, D.; Wagner, S.; Murty, B.; Balaji, N.; Lakshmi, N.K.; Sudheer, K.P.; Shamita, K.; Karl, S.; Peter, F. Dynamic integration of land use changes in a hydrologic assessment of a rapidly developing Indian catchment. Sci. Total Environ. 2016, 539, 153–164. [Google Scholar] [CrossRef]
- Helen, A.; Naghmeh, M.D.; Ali, M.; Zahra, A.; Majid, D.; Nicola, F.; Paul, D.W. Effects of dynamic land use/land cover change on water resources and sediment yield in the Anzali wetland catchment, Gilan, Iran. Sci. Total Environ. 2020, 712, 136449. [Google Scholar] [CrossRef]
- Li, L.J.; Zhang, L.; Wang, H.; Wang, J.; Yang, J.W.; Jiang, D.J.; Li, J.Y.; Qin, D.Y. Assessing the impact of climate variability and human activities on streamflow from the Wuding River basin in China. Hydrol. Process 2007, 10, 3485–3491. [Google Scholar] [CrossRef]
- Zhang, X.P.; Zhang, L.; Zhao, J.; Paul, R.; Peter, H. Response of streamflow to changes in climate and land use/cover in the Loess Plateau, China. Water Resour. Res. 2008, 44, 56–64. [Google Scholar] [CrossRef]
- Zhao, G.J.; Tian, P.; Mu, X.M.; Jiao, J.Y.; Wang, F.; Gao, P. Quantifying the impact of climate variability and human activities on streamflow in the middle reaches of the Yellow River basin. China J. Hydrol. 2014, 519, 387–398. [Google Scholar] [CrossRef]
- Zeng, S.D.; Zhan, C.S.; Sun, F.B.; Du, H.; Wang, F.Y. Effects of climate change and human activities on surface runoff in the Luan River Basin. Adv. Meteorol. 2015, 2015, 740239. [Google Scholar] [CrossRef]
- Ye, X.C.; Zhang, Q.; Liu, J.; Li, X.H.; Xu, C.Y. Distinguishing the relative impacts of cli–mate change and human activities on variation of streamflow in the Poyang Lake catchment, China. J. Hydrol. 2013, 494, 83–95. [Google Scholar] [CrossRef]
- Zuo, D.P.; Xu, Z.X.; Wu, W.; Zhao, J.; Zhao, F.F. Identification of streamflow response to climate change and human activities in the Wei River Basin, China. Water Resour. Manag. 2014, 28, 833–851. [Google Scholar] [CrossRef]
- Gao, G.; Fu, B.; Wang, S.; Liang, W.; Jiang, X.H. Determining the hydrological responses to climate variability and land use/cover change in the Loess Plateau with the Budyko framework. Sci. Total Environ. 2016, 557–558, 331–342. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, J.Y.; Singh, V.P.; Gu, X.H.; Chen, X.H. Evaluation of impacts of climate change and human activities on streamflow in the Poyang Lake basin, China. Hydrol. Process 2016, 30, 2562–2576. [Google Scholar] [CrossRef]
- Lyu, J.Q.; Mo, S.H.; Luo, P.P.; Zhou, M.M.; Shen, B.; Nover, D. A quantitative assessment of hydrological responses to climate change and human activities at spatiotemporal within a typical catchment on the Loess Plateau, China. Quat. Int. 2019, 527, 1–11. [Google Scholar] [CrossRef]
- Gbohoui, Y.P.; Paturel, J.; Fowe, T.; Mounirou, L.A.; Yonaba, R.; Karambiri, H.; Yacouba, H. Impacts of climate and environmental changes on water resources: A multi-scale study based on Nakanbé nested watersheds in West African Sahel. J. Hydrol. Reg. Stud. 2012, 35, 100828. [Google Scholar] [CrossRef]
- Xu, Z.X.; Ban, C.G.; Zhang, R. Evolution law, attribution regional characteristics of runoff for major rivers in China. Adv. Sci. Technol. Water Resour. 2024, 44, 1–8. [Google Scholar] [CrossRef]
- Wu, J.W.; Miao, C.Y.; Zhang, X.M.; Yang, T.T.; Duan, Q.Y. Detecting the quantitative hydrological response to changes in climate and human activities. Sci. Total Environ. 2017, 586, 328–337. [Google Scholar] [CrossRef]
- Liu, Z.P.; Wang, Y.Q.; Shao, M.G.; Jia, X.X.; Li, X.L. Spatiotemporal analysis of multiscalar drought characteristics across the loess plateau of China. J. Hydrol. 2016, 534, 281–299. [Google Scholar] [CrossRef]
- Wang, H.J.; Yang, Z.S.; Saito, Y.; Liu, J.P.; Sun, X.X. Interannual and seasonal variation of the Huanghe (Yellow River) water discharge over the past 50 years: Connections to impacts from ENSO events and dams. Glob. Planet. Chang. 2006, 50, 212–225. [Google Scholar] [CrossRef]
- Li, Y.Y.; Rong, T.Q.; Qin, M.Z.; Zhang, P.Y.; Yang, D.; Liu, Z.Y.; Zhang, Y.; Zhu, H.; Song, M.L. Spatiotemporal characteristics of soil erosion in a typical watershed consisting of different landscape: A case study of the Qin River Basin. PLoS ONE 2022, 17, e0275470. [Google Scholar] [CrossRef]
- Lyu, J.Q. The Hydrological Response to Climate Change and Human Activity in Typical Regions, Northwest China. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2012. [Google Scholar]
- Liu, Y.Q.; Huang, S.Z.; Guo, Y.; Liu, Y.J.; Li, Z.Y.; Huang, Q. Propagation threshold of meteorological drought to different levels of hydrological drought: A case study of Qinhe River Basin. J. Hydraul. Eng. 2022, 41, 9–19. [Google Scholar] [CrossRef]
- Yang, D.W.; Li, C.; Hu, H.P.; Lei, Z.D.; Yang, S.X.; Tetsuya, K.; Toshio, K.; Katumi, M. Analysis of water resources variability in the Yellow River of China during the last half century using historical data. Water Resour. Res. 2004, 40, W06502. [Google Scholar] [CrossRef]
- Liu, J. Remote Sensing Monitoring Dataset of Land Use Status in Six Provinces in Western China for Many Years (1970s, 1980s, 1995, 2000, 2005, 2010, 2015); National Tibetan Plateau Data Center: Xining, China, 2019. [Google Scholar] [CrossRef]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; Saleous, N.E. An extended AVHRR-8km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Jain, S.; Lall, U. Magnitude and timing of annual maximum floods: Trends and large scale climatic associations for the Blacksmith Fork River, Utah. Water Resour. Res. 2000, 36, 3641–3651. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend detection in hydrologic data: The Mann-Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Zhang, J.; Man, Z.M.; Xiao, W.W.; Shen, Z.Z. Research on sequence reconstruction and characteristics diagnosis of droughts and floods in the Middle Yellow River since the Qing Dynasty: 1644–2009. Geogr. Res. 2013, 32, 1579–1590. [Google Scholar] [CrossRef]
- Sun, S.; Barraud, S.; Branger, F.; Braud, I.; Castebrunet, H. Urban hydrologic trend analysis based on rainfall and runoff data analysis and conceptual model calibration. Hydrol. Process 2017, 31, 1349–1359. [Google Scholar] [CrossRef]
- Cao, L.; Xu, J.H.; Chen, Y.N.; Li, W.H.; Yang, Y.; Hong, Y.L.; Li, Z. Understanding the dynamic coupling between vegetation cover and climatic factors in a semiarid region—A case study of Inner Mongolia, China. Ecohydrology 2012, 6, 917–926. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Zhou, Y.Q.; Shao, M.; Li, X. Temporal and Spatial Evolution, Prediction, and Driving-Factor Analysis of Net Primary Productivity of Vegetation at City Scale: A Case Study from Yangzhou City, China. Sustainability 2023, 15, 14518. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar] [CrossRef]
- Lunetta, R.S.; Knight, J.F.; Ediriwickrema, J.; Lyon, J.G.; Worthy, L.D. Land–cover change detection using multitemporal MODIS NDVI data. Remote Sens. Environ. 2009, 105, 142–154. [Google Scholar] [CrossRef]
- Zhang, Y.R.; He, Y.; Li, Y.L.; Jia, L.P. Spatiotemporal variation and driving forces of NDVI from 1982 to 2015 in the Qinba Mountains, China. Environ. Sci. Pollut. Res. 2022, 29, 52277–52288. [Google Scholar] [CrossRef]
- Kundzewicz, W.Z.; Robson, A.J. Change detection in hydrological records-a review of the methodology/Revue methodologique de la detection de changements dans les chroniques hydrologiques. Hydrol. Sci. J. 2004, 49, 7–19. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-parametric approach to the change-point problem. J. R. Stat. Soc. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, G.J.; Mu, X.M.; Gao, P.; Sun, W.Y. Regime shift identification of runoff and sediment loads in Yellow River Basin, China. Water 2014, 6, 3012–3032. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Gachon, P.; Sushama, L.; St-Hilaire, A. Identification of hydrological trends in the presence of serial and cross correlations: A review of selected methods and their application to annual flow regimes of Canadian rivers. J. Hydrol. 2009, 368, 117–130. [Google Scholar] [CrossRef]
- Zhao, C.S.; Liu, C.M.; Dai, X.Q.; Liu, T.; Duan, Z.; Liu, L.F.; Mitrovic, S.M. Separation of the impacts of climate change and human activity on runoff variations. J. Hydrol. 2015, 60, 234–246. [Google Scholar] [CrossRef]
- Jiang, S.H.; Ren, L.L.; Yong, B.; Yang, X.L.; Liu, X.F. Analysing the effects of climate variability and human activities on runoff from the Laohahe Basin in northern China. Hydrol. Res. 2012, 43, 3–13. [Google Scholar] [CrossRef]
- Budyko, M.I. Evaporation under Natural Conditions; Office of Technical Services, U.S. Department of Commerce: Washington, DC, USA, 1948.
- Budyko, M.I. Climate and Life; Academic Press: Cambridge, MA, USA, 1976; Volume 6, pp. 461–463. [Google Scholar] [CrossRef]
- Fuh, B.P. On the calculation of the evaporation from land surface. Chin. J. Atmos. Sci. 1981, 5, 23–31. [Google Scholar] [CrossRef]
- Yang, H.B.; Yang, D.W.; Hu, Q.F. An error analysis of the Budyko hypothesis for assessing the contribution of climate change to runoff. Water Resour. Res. 2014, 50, 9620–9629. [Google Scholar] [CrossRef]
- Choudhury, B.J. Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model. J. Hydrol. 1999, 216, 99–110. [Google Scholar] [CrossRef]
- Wang, D.B.; Tang, Y. A one-parameter Budyko model for water balance captures emergent behavior in darwinian hydrologic models. Geophys. Res. Lett. 2014, 41, 4569–4577. [Google Scholar] [CrossRef]
- Gong, Y.; Mo, S.H.; Li, Z.L.; Shen, B. Study on runoff response in Xiaoli Basin based on Budyko equation. J. Xi’an Univ. Technol. 2018, 34, 439–446. [Google Scholar] [CrossRef]
- Liang, X.; Wood, E.F.; Lettenmaier, D.P. One–dimensional statistical dynamic representation of subgrid spatial variability of precipitation in the two–layer variable infiltration capacity model. J. Geophys. Res. 1996, 101, 21403–21422. [Google Scholar] [CrossRef]
- Yang, D.W.; Herath, S.; Musiake, K. A hillslope–based hydrological model using catchment area and width function. Hydrol. Sci. J. 2022, 47, 49–65. [Google Scholar] [CrossRef]
- Xu, X.Y.; Yang, H.B.; Yang, D.W.; Ma, H. Assessing the impacts of climate variability and human activities on annual runoff in the Luan River basin, China. Hydrol Res. 2013, 44, 940–952. [Google Scholar] [CrossRef]
- Mu, X.M.; Zhang, L.; Mcvicar, T.R.; Chille, B.S.; Gau, P. Analysis of the impact of conservation measures on stream flow regime in catchments of the Loess Plateau, China. Hydrol. Process 2007, 21, 2124–2134. [Google Scholar] [CrossRef]
- Zhao, G.J.; Mu, X.M.; Jiao, J.Y.; An, Z.F.; Klik, A.; Wang, F.; Jiao, F.; Yue, X.L.; Gao, P.; Sun, W.Y. Evidence and Causes of Spatiotemporal Changes in Runoff and Sediment Yield on the Chinese Loess Plateau. Land Degrad. Dev. 2017, 28, 579–590. [Google Scholar] [CrossRef]
- Rungee, J.; Bales, R.; Goulden, M. Evapotranspiration response to multiyear dry periods in the semiarid western United States. Hydrol. Process 2019, 33, 182–194. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, P.D.; Liu, M.; Xu, K.R.; Zhang, N.; Jiang, P.; Wang, W.J.; Jiang, Y.G. Spatial pattern of water conservation function and ecological management suggestions in the catchment area of the upper reaches of Qinhe River in the Yellow River Basin from 1990 to 2020. Geology 2024, 1–15. Available online: https://link.cnki.net/urlid/11.1167.P.20231120.1259.012 (accessed on 1 April 2024).
- Bai, P.; Liu, W.H.; Guo, M.J. Impacts of climate variability and human activities on decrease in streamflow in the Qinhe River, China. Theor. Appl. Climatol. 2014, 117, 293–301. [Google Scholar] [CrossRef]
- Yan, D.N.; Wu, X.Y.; Wang, B.H.; Hao, H.K. Characteristics and driving forces of changes in vegetation coverage on the Loess Plateau, 1982–2015. Acta Ecol. Sin. 2023, 43, 9794–9804. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Shao, M.X.; Zhu, Y.J.; Liu, Z.P. Impacts of land use and plant characteristics on dried soil layers in different climatic regions on the Loess Plateau of China. Agric. For. Meteorol. 2010, 151, 437–448. [Google Scholar] [CrossRef]
- Cao, S.X. Impact of China’s Large-Scale Ecological Restoration Program on the Environment and Society in Arid and Semiarid Areas of China: Achievements, Problems, Synthesis, and Applications. Crit. Rev. Environ. Sci. Technol. 2011, 41, 317–335. [Google Scholar] [CrossRef]
- Feng, X.M.; Fu, B.J.; Piao, S.L.; Wang, S.; Ciais, P.; Zeng, Z.Z.; Lv, Y.H.; Zeng, Y.; Li, Y.; Jiang, X.H.; et al. Revegetation in China’s Loess Plateau is approaching sustainable water resource limits. Nat. Clim. Chang. 2016, 6, 1019–1022. [Google Scholar] [CrossRef]
- Liu, X.Q.; Zhao, J.B.; Yu, X.F. Study on the Climatic Warming-drying Trend in the Loess Plateau and the Countermeasures. Arid Zone Res. 2006, 4, 627–631. [Google Scholar] [CrossRef]
- Tian, P.; Mu, X.M.; Liu, J.L.; Hu, J.F.; Gu, C.J. Impacts of Climate Variability and Human Activities on the Changes of Runoff and Sediment Load in a Catchment of the Loess Plateau, China. Adv. Meteorol. 2016, 2016, 4724067. [Google Scholar] [CrossRef]
- Chang, Y.P.; Ding, Y.J.; Zhao, Q.D.; Zhang, S.Q. Attributing Evapotranspiration Changes with an Extended Budyko Framework Considering Glacier Changes in a Cryospheric-Dominated Watershed. Remote Sens. 2023, 15, 558. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, L.; Zhu, R.; Liu, C.; Sato, Y.; Fukushima, Y. Responses of streamflow to climate and land surface change in the headwaters of the Yellow River Basin. Water Resour Res. 2009, 45, 56–64. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).