Trajectory Deviation Estimation Method for UAV-Borne Through-Wall Radar
Abstract
1. Introduction
2. UAV-Based Signal Model for Through-Wall Radar
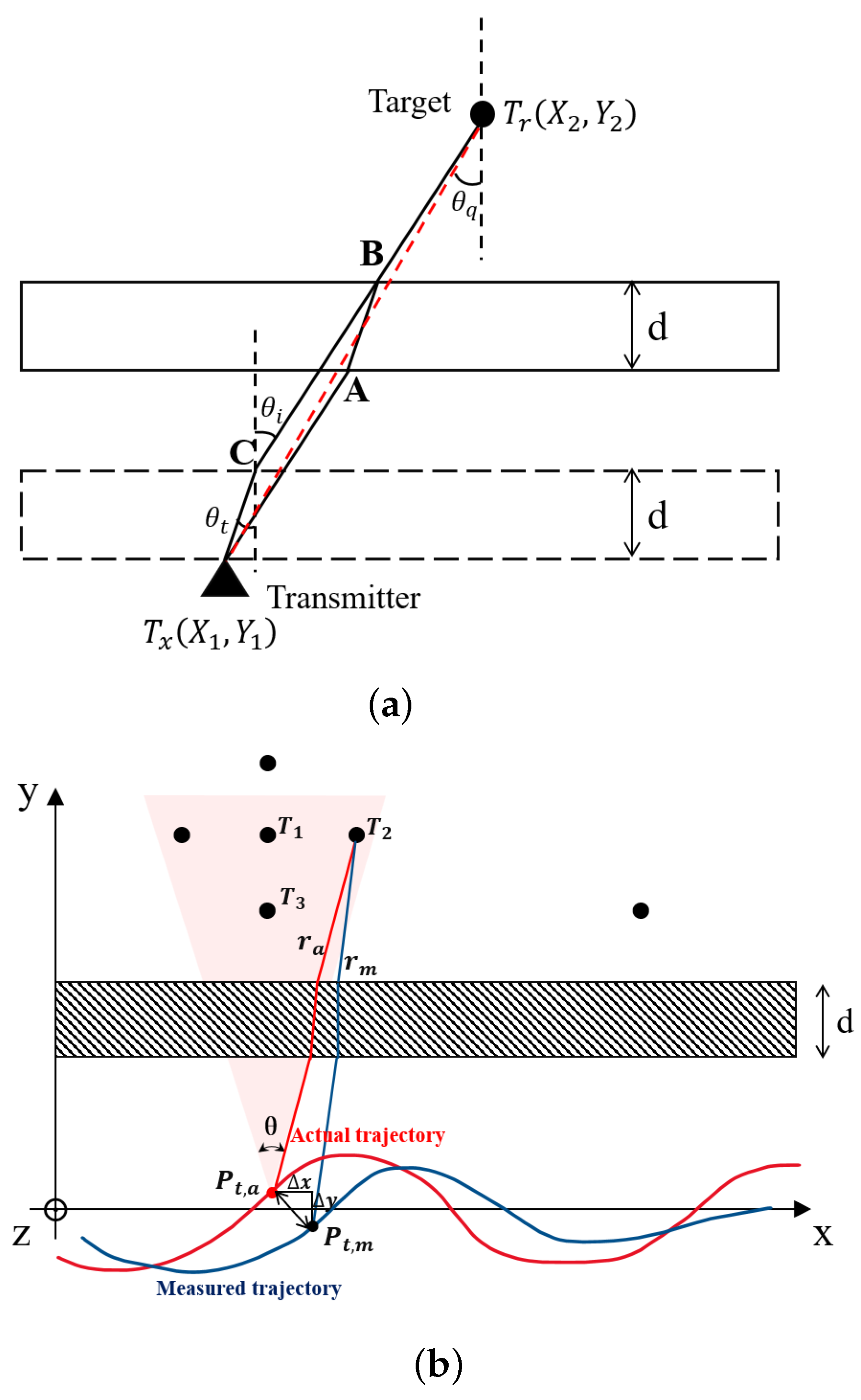
2.1. Propagation Model of Electromagnetic Waves in a Through-Wall Scenario
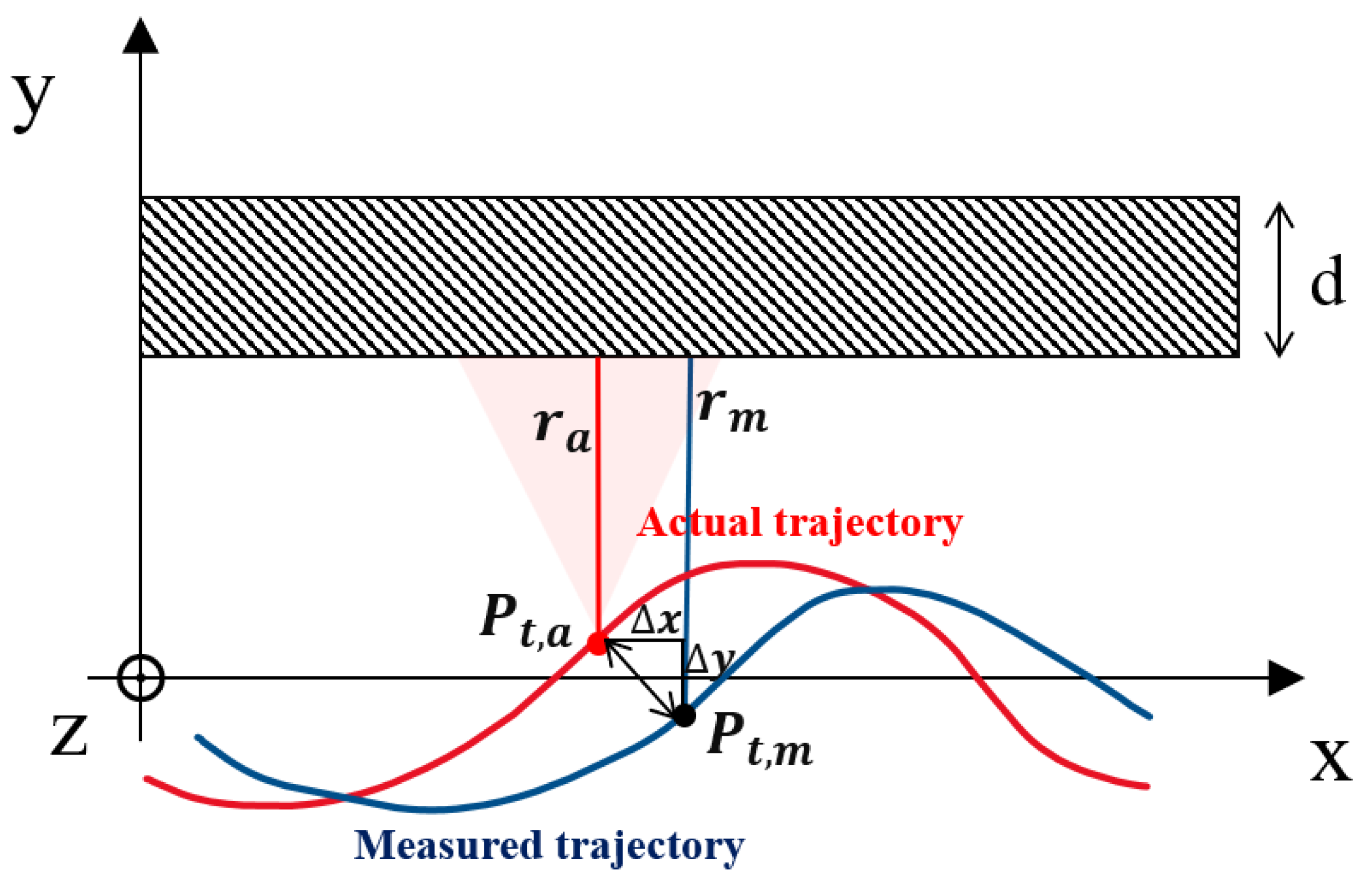
2.2. Signal Model of Trajectory Deviation
3. Trajectory Deviation Estimation Algorithm
3.1. Estimation of Trajectory Deviation in the Line-of-Sight Direction
| Algorithm 1 PSO |
for each particle i do for each dimension d do Initialize velocity and position end for end for Initialize and k = 1 while not stop do for each particle i do Update the velocity and position of particle i: Calculate fitness value of if then ; end if if then ; end if end for k = k + 1 end while print |
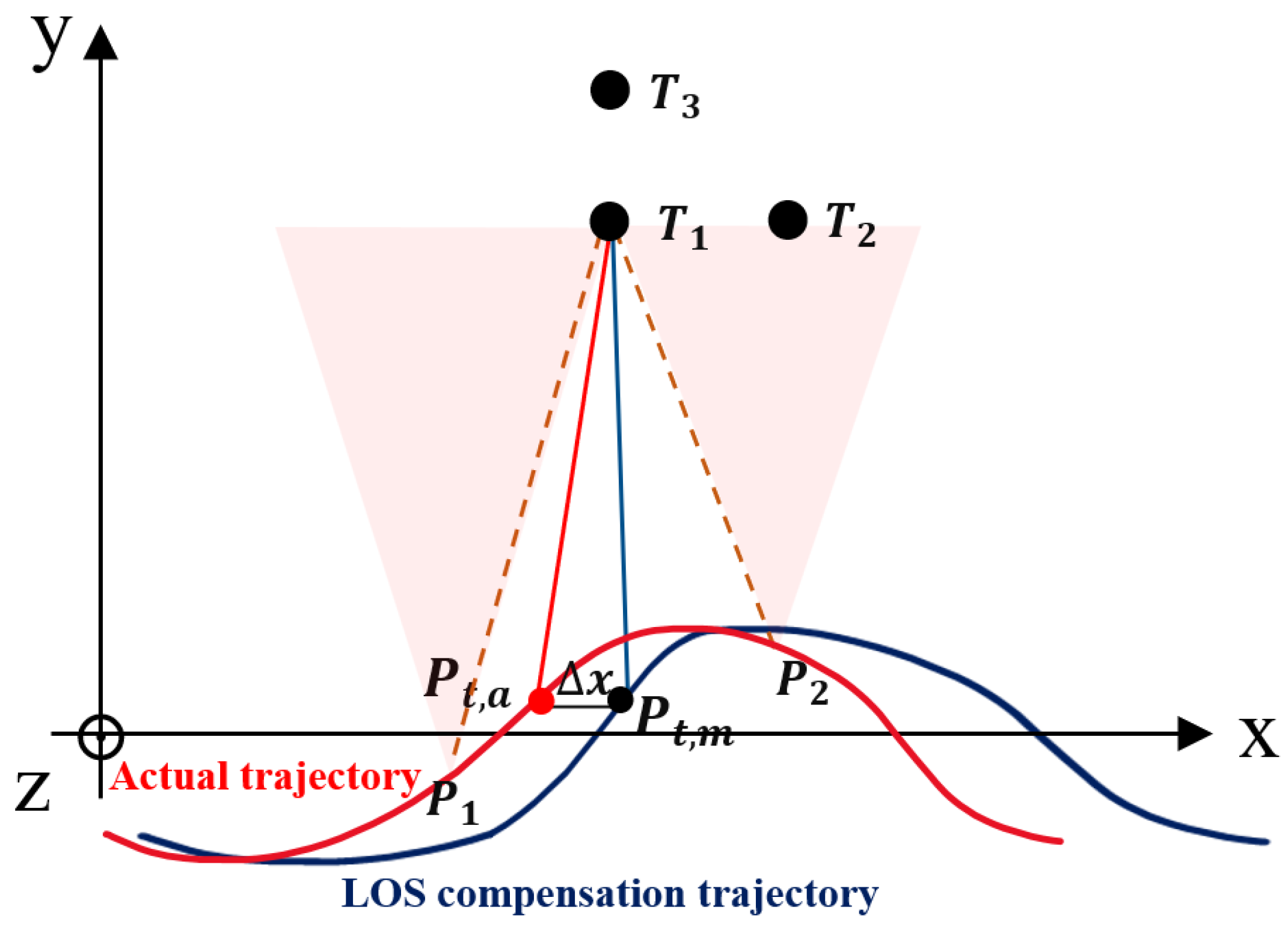
3.2. Estimation of the Trajectory Deviation along the Track
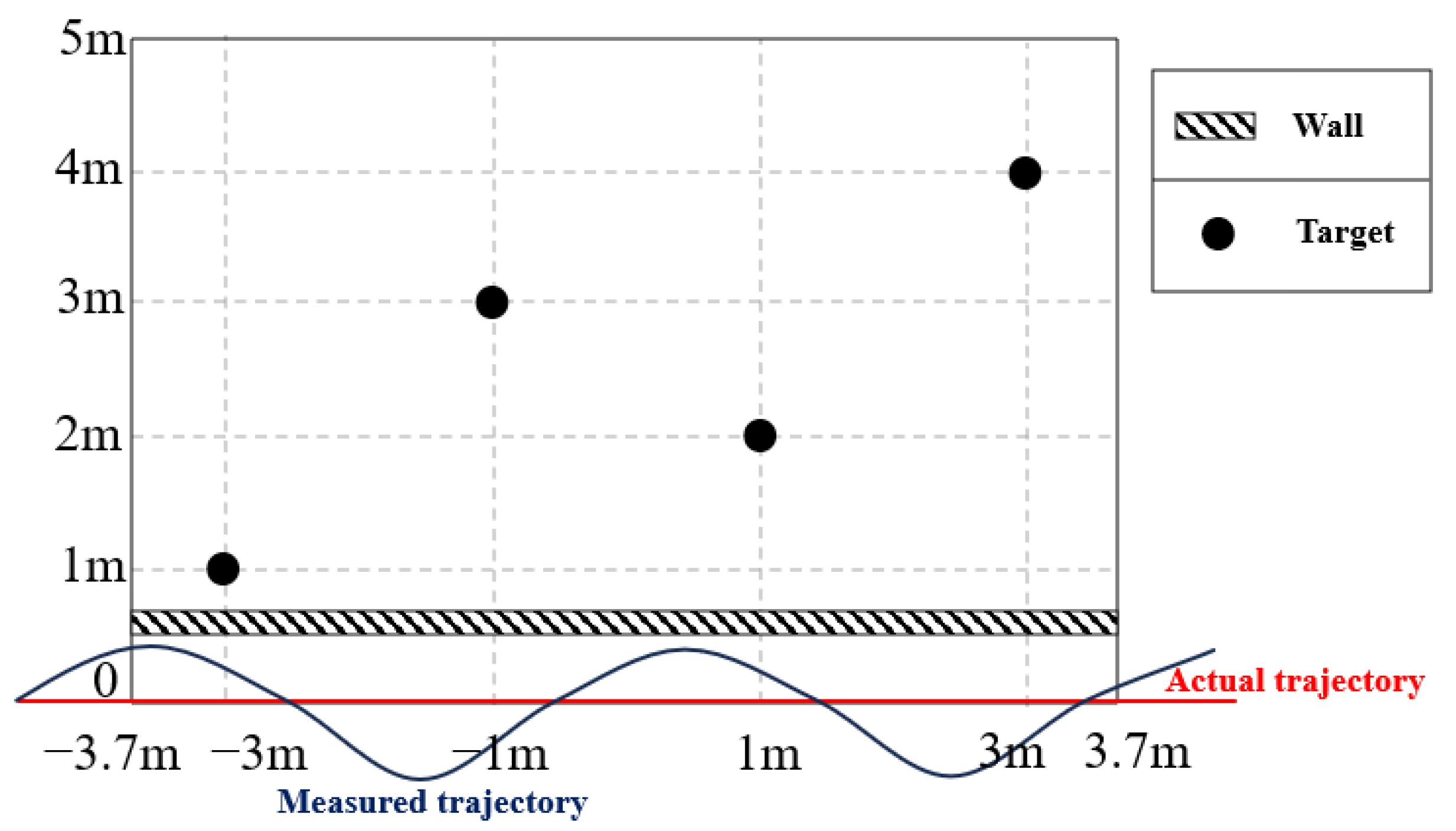
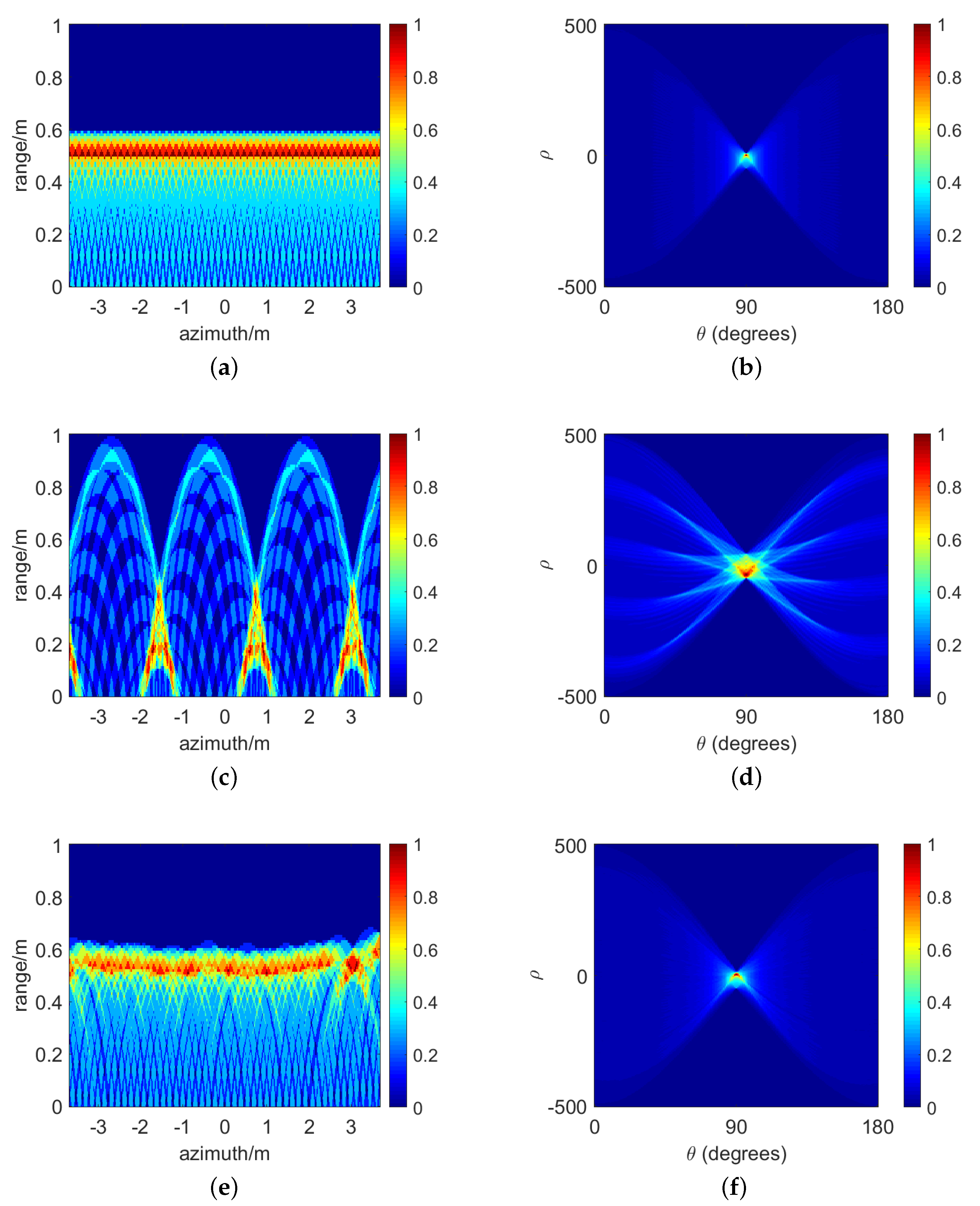
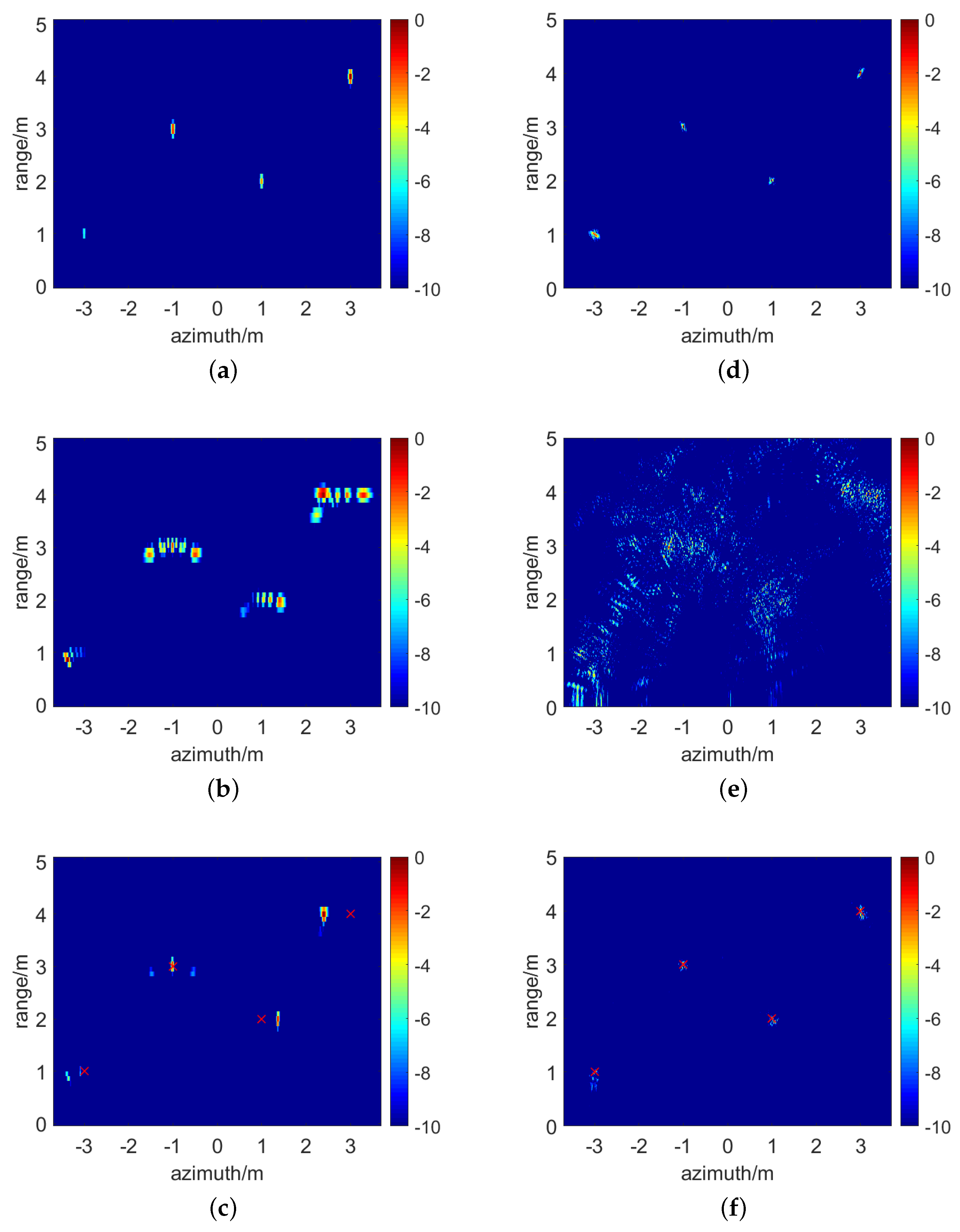
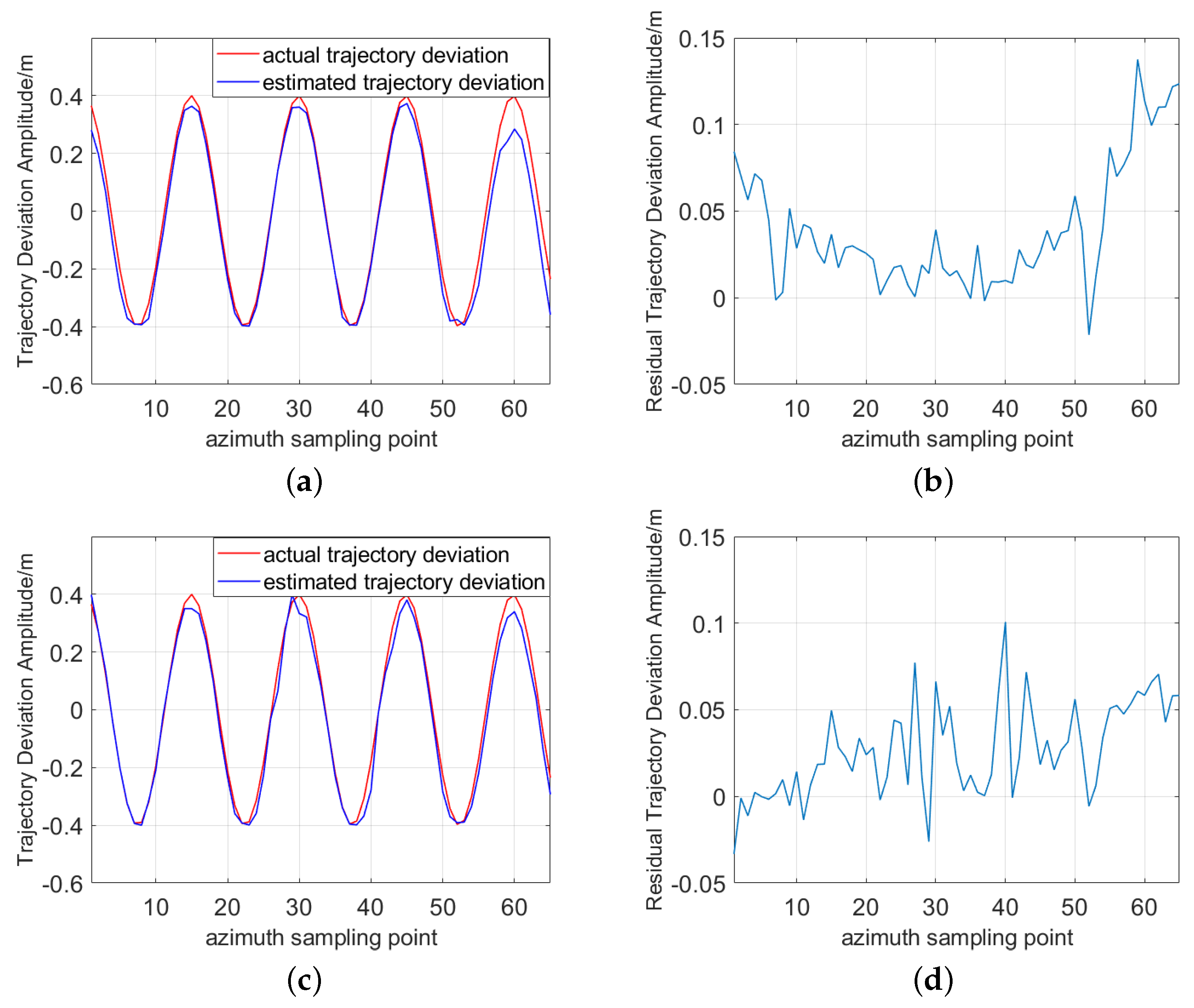
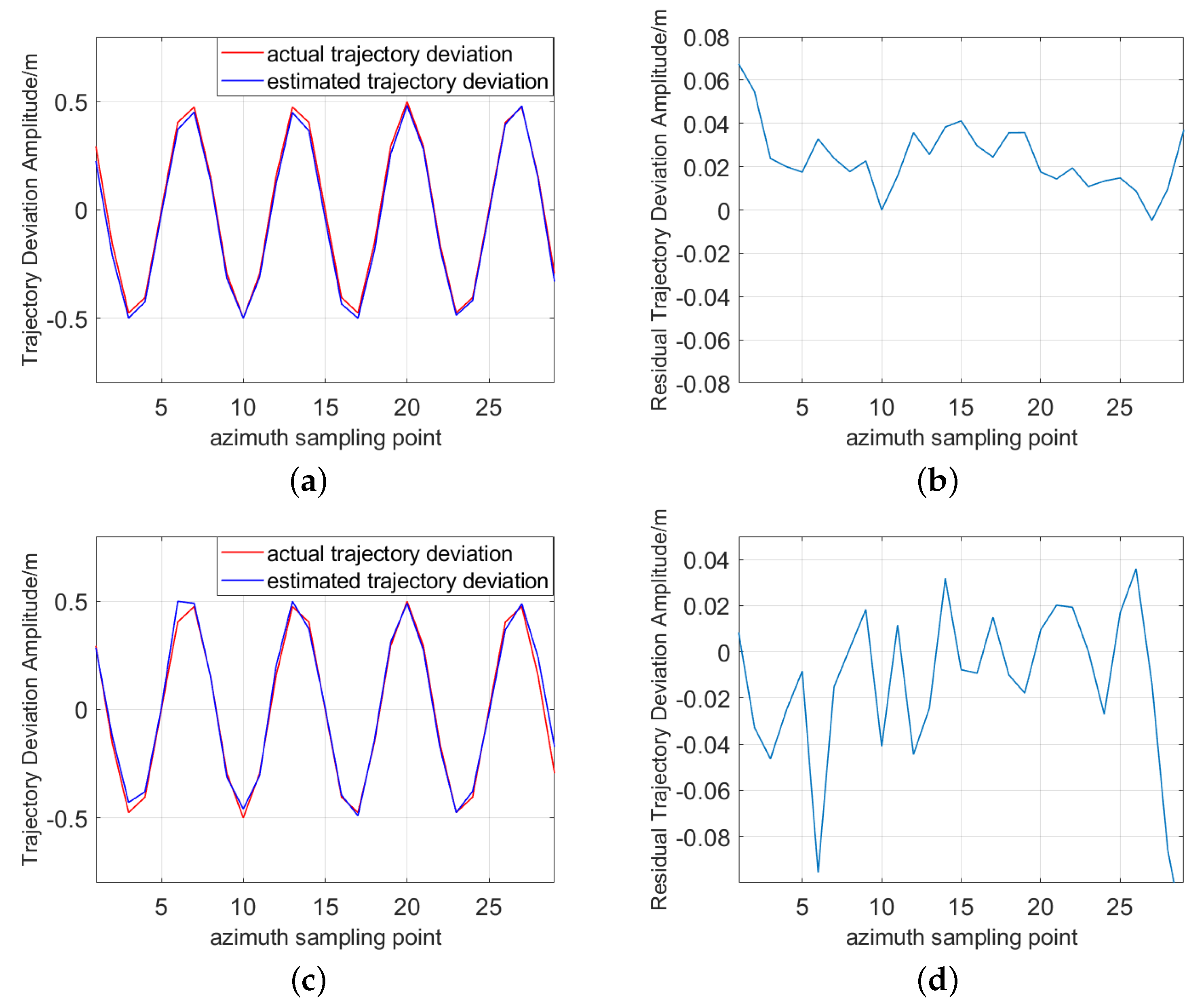
4. Simulation and Experimental Results
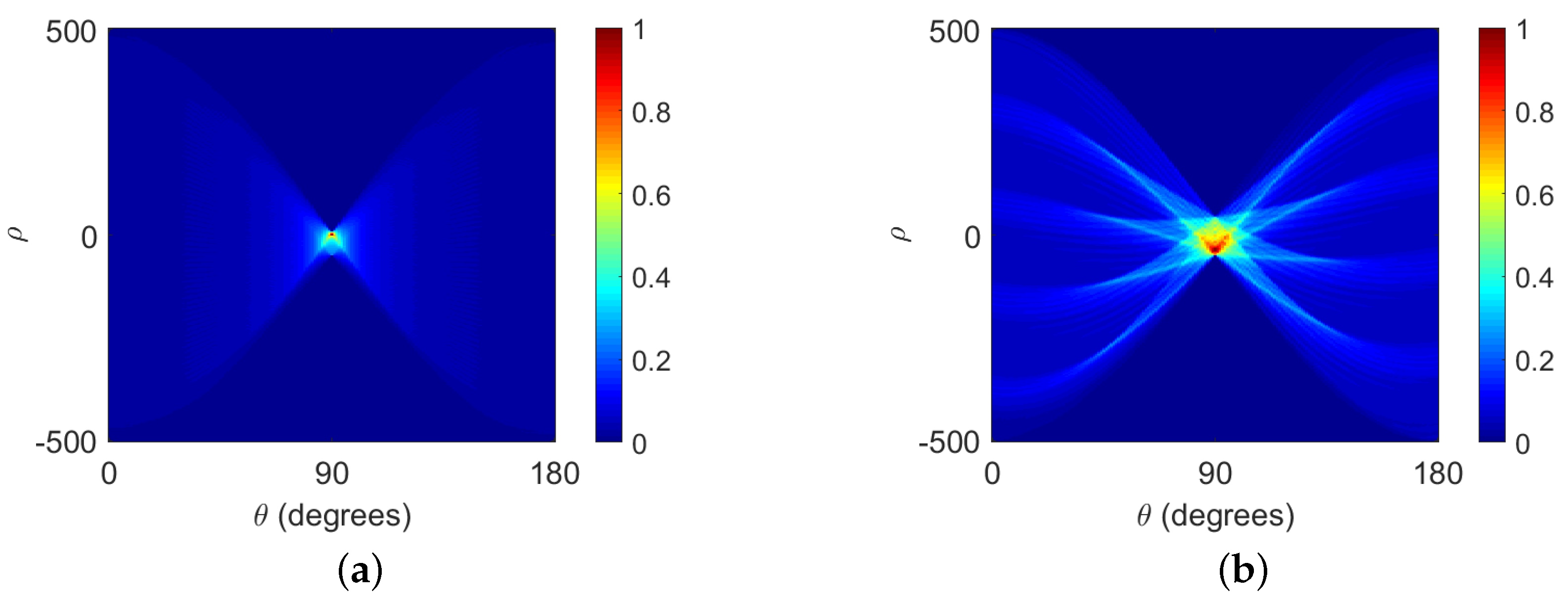
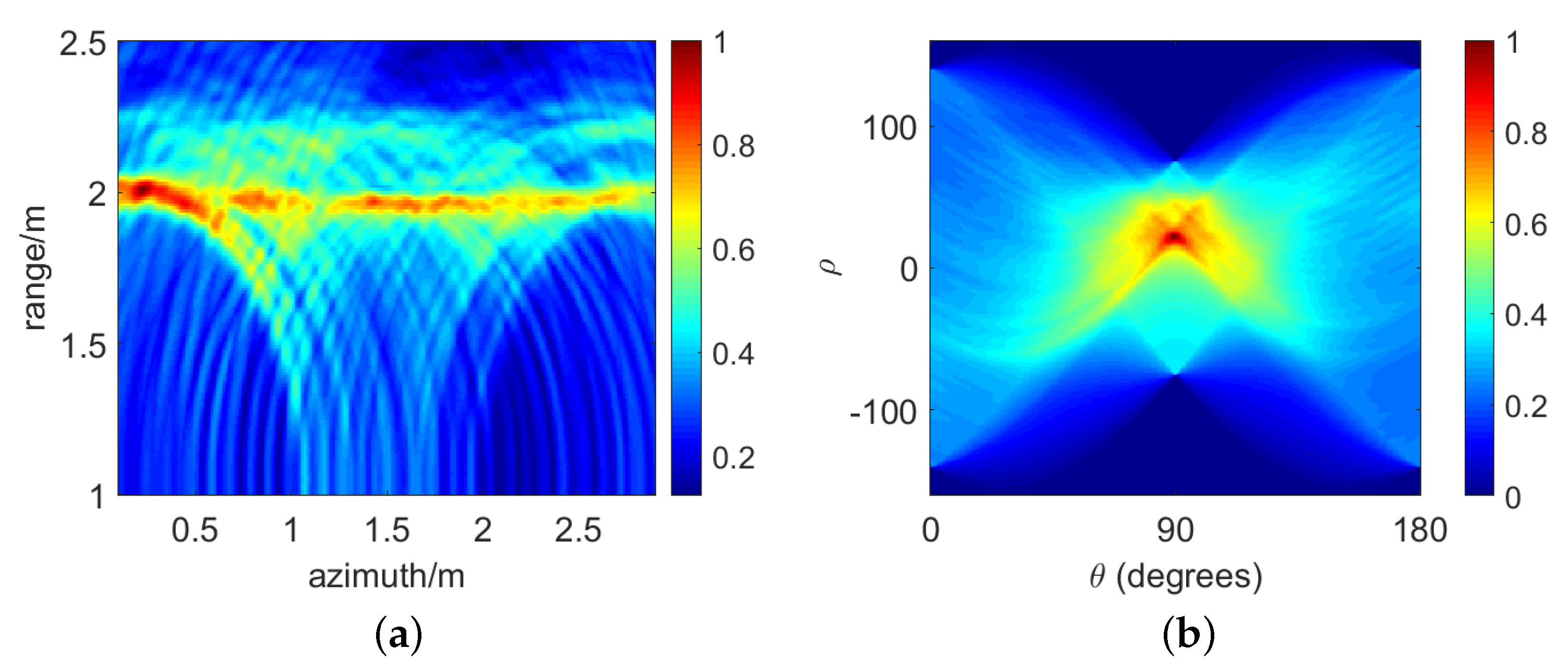
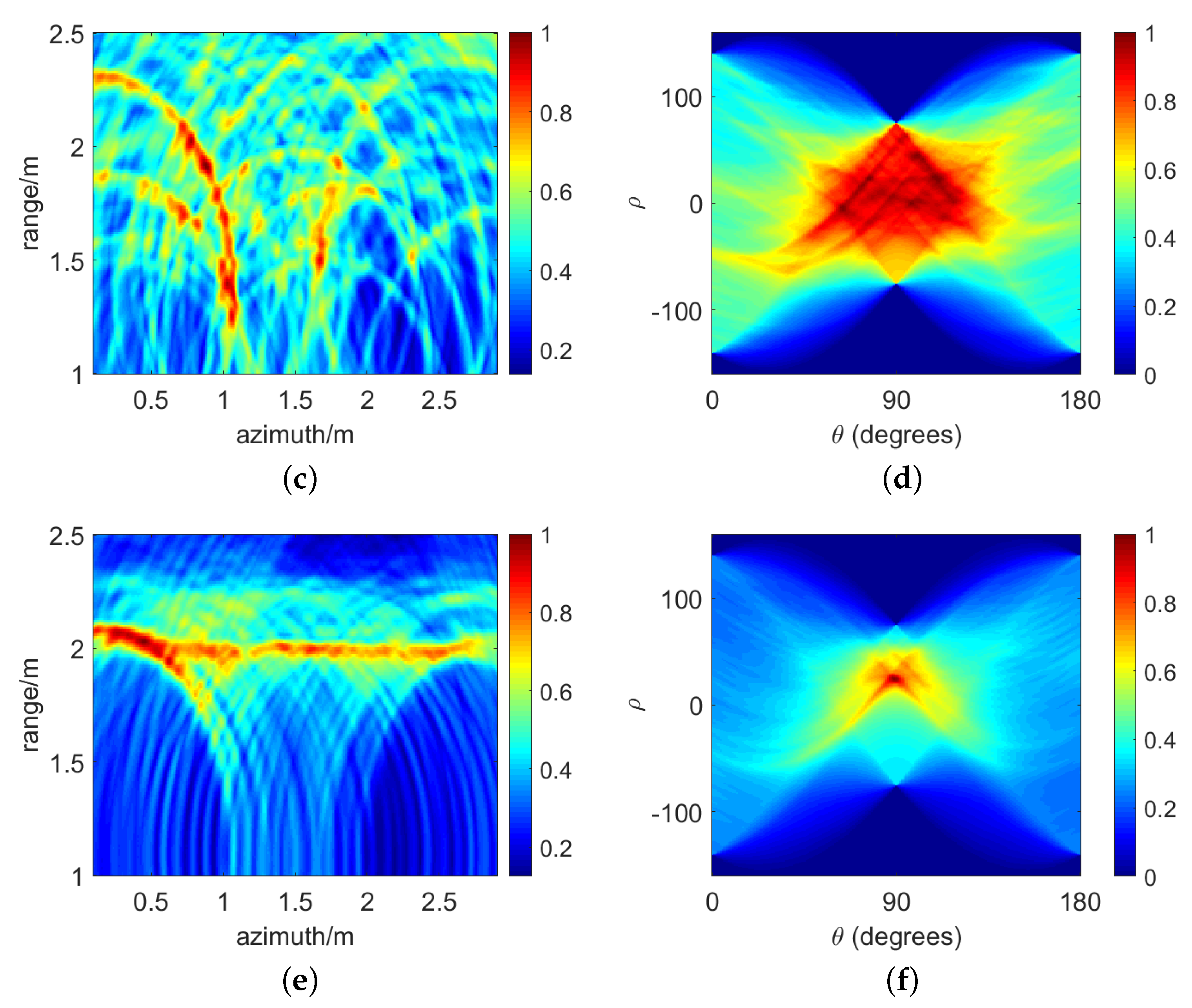
4.1. Simulation Results
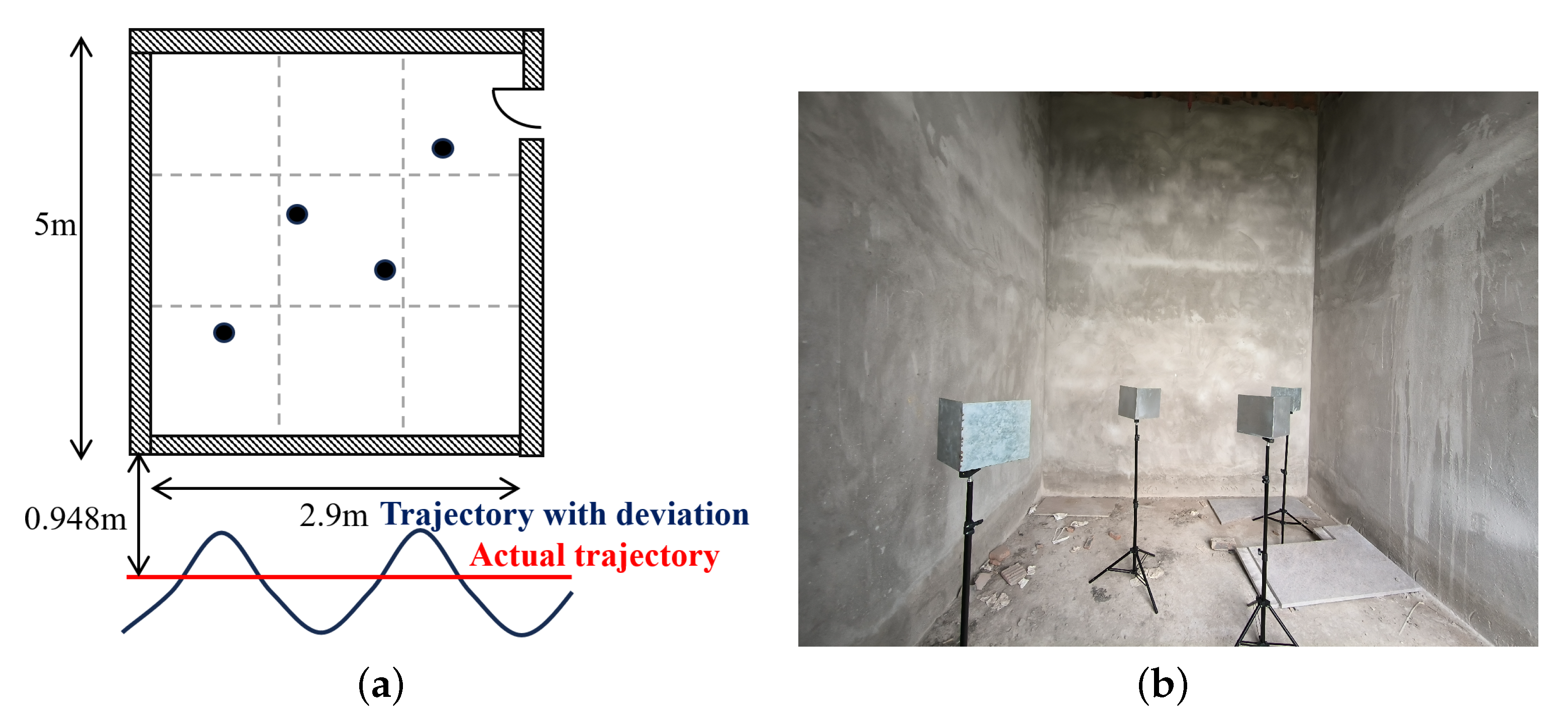
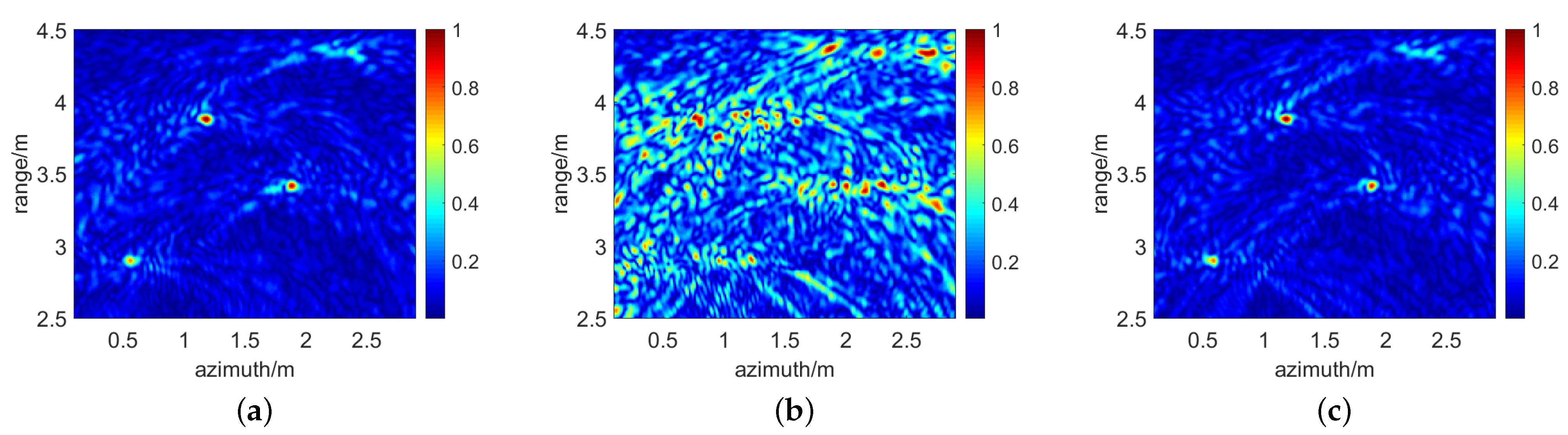
4.2. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chaves, C.S.; Geschke, R.H.; Shargorodskyy, M.; Brauns, R.; Herschel, R.; Krebs, C. Polarimetric UAV-deployed FMCW Radar for Buried People Detection in Rescue Scenarios. In Proceedings of the 2021 18th European Radar Conference (EuRAD), London, UK, 5–7 April 2022; pp. 5–8. [Google Scholar] [CrossRef]
- Stockel, P.; Wallrath, P.; Herschel, R.; Pohl, N. Detection and Monitoring of People in Collapsed Buildings Using a Rotating Radar on a UAV. IEEE Trans. Radar Syst. 2024, 2, 13–23. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y. The best way to promote efficiency and precision of laser scanning for ancient architectures mapping—An ideal rotary-UAV with minimum vibration for LIDAR. In Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 24–26 June 2011; pp. 1761–1766. [Google Scholar] [CrossRef]
- Qu, J.; Huang, Y.; Li, H. Research on UAV Image Detection Method in Urban Low-altitude Complex Background. In Proceedings of the 2023 International Conference on Cyber-Physical Social Intelligence (ICCSI), Xi’an, China, 20–23 October 2023; pp. 26–31. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, F.; Zeng, T.; Wang, C. A Novel Motion Compensation Algorithm Based on Motion Sensitivity Analysis for Mini-UAV-Based BiSAR System. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Joyo, M.K.; Hazry, D.; Faiz Ahmed, S.; Tanveer, M.H.; Warsi, F.A.; Hussain, A.T. Altitude and horizontal motion control of quadrotor UAV in the presence of air turbulence. In Proceedings of the 2013 IEEE Conference on Systems, Process and Control (ICSPC), Kuala Lumpur, Malaysia, 13–15 December 2013; pp. 16–20. [Google Scholar] [CrossRef]
- Quegan, S. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms. J. Atmos. Sol.-Terr. Phys. 1995, 59, 246–260. [Google Scholar] [CrossRef]
- Niho, Y.G.; Day, E.W.; Flanders, T.L. Fast Phase Difference Autofocus. 1993. Available online: http://patents.google.com/patent/CA2083906A1 (accessed on 14 April 2024).
- Zhang, L.; Li, H.l.; Qiao, Z.j.; Xing, M.d.; Bao, Z. Integrating Autofocus Techniques with Fast Factorized Back-Projection for High-Resolution Spotlight SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1394–1398. [Google Scholar] [CrossRef]
- Mancill, C.E.; Swiger, J.M. A Map Drift Autofocus Technique for Correcting Higher Order SAR Phase Errors. In Proceedings of the 27th Annual Tri-service Radar Symposium Record, Monterey, Monterey, CA, USA, 23–25 June 1981; pp. 391–400. [Google Scholar]
- Berizzi, F.; Corsini, G.; Diani, M.; Veltroni, M. Autofocus of wide azimuth angle SAR images by contrast optimisation. In Proceedings of the IGARSS ’96, 1996 International Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 31–31 May 1996; Volume 2, pp. 1230–1232. [Google Scholar] [CrossRef]
- Ahmed, N.; Natarajan, T.; Rao, K. Discrete Cosine Transform. IEEE Trans. Comput. 1974, C-23, 90–93. [Google Scholar] [CrossRef]
- Azouz, A.; Li, Z. Improved phase gradient autofocus algorithm based on segments of variable lengths and minimum entropy phase correction. In Proceedings of the 2014 IEEE China Summit and International Conference on Signal and Information Processing (ChinaSIP), Xi’an, China, 9–13 July 2014; pp. 194–198. [Google Scholar] [CrossRef]
- Wahl, D.; Eichel, P.; Ghiglia, D.; Jakowatz, C. Phase gradient autofocus-a robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef]
- Ye, W.; Yeo, T.S.; Bao, Z. Weighted least-squares estimation of phase errors for SAR/ISAR autofocus. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2487–2494. [Google Scholar] [CrossRef]
- Ash, J.N. An Autofocus Method for Backprojection Imagery in Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2012, 9, 104–108. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.; Pu, W.; Yang, J.; Huang, Y.; Li, W.; Yang, H.; Huo, W. An autofocus method based on maximum image sharpness for Fast Factorized Back-projection. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1201–1204. [Google Scholar] [CrossRef]
- Wei, S.J.; Zhang, X.L.; Hu, K.B.; Wu, W.J. LASAR autofocus imaging using maximum sharpness back projection via semidefinite programming. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 1311–1315. [Google Scholar] [CrossRef]
- Torgrimsson, J.; Dammert, P.; Hellsten, H.; Ulander, L.M.H. Factorized Geometrical Autofocus for Synthetic Aperture Radar Processing. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6674–6687. [Google Scholar] [CrossRef]
- Xing, M.; Jiang, X.; Wu, R.; Zhou, F.; Bao, Z. Motion Compensation for UAV SAR Based on Raw Radar Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2870–2883. [Google Scholar] [CrossRef]
- Ding, Z.; Li, L.; Wang, Y.; Zhang, T.; Gao, W.; Zhu, K.; Zeng, T.; Yao, D. An Autofocus Approach for UAV-Based Ultrawideband Ultrawidebeam SAR Data With Frequency-Dependent and 2-D Space-Variant Motion Errors. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, X.; He, S.; Zhao, H.; Shi, J. A Less-Memory and High-Efficiency Autofocus Back Projection Algorithm for SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 890–894. [Google Scholar] [CrossRef]
- Ran, L.; Liu, Z.; Zhang, L.; Li, T.; Xie, R. An Autofocus Algorithm for Estimating Residual Trajectory Deviations in Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3408–3425. [Google Scholar] [CrossRef]
- Chen, J.; Xing, M.; Sun, G.C.; Li, Z. A 2-D Space-Variant Motion Estimation and Compensation Method for Ultrahigh-Resolution Airborne Stepped-Frequency SAR With Long Integration Time. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6390–6401. [Google Scholar] [CrossRef]
- Kraus, J.D.; Marhefka, R.J. Antennas for All Applications, 3rd ed.; Publishing House of Electronics Industry: Beijing, China, 2008; pp. 21–22. [Google Scholar]
- Zeng, X.; Yang, M.; Chen, B.; Jin, Y. Estimation of Direction of Arrival by Time Reversal for Low-Angle Targets. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2675–2694. [Google Scholar] [CrossRef]
- Wang, F.; Zeng, X.; Wu, C.; Wang, B.; Liu, K.J.R. Driver Vital Signs Monitoring Using Millimeter Wave Radio. IEEE Internet Things J. 2022, 9, 11283–11298. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, F.; Wu, C.; Wang, B.; Liu, K.J.R. ViMo: Multiperson Vital Sign Monitoring Using Commodity Millimeter-Wave Radio. IEEE Internet Things J. 2021, 8, 1294–1307. [Google Scholar] [CrossRef]
- Jin, T.; Chen, B.; Zhou, Z. Image-Domain Estimation of Wall Parameters for Autofocusing of Through-the-Wall SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1836–1843. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, X.; Zhao, H.; Dai, A.; Zhou, H. Three-dimensional fuzzy control of mini quadrotor UAV trajectory tracking under impact of wind disturbance. In Proceedings of the 2016 International Conference on Advanced Mechatronic Systems (ICAMechS), Melbourne, VIC, Australia, 30 November–3 December 2016; pp. 372–377. [Google Scholar] [CrossRef]
- Berizzi, F.; Corsini, G. Autofocusing of inverse synthetic aperture radar images using contrast optimization. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1185–1191. [Google Scholar] [CrossRef]
- GB 50003-2011; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. China Architecture and Building Press: Beijing, China, 2011.
- Giri, D.V.; Tesche, F.M. Electromagnetic attenuation through various types of buildings. In Proceedings of the 2013 Asia-Pacific Symposium on Electromagnetic Compatibility (APEMC), Melbourne, VIC, Australia, 20–23 May 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Ali-Rantala, P.; Ukkonen, L.; Sydanheimo, L.; Keskilammi, M.; Kivikoski, M. Different kinds of walls and their effect on the attenuation of radiowaves indoors. In Proceedings of the IEEE Antennas and Propagation Society International Symposium. Digest. Held in conjunction with: USNC/CNC/URSI North American Radio Sci. Meeting (Cat. No.03CH37450), Columbus, OH, USA, 22–27 June 2003; Volume 3, pp. 1020–1023. [Google Scholar] [CrossRef]
- Ferreira, D.; Fernandes, T.R.; Caldeirinha, R.F.S.; Cuinas, I. Characterization of wireless propagation through traditional Iberian brick walls. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 2454–2458. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, Y.; Zhang, Q.; Dong, Z.; Ji, Y.; Qin, B. A Novel Ionospheric Scintillation Mitigation Method Based on Minimum-Entropy Autofocus in P-band SAR Imaging. In Proceedings of the 2019 IEEE 4th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 19–21 July 2019; pp. 198–202. [Google Scholar] [CrossRef]

| Material | Relative Permittivity | Conductivity (S/m) |
|---|---|---|
| Brick | 4∼7 | ∼ |
| Cement | 6∼7 | ∼ |
| Concrete | 5∼7 | ∼ |
| Wood | 1.5∼2.5 | ∼ |
| Glass | 3∼7 | ∼ |
| Parameter | Value |
|---|---|
| Carrier frequency | 3 GHz |
| Signal band | 1 GHz |
| PRT | 1300 |
| Sampling rate | 2 MHz |
| Beam width in azimuth | |
| Length of synthetic aperture | 10 m |
| Squint angle | |
| Range resolution | 0.15 m |
| Parameter | Value |
|---|---|
| Minimum frequency | 0.1 GHz |
| Maximum frequency | 6 GHz |
| Frequency step | 0.1 GHz |
| Measurement speed | 0.36 ms/point |
| Beam width in azimuth | |
| Antenna type | Vivaldi |
| Antenna distance | 8 cm |
| Height | 1.1 m |
| Range resolution | 0.025 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Zeng, X.; Zhong, S.; Gong, J.; Yang, X. Trajectory Deviation Estimation Method for UAV-Borne Through-Wall Radar. Remote Sens. 2024, 16, 1593. https://doi.org/10.3390/rs16091593
Chen L, Zeng X, Zhong S, Gong J, Yang X. Trajectory Deviation Estimation Method for UAV-Borne Through-Wall Radar. Remote Sensing. 2024; 16(9):1593. https://doi.org/10.3390/rs16091593
Chicago/Turabian StyleChen, Luying, Xiaolu Zeng, Shichao Zhong, Junbo Gong, and Xiaopeng Yang. 2024. "Trajectory Deviation Estimation Method for UAV-Borne Through-Wall Radar" Remote Sensing 16, no. 9: 1593. https://doi.org/10.3390/rs16091593
APA StyleChen, L., Zeng, X., Zhong, S., Gong, J., & Yang, X. (2024). Trajectory Deviation Estimation Method for UAV-Borne Through-Wall Radar. Remote Sensing, 16(9), 1593. https://doi.org/10.3390/rs16091593







