Abstract
The intermittency of gravity wave potential energy (GWPE) in the upper troposphere and stratosphere was investigated using the Constellation Observing System for Meteorology, Ionosphere, and Climate-2 (COSMIC-2) temperature data over three typical mountains (Tibetan Plateau, Rocky Mountains, and Andes). These typical mountains have high sea level elevations but different land–sea contrast. The probability density function (PDF) of GWPE has the independent variable of GWPE and dependent variable of occurrence probability of GWPE over a region. Our analysis showed that the PDFs of GWPE over these three mountains roughly followed lognormal distributions in all heights and months. But, the key parameters (mean value and standard deviation) of lognormal distribution varied with heights and months. Above each mountain, the two key parameters exhibited similar temporal and spatial distributions. They had the largest values around the tropopause region, smaller values in the lower stratosphere (~20–30 km), and larger values in the upper stratosphere (~35–45 km). The intermittency of GWs is represented as the ratio of the GWPE at 50th percentile to the GWPE at 90th percentile. The weakest intermittency was at ~20–30 km (above the zonal mean winds of zero) over the Tibetan Plateau and Rocky Mountains in all months and over the Andes from November to March, respectively. Generally, the weakest intermittency (~0.4) occurred in the region where the key parameters were the smallest around summer. The key parameters of lognormal distribution were dominated by annual variation over the Andes throughout the height range, 8–50 km. However, the semiannual variations are also significant in the lower stratosphere over the Tibetan Plateau and Rocky Mountains. The seasonal variations in the intermittency were not as obvious as those of the key parameters. The lognormal distributions and the intermittencies derived here provide an observational constraint on the tunable parameters in GW parameterization schemes.
1. Introduction
Atmospheric gravity waves (GWs) are widespread in the atmosphere and are important in coupling the atmosphere of different layers and regions. Many GW sources are located in the troposphere and lower stratosphere. Sources of the GWs may be the flow over mountains, convection, strong wind jets and shear, and wave–wave interactions [1]. Moreover, GWs may also be generated by the body force caused by localized wave dissipation, wave–wave interactions after they propagate far from their initial source region [2,3,4,5,6]. Among the various GW sources, GWs triggered by flow over the mountain, also known as mountain waves (MWs), are directly related to both the flow and the spectral of the mountain. The variations in the strength and directions of the flow over a certain mountain induce the intermittence of GWs over the mountain [7,8]. On the other hand, secondary GWs triggered by unstable and/or breaking MWs during the upward propagation of the primary MWs may also be intermittent. This is because the GWs may not always have their averaged strength (such as potential energy and momentum flux, etc.) but may vary within a given time interval and region. This introduces the term of intermittence, which is used to characterize the non-uniform distributions of GW’s strength on the aspects of both time and space. Thus, the intermittence of GWs is an important parameter in characterizing the strength of GWs within a given time interval and region.
The intermittency of GWs is represented by many indices, such as the percentile ratio of the GW’s strength [9,10,11], Gini coefficient [11,12,13,14,15,16], and Bernoulli coefficient [9,17]. Specifically, the percentile ratio is the ratio of the GW’s strength at the 50th percentile to the GW’s strength at the 90th percentile of probability density functions (PDFs) of the GW’s strength [9,10,11]. In a statistical sense, PDFs can reflect comprehensive information about GW parameters in a given time interval and region; the intermittency of GWs over specific regions is usually quantified using the percentile ratio of the PDF of GW parameters in that region.
Previous studies on the PDF and intermittency of GW parameters in the upper troposphere and lower stratosphere (UTLS) focused on the southern hemisphere (Antarctica and the Southern Ocean) [7,11,13,14,18,19] and tropical regions [11,20]. The three typical mountains of the Tibetan Plateau, Rocky Mountains, and Andes have different background winds and land–sea contrast from Antarctica, the Southern Ocean, and the tropical regions. The Tibetan Plateau is one of the most complex topographies in the world, with frequent atmospheric convection activities [21,22] and the highest mountain in the word (the Himalayas). The Rocky Mountains, along the north–south direction, have a similar land–sea contrast to the Andes, but their altitude is lower elevation than the Andes. Moreover, both the Rocky Mountains and the Andes have a different land–sea contrast from the Tibetan Plateau. The longitudinal and latitudinal ranges of these three topographic regions are shown in Figure 1. However, there is insufficient research on the PDFs and intermittency over the three typical mountains (Tibetan Plateau, Rocky Mountains, and Andes) due to the limited sampling profiles per day available and height resolution. Fortunately, the dense sampling and better height resolution profiles of the Constellation Observing System for Meteorology, Ionosphere, and Climate-2 (COSMIC-2) provide a good opportunity to study the detailed height variations in intermittency of GWs over the three typical mountains. Thus, we focus on the seasonal dependence and height variations in the intermittency of GWs over the three typical mountains.
Figure 1.
The latitudinal and longitudinal ranges of the Tibetan Plateau (red box), Andes (green box), and Rocky Mountains (blue box).
The remainder of this paper is organized as follows. Data and methods are introduced in Section 2. Section 3 presents the PDFs of gravity wave potential energy (GWPE) and Section 4 presents the intermittency of GWPE over the Tibetan Plateau, Rocky Mountains, and Andes. The discussions and conclusions are presented in Section 5 and Section 6, respectively.
2. Data and Methods
2.1. Data
The COSMIC-2 mission was composed of six satellites and was launched into low Earth orbit on 25 June 2019. The next-generation GNSS RO payloads onboard the COSMIC-2 mission have provided approximately 4000 temperature profiles since September 2019 [23,24] and approximately 6000 since May 2021 [24]. These profiles have vertical resolutions of 0.05 km and 0.1 km below and above 10 km, respectively. The temperature error is less than 0.05 K [24]. Compared to previous missions, the COSMIC-2 mission provides more temperature profiles in the latitude range of 40°S–40°N (~70% of the profiles) and 20°S–20°N (see also the Figure 2 of Reference [25]). The dense samplings provide an opportunity of obtain the robust PDFs and intermittency of GWs in these latitudes. The temperature data were obtained from the COSMIC Data Analysis and Archive Center (CDACC) website https://cdaac-www.cosmic.ucar.edu/, accessed on 5 February 2024. We focused on the temperature data from December 2020 to November 2023. Before performing further analysis, each temperature profile was interpolated within a height range of ~8–60 km at intervals of 0.1 km. The upper limit of 60 km is only used in the procedure for extracting GW profiles. The physical analysis is limited to 8–50 km because of the lower signal-to-noise ratio of the RO profiles above 50 km [26] and the edge effect of the GW extraction method.
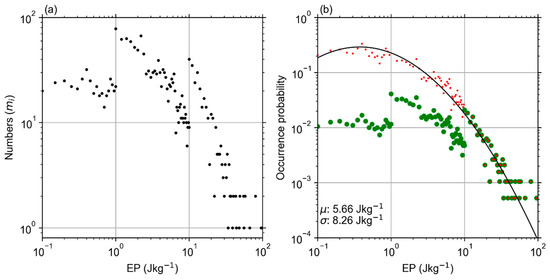
Figure 2.
Procedure for calculation of the PDF of GWPE at 15 km over the Andes in July. (a) The profiles number of GWPE in each sub-interval. (b) The occurrence probability (green dots) and the PDF (red dots). The black line is the least-square fitting of the lognormal distribution to PDF.
To explore the physics of GW intermittency, we used wind data (same time period as COSMIC-2 temperature data) from Modern-Era Retrospective Analysis for Research and Application, Version 2 (MERRA-2), a new version of the atmospheric reanalysis dataset developed by NASA’s Global Modeling and Assimilation Office [27]. Validation studies have shown the monthly zonal mean wind of MERRA-2 coincides well with that measured by radiosonde in Singapore and also coincides well with the subtropical and polar jets obtained from other reanalyzed data (e.g., MERRA, European Centre for Medium-Range Weather Forecasts Re-Analysis Interim (ERA-Interim), Japanese 55-year Reanalysis (JRA-55), and National Centers for Environmental Prediction Climate Forecast System Reanalysis (NCEP CFSR) [28,29]. MERRA-2 data were downloaded from https://goldsmr5.gesdisc.eosdis.nasa.gov/data/MERRA2/M2I3NVASM.5.12.4/, accessed on 1 March 2024.
2.2. Calculating Gravity Wave Potential Energy
The main idea of calculating gravity wave potential energy (GWPE) per unit mass () is similar as that used in references [30,31,32]. Based on the dense samplings of COSMIC-2, the procedure was summarized as the following four steps.
Firstly, we divided the COSMIC-2 temperature profiles within a day into several latitudinal bands by fixing the number of profiles (~60) so that the robustness of the harmonic used in the next step does not vary with latitude.
Secondly, at each latitudinal band and each height, the observed temperature data () are fitted using the following equation:
Here, the first term () on the right side of Equation (1) is the background temperature. The second term on the right side of Equation (1) represents the large-scale waves with zonal wavenumbers 1–6 (i.e., tides and planetary waves). is longitude (unit: °) and are the amplitudes. The third term () on the right side of Equation (1) is the temperature residual.
Thirdly, the discrete wavelet transform [33] was applied to each temperature residual profile (). Then, a new profile () was reconstructed via inverse discrete wavelet transform and by restricting the vertical wavelength in the range of 2–10 km [30,31,32]. The reconstruction procedure ensures the new profile has coherent structure and eliminates observational noise to some extent. Thus, the reconstructed profile () is regarded as GW perturbation.
Finally, the GWPE of each profile () is calculated as [30,34,35,36] (Tsuda et al., 2000; Wang L and Geller, 2003; Liu X et al., 2014, 2017):
In Equation (2), the GW amplitude () can be obtained through applying the Hilbert transform to the GW profile () [37]. is the gravitational acceleration. The Brunt–Väisälä frequency in Equation (2) is calculated as
In Equation (3), is the specific heat of dry air at constant pressure. is the altitude.
2.3. Calculating the PDF of GWPE
The PDF of GWPE can be simply understood as a function, which is the independent variable of the magnitude of the GWPE. Comparatively, the dependent variable is the occurrence probability of the GW profiles and has the same magnitude of GWPE within a fixed temporal and spatial region. The occurrence provability is calculated as the ratio between the number of GW profiles with a certain magnitude of GWPE and the total GW profiles within the fixed temporal and spatial region. The detailed procedure of calculating the PDF of GWPE is as follows
Firstly, at a given region, height, and temporal interval, the GWPE varies from its minimum () to maximum (). As an example, the GWPE varies in the range of 0.1–100 J/kg at 15 km over the Andes in July. This means that and .
Secondly, we divided the interval of into sub-intervals. Since the magnitudes of GWPE vary from a very small value to about one hundred, the length of sub-intervals () varies with the magnitude range of [10,12].
Here, we set to 0.05 J/kg in the GWPE range of <1 J/kg, 0.2 J/kg in the GWPE range of 1–10 J/kg, and 1 J/kg in the GWPE range of >10 J/kg. The magnitude of chosen here is a compromise between the profile numbers in each sub-interval and the resolution of PDFs.
Thirdly, we calculated the number of GW profiles and their occurrence probabilities in each sub-interval. The number of GW profiles in each sub-interval is denoted (Figure 2a). Correspondingly, its occurrence probability is calculated as (green dots in Figure 2b). Here is the total number of GW profiles within the target region.
Fourthly, the occurrence probability () in each sub-interval is normalized (i.e., divided by ) to obtain the probability density function (PDF) and is shown as red dots in Figure 2b. Normalization converts the occurrence probability of GWPE at a non-uniform scale to PDFs at a linear scale.
Finally, we fit the PDFs of GWPE with lognormal distribution (black line in Figure 2b). The lognormal distribution is expressed as
Here, means , ranging from to ; means the PDF at the center height of the target region. and are, respectively, the mean and standard deviation of at the logarithmic scale. The actual mean and standard deviation of are and (denoted at the lower left corner of Figure 2b), respectively.
2.4. Calculating the GWPE Intermittency
The intermittency of the GWPE is a metric of the non-uniformness of the distributions of GWPE within a certain region and temporal interval. Based on the occurrence probability calculated in Section 2.3, the GWPE at 15 km over the Andes in July was taken as an example to illustrate the procedure of calculating the GWPE intermittency. The detailed procedure involves the following three steps.
Firstly, we calculated the cumulative probability of GWPE. The cumulative probability of (noted as ) was calculated by summing the occurrence probabilities of with ranging from 1 to . This can be formulated as . Figure 3a shows the occurrence probability of GWPE at 15 km over the Andes in July. The corresponding cumulative probability is shown as a black line in Figure 3c. This means that the cumulative probability () is a function of .
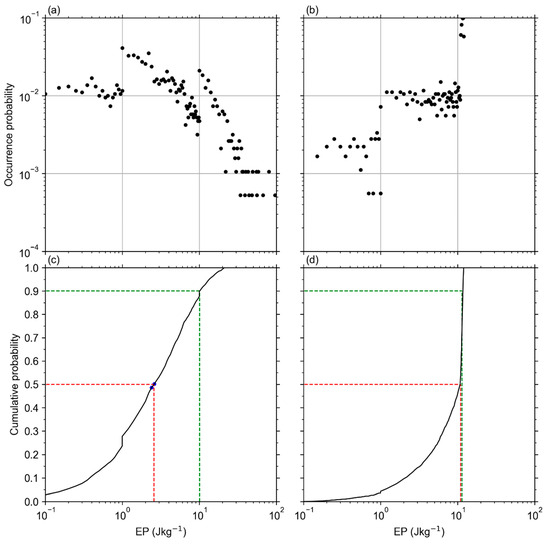
Figure 3.
The procedure of calculating the intermittency of GWPE. (a) The occurrence probability of GWPE at 15 km over Andes in July. (b) The occurrence probability of GWPE generated artificially to form a uniform distribution of occurrence probability in 0.1–12 J/kg. (c,d) The cumulative probabilities (black line) corresponding to those shown in (a) and (b), respectively. The blue dots in (c,d) are cumulative probabilities of around 0.5; red and green dashed lines in (c) and (d) indicate the magnitude of GWPE corresponding to the cumulative probabilities of 0.5 and 0.9, respectively.
Secondly, we calculated the magnitude of GWPE corresponding to certain cumulative probability. For example, the GWPE corresponding to the cumulative probability of 0.5 (noted as ) is calculated as follows. We chose two if their cumulative probability was around 0.5 (horizontal red dashed line in Figure 3c). In this case, the two were denoted as the two blue dots in Figure 3c. Then, a linear fitting of the cumulative probabilities was performed on the two to obtains the actual value of , which is just the intersection of the vertical red dashed line and x-axis in Figure 3c. Similarly, can also be calculated (the green dashed line in Figure 3c).
Finally, we calculated the intermittency of GWPE. Here, the intermittency of GWPE () was quantified as the ratio of GWPE at two different percentiles (i.e., at two different cumulative probabilities) [9]. Specifically, the intermittency of GWPE () is defined as . Reference [9] explained that when closes to 1 it indicates the most uniform occurrence (or weakest intermittency) and when closes to 0 it indicates the most non-uniform occurrence (or strongest intermittency). For example, Figure 3b shows that the occurrence probabilities of GWPE generated artificially to meet that the occurrence probabilities are uniformly distributed from J/kg to J/kg. This induces that closes to , that is to say, closes to 1. This is an example to illustrate the case of the most uniform occurrence (or weakest intermittency).
3. PDFs of GWPE over Mountains
Figure 4 shows the occurrence probability and PDF of GWPE and its lognormal distribution fitting result at 20 km during July over the Tibetan Plateau, Rocky Mountains, and Andes, respectively. In Figure 5, we show the month–height distributions of two key parameters (the mean value and the standard deviation ) of the lognormal distribution over the three typical mountains.
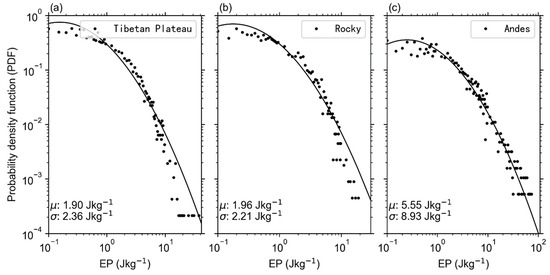
Figure 4.
The occurrence probability and PDF of GWPE and its lognormal distribution fitting results at 20 km during July: (a) Tibetan Plateau; (b) Rocky Mountains; (c) Andes.
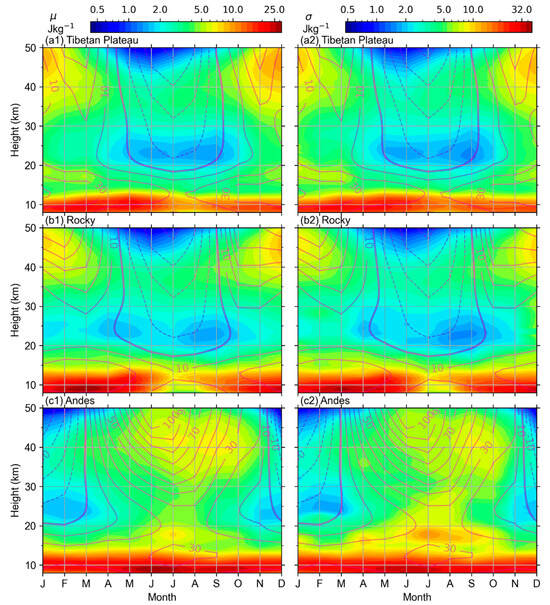
Figure 5.
Month–height distributions of the mean value (the first columns, (a1)–(c1)) and the standard deviation (the second columns, (a2)–(c2)) of GWPE over the Tibetan Plateau, Rocky Mountains, and Andes. Also plotted in each panel is the monthly mean zonal wind calculated from MERRA-2 (the magenta contour lines in each panel have a contour interval of 20 m/s; the thin, solid, dashed lines and the thick, solid contour lines represent the eastward and westward winds, 0 m/s, respectively.
From Figure 4, the PDF of GWPE over the Tibetan Plateau, Rocky Mountains, and Andes at 20 km during July roughly follows lognormal distributions. This has been pointed out before by reference [38]. The lognormal distribution overestimated the PDF of GWPE (0.1–0.8 J/kg and >10 J/kg) and underestimated the PDF of GWPE (0.8–10 J/kg) over the Tibetan Plateau. The lognormal distribution overestimated the PDF of GWPE (0.1–0.8 J/kg and >10 J/kg), described well the PDF of GWPE (0.8–2 J/kg and 4–8 J/kg), and underestimated the PDF of GWPE (2–4 J/kg) over the Rocky Mountains. The lognormal distribution overestimated the PDF of GWPE (0.1–2 J/kg) and described well the PDF of GWPE (>2 J/kg) over Andes. Overall, the PDF of GWPE over the Andes best followed lognormal distributions, then over the Rocky Mountains, and, finally, over Tibetan Plateau.
From Figure 5(a1)–(c1), at 8–15 km, the mean value was the largest (7–30 J/kg) in all months over the Tibetan Plateau, Rocky Mountains, and Andes, respectively. The mean value firstly decreased, reaching its minima at ~20–30 km (called the dissipation layer of GWPE; the eastward zonal wind reached to 0 m/s there), then increased, and finally decreased with increasing height in all months over these three typical regions. Overall, the mean value over these three typical regions has the largest values around the tropopause region, smaller values in the lower stratosphere (~20–30 km), and larger values in the upper stratosphere (~35–45 km).
In addition, at 8–15 km and from November to May, the mean values was the largest over the Rocky Mountains, followed by over the Tibetan Plateau, and then over the Andes. Also, at 8–15 km and from June to October, the mean values was the largest over Andes, followed by over the Tibetan Plateau, and finally over the Rocky Mountains. At 15–50 km, the mean values over Tibetan Plateau and Rocky Mountains in the northern hemisphere were almost the same in all months. Comparing the mean values over two mountains in the northern hemisphere with that over the Andes, the mean values over the Andes was the largest from April to October and was the smallest from November to March.
Moreover, we found that the mean value is dominated by annual variation (with a peak in boreal summer) over the Andes throughout the height range. Over the Tibetan Plateau and Rocky Mountains, the annual variation (with a peak in boreal winter) is dominant in the upper stratosphere and around the troposphere, while both annual and semiannual variations are dominant in the lower stratosphere (~20–30 km). From Figure 5(a2)–(c2), the temporal and spatial distributions of the standard deviation were similar to the mean value over the Tibetan Plateau, Rocky Mountains, and Andes, respectively.
4. Intermittency of GWPE over Mountains
Figure 6 shows the month–height distributions of the , , and the intermittency over the Tibetan Plateau, Rocky Mountains, and Andes, respectively.
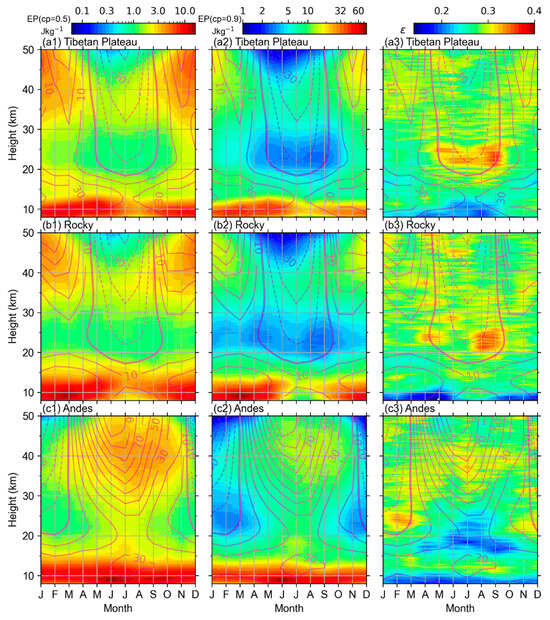
Figure 6.
Month–height distributions of (the first columns, (a1)–(c1)), (the second columns, (a2)–(c2)), and (the third columns, (a3)–(c3)) over the Tibetan Plateau, Rocky Mountains, and Andes. Also plotted in each panel is the monthly mean zonal wind calculated from MERRA-2 (the magenta contour lines in each panel have a contour interval of 20 m/s; the thin, solid, dashed lines and thick, solid contour lines represent the eastward and westward winds, 0 m/s, respectively).
From Figure 6(a1)–(c1),(a2)–(c2), the temporal and spatial distributions of the and over the Tibetan Plateau, Rocky Mountains, and Andes are similar to the temporal and spatial distributions of the mean value in Figure 5(a1)–(c1). In other word, the and over these three typical mountains have largest values around the tropopause region, smaller values in the lower stratosphere (~20–30 km), and larger values in the upper stratosphere (~35–45 km). Moreover, the and were dominated by annual variation (with a peak in boreal summer) over the Andes throughout the height range. Over the Tibetan Plateau and Rocky Mountains, the annual variation (with a peak in boreal winter) was dominant in the upper stratosphere and around the troposphere, while both annual and semiannual variations were dominant in the lower stratosphere. But. the magnitudes of were generally larger than over the Tibetan Plateau, Rocky Mountains, and Andes, respectively.
From Figure 6(a3), in the region of the Tibetan Plateau, the percentile ratio was the smallest (0.14–0.2) at 8–10 km from January to October and at 10–13 km from June to October. This indicates that the intermittency of GWPE was the strongest at 8–10 km from January to October and at 10–13 km from June to October. The percentile ratio was smaller (0.2–0.3) at 10–20 km from November to May. This indicates that the intermittency of GWPE was stronger at 10–20 km from November to May. The percentile ratio was the largest (0.3–0.4) at 20–30 km from May to October. This indicates that the intermittency of GWPE was the weakest at 20–30 km from May to October. The percentile ratio was larger (0.25–0.35) at 30–50 km in all months. This indicates that the intermittency of GWPE was weaker at 30–50 km in all months. Overall, the intermittency of GWPE over the Tibetan Plateau was stronger at 8–10 km from January to October and at 10–13 km from June to October, the weakest at 20–30 km from May to October, and weaker at 30–50 km in all months. Moreover, while the mean value of GWPE had a larger value (Figure 5(a1)) at 8–10 km from October to December, the intermittency of GWs was weaker. This indicates the distribution of GWPE is more uniform.
From Figure 6(b3), in the region of the Rocky Mountains, the percentile ratio was the smallest (0.14–0.2) at 8–10 km from September to June. This indicates that the intermittency of GWs was the strongest at 8–10 km from September to June. The percentile ratio was smaller (0.2–0.3) at 10–20 km from September to June. This indicates that the intermittency of GWPE was stronger at 10–20 km from September to June. The percentile ratio was the largest (0.3–0.4) at 20–30 km from July to September. This indicates that the intermittency of GWPE was the weakest at 20–30 km from July to September. The percentile ratio was larger (0.25–0.35) at 30–50 km in all months. This indicates that the intermittency of GWPE was weaker at 30–50 km in all months. Overall, the intermittency of GWPE over the Rocky Mountains was stronger at 8–20 km from September to June, weaker at 30–50 km in all months, and weakest at 20–30 km from July to September.
From Figure 6(c3), in the region of the Andes, the percentile ratio was the smallest (0.14–0.2) at 8–10 km in all months, at 15–20 km from April to October, and at 20–25 km from June to September. This indicates that the intermittency of GWs was the strongest at 8–10 km in all months, at 15–20 km from April to October, and at 20–25 km from June to September. The percentile ratio was the largest (0.3–0.4) at 20–30 km from November to March. This indicates that the intermittency of GWPE was the weakest at 20–30 km from November to March. The percentile ratio was larger (0.25–0.35) at 30–50 km in all months. This indicates that the intermittency of GWPE was weaker at 30–50 km in all months. Overall, the intermittency of GWPE over the Andes was the strongest at 8–10 km in all months, at 15–20 km from April to October, and at 20–25 km from June to September; weaker at 30–50 km in all months; and the weakest at 20–30 km from November to March. Moreover, the intermittency of GWPE over the Andes was the strongest at 8–10 km in all months; it was then weaker at 10–15 km in all months (zonal mean wind was 30 m/s), before becoming relatively stronger at 15–30 km from April to October when the mean value of GWPE had the smallest value (Figure 5(c1)) at 20–30 km.
In Figure 6(a3)–(c3), the intermittency of GWPE was the strongest over the Rocky Mountains, weaker over the Andes, and weakest over the Tibetan Plateau at 8–10 km from September to June. The intermittency of GWPE was the strongest over the Tibetan Plateau, weaker over the Andes, and weakest over the Rocky Mountains at 8–10 km from July to August. The intermittency of GWPE was the strongest over Andes, weaker over the Rocky Mountains, and the weakest over the Tibetan Plateau at 15–20 km from April to October. The intermittency of GWPE was the strongest over the Andes, weaker over the Rocky Mountains, the weakest over the Tibetan Plateau at 20–30 km from May to September. The intermittency of GWPE was the weakest over the Andes, stronger over the Rocky Mountains, and strongest over the Tibetan Plateau at 20–30 km from November to March.
We have summarized the temporal and spatial distributions of ratio (intermittency) over the Tibetan Plateau, Rocky Mountains, and Andes in Table 1. The boreal spring, boreal summer, boreal autumn, and boreal winter in Table 1 represent March–May, June–August, September–November, and December–February, respectively.

Table 1.
The temporal and spatial distributions of ratio (intermittency) over the Tibetan Plateau, Rocky, and Andes.
Moreover, we found that the intermittency of GWPE over the Tibetan Plateau was dominated by annual variation in the lower and upper stratosphere, while neither annual nor semiannual variations were dominant around the troposphere. Over the Rocky Mountains and Andes, the intermittency of GWPE was dominated by annual variation in the upper stratosphere and around the troposphere, while both annual and semiannual variations were dominant in the lower stratosphere. The seasonal variations in the intermittency were not as obvious as those of the key parameters, and . Further examination showed that the intermittency of GWPE was stronger over the Rocky Mountains at 8–10 km from September to June and was stronger over the Tibetan Plateau at 8–14 km from July to August when the zonal mean wind was eastward.
5. Discussion
The main features found in the previous section are as follows: (1) The weakest intermittency occurred at ~20–30 km (above the zonal mean winds of zero) over the Tibetan Plateau in all months, over the Rocky Mountains in all months, and over the Andes from November to March, respectively. Possible mechanisms can be ascribed to the saturation of GWs or the loss of energy due to the nonlinear interactions with other waves, resulting in the transfer of GWPE to the background flow or other waves [39,40]. According to these mechanisms and height-dependent wind structures, we propose that the activities of GWs are filtered as they propagate upward to the region of zero-speed wind at ~20–30 km. (2) From Figure 6(c3), stronger intermittency of GWs over the Andes at 15–30 km from April to October. The GWs over the Andes were mainly excited by flow over the topography (MWs) [26,41,42,43,44]. The corresponding sources of GW are highly variable, as they depend strongly on variable near-surface winds. (3) While the mean value of GWPE had larger value (Figure 5(a1)) at 8–10 km from October to December, the intermittency of GWs was weaker. Reference [45] indicated that it is impossible to distinguish MWs from other GW sources in the COSMIC data because individual phase speeds were indeterminable and did not show strong GWPE above the Himalayas at 17–23 km during boreal winter. Therefore, there may be other strong GW sources (such as convection sources). The Tibetan Plateau is one of the most complex topographies in the world, with frequent atmospheric convection activities, we need to study the proportion of different GW sources over the region in future work.
6. Conclusions
The intermittency of gravity wave potential energy (GWPE) in the upper troposphere and stratosphere was investigated using the COSMIC-2 temperature data from December 2020 to November 2023 over three typical mountains (Tibetan Plateau, Rocky Mountains, and Andes). These typical mountains have high sea level elevations but different land–sea contrasts. We have described, in detail, the method of the probability density function (PDF) and the intermittency of GWPE in Section 2.3 and Section 2.4. Here, the key parameters of lognormal distribution are the mean value and the standard deviation , and the intermittency of GWs is represented by the percentile ratio . The main findings are as follows.
Firstly, the PDFs of the GWPE over the Tibetan Plateau, Rocky Mountains, and Andes roughly followed lognormal distributions in all heights and months. Above each mountain, the two key parameters of lognormal distribution (the mean value and the standard deviation ) exhibit similar temporal and spatial distributions. They had the largest values around the tropopause region, smaller values in the lower stratosphere (~20–30 km), and larger values in the upper stratosphere (~35–45 km). At 15–50 km, the two key parameters over the Tibetan Plateau and Rocky Mountains in the northern hemisphere were almost the same in all months. Compared to the two key parameters over the two mountains in the northern hemisphere with that over Andes, the two key parameters over the Andes were the largest from April to October and the smallest from November to March.
Secondly, we showed the weakest intermittency at ~20–30 km (above the region having zero zonal mean winds) over the Tibetan Plateau and Rocky Mountains in all months and over the Andes from November to March, respectively. The intermittency of the GWs was the strongest over the Rocky Mountains, strong over the Andes, and weaker over the Tibetan Plateau at 8–10 km from September to June. The intermittency of GWs was the strongest over the Andes, weaker over the Rocky Mountains, and the weakest over the Tibetan Plateau at 20–30 km from May to September. Over the Tibetan Plateau and Rocky Mountains, the intermittency of GWs was stronger over the Rocky Mountains at 8–10 km from September to June and was stronger over the Tibetan Plateau at 8–14 km from July to August when the zonal mean wind was eastward.
Finally, the intermittency of GWPE over the Tibetan Plateau was dominated by annual variation in the lower and upper stratosphere, while neither annual nor semiannual variations were dominant around the troposphere. Over the Rocky Mountains and Andes, the intermittency of GWPE was dominated by annual variation in the upper stratosphere and around the troposphere, while both annual and semiannual variations were dominant in the lower stratosphere. The seasonal variations in the intermittency were not as obvious as those of the key parameters.
Author Contributions
J.X.: conceptualization, supervision; J.W.: software, calculation, formal analysis, writing—original draft preparation; X.L.: methodology, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant Nos. 41831073, 42174196), the Project of Stable Support for Youth Team in Basic Research Field, CAS (grant No. YSBR-018), the Informatization Plan of Chinese Academy of Sciences (grant No. CAS-WX2022SF-0103), the National Program on Key Research Project (grant No. 2022YFF0711400), and the Open Research Project of Large Research Infrastructures of CAS “Study on the interaction between low/mid-latitude atmosphere and ionosphere based on the Chinese Meridian Project”. This research was also supported, in part, by the Specialized Research Fund and the Open Research Program of the State Key Laboratory of Space Weather.
Data Availability Statement
Publicly available datasets were analyzed in this study. They can be found as follows: the COSMIC-2 (Constellation Observing System for Meteorology, Ionosphere, and Climate-2) temperature data are available at https://cdaac-www.cosmic.ucar.edu/, accessed on 5 February 2024; the MERRA-2 (Modern-Era Retrospective Analysis for Research and Application, Version 2) wind data were accessed from https://goldsmr5.gesdisc.eosdis.nasa.gov/data/MERRA2/M2I3NVASM.5.12.4/, accessed on 1 March 2024.
Acknowledgments
We are grateful to the anonymous reviewers for their constructive comments and suggestions to improve this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1–64. [Google Scholar] [CrossRef]
- Bacmeister, J.T.; Schoeberl, M.R. Breakdown of vertically propagating two-dimensional gravity waves forced by orography. J. Atmos. Sci. 1989, 46, 2109–2134. [Google Scholar] [CrossRef]
- Vadas, S.L.; Fritts, D.C. The importance of spatial variability in the generation of secondary gravity waves from local body forces. Geophys. Res. Lett. 2002, 29, 45-1–45-4. [Google Scholar] [CrossRef]
- Vadas, S.L.; Fritts, D.C.; Alexander, M.J. Mechanism for the generation of secondary waves in wave breaking regions. J. Atmos. Sci. 2003, 60, 194–214. [Google Scholar] [CrossRef]
- Vadas, S.L.; Becker, E. Numerical modeling of the generation of tertiary gravity waves in the mesosphere and thermosphere during strong mountain wave events over the Southern Andes. J. Geophys. Res. Space Phys. 2019, 124, 7687–7718. [Google Scholar] [CrossRef]
- Vadas, S.L.; Xu, S.; Yue, J.; Bossert, K.; Becker, E.; Baumgarten, G. Characteristics of the quiet-time hot spot gravity waves observed by GOCEE over the Southern Andes on 5 July 2010. J. Geophys. Res. Space Phys. 2019, 124, 7034–7061. [Google Scholar] [CrossRef]
- Hertzog, A.; Alexander, M.J.; Plougonven, R. On the intermittency of gravity wave momentum flux in the stratosphere. J. Atmos. Sci. 2012, 69, 3433–3448. [Google Scholar] [CrossRef]
- Kuchar, A.; Sacha, P.; Eichinger, R.; Jacobi, C.; Pisoft, P.; Rieder, H.E. On the intermittency of orographic gravity wave hotspots and its importance for middle atmosphere dynamics. Weather. Clim. Dyn. 2020, 1, 481–495. [Google Scholar] [CrossRef]
- Hertzog, A.; Boccara, G.; Vincent, R.A.; Vial, F.; Cocquerez, P. Estimation of gravity wave momentum flux and phase speeds from quasi-lagrangian stratospheric balloon flights. Part II: Results from the vorcore campaign in antarctica. J. Atmos. Sci. 2008, 65, 3056–3070. [Google Scholar] [CrossRef]
- Cao, B.; Liu, A.Z. Intermittency of gravity wave momentum flux in the mesopause region observed with an all-sky airglow imager. J. Geophys. Res. Atmos. 2016, 121, 650–663. [Google Scholar] [CrossRef]
- Ern, M.; Preusse, P.; Riese, M. Intermittency of gravity wave potential energies and absolute momentum fluxes derived from infrared limb sounding satellite observations. Atmos. Chem. Phys. 2022, 22, 15093–15133. [Google Scholar] [CrossRef]
- Wright, C.J.; Osprey, S.M.; Gille, J.C. Global observations of gravity wave intermittency and its impact on the observed momentum flux morphology. J. Geophys. Res. Atmos. 2013, 118, 10980–10993. [Google Scholar] [CrossRef]
- Jewtoukoff, V.; Hertzog, A.; Plougonven, R.; de la Cámara, A.; Lott, F. Comparison of gravity waves in the southern hemisphere derived from balloon observations and the ECMWF analyses. J. Atmos. Sci. 2015, 72, 3449–3468. [Google Scholar] [CrossRef]
- Alexander, S.P.; Sato, K.; Watanabe, S.; Kawatani, Y.; Murphy, D.J. Southern hemisphere extratropical gravity wave sources and intermittency revealed by a middle-atmosphere general circulation model. J. Atmos. Sci. 2016, 73, 1335–1349. [Google Scholar] [CrossRef]
- Love, P.T.; Murphy, D.J. Gravity wave momentum flux in the mesosphere measured by VHF radar at Davis, Antarctica. J. Geophys. Res. Atmos. 2016, 121, 12723–12736. [Google Scholar] [CrossRef]
- Minamihara, Y.; Sato, K.; Tsutsumi, M. Intermittency of gravity waves in the Antarctic troposphere and lower stratosphere revealed by the PANSY radar observation. J. Geophys. Res. Atmos. 2020, 125, e2020JD032543. [Google Scholar] [CrossRef]
- Bühler, O. Equatorward propagation of inertia-gravity waves due to steady and intermittent wave sources. J. Atmos. Sci. 2003, 60, 1410–1419. [Google Scholar] [CrossRef]
- Plougonven, R.; Hertzog, A.; Guez, L. Gravity waves over antarctica and the southern ocean: Consistent momentum fluxes in mesoscale simulations and stratospheric balloon observations. Q. J. R. Meteor. Soc. 2013, 139, 101–118. [Google Scholar] [CrossRef]
- de la Cámara, A.; Lott, F. A parameterization of gravity waves emitted by fronts and jets. Geophys. Res. Lett. 2015, 42, 2071–2078. [Google Scholar] [CrossRef]
- Jewtoukoff, V.; Plougonven, R.; Hertzog, A. Gravity waves generated by deep tropical convection: Estimates from balloon observations and mesoscale simulations. J. Geophys. Res. Atmos. 2013, 118, 9690–9707. [Google Scholar] [CrossRef]
- Ding, Y.H. Effects of the Qinghai-Xizang (Tibetan) plateau on the circulation features over the plateau and its surrounding areas. Adv. Atmos. Sci. 1992, 9, 112–130. [Google Scholar]
- Lin, Y.H.; Zhang, L.J. Characteristics of gravity waves over the Tibetan Plateau during the PRC-Japan Cooperative JICA Project in 2008. J. Meteorol. Soc. Jpn. 2012, 90C, 215–223. [Google Scholar] [CrossRef]
- Anthes, R.; Schreiner, W. Six new satellites watch the atmosphere over Earth’s equator. Eos 2019, 100. [Google Scholar] [CrossRef]
- Schreiner, W.S.; Weiss, J.P.; Anthes, R.A.; Braun, J.; Chu, V.; Fong, J. COSMIC-2 radio occultation constellation: First results. Geophys. Res. Lett. 2020, 47, e2019GL086841. [Google Scholar] [CrossRef]
- Ho, S.P.; Zhou, X.; Shao, X.; Zhang, B.; Adhikari, L.; Kireev, S. Initial assessment of the COSMIC-2/FORMOSAT-7 neutral atmosphere data quality in nesdis/star using in situ and satellite data. Remote Sens. 2020, 12, 4099. [Google Scholar] [CrossRef]
- Hindley, N.P.; Wright, C.J.; Smith, N.D.; Mitchell, N.J. The southern stratospheric gravity-wave hot spot: Individual waves and their momentum fluxes measured by COSMIC GPS-RO. Atmos. Chem. Phys. 2015, 15, 7797–7818. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Coy, L.; Wargan, K.; Molod, A.M.; McCarty, W.R.; Pawson, S. Structure and dynamics of the quasi-biennial oscillation in merra-2. J. Clim. 2016, 29, 5339–5354. [Google Scholar] [CrossRef]
- Manney, G.L.; Hegglin, M.I. Seasonal and regional variations of long-term changes on upper-tropospheric jets from reanalyses. J. Clim. 2018, 31, 423–448. [Google Scholar] [CrossRef]
- Liu, X.; Yue, J.; Xu, J.; Garcia, R.R.; Russell, J.M.; Mlynczak, M. Variations of global gravity waves derived from 14 years of saber temperature observations. J. Geophys. Res. Atmos. 2017, 122, 6231–6249. [Google Scholar] [CrossRef]
- Liu, X.; Xu, J.; Yue, J.; Vadas, S.L.; Becker, E. Orographic primary and secondary gravity waves in the middle atmosphere from 16-year saber observations. Geophys. Res. Lett. 2019, 46, 4512–4522. [Google Scholar] [CrossRef]
- Liu, X.; Xu, J.; Yue, J.; Liu, H. Gravity-wave-perturbed wind shears derived from saber temperature observations. Atmos. Chem. Phys. 2020, 20, 14437–14456. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteor. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Tsuda, T.; Nishida, M.; Rocken, C.; Ware, R.H. A global morphology of gravity wave activity in the stratosphere revealed by the GPS occultation data (GPS/MET). J. Geophys. Res. Atmos. 2000, 105, 7257–7273. [Google Scholar] [CrossRef]
- Wang, L.; Geller, M.A. Morphology of gravity-wave energy as observed from 4 years (1998–2001) of high vertical resolution U.S. radiosonde data. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Liu, X.; Yue, J.; Xu, J.; Wang, L.; Yuan, W.; Russell, J.M., III; Hervig, M.E. Gravity wave variations in the polar stratosphere and mesosphere from SOFIE/AIM temperature observations. J. Geophys. Res. Atmos. 2014, 119, 7368–7381. [Google Scholar] [CrossRef]
- Schoon, L.; Zülicke, C. A novel method for the extraction of local gravity wave parameters from gridded three-dimensional data: Description, validation, and application. Atmos. Chem. Phys. 2018, 18, 6971–6983. [Google Scholar] [CrossRef]
- Baumgaertner, A.J.G.; McDonald, A.J. A gravity wave climatology for Antarctica compiled from Challenging Minisatellite Payload/Global Positioning System (CHAMP/GPS) radio occultations. J. Geophys. Res. Atmos. 2007, 112, D5. [Google Scholar] [CrossRef]
- Liu, X.; Xu, J.; Liu, H.L.; Ma, R. Nonlinear interactions between gravity waves with different wavelengths and diurnal tide. J. Geophys. Res. 2008, 113, D08112. [Google Scholar] [CrossRef]
- Li, T.; Leblanc, T.; McDermid, I.S.; Wu, D.L.; Dou, X.; Wang, S. Seasonal and interannual variability of gravity wave activity revealed by long-term lidar observations over Mauna Loa Observatory, Hawaii. J. Geophys. Res. 2010, 115, D13103. [Google Scholar] [CrossRef]
- Hei, H.; Tsuda, T.; Hirooka, T. Characteristics of atmospheric gravity wave activity in the polar regions revealed by GPS radio occultation data with CHAMP. J. Geophys. Res. 2008, 113, D04107. [Google Scholar] [CrossRef]
- Yan, X.; Arnold, N.; Remedios, J. Global observations of gravity waves from High Resolution Dynamics Limb Sounder temperature measurements: A yearlong record of temperature amplitude and vertical wavelength. J. Geophys. Res. Atmos. 2010, 115, D10113. [Google Scholar] [CrossRef]
- Faber, A.; Llamedo, P.; Schmit, T.; de la Torre, A.; Wickert, J. On the determination of gravity wave momentum flux from GPS radio occultation data. Atmos. Meas. Technol. 2013, 6, 3169–3180. [Google Scholar] [CrossRef]
- Ern, M.; Trinh, Q.T.; Preusse, P.; Gille, J.C.; Mlynczak, M.G.; Iii, J.M.R.; Riese, M. GRACILE: A comprehensive climatology of atmospheric gravity wave parameters based on satellite limb soundings. Earth Syst. Sci. Data 2018, 10, 857–892. [Google Scholar] [CrossRef]
- Alexander, S.P.; Tsuda, T.; Kawatani, Y. COSMIC GPS observations of Northern Hemisphere winter stratospheric gravity waves and comparisons with an atmospheric general circultation model. Geophys. Res. Lett. 2008, 35, L10808. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).