A Multi-Satellite SBAS for Retrieving Long-Term Ground Displacement Time Series
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Study Area
2.1.2. Dataset
2.2. Methods
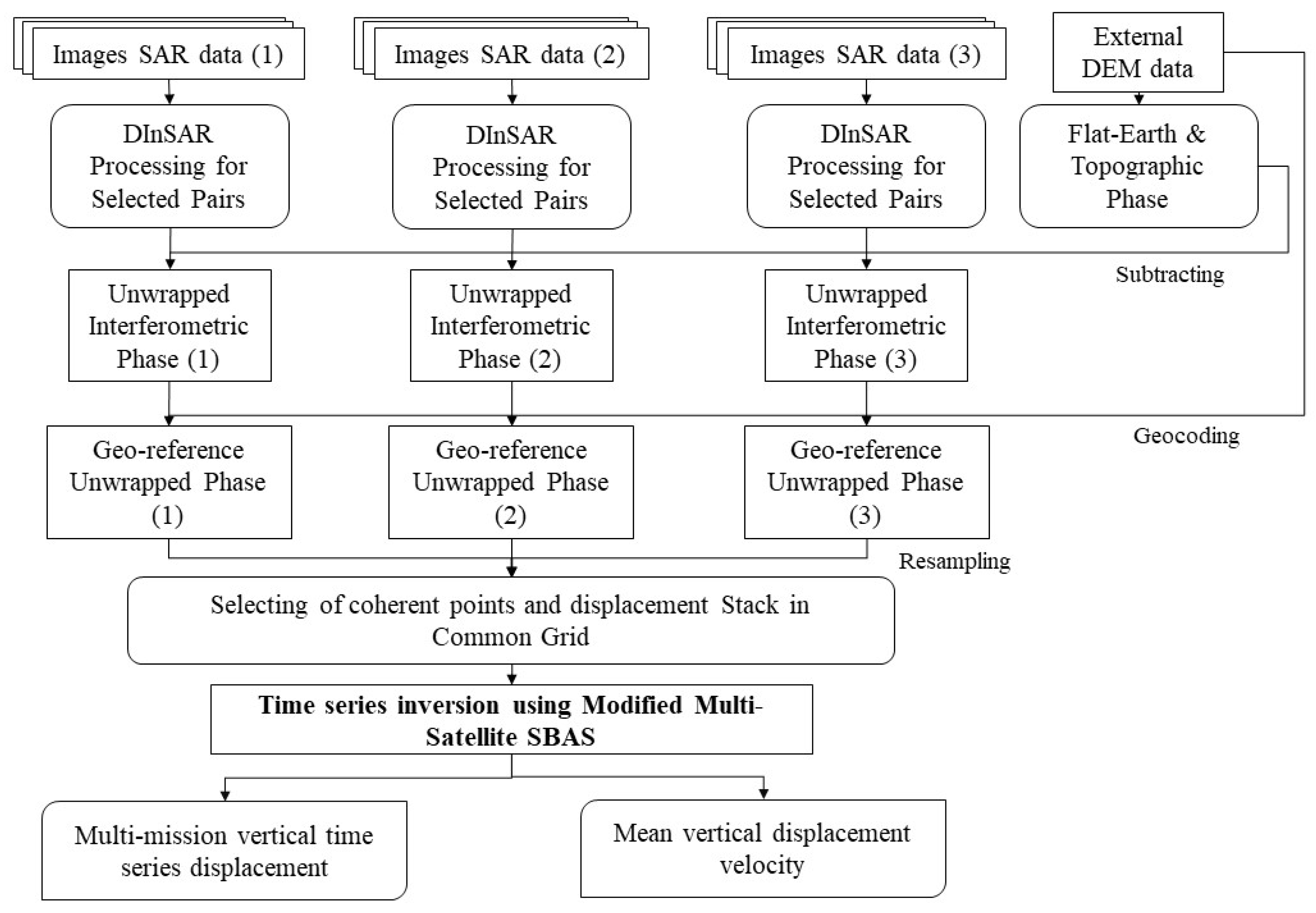
2.2.1. Surface Displacement Using Multi-Baseline DInSAR
2.2.2. Selection of High Coherent Points
2.2.3. Multi-Satellite SBAS Integration
2.2.4. Evaluation Criteria
3. Results and Analysis
3.1. Multi-Baseline DInSAR Displacement
3.2. Multi-Satellite SBAS Displacement
3.3. Displacement from Individual Datasets
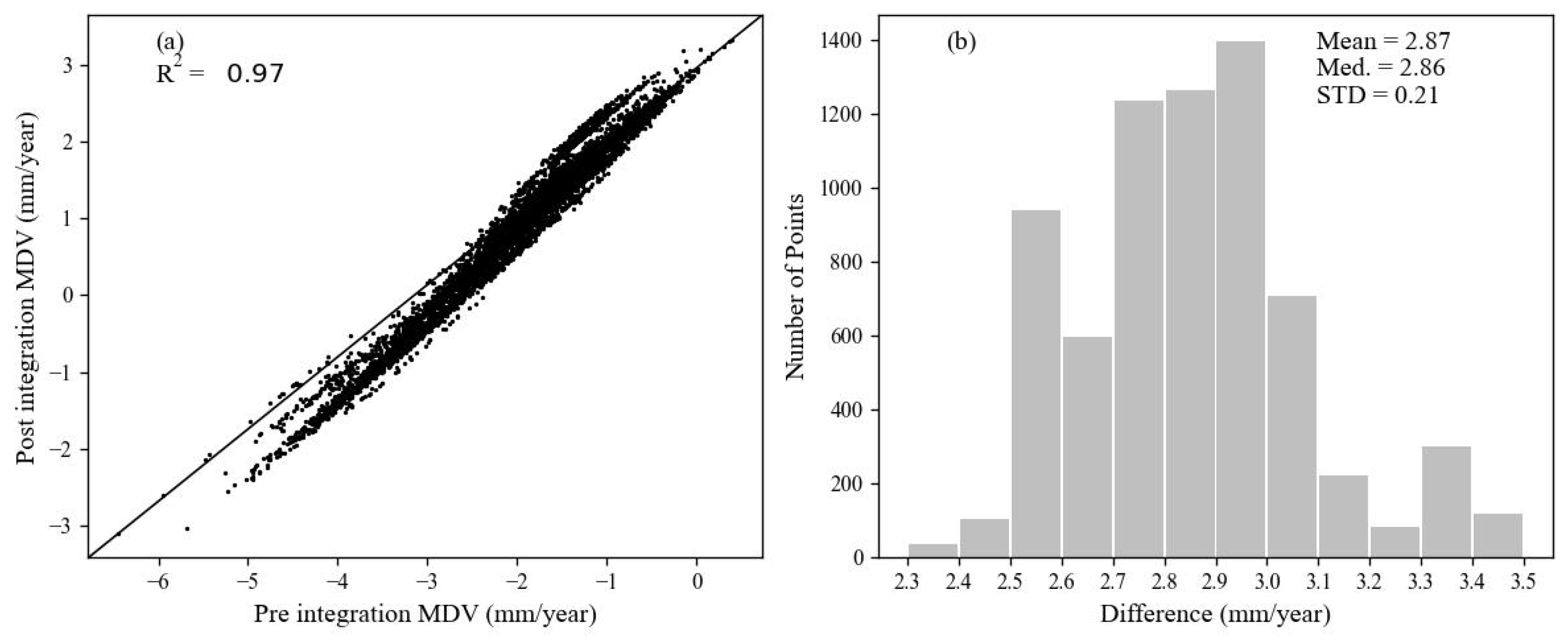
3.4. Evaluation
3.4.1. Displacement Based on All Interferograms
3.4.2. Displacement from Individual Datasets
4. Discussion
4.1. Displacement in Almokattam City, Causes and Implications
4.2. Multi-Satellite SBAS for SAR Data Integration
4.3. Comparison with Previous Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aboushook, M.; EL-Sohby, M.; Mazen, O. Slope degradation and analysis of Mokattam plateau, Egypt. In Proceedings of the 2nd International Conference on Geotechnical Site Characterization (ISC-2), Porto, Portugal, 19–22 September 2004; pp. 1081–1887. [Google Scholar]
- Aimaiti, Y.; Yamazaki, F.; Liu, W. Multi-Sensor InSAR Analysis of Progressive Land Subsidence over the Coastal City of Urayasu, Japan. Remote Sens. 2018, 10, 1304. [Google Scholar] [CrossRef]
- Luo, Q.; Perissin, D.; Lin, H.; Li, Q.; Duering, R. Railway subsidence monitoring by high-resolution INSAR time series analysis in Tianjin. In Proceedings of the 2011 19th International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Sun, Q.; Hu, J.; Zhang, L.; Ding, X. Towards Slow-Moving Landslide Monitoring by Integrating Multi-Sensor InSAR Time Series Datasets: The Zhouqu Case Study, China. Remote Sens. 2016, 8, 908. [Google Scholar] [CrossRef]
- Wang, L.; Marzahn, P.; Bernier, M.; Ludwig, R. Sentinel-1 InSAR measurements of deformation over discontinuous permafrost terrain, Northern Quebec, Canada. Remote Sens. Environ. 2020, 248, 111965. [Google Scholar] [CrossRef]
- Ren, H.; Feng, X. Calculating vertical deformation using a single InSAR pair based on singular value decomposition in mining areas. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102115. [Google Scholar] [CrossRef]
- Peng, M.; Zhao, C.; Zhang, Q.; Lu, Z.; Bai, L.; Bai, W. Multi-Scale and Multi-Dimensional Time Series InSAR Characterizing of Surface Deformation over Shandong Peninsula, China. Appl. Sci. 2020, 10, 2294. [Google Scholar] [CrossRef]
- Pawluszek-Filipiak, K.; Borkowski, A. Integration of DInSAR and SBAS Techniques to Determine Mining-Related Deformations Using Sentinel-1 Data: The Case Study of Rydułtowy Mine in Poland. Remote Sens. 2020, 12, 242. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arıkan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514–517, 1–13. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Werner, C.L.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. Interferometric point target analysis for deformation mapping. In Proceedings of the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003; Volume 7, pp. 4362–4364. [Google Scholar]
- Kampes, B.M. Radar Interferometry; Springer: Berlin/Heidelberg, Germany, 2006; Volume 12. [Google Scholar]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Mora, O.; Mallorqui, J.; Broquetas, A. Linear and nonlinear terrain deformation maps from a reduced set of interferometric SAR images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2243–2253. [Google Scholar] [CrossRef]
- Crosetto, M.; Crippa, B. State of the art of land deformation monitoring using differential SAR interferometry. In Proceedings of the ISPRS Hann, ISPRS Hannover Workshop 2005, Hannover, Germany, 17–20 May 2005. [Google Scholar]
- Fornaro, G.; Pauciullo, A.; Serafino, F. Deformation monitoring over large areas with multipass differential SAR interferometry: A new approach based on the use of spatial differences. Int. J. Remote Sens. 2009, 30, 1455–1478. [Google Scholar] [CrossRef]
- Pepe, A.; Solaro, G.; Calò, F.; Dema, C. A Minimum Acceleration Approach for the Retrieval of Multiplatform InSAR Deformation Time Series. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3883–3898. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, G.; Wang, Q.; Yang, T.; Liu, M.; Gao, W.; Falabella, F.; Mastro, P.; Pepe, A. Generation of long-term InSAR ground displacement time-series through a novel multi-sensor data merging technique: The case study of the Shanghai coastal area. ISPRS J. Photogramm. Remote Sens. 2019, 154, 10–27. [Google Scholar] [CrossRef]
- Gray, L. Using multiple RADARSAT InSAR pairs to estimate a full three-dimensional solution for glacial ice movement. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Gudmundsson, S.; Sigmundsson, F.; Carstensen, J.M. Three-dimensional surface motion maps estimated from combined interferometric synthetic aperture radar and GPS data. J. Geophys. Res. Solid Earth 2002, 107, ETG 13-1–ETG 13-14. [Google Scholar] [CrossRef]
- Hu, J.; Ding, X.L.; Li, Z.W.; Zhu, J.J.; Sun, Q.; Zhang, L.; Omura, M. A kalman filter based mtinsar methodology for derving 3d surface displacement evolutions. North 2012, 2011, 19–23. [Google Scholar]
- Lu, J. Sentinel-1 Toolbox Offset Tracking Tutorial; ESA: Montreal, QC, Canada, 2016. [Google Scholar]
- Wright, T.J.; Parsons, B.E.; Lu, Z. Toward mapping surface deformation in three dimensions using InSAR. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Saraswat, A.; Tsai, Y.L.S.; Chen, F.C.; Han, J.Y. 3d Deformation Analysis in a Metropolitan Area During Ongoing Subway Construction Using Time Series Insar. Preprint. 2024. Available online: https://ssrn.com/abstract=4726193 (accessed on 21 April 2024).
- Jo, M.J.; Jung, H.S.; Won, J.S.; Poland, M.P.; Miklius, A.; Lu, Z. Measurement of slow-moving along-track displacement from an efficient multiple-aperture SAR interferometry (MAI) stacking. J. Geod. 2015, 89, 411–425. [Google Scholar] [CrossRef]
- Jung, H.S.; Won, J.S.; Kim, S.W. An Improvement of the Performance of Multiple-Aperture SAR Interferometry (MAI). IEEE Trans. Geosci. Remote Sens. 2009, 47, 2859–2869. [Google Scholar] [CrossRef]
- Fialko, Y.; Sandwell, D.; Simons, M.; Rosen, P. Three-dimensional deformation caused by the Bam, Iran, earthquake and the origin of shallow slip deficit. Nature 2005, 435, 295–299. [Google Scholar] [CrossRef] [PubMed]
- Fialko, Y.; Simons, M.; Agnew, D. The complete (3-D) surface displacement field in the epicentral area of the 1999 MW7.1 Hector Mine Earthquake, California, from space geodetic observations. Geophys. Res. Lett. 2001, 28, 3063–3066. [Google Scholar] [CrossRef]
- Samsonov, S.; Tiampo, K.F.; Gonzalez, P.; Prieto, J.F.; Camacho, A.G.; Fernández, J. Surface deformation studies of Tenerife Island, Spain from joint GPS-DInSAR observations. In Proceedings of the 2008 Second Workshop on Use of Remote Sensing Techniques for Monitoring Volcanoes and Seismogenic Areas, Napoli, Italy, 11–14 November 2008; pp. 1–6. [Google Scholar]
- Chen, M.; Xu, G.; Zhang, T.; Xie, X.; Chen, Z. A novel method for inverting coseismic 3D surface deformation using InSAR considering the weight influence of the spatial distribution of GNSS points. Adv. Space Res. 2024, 73, 585–596. [Google Scholar] [CrossRef]
- Joughin, I.; Kwok, R.; Fahnestock, M. Interferometric estimation of three-dimensional ice-flow using ascending and descending passes. IEEE Trans. Geosci. Remote Sens. 1998, 36, 25–37. [Google Scholar] [CrossRef]
- Samsonov, S. Three-dimensional deformation time series of glacier motion from multiple-aperture DInSAR observation. J. Geod. 2019, 93, 2651–2660. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Yi, H.; Hu, J.; Feng, G. Deriving Dynamic Subsidence of Coal Mining Areas Using InSAR and Logistic Model. Remote Sens. 2017, 9, 125. [Google Scholar] [CrossRef]
- Casu, F.; Manconi, A.; Pepe, A.; Lanari, R. Deformation Time-Series Generation in Areas Characterized by Large Displacement Dynamics: The SAR Amplitude Pixel-Offset SBAS Technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2752–2763. [Google Scholar] [CrossRef]
- Samsonov, S.; d’Oreye, N. Multidimensional time-series analysis of ground deformation from multiple InSAR data sets applied to Virunga Volcanic Province. Geophys. J. Int. 2012, 191, 1095–1108. [Google Scholar] [CrossRef]
- Pepe, A.; Solaro, G.; Dema, C. A Minimum Curvature Combination Method for the Generation of Multi-Platform DInSAR Deformation Time-Series. In Proceedings of the FRINGE 2015: Advances in the Science and Applications of SAR Interferometry and Sentinel-1 InSAR Workshop, Frascati, Italy, 23–27 March 2015; Ouwehand, L., Ed.; ESA: Frascati, Italy, 2015; Volume 731, p. 9. [Google Scholar]
- Samsonov, S.V.; Blais-Stevens, A. Estimating volume of large slow-moving deep-seated landslides in northern Canada from DInSAR-derived 2D and constrained 3D deformation rates. Remote Sens. Environ. 2024, 305, 114049. [Google Scholar] [CrossRef]
- Tao, Q.; Zheng, Z.; Zhai, M.; Zhang, S.; Hu, L.; Liu, T. Sensitivity and reliability analysis to MSBAS regularization for the estimation of surface deformation over a mine. Geocarto Int. 2024, 39, 2329669. [Google Scholar] [CrossRef]
- Tang, W.; Gong, Z.; Sun, X.; Liu, Y.; Motagh, M.; Li, Z.; Li, J.; Malinowska, A.; Jiang, J.; Wei, L.; et al. Three-dimensional surface deformation from multi-track InSAR and oil reservoir characterization: A case study in the Liaohe Oilfield, northeast China. Int. J. Rock Mech. Min. Sci. 2024, 174, 105637. [Google Scholar] [CrossRef]
- Kamel, A.; El Sokkary, A. Geologic hazards assessment of Cairo and vicinity. Nat. Hazards 1996, 13, 253–274. [Google Scholar] [CrossRef]
- Cuvillier, J. Revision du Nummulitique Egyptein; MWRI Central Library: Cairo, Egypt, 1930. [Google Scholar]
- Cuvillier, J. A conglomerate in the nummulitic formation of Gebel Moqattam, near Cairo. Geol. Mag. 1927, 64, 522–523. [Google Scholar] [CrossRef]
- Liang, H.; Li, X.; Zhang, L.; Chen, R.F.; Ding, X.; Chen, K.L.; Wang, C.S.; Chang, C.S.; Chi, C.Y. Investigation of Slow-Moving Artificial Slope Failure with Multi-Temporal InSAR by Combining Persistent and Distributed Scatterers: A Case Study in Northern Taiwan. Remote Sens. 2020, 12, 2403. [Google Scholar] [CrossRef]
- Hansen, P.C. The truncatedSVD as a method for regularization. BIT Numer. Math. 1987, 27, 534–553. [Google Scholar] [CrossRef]
- Goldstein, R.; Werner, C. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Chen, C.; Zebker, H. Phase unwrapping for large SAR interferograms: Statistical segmentation and generalized network models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef]
- von Zittel, K.A. Beitraege zur Geologie und Palaeontologie der libyschen Wüste und der Angrenzenden Gebiete von Aegypten I Theil; Fischer, T., Ed.; Hansebooks: Norderstedt, Germany, 1883. [Google Scholar]
- El Shazly, E.; Hady, M.A.; Salman, A.; El Rakaiby, M.; Morsy, M.; El Aassy, I.; El Shazly, M. Geological Investigations on Gebel El Mokattam Area; Remote Sensing Center: Cairo, Egypt, 1976; Volume 23. [Google Scholar]
- Moustafa, A.; El-Nahhas, F.; Tawab, S.A. Engineering geology of Mokattam city and vicinity, eastern Greater Cairo, Egypt. Eng. Geol. 1991, 31, 327–344. [Google Scholar] [CrossRef]
- Poscolieri, M.; Parcharidis, I.; Foumelis, M.; Rafanelli, C. Ground Deformation Monitoring in the Greater Cairo Metropolitan Region (Egypt) by SAR Interferometry. Environ. Semeiot. 2011, 4, 17–45. [Google Scholar] [CrossRef]
- Aly, M.H.; Zebker, H.A.; Giardino, J.R.; Klein, A.G. Permanent Scatterer investigation of land subsidence in Greater Cairo, Egypt. Geophys. J. Int. 2009, 178, 1238–1245. [Google Scholar] [CrossRef]



| Satellite | ENVISAT | ERS | Sentinel-1 | |||
|---|---|---|---|---|---|---|
| Orbit | Ascending | Descending | Ascending | Descending | Ascending | Descending |
| Period | 21 March 2008–16 March 2009 | 13 May 2004–06 March 2012 | 09 February 2009–27 September 2010 | 20 January 2000–17 February 2005 | 9 October 2014–15 July 2020 | 30 September 2016–29 June 2020 |
| No. of images | 3 | 22 | 4 | 23 | 21 | 17 |
| Satellite | ERS | ENVISAT | Sentinel-1 |
|---|---|---|---|
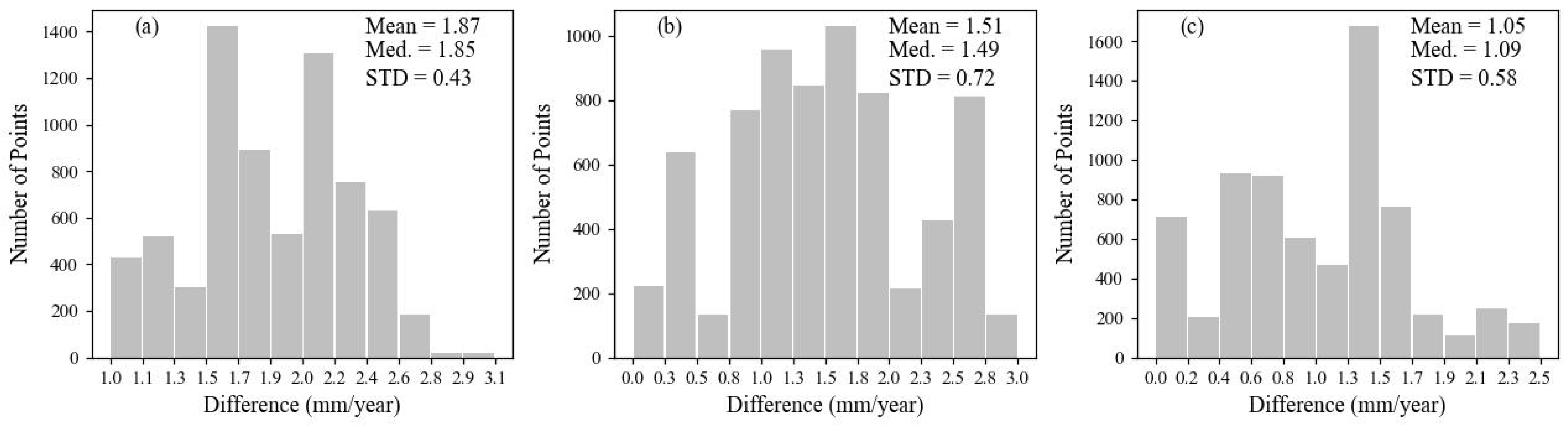
| Min. Difference | 0.97 | 0.002 | 0.0003 |
| Max. Difference | 3.11 | 3.02 | 2.5 |
| Mean. Difference | 1.87 | 1.5 | 1.04 |
| 1.92 | 1.66 | 1.19 | |
| STD | 0.42 | 0.72 | 0.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amr, D.; Ding, X.-L.; Fekry, R. A Multi-Satellite SBAS for Retrieving Long-Term Ground Displacement Time Series. Remote Sens. 2024, 16, 1520. https://doi.org/10.3390/rs16091520
Amr D, Ding X-L, Fekry R. A Multi-Satellite SBAS for Retrieving Long-Term Ground Displacement Time Series. Remote Sensing. 2024; 16(9):1520. https://doi.org/10.3390/rs16091520
Chicago/Turabian StyleAmr, Doha, Xiao-Li Ding, and Reda Fekry. 2024. "A Multi-Satellite SBAS for Retrieving Long-Term Ground Displacement Time Series" Remote Sensing 16, no. 9: 1520. https://doi.org/10.3390/rs16091520
APA StyleAmr, D., Ding, X.-L., & Fekry, R. (2024). A Multi-Satellite SBAS for Retrieving Long-Term Ground Displacement Time Series. Remote Sensing, 16(9), 1520. https://doi.org/10.3390/rs16091520






