Fluctuations in Refracted Star Signals Caused by the Stratospheric Internal Gravity Waves
Abstract
1. Introduction
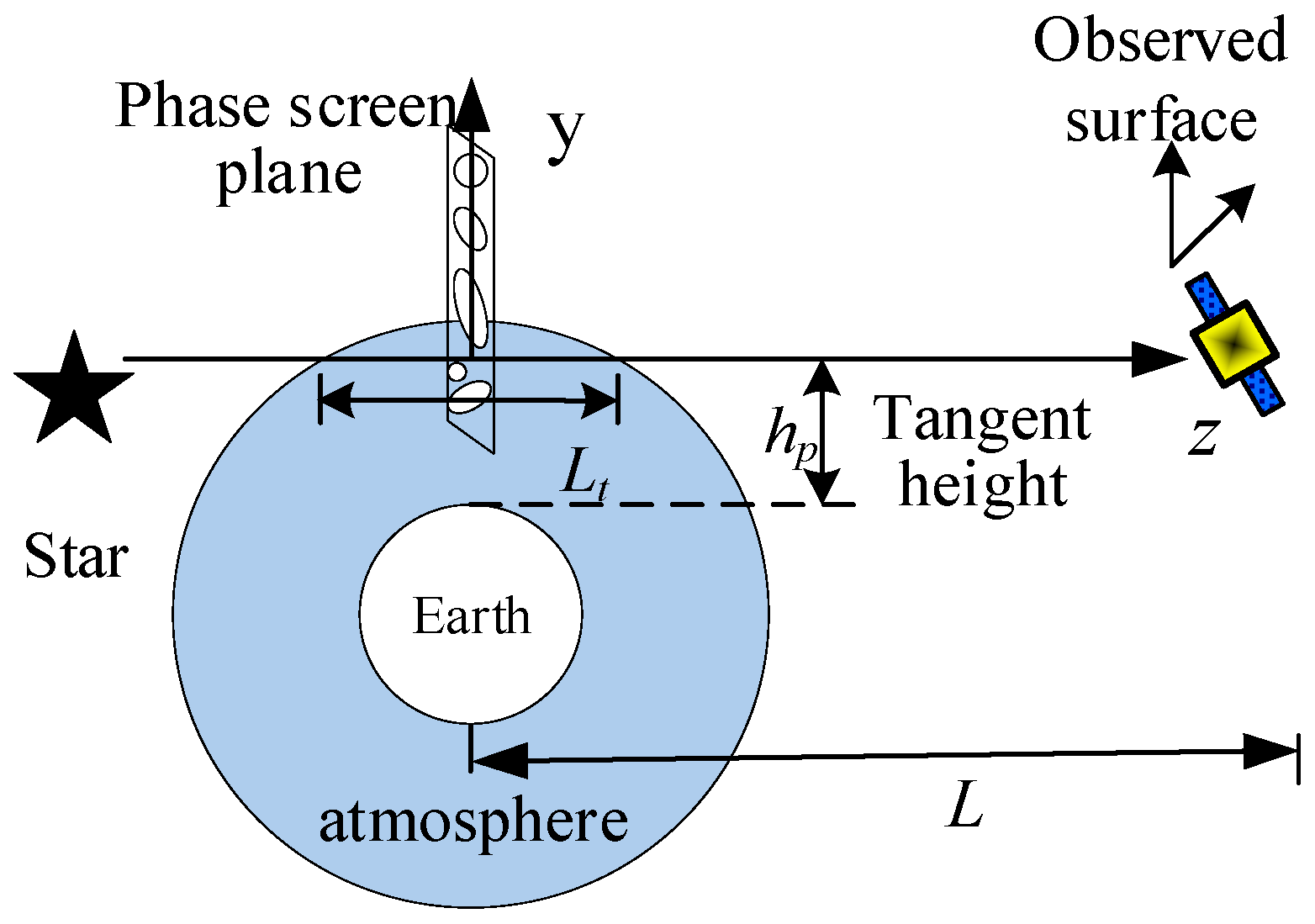
2. Spectral Model of Refractivity Fluctuation
3. Relative Intensity and Refraction Angle Fluctuations
3.1. Relative Intensity Fluctuations
3.2. Refraction Angle Fluctuations
4. Experimental Results and Analysis
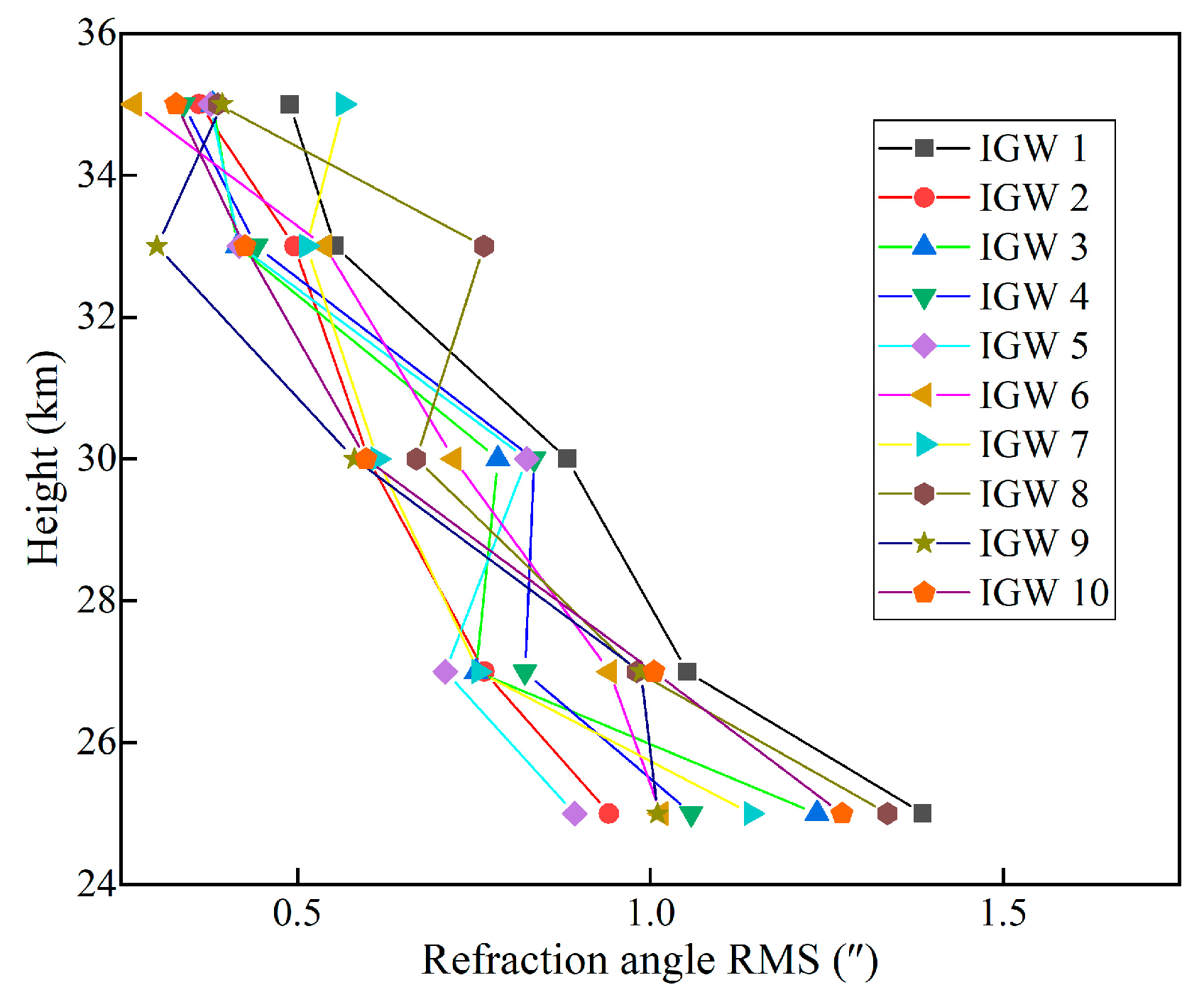
4.1. Experimental Dataset
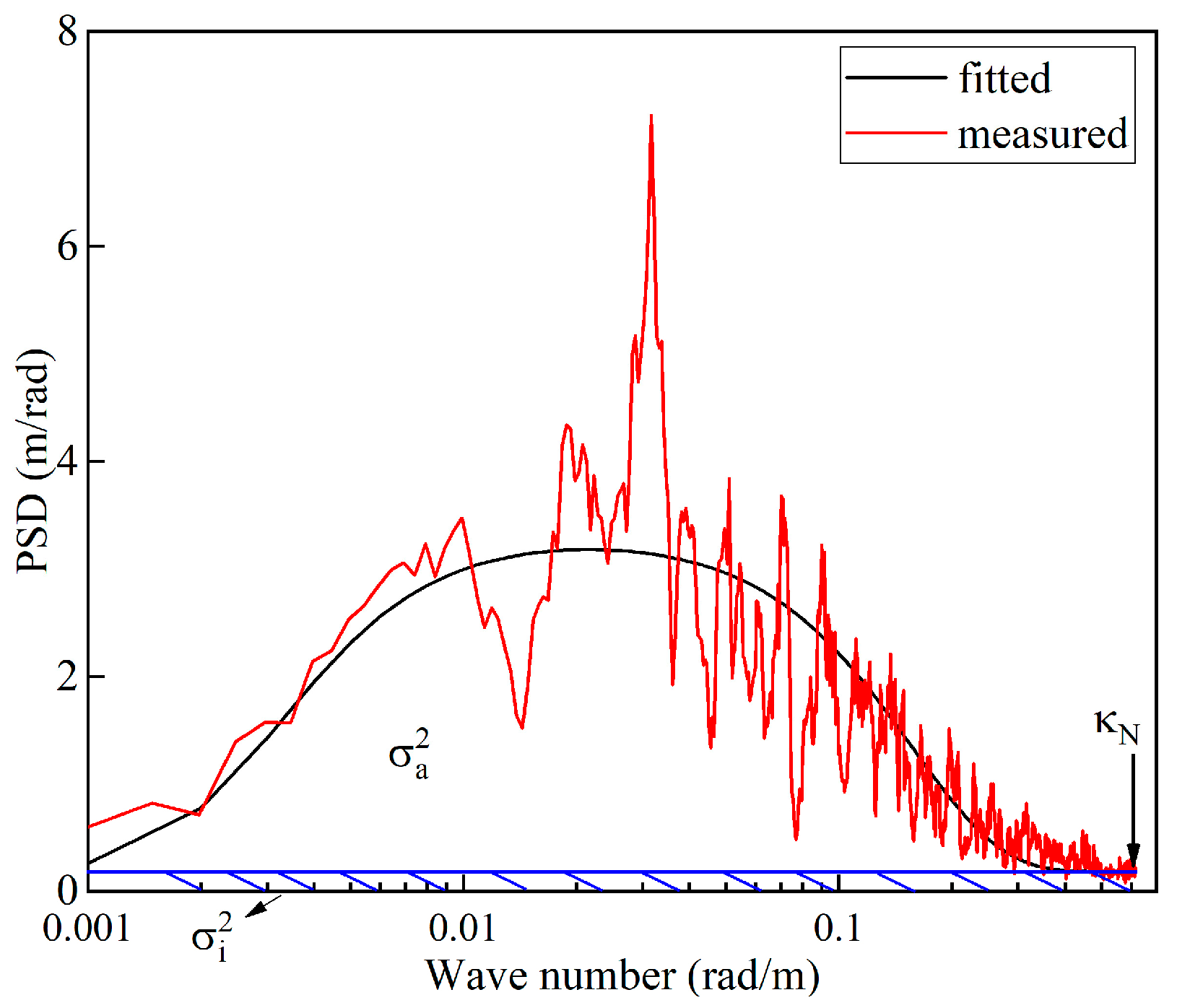
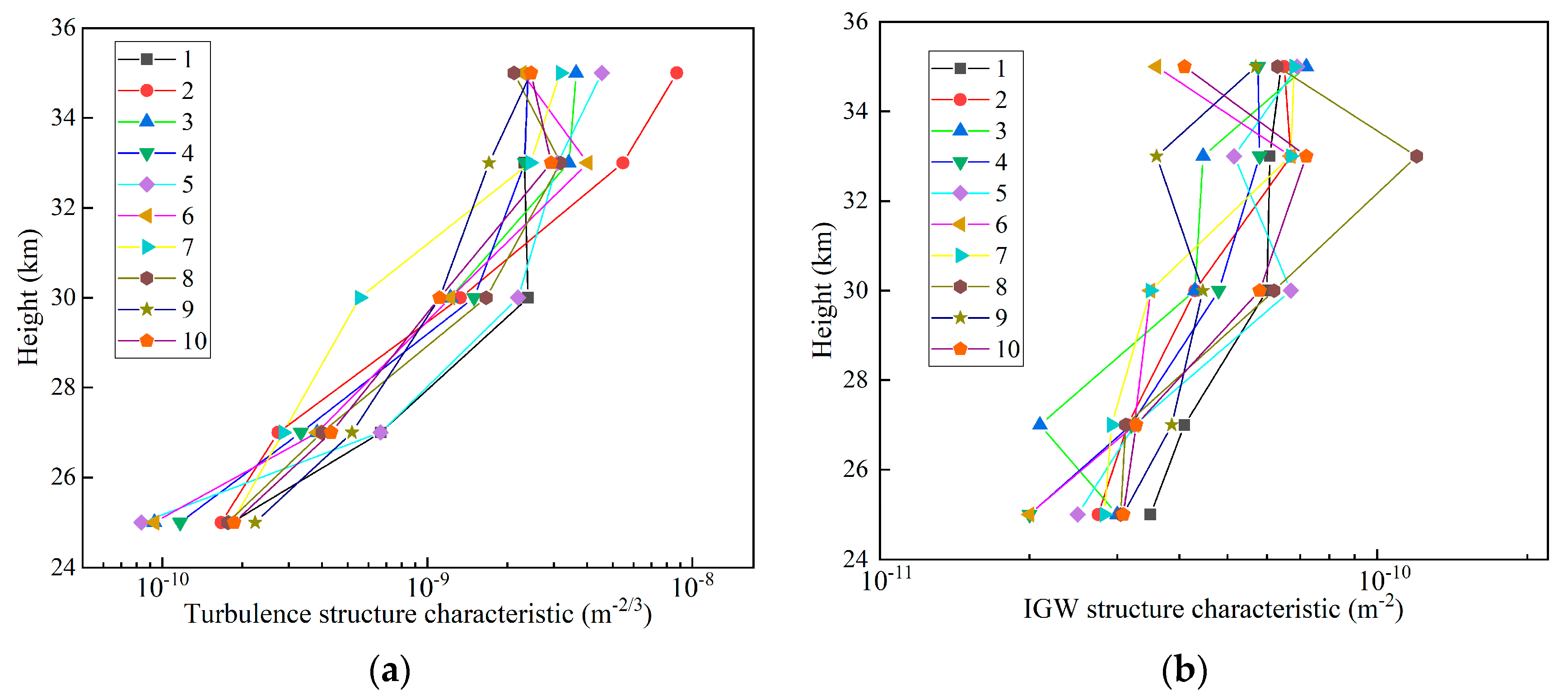
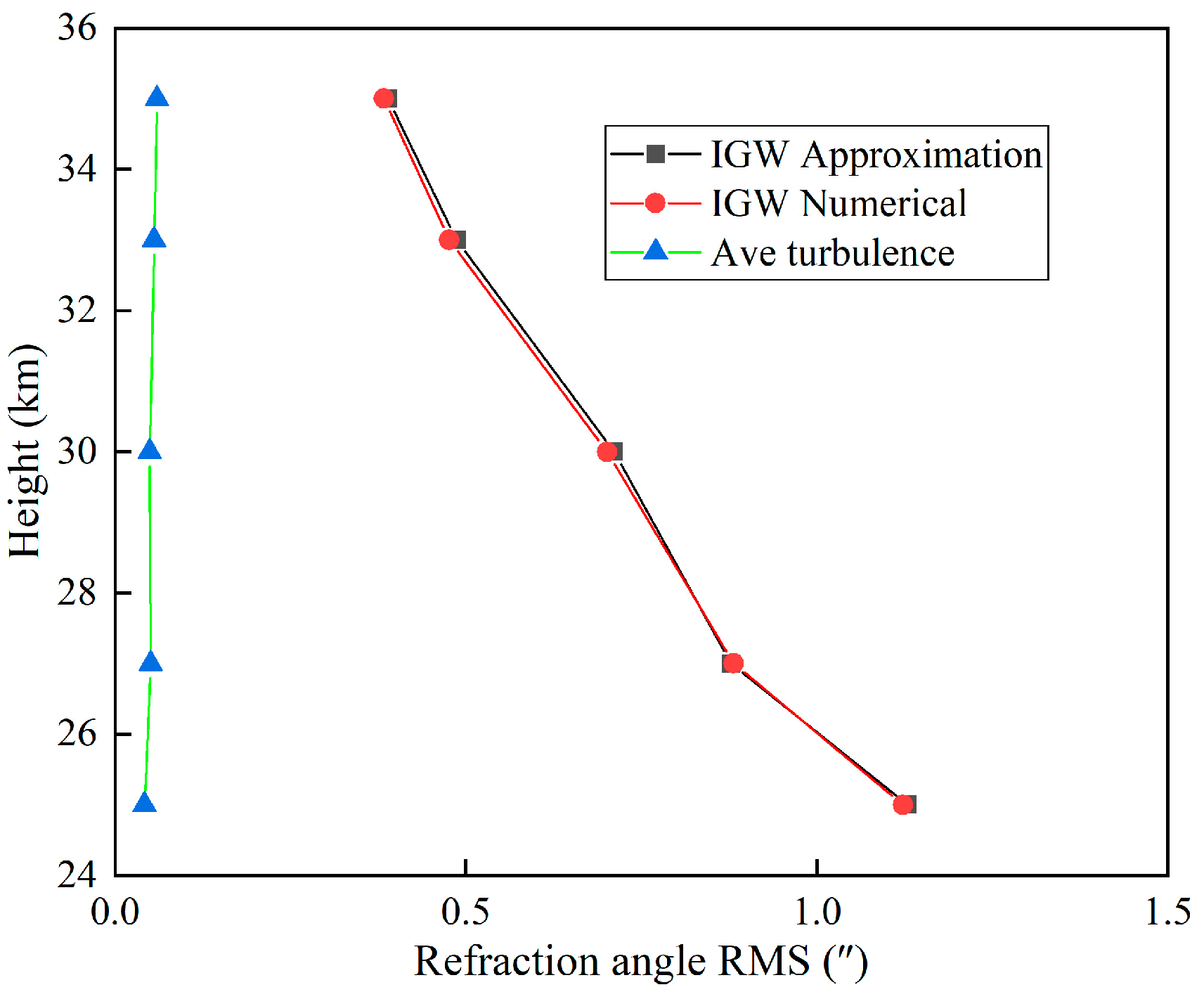
4.2. Results and Analysis
4.2.1. Relative Intensity Fluctuations
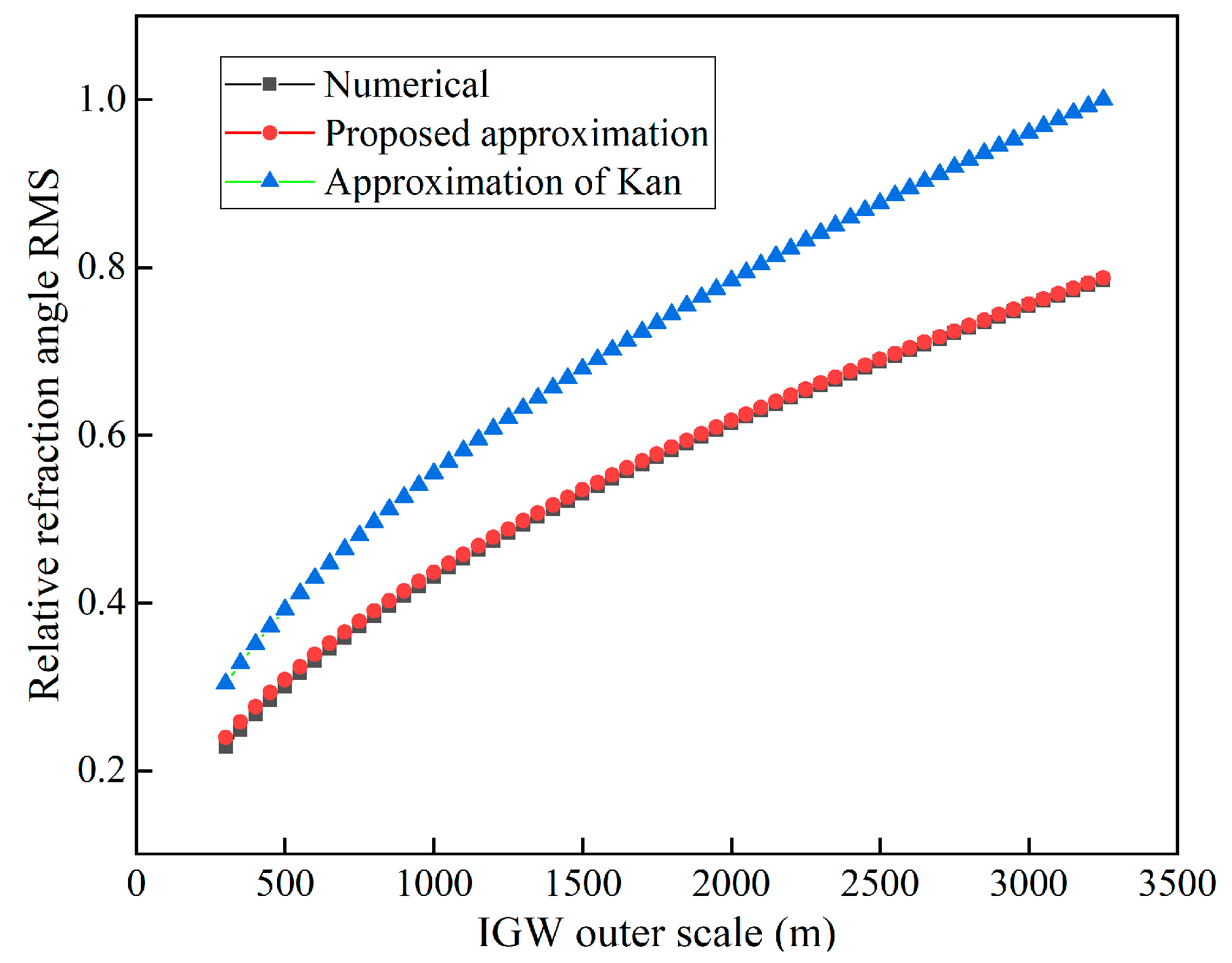
4.2.2. Refraction Angle Fluctuations
4.2.3. Other Parameter Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Wu, S.; Wang, B.; Yan, Z.; Yao, S.; Zeliu, C. Near-infrared Star Map Simulation for Starlight Refraction Sensor based on Ray Tracing. Infrared Phys. Technol. 2023, 132, 104760. [Google Scholar] [CrossRef]
- White, R.L.; Thurman, S.W.; Barnes, F.A. Autonomous Satellite Navigation Using Observations of Starlight Atmospheric Refraction. Navigation 1985, 32, 317–333. [Google Scholar] [CrossRef]
- Fan, S.; Yan, Z.; Lin, Y. Adaptively tuning sampling weights of the unscented Kalman filter in starlight refraction navigation. Optik 2017, 148, 300–311. [Google Scholar]
- Bi, C.; Qing, C.; Wu, P.; Jin, X.; Liu, Q.; Qian, X.; Weng, N. Optical turbulence profile in marine environment with artificial neural network model. Remote Sens. 2022, 14, 2267. [Google Scholar] [CrossRef]
- Grechko, G.M.; Gurvich, A.S.; Kan, V.; Kireev, S.V.; Savchenko, S.A. Anisotropy of spatial structures in the middle atmosphere. Adv. Space Res. 1992, 12, 169–175. [Google Scholar] [CrossRef]
- Cheng, X.; Yang, J.; Xiao, C.; Hu, X. Density Correction of NRLMSISE-00 in the Middle Atmosphere (20–100 km) based on TIMED/SABER Density Data. Atmosphere 2020, 11, 341. [Google Scholar] [CrossRef]
- Gorbunov, M.; Kan, V. The Study of Internal Gravity Waves in the Earth’s Atmosphere by Radio Occultations: A Review. Remote Sens. 2024, 16, 221. [Google Scholar] [CrossRef]
- Sofieva, V.F.; Gurvich, A.S.; Dalaudier, F.; Kan, V. Reconstruction of internal gravity wave and turbulence parameters in the stratosphere using GOMOS scintillation measurements. J. Geophys. Res. Atmos. 2007, 112, 1–14. [Google Scholar] [CrossRef]
- Robert, C.; Conan, J.M.; Michau, V.; Renard, J.B.; Robert, C.; Dalaudier, F. Retrieving parameters of the anisotropic refractive index fluctuations spectrum in the stratosphere from balloon-borne observations of stellar scintillation. J. Opt. Soc. Am. A 2008, 25, 379–393. [Google Scholar] [CrossRef] [PubMed]
- Gurvich, A.S.; Belen’kii, M.S. Influence of stratospheric turbulence on infrared imaging. J. Opt. Soc. Am. A 1995, 12, 2517–2522. [Google Scholar] [CrossRef]
- Du Wenhe, Z.Z.; Daosen, L.; Chengjiang, C.; Rui, L.; Guangyu, Z.; Yuqiang, Y. Effect of non-Kolmogorov turbulence on fluctuations in angle of arrival of starlight. Infrared Laser Eng. 2013, 42, 2779–2783. [Google Scholar]
- Gorbunov, M.E.; Kirchengast, G. Influence of anisotropic turbulence on X/K band radio occultation signals and related transmission retrieval quality. In Prodex-CN1 Task 2.2 Report to ESA/ESTEC-Draft Version; University of Graz: Graz, Austria, 2007. [Google Scholar]
- Yang, B.; Zhu, X.Y. Influence of Atmospheric Turbulence on Starlight Transmission during Satellite Celestial Navigation in Stratosphere. Yuhang Xuebao J. Astronaut. 2017, 38, 359–366. [Google Scholar]
- Kan, V.; Gorbunov, M.E.; Sofieva, V.F. Fluctuations of radio occultation signals in sounding the Earth’s atmosphere. Atmos. Meas. Tech. 2018, 11, 663–680. [Google Scholar] [CrossRef]
- Wu, S.; Wang, H.; Wang, B. Construction of a backpropagation starlight atmospheric refraction model based on ray tracing. Appl. Opt. 2023, 62, 3778–3787. [Google Scholar] [CrossRef] [PubMed]
- Salpeter, E.E. Interplanetary scintillations. I. Theory. Astrophys. J. 1967, 147, 433. [Google Scholar] [CrossRef]
- Gurvich, A.S.; Brekhovskikh, V.L. Study of the turbulence and inner waves in the stratosphere based on the observations of stellar scintillations from space: A model of scintillation spectra. Waves Random Media 2001, 11, 163–181. [Google Scholar] [CrossRef]
- Bertaux, J.L.; Kyrölä, E.; Fussen, D.; Hauchecorne, A.; Dalaudier, F.; Sofieva, V.; Tamminen, J.; Vanhellemont, F.; Fanton d’Andon, O.; Barrot, G.; et al. Global ozone monitoring by occultation of stars: An overview of GOMOS measurements on ENVISAT. Atmos. Chem. Phys. 2010, 10, 12091–12148. [Google Scholar] [CrossRef]
- Wu, S.; Wang, H.; Yan, Z. Optical system design method of the all-day starlight refraction navigation system. J. Eur. Opt. Soc.-Rapid Publ. 2023, 19, 43. [Google Scholar] [CrossRef]
- Gurvich, A.S.; Kan, V. Structure of air density irregularities in the stratosphere from spacecraft observations of stellar scintillation: 2. Characteristic scales, structure characteristics, and kinetic energy dissipation. Izv. Atmos. Ocean. Phys. 2003, 39, 311–321. [Google Scholar]
- Gounley, R.; White, R.L.; Gai, E. Autonomous satellite navigation by stellar refraction. J. Guid. Control. Dyn. 1984, 7, 129–134. [Google Scholar] [CrossRef]





| Num | Orbit | Star | α, ° | Tangent Point | Time | Vs, km/s |
|---|---|---|---|---|---|---|
| 1 | 2908 | 9Alp CMa | 67.1 | 35°S, 105°W | 20 September | 4.3 |
| 2 | 2911 | 9Alp CMa | 67.4 | 35°S, 179°E | 20 September | 4.3 |
| 3 | 2914 | 9Alp CMa | 67.4 | 33°S, 104°E | 20 September | 4.3 |
| 4 | 2915 | 9Alp CMa | 67.4 | 33°S, 179°E | 20 September | 4.3 |
| 5 | 2926 | 9Alp CMa | 68.0 | 32°S, 162°E | 21 September | 4.4 |
| 6 | 2928 | 9Alp CMa | 68.1 | 32°S, 111°E | 21 September | 4.3 |
| 7 | 3059 | Alp Eri | 28.4 | 26°N, 50°E | 30 September | 2.7 |
| 8 | 3060 | Alp Eri | 28.3 | 26°N, 26°E | 30 September | 2.7 |
| 9 | 3067 | Alp Eri | 28.1 | 26°N, 150°W | 1 October | 2.6 |
| 10 | 3077 | Alp Eri | 27.4 | 26°N, 42°W | 1 October | 2.6 |
| Proposed Approximation | Approximation of Kan | |
|---|---|---|
| Intensity fluctuation | 7.3% | 50.4% |
| Refraction angle fluctuation | 1.0% | 30.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Wang, H.; Zheng, X.; Yan, Z. Fluctuations in Refracted Star Signals Caused by the Stratospheric Internal Gravity Waves. Remote Sens. 2024, 16, 1519. https://doi.org/10.3390/rs16091519
Wu S, Wang H, Zheng X, Yan Z. Fluctuations in Refracted Star Signals Caused by the Stratospheric Internal Gravity Waves. Remote Sensing. 2024; 16(9):1519. https://doi.org/10.3390/rs16091519
Chicago/Turabian StyleWu, Shaochong, Hongyuan Wang, Xunjiang Zheng, and Zhiqiang Yan. 2024. "Fluctuations in Refracted Star Signals Caused by the Stratospheric Internal Gravity Waves" Remote Sensing 16, no. 9: 1519. https://doi.org/10.3390/rs16091519
APA StyleWu, S., Wang, H., Zheng, X., & Yan, Z. (2024). Fluctuations in Refracted Star Signals Caused by the Stratospheric Internal Gravity Waves. Remote Sensing, 16(9), 1519. https://doi.org/10.3390/rs16091519






