Speckle Noise Reduction via Linewidth Broadening for Planetary Laser Reflectance Spectrometers
Abstract
1. Introduction
2. Materials and Methods
2.1. Laser and Illumination Sources
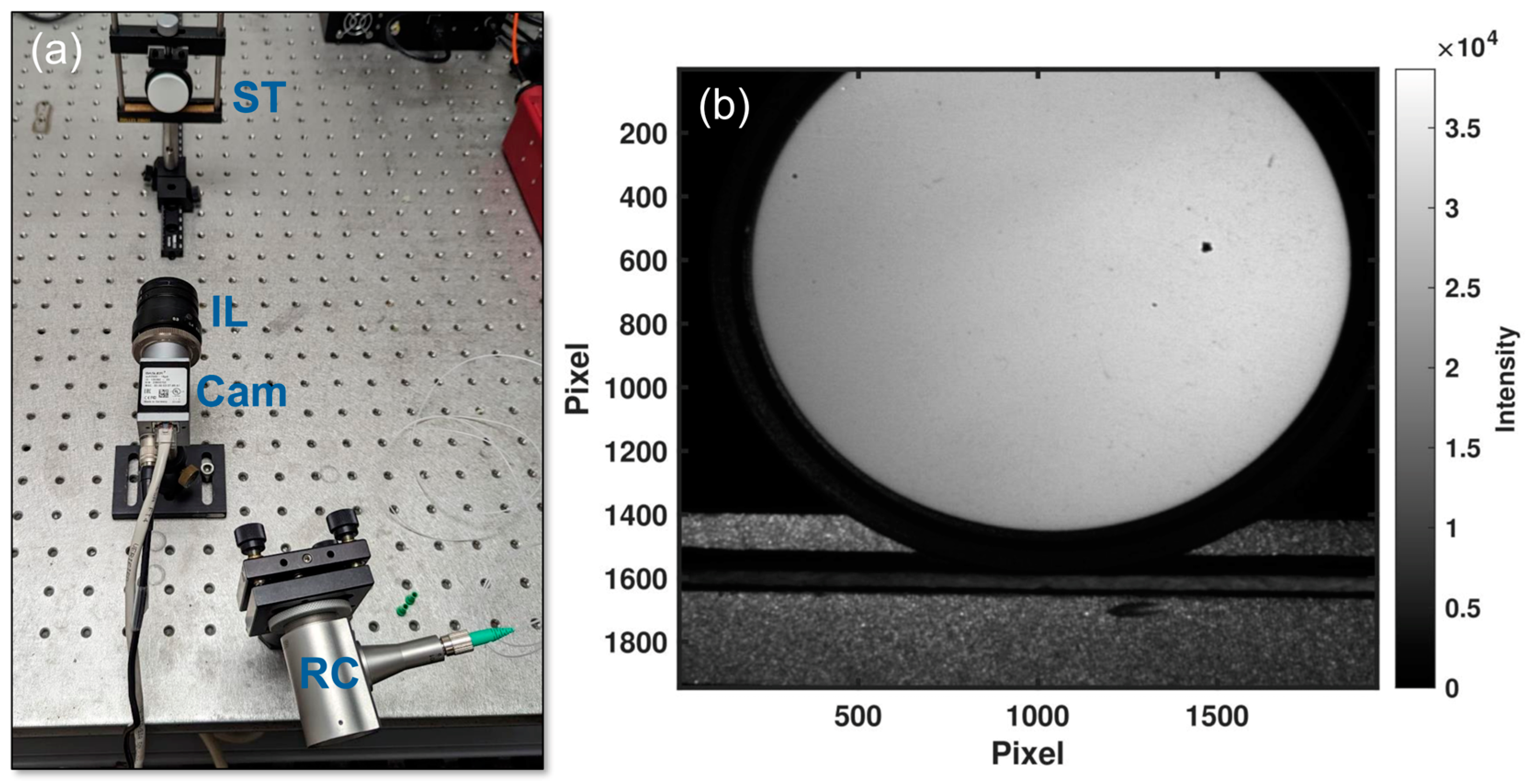
2.2. Speckle Imaging Tests
2.3. Speckle Pattern Simulations
3. Results
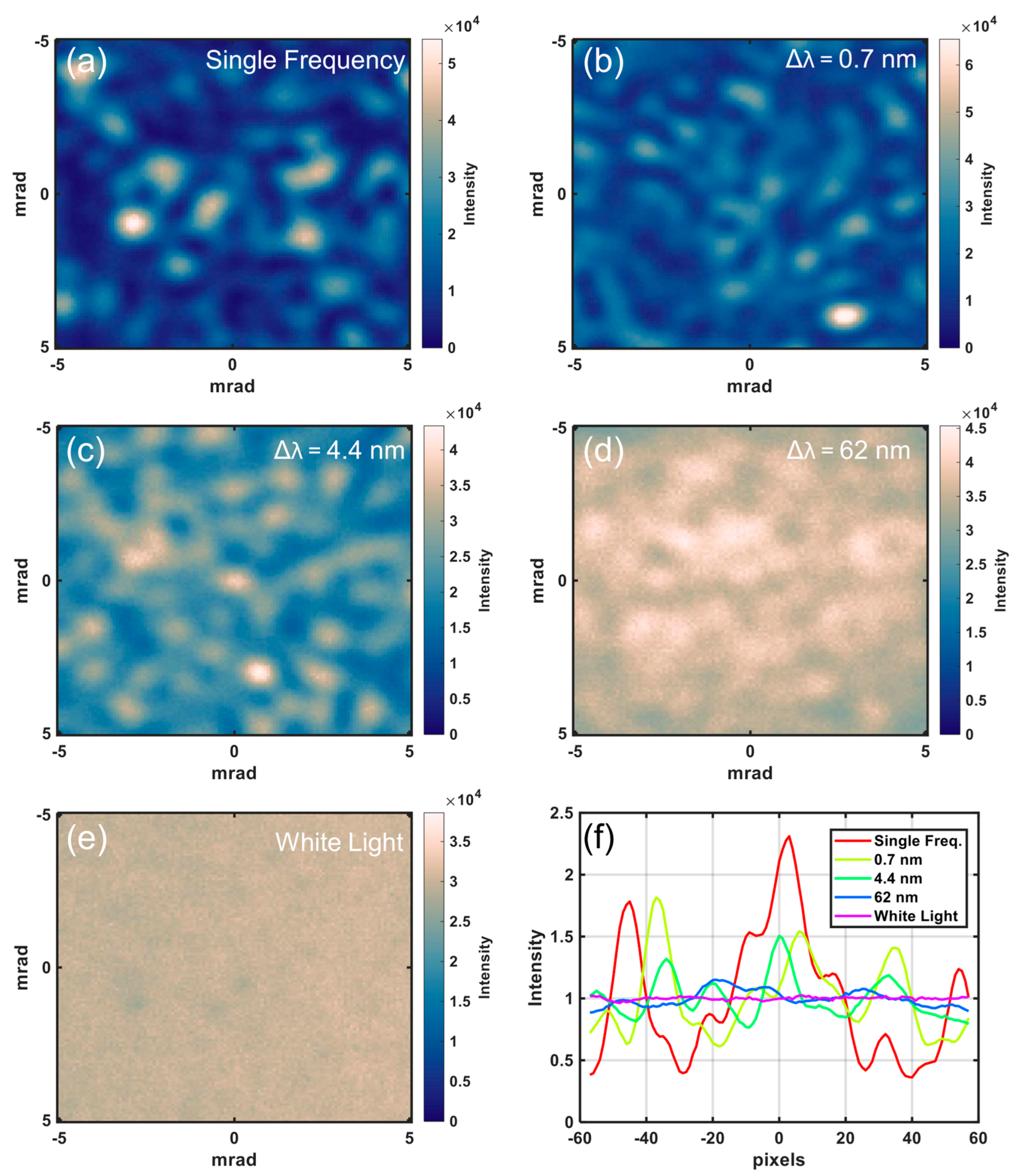
3.1. Experimental and Simulated Speckle Patterns
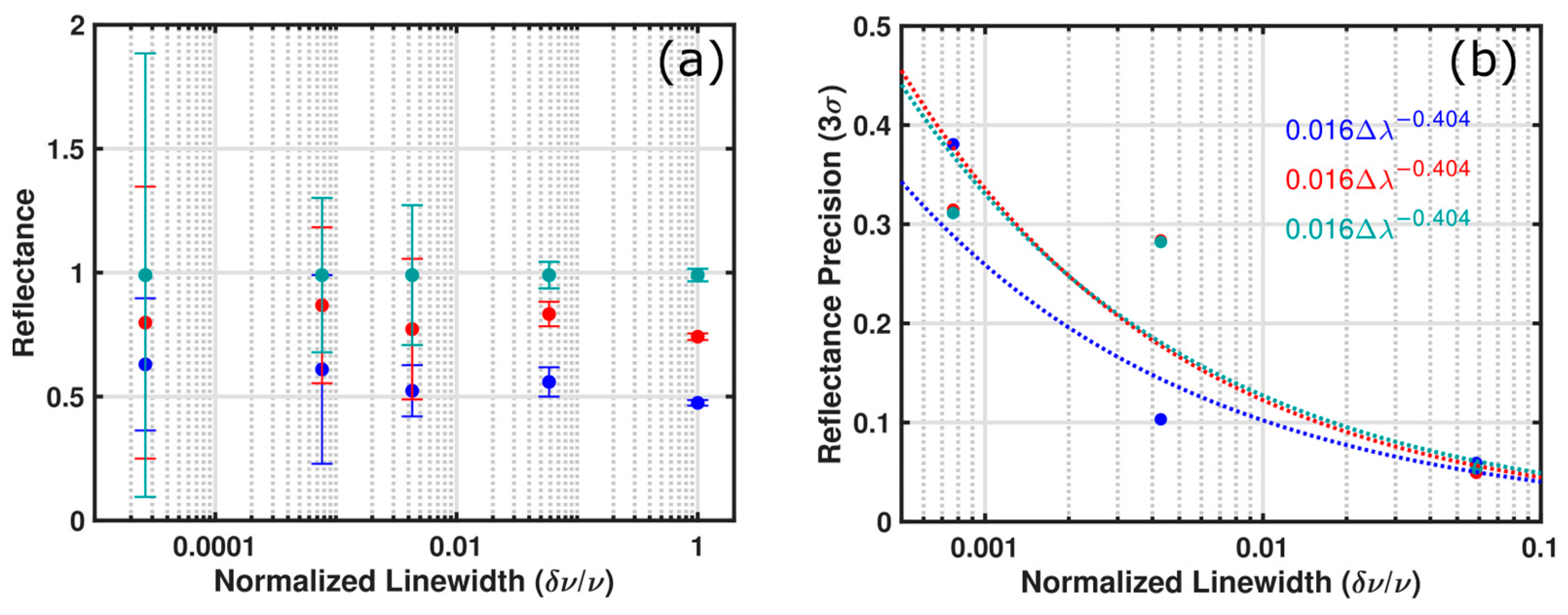
3.2. Regions of Interest and Speckle Contrast
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adams, J.B. Lunar and Martian Surfaces: Petrologic Significance of Absorption Bands in the Near-Infrared. Science 1968, 159, 1453–1455. [Google Scholar] [CrossRef] [PubMed]
- McCord, T.B. Color Differences on the Lunar Surface. J. Geophys. Res. 1969, 74, 3131–3142. [Google Scholar] [CrossRef]
- Nozette, S.; Rustan, P.; Pleasance, L.P.; Kordas, J.F.; Lewis, I.T.; Park, H.S.; Priest, R.E.; Horan, D.M.; Regeon, P.; Lichtenberg, C.L.; et al. The Clementine Mission to the Moon: Scientific Overview. Science 1994, 266, 1835–1839. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.; Craig, D.; Herrmann, N.; Mahoney, E.; Krezel, J.; McIntyre, N.; Goodliff, K. The Artemis Program: An Overview of NASA’s Activities to Return Humans to the Moon. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–10. [Google Scholar]
- Kleinhenz, J.E.; Paz, A. Case Studies for Lunar ISRU Systems Utilizing Polar Water. In Proceedings of the ASCEND 2020: American Institute of Aeronautics and Astronautics, Virtual, 16 November 2020. [Google Scholar]
- Fisher, E.A.; Lucey, P.G.; Lemelin, M.; Greenhagen, B.T.; Siegler, M.A.; Mazarico, E.; Aharonson, O.; Williams, J.-P.; Hayne, P.O.; Neumann, G.A.; et al. Evidence for Surface Water Ice in the Lunar Polar Regions Using Reflectance Measurements from the Lunar Orbiter Laser Altimeter and Temperature Measurements from the Diviner Lunar Radiometer Experiment. Icarus 2017, 292, 74–85. [Google Scholar] [CrossRef] [PubMed]
- Brown, H.M.; Boyd, A.K.; Denevi, B.W.; Henriksen, M.R.; Manheim, M.R.; Robinson, M.S.; Speyerer, E.J.; Wagner, R.V. Resource Potential of Lunar Permanently Shadowed Regions. Icarus 2022, 377, 114874. [Google Scholar] [CrossRef]
- Spudis, P.D. The Value of the Moon: How to Explore, Live, and Prosper in Space Using the Moon’s Resources; Smithsonian Books: Washington, DC, USA, 2016; ISBN 978-1-58834-503-5. [Google Scholar]
- Lucey, P.G.; Petro, N.; Hurley, D.M.; Farrell, W.M.; Prem, P.; Costello, E.S.; Cable, M.L.; Barker, M.K.; Benna, M.; Dyar, M.D.; et al. Volatile Interactions with the Lunar Surface. Geochemistry 2021, 82, 125858. [Google Scholar] [CrossRef]
- Potter, R.W.K.; Collins, G.S.; Kiefer, W.S.; McGovern, P.J.; Kring, D.A. Constraining the Size of the South Pole-Aitken Basin Impact. Icarus 2012, 220, 730–743. [Google Scholar] [CrossRef]
- Moriarty, D.P.; Pieters, C.M. The Character of South Pole-Aitken Basin: Patterns of Surface and Subsurface Composition. J. Geophys. Res. Planets 2018, 123, 729–747. [Google Scholar] [CrossRef]
- Speyerer, E.J.; Robinson, M.S. Persistently Illuminated Regions at the Lunar Poles: Ideal Sites for Future Exploration. Icarus 2013, 222, 122–136. [Google Scholar] [CrossRef]
- Bussey, D.B.J.; McGovern, J.A.; Spudis, P.D.; Neish, C.D.; Noda, H.; Ishihara, Y.; Sørensen, S.-A. Illumination Conditions of the South Pole of the Moon Derived Using Kaguya Topography. Icarus 2010, 208, 558–564. [Google Scholar] [CrossRef]
- Mazarico, E.; Barker, M.K.; Jagge, A.M.; Britton, A.W.; Lawrence, S.J.; Bleacher, J.E.; Petro, N.E. Sunlit Pathways between South Pole Sites of Interest for Lunar Exploration. Acta Astronaut. 2023, 204, 49–57. [Google Scholar] [CrossRef]
- Lucey, P.G.; Hayne, P.O.; Costello, E.; Green, R.; Hibbitts, C.; Goldberg, A.; Mazarico, E.; Li, S.; Honniball, C. The Spectral Radiance of Indirectly Illuminated Surfaces in Regions of Permanent Shadow on the Moon. Acta Astronaut. 2021, 180, 25–34. [Google Scholar] [CrossRef]
- Cloutis, E.A.; Caudill, C.; Lalla, E.A.; Newman, J.; Daly, M.; Lymer, E.; Freemantle, J.; Kruzelecky, R.; Applin, D.; Chen, H.; et al. LunaR: Overview of a Versatile Raman Spectrometer for Lunar Exploration. Front. Astron. Space Sci. 2022, 9, 1016359. [Google Scholar] [CrossRef]
- Wang, A.; Jolliff, B.L.; Haskin, L.A. Raman Spectroscopy as a Method for Mineral Identification on Lunar Robotic Exploration Missions. J. Geophys. Res. 1995, 100, 21189–21199. [Google Scholar] [CrossRef]
- Lucey, P.; Petro, N.; Hurley, D.; Farrell, W.; Sun, X.; Green, R.; Greenberger, R.; Cameron, D. The Lunar Volatiles Orbiter: A Lunar Discovery Mission Concept. In Proceedings of the 2017 Annual Meeting of the Lunar Exploration Analysis Group, Columbia, MD, USA, 9–11 October 2017; Volume 2041, p. 5048. [Google Scholar]
- Cohen, B.A.; Hayne, P.O.; Greenhagen, B.; Paige, D.A.; Seybold, C.; Baker, J. Lunar Flashlight: Illuminating the Lunar South Pole. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 46–52. [Google Scholar] [CrossRef]
- Cohen, B.A.; Petersburg, R.R.; Cremons, D.R.; Russell, P.S.; Hayne, P.O.; Greenhagen, B.T.; Paige, D.A.; Camacho, J.M.; Cheek, N.; Sullivan, M.T.; et al. Lunar Flashlight Science Ground and Flight Measurements and Operations Using a Multi-Band Laser Reflectometer. Icarus 2024, 413, 116013. [Google Scholar] [CrossRef]
- Lucey, P.G.; Neumann, G.A.; Riner, M.A.; Mazarico, E.; Smith, D.E.; Zuber, M.T.; Paige, D.A.; Bussey, D.B.; Cahill, J.T.; McGovern, A.; et al. The Global Albedo of the Moon at 1064 Nm from LOLA. J. Geophys. Res. Planets 2014, 119, 1665–1679. [Google Scholar] [CrossRef]
- Hayne, P.O.; Hendrix, A.; Sefton-Nash, E.; Siegler, M.A.; Lucey, P.G.; Retherford, K.D.; Williams, J.-P.; Greenhagen, B.T.; Paige, D.A. Evidence for Exposed Water Ice in the Moon’s South Polar Regions from Lunar Reconnaissance Orbiter Ultraviolet Albedo and Temperature Measurements. Icarus 2015, 255, 58–69. [Google Scholar] [CrossRef]
- Lemelin, M.; Lucey, P.G.; Neumann, G.A.; Mazarico, E.M.; Barker, M.K.; Kakazu, A.; Trang, D.; Smith, D.E.; Zuber, M.T. Improved Calibration of Reflectance Data from the LRO Lunar Orbiter Laser Altimeter (LOLA) and Implications for Space Weathering. Icarus 2016, 273, 315–328. [Google Scholar] [CrossRef]
- Cremons, D.R.; Honniball, C.I. Simulated Lunar Surface Hydration Measurements Using Multispectral Lidar at 3 Μm. Earth Space Sci. 2022, 9, e2022EA002277. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Speckle Phenomena in Optics: Theory and Applications, 2nd ed.; The International Society for Optical Engineering: Bellingham, WA, USA, 2020; ISBN 978-1-5106-3149-6. [Google Scholar]
- Cassé, V.; Gibert, F.; Edouart, D.; Chomette, O.; Crevoisier, C. Optical Energy Variability Induced by Speckle: The Cases of MERLIN and CHARM-F IPDA Lidar. Atmosphere 2019, 10, 540. [Google Scholar] [CrossRef]
- Akram, M.N.; Chen, X. Speckle Reduction Methods in Laser-Based Picture Projectors. Opt. Rev. 2016, 23, 108–120. [Google Scholar] [CrossRef]
- Lee, S.; Kim, D.; Nam, S.-W.; Lee, B.; Cho, J.; Lee, B. Light Source Optimization for Partially Coherent Holographic Displays with Consideration of Speckle Contrast, Resolution, and Depth of Field. Sci. Rep. 2020, 10, 18832. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.-T.-K.; Svensen, Ø.; Chen, X.; Akram, M.N. Speckle Reduction in Laser Projection Displays through Angle and Wavelength Diversity. Appl. Opt. 2016, 55, 1267–1274. [Google Scholar] [CrossRef] [PubMed]
- Kozacki, T.; Chlipala, M. Color Holographic Display with White Light LED Source and Single Phase Only SLM. Opt. Express 2016, 24, 2189–2199. [Google Scholar] [CrossRef]
- Trisnadi, J.I. Speckle Contrast Reduction in Laser Projection Displays; Wu, M.H., Ed.; SPIE Press: San Jose, CA, USA, 2002; pp. 131–137. [Google Scholar]
- Yu, N.E.; Choi, J.W.; Kang, H.; Ko, D.-K.; Fu, S.-H.; Liou, J.-W.; Kung, A.H.; Choi, H.J.; Kim, B.J.; Cha, M.; et al. Speckle Noise Reduction on a Laser Projection Display via a Broadband Green Light Source. Opt. Express 2014, 22, 3547–3556. [Google Scholar] [CrossRef] [PubMed]
- Kuksenkov, D.V.; Roussev, R.V.; Li, S.; Wood, W.A.; Lynn, C.M. Multiple-Wavelength Synthetic Green Laser Source for Speckle Reduction; Vodopyanov, K.L., Ed.; SPIE Press: San Francisco, CA, USA, 2011; p. 79170B. [Google Scholar]
- Ehret, G.; Bousquet, P.; Pierangelo, C.; Alpers, M.; Millet, B.; Abshire, J.B.; Bovensmann, H.; Burrows, J.P.; Chevallier, F.; Ciais, P.; et al. MERLIN: A French-German Space Lidar Mission Dedicated to Atmospheric Methane. Remote Sens. 2017, 9, 1052. [Google Scholar] [CrossRef]
- Riris, H.; Li, S.; Numata, K.; Wu, S.; Yu, A.; Burris, J.; Krainak, M.; Abshire, J. LIDAR Technology for Measuring Trace Gases on Mars and Earth. In Proceedings of the Lidar Remote Sensing for Environmental Monitoring XII, San Diego, CA, USA, 21–22 August 2011; p. 8159. [Google Scholar]
- Abshire, J.B.; Riris, H.; Allan, G.R.; Weaver, C.J.; Mao, J.; Sun, X.; Hasselbrack, W.E.; Kawa, S.R.; Biraud, S. Pulsed Airborne Lidar Measurements of Atmospheric CO2 Column Absorption. Tellus B Chem. Phys. Meteorol. 2010, 62, 770. [Google Scholar] [CrossRef]
- Pierrottet, D.F.; Amzajerdian, F.; Petway, L.B.; Hines, G.D.; Barnes, B. Field Demonstration of a Precision Navigation Lidar System for Space Vehicles. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference: American Institute of Aeronautics and Astronautics, Boston, MA, USA, 19 August 2013. [Google Scholar]
- Dunmeyer, D. Laser Speckle Modeling for Three-Dimensional Metrology and LADAR. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2001. [Google Scholar]
- Schwenger, F.; Braesicke, K. Simulation of Laser Speckle Patterns Generated by Random Rough Surfaces. In Proceedings of the Infrared Imaging Systems: Design, Analysis, Modeling, and Testing XXXI, Online, 23 April 2020; Holst, G.C., Haefner, D.P., Eds.; SPIE Press: San Jose, CA, USA; p. 14. [Google Scholar]
- Paschotta, R. Field Guide to Laser Pulse Generation; SPIE Field Guides; SPIE Press: Bellingham, WA, USA, 2008; ISBN 978-0-8194-7248-9. [Google Scholar]
- Siegman, A.E. Lasers; University Science Books: Mill Valley, CA, USA, 1986; ISBN 978-0-935702-11-8. [Google Scholar]
- Brosnan, S.; Byer, R. Optical Parametric Oscillator Threshold and Linewidth Studies. IEEE J. Quantum Electron. 1979, 15, 415–431. [Google Scholar] [CrossRef]
- Green, R.; Pieters, C.; Mouroulis, P.; Eastwood, M.; Boardman, J.; Glavich, T.; Isaacson, P.; Annadurai, M.; Besse, S.; Barr, D.; et al. The Moon Mineralogy Mapper (M3) Imaging Spectrometer for Lunar Science: Instrument Description, Calibration, on-Orbit Measurements, Science Data Calibration and on-Orbit Validation. J. Geophys. Res. Planets 2011, 116, E00G19. [Google Scholar] [CrossRef]
- Colaprete, A.; Andrews, D.; Bluethmann, W.; Elphic, R.C.; Bussey, B.; Trimble, J.; Zacny, K.; Captain, J.E.; Colaprete, A.; Andrews, D.; et al. An Overview of the Volatiles Investigating Polar Exploration Rover (VIPER) Mission. In Proceedings of the American Geophysical Union, San Francisco, CA, USA, 9–13 December 2019; Volume 2019, p. P34B–03. [Google Scholar]
- Roush, T.; Colaprete, A.; Cook, A.; Bielawski, R.; Ennico-Smith, K.; Noe Dobrea, E.; Benton, J.; Forgione, J.; White, B.; McMurray, R.; et al. The Volatiles Investigating Polar Exploration Rover (VIPER) Near Infrared Volatile Spectrometer System (NIRVSS). In Proceedings of the Lunar and Planetary Science Conference, Online, 15–19 March 2021; p. 1678. [Google Scholar]
- Bender, H.A.; Smith, C.D.; Ehlmann, B.L.; Thompson, D.R.; Vinckier, Q.P.; Mouroulis, P. Optical Design and Performance of the Lunar Trailblazer High-Resolution Volatiles and Minerals Moon Mapper (HVM3). In Proceedings of the Imaging Spectrometry XXV: Applications, Sensors, and Processing, San Diego, CA, USA, 22 August 2022; Ientilucci, E.J., Bradley, C.L., Eds.; SPIE Press: San Diego, CA, USA, 2022; p. 3. [Google Scholar]
- Ehlmann, B.L.; Klima, R.L.; Seybold, C.C.; Klesh, A.T.; Au, M.H.; Bender, H.A.; Bennett, C.L.; Blaney, D.L.; Bowles, N.; Calcutt, S.; et al. NASA’s Lunar Trailblazer Mission: A Pioneering Small Satellite for Lunar Water and Lunar Geology. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–14. [Google Scholar]
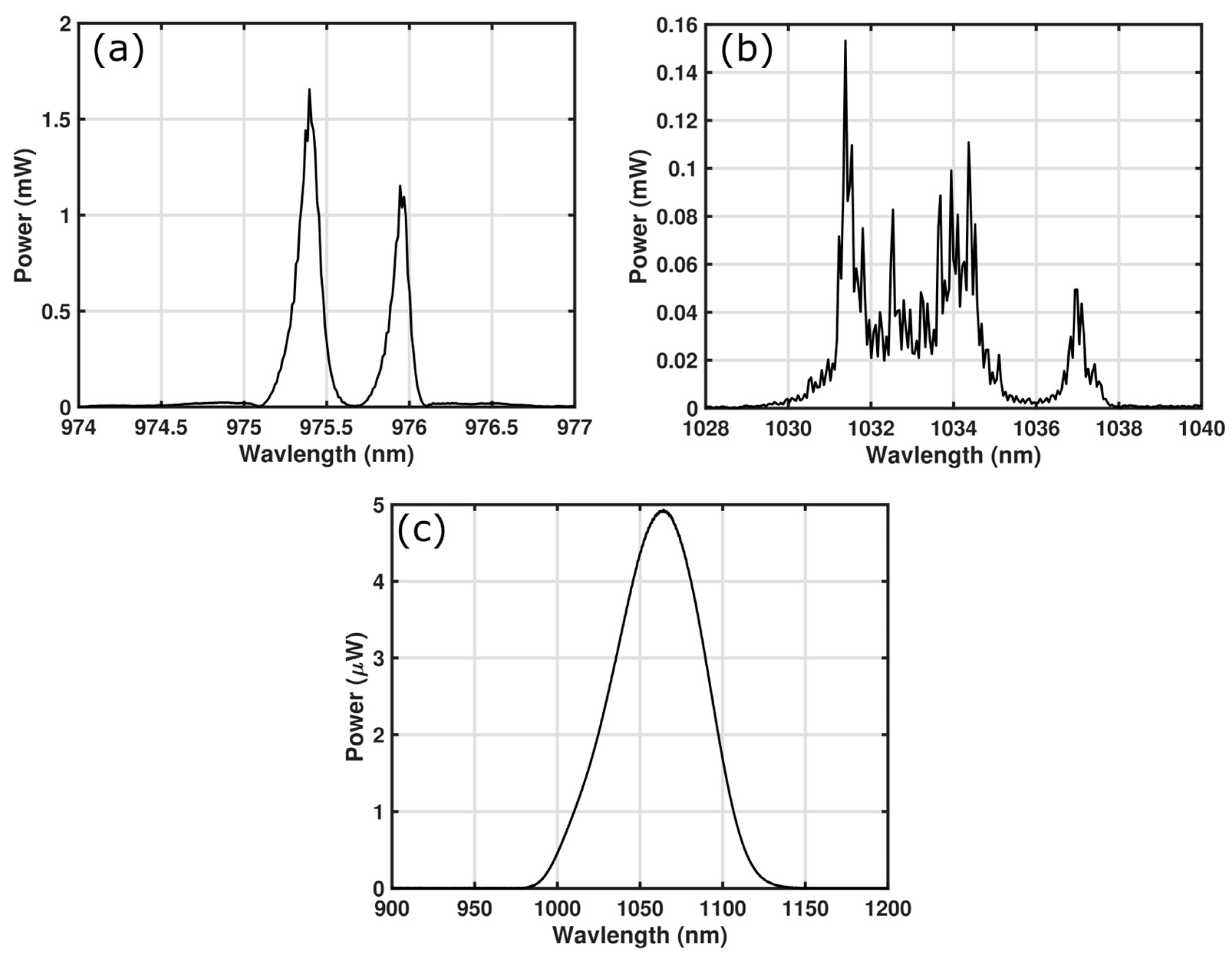


| Illumination Source | Center Wavelength | Linewidth 1 | Normalized Linewidth 2 |
|---|---|---|---|
| Single Frequency Diode | 1063.9894 nm | <0.03 nm | 2.6 × 10−5 |
| Dual Mode Pump Diode | 975.69 nm | 0.75 nm | 7.7 × 10−4 |
| Fabry–Perot Diode | 1034.4 nm | 4.4 nm | 0.0043 |
| Superluminescent Diode | 1068 nm | 62.5 nm | 0.059 |
| Halogen White Light Source | 360–2400 nm 3 | ||
| Laser Source | Normalized Linewidth | 50% Target | 75% Target | 99% Target 1 |
|---|---|---|---|---|
| Single Frequency Diode | 2.6 × 10−5 | 0.6 ± 0.3 | 0.8 ± 0.6 | 0.99 ± 0.9 |
| Dual Mode Pump Diode | 7.7 × 10−4 | 0.5 ± 0.4 | 0.9 ± 0.3 | 0.99 ± 0.3 |
| Fabry–Perot Diode | 0.0043 | 0.5 ± 0.1 | 0.8 ± 0.3 | 0.99 ± 0.3 |
| Superluminescent Diode | 0.059 | 0.56 ± 0.06 | 0.83 ± 0.05 | 0.99 ± 0.05 |
| Halogen White Light Source | N/A | 0.47 ± 0.01 | 0.74 ± 0.01 | 0.99 ± 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cremons, D.R.; Clarke, G.B.; Sun, X. Speckle Noise Reduction via Linewidth Broadening for Planetary Laser Reflectance Spectrometers. Remote Sens. 2024, 16, 1515. https://doi.org/10.3390/rs16091515
Cremons DR, Clarke GB, Sun X. Speckle Noise Reduction via Linewidth Broadening for Planetary Laser Reflectance Spectrometers. Remote Sensing. 2024; 16(9):1515. https://doi.org/10.3390/rs16091515
Chicago/Turabian StyleCremons, Daniel R., Gregory B. Clarke, and Xiaoli Sun. 2024. "Speckle Noise Reduction via Linewidth Broadening for Planetary Laser Reflectance Spectrometers" Remote Sensing 16, no. 9: 1515. https://doi.org/10.3390/rs16091515
APA StyleCremons, D. R., Clarke, G. B., & Sun, X. (2024). Speckle Noise Reduction via Linewidth Broadening for Planetary Laser Reflectance Spectrometers. Remote Sensing, 16(9), 1515. https://doi.org/10.3390/rs16091515










