Remote Quantification of Soil Organic Carbon: Role of Topography in the Intra-Field Distribution
Abstract
1. Introduction
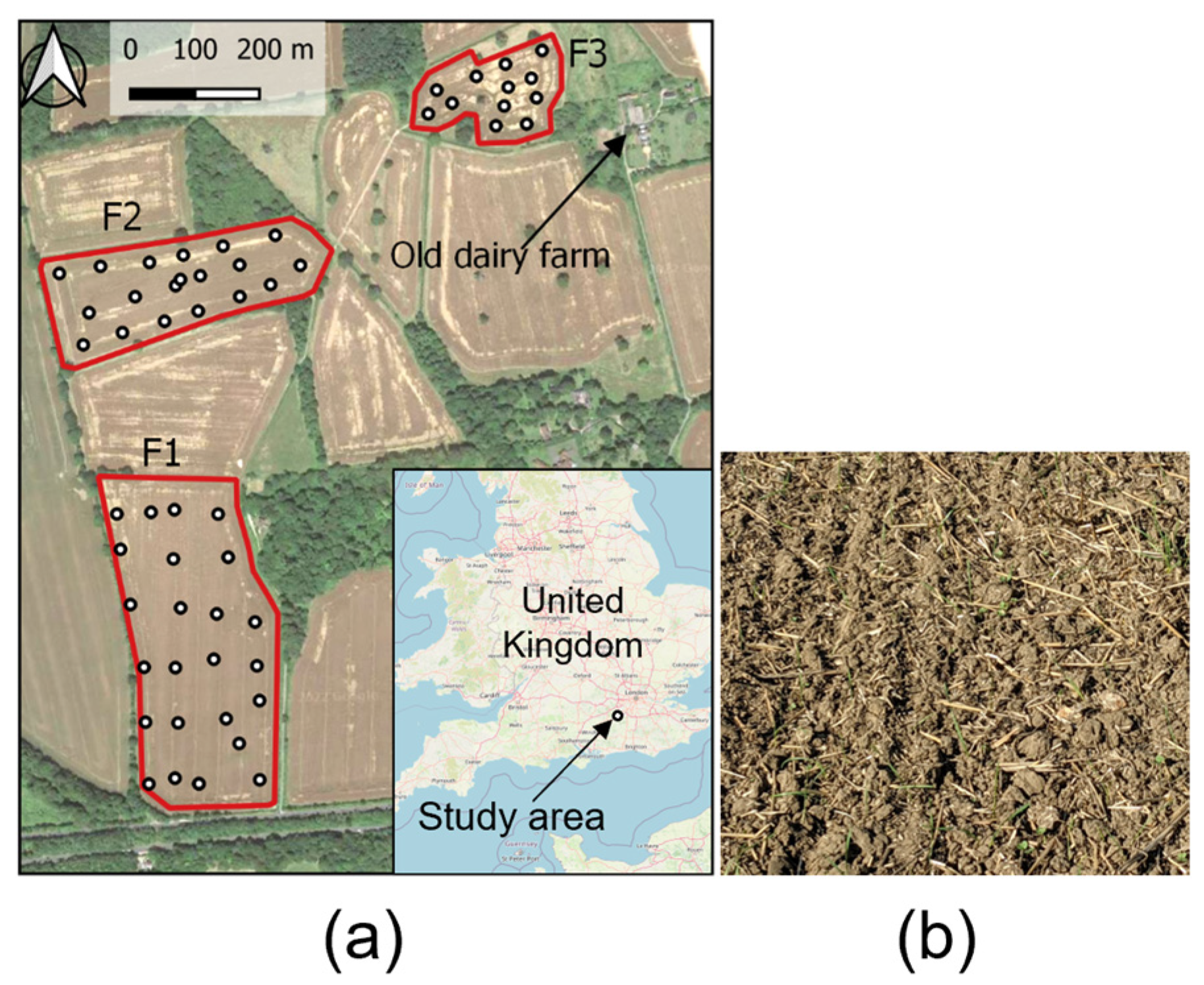
2. Study Area
3. Materials and Methods
3.1. Onsite Sampling
3.2. Laboratory Analysis of Soil Organic Carbon
3.3. Satellite Data, Image Pre-Processing and Indices Calculation
3.4. Extraction of Topographical Features
3.5. Machine Learning Models for SOC Prediction
3.6. Random Forest
3.7. Support Vector Machine
3.8. Model Assessment and Optimisation
3.9. Variable Importance Analysis
4. Results
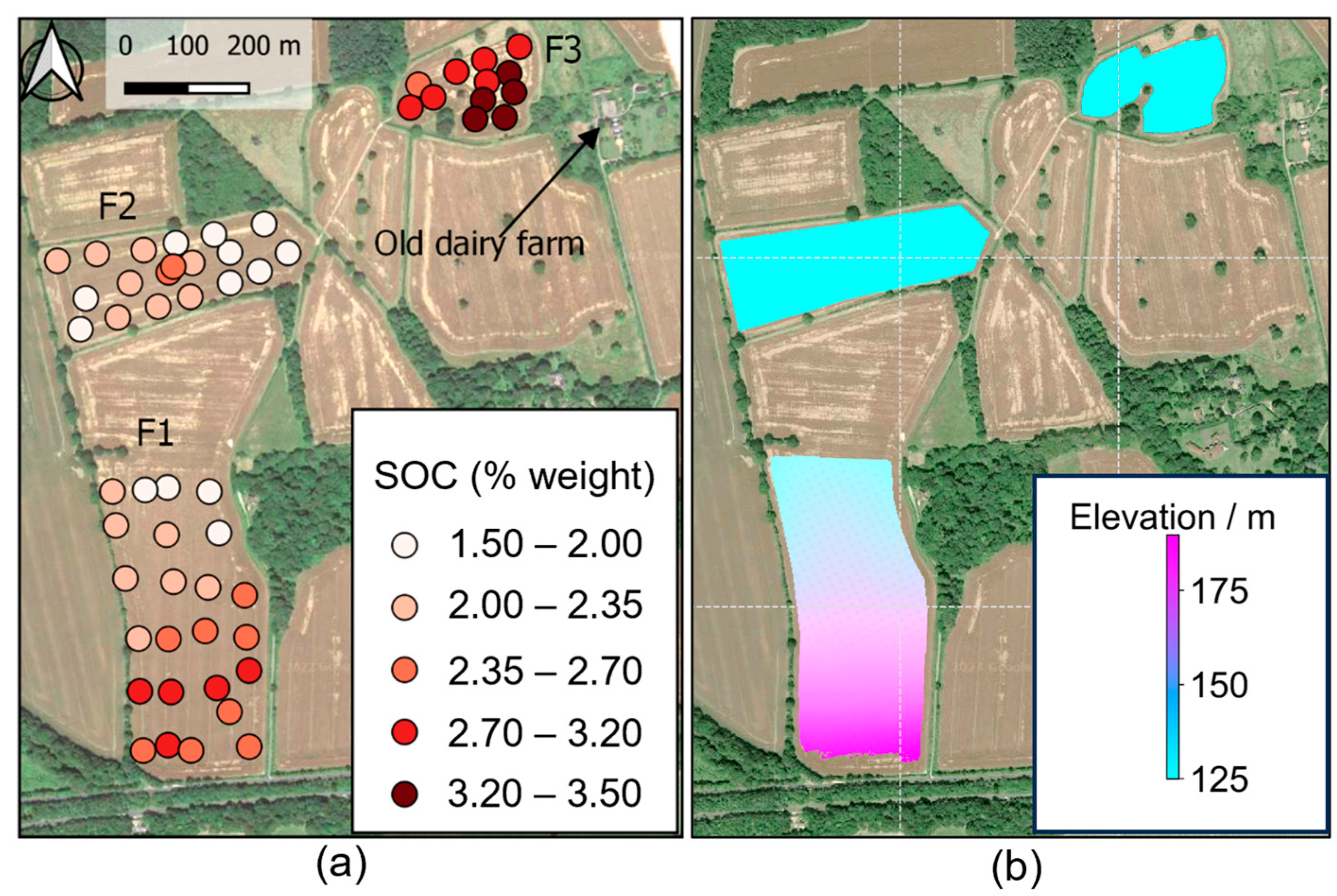
4.1. SOC Analysis of the Soil Samples
4.2. SOC Model Performance for SVR and RF
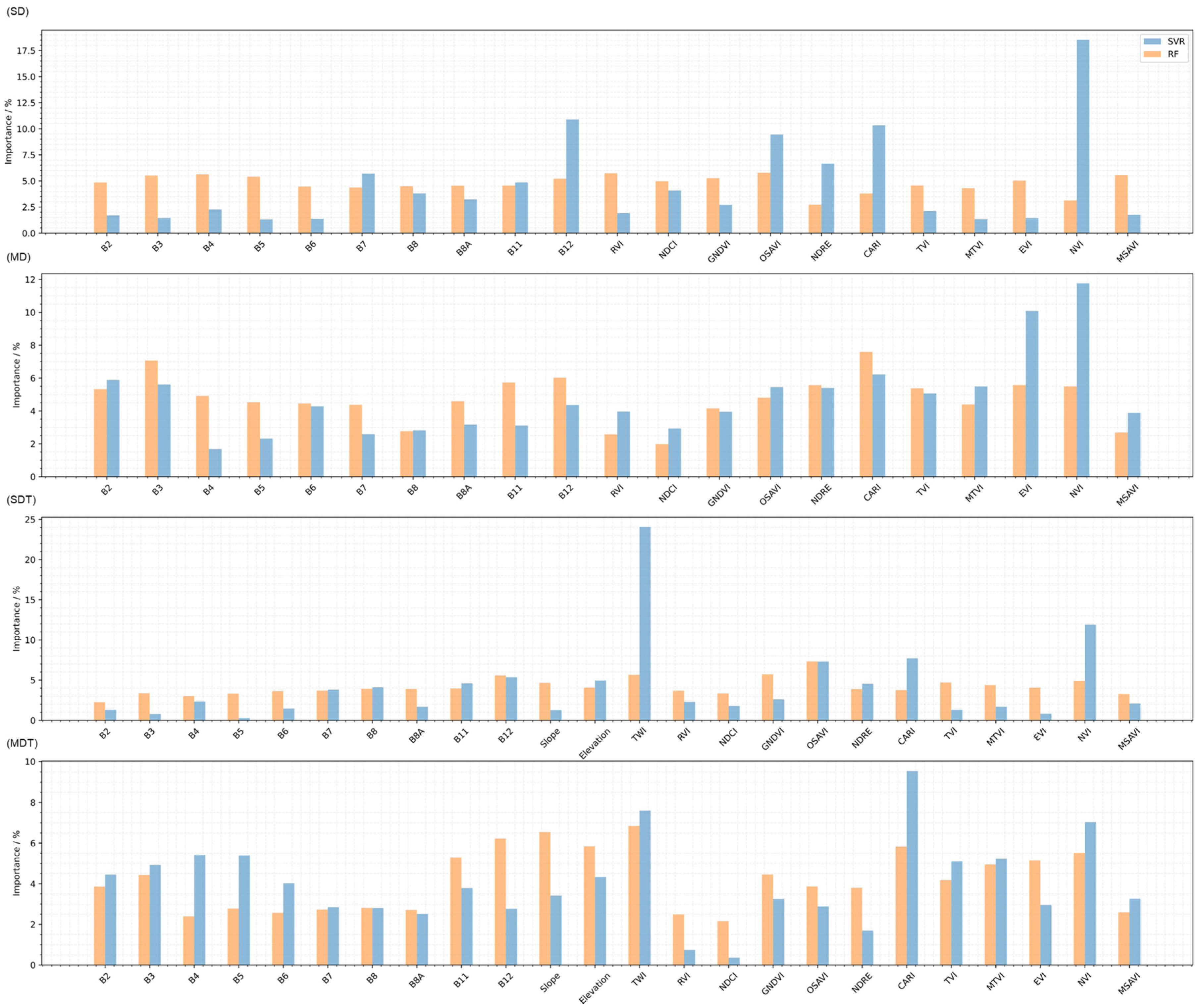
4.3. Permutation Importance
4.4. Model Extrapolation over Sample Area
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, W.; Guan, K.; Peng, B.; Margenot, A.; Lee, D.; Tang, J.; Jin, Z.; Grant, R.; DeLucia, E.; Qin, Z.; et al. How does uncertainty of soil organic carbon stock affect the calculation of carbon budgets and soil carbon credits for croplands in the U.S. Midwest? Geoderma 2023, 429, 116254. [Google Scholar] [CrossRef]
- Caruso, T.; De Vries, F.T.; Bardgett, R.D.; Lehmann, J. Soil organic carbon dynamics matching ecological equilibrium theory. Ecol. Evol. 2018, 8, 11169–11178. [Google Scholar] [CrossRef] [PubMed]
- Manns, H.R.; Berg, A.A. Importance of soil organic carbon on surface soil water content variability among agricultural fields. J. Hydrol. 2014, 516, 297–303. [Google Scholar] [CrossRef]
- Lal, R.; Negassa, W.; Lorenz, K. Carbon sequestration in soil. Curr. Opin. Environ. Sustain. 2015, 15, 79–86. [Google Scholar] [CrossRef]
- Oelkers, E.H.; Cole, D.R. Carbon dioxide sequestration; a solution to a global problem. Elements 2008, 4, 305–310. [Google Scholar] [CrossRef]
- Lei, Z.; Yu, D.; Zhou, F.; Zhang, Y.; Yu, D.; Zhou, Y.; Han, Y. Changes in soil organic carbon and its influencing factors in the growth of Pinus sylvestris var. mongolica plantation in Horqin Sandy Land, Northeast China. Sci. Rep. 2019, 9, 16412–16453. [Google Scholar] [CrossRef] [PubMed]
- Monger, H.C. Soils as Generators and Sinks of Inorganic Carbon in Geologic Time. In Soil Carbon; Springer International Publishing: Cham, Switzerland, 2014; pp. 27–36. [Google Scholar]
- Bellassen, V.; Stephan, N. Accounting for Carbon: Monitoring, Reporting and Verifying Emissions in the Climate Economy; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Jacquemoud, S.; Baret, F.; Hanocq, J.F. Modeling spectral and bidirectional soil reflectance. Remote Sens. Environ. 1992, 41, 123–132. [Google Scholar] [CrossRef]
- Ymeti, I.; Pikha Shrestha, D.; van der Meer, F. Monitoring soil surface mineralogy at different moisture conditions using visible near-infrared spectroscopy data. Remote Sens. 2019, 11, 2526. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Inbar, Y.; Chen, Y. The reflectance spectra of organic matter in the visible near-infrared and short wave infrared region (400–2500 nm) during a controlled decomposition process. Remote Sens. Environ. 1997, 61, 1–15. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Žižala, D.; Saberioon, M.; Borůvka, L. Soil organic carbon and texture retrieving and mapping using proximal, airborne and Sentinel-2 spectral imaging. Remote Sens. Environ. 2018, 218, 89–103. [Google Scholar] [CrossRef]
- Renata Teixeira de Almeida, M.; Scudiero, E.; Zaccaria, D.; Saad, J.C.C. Multitemporal satellite imagery analysis for soil organic carbon assessment in an agricultural farm in southeastern Brazil. Sci. Total Environ. 2021, 784, 147216. [Google Scholar]
- Gianinetto, M.; Lechi, G. The development of Superspectral approaches for the improvement of land cover classification. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2670–2679. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Minaei, F.; Talebi-khiyavi, H.; Xu, T.; Homaee, M. Synergetic use of multi-temporal Sentinel-1, Sentinel-2, NDVI, and topographic factors for estimating soil organic carbon. Catena 2022, 212, 106077. [Google Scholar] [CrossRef]
- Chabrillat, S.; Milewski, R.; Schmid, T.; Rastrero, M.; Escribano, P.; Pelayo, M.; Palacios-Orueta, A. Potential of hyperspectral imagery for the spatial assessment of soil erosion stages in agricultural semi-arid Spain at different scales. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Moore, I.D.; Gessler, P.E.; Nielsen, G.A.; Peterson, G.A. Soil Attribute Prediction Using Terrain Analysis. Soil Sci. Soc. Am. J. 1993, 57, 443–452. [Google Scholar] [CrossRef]
- Fathololoumi, S.; Vaezi, A.R.; Alavipanah, S.K.; Ghorbani, A.; Saurette, D.; Biswas, A. Improved digital soil mapping with multitemporal remotely sensed satellite data fusion: A case study in Iran. Sci. Total Environ. 2020, 721, 137703. [Google Scholar] [CrossRef] [PubMed]
- Tao, P.; Cheng-Zhi, Q.; Zhu, A.X.; Lin, Y.; Ming, L.; Baolin, L.; Chenghu, Z. Mapping soil organic matter using the topographic wetness index: A comparative study based on different flow-direction algorithms and kriging methods. Ecol. Indic. 2010, 10, 610–619. [Google Scholar] [CrossRef]
- André Geraldo de Lima, M.; Marcio Rocha, F.; Waldir de Carvalho, J.; Marcos Gervasio, P.; André, T.; Carlos Ernesto Gonçalves Reynaud, S. Environmental Correlation and Spatial Autocorrelation of Soil Properties in Keller Peninsula, Maritime Antarctica. Rev. Bras. Ciência Solo 2017, 41, e0170021. [Google Scholar]
- Kingsley, J.; Isong Isong, A.; Ndiye, M.K.; Chapman, A.P.; Okon, A.E.; Ahado, S.K. Soil organic carbon prediction with terrain derivatives using geostatistics and sequential Gaussian simulation. J. Saudi Soc. Agric. Sci. 2021, 20, 379–389. [Google Scholar]
- Mirchooli, F.; Kiani-Harchegani, M.; Khaledi Darvishan, A.; Falahatkar, S.; Sadeghi, S.H. Spatial distribution dependency of soil organic carbon content to important environmental variables. Ecol. Indic. 2020, 116, 106473. [Google Scholar] [CrossRef]
- Zhao, R.; Biswas, A.; Zhou, Y.; Zhou, Y.; Shi, Z.; Li, H. Corrigendum to “Identifying localized and scale-specific multivariate controls of soil organic matter variations using multiple wavelet coherence”. Sci. Total Environ. 2018, 643, 548–558, Erratum in Sci. Total Environ. 2019, 649, 1661–1662. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, R.; Zeng, Y.; Shi, Z.; Zhou, Q. Identifying scale-specific controls of soil organic matter distribution in mountain areas using anisotropy analysis and discrete wavelet transform. Catena 2018, 160, 1–9. [Google Scholar] [CrossRef]
- Vuolo, F.; Neuwirth, M.; Immitzer, M.; Atzberger, C.; Ng, W.-T. How much does multi-temporal Sentinel-2 data improve crop type classification? Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 122–130. [Google Scholar] [CrossRef]
- Zhou, T.; Geng, Y.; Chen, J.; Pan, J.; Haase, D.; Lausch, A. High-resolution digital mapping of soil organic carbon and soil total nitrogen using DEM derivatives, Sentinel-1 and Sentinel-2 data based on machine learning algorithms. Sci. Total Environ. 2020, 729, 138244. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Garosi, Y.; Reza Owliaie, H.; Ayoubi, S.; Taghizadeh-Mehrjardi, R.; Scholten, T.; Xu, M. Improving the spatial prediction of soil organic carbon using environmental covariates selection: A comparison of a group of environmental covariates. Catena 2022, 208, 105723. [Google Scholar] [CrossRef]
- Vaudour, E.; Gomez, C.; Lagacherie, P.; Loiseau, T.; Baghdadi, N.; Urbina-Salazar, D.; Loubet, B.; Arrouays, D. Temporal mosaicking approaches of Sentinel-2 images for extending topsoil organic carbon content mapping in croplands. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102277. [Google Scholar] [CrossRef]
- Cranfield University UK. The Soils Guide-Upton. Available online: https://www.landis.org.uk/soilsguide/series.cfm?serno=2004 (accessed on 22 April 2024).
- Cranfield University UK. The Soils Guide-Wickham. Available online: https://www.landis.org.uk/soilsguide/mapunit.cfm?mu=71108&sorttype_association=map_unit_name (accessed on 22 April 2024).
- The Farm Carbon Toolkit. Soil Sampling: What to Expect. 2021. Available online: https://farmcarbontoolkit.org.uk/wp-content/uploads/2021/09/Soil-Sampling_-What-To-Expect.pdf (accessed on 24 April 2024).
- Emmett, B.A.; Reynolds, B.; Chamberlain, P.M.; Rowe, E.; Spurgeon, D.; Brittain, S.A.; Frogbrook, Z.; Hughes, S.; Lawlor, A.J.; Poskitt, J.; et al. Countryside Survey: Soils Report from 2007. NERC/Cent. Ecol. Hydrol. 2010, 192, 10. [Google Scholar]
- BS 1377-1:2016; Methods of Test for Soils for Civil Engineering Purposes: General Requirements and Sample Preparation. British Standards Institution: London, UK, 2016.
- Lebron, I.; Cooper, D.M.; Brentegani, M.A.; Bentley, L.A.; Dos Santos Pereira, G.; Keenan, P.; Cosby, J.B.; Emmet, B.; Robinson, D.A. Soil carbon determination for long-term monitoring revisited using thermo-gravimetric analysis. Vadose Zone J. 2024, 23, e20300. [Google Scholar] [CrossRef]
- Ball, D. Loss-on-Ignition as an Estimate of Organic Matter and Organic Carbon in Non-Calcareous Soils. J. Soil Sci. 2006, 15, 84–92. [Google Scholar] [CrossRef]
- Sparks, D.L.; Page, A.L.; Helmke, P.A.; Loeppert, R.H.; Soltanpour, P.N.; Tabatabai, M.A.; Johnston, C.T.; Sumner, M.E. Methods of Soil Analysis. Part 3, Chemical Methods; Soil Science Society of America Inc.: Madison, WI, USA, 1996. [Google Scholar]
- Karunadasa, K.S.P.; Manoratne, C.H.; Pitawala, H.M.T.G.A.; Rajapakse, R.M.G. Thermal decomposition of calcium carbonate (calcite polymorph) as examined by in-situ high-temperature X-ray powder diffraction. J. Phys. Chem. Solids 2019, 134, 21–28. [Google Scholar] [CrossRef]
- Reynolds, B.; Chamberlain, P.M.; Poskitt, J.; Woods, C.; Scott, W.A.; Rowe, E.C.; Robinson, D.A.; Frogbrook, Z.L.; Keith, A.M.; Henrys, P.A.; et al. Countryside Survey: National “Soil Change” 1978–2007 for Topsoils in Great Britain—Acidity, Carbon, and Total Nitrogen Status. Vadose Zone J. 2013, 12, vzj2012.0114. [Google Scholar] [CrossRef]
- Elhag, M.; Bahrawi, J.A. Soil salinity mapping and hydrological drought indices assessment in arid environments based on remote sensing techniques. Geosci. Instrum. Methods Data Syst. 2017, 6, 149–158. [Google Scholar] [CrossRef]
- Bertini, F.; Brand, O.; Carlier, S.; Del Bello, U.; Drusch, M.; Duca, R.; Fernandez, V.; Ferrario, C.; Ferreira, M.H.; Isola, C.; et al. Sentinel-2 ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar]
- Kemper, T.; Sommer, S. Estimate of heavy metal contamination in soils after a mining accident using reflectance spectroscopy. Environ. Sci. Technol. 2002, 36, 2742–2747. [Google Scholar] [CrossRef] [PubMed]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. Solid Earth 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Deventer, V.; Ward, A.; Gowda, P.; Lyon, J. Using Thematic Mapper Data to Identify Contrasting Soil Plains and Tillage Practices. Photogramm. Eng. Remote Sens. 1997, 63, 87–93. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Pouladi, N.; Gholizadeh, A.; Khosravi, V.; Borůvka, L. Digital mapping of soil organic carbon using remote sensing data: A systematic review. Catena 2023, 232, 107409. [Google Scholar] [CrossRef]
- Liu, H.Q.; Huete, A. Feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar] [CrossRef]
- Huete, A.R.; Liu, H.Q.; Batchily, K.W. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Marshak, A.; Knyazikhin, Y.; Davis, A.B.; Wiscombe, W.J.; Pilewskie, P. Cloud-vegetation interaction: Use of normalized difference cloud index for estimation of cloud optical thickness. Geophys. Res. Lett. 2000, 27, 1695–1698. [Google Scholar] [CrossRef]
- Geneviève, R.; Michael, S.; Frédéric, B. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Birth, G.S.; McVey, G.R. Measuring the Color of Growing Turf with a Reflectance Spectrophotometer1. Agron. J. 1968, 60, 640–643. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Gupta, R.K.; Vijayan, D.; Prasad, T.S. New hyperspectral vegetation characterization parameters. Adv. Space Res. 2001, 28, 201–206. [Google Scholar] [CrossRef]
- De Rosa, D.; Ballabio, C.; Lugato, E.; Fasiolo, M.; Jones, A.; Panagos, P. Soil organic carbon stocks in European croplands and grasslands: How much have we lost in the past decade? Glob. Chang. Biol. 2024, 30, e16992. [Google Scholar] [CrossRef]
- Stevenson, A.; Zhang, Y.; Huang, J.; Hu, J.; Paustian, K.; Hartemink, A.E. Rates of soil organic carbon change in cultivated and afforested sandy soils. Agric. Ecosyst. Environ. 2024, 360, 108785. [Google Scholar] [CrossRef]
- Hurst, M.D.; Mudd, S.M.; Walcott, R.; Attal, M.; Yoo, K. Using hilltop curvature to derive the spatial distribution of erosion rates. J. Geophys. Res. Earth Surf. 2012, 117, 108785. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Wang, T.; Zhou, W.; Xiao, J.; Li, H.; Yao, L.; Xie, L.; Wang, K. Soil Organic Carbon Prediction Using Sentinel-2 Data and Environmental Variables in a Karst Trough Valley Area of Southwest China. Remote Sens. 2023, 15, 2118. [Google Scholar] [CrossRef]
- Minasny, B.; Setiawan, B.I.; Saptomo, S.K.; McBratney, A.B. Open digital mapping as a cost-effective method for mapping peat thickness and assessing the carbon stock of tropical peatlands. Geoderma 2018, 313, 25–40. [Google Scholar] [CrossRef]
- Wang, B.; Waters, C.; Orgill, S.; Gray, J.; Cowie, A.; Clark, A.; Liu, D.L. High resolution mapping of soil organic carbon stocks using remote sensing variables in the semi-arid rangelands of eastern Australia. Sci. Total Environ. 2018, 630, 367–378. [Google Scholar] [CrossRef] [PubMed]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 271, pp. 278–282. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Korhonen, L.; Hadi; Packalen, P.; Rautiainen, M. Comparison of Sentinel-2 and Landsat 8 in the estimation of boreal forest canopy cover and leaf area index. Remote Sens. Environ. 2017, 195, 259–274. [Google Scholar] [CrossRef]
- Castaldi, F. Sentinel-2 and Landsat-8 Multi-Temporal Series to Estimate Topsoil Properties on Croplands. Remote Sens. 2021, 13, 3345. [Google Scholar] [CrossRef]
- An, D.; Chen, Y. Non-intrusive soil carbon content quantification methods using machine learning algorithms: A comparison of microwave and millimeter wave radar sensors. J. Autom. Intell. 2023, 2, 152–166. [Google Scholar] [CrossRef]
- Dvorakova, K.; Heiden, U.; Pepers, K.; Staats, G.; van Os, G.; van Wesemael, B. Improving soil organic carbon predictions from a Sentinel–2 soil composite by assessing surface conditions and uncertainties. Geoderma 2023, 429, 116128. [Google Scholar] [CrossRef]
- Cartopy: A Cartographic Python Library with a Matplotlib Interface. 2010. Available online: https://scitools.org.uk/cartopy (accessed on 24 April 2024).
- Maussion, F.; Roth, T.; Landmann, J.; Dusch, M.; Bell, R. Salem. Zenodo. 2021. Available online: https://salem.readthedocs.io/en/stable/index.html (accessed on 24 April 2024).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Lamichhane, S.; Kumar, L.; Wilson, B. Digital soil mapping algorithms and covariates for soil organic carbon mapping and their implications: A review. Geoderma 2019, 352, 395–413. [Google Scholar] [CrossRef]
- Meng, X.; Bao, Y.; Liu, J.; Liu, H.; Zhang, X.; Zhang, Y.; Wang, P.; Tang, H.; Kong, F. Regional soil organic carbon prediction model based on a discrete wavelet analysis of hyperspectral satellite data. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102111. [Google Scholar] [CrossRef]
- Yang, J.; Fan, J.; Lan, Z.; Mu, X.; Wu, Y.; Xin, Z.; Miping, P.; Zhao, G. Improved Surface Soil Organic Carbon Mapping of SoilGrids250m Using Sentinel-2 Spectral Images in the Qinghai–Tibetan Plateau. Remote Sens. 2023, 15, 114. [Google Scholar] [CrossRef]
- Vaudour, E.; Gomez, C.; Fouad, Y.; Lagacherie, P. Sentinel-2 image capacities to predict common topsoil properties of temperate and Mediterranean agroecosystems. Remote Sens. Environ. 2019, 223, 21–33. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.; Chappell, A.; De Caritat, P.; McKenzie, N. On the soil information content of visible–near infrared reflectance spectra. Eur. J. Soil Sci. 2011, 62, 442–453. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Saberioon, M.; Viscarra Rossel, R.A.; Boruvka, L.; Klement, A. Spectroscopic measurements and imaging of soil colour for field scale estimation of soil organic carbon. Geoderma 2020, 357, 113972. [Google Scholar] [CrossRef]
- Sena, N.C.; Veloso, G.V.; Fernandes-Filho, E.I.; Francelino, M.R.; Schaefer, C.E.G.R. Analysis of terrain attributes in different spatial resolutions for digital soil mapping application in southeastern Brazil. Geoderma Reg. 2020, 21, e00268. [Google Scholar] [CrossRef]
- Li, X.; McCarty, G.W.; Karlen, D.L.; Cambardella, C.A. Topographic metric predictions of soil redistribution and organic carbon in Iowa cropland fields. Catena 2018, 160, 222–232. [Google Scholar] [CrossRef]

| Band | Spectral Range (nm) | Spectral Position (nm) | Bandwidth (nm) | Spatial Resolution (m) |
|---|---|---|---|---|
| B2 | 458–523 | 490 | 65 | 10 |
| B3 | 543–578 | 560 | 35 | 10 |
| B4 | 650–680 | 665 | 30 | 10 |
| B5 | 698–713 | 705 | 15 | 20 |
| B6 | 733–748 | 740 | 15 | 20 |
| B7 | 773–793 | 783 | 20 | 20 |
| B8 | 785–900 | 842 | 115 | 10 |
| B8a | 855–875 | 865 | 20 | 20 |
| B11 | 1565–1655 | 1610 | 90 | 20 |
| B12 | 2100–2280 | 2190 | 180 | 20 |
| Index | Definition | Reference |
|---|---|---|
| Normalised Difference Vegetation Index (NDVI) | Rouse et al. [44] | |
| Normalised Burn Ratio (NBR2) | Van Deventer et al. [43] | |
| Enhanced Vegetation Index (EVI) | Liu & Huete [46,47] | |
| Green Normalised Difference Vegetation Index (GNDVI) | Gitelson, Kaufman & Merzlyak [48] | |
| Normalised Difference Red Edge (NDRE) | Huete et al. [47] | |
| Modified Triangular Vegetation Index 1 (MTVI) | Haboudane et al. [49] | |
| Normalised Difference Cloud Index (NDCI) | Marshak et al. [50] | |
| Optimised Soil-Adjusted Vegetation Index (OSAVI) | Rondeaux, Steven & Baret [51] | |
| Triangular Vegetation Index (TVI) | Broge & Leblanc [52] | |
| Ratio Vegetation Index (RVI) | Birth & McVey [53] | |
| Chlorophyll Absorption Reflectance Index (CARI) | Haboudane et al. [54] | |
| Modified Soil-Adjusted Vegetation Index (MSAVI) | Qi et al. [55] | |
| New Vegetation Index (NVI) | Gupta, Vijayan & Prasad [56] |
| Model | Hyperparameter | Description | Search Range |
|---|---|---|---|
| RF | Estimator number | The number of decision trees generated. | 500–25,000 |
| Maximum Depth | The maximum depth a given tree can reach. | 5–4000 | |
| Feature proportion | The proportion of the total feature set used in decision tree construction. | 0.1–1.0 | |
| SVR | Regularisation, C | The penalty associated with point distance. | 0.1–100 |
| Epsilon, | The distance from the hyperplane within which no penalty is applied. | 0.001–100 | |
| Gamma, | An RBF kernel coefficient determining the range of influence each point exerts. | 0.001–100 |
| Model Name | Input Data |
|---|---|
| Single-date spectral (SD) | Sentinel-2 spectral reflectance taken from one day only |
| Multidate spectral (MD) | Median spectral reflectance of time series taken from Sentinel-2 over a 3 year period |
| Topographical (T) | Topographical covariates (relative height, slope, TWI) extracted from high resolution DEM only |
| Single-date spectral and topographical (SDT) | Both Sentinel-2 spectral reflectance data (target date only) and topographical covariates |
| Multidate spectral and topographical (MDT) | Both median Sentinel-2 spectral reflectance data (3 year period) and topographical covariates |
| Field | Minimum (%) | Maximum (%) | Mean (%) | Standard Deviation (%) | Kurtosis | Skewness | Coefficient of Variation (%) |
|---|---|---|---|---|---|---|---|
| F1 | 1.52 | 3.19 | 2.35 | 0.41 | −0.19 | 0.16 | 17.65% |
| F2 | 1.63 | 2.52 | 2.06 | 0.25 | −0.78 | 0.12 | 12.11% |
| F3 | 2.65 | 3.52 | 3.16 | 0.24 | 0.32 | −0.32 | 7.44% |
| Model | Algorithm | Metric | RMSE | MAE | |
|---|---|---|---|---|---|
| SD | RF | Cross-validation | |||
| Validation test | |||||
| SVR | Cross-validation | ||||
| Validation test | |||||
| MD | RF | Cross-validation | |||
| Validation test | |||||
| SVR | Cross-validation | ||||
| Validation test | |||||
| T | RF | Cross-validation | |||
| Validation test | |||||
| SVR | Cross-validation | ||||
| Validation test | |||||
| SDT | RF | Cross-validation | |||
| Validation test | |||||
| SVR | Cross-validation | ||||
| Validation test | |||||
| MDT | RF | Cross-validation | |||
| Validation test | |||||
| SVR | Cross-validation | ||||
| Validation test |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cutting, B.J.; Atzberger, C.; Gholizadeh, A.; Robinson, D.A.; Mendoza-Ulloa, J.; Marti-Cardona, B. Remote Quantification of Soil Organic Carbon: Role of Topography in the Intra-Field Distribution. Remote Sens. 2024, 16, 1510. https://doi.org/10.3390/rs16091510
Cutting BJ, Atzberger C, Gholizadeh A, Robinson DA, Mendoza-Ulloa J, Marti-Cardona B. Remote Quantification of Soil Organic Carbon: Role of Topography in the Intra-Field Distribution. Remote Sensing. 2024; 16(9):1510. https://doi.org/10.3390/rs16091510
Chicago/Turabian StyleCutting, Benjamin J., Clement Atzberger, Asa Gholizadeh, David A. Robinson, Jorge Mendoza-Ulloa, and Belen Marti-Cardona. 2024. "Remote Quantification of Soil Organic Carbon: Role of Topography in the Intra-Field Distribution" Remote Sensing 16, no. 9: 1510. https://doi.org/10.3390/rs16091510
APA StyleCutting, B. J., Atzberger, C., Gholizadeh, A., Robinson, D. A., Mendoza-Ulloa, J., & Marti-Cardona, B. (2024). Remote Quantification of Soil Organic Carbon: Role of Topography in the Intra-Field Distribution. Remote Sensing, 16(9), 1510. https://doi.org/10.3390/rs16091510








