A Simple Artificial Neural Model to Predict Dambovita River Temperature Affected by Urban Heat Islands in Bucharest City
Abstract
1. Introduction
2. Materials and Methods
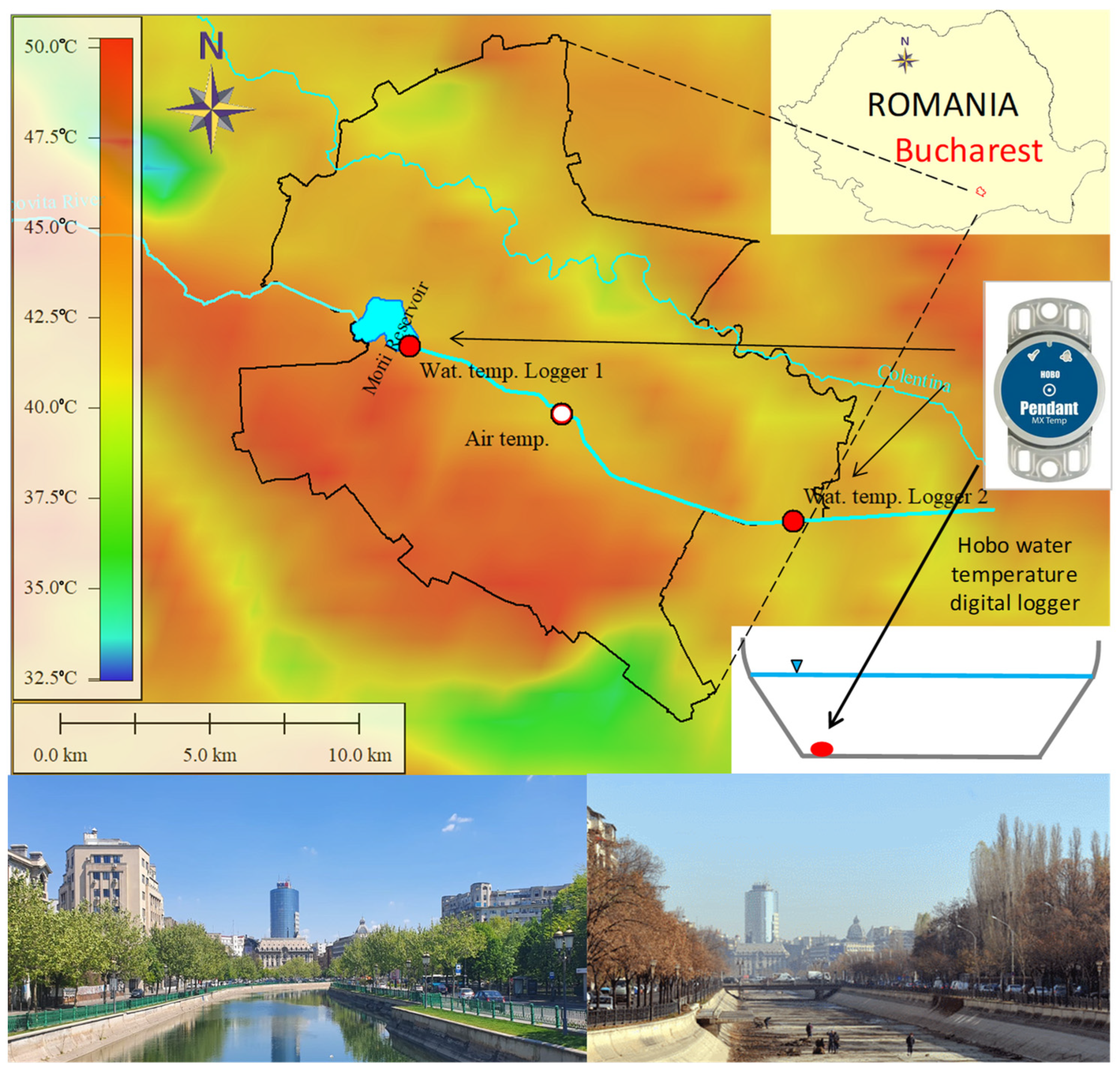
2.1. Study Area
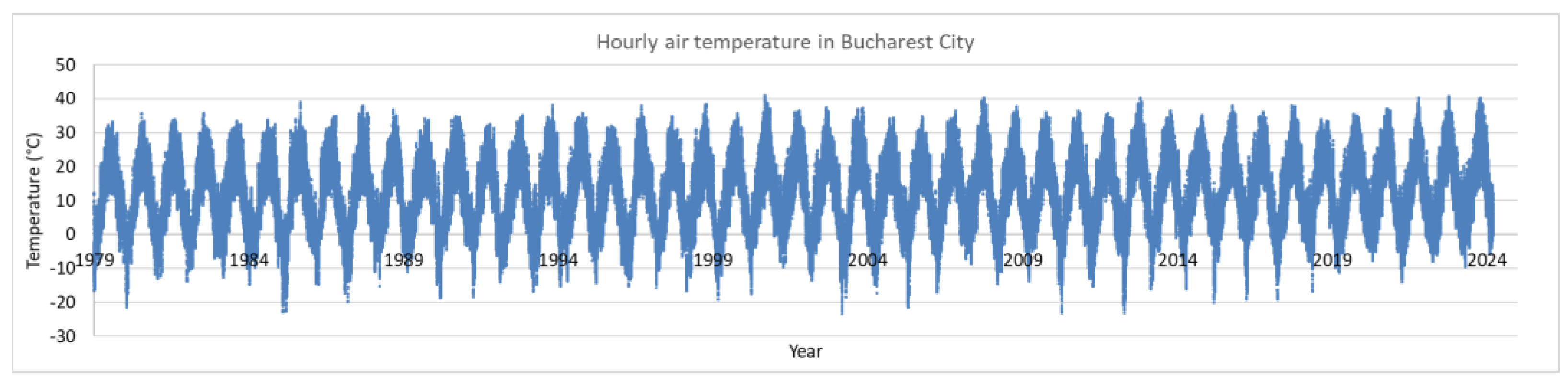
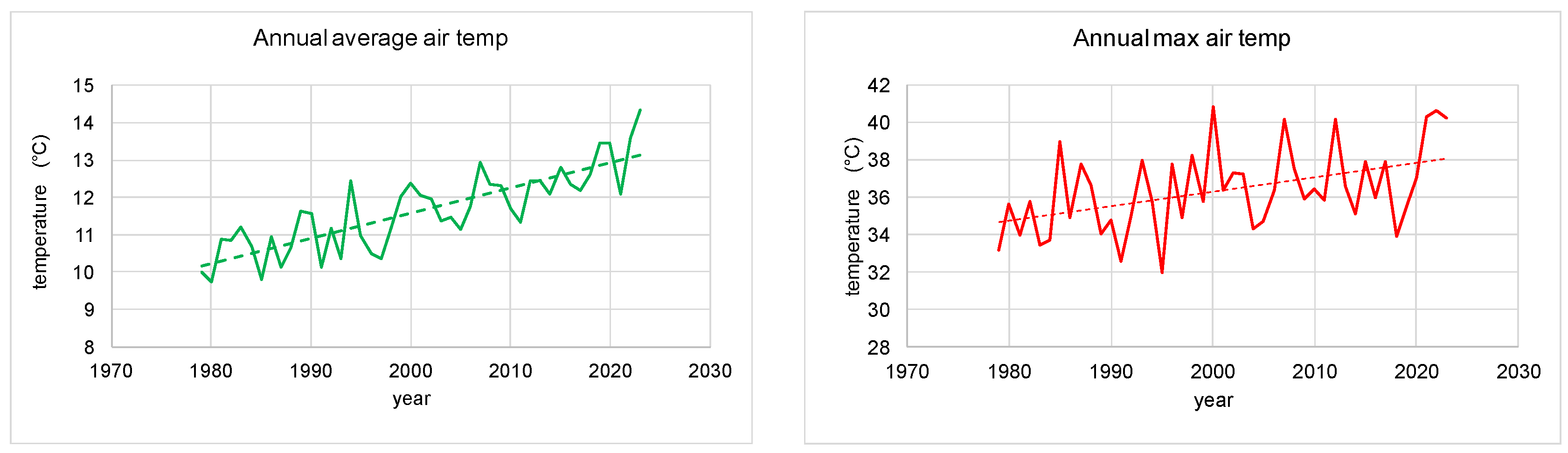
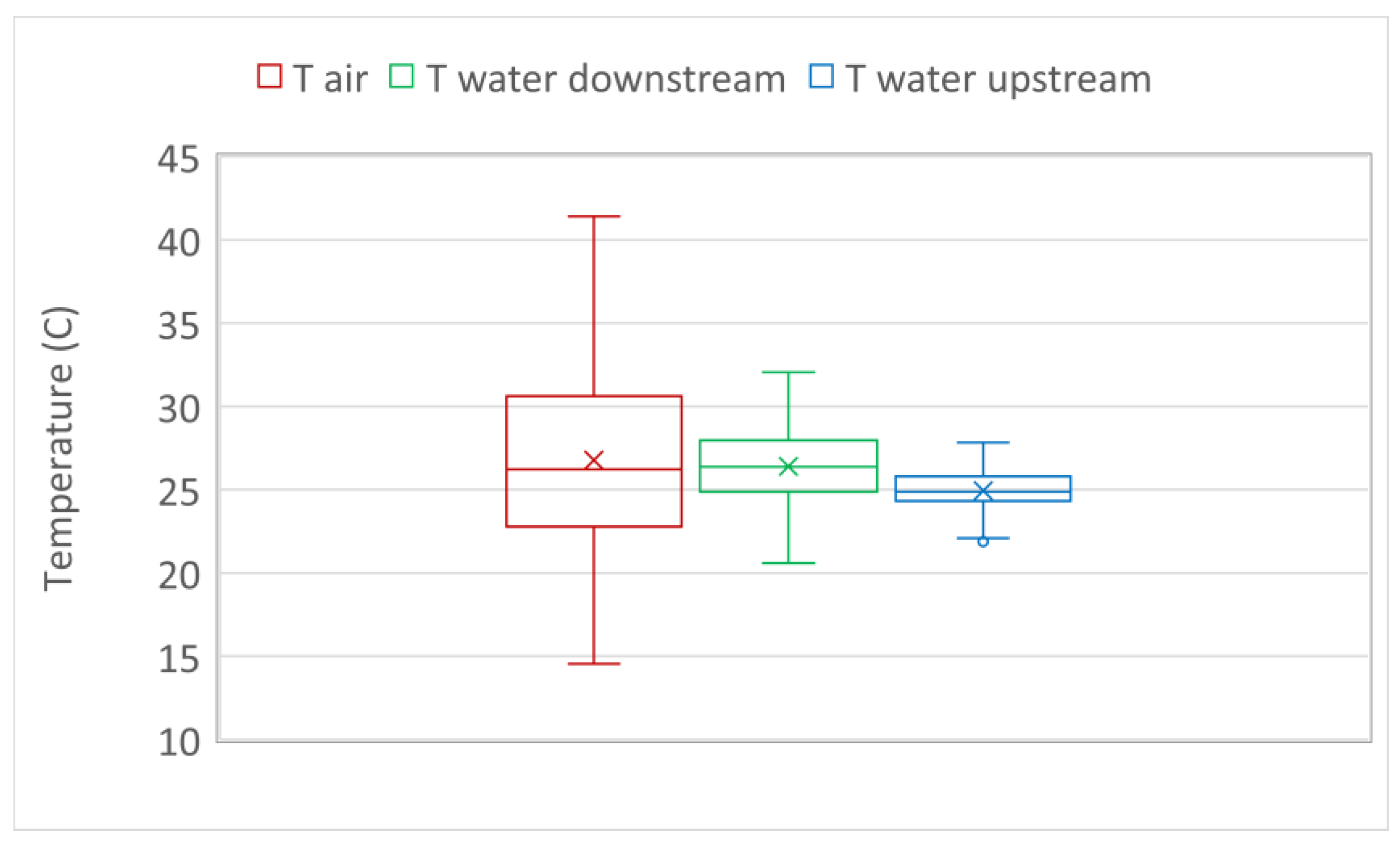
2.2. Air and Water Temperature Data
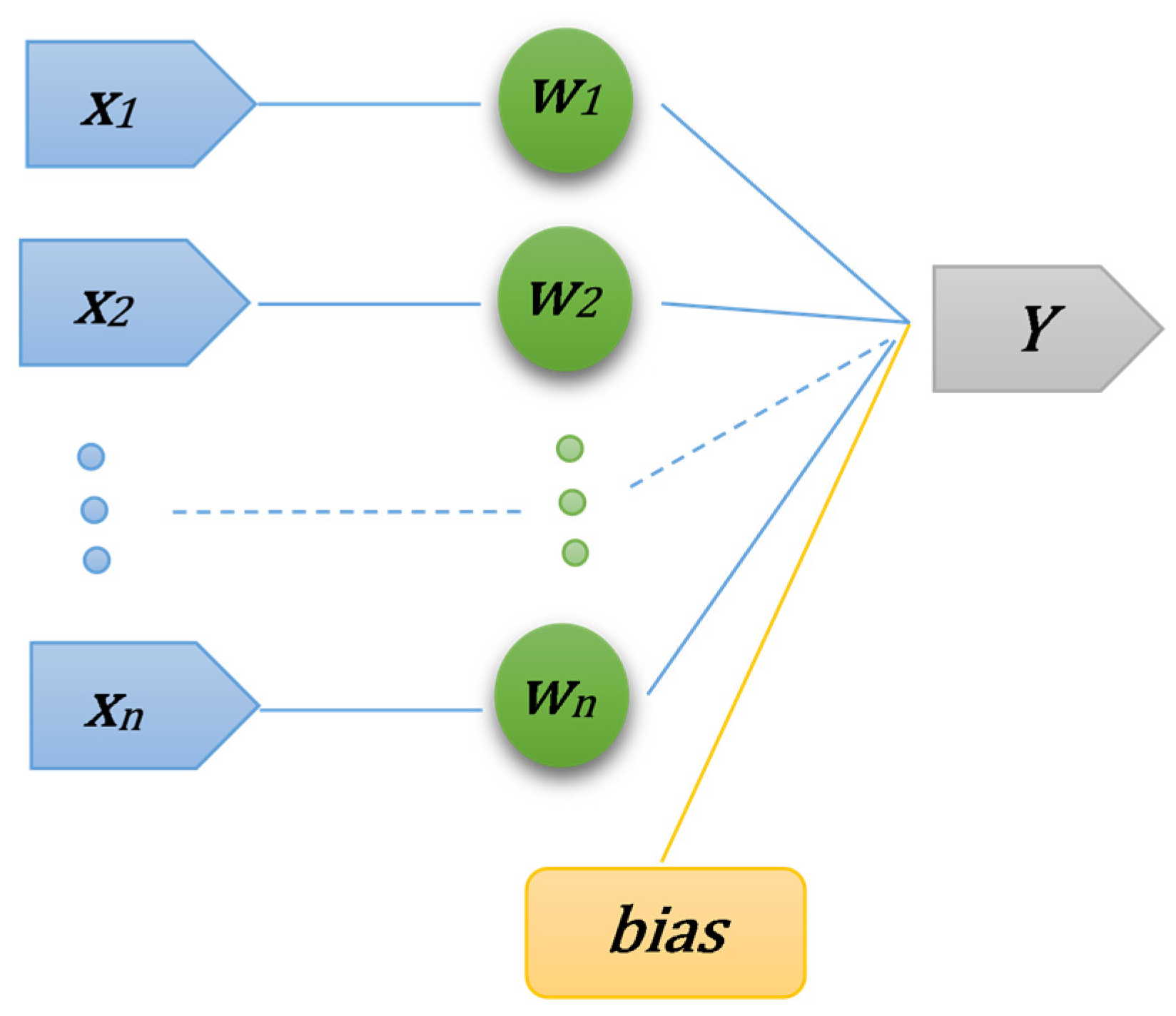
2.3. The ANN Water Temperature Prediction Model
- Forward propagation—computation of input weights and calculation of the error (by using a second-order derivatives algorithm) are progressing in a forward step;
- Backward propagation (the steepest descent algorithm)—adjustment of weights based on the error (by using a first-order derivatives algorithm) are progressing in a backward step.
- Note that the Hessian matrix is as follows:
- For small μ values (nearly zero)—the Gauss–Newton second-order algorithm is used and can be approximated using the following:
- For larger μ values—the steepest descent first-order algorithm is used, as follows:
- Five neurons in the input layer for air and water temperature values measured at the exit from the Morii Reservoir for two different time moments and the discharge (the influence of other meteorological and hydrological parameters, e.g., wind, solar radiation, cloudiness, and precipitation, was not taken into account);
- Ten neurons in the intermediate hidden layer;
- One neuron in the output layer, consisting of water temperature at the downstream cross-section of the Dâmbovița River, at its exit from Bucharest City.

- for ANN training (computation weights): ann_ffbp_init(N, r);
- for ANN run and prediction of temperatures: ann_FFBP_run(X,W).
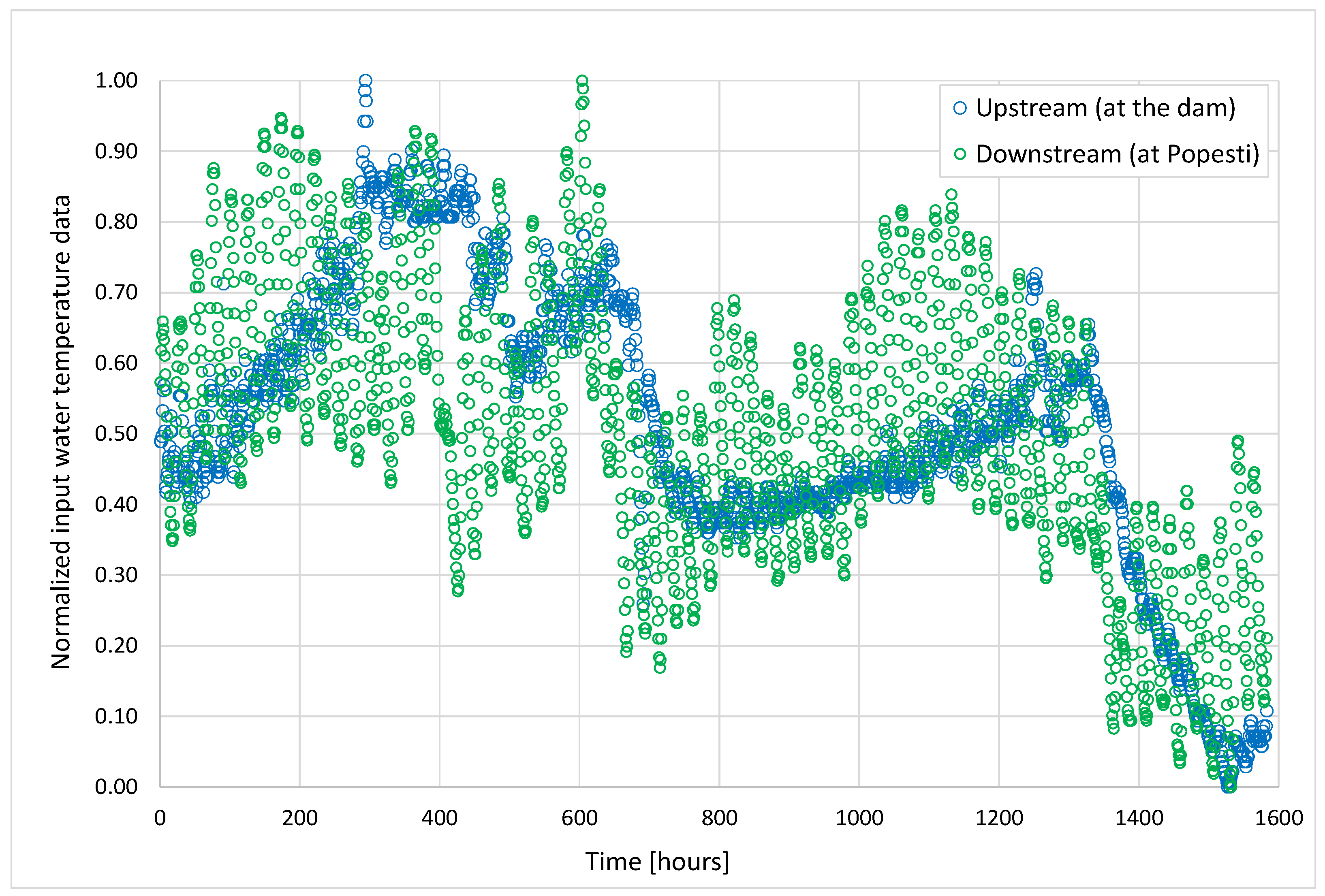
2.4. Input Data for the ANN Model
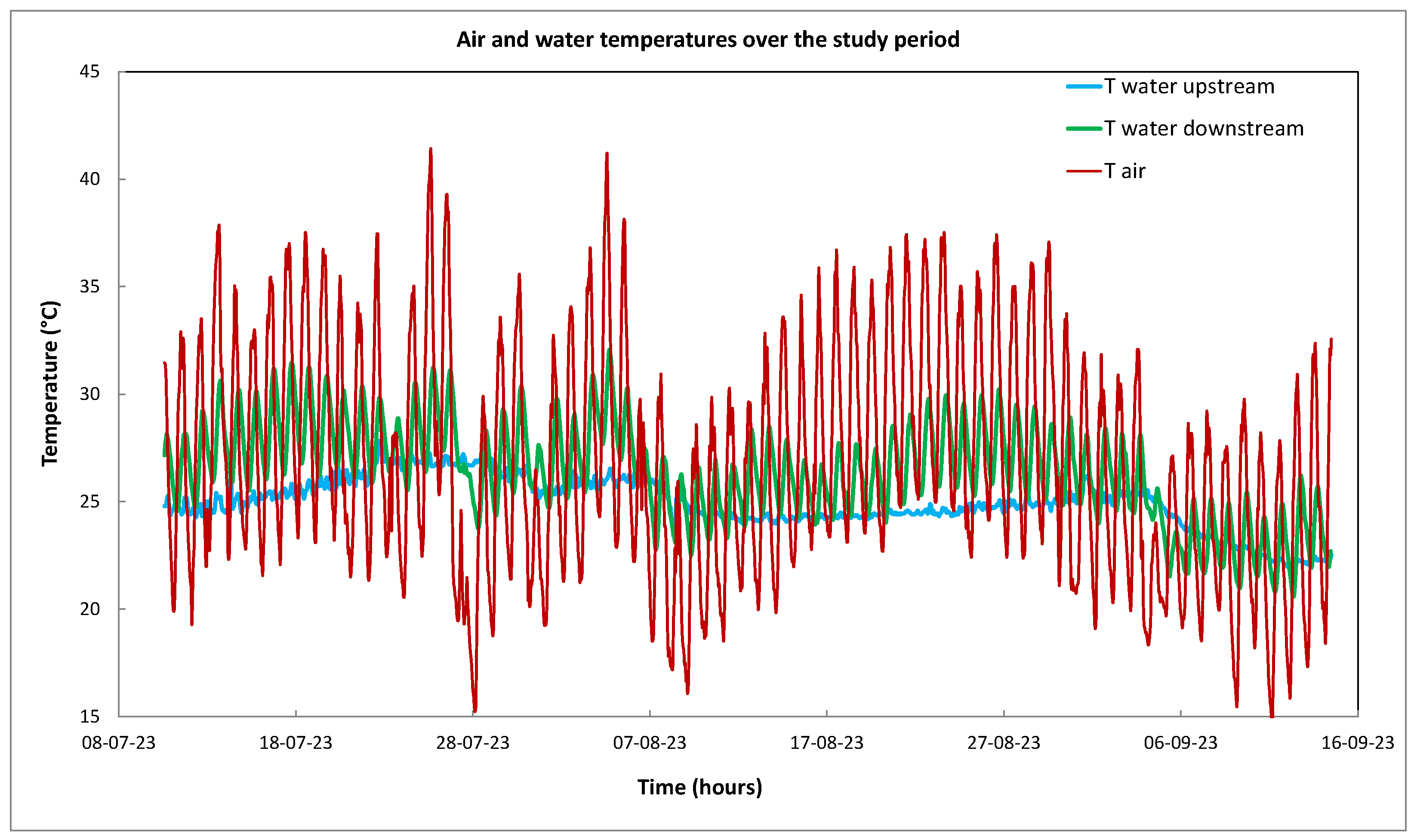
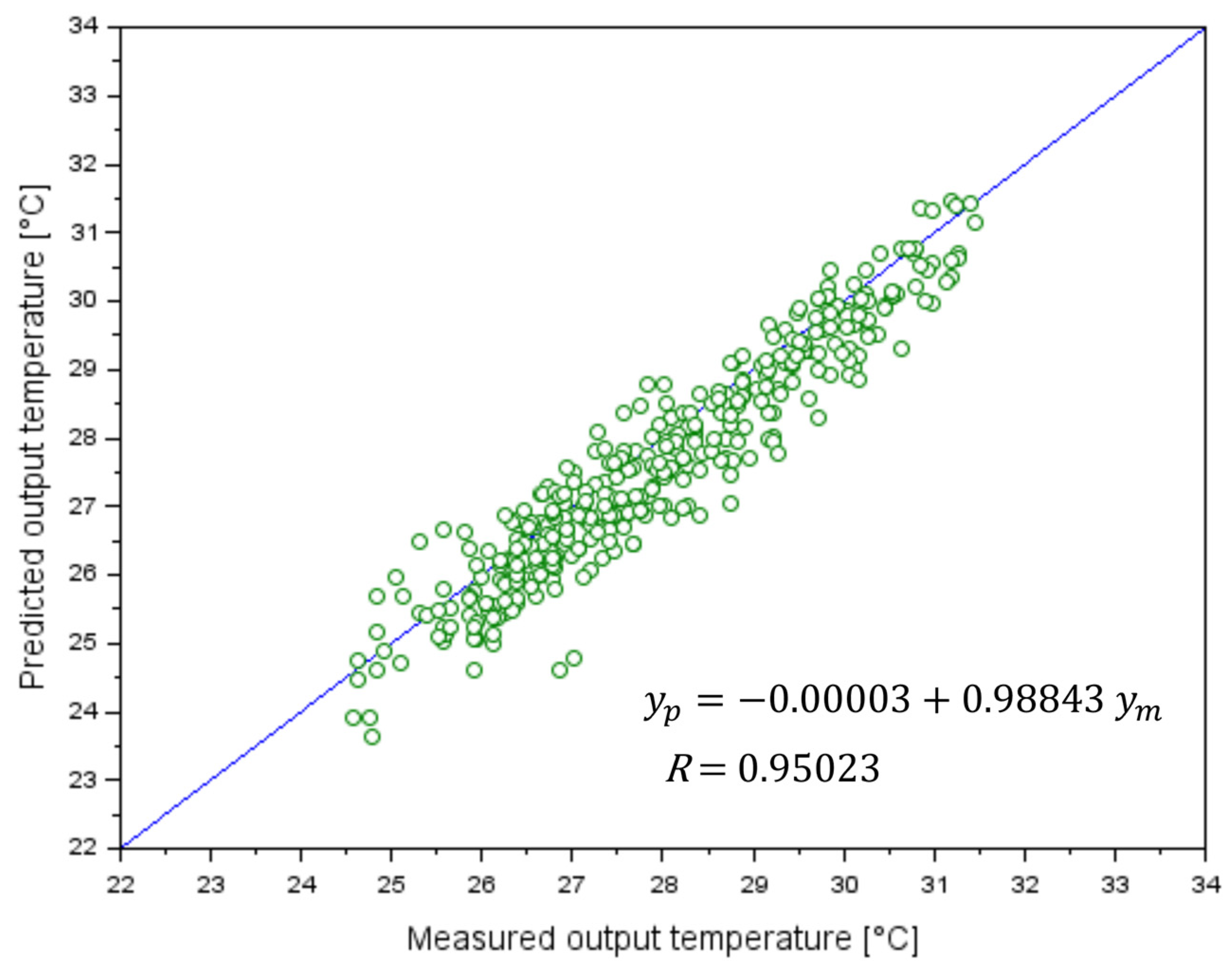
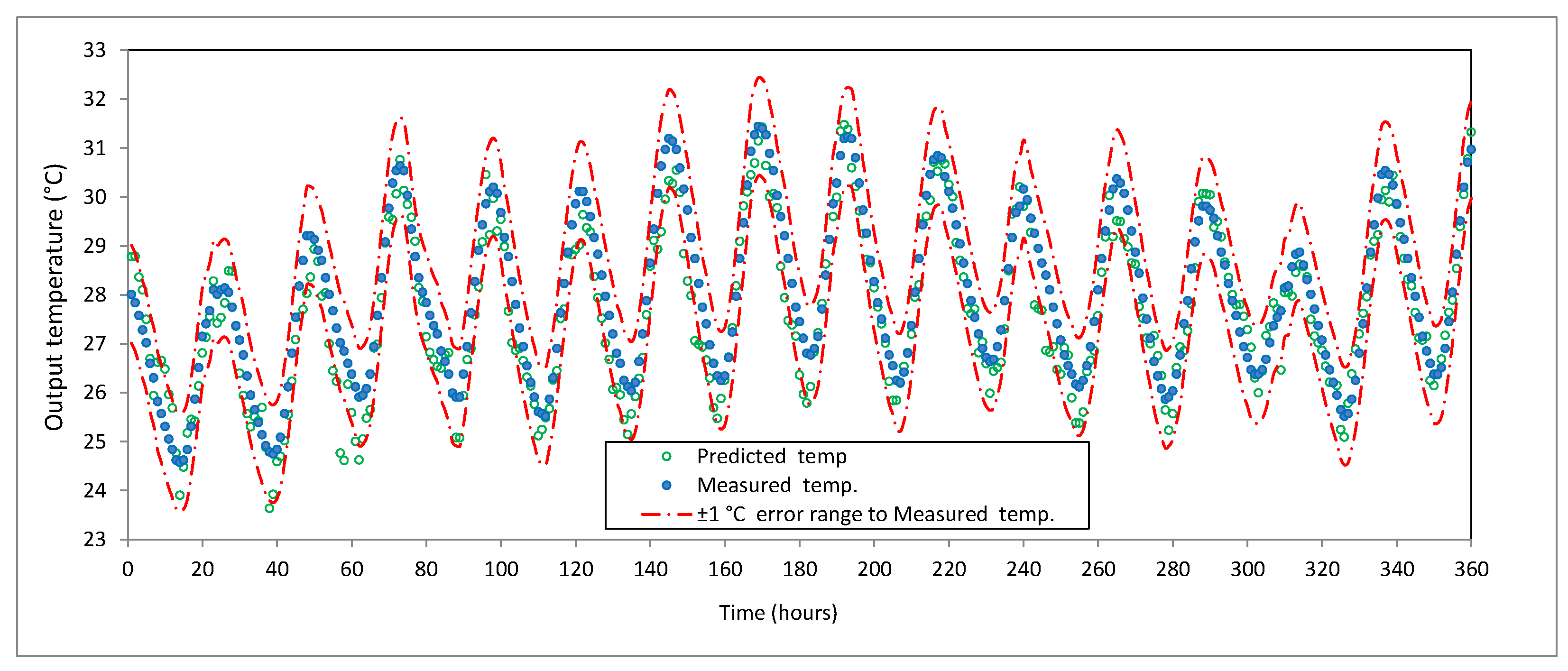
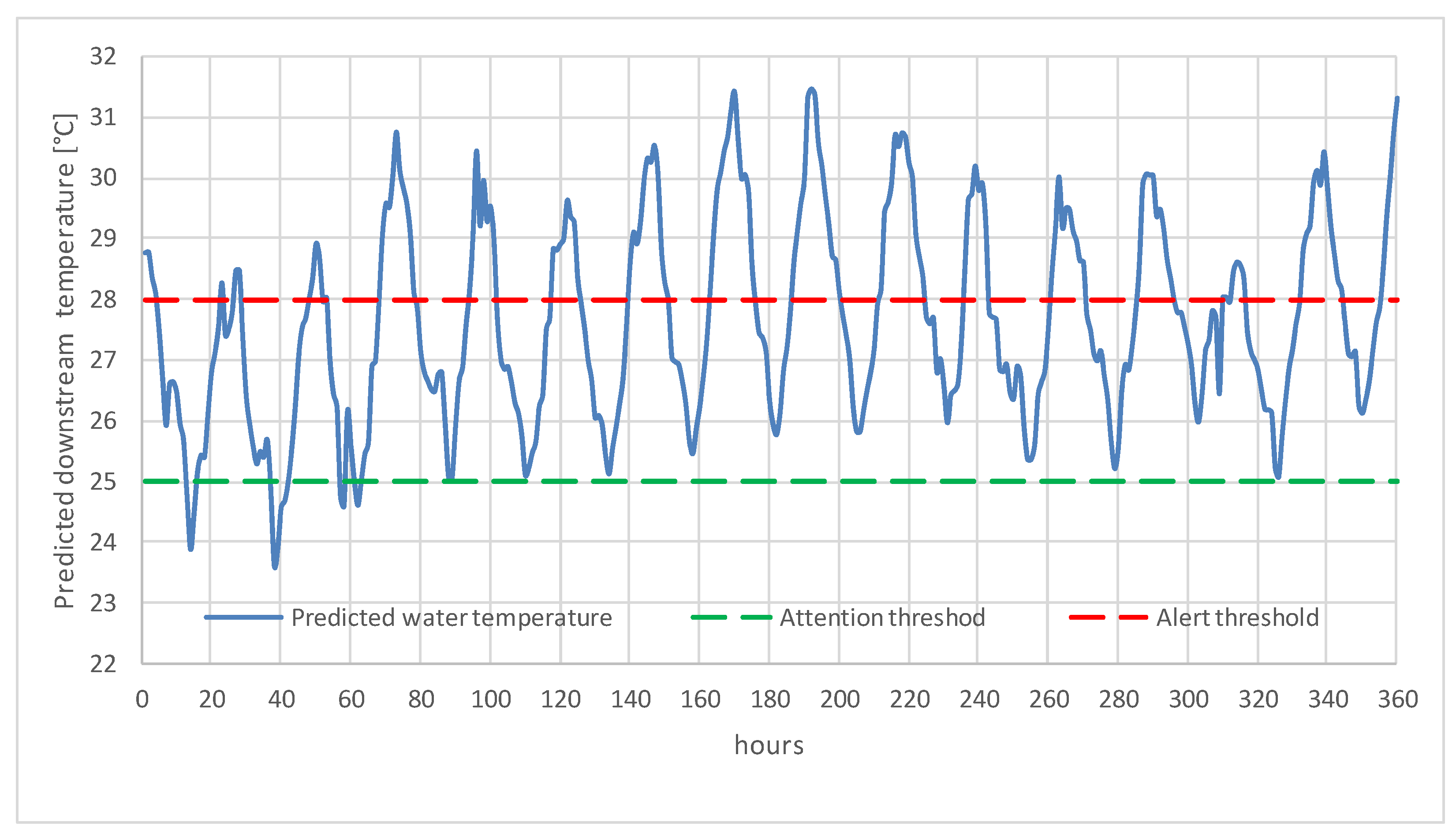
3. Results
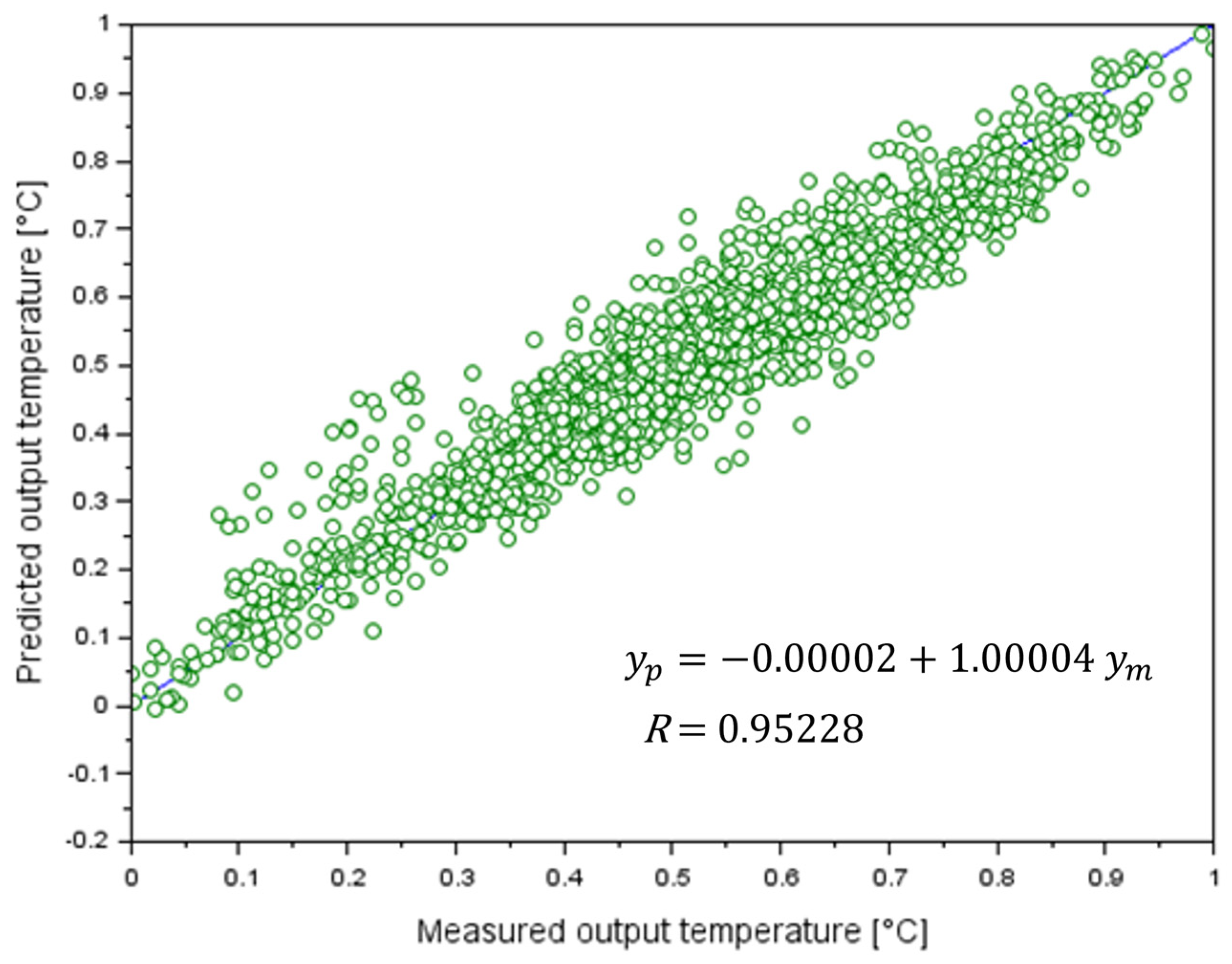
ANN Training
4. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, L.; Qian, F.; Song, D.X.; Zheng, K.J. Research on Urban Heat-Island Effect. Procedia Eng. 2016, 169, 11–18. [Google Scholar] [CrossRef]
- Li, Y.-y.; Zhang, H.; Kainz, W. Monitoring patterns of urban heat islands of the fast-growing Shanghai metropolis, China: Using time-series of Landsat TM/ETM+ data. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 127–138. [Google Scholar] [CrossRef]
- Santamouris, M.; Yun, G.Y. Recent development and research priorities on cool and super cool materials to mitigate urban heat island. Renew. Energy 2020, 161, 792–807. [Google Scholar] [CrossRef]
- Ulpiani, G. On the linkage between urban heat island and urban pollution island: Three-decade literature review towards a conceptual framework. Sci. Total Environ. 2021, 751, 141727. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Chen, Y. Characterizing the indicator-based, day-and-night, and climate-based variations in response of surface urban heat island during heat wave across global 561 cities. Sustain. Cities Soc. 2023, 99, 104877. [Google Scholar] [CrossRef]
- Bhatti, M.; Singh, A.; McBean, E.; Vijayakumar, S.; Fitzgerald, A.; Siwierski, J.; Murison, L. Climate Change Impacts on Water Temperatures in Urban Lakes: Implications for the Growth of Blue Green Algae in Fairy Lake. Water 2024, 16, 587. [Google Scholar] [CrossRef]
- Gupta, N.; Mathew, A.; Khandelwal, S. Analysis of cooling effect of water bodies on land surface temperature in nearby region: A case study of Ahmedabad and Chandigarh cities in India. Egypt. J. Remote Sens. Space Sci. 2019, 22, 81–93. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y. Water Bodies’ Cooling Effects on Urban Land Daytime Surface Temperature: Ecosystem Service Reducing Heat Island Effect. Sustainability 2019, 11, 787. [Google Scholar] [CrossRef]
- Saaroni, H.; Ziv, B. The impact of a small lake on heat stress in a Mediterranean urban park: The case of Tel Aviv, Israel. Int. J. Biometeorol. 2003, 47, 156–165. [Google Scholar] [CrossRef]
- Kim, H.; Lee, G.; Lee, C.-G.; Park, S.-J. Algae development in rivers with artificially constructed weirs: Dominant influence of discharge over temperature. J. Environ. Manag. 2024, 355, 120551. [Google Scholar] [CrossRef]
- Feisal, N.A.S.; Kamaludin, N.H.; Sani, M.F.A.; Ahmad, D.K.A.; Ahmad, M.A.; Razak, N.F.A.; Ibrahim, T.N.B.T. Anthropogenic disturbance of aquatic biodiversity and water quality of an urban river in Penang, Malaysia. Water Sci. Eng. 2023, 16, 234–242. [Google Scholar] [CrossRef]
- Graf, R.; Aghelpour, P. Daily River Water Temperature Prediction: A Comparison between Neural Network and Stochastic Techniques. Atmosphere 2021, 12, 1154. [Google Scholar] [CrossRef]
- Zhu, S.; Piotrowski, A.P. River/stream water temperature forecasting using artificial intelligence models: A systematic review. Acta Geophys. 2020, 68, 1433–1442. [Google Scholar] [CrossRef]
- Qiu, R.; Wang, Y.; Rhoads, B.; Wang, D.; Qiu, W.; Tao, Y.; Wu, J. River water temperature forecasting using a deep learning method. J. Hydrol. 2021, 595, 126016. [Google Scholar] [CrossRef]
- Qiu, R.; Wang, Y.; Wang, D.; Qiu, W.; Wu, J.; Tao, Y. Water temperature forecasting based on modified artificial neural network methods: Two cases of the Yangtze River. Sci. Total Environ. 2020, 737, 139729. [Google Scholar] [CrossRef] [PubMed]
- Graf, R.; Zhu, S.; Sivakumar, B. Forecasting river water temperature time series using a wavelet–neural network hybrid modelling approach. J. Hydrol. 2019, 578, 124115. [Google Scholar] [CrossRef]
- Cole, J.C.; Maloney, K.O.; Schmid, M.; McKenna, J.E., Jr. Developing and testing temperature models for regulated systems: A case study on the Upper Delaware River. J. Hydrol. 2014, 519, 588–598. [Google Scholar] [CrossRef]
- Letcher, B.H.; Hocking, D.J.; O’Neil, K.; Whiteley, A.R.; Nislow, K.H.; O’Donnell, M.J. A hierarchical model of daily stream temperature using air-water temperature synchronization, autocorrelation, and time lags. PeerJ 2016, 4, e1727. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, M.J.; Napiorkowski, J.J.; Osuch, M. Comparing various artificial neural network types for water temperature prediction in rivers. J. Hydrol. 2015, 529, 302–315. [Google Scholar] [CrossRef]
- Mosavi, A.; Salimi, M.; Faizollahzadeh Ardabili, S.; Rabczuk, T.; Shamshirband, S.; Varkonyi-Koczy, A. State of the art of machine learning models in energy systems, a systematic review. Energies 2019, 12, 1301. [Google Scholar] [CrossRef]
- Zhu, S.; Nyarko, E.K.; Hadzima-Nyarko, M. Modelling daily water temperature from air temperature for the Missouri River. PeerJ 2018, 6, e4894. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, A.; Lahiri, S.N.; Wilson, A. A statistical analysis of noisy crowdsourced weather data. Ann. Appl. Stat. 2020, 14, 116–142. [Google Scholar] [CrossRef]
- Shaik, N.B.; Pedapati, S.R.; Taqvi, S.A.A.; Othman, A.R.; Dzubir, F.A.A. A feed-forward back propagation neural network approach to predict the life condition of crude oil pipeline. Processes 2020, 8, 661. [Google Scholar] [CrossRef]
- Gogoașe-Nistoran, D.E.; Ionescu, C.S.; Opriș, I.; Enache, I. Extreme Heatwave Scenarios with Impact on Thermal Regime of Dâmbovița River in Bucharest, Romania. IOP Conf. Ser. Earth Environ. Sci. 2021, 664, 012026. [Google Scholar] [CrossRef]
- Zaharia, L.; Ioana-Toroimac, G.; Cocoş, O.; Ghiţă, F.A.; Mailat, E. Urbanization effects on the river systems in the Bucharest City region (Romania). Ecosyst. Health Sustain. 2016, 2, e01247. [Google Scholar] [CrossRef]
- Stematiu, D.; Teodorescu, D.R. Dâmbovița in Bucharest—Flood defense system. In Proceedings of the Annual conference of the Romanian Academy of Technical Sciences. In Annual Conference of the Romanian Academy of Technical Sciences; A.G.I.R. Publishing House: Bucharest, Romania, 2012; pp. 143–150. (In Romanian) [Google Scholar]
- Gogoașe Nistoran, D.-E.; Dragomirescu, A.; Ionescu, C.-S.; Schiaua, M.; Vasiliu, N.; Georgescu, M. A procedure to develop elevation-area-capacity curves of reservoirs from depth sounding surveys. In Proceedings of the 2017 International Conference on ENERGY and ENVIRONMENT (CIEM), Bucharest, Romania, 19–20 October 2017; pp. 92–96. [Google Scholar] [CrossRef]
- Cheval, S.; Dumitrescu, A. The summer surface urban heat island of Bucharest (Romania) retrieved from MODIS images. Theor. Appl. Climatol. 2015, 121, 631–640. [Google Scholar] [CrossRef]
- Land Process Distributed Active Archive Center (LP DAAC). Available online: https://lpdaac.usgs.gov (accessed on 14 September 2020).
- Dewan, A.M.; Corner, R.J. The Impact of Land Use and Land Cover Changes on Land Surface Temperature in a Rapidly Urbanizing Megacity. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 6337–6339. Available online: https://ieeexplore.ieee.org/document/6352709 (accessed on 10 February 2024).
- Gogoașe Nistoran, D.E.; Ionescu, C.S.; Georgescu, M.; David, D.S. Hydraulic model for water management along Dâmboviţa River through Bucharest City, Romania. E3S Web Conf. 2019, 85, 06007. [Google Scholar] [CrossRef]
- Singh, S.P.; Singh, P. Effect of temperature and light on the growth of algae species: A. review. Renew. Sustain. Energy Rev. 2015, 50, 431–444. [Google Scholar] [CrossRef]
- Available online: https://openweather.co.uk/products/historical-weather-collection (accessed on 25 January 2024).
- Available online: https://openweathermap.org/technology (accessed on 25 January 2024).
- Available online: https://openweathermap.org/accuracy-and-quality (accessed on 25 January 2024).
- Onset, 470 MacArthur Blvd., Bourne, MA 02532, USA. Available online: https://www.onsetcomp.com/products/data-loggers/mx2201#specifications (accessed on 15 February 2024).
- Briciu, A.-E.; Mihăilă, D.; Graur, A.; Oprea, D.I.; Prisăcariu, A.; Bistricean, P.I. Changes in the Water Temperature of Rivers Impacted by the Urban Heat Island: Case Study of Suceava City. Water 2020, 12, 1343. [Google Scholar] [CrossRef]
- Jallal, M.A.; Chabaa, S.; Chabaa, S.; Zeroual, A. Half-hour global solar radiation forecasting based on static and dynamic multivariate neural networks. J. Eng. Res. 2021, 9, 203–217. [Google Scholar] [CrossRef]
- Puiseux, T. Simulations Numériques Pour l’Imagerie par Résonance Magnétique à Contraste de Phase. Ph.D. Thesis, Universite de Montpellier, Montpellier, France, 2019. [Google Scholar]
- Meza, J.C. Steepest descent. WIREs Comput. Stat. 2010, 2, 719–722. [Google Scholar] [CrossRef]
- Prashanthi, A.; Reddy, R.R. A Feed-Forward and Back Propagation Neural Network Approach for Identifying Network Anomalies. In Proceedings of the 2023 International Conference for Advancement in Technology (ICONAT), Goa, India, 24–26 January 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Bebis, G.; Georgiopoulos, M. Feed-forward neural networks. IEEE Potentials 1994, 13, 27–31. [Google Scholar] [CrossRef]
- Yagli, G.M.; Yang, D.; Srinivasan, D. Automatic hourly solar forecasting using machine learning models. Renew. Sustain. Energy Rev. 2019, 105, 487–498. [Google Scholar] [CrossRef]
- Wilamowski, B.M.; Yu, H. Improved Computation for Levenberg Marquardt Training. IEEE Trans. Neural Netw. 2010, 21, 930–937. [Google Scholar] [CrossRef] [PubMed]
- Sushmi, N.B.; Subbulekshmi, D. Performance Analysis of FFBP-LM-ANN Based Hourly GHI Prediction Using Environmental Variables: A Case Study in Chennai. Math. Probl. Eng. 2022, 2022, 1713657. [Google Scholar] [CrossRef]
- Pourpasha, H.; Farshad, P.; Zeinali, S.H. Modeling and optimization the effective parameters of nanofluid heat transfer performance using artificial neural network and genetic algorithm method. Energy Rep. 2021, 7, 8447–8464. [Google Scholar] [CrossRef]
- Scilab Enterprises. Scilab Version 6.0.1. Available online: https://www.scilab.org/ (accessed on 20 April 2023).
- Souchon, Y.; Tissot, L. Synthesis of Thermal Tolerances of the Common Freshwater Fish Species in Large Western Europe Rivers. Knowl. Manag. Aquat. Ecosyst. 2012, 405, 3. [Google Scholar] [CrossRef]
- Zhu, S.; Hadzima-Nyarko, M.; Gao, A.; Wang, F.; Wu, J.; Wu, S. Two hybrid data-driven models for modeling water-air temperature relationship in rivers. Environ. Sci. Pollut. Res. 2019, 26, 12622–12630. [Google Scholar] [CrossRef]
- Intergovernmental Panel for Climate Change (IPCC). AR6 Synthesis Report Climate Change 2023. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023; pp. 35–115. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ionescu, C.-S.; Opriș, I.; Gogoașe Nistoran, D.-E.; Copilău, C. A Simple Artificial Neural Model to Predict Dambovita River Temperature Affected by Urban Heat Islands in Bucharest City. Remote Sens. 2024, 16, 1513. https://doi.org/10.3390/rs16091513
Ionescu C-S, Opriș I, Gogoașe Nistoran D-E, Copilău C. A Simple Artificial Neural Model to Predict Dambovita River Temperature Affected by Urban Heat Islands in Bucharest City. Remote Sensing. 2024; 16(9):1513. https://doi.org/10.3390/rs16091513
Chicago/Turabian StyleIonescu, Cristina-Sorana, Ioana Opriș, Daniela-Elena Gogoașe Nistoran, and Cristian Copilău. 2024. "A Simple Artificial Neural Model to Predict Dambovita River Temperature Affected by Urban Heat Islands in Bucharest City" Remote Sensing 16, no. 9: 1513. https://doi.org/10.3390/rs16091513
APA StyleIonescu, C.-S., Opriș, I., Gogoașe Nistoran, D.-E., & Copilău, C. (2024). A Simple Artificial Neural Model to Predict Dambovita River Temperature Affected by Urban Heat Islands in Bucharest City. Remote Sensing, 16(9), 1513. https://doi.org/10.3390/rs16091513







