Classification of Lakebed Geologic Substrate in Autonomously Collected Benthic Imagery Using Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Dataset
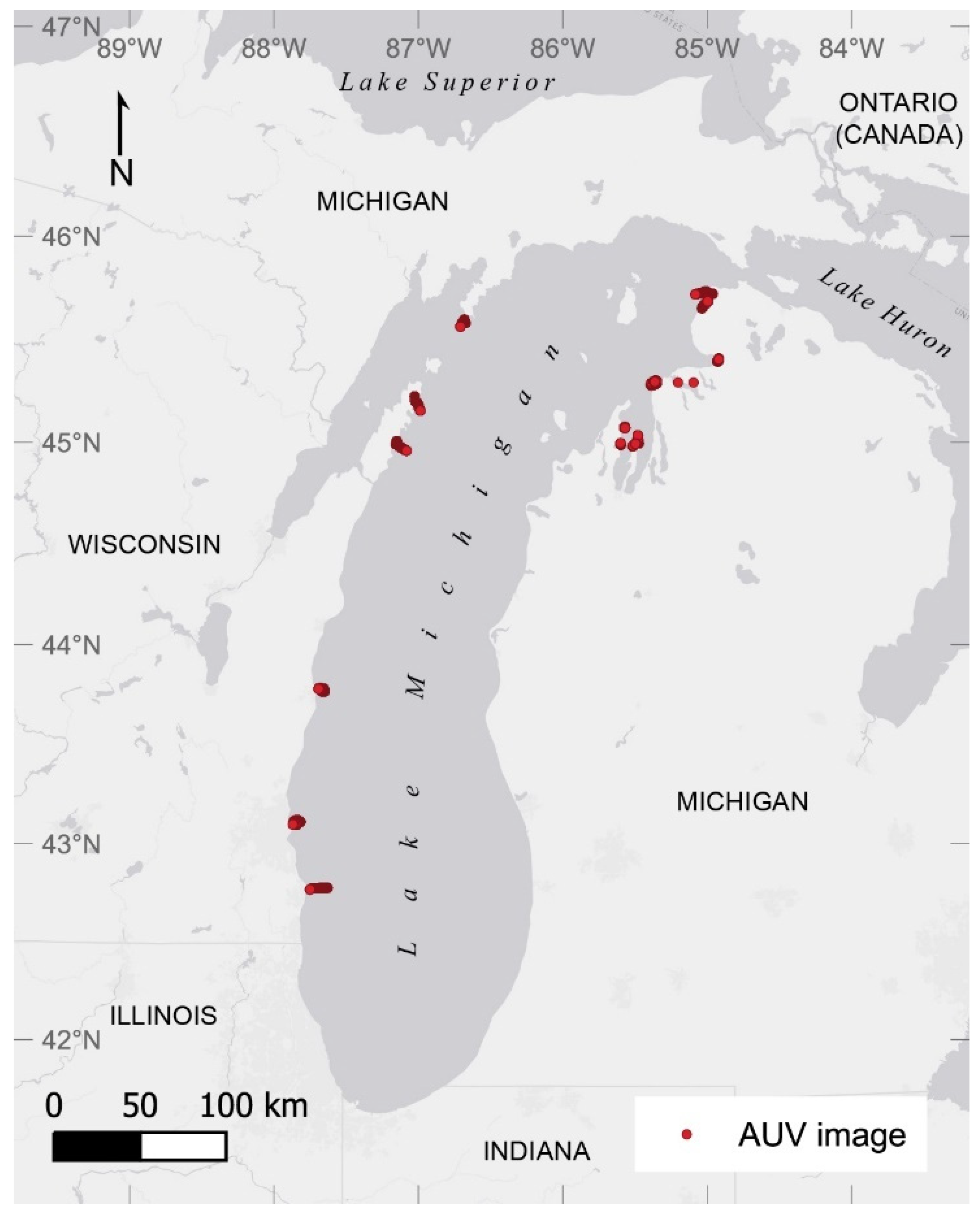
2.1.1. AUV Image Dataset
2.1.2. Classification Scheme
2.1.3. Creation of Training Dataset
2.2. Machine Learning Classification Models
2.2.1. Random Forest (RF) Models
- Intensity Variance: The brightness, or intensity, of a pixel in a grayscale image is simply an 8-bit integer, a number between 0 to 256. The variance of these values indicates how much these numbers are dispersed about their mean. Heuristically, we would expect to see more variation where there are more shadows and reflective surfaces.
- Edgeness: We would expect images with more “things” in them—usually rocks or shells or plants—would have more edges. We apply a canny edge detection algorithm [40] with sigma set to 3 to the image and calculate the proportion of pixels in the image that are considered edges. This metric we call “Edgeness”.
- Gray Level Co-Occurrence Matrix: Gray Level Co-Occurrence Matrices (GLCMs) are often used for analyzing texture in images. Four GLCMs were calculated for each pre-processed image, using an offset of 1 and angles of 0, π/4, π/2, and 3π/4. The contrast, dissimilarity, ASM, energy, and correlation, all defined in paper [41], were calculated from these matrices and averaged over the four angles. Each metric was a separate feature in the feature vector.
- Local Binary Patterns: Local Binary Patterns (LBPs), first defined in [42], are commonly used for texture analysis. Using only 4 neighbors 1 pixel away, a histogram of the number of pixels falling into each of the 16 local binary pattern bins in the image was obtained. The number of pixels in each bin became a metric in the feature vector, resulting in 16 features.
- Fourier Metrics: The discrete 2D Fast Fourier Transform (FFT) of each image was taken [43]. Then, the Frobenius Norm was taken, first of the entire FFT matrix, then of the FFT matrix masked to highlight certain frequencies in the image. In total, 4 annuli-shaped masks were used so that the angle of the frequency was ignored. With the minimum side length of the images being 1306 pixels, the 4 masks were from 0 to 326 pixels, 326 to 653 pixels, 653 to 979 pixels, and 979 to 1306 pixels. The norms for each of the different matrices each gave a metric for the feature vector, totaling 5 feature metrics.
- Point Cloud Standard Deviation: In addition to color images, the AUV collects stereo imagery from two 2 Mp grayscale cameras and calculates disparity maps and point clouds at four frames per second (the cameras are not synchronized so there may have been some offset to the images). The roughness of the point clouds was assumed to correlate to the roughness of the benthic surface in the color image. We calculated the standard deviation of the heights of the points as a measure of roughness, where height is defined to be the distance from the plane of best fit through the point cloud. The plane of best fit was identified using principal components analysis (PCA) by taking the first and second principal components (PC1 and PC2) to represent lateral dimensions of the data. The third principal component (PC3) is orthogonal to the lateral plane and should capture vertical dispersion in the data. This metric was calculated for each point cloud in a mission and treated as a time series. Each color image was assigned a plane standard deviation value by linearly interpolating the plane standard deviation time series to the timestamp of the image.
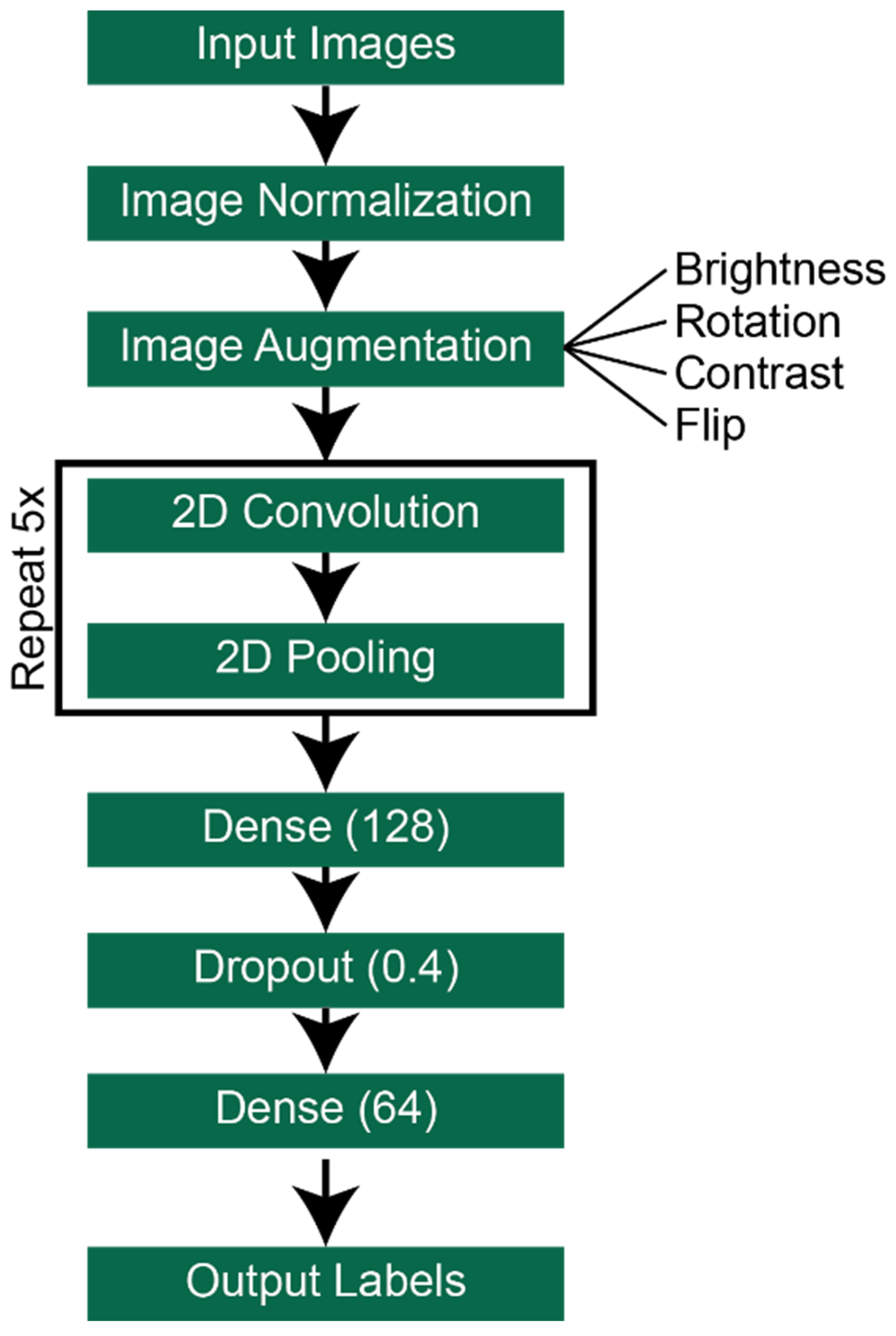
2.2.2. Deep Neural Network (DNN) Models
3. Results
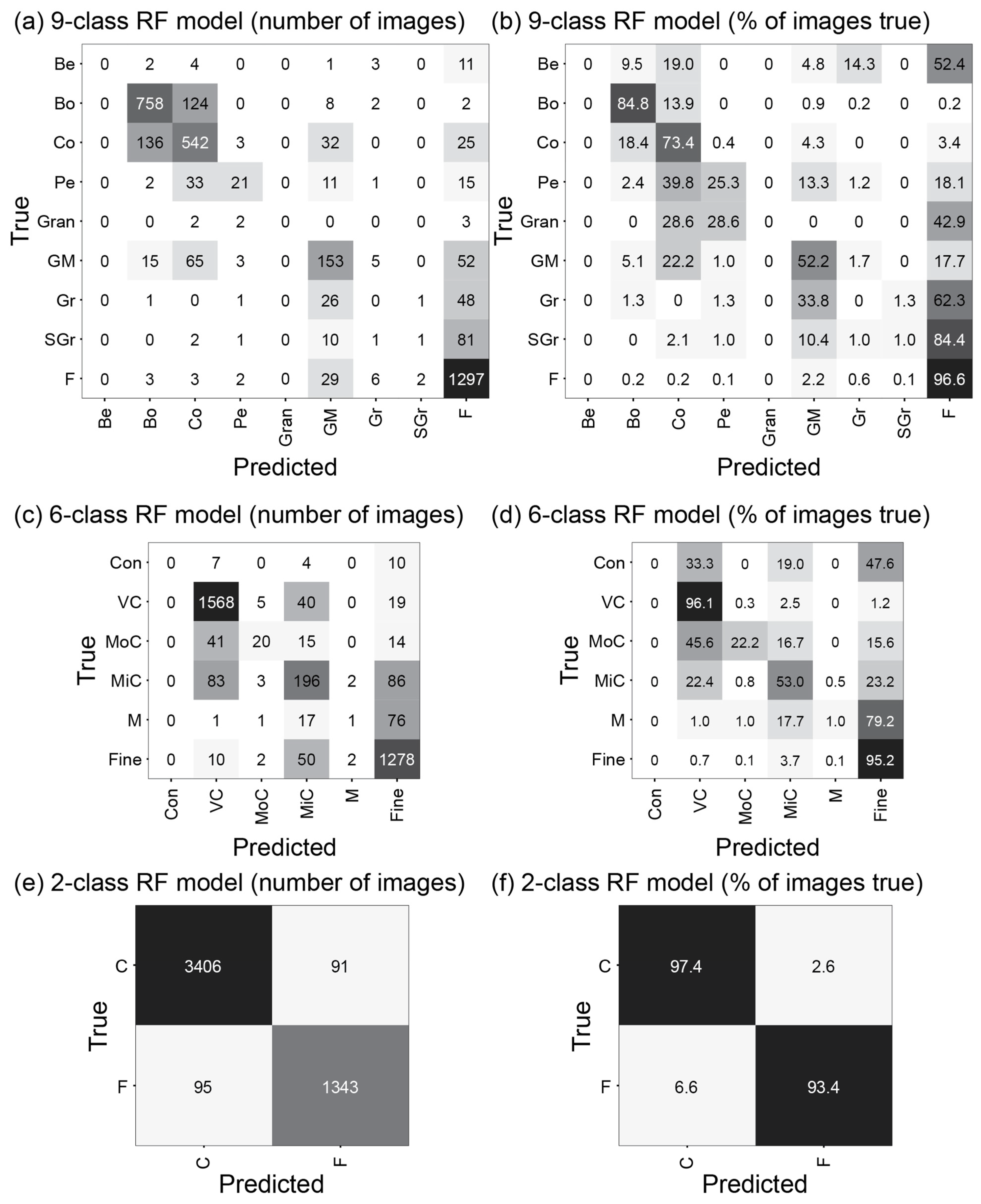
3.1. RF Image Classification Models
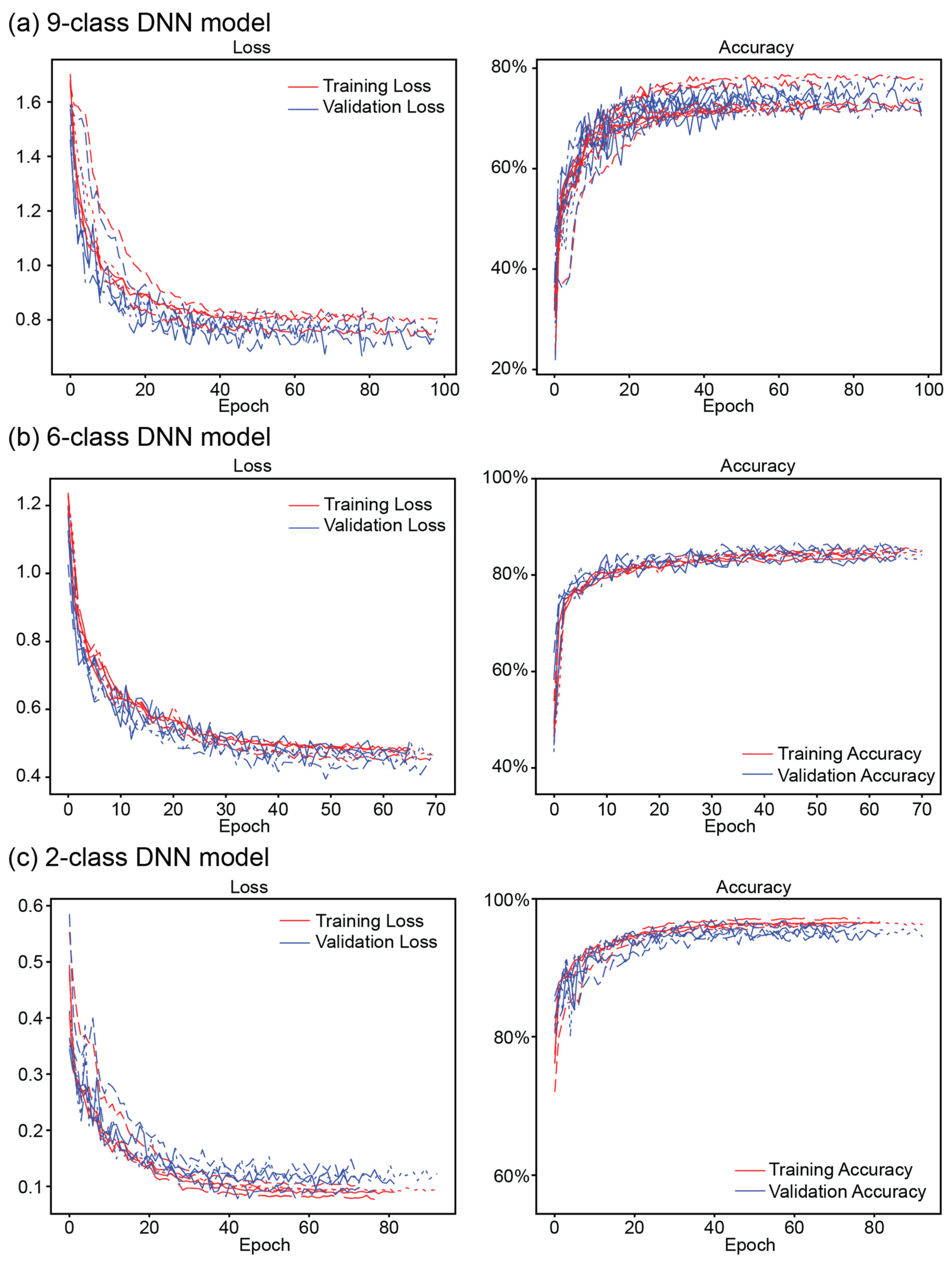
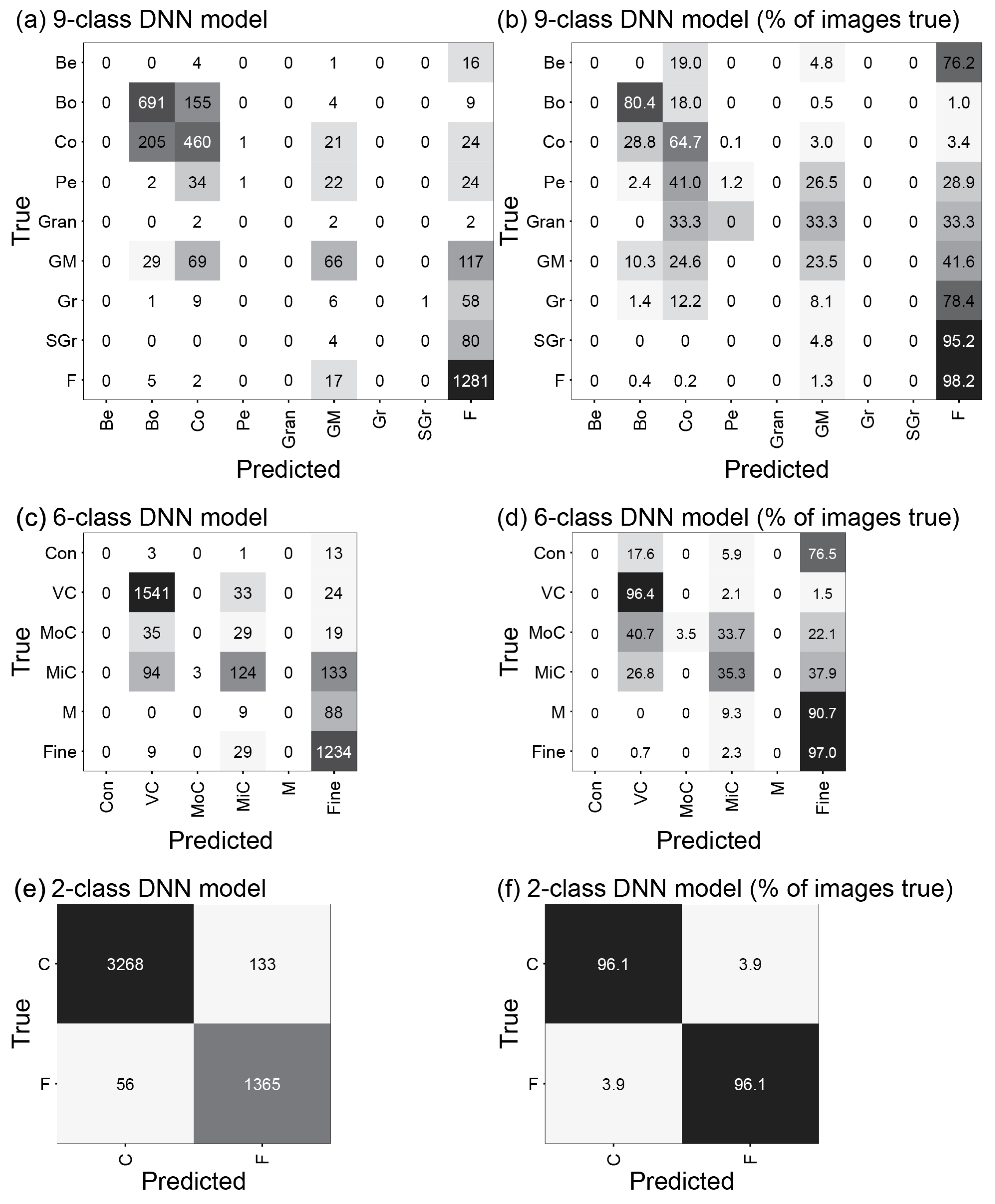
3.2. DNN Image Classification Models
4. Discussion
4.1. Manual Image Labeling
4.2. RF Image Classification Models
4.3. DNN Image Classification Models
4.4. Model Comparison
4.5. Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Appendix A
| Full Dataset (All AUV Images) | 1.25–3.00 m AUV Images | 1.60–2.10 m AUV Images | |
|---|---|---|---|
| Bedrock | 46 | 43 | 21 |
| Boulder | 1488 | 1435 | 894 |
| Cobble | 1133 | 1096 | 738 |
| Pebble | 136 | 127 | 83 |
| Granule | 13 | 13 | 7 |
| Gravel Mix | 500 | 475 | 293 |
| Gravelly | 124 | 120 | 77 |
| Slightly Gravelly | 138 | 136 | 96 |
| Fine | 1768 | 1740 | 1342 |
| Coarse Algae | 1936 | 1901 | 1405 |
| Total Images | 7282 | 7086 | 4956 |
| Altitude | GSR (mm) | ||
|---|---|---|---|
| Dataset | Programmed AUV altitude | 1.75 | 0.477 |
| Full | Minimum | 0.51 | 0.139 |
| Mean | 2.01 | 0.548 | |
| Maximum | 4.91 | 1.339 | |
| 1.25–3.00 m | Minimum | 1.25 | 0.341 |
| Mean | 1.98 | 0.540 | |
| Maximum | 3.00 | 0.818 | |
| 1.60–2.10 m | Minimum | 1.60 | 0.436 |
| Mean | 1.88 | 0.513 | |
| Maximum | 2.10 | 0.573 |
| Dataset | Model Type | Number of Classes | Without Altitude | With Altitude |
|---|---|---|---|---|
| Full | RF | 9 | 74.8 ± 0.4% | 75.3 ± 0.5% |
| 6 | 85.8 ± 0.5% | 85.8 ± 0.6% | ||
| 2 | 96 ± 0.6% | 96.1 ± 0.7% | ||
| DNN | 9 | 72.1 ± 3.2% | 33.2 ± 1% | |
| 6 | 83.8 ± 2.4% | 49.4 ± 0.7% | ||
| 2 | 96.5 ± 0.9% | 73.9 ± 1.3% | ||
| 1.25–3.00 m | RF | 9 | 75.5 ± 0.8% | 75.4 ± 0.5% |
| 6 | 85.7 ± 1.1% | 85.8 ± 1.1% | ||
| 2 | 96.2 ± 0.3% | 96.1 ± 0.4% | ||
| DNN | 9 | 72.3 ± 3.7% | 33.6 ± 0.8% | |
| 6 | 84.5 ± 1.7% | 48.8 ± 1.4% | ||
| 2 | 95.4 ± 0.7% | 73.3 ± 1.1% | ||
| 1.60–2.10 m | RF | 9 | 78.1 ± 0.9% | 78.2 ± 0.8% |
| 6 | 86.3 ± 0.9% | 86.6 ± 1.1% | ||
| 2 | 96.2 ± 1% | 96.2 ± 1.1% | ||
| DNN | 9 | 73.1 ± 0.9% | 37.9 ± 1.5% | |
| 6 | 84.1 ± 1.4% | 46.5 ± 1.9% | ||
| 2 | 96.2 ± 0.8% | 70.7 ± 1.7% |
References
- Valentine, P.C. Sediment Classification and the Characterization, Identification, and Mapping of Geologic Substrates for the Glaciated Gulf of Maine Seabed and Other Terrains, Providing a Physical Framework for Ecological Research and Seabed Management; Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2019; p. 50. [Google Scholar]
- Gibbs, A.G.; Cochrane, S.A. An Integrated Approach to Benthic Habitat Mapping Using Remote Sensing and GIS: An Example from the Hawaiian Islands. In Remote Sensing and Geospatial Technologies for Coastal Ecosystem Assessment and Management; Lecture Notes in Geoinformation and Cartography; Springer: Berlin/Heidelberg, Germany, 2009; pp. 211–231. ISBN 978-3-540-88182-7. [Google Scholar]
- Lucieer, V.; Hill, N.A.; Barrett, N.S.; Nichol, S. Do Marine Substrates ‘Look’ and ‘Sound’ the Same? Supervised Classification of Multibeam Acoustic Data Using Autonomous Underwater Vehicle Images. Estuar. Coast. Shelf Sci. 2013, 117, 94–106. [Google Scholar] [CrossRef]
- Montereale Gavazzi, G.; Kapasakali, D.A.; Kerchof, F.; Deleu, S.; Degraer, S.; Van Lancker, V. Subtidal Natural Hard Substrate Quantitative Habitat Mapping: Interlinking Underwater Acoustics and Optical Imagery with Machine Learning. Remote Sens. 2021, 13, 4608. [Google Scholar] [CrossRef]
- Reif, M.K.; Krumwiede, B.S.; Brown, S.E.; Theuerkauf, E.J.; Harwood, J.H. Nearshore Benthic Mapping in the Great Lakes: A Multi-Agency Data Integration Approach in Southwest Lake Michigan. Remote Sens. 2021, 13, 3026. [Google Scholar] [CrossRef]
- Mabrouk, A.; Menza, C.; Sautter, W. Best Practices for Ground-Truthing and Accuracy Assessment of Lakebed Maps in the Great Lakes: A Case Study Offshore the Bayfield Peninsula in Lake Superior; Springer: Berlin/Heidelberg, Germany, 2022; p. 25. [Google Scholar] [CrossRef]
- Benoist, N.M.A.; Morris, K.J.; Bett, B.J.; Durden, J.M.; Huvenne, V.A.I.; Le Bas, T.P.; Wynn, R.B.; Ware, S.J.; Ruhl, H.A. Monitoring Mosaic Biotopes in a Marine Conservation Zone by Autonomous Underwater Vehicle. Conserv. Biol. 2019, 33, 1174–1186. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, A.; Ospina, A.G.; Bennamoun, M.; An, S.; Sohel, F.; Boussaid, F.; Hovey, R.; Fisher, R.B.; Kendrick, G.A. Automatic Hierarchical Classification of Kelps Using Deep Residual Features. Sensors 2020, 20, 447. [Google Scholar] [CrossRef]
- Mohamed, H.; Nadaoka, K.; Nakamura, T. Semiautomated Mapping of Benthic Habitats and Seagrass Species Using a Convolutional Neural Network Framework in Shallow Water Environments. Remote Sens. 2020, 12, 4002. [Google Scholar] [CrossRef]
- Mohamed, H.; Nadaoka, K.; Nakamura, T. Towards Benthic Habitat 3D Mapping Using Machine Learning Algorithms and Structures from Motion Photogrammetry. Remote Sens. 2020, 12, 127. [Google Scholar] [CrossRef]
- Wentworth, C.K. A Scale of Grade and Class Terms for Clastic Sediments. J. Geol. 1922, 30, 377–392. [Google Scholar] [CrossRef]
- Trefethen, J.M. Classification of Sediments. Am. J. Sci. 1950, 248, 55–62. [Google Scholar] [CrossRef]
- Schlee, J.S. Atlantic Continental Shelf and Slope of the United States: Sediment Texture of the Northeastern Part; Professional Paper; US Geological Survey: Seattle, WA, USA, 1973. [Google Scholar]
- Shepard, F.P. Nomenclature Based on Sand-Silt-Clay Ratios. J. Sediment. Res. 1954, 24, 151–158. [Google Scholar]
- Folk, R.L. Petrology of Sedimentary Rocks; Hemphill Publishing Company: Austin, TX, USA, 1980. [Google Scholar]
- United States. National Ocean Service and United States. Federal Geographic Data Committee. Coastal and Marine Ecological Classification Standard (CMECS). 2012. Available online: https://repository.library.noaa.gov/view/noaa/27552 (accessed on 6 June 2022).
- Harter, S.L.; Paxton, A.B.; Winship, A.J.; Hile, S.D.; Taylor, J.C.; Poti, M.; Menza, C. Workshop Report for Approaches to Mapping, Ground-Truthing, and Predictive Habitat Modeling of the Distribution and Abundance of Mesophotic and Deep Benthic Communities; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2022; p. 38. [Google Scholar]
- Burns, C.; Bollard, B.; Narayanan, A. Machine-Learning for Mapping and Monitoring Shallow Coral Reef Habitats. Remote Sens. 2022, 14, 2666. [Google Scholar] [CrossRef]
- Chen, X.; Hassan, M.A.; Fu, X. Convolutional Neural Networks for Image-Based Sediment Detection Applied to a Large Terrestrial and Airborne Dataset. Earth Surf. Dynam. 2022, 10, 349–366. [Google Scholar] [CrossRef]
- González-Rivero, M.; Beijbom, O.; Rodriguez-Ramirez, A.; Bryant, D.E.P.; Ganase, A.; Gonzalez-Marrero, Y.; Herrera-Reveles, A.; Kennedy, E.V.; Kim, C.J.S.; Lopez-Marcano, S.; et al. Monitoring of Coral Reefs Using Artificial Intelligence: A Feasible and Cost-Effective Approach. Remote Sens. 2020, 12, 489. [Google Scholar] [CrossRef]
- Pavoni, G.; Corsini, M.; Pedersen, N.; Petrovic, V.; Cignoni, P. Challenges in the Deep Learning-Based Semantic Segmentation of Benthic Communities from Ortho-Images. Appl. Geomat. 2021, 13, 131–146. [Google Scholar] [CrossRef]
- Raphael, A.; Dubinsky, Z.; Iluz, D.; Netanyahu, N.S. Neural Network Recognition of Marine Benthos and Corals. Diversity 2020, 12, 29. [Google Scholar] [CrossRef]
- Raphael, A.; Dubinsky, Z.; Netanyahu, N.S.; Iluz, D. Deep Neural Network Analysis for Environmental Study of Coral Reefs in the Gulf of Eilat (Aqaba). BDCC 2021, 5, 19. [Google Scholar] [CrossRef]
- Wang, H.; Fu, X.; Zhao, C.; Luan, Z.; Li, C. A Deep Learning Model to Recognize and Quantitatively Analyze Cold Seep Substrates and the Dominant Associated Species. Front. Mar. Sci. 2021, 8, 775433. [Google Scholar] [CrossRef]
- Ternon, Q.; Danet, V.; Thiriet, P.; Ysnel, F.; Feunteun, E.; Collin, A. Classification of Underwater Photogrammetry Data for Temperate Benthic Rocky Reef Mapping. Estuar. Coast. Shelf Sci. 2022, 270, 107833. [Google Scholar] [CrossRef]
- Diesing, M.; Green, S.L.; Stephens, D.; Lark, R.M.; Stewart, H.A.; Dove, D. Mapping Seabed Sediments: Comparison of Manual, Geostatistical, Object-Based Image Analysis and Machine Learning Approaches. Cont. Shelf Res. 2014, 84, 107–119. [Google Scholar] [CrossRef]
- Mohamed, H.; Nadaoka, K.; Nakamura, T. Assessment of Machine Learning Algorithms for Automatic Benthic Cover Monitoring and Mapping Using Towed Underwater Video Camera and High-Resolution Satellite Images. Remote Sens. 2018, 10, 773. [Google Scholar] [CrossRef]
- Wicaksono, P.; Aryaguna, P.A.; Lazuardi, W. Benthic Habitat Mapping Model and Cross Validation Using Machine-Learning Classification Algorithms. Remote Sens. 2019, 11, 1279. [Google Scholar] [CrossRef]
- Cui, X.; Liu, H.; Fan, M.; Ai, B.; Ma, D.; Yang, F. Seafloor Habitat Mapping Using Multibeam Bathymetric and Backscatter Intensity Multi-Features SVM Classification Framework. Appl. Acoust. 2021, 174, 107728. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; ISBN 978-0-521-54051-3. [Google Scholar]
- Geisz, J.K.; Wernette, P.A.; Esselman, P.C.; Morris, J.M. Autonomously Collected Benthic Imagery for Substrate Prediction, Lake Michigan 2020–2021; U.S. Geological Survey: Reston, VA, USA, 2024. [Google Scholar] [CrossRef]
- Fincham, J.I.; Wilson, C.; Barry, J.; Bolam, S.; French, G. Developing the Use of Convolutional Neural Networking in Benthic Habitat Classification and Species Distribution Modelling. ICES J. Mar. Sci. 2020, 77, 3074–3082. [Google Scholar] [CrossRef]
- Gómez-Ríos, A.; Tabik, S.; Luengo, J.; Shihavuddin, A.; Krawczyk, B.; Herrera, F. Towards Highly Accurate Coral Texture Images Classification Using Deep Convolutional Neural Networks and Data Augmentation. Expert Syst. Appl. 2019, 118, 315–328. [Google Scholar] [CrossRef]
- Elith, J. Machine Learning, Random Forests and Boosted Regression Trees. In Quantitative Analyses in Wildlife Science; Wildlife Management and Conservation; Johns Hopkins University Press: Baltimore, MD, USA, 2019; p. 281. ISBN 978-1-4214-3107-9. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Bradski, G. The OpenCV Library. Dr. Dobb’s J. Softw. Tools 2000, 120, 122–125. [Google Scholar]
- The Pandas Development Team. Pandas-Dev/Pandas: Pandas 2020. Available online: https://zenodo.org/records/10697587 (accessed on 5 September 2023).
- van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef] [PubMed]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973; SMC-3, 610–621. [Google Scholar] [CrossRef]
- Wang, L.; He, D.-C. Texture Classification Using Texture Spectrum. Pattern Recognit. 1990, 23, 905–910. [Google Scholar] [CrossRef]
- Strang, G. Wavelets. Am. Sci. 1994, 82, 250–255. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- Keras 2015. Available online: https://keras.io (accessed on 5 September 2023).
- Zhang, L.; Tanno, R.; Xu, M.-C.; Jin, C.; Jacob, J.; Ciccarelli, O.; Barkhof, F.; Alexander, D.C. Disentangling Human Error from the Ground Truth in Segmentation of Medical Images. In Proceedings of the Advances in Neural Information Processing Systems 33 (NeurIPS 2020), Virtual, 6–12 December 2020; Neural Information Processing Systems Foundation, Inc. (NeurIPS): Vancouver, BC, Canada, 2021. [Google Scholar]
- Ontario Geological Survey 1:250 000 Scale Bedrock Geology of Ontario 2011. Available online: https://www.geologyontario.mndm.gov.on.ca/mndmfiles/pub/data/records/MRD126-REV1.html (accessed on 5 September 2023).
- Schruben, P.G.; Arndt, R.E.; Bawiec, W.J.; King, P.B.; Beikman, H.M. Geology of the Conterminous United States at 1:2,500,000 Scale a Digital Representation of the 1974 P.B. King and H.M. Beikman Map; Data Series; Release 2, 1998; U.S. Geological Survey: Reston, VA, USA, 1998. [Google Scholar]
- Shihavuddin, A.S.M.; Gracias, N.; Garcia, R.; Gleason, A.; Gintert, B. Image-Based Coral Reef Classification and Thematic Mapping. Remote Sens. 2013, 5, 1809–1841. [Google Scholar] [CrossRef]
- Stokes, M.D.; Deane, G.B. Automated Processing of Coral Reef Benthic Images: Coral Reef Benthic Imaging. Limnol. Oceanogr. Methods 2009, 7, 157–168. [Google Scholar] [CrossRef]
- Mohammed, R.; Rawashdeh, J.; Abdullah, M. Machine Learning with Oversampling and Undersampling Techniques: Overview Study and Experimental Results. In Proceedings of the 2020 11th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 7–9 April 2020; pp. 243–248. [Google Scholar]
- Ellen Marsden, J.; Casselman, J.M.; Edsall, T.A.; Elliott, R.F.; Fitzsimons, J.D.; Horns, W.H.; Manny, B.A.; McAughey, S.C.; Sly, P.G.; Swanson, B.L. Lake Trout Spawning Habitat in the Great Lakes—A Review of Current Knowledge. J. Great Lakes Res. 1995, 21, 487–497. [Google Scholar] [CrossRef]
- Buscombe, D. Shallow Water Benthic Imaging and Substrate Characterization Using Recreational-Grade Sidescan-Sonar. Environ. Model. Softw. 2017, 89, 1–18. [Google Scholar] [CrossRef]
- Galloway, A.; Brunet, D.; Valipour, R.; McCusker, M.; Biberhofer, J.; Sobol, M.K.; Moussa, M.; Taylor, G.W. Predicting Dreissenid Mussel Abundance in Nearshore Waters Using Underwater Imagery and Deep Learning. Limnol. Ocean Methods 2022, 20, 233–248. [Google Scholar] [CrossRef]

| CMECS Substrate Class | CMECS Substrate Subclass | CMECS Substrate Group | CMECS Substrate Subgroup | Label |
|---|---|---|---|---|
| Consolidated Mineral | Bedrock | Bedrock | ||
| Megaclast | (>4096 mm) | |||
| Unconsolidated Mineral | Coarse Unconsolidated | Gravel | Boulder | Boulder |
| (256 mm to <4096 mm) | ||||
| Cobble | Cobble | |||
| (64 mm to <256 mm) | ||||
| Pebble | Pebble | |||
| (4 mm to <64 mm) | ||||
| Granule | Granule | |||
| (2–4 mm) | ||||
| Gravel Mixes | Sandy Gravel | Gravel Mixes | ||
| Muddy Sandy Gravel | ||||
| Muddy Gravel | ||||
| Gravelly | Gravelly Sand | Gravelly | ||
| Gravelly Muddy Sand | ||||
| Gravelly Mud | ||||
| Fine Unconsolidated | Slightly Gravelly | Slightly Gravelly Sand | Slightly Gravelly | |
| Slightly Gravelly Muddy Sand | ||||
| Slightly Gravelly Sandy Mud | ||||
| Slightly Gravelly Mud | ||||
| Sand | Very Coarse Sand | Fine (<2 mm) | ||
| Coarse Sand | ||||
| Medium Sand | ||||
| Fine Sand | ||||
| Very Fine Sand | ||||
| Muddy Sand | Silty Sand | |||
| Silty-Clayey Sand | ||||
| Clayey Sand | ||||
| Sandy Mud | Sandy Silt | |||
| Sandy Silt-Clay | ||||
| Sandy Clay | ||||
| Mud | Silt | |||
| Silt-Clay | ||||
| Clay |
| Label (Abbreviation) | Image Class Definition |
|---|---|
| Bedrock (Be) | The substrate in the image belongs to the Rock CMECS class, either bedrock or megaclast. This is a substrate with continuous formations of bedrock or megaclast (particles ≥ 4.0 m) that cover 50% or more of the image surface. |
| Boulder (Bo) | The substrate in the image belongs to the CMECS Boulder Subgroup. The Geologic Substrate contains >80% Gravel, with the areal extent dominated by Gravel particles of size 256 mm to <4096 mm. |
| Cobble (Co) | The substrate in the image belongs to the CMECS Cobble Subgroup. The Geologic Substrate contains >80% Gravel, with the areal extent dominated by Gravel particles of size 64 mm to <256 mm |
| Pebble (Pe) | The substrate in the image belongs to the CMECS Boulder Subgroup. The Geologic Substrate contains >80% Gravel, with the areal extent dominated by Gravel particles of size 4 mm to <64 mm. |
| Granule (Gran) | The substrate in the image belongs to the CMECS Boulder Subgroup. The Geologic Substrate contains >80% Gravel, with the areal extent dominated by Gravel particles of size 2 mm to <4 mm. |
| Gravel Mixes (GM) | The substrate in the image belongs to the CMECS Gravel Mixes Group. The Geologic Substrate surface layer contains 30% to <80% Gravel (particles 2 mm to <4096 mm). |
| Gravelly (Gr) | The substrate in the image belongs to the CMECS Gravelly Group. The Geologic Substrate surface layer contains 5% to <30% Gravel (particles 2 mm to <4096 mm). |
| Slightly Gravelly (SGr) | The substrate in the image belongs to the CMECS Slightly Gravelly Group. The Geologic Substrate surface layer contains from a trace (0.01%) of Gravel to 5% Gravel (particles 2 mm to <4096 mm). |
| Fine (F) | The substrate in the image belongs to the CMECS Fine Unconsolidated Substrate Subclass, but not the Slightly Gravelly Group. The Geologic Substrate surface layer contains no trace of Gravel and is composed entirely of particles <2 mm, including sand, mud (clay and silt), and mixed types. |
| 9-Class | 6-Class | 2-Class |
|---|---|---|
| Bedrock (Be) (21) | Consolidated (Con) (21) | |
| Boulder (Bo) (894) | Very Coarse (VC) (1632) | Coarse * (C) (3497) |
| Cobble (Co) (738) | ||
| Pebble (Pe) (83) | Moderately Coarse (MoC) (90) | |
| Granule (Gran) (7) | ||
| Gravel Mix (GM) (293) | Mixed Coarse (MiC) (370) | |
| Gravelly (Gr) (77) | ||
| Slightly Gravelly (SGr) (96) | Mixed (M) (96) | Fine (F) (1438) |
| Fine (F) (1342) | Fine (F) (1342) | |
| Coarse Algae (CA) (1405) | ||
| Condition | Final Label |
|---|---|
| All three labelers agree on classification | Three-way agreed-upon class |
| Two labelers agree on the classification, one labeler assigns a different classification | Two-way agreed-upon class |
| No labelers agree on classification | Arbitrated by senior author and assigned final class |
| Feature Vector Index | Metric |
|---|---|
| 1 | Intensity Variance |
| 2 | Edgeness |
| 3 | GLCM Contrast |
| 4 | GLCM Dissimilarity |
| 5 | GLCM Homogeneity |
| 6 | GLCM ASM |
| 7 | GLCM Energy |
| 8 | GLCM Correlation |
| 9–24 | LBP 1–16 |
| 25 | FFT Norm |
| 26–29 | FFT Annulus Norms |
| 30 | Plane Standard Deviation |
| RF | DNN | |
|---|---|---|
| 9-class | 78.1 ± 0.9% | 73.1 ± 0.9% |
| 6-class | 86.3 ± 0.9% | 84.1 ± 1.4% |
| 2-class | 96.2 ± 1% | 96.2 ± 0.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geisz, J.K.; Wernette, P.A.; Esselman, P.C. Classification of Lakebed Geologic Substrate in Autonomously Collected Benthic Imagery Using Machine Learning. Remote Sens. 2024, 16, 1264. https://doi.org/10.3390/rs16071264
Geisz JK, Wernette PA, Esselman PC. Classification of Lakebed Geologic Substrate in Autonomously Collected Benthic Imagery Using Machine Learning. Remote Sensing. 2024; 16(7):1264. https://doi.org/10.3390/rs16071264
Chicago/Turabian StyleGeisz, Joseph K., Phillipe A. Wernette, and Peter C. Esselman. 2024. "Classification of Lakebed Geologic Substrate in Autonomously Collected Benthic Imagery Using Machine Learning" Remote Sensing 16, no. 7: 1264. https://doi.org/10.3390/rs16071264
APA StyleGeisz, J. K., Wernette, P. A., & Esselman, P. C. (2024). Classification of Lakebed Geologic Substrate in Autonomously Collected Benthic Imagery Using Machine Learning. Remote Sensing, 16(7), 1264. https://doi.org/10.3390/rs16071264







