Fusion of Hyperspectral and Multispectral Images with Radiance Extreme Area Compensation
Abstract
1. Introduction
- (1)
- The novel RECF method is the first to focus on the impact of radiance extreme regions on hyperspectral fusion and explicitly proposes a solution framework.
- (2)
- To address the underexposed areas, effective region extraction is achieved through the reconstruction error map. By utilizing piecewise constrained non-negative matrix factorization, the influence of spectral noise caused by underexposed areas on fusion is effectively suppressed.
- (3)
- For overexposed regions, optimal replacement compensation is calculated with the help of multispectral data.
- (4)
- RECF is an unsupervised method that can be applied to the fusion of HS and MS remote sensing data in real-world applications. Through experiments with simulated and real data, its fusion effect on overexposed and underexposed regions is significantly better compared to the current advanced methods.
2. Materials and Methods
2.1. Unmixing-Based Fusion Model
2.2. Piecewise Smoothness Constrained Non-Negative Matrix Factorization
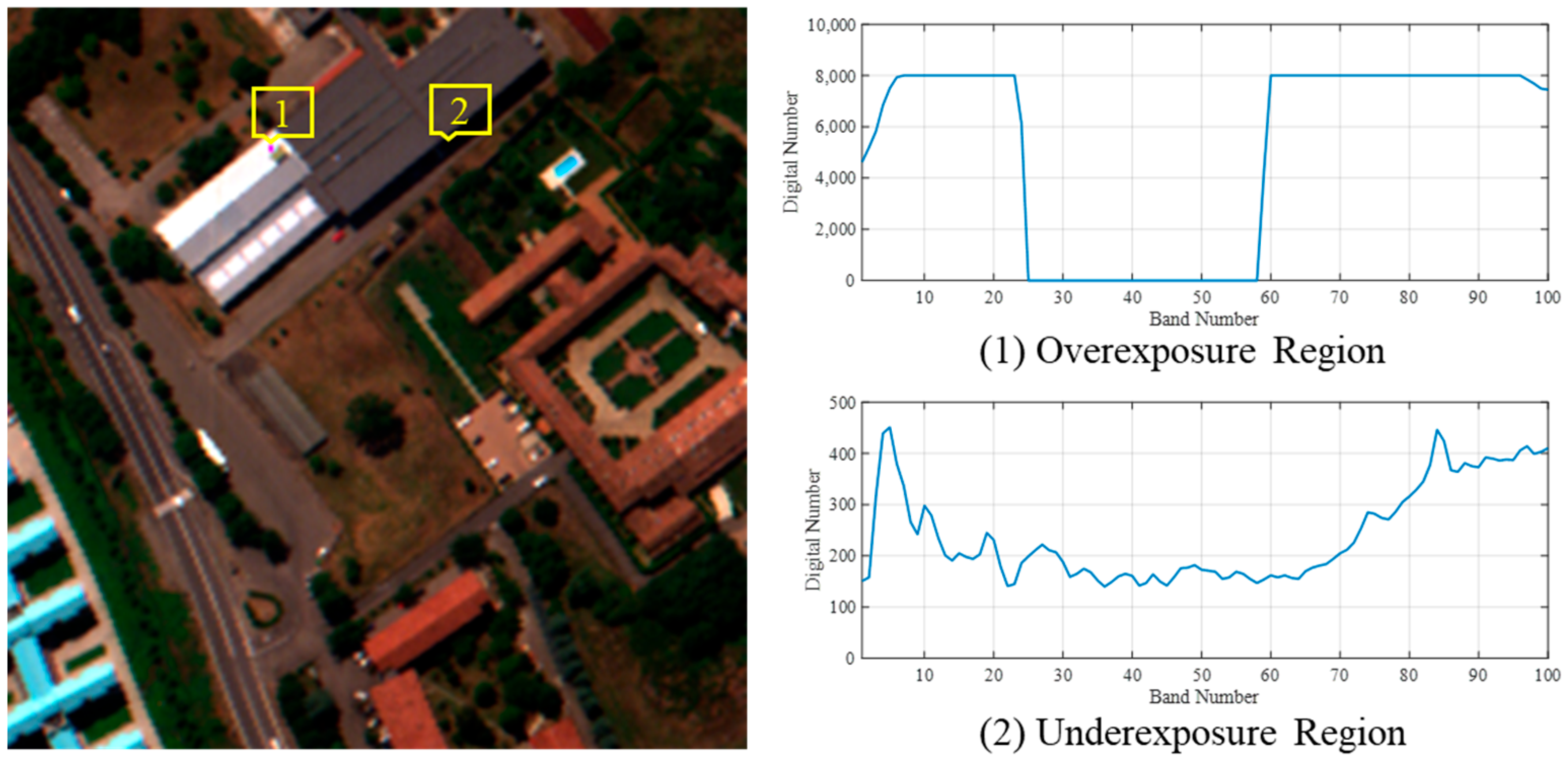
2.3. The Impact of Radiance Extreme Areas on Fusion
3. Proposed Method
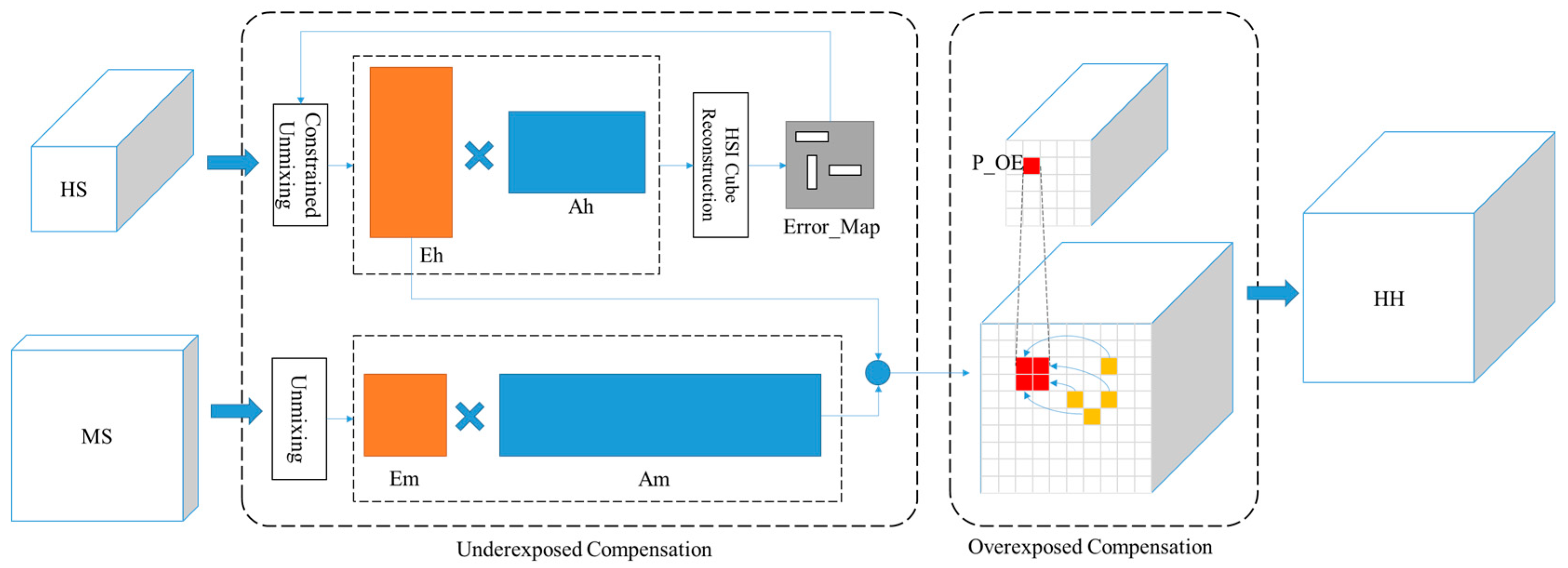
3.1. Idea of RECF
3.2. Error Map
3.3. Local Smoothing Constraint for the Abundance Matrix
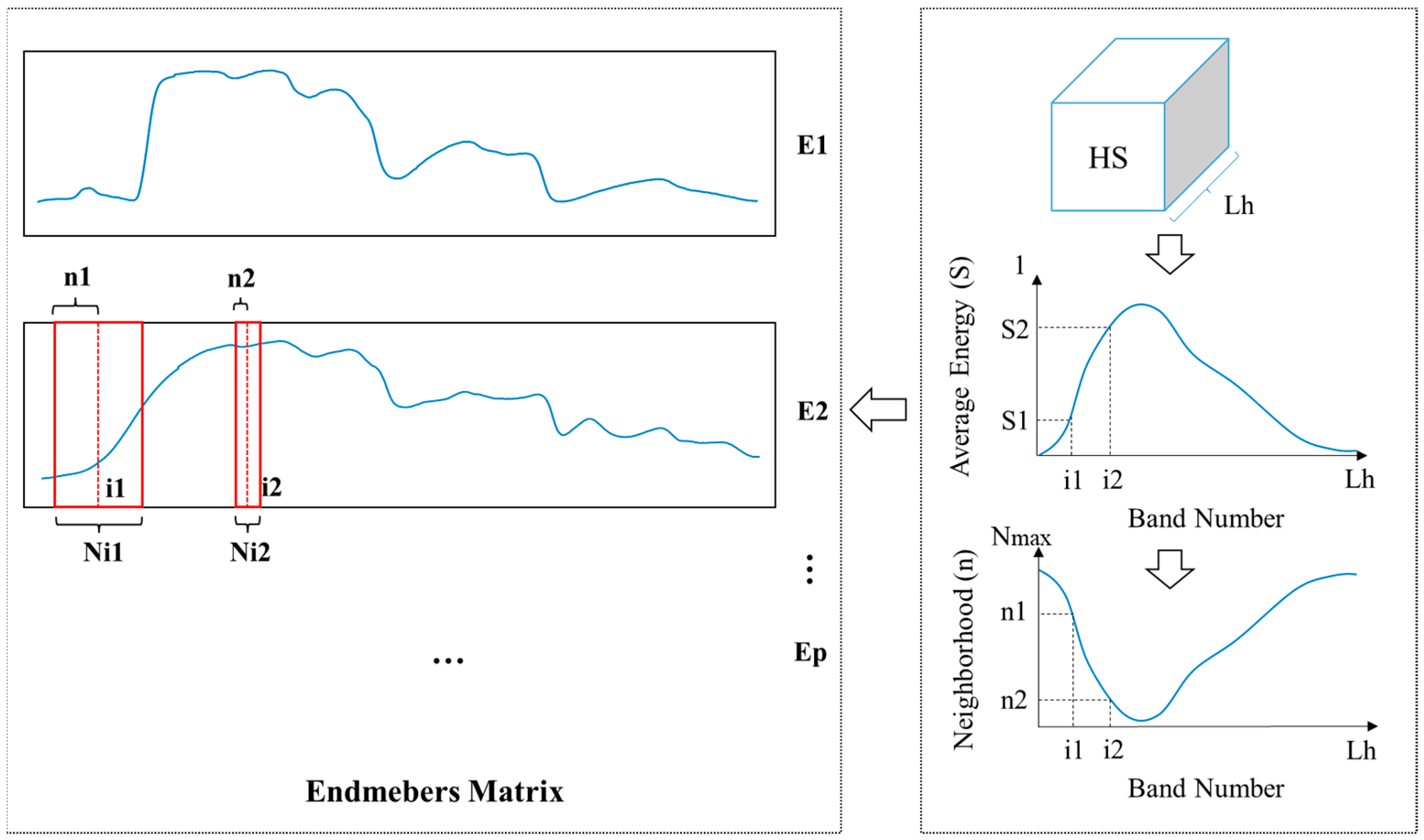
3.4. Local Smoothing Constraint for the Endmember Matrix
3.5. The Iterative Update Rule for PSNMF Fusion
3.6. Compensation for Overexposed Areas
4. Experiments
4.1. Experimental Data
- (1)
- Pavia University Datasets:
- (2)
- Chikusei Datasets:
- (3)
- Xiong’an Datasets:
- (4)
- HJ-2 satellite hyperspectral and multispectral data
4.2. Compared Methods
4.3. Evaluation Metrics
- (1)
- PSNR
- (2)
- SAM
- (3)
- ERGAS
- (4)
- Q2n
- (5)
- CC
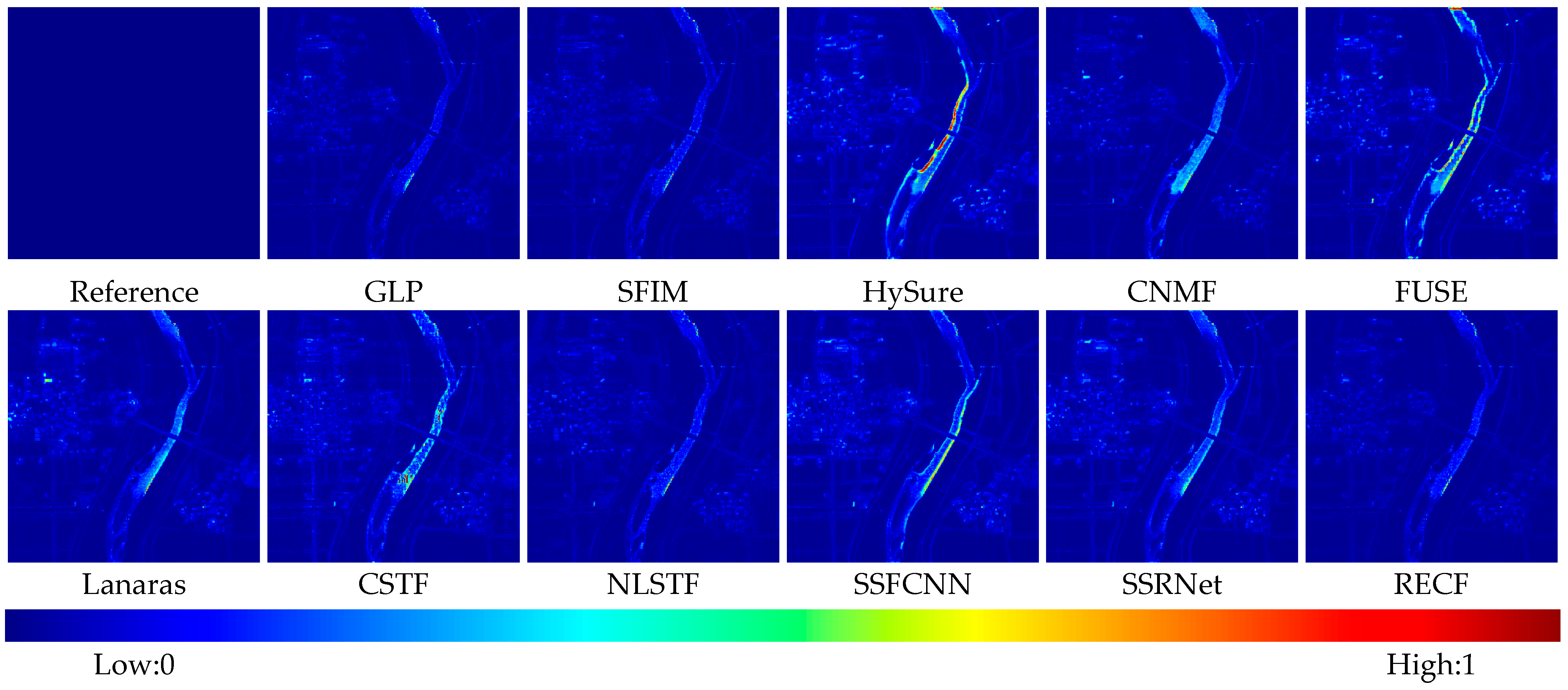
4.4. Experimental Results
- (1)
- Results on the airborne HS dataset
- (2)
- Results on HJ-2 satellite HS remote sensing images
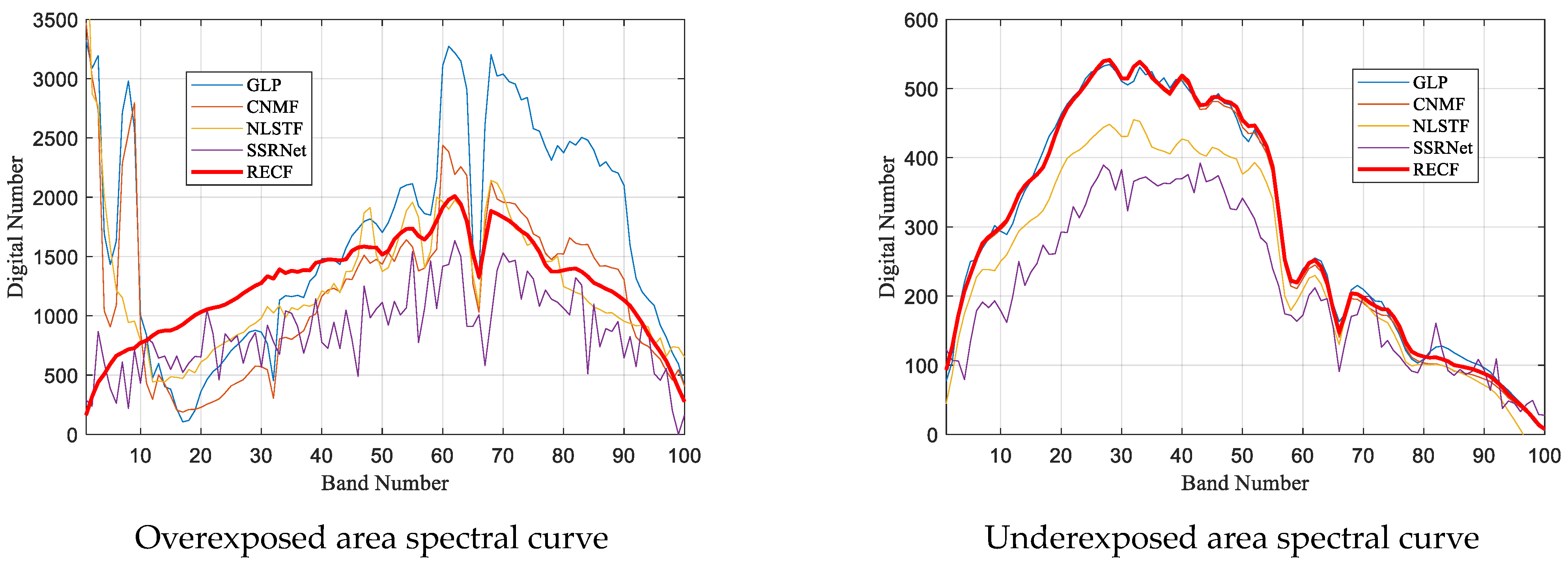
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, S.; Zhang, M.; Cheng, X.; Wang, L.; Xu, M.; Wang, H. Hyperspectral Anomaly Detection via Dual Dictionaries Construction Guided by Two-Stage Complementary Decision. Remote Sens. 2022, 14, 1784. [Google Scholar] [CrossRef]
- Liu, M.; Yu, T.; Gu, X.; Sun, Z.; Li, J. The Impact of Spatial Resolution on the Classification of Vegetation Types in Highly Fragmented Planting Areas Based on Unmanned Aerial Vehicle Hyperspectral Images. Remote Sens. 2020, 12, 146. [Google Scholar] [CrossRef]
- Bannari, A.; Staenz, K.; Champagne, C.; Khurshid, K.S. Spatial variability mapping of crop residue using hyperion (eo-1) hyperspectral data. Remote Sens. 2018, 7, 8107–8127. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and Multispectral Data Fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Ren, K.; Sun, W.; Meng, X.; Yang, G.; Du, Q. Fusing China GF-5 Hyperspectral Data with GF-1, GF-2 and Sentinel-2A Multispectral Data: Which Methods Should Be Used? Remote Sens. 2020, 12, 882. [Google Scholar] [CrossRef]
- Pignatti, S.; Acito, N.; Amato, U.; Casa, R.; Castaldi, F.; Coluzzi, R.; De, B.R.; Diani, M.; Imbrenda, V.; Laneve, G. Environmental products overview of the Italian hyperspectral prisma mission: The SAP4PRISMA project. In Proceedings of the Geoscience & Remote Sensing Symposium, Milan, Italy, 26–31 July 2015. [Google Scholar]
- Stuffler, T.; Kaufmann, C.; Hofer, S.; FöRster, K.P.; Schreier, G.; Mueller, A.; Eckardt, A.; Bach, H.; Penné, B.; Benz, U. EnMAP Hyperspectral Imager: An advanced optical payload for future applications in Earth observation programs. Acta Astronaut. 2007, 61, 115–120. [Google Scholar] [CrossRef]
- Keller, S.; Braun, A.C.; Hinz, S.; Weinmann, M. Investigation of the impact of dimensionality reduction and feature selection on the classification of hyperspectral EnMAP data. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016. [Google Scholar]
- Ye, X.; Ren, H.; Liu, R.; Qin, Q.; Liu, Y.; Dong, J. Land Surface Temperature Estimate From Chinese Gaofen-5 Satellite Data Using Split-Window Algorithm. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5877–5888. [Google Scholar] [CrossRef]
- Sun, W.; Liu, K.; Ren, G.; Liu, W.; Yang, G.; Meng, X.; Peng, J. A simple and effective spectral-spatial method for mapping large-scale coastal wetlands using China ZY1-02D satellite hyperspectral images. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102572. [Google Scholar] [CrossRef]
- Chen, T.; Su, X.; Li, H.; Li, S.; Liu, J.; Zhang, G.; Feng, X.; Wang, S.; Liu, X.; Wang, Y.; et al. Learning a Fully Connected U-Net for Spectrum Reconstruction of Fourier Transform Imaging Spectrometers. Remote Sens. 2022, 14, 900. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Mura, M.D.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A Critical Comparison Among Pansharpening Algorithms. IEEE Trans. Geoence Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Selva, M.; Aiazzi, B.; Butera, F.; Chiarantini, L.; Baronti, S. Hyper-Sharpening: A First Approach on SIM-GA Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3008–3024. [Google Scholar] [CrossRef]
- Chen, Z.; Pu, H.; Wang, B.; Jiang, G.M. Fusion of Hyperspectral and Multispectral Images: A Novel Framework Based on Generalization of Pan-Sharpening Methods. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1418–1422. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving Component Substitution Pansharpening through Multivariate Regression of MS+Pan Data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Gomez, R.B.; Jazaeri, A.; Kafatos, M. Wavelet-based hyperspectral and multispectral image fusion. Proc. SPIE—Int. Soc. Opt. Eng. 2001, 4383, 36–42. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-Tailored Multiscale Fusion of High-Resolution MS and Pan Imagery. Photogramm. Eng. Remote Sens. 2015, 72, 591–596. [Google Scholar] [CrossRef]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J.Y. Hyperspectral and Multispectral Image Fusion based on a Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3658–3668. [Google Scholar] [CrossRef]
- Akhtar, N.; Shafait, F.; Mian, A. Bayesian sparse representation for hyperspectral image super resolution. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Wei, Q.; Dobigeon, N.; Tourneret, J.Y. Bayesian Fusion of Multi-Band Images. IEEE J. Sel. Top. Signal Process. 2015, 9, 1117–1127. [Google Scholar] [CrossRef]
- Hardie, R.C.; Eismann, M.T.; Wilson, G.L. MAP Estimation for Hyperspectral Image Resolution Enhancement Using an Auxiliary Sensor. IEEE Trans. Image Process. 2004, 13, 1174–1184. [Google Scholar] [CrossRef] [PubMed]
- Bresson, X.; Chan, T.F.; Chan, T.F.C. Fast dual minimization of the vectorial total variation norm and applications to color image processing. Inverse Probl. Imaging 2017, 2, 455–484. [Google Scholar] [CrossRef]
- Rong, K.; Jiao, L.; Wang, S.; Liu, F. Pansharpening Based on Low-Rank and Sparse Decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 7, 4793–4805. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, M.; Yang, S. Multispectral and Hyperspectral Image Fusion Based on Group Spectral Embedding and Low-Rank Factorization. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1363–1371. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled Nonnegative Matrix Factorization Unmixing for Hyperspectral and Multispectral Data Fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Akhtar, N.; Shafait, F.; Mian, A. Sparse Spatio-Spectral Representation for Hyperspectral Image Super-Resolution. In Proceedings of the European conference on computer vision, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Lanaras, C.; Baltsavias, E.; Schindler, K. Hyperspectral Super-Resolution by Coupled Spectral Unmixing. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Fu, Y.; Zhang, T.; Zheng, Y.; Zhang, D.; Huang, H. Hyperspectral Image Super-Resolution With Optimized RGB Guidance. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Liu, J.; Wu, Z.; Xiao, L.; Sun, J.; Yan, H. A Truncated Matrix Decomposition for Hyperspectral Image Super-Resolution. IEEE Trans. Image Process. 2020, 29, 8028–8042. [Google Scholar] [CrossRef]
- Nezhad, Z.H.; Karami, A.; Heylen, R.; Scheunders, P. Fusion of Hyperspectral and Multispectral Images Using Spectral Unmixing and Sparse Coding. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2377–2389. [Google Scholar] [CrossRef]
- Dian, R.; Fang, L.; Li, S. Hyperspectral Image Super-Resolution via Non-Local Sparse Tensor Factorization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Xu, Y.; Wu, Z.; Chanussot, J.; Comon, P.; Wei, Z. Nonlocal Coupled Tensor CP Decomposition for Hyperspectral and Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2020, 58, 348–362. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Chanussot, J.; Wei, Z. Hyperspectral Images Super-Resolution via Learning High-Order Coupled Tensor Ring Representation. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4747–4760. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, M.; Yang, S.; Jiao, L. Spatial–Spectral-Graph-Regularized Low-Rank Tensor Decomposition for Multispectral and Hyperspectral Image Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1030–1040. [Google Scholar] [CrossRef]
- Li, S.; Dian, R.; Fang, L.; Bioucas-Dias, J.M. Fusing Hyperspectral and Multispectral Images via Coupled Sparse Tensor Factorization. IEEE Trans. Image Process. 2018, 27, 4118–4130. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Xia, G.-S.; Hu, J.; Zhang, L. Transferring Deep Convolutional Neural Networks for the Scene Classification of High-Resolution Remote Sensing Imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.; Tiede, D.; Aryal, J. Evaluation of Different Machine Learning Methods and Deep-Learning Convolutional Neural Networks for Landslide Detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef]
- Nijaguna, G.S.; Manjunath, D.R.; Abouhawwash, M.; Askar, S.S.; Basha, D.K.; Sengupta, J. Deep Learning-Based Improved WCM Technique for Soil Moisture Retrieval with Satellite Images. Remote Sens. 2023, 15, 2005. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. Multispectral and Hyperspectral Image Fusion Using a 3-D-Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 639–643. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.-Q.; Chan, J.C.-W. Hyperspectral and Multispectral Image Fusion via Deep Two-Branches Convolutional Neural Network. Remote Sens. 2018, 10, 800. [Google Scholar] [CrossRef]
- Zhou, F.; Hang, R.; Liu, Q.; Yuan, X. Pyramid Fully Convolutional Network for Hyperspectral and Multispectral Image Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1549–1558. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Bu, Y.; Liao, W.; Philips, W. Spatial-Spectral Structured Sparse Low-Rank Representation for Hyperspectral Image Super-Resolution. IEEE Trans. Image Process. 2021, 30, 3084–3097. [Google Scholar] [CrossRef]
- Su, L.; Sui, Y.; Yuan, Y. An Unmixing-Based Multi-Attention GAN for Unsupervised Hyperspectral and Multispectral Image Fusion. Remote Sens. 2023, 15, 936. [Google Scholar] [CrossRef]
- Li, J.; Cui, R.; Li, B.; Song, R.; Du, Q. Hyperspectral Image Super-Resolution by Band Attention Through Adversarial Learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4304–4318. [Google Scholar] [CrossRef]
- Zhou, Y.; Rangarajan, A.; Gader, P.D. An Integrated Approach to Registration and Fusion of Hyperspectral and Multispectral Images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3020–3033. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L. Total Variation Regularized Reweighted Sparse Nonnegative Matrix Factorization for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3909–3921. [Google Scholar] [CrossRef]
- Liu, X.; Xia, W.; Wang, B.; Zhang, L. An Approach Based on Constrained Nonnegative Matrix Factorization to Unmix Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 757–772. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Jia, S.; Qian, Y. Constrained Nonnegative Matrix Factorization for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2009, 47, 161–173. [Google Scholar] [CrossRef]
- IEEE. IEEE Xplore Abstract—A Threshold Selection Method from Gray-Level Histograms. Syst. Man Cybern. IEEE Trans. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Simoes, M.; Bioucas-Dias, J.; Almeida, L.B.; Chanussot, J. A Convex Formulation for Hyperspectral Image Superresolution via Subspace-Based Regularization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3373–3388. [Google Scholar] [CrossRef]
- Wei, Q.; Dobigeon, N.; Tourneret, J. Fast Fusion of Multi-Band Images Based on Solving a Sylvester Equation. IEEE Trans. Image Process. A Publ. IEEE Signal Process. Soc. 2015, 24, 4109–4121. [Google Scholar] [CrossRef]
- Han, X.H.; Shi, B.; Zheng, Y.Q. SSF-CNN: Spatial and Spectral Fusion with CNN for Hyperspectral Image Super-Resolution. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018. [Google Scholar]
- Zhang, X.; Huang, W.; Wang, Q.; Li, X. SSR-NET: Spatial-Spectral Reconstruction Network for Hyperspectral and Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5953–5965. [Google Scholar] [CrossRef]














| Algorithm Flowchart: Radiance Extreme Area Compensation Fusion |
| Input: HS, MS, Algorithm parameters αE, αA, γE, γA, ρ |
| Output: HH |
| Step1: Identify and extract overexposed areas from HS as R_OE_HS |
Step2: Fusion radiance normal light region based on PSNMF
while not converge do
end
|
| Step3: Compensate overexposed areas of fused HH by (15) and (16) |
| Datasets | Platform | Bands | Resolutions (m) | Image Size | Scene Size |
|---|---|---|---|---|---|
| Pavia University | Airborne | 224 | 1.3 | 610 × 340 | 320 × 320 |
| Chikusei | Airborne | 128 | 2.5 | 2517 × 2335 | 320 × 320 |
| Xiong’an | Airborne | 250 | - | 3750 × 1580 | 320 × 320 |
| HJ-2 HSI | Satellite | 100 | 48 | 2048 × 2048 | 180 × 180 |
| HJ-2 MSI | Satellite | 5 | 16 | 6144 × 6144 | 540 × 540 |
| Method | Pavia University | ||||
|---|---|---|---|---|---|
| PSNR | SAM | ERGAS | Q2n | CC | |
| GS | 39.1229 | 2.9641 | 2.0209 | 0.9810 | 0.9903 |
| GLP | 35.9758 | 2.2076 | 2.9290 | 0.9830 | 0.9858 |
| SFIM | 34.5101 | 2.2498 | 3.4474 | 0.9800 | 0.9806 |
| HySure | 37.1035 | 3.4303 | 2.6331 | 0.9776 | 0.9886 |
| CNMF | 38.7076 | 2.2799 | 2.2632 | 0.9833 | 0.9921 |
| FUSE | 37.5293 | 3.0178 | 2.6681 | 0.9803 | 0.9869 |
| Lanaras | 37.6645 | 2.7155 | 2.3391 | 0.9806 | 0.9895 |
| CSTF | 37.6332 | 2.6852 | 2.3087 | 0.8012 | 0.9878 |
| NLSTF | 44.0807 | 2.3732 | 1.4578 | 0.9075 | 0.9945 |
| SSFCNN | 39.9397 | 2.7074 | 1.8341 | 0.9816 | 0.9922 |
| SSRNET | 41.2645 | 2.5188 | 1.7124 | 0.9844 | 0.9935 |
| RECF | 44.6691 | 2.2393 | 1.4514 | 0.9866 | 0.9949 |
| Method | Chikusei | ||||
|---|---|---|---|---|---|
| PSNR | SAM | ERGAS | Q2n | CC | |
| GS | 43.6715 | 2.0144 | 2.8178 | 0.9772 | 0.9897 |
| GLP | 41.3536 | 1.2231 | 3.4620 | 0.9811 | 0.9868 |
| SFIM | 40.4918 | 1.2953 | 3.6851 | 0.9794 | 0.9852 |
| HySure | 42.2294 | 2.4063 | 3.7914 | 0.9524 | 0.9852 |
| CNMF | 43.2031 | 1.5914 | 3.2515 | 0.9739 | 0.9884 |
| FUSE | 41.7854 | 2.1761 | 3.4878 | 0.9698 | 0.9876 |
| Lanaras | 42.8317 | 1.8481 | 3.4735 | 0.9698 | 0.9854 |
| CSTF | 40.1310 | 2.0358 | 3.7386 | 0.9971 | 0.9832 |
| NLSTF | 49.6090 | 1.6227 | 2.2853 | 0.9982 | 0.9916 |
| SSFCNN | 39.0689 | 2.1279 | 3.1738 | 0.9654 | 0.9874 |
| SSRNET | 40.1855 | 1.9724 | 3.0532 | 0.9613 | 0.9855 |
| RECF | 49.9857 | 1.3416 | 2.2541 | 0.9792 | 0.9926 |
| Method | Xiong’an | ||||
|---|---|---|---|---|---|
| PSNR | SAM | ERGAS | Q2n | CC | |
| GS | 38.6550 | 0.8677 | 1.0265 | 0.9481 | 0.9905 |
| GLP | 36.6875 | 0.6300 | 1.1409 | 0.9652 | 0.9878 |
| SFIM | 36.0686 | 0.6725 | 1.2092 | 0.9646 | 0.9862 |
| HySure | 37.0925 | 1.4416 | 1.2198 | 0.9267 | 0.9870 |
| CNMF | 37.2273 | 0.8035 | 1.1261 | 0.9667 | 0.9881 |
| FUSE | 37.6000 | 0.8757 | 1.1778 | 0.9622 | 0.9872 |
| Lanaras | 37.7233 | 0.9458 | 0.9180 | 0.9543 | 0.9921 |
| CSTF | 39.2185 | 0.8638 | 0.8334 | 0.8629 | 0.9926 |
| NLSTF | 46.4314 | 0.6905 | 0.4492 | 0.9529 | 0.9975 |
| SSFpecCNN | 33.9311 | 1.7599 | 1.7292 | 0.9824 | 0.9844 |
| SSRNET | 33.3463 | 1.6577 | 1.9545 | 0.9209 | 0.98197 |
| RECF | 47.6076 | 0.5964 | 0.3739 | 0.9844 | 0.9985 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, J.; Mou, X.; Chen, T.; Chen, J.; Liu, J.; Feng, X.; Li, H.; Zhang, G.; Wang, S.; et al. Fusion of Hyperspectral and Multispectral Images with Radiance Extreme Area Compensation. Remote Sens. 2024, 16, 1248. https://doi.org/10.3390/rs16071248
Wang Y, Chen J, Mou X, Chen T, Chen J, Liu J, Feng X, Li H, Zhang G, Wang S, et al. Fusion of Hyperspectral and Multispectral Images with Radiance Extreme Area Compensation. Remote Sensing. 2024; 16(7):1248. https://doi.org/10.3390/rs16071248
Chicago/Turabian StyleWang, Yihao, Jianyu Chen, Xuanqin Mou, Tieqiao Chen, Junyu Chen, Jia Liu, Xiangpeng Feng, Haiwei Li, Geng Zhang, Shuang Wang, and et al. 2024. "Fusion of Hyperspectral and Multispectral Images with Radiance Extreme Area Compensation" Remote Sensing 16, no. 7: 1248. https://doi.org/10.3390/rs16071248
APA StyleWang, Y., Chen, J., Mou, X., Chen, T., Chen, J., Liu, J., Feng, X., Li, H., Zhang, G., Wang, S., Li, S., & Liu, Y. (2024). Fusion of Hyperspectral and Multispectral Images with Radiance Extreme Area Compensation. Remote Sensing, 16(7), 1248. https://doi.org/10.3390/rs16071248







