PointMM: Point Cloud Semantic Segmentation CNN under Multi-Spatial Feature Encoding and Multi-Head Attention Pooling
Abstract
1. Introduction
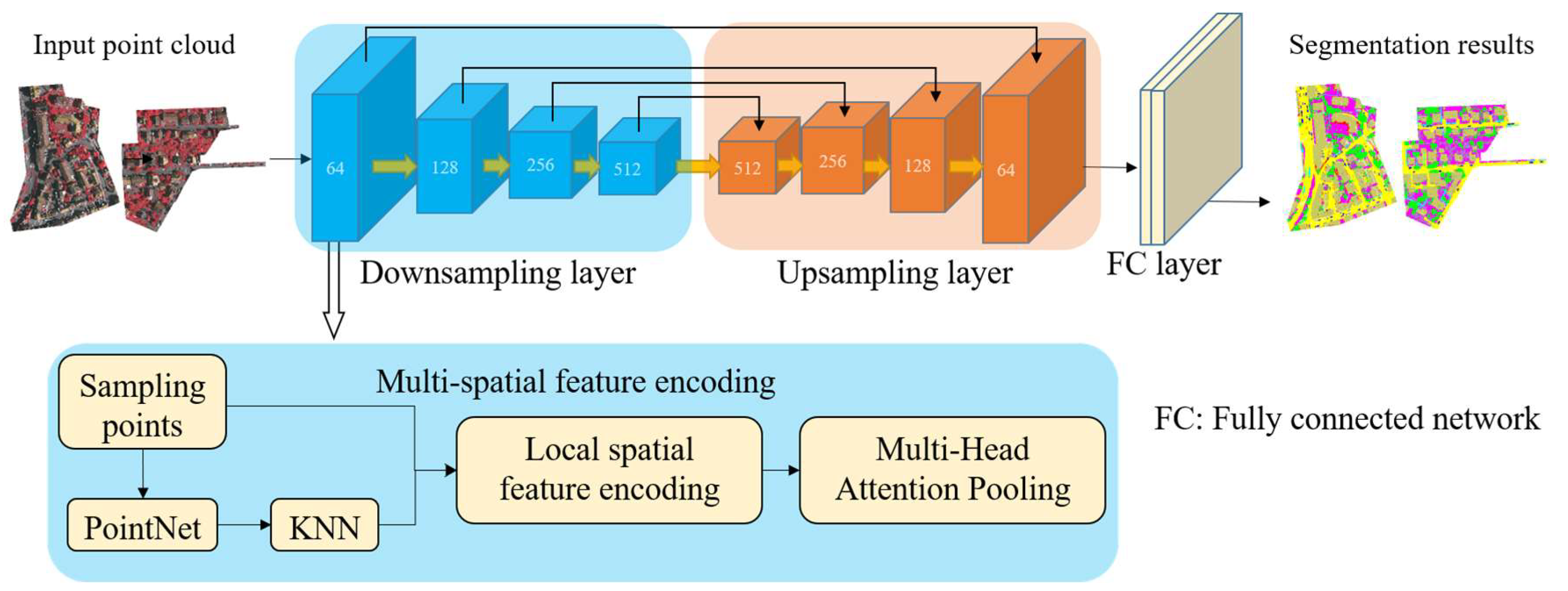
2. Our Method
2.1. Network Overview
2.2. Multi-Spatial Feature Encoding
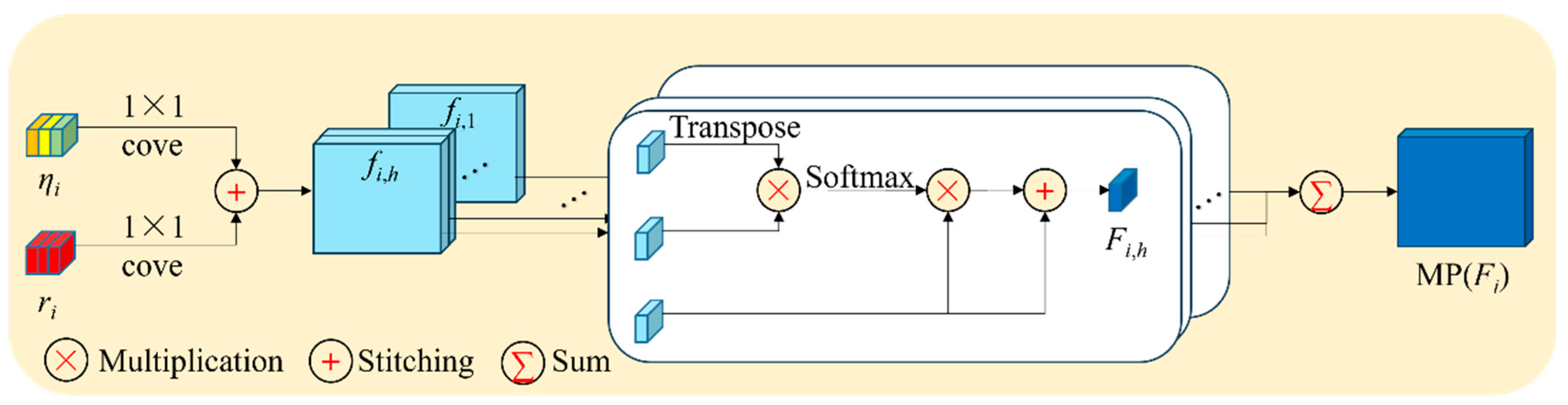
2.3. Multi-Head Attention Pooling
3. Results
3.1. Experimental Environment and Evaluation
3.2. Semantic Segmentation of S3DIS Dataset
3.2.1. Ablation Experiment
3.2.2. Six-Fold Cross-Validation
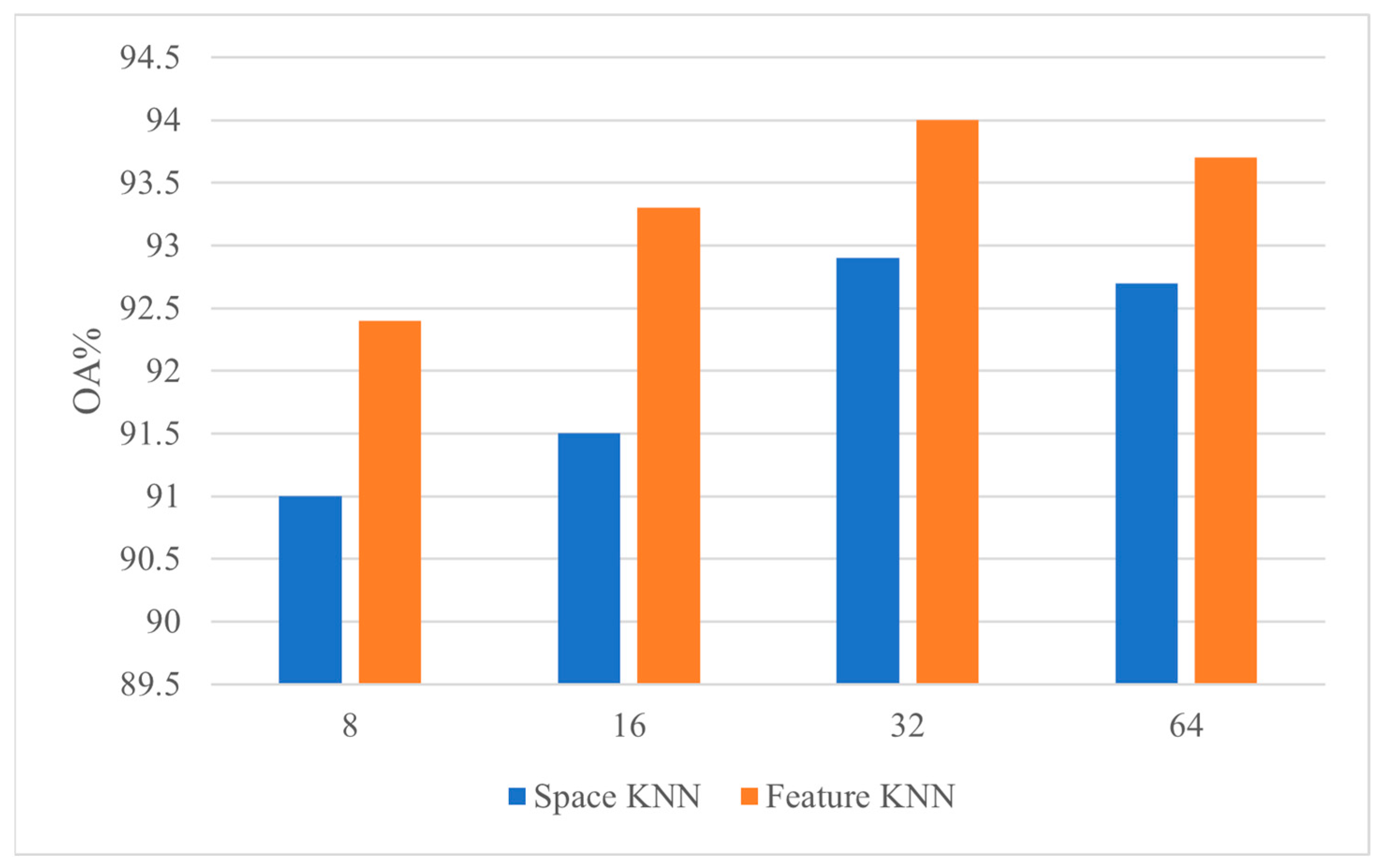
3.2.3. The Experiments of Sampling Points and Neighborhood Points
3.3. Semantic Segmentation of Vaihingen Dataset
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Xie, H.; Zhang, L.; Lu, Z. Information Extraction and Three-Dimensional Contour Reconstruction of Vehicle Target Based on Multiple Different Pitch-Angle Observation Circular Synthetic Aperture Radar Data. Remote Sens. 2024, 16, 401. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, Y.; Wang, Z.; Yu, Y.; Zhang, Z.; Zhang, M.; Zhang, L.; Cheng, B. Inter-Domain Invariant Cross-Domain Object Detection Using Style and Content Disentanglement for In-Vehicle Images. Remote Sens. 2024, 16, 304. [Google Scholar] [CrossRef]
- Caciora, T.; Jubran, A.; Ilies, D.C.; Hodor, N.; Blaga, L.; Ilies, A.; Grama, V.; Sebesan, B.; Safarov, B.; Ilies, G.; et al. Digitization of the Built Cultural Heritage: An Integrated Methodology for Preservation and Accessibilization of an Art Nouveau Museum. Remote Sens. 2023, 15, 5763. [Google Scholar] [CrossRef]
- Muumbe, T.P.; Singh, J.; Baade, J.; Raumonen, P.; Coetsee, C.; Thau, C.; Schmullius, C. Individual Tree-Scale Aboveground Biomass Estimation of Woody Vegetation in a Semi-Arid Savanna Using 3D Data. Remote Sens. 2024, 16, 399. [Google Scholar] [CrossRef]
- Yu, H.; Yang, Z.; Tan, L.; Wang, Y.; Sun, W.; Sun, M.; Tang, Y. Methods and datasets on semantic segmentation: A review. Neurocomputing 2018, 304, 82–103. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep learning for 3d point clouds: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 4338–4364. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Tan, B.; Pei, H.; Jiang, W. Segmentation and multi-scale convolutional neural network-based classification of airborne laser scanner data. Sensors 2018, 18, 3347. [Google Scholar] [CrossRef]
- Zhao, R.; Pang, M.; Wang, J. Classifying airborne LiDAR point clouds via deep features learned by a multi-scale convolutional neural network. Int. J. Geogr. Inf. Sci. 2018, 32, 960–979. [Google Scholar] [CrossRef]
- Gerdzhev, M.; Razani, R.; Taghavi, E.; Bingbing, L. Tornado-net: Multiview total variation semantic segmentation with diamond inception module. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 9543–9549. [Google Scholar]
- Qiu, H.; Yu, B.; Tao, D. GFNet: Geometric Flow Network for 3D Point Cloud Semantic Segmentation. arXiv 2022, arXiv:2207.02605. [Google Scholar]
- Jing, W.; Zhang, W.; Li, L.; Di, D.; Chen, G.; Wang, J. AGNet: An attention-based graph network for point cloud classification and segmentation. Remote Sens. 2022, 14, 1036. [Google Scholar] [CrossRef]
- Lee, M.S.; Yang, S.W.; Han, S.W. Gaia: Graphical information gain based attention network for weakly supervised point cloud semantic segmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 582–591. [Google Scholar]
- Liu, Z.; Tang, H.; Lin, Y.; Han, S. Point-voxel cnn for efficient 3d deep learning. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, F. VoxSegNet: Volumetric CNNs for Semantic Part Segmentation of 3D Shapes; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Liu, M.; Zhou, Q.; Zhao, H.; Li, J.; Du, Y.; Keutzer, K.; Du, L.; Zhang, S. Prototype-Voxel Contrastive Learning for LiDAR Point Cloud Panoptic Segmentation. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 9243–9250. [Google Scholar]
- Zhou, W.; Zhang, X.; Hao, X.; Wang, D.; He, Y. Multi point-voxel convolution (MPVConv) for deep learning on point clouds. Comput. Graph. 2023, 112, 72–80. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. Adv. Neural Inf. Process. Syst. 2017. [Google Scholar] [CrossRef]
- Jiang, M.; Wu, Y.; Zhao, T.; Zhao, Z.; Lu, C. Pointsift: A sift-like network module for 3d point cloud semantic segmentation. arXiv 2018, arXiv:1807.00652. [Google Scholar]
- Zhao, H.; Jiang, L.; Fu, C.W.; Jia, J. Pointweb: Enhancing local neighborhood features for point cloud processing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 5565–5573. [Google Scholar]
- Su, Z.; Zhou, G.; Luo, F.; Li, S.; Ma, K.K. Semantic Segmentation of 3D Point Clouds Based on High Precision Range Search Network. Remote Sens. 2022, 14, 5649. [Google Scholar] [CrossRef]
- Yan, K.; Hu, Q.; Wang, H.; Huang, X.; Li, L.; Ji, S. Continuous mapping convolution for large-scale point clouds semantic segmentation. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Zhao, L.; Tao, W. Jsnet++: Dynamic filters and pointwise correlation for 3d point cloud instance and semantic segmentation. IEEE Trans. Circuits Syst. Video Technol. 2022, 33, 1854–1867. [Google Scholar] [CrossRef]
- Zhao, L.; Tao, W. JSNet: Joint instance and semantic segmentation of 3D point clouds. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12951–12958. [Google Scholar]
- Luo, N.; Yu, H.; Huo, Z.; Liu, J.; Wang, Q.; Xu, Y.; Gao, Y. KVGCN: A KNN searching and VLAD combined graph convolutional network for point cloud segmentation. Remote Sens. 2021, 13, 1003. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Zhong, R.; Sun, L.; Leng, S.; Wang, Q. Densely connected graph convolutional network for joint semantic and instance segmentation of indoor point clouds. ISPRS J. Photogramm. Remote Sens. 2021, 182, 67–77. [Google Scholar] [CrossRef]
- Zeng, Z.; Xu, Y.; Xie, Z.; Wan, J.; Wu, W.; Dai, W. RG-GCN: A random graph based on graph convolution network for point cloud semantic segmentation. Remote Sens. 2022, 14, 4055. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Q. DDGCN: Graph convolution network based on direction and distance for point cloud learning. Vis. Comput. 2023, 39, 863–873. [Google Scholar] [CrossRef]
- Zhang, F.; Xia, X. Cascaded Contextual Reasoning for Large-Scale Point Cloud Semantic Segmentation. IEEE Access 2023, 11, 20755–20768. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Randla-net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 11108–11117. [Google Scholar]
- Du, J.; Cai, G.; Wang, Z.; Huang, S.; Su, J.; Junior, J.M.; Smit, J.; Li, J. ResDLPS-Net: Joint residual-dense optimization for large-scale point cloud semantic segmentation. ISPRS J. Photogramm. Remote Sens. 2021, 182, 37–51. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, X.; Hu, B.; Zhang, Q.; Ye, M.; Zhou, G. A large-scale point cloud semantic segmentation network via local dual features and global correlations. Comput. Graph. 2023, 111, 133–144. [Google Scholar] [CrossRef]
- Yin, F.; Huang, Z.; Chen, T.; Luo, G.; Yu, G.; Fu, B. Dcnet: Large-scale point cloud semantic segmentation with discriminative and efficient feature aggregation. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 4083–4095. [Google Scholar] [CrossRef]
- Deng, C.; Peng, Z.; Chen, Z.; Chen, R. Point Cloud Deep Learning Network Based on Balanced Sampling and Hybrid Pooling. Sensors 2023, 23, 981. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Qi, Z.; Fuxin, L. Pointconv: Deep convolutional networks on 3d point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9621–9630. [Google Scholar]
- Yan, X.; Zheng, C.; Li, Z.; Wang, S.; Cui, S. Pointasnl: Robust point clouds processing using nonlocal neural networks with adaptive sampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 5589–5598. [Google Scholar]
- Zarzar, J.; Giancola, S.; Ghanem, B. PointRGCN: Graph convolution networks for 3D vehicles detection refinement. arXiv 2019, arXiv:1911.12236. [Google Scholar]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 16259–16268. [Google Scholar]
- Bai, X.; Luo, Z.; Zhou, L.; Chen, H.; Li, L.; Hu, Z.; Fu, H.; Tai, C.L. Pointdsc: Robust point cloud registration using deep spatial consistency. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 15859–15869. [Google Scholar]
- Yew, Z.J.; Lee, G.H. Rpm-net: Robust point matching using learned features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11824–11833. [Google Scholar]
- Deng, H.; Birdal, T.; Ilic, S. Ppfnet: Global context aware local features for robust 3d point matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 195–205. [Google Scholar]
- Huang, R.; Xu, Y.; Stilla, U. GraNet: Global relation-aware attentional network for semantic segmentation of ALS point clouds. ISPRS J. Photogramm. Remote Sens. 2021, 177, 1–20. [Google Scholar] [CrossRef]
- Wen, C.; Li, X.; Yao, X.; Peng, L.; Chi, T. Airborne LiDAR point cloud classification with global-local graph attention convolution neural network. ISPRS J. Photogramm. Remote Sens. 2021, 173, 181–194. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, X.; Li, J.; Fang, Z.; Jiang, X.; Huq, K.M. LFT-Net: Local feature transformer network for point clouds analysis. IEEE Trans. Intell. Transp. Syst. 2022, 24, 2158–2168. [Google Scholar] [CrossRef]
- Zhang, M.; Kadam, P.; Liu, S.; Kuo, C.C. GSIP: Green semantic segmentation of large-scale indoor point clouds. Pattern Recognit. Lett. 2022, 164, 9–15. [Google Scholar] [CrossRef]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. Kpconv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6411–6420. [Google Scholar]
- Huang, R.; Xu, Y.; Hong, D.; Yao, W.; Ghamisi, P.; Stilla, U. Deep point embedding for urban classification using ALS point clouds: A new perspective from local to global. ISPRS J. Photogramm. Remote Sens. 2020, 163, 62–81. [Google Scholar] [CrossRef]
- Ye, Z.; Xu, Y.; Huang, R.; Tong, X.; Li, X.; Liu, X.; Luan, K.; Hoegner, L.; Stilla, U. LASDU: A Large-Scale Aerial LiDAR Dataset for Semantic Labeling in Dense Urban Areas. Int. J. Geo-Inf. 2020, 9, 450. [Google Scholar] [CrossRef]
- Wen, C.; Yang, L.; Li, X.; Peng, L.; Chi, T. Directionally constrained fully convolutional neural network for airborne LiDAR point cloud classification. ISPRS J. Photogramm. Remote Sens. 2020, 162, 50–62. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Wang, M.; Wen, C.; Fang, Y. DANCE-NET: Density-aware convolution networks with context encoding for airborne LiDAR point cloud classification. ISPRS J. Photogramm. Remote Sens. 2020, 166, 128–139. [Google Scholar] [CrossRef]
- Li, W.; Wang, F.D.; Xia, G.S. A geometry-attentional network for ALS point cloud classification. ISPRS J. Photogramm. Remote Sens. 2020, 164, 26–40. [Google Scholar]
- Deng, C.; Chen, R.; Tang, W.; Chu, H.; Xu, G.; Cui, Y.; Peng, Z. PointNAC: Copula-Based Point Cloud Semantic Segmentation Network. Symmetry 2023, 15, 2021. [Google Scholar] [CrossRef]



| Class | Number | Proportion | Class | Number | Proportion |
|---|---|---|---|---|---|
| ceiling | 5,721,636 | 21.6 | table | 715,205 | 2.7 |
| floor | 5,138,877 | 19.4 | chair | 953,606 | 3.6 |
| wall | 6,887,155 | 26.0 | sofa | 105,956 | 0.4 |
| beam | 317,869 | 1.2 | Bookcase | 1,456,898 | 5.5 |
| column | 397,336 | 1.5 | board | 264,890 | 1.0 |
| window | 529,781 | 2.0 | clutter | 2,595,927 | 9.8 |
| door | 1,403,920 | 5.3 | All | 26,489,056 | 100 |
| Name | Module |
|---|---|
| PointNet++ | Baseline |
| +MHP | Multi-head attention pooling |
| +MSF | Multi-spatial feature encoding |
| ALL | PointMM |
| Module | MIoU | OA | Ceiling | Floor | Wall | Beam | Column | Window | Door | Table | Chair | Sofa | Bookcase | Board | Clutter |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baseline | 70.2 | 87.7 | 93.0 | 97.3 | 74.8 | 68.7 | 43.2 | 77.8 | 78.9 | 72.4 | 76.8 | 41.9 | 58.7 | 66.2 | 63.2 |
| MHP | 73.3 | 90.7 | 91.4 | 97.9 | 76.9 | 68.0 | 46.5 | 72.6 | 79.2 | 75.3 | 83.6 | 63.2 | 64.7 | 65.3 | 67.8 |
| MSF | 78.0 | 92.7 | 93.3 | 97.2 | 80.6 | 76.4 | 59.5 | 73.5 | 83.8 | 74.5 | 83.5 | 76.8 | 68.5 | 77.0 | 69.7 |
| ALL | 80.4 | 94.0 | 94.6 | 97.8 | 82.7 | 76.2 | 52.9 | 77.5 | 83.6 | 77.8 | 86.6 | 83.7 | 79.1 | 76.9 | 75.8 |
| Module | Training Duration for One Epoch |
|---|---|
| Baseline | 233.3703 |
| +MHP | 1104.0414 |
| +MSF | 681.2939 |
| ALL | 1604.5551 |
| Method | GSIP | HPRS | MCS | KVGCN | RGGCN | LG-Net | JSNet++ | KPConv | RandLA-Net | BSH-Net | PointNAC | PointTr | Ours |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OA | 79.8 | 84.7 | 86.8 | 87.4 | 88.1 | 88.3 | 88.7 | - | 88.0 | 90.5 | 90.9 | 90.2 | 90.4 |
| Miou | 48.5 | 61.3 | 66.8 | 60.9 | 63.7 | 70.8 | 62.4 | 70.6 | 70.0 | 66.1 | 67.4 | 73.5 | 70.7 |
| Ceiling | 91.8 | 92.7 | 92.4 | 94.5 | 94.0 | 93.7 | 94.1 | 93.6 | 93.1 | - | - | - | 95.4 |
| Floor | 89.8 | 94.5 | 95.8 | 94.1 | 96.2 | 96.4 | 97.3 | 92.4 | 96.1 | - | - | - | 97.5 |
| Wall | 73.0 | 76.3 | 79.5 | 79.5 | 79.1 | 81.3 | 78.0 | 83.1 | 80.6 | - | - | - | 81.1 |
| Beam | 26.3 | 30.1 | 55.8 | 53.4 | 60.4 | 65.2 | 41.3 | 63.9 | 62.4 | - | - | - | 59.5 |
| Column | 24.0 | 25.5 | 43.6 | 36.3 | 44.3 | 51.8 | 32.2 | 54.3 | 48.0 | - | - | - | 38.8 |
| Window | 44.6 | 63.1 | 59.6 | 56.8 | 60.1 | 66.2 | 52.0 | 66.1 | 64.4 | - | - | - | 66.5 |
| Door | 55.8 | 61.8 | 63.4 | 63.2 | 65.9 | 69.7 | 70.0 | 76.6 | 69.4 | - | - | - | 73.9 |
| Table | 55.5 | 65.6 | 67.3 | 64.3 | 70.8 | 69.1 | 69.9 | 57.8 | 69.4 | - | - | - | 73.0 |
| Chair | 51.1 | 69.3 | 70.2 | 67.5 | 64.9 | 75.1 | 72.7 | 64.0 | 76.4 | - | - | - | 84.0 |
| Sofa | 10.2 | 47.0 | 63.1 | 54.3 | 30.8 | 63.9 | 37.9 | 69.3 | 60.0 | - | - | - | 53.3 |
| Bookcase | 43.8 | 56.1 | 59.3 | 23.6 | 51.9 | 63.5 | 54.1 | 74.9 | 64.2 | - | - | - | 68.1 |
| Board | 21.8 | 60.1 | 61.8 | 43.1 | 52.6 | 66.0 | 51.3 | 61.3 | 65.9 | - | - | - | 58.6 |
| Clutter | 43.2 | 55.1 | 56.2 | 53.2 | 56.4 | 58.4 | 60.2 | 60.3 | 60.1 | - | - | - | 69.5 |
| Model | Power Line | Car | Facade | Hedge | Impervious Surface | Low Vegetation | Roof | Shrub | Tree |
|---|---|---|---|---|---|---|---|---|---|
| Training-N | 546 | 4614 | 27,250 | 12,070 | 193,723 | 180,850 | 152,045 | 47,605 | 135,173 |
| Training-P | 0.072% | 0.612% | 3.615% | 1.601% | 25.697% | 23.989% | 20.168% | 6.315% | 17.931% |
| Testing-N | 600 | 3708 | 11,224 | 7422 | 101,986 | 98,690 | 109,048 | 24,818 | 54,226 |
| Testing-P | 0.146% | 0.900% | 2.726% | 1.803% | 24.770% | 23.970% | 26.486% | 6.027% | 13.170% |
| Model | Power Line | Car | Facade | Hedge | Impervious Surface | Low Vegetation | Roof | Shrub | Tree | OA | Average F1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| HDA | 64.2 | 68.9 | 36.5 | 19.2 | 99.2 | 85.1 | 88.2 | 37.7 | 69.2 | 81.2 | 63.1 |
| DPE | 68.1 | 75.2 | 44.2 | 19.5 | 99.3 | 86.5 | 91.1 | 39.4 | 72.6 | 83.2 | 66.2 |
| NANJ2 | 62.0 | 66.7 | 42.6 | 40.7 | 91.2 | 88.8 | 93.6 | 55.9 | 82.6 | 85.2 | 69.3 |
| BSH-NET | 46.5 | 77.8 | 57.9 | 37.9 | 92.9 | 82.3 | 94.8 | 48.6 | 86.3 | 85.4 | 69.5 |
| PointNAC | 52.9 | 76.7 | 57.5 | 41.1 | 93.6 | 83.2 | 94.9 | 50.5 | 85.2 | 85.9 | 70.6 |
| Randla-Net | 68.8 | 76.6 | 61.9 | 43.8 | 91.3 | 82.1 | 91.1 | 45.2 | 77.4 | 82.1 | 70.9 |
| D-FCN | 70.4 | 78.1 | 60.5 | 37.0 | 91.4 | 80.2 | 93.0 | 46.0 | 79.4 | 82.2 | 70.7 |
| Dance-Net | 68.4 | 77.2 | 60.2 | 38.6 | 92.8 | 81.6 | 93.9 | 47.2 | 81.4 | 83.9 | 71.2 |
| GACNN | 76.0 | 77.7 | 58.9 | 37.8 | 93.0 | 81.8 | 93.1 | 46.7 | 78.9 | 83.2 | 71.5 |
| GANet | 75.4 | 77.8 | 61.5 | 44.2 | 91.6 | 82.0 | 94.4 | 49.6 | 82.6 | 84.5 | 73.2 |
| GraNet | 67.7 | 80.9 | 62.0 | 51.1 | 91.7 | 82.7 | 94.5 | 49.9 | 82.0 | 84.5 | 73.6 |
| PointMM | 60.6 | 77.3 | 62.3 | 37.0 | 93.5 | 84.0 | 96.1 | 57.8 | 86.4 | 87.7 | 72.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Wu, J.; Luo, Y.; Xu, G. PointMM: Point Cloud Semantic Segmentation CNN under Multi-Spatial Feature Encoding and Multi-Head Attention Pooling. Remote Sens. 2024, 16, 1246. https://doi.org/10.3390/rs16071246
Chen R, Wu J, Luo Y, Xu G. PointMM: Point Cloud Semantic Segmentation CNN under Multi-Spatial Feature Encoding and Multi-Head Attention Pooling. Remote Sensing. 2024; 16(7):1246. https://doi.org/10.3390/rs16071246
Chicago/Turabian StyleChen, Ruixing, Jun Wu, Ying Luo, and Gang Xu. 2024. "PointMM: Point Cloud Semantic Segmentation CNN under Multi-Spatial Feature Encoding and Multi-Head Attention Pooling" Remote Sensing 16, no. 7: 1246. https://doi.org/10.3390/rs16071246
APA StyleChen, R., Wu, J., Luo, Y., & Xu, G. (2024). PointMM: Point Cloud Semantic Segmentation CNN under Multi-Spatial Feature Encoding and Multi-Head Attention Pooling. Remote Sensing, 16(7), 1246. https://doi.org/10.3390/rs16071246






