Measurement of Downwelling Radiance Using a Low-Cost Compact Fourier-Transform Infrared System for Monitoring Atmospheric Conditions
Abstract
1. Introduction
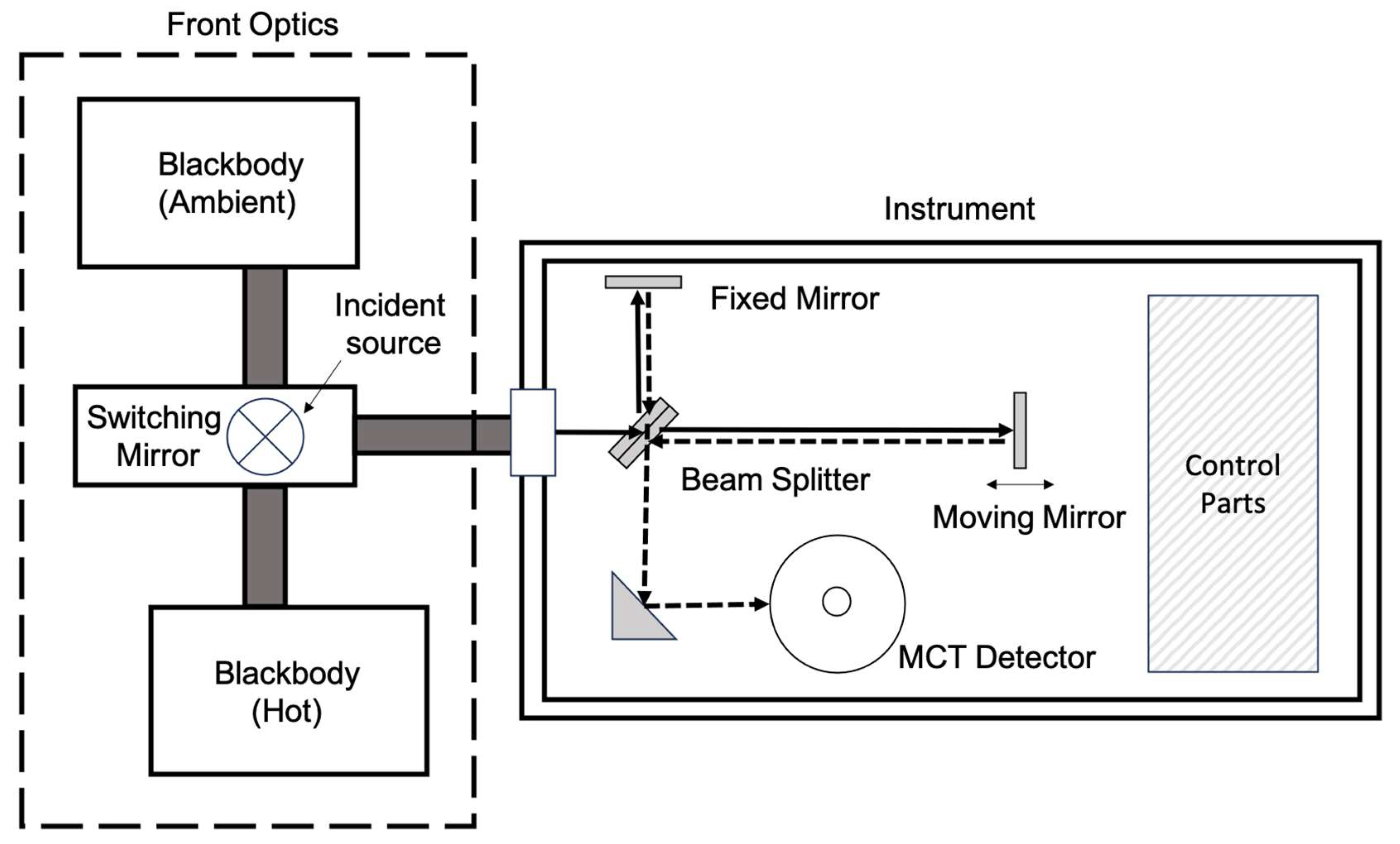
2. Instrumentation Construction of Instrument Hardware
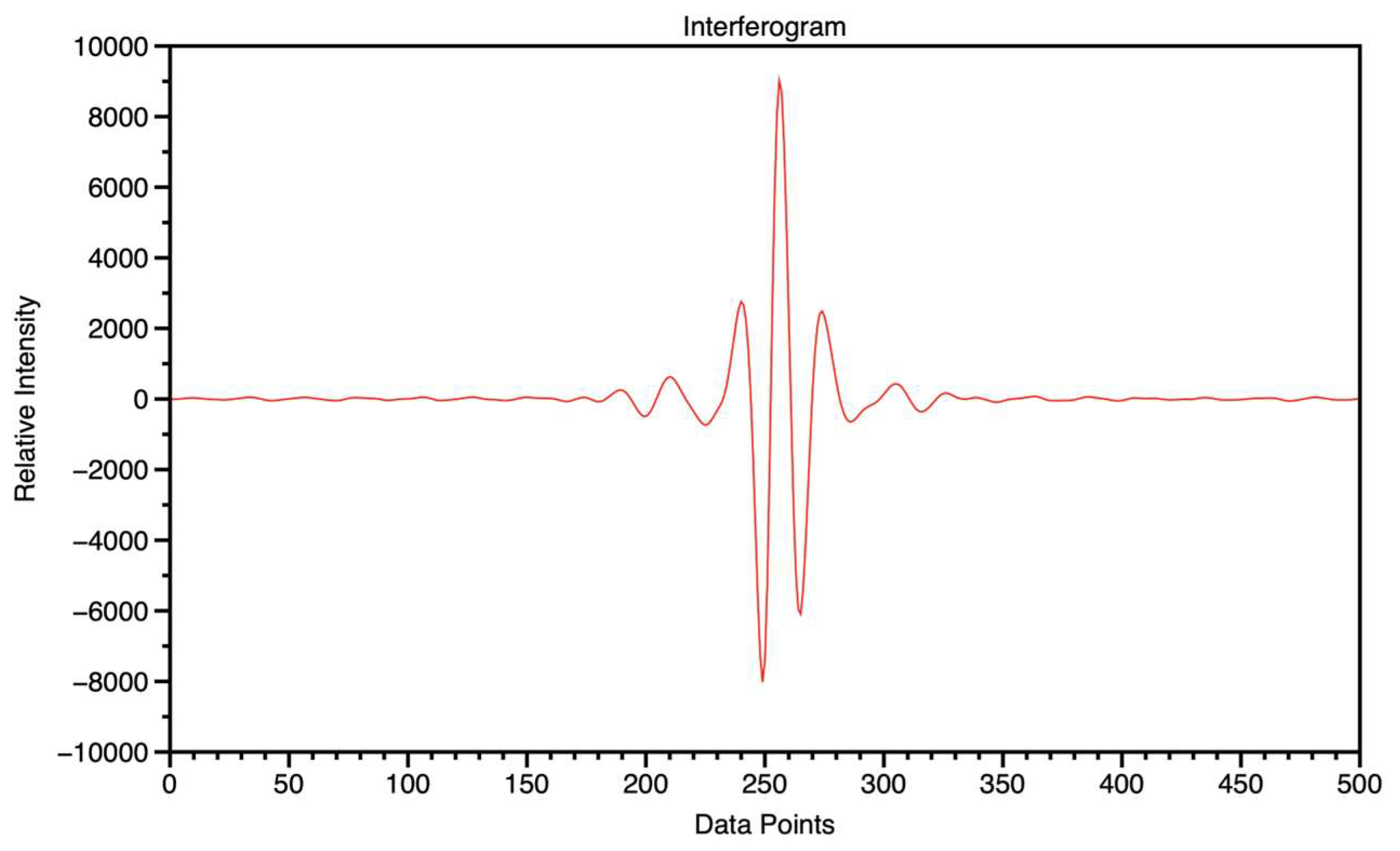
3. Signal Processing
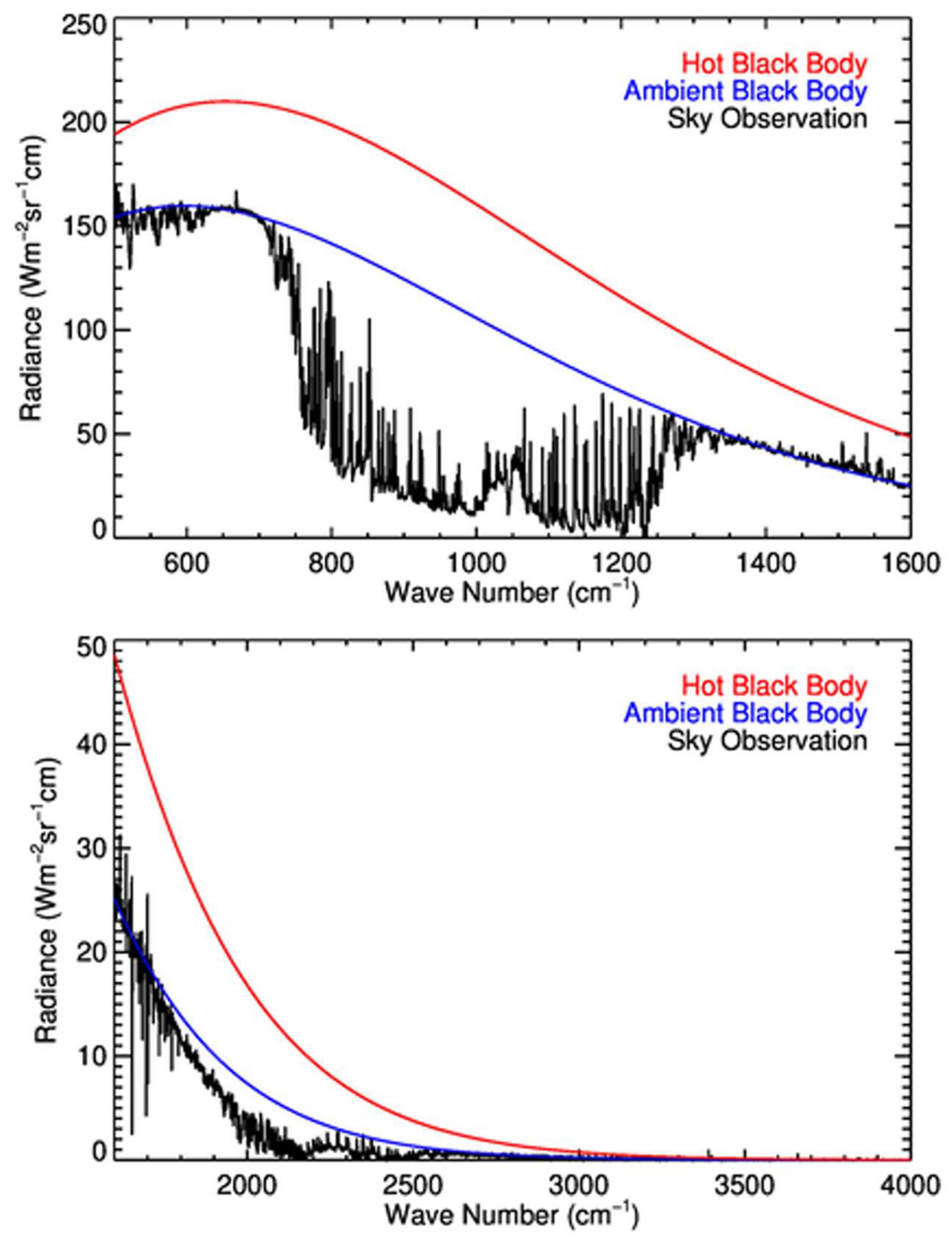
3.1. Radiometric Calibration
3.2. Noise-Equivalent Spectral Radiance
4. The Thermodynamic Profile Retrieval Algorithm
4.1. The Line-by-Line Radiative Transfer Model
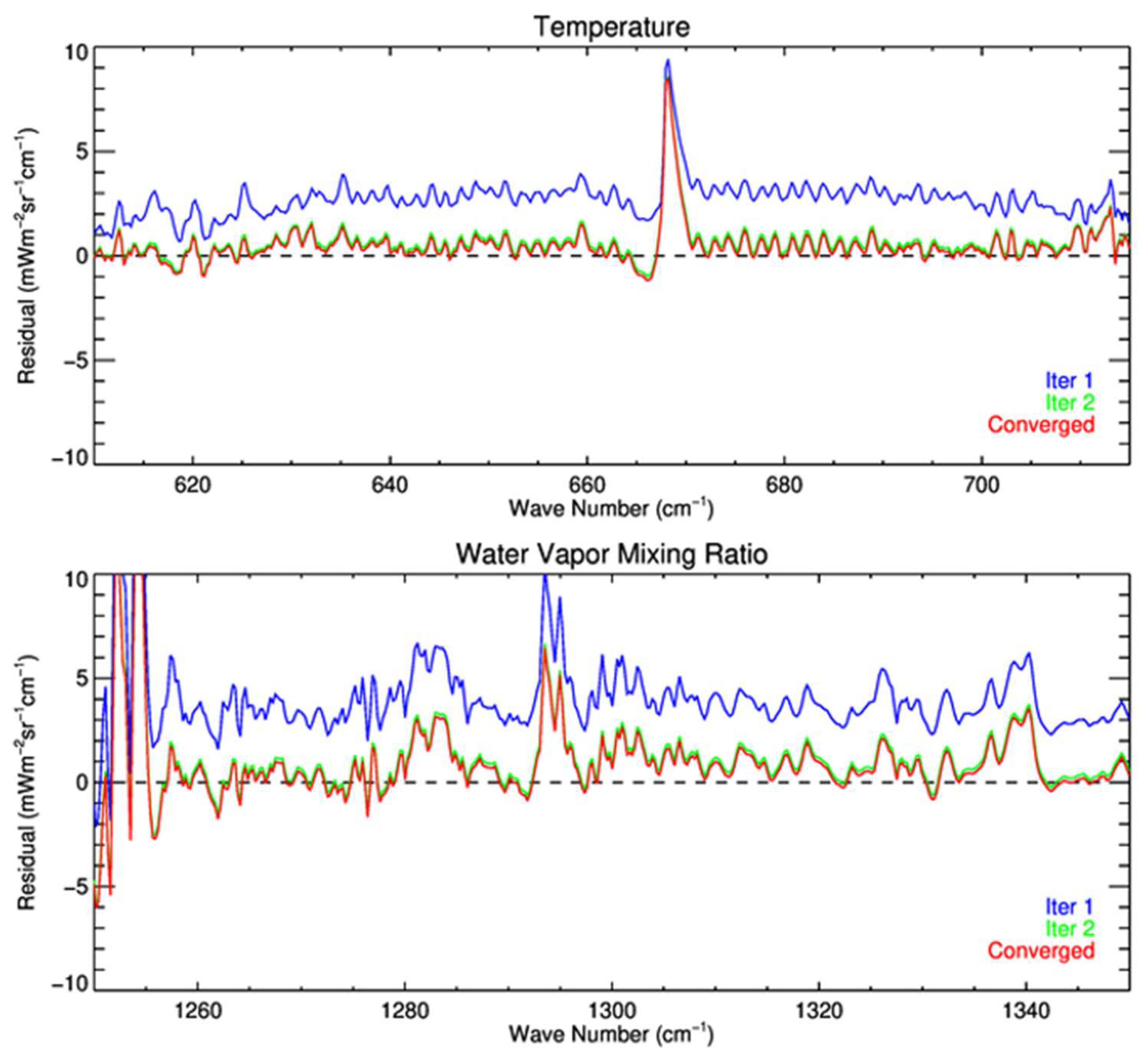
4.2. Optimal Estimation Retreival
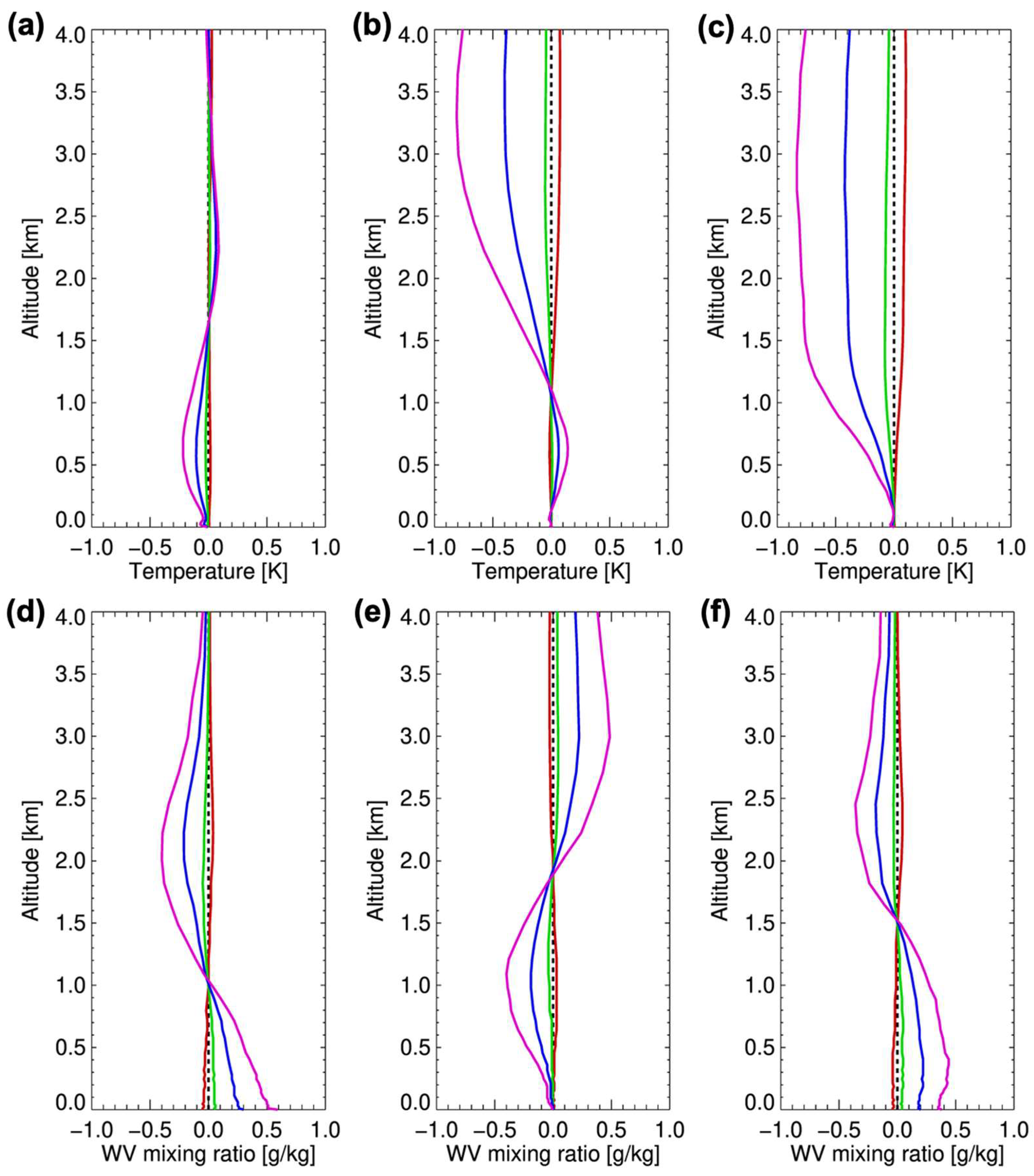
5. Results
6. Discussion
7. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AERI | Atmospheric Emitted Radiance Interferometer |
| ARM | Atmospheric Radiation Measurement |
| ASOS | Automated Synoptic Observing System |
| BOA | Bottom Of the Atmosphere |
| COMS | Communication, Oceanography, and Meteorology Satellite |
| CRIS | CRoss-track Infrared Sounder |
| DISORT | Discrete Ordinates Radiative Transfer |
| ECMWF | European Centre for Medium-RangeWeather Forecasts |
| ERA-5 | ECMWF Reanalysis version 5 |
| FFT | Fast Fourier Transform |
| FTIR | Fourier Transfer Infrared |
| GOS | Global Observing System |
| HITRAN | HIgh-Resolution Transmission molecular absorption database |
| IASI | Infrared Atmospheric Sounding Interferometer |
| KMA | Korea Meteorological Administration |
| KNU | Kyungpook National University |
| LBLRTM | Line-By-Line Radiative Transfer Model |
| LN2 | Liquid nitrogen |
| LP | Levenberg Parameter |
| MCT | Mercury–Cadmium–Telluride |
| METOP | METeorological OPerational |
| MI | Meteorological Imager |
| MT_CKD | MlawerTobinCloughKneizysDavies |
| MWR | Microwave Radiometer |
| NASA | National Aeronautics and Space Administration |
| NCEP | National Centers for Environmental Prediction |
| NESR | Noise-Equivalent Spectral Radiance |
| NOAA | National Oceanic and Atmospheric Administration |
| NRC | National Research Council |
| NPP | National Polar-orbiting Partnership |
| NWP | Numerical Weather Prediction |
| OEM | Optimal Estimation Method |
| PBL | Planetary Boundary Layer |
| PID | Proportional Integral Differential |
| RMSE | Root Mean Square Error |
| RU | Radiance Units |
| RTM | Radiative Transfer Model |
| TROPoe | Tropospheric Optimal Estimation Retrieval Algorithm |
| WACCM | Whole Atmosphere Community Climate Model |
| WMO | World Meteorological Organization |
| ZPD | Zero Path Difference |
References
- Trenberth, K.E. Atmospheric moisture residence times and cycling: Implications for rainfall rates and climate change. Clim. Chang. 1998, 39, 667–694. [Google Scholar] [CrossRef]
- Wulfmeyer, V.; Hardesty, R.M.; Turner, D.D.; Behrendt, A.; Cadeddu, M.P.; Di Girolamo, P.; Schlüssel, P.; Van Baelen, J.; Zus, F. A review of the remote sensing of lower tropospheric thermodynamic profiles and its indispensable role for the understanding and the simulation of water and energy cycles. Rev. Geophys. 2015, 53, 819–895. [Google Scholar] [CrossRef]
- Charlesworth, E.; Plöger, F.; Birner, T.; Baikhadzhaev, R.; Abalos, M.; Abraham, N.L.; Akiyoshi, H.; Bekki, S.; Dennison, F.; Jöckel, P. Stratospheric water vapor affecting atmospheric circulation. Nat. Commun. 2023, 14, 3925. [Google Scholar] [CrossRef]
- Wagner, T.J.; Feltz, W.F.; Ackerman, S.A. The temporal evolution of convective indices in storm-producing environments. Weather Forec. 2008, 23, 786–794. [Google Scholar] [CrossRef]
- Dimitrova, R.; Silver, Z.; Zsedrovits, T.; Hocut, C.M.; Leo, L.S.; Di Sabatino, S.; Fernando, H.J.S. Assessment of planetary boundary-layer schemes in the weather research and forecasting mesoscale model using MATERHORN field data. Boundary-Layer Meteorol. 2016, 159, 589–609. [Google Scholar] [CrossRef]
- Miao, Y.; Liu, S. Linkages between aerosol pollution and planetary boundary layer structure in China. Sci. Total Environ. 2019, 650, 288–296. [Google Scholar] [CrossRef]
- Pan, H.-L.; Mahrt, L. Interaction between soil hydrology and boundary-layer development. Boundary-Layer Meteorol. 1987, 38, 185–202. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Scientific Assessment of Ozone Depletion: 2014; World Meteorological Organization (WMO): Geneva, Switzerland, 2014; ISBN 9789966076014. [Google Scholar]
- Board, S.S.; National Academies of Sciences, Engineering, Medicine. Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space; National Academies Press: New York, NY, USA, 2019; ISBN 0309467578. [Google Scholar]
- Cayla, F.R. IASI infrared interferometer for operations and research. In High Spectral Resolution Infrared Remote Sensing for Earth’s Weather and Climate Studies; Springer: Berlin/Heidelberg, Germany, 1993; pp. 9–19. [Google Scholar]
- Han, Y.; Revercomb, H.; Cromp, M.; Gu, D.; Johnson, D.; Mooney, D.; Scott, D.; Strow, L.; Bingham, G.; Borg, L. Suomi NPP CrIS measurements, sensor data record algorithm, calibration and validation activities, and record data quality. J. Geophys. Res. Atmos. 2013, 118, 12734–12748. [Google Scholar] [CrossRef]
- Hilton, F.I.; Newman, S.M.; Collard, A.D. Identification of NWP humidity biases using high-peaking water vapour channels from IASI. Atmos. Sci. Lett. 2012, 13, 73–78. [Google Scholar] [CrossRef]
- Huang, H.-L.; Smith, W.L.; Woolf, H.M. Vertical resolution and accuracy of atmospheric infrared sounding spectrometers. J. Appl. Meteorol. Climatol. 1992, 31, 265–274. [Google Scholar] [CrossRef][Green Version]
- Löhnert, U.; Crewell, S.; Simmer, C. An integrated approach toward retrieving physically consistent profiles of temperature, humidity, and cloud liquid water. J. Appl. Meteorol. Climatol. 2004, 43, 1295–1307. [Google Scholar] [CrossRef]
- Cadeddu, M.P.; Liljegren, J.C.; Turner, D.D. The Atmospheric Radiation Measurement (ARM) program network of microwave radiometers: Instrumentation, data, and retrievals. Atmos. Meas. Tech. Discuss. 2013, 6, 3723–3763. [Google Scholar] [CrossRef]
- Feltz, W.F.; Smith, W.L.; Howell, H.B.; Knuteson, R.O.; Woolf, H.; Revercomb, H.E. Near-continuous profiling of temperature, moisture, and atmospheric stability using the Atmospheric Emitted Radiance Interferometer (AERI). J. Appl. Meteorol. 2003, 42, 584–597. [Google Scholar] [CrossRef]
- Council, N.R. Committee on developing mesoscale meteorological observational capabilities to meet multiple national needs. In Observing Weather and Climate from the Ground Up: A Nationwide Network of Networks; The National Academies Press: Washington, DC, USA, 2009. [Google Scholar]
- Turner, D.D.; Feltz, W.F.; Ferrare, R.A. Continuous water vapor profiles from operational ground-based active and passive remote sensors. Bull. Am. Meteorol. Soc. 2000, 81, 1301–1318. [Google Scholar] [CrossRef][Green Version]
- Wagner, T.J.; Turner, D.D.; Berg, L.K.; Krueger, S.K. Ground-based remote retrievals of cumulus entrainment rates. J. Atmos. Ocean. Technol. 2013, 30, 1460–1471. [Google Scholar] [CrossRef]
- Turner, D.D. Ground-based infrared retrievals of optical depth, effective radius, and composition of airborne mineral dust above the Sahel. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Seo, J.; Choi, H.; Oh, Y. Potential of AOD retrieval using atmospheric emitted radiance interferometer (AERI). Remote Sens. 2022, 14, 407. [Google Scholar] [CrossRef]
- Lee, Y.-J.; Park, J.-H.; Lee, K.-M. Infrared emissivity of major minerals measured by FT-IR. Atmosphere 2015, 25, 601–610. [Google Scholar] [CrossRef]
- Park, J.; Kim, D.; Kim, H.; Lee, J.; Chung, W. Thermal radiative copper oxide layer for enhancing heat dissipation of metal surface. Nanomaterials 2021, 11, 2819. [Google Scholar] [CrossRef] [PubMed]
- Sellitto, P.; Salerno, G.; La Spina, A.; Caltabiano, T.; Scollo, S.; Boselli, A.; Leto, G.; Zanmar Sanchez, R.; Crumeyrolle, S.; Hanoune, B. Small-scale volcanic aerosols variability, processes and direct radiative impact at Mount Etna during the EPL-RADIO campaigns. Sci. Rep. 2020, 10, 15224. [Google Scholar] [CrossRef]
- Revercomb, H.E.; Buijs, H.; Howell, H.B.; LaPorte, D.D.; Smith, W.L.; Sromovsky, L.A. Radiometric calibration of IR Fourier transform spectrometers: Solution to a problem with the High-Resolution Interferometer Sounder. Appl. Opt. 1988, 27, 3210–3218. [Google Scholar] [CrossRef]
- Bianchini, G.; Palchetti, L. REFIR-PAD level 1 data analysis and performance characterization. Atmos. Chem. Phys. 2008, 8, 3817–3826. [Google Scholar] [CrossRef]
- Knuteson, R.O.; Revercomb, H.E.; Best, F.A.; Ciganovich, N.C.; Dedecker, R.G.; Dirkx, T.P.; Ellington, S.C.; Feltz, W.F.; Garcia, R.K.; Howell, H.B. Atmospheric emitted radiance interferometer. Part I: Instrument design. J. Atmos. Ocean. Technol. 2004, 21, 1763–1776. [Google Scholar] [CrossRef]
- Knuteson, R.O.; Revercomb, H.E.; Best, F.A.; Ciganovich, N.C.; Dedecker, R.G.; Dirkx, T.P.; Ellington, S.C.; Feltz, W.F.; Garcia, R.K.; Howell, H.B. Atmospheric emitted radiance interferometer. Part II: Instrument performance. J. Atmos. Ocean. Technol. 2004, 21, 1777–1789. [Google Scholar] [CrossRef]
- Mathew, G.; Nair, A.; Gundu Rao, T.K.; Pande, K. Laboratory technique for quantitative thermal emissivity measurements of geological samples. J. Earth Syst. Sci. 2009, 118, 391–404. [Google Scholar] [CrossRef]
- Clough, S.A.; Iacono, M.J.; Moncet, J. Line-by-line calculations of atmospheric fluxes and cooling rates: Application to water vapor. J. Geophys. Res. Atmos. 1992, 97, 15761–15785. [Google Scholar] [CrossRef]
- Clough, S.A.; Shephard, M.W.; Mlawer, E.J.; Delamere, J.S.; Iacono, M.J.; Cady-Pereira, K.; Boukabara, S.; Brown, P.D. Atmospheric radiative transfer modeling: A summary of the AER codes. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 233–244. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.; Istvan, L. DISORT, a general-purpose Fortran program for discrete-ordinate-method radiative transfer in scattering and emitting layered media: Documentation of methodology. In DISORT Report v1.1; Deptartment of Physics and Engineering Physics, Stevens Institute of Technology: Hoboken, NJ, USA, 2000. [Google Scholar]
- Stamnes, K.; Tsay, S.-C.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef]
- Rothman, L.S.; Gordon, I.E.; Babikov, Y.; Barbe, A.; Chris Benner, D.; Bernath, P.F.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.R.; et al. The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef]
- Lechevallier, L.; Vasilchenko, S.; Grilli, R.; Mondelain, D.; Romanini, D.; Campargue, A. The water vapour self-continuum absorption in the infrared atmospheric windows: New laser measurements near 3.3 and 2.0 µm. Atmos. Meas. Tech. 2018, 11, 2159–2171. [Google Scholar] [CrossRef]
- Wells, R.J. Rapid approximation to the Voigt/Faddeeva function and its derivatives. J. Quant. Spectrosc. Radiat. Transf. 1999, 62, 29–48. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000; Volume 2, ISBN 9814498688. [Google Scholar]
- Turner, D.D.; Löhnert, U. Information content and uncertainties in thermodynamic profiles and liquid cloud properties retrieved from the ground-based Atmospheric Emitted Radiance Interferometer (AERI). J. Appl. Meteorol. Climatol. 2014, 53, 752–771. [Google Scholar] [CrossRef]
- Marsh, D.; Mills, M.; Kinnison, D.E.; Lamarque, J.-F. Climate change from 1850 to 2005 simulated in CESM1 (WACCM). J. Clim. 2013, 26, 7372–7391. [Google Scholar] [CrossRef]
- Ben-David, A.; Ifarraguerri, A. Computation of a spectrum from a single-beam Fourier-transform infrared interferogram. Appl. Opt. 2002, 41, 1181–1189. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- National Centers for Environmental Prediction/National Weather Service/NOAA/U.S. Department of Commerce. 2015, Updated Daily. NCEP GDAS/FNL 0.25 Degree Global Tropospheric Analyses and Forecast Grids. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. Available online: https://rda.ucar.edu/datasets/ds083.3/ (accessed on 23 March 2024).







| Parameter | Values |
|---|---|
| FTIR Spectrometer | |
| Instrument | MIDAC M4400 |
| Type | Michelson interferometer |
| Mirrors | Gold coated, diamond tuned, permanently aligned |
| Beam Splitter | KBr |
| Detector | HgCdTe (MCT; Mercury–Cadmium–Telluride) w/Liquid N2 cooling |
| Metrology Laser | HeLe laser |
| Spectral Range | 500 to 4000 cm−1 |
| Spectral Resolution * | 1.0 cm−1 |
| Accuracy | >0.01 cm−1 |
| Size | 19″ × 11.5″ × 8″ (W × L × H) |
| Blackbody | |
| Instrument | MIKRON M340 |
| Temperature Range | −20 °C to 150 °C |
| Temperature Resolution | 0.1 °C |
| Operating Ambient Temperature | 5 °C to 40 °C |
| Temperature Sensor | Precision Platinum RTD |
| Stability | 0.1 °C per 8 h period |
| Emitter Diameter | 2.0″ |
| Emissivity | 0.9756 ± 0.0039 @ 8–15 μm 0.9713 ± 0.0049 @ 3–5 μm |
| Size | 11″ × 11″ × 6.5″ (W × L × H) |
| Temperature | Water Vapor Mixing Ratio |
|---|---|
| 612.0–618.0 cm−1 624.0–660.0 cm−1 674.0–713.0 cm−1 | 1250.0–1350.0 cm−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, H.; Seo, J. Measurement of Downwelling Radiance Using a Low-Cost Compact Fourier-Transform Infrared System for Monitoring Atmospheric Conditions. Remote Sens. 2024, 16, 1136. https://doi.org/10.3390/rs16071136
Choi H, Seo J. Measurement of Downwelling Radiance Using a Low-Cost Compact Fourier-Transform Infrared System for Monitoring Atmospheric Conditions. Remote Sensing. 2024; 16(7):1136. https://doi.org/10.3390/rs16071136
Chicago/Turabian StyleChoi, Haklim, and Jongjin Seo. 2024. "Measurement of Downwelling Radiance Using a Low-Cost Compact Fourier-Transform Infrared System for Monitoring Atmospheric Conditions" Remote Sensing 16, no. 7: 1136. https://doi.org/10.3390/rs16071136
APA StyleChoi, H., & Seo, J. (2024). Measurement of Downwelling Radiance Using a Low-Cost Compact Fourier-Transform Infrared System for Monitoring Atmospheric Conditions. Remote Sensing, 16(7), 1136. https://doi.org/10.3390/rs16071136








